NAM-NMM Temperature Downscaling Using Personal Weather Stations to Study Urban Heat Hazards
Abstract
:1. Introduction
1.1. Urban Temperature Increase Due to Climate Change
1.2. Temperature Downscaling in Urban Areas
2. Materials and Methods
2.1. Data Sources
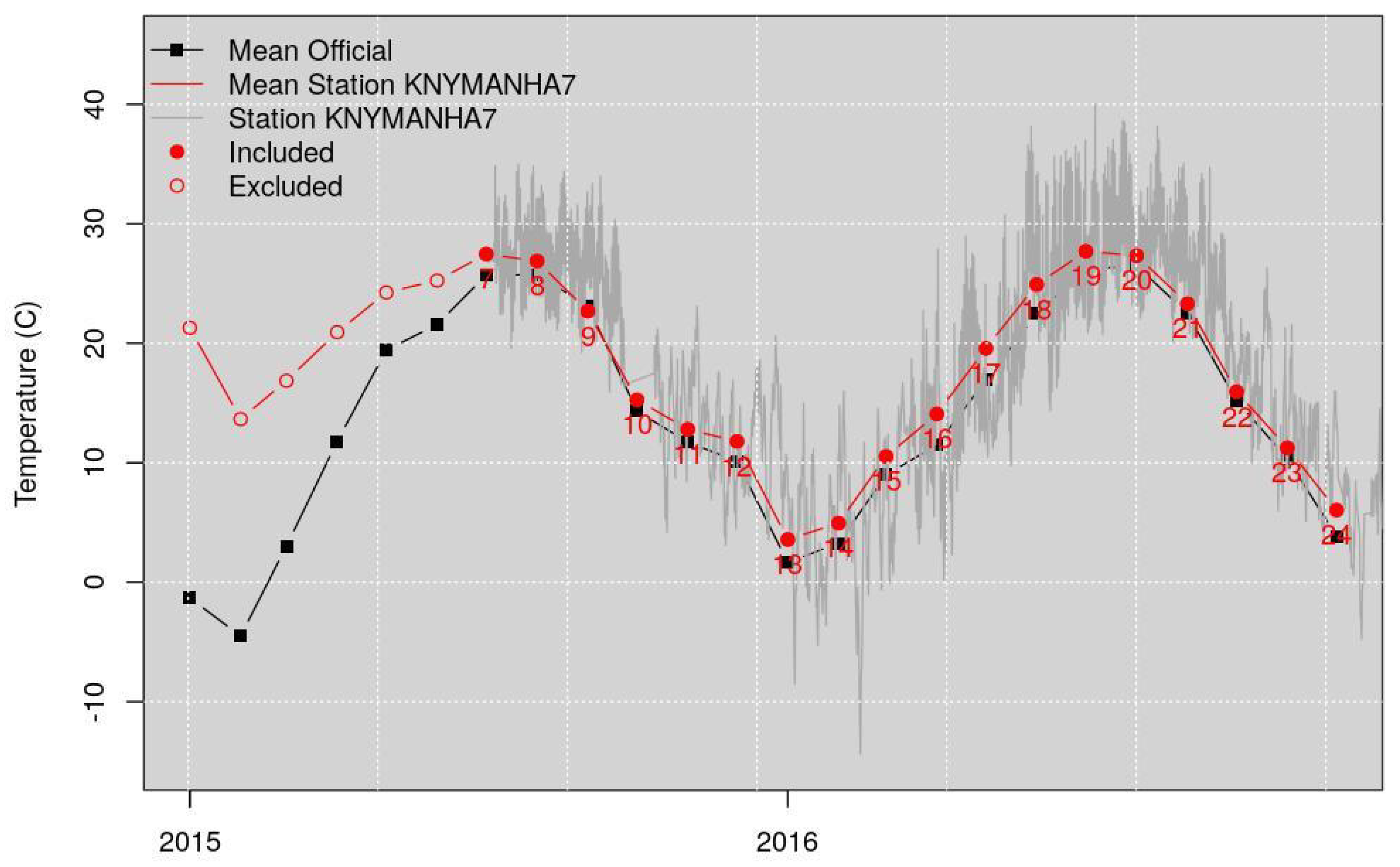
2.2. Weather Underground Data Quality Control
- All the stations with no data were excluded, reducing immediately the stations number to 105.
- Among the remaining stations, four are part of the METARs weather station network, namely: KLGA—LaGuardia Airport, KTEB—Teterboro Airport, KJRB: Wall Street station and KNYC—Central Park. Stations belonging to the METARs network have a more rigorous quality control, as they are officially operated by entities and not private citizens. This does not mean that do not include errors or noise, but rather that they can be assumed to be more reliable than regular PWSs. Because of this consideration, these four stations were used as reliable representatives for the area, and used to filter PWSs that drastically deviated from their measurements. Going forward, we assume to have 105 valid stations, four of them being the more reliable METARs stations, and 101 regular PWSs.
- A set of monthly statistics for all the 105 WU stations were calculated, including average, minimum, first quartile, median, third quartile, and maximum.
- Additionally, statistics were computed between the four METARs stations and all the 101 PWSs.
- a
- The monthly Root Mean Square Error (RMSE). This shows the monthly variation of each of the PWS with respect to METARs stations and shows bias that might change with values (e.g., inability to identify extreme values), season (for example installation problems related to shading). This method was not used to eliminate individual stations, but individual hourly observations that deviate from the general trend. This step is further explained later.
- b
- The yearly RMSE. This shows the yearly variation among all values, and is primarily an indication of very strong deviation from the METARs representative. Examples are stations that are installed indoors or close to exhaust vents, recording values that are not usable for the intended purposes of this article. This method was used to eliminate 17 stations from the analysis. This step is further explained later.
- Five more PWSs show drastically different values than the four METARs stations; however, they show very strong similarities among each other, creating a nice cluster. They were separated and further investigated and analyzed. Their anomaly distributions make them outliers stations compared to the distribution of the other PWSs; however, their similarities, which do not correspond to spatial proximity, make them an interesting case for future studies. However, they were excluded from the analysis in this work.
2.2.1. Filtering of Entire Stations Based on Yearly Statistics
2.2.2. Filtering of Entire Stations Based on Monthly Statistics
2.2.3. Filtering of Individual Hourly Values Based on Monthly Statistics
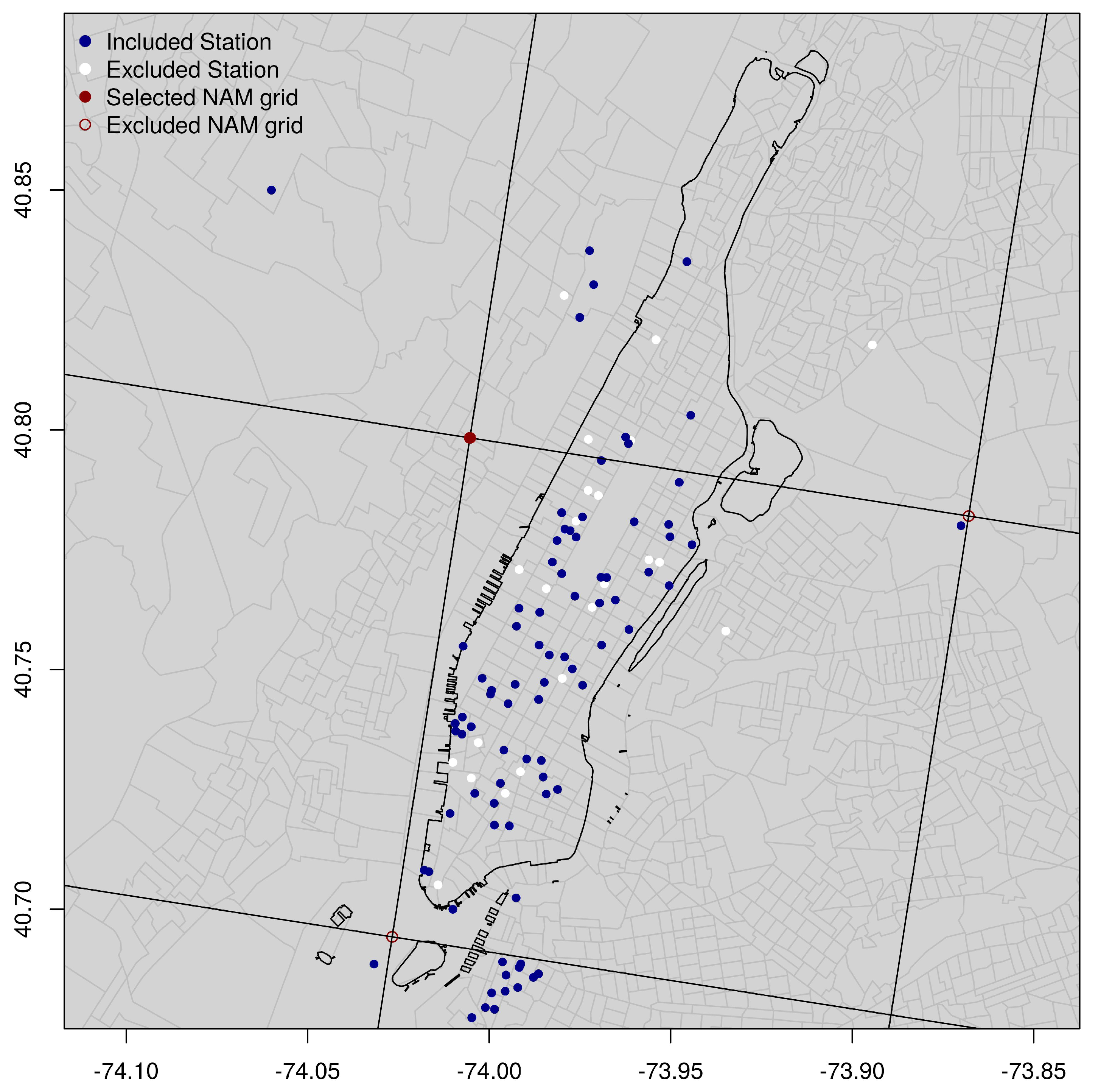
2.3. NAM-NMM Station Identification
2.4. Analog Ensemble
- The generation of an ensemble without the need for any perturbation strategy (e.g., of the initial conditions, physical parameterizations, models, etc.);
- The need in real time of only one deterministic prediction, which could result in significant real-time computational savings concerning traditional ensemble methods based on several model runs. Alternatively, if the same resources as the ones needed to generate a traditional ensemble are used, AnEn allows for the generation in real time of a higher fidelity prediction (with finer horizontal and vertical resolution);
- The prediction is based on past observed values, i.e., not on model estimates, which results in low-bias and well-calibrated forecasts;
- More accurate deterministic predictions of the deterministic system used to generate AnEn;
- Sharp and reliable probabilistic predictions.
- Starting from a current deterministic NWP forecast, the best matching historical forecasts (analogs) for the current prediction are chosen, at the same FLT (see Equation (2));
- For each FLT, the observations corresponding to the analog forecasts are retrieved from the historical data set;
- These observations form the analog ensemble future prediction at that location and FLT [20].
2.5. AnEn Generation
2.6. Spatial Downscaling
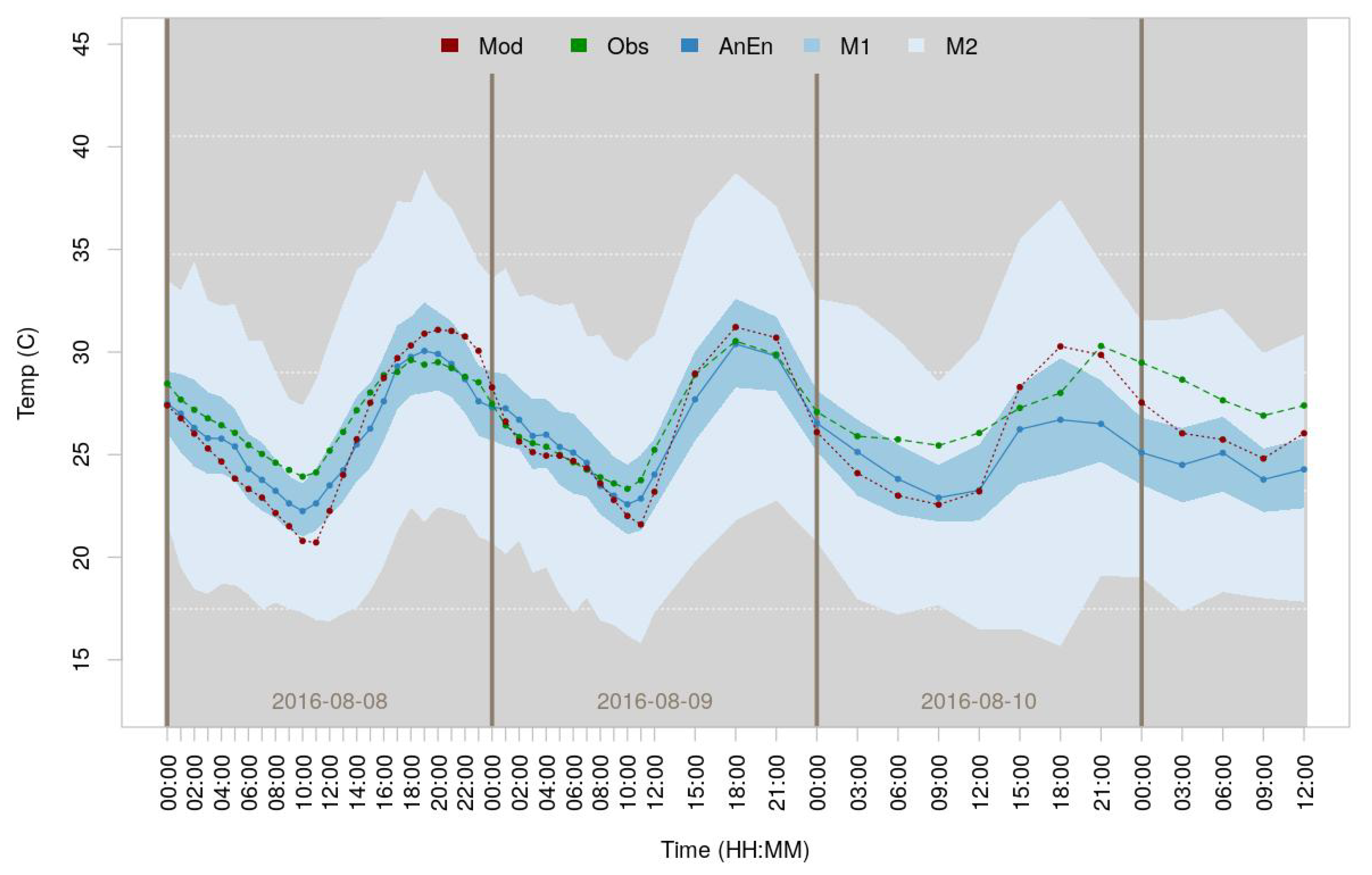
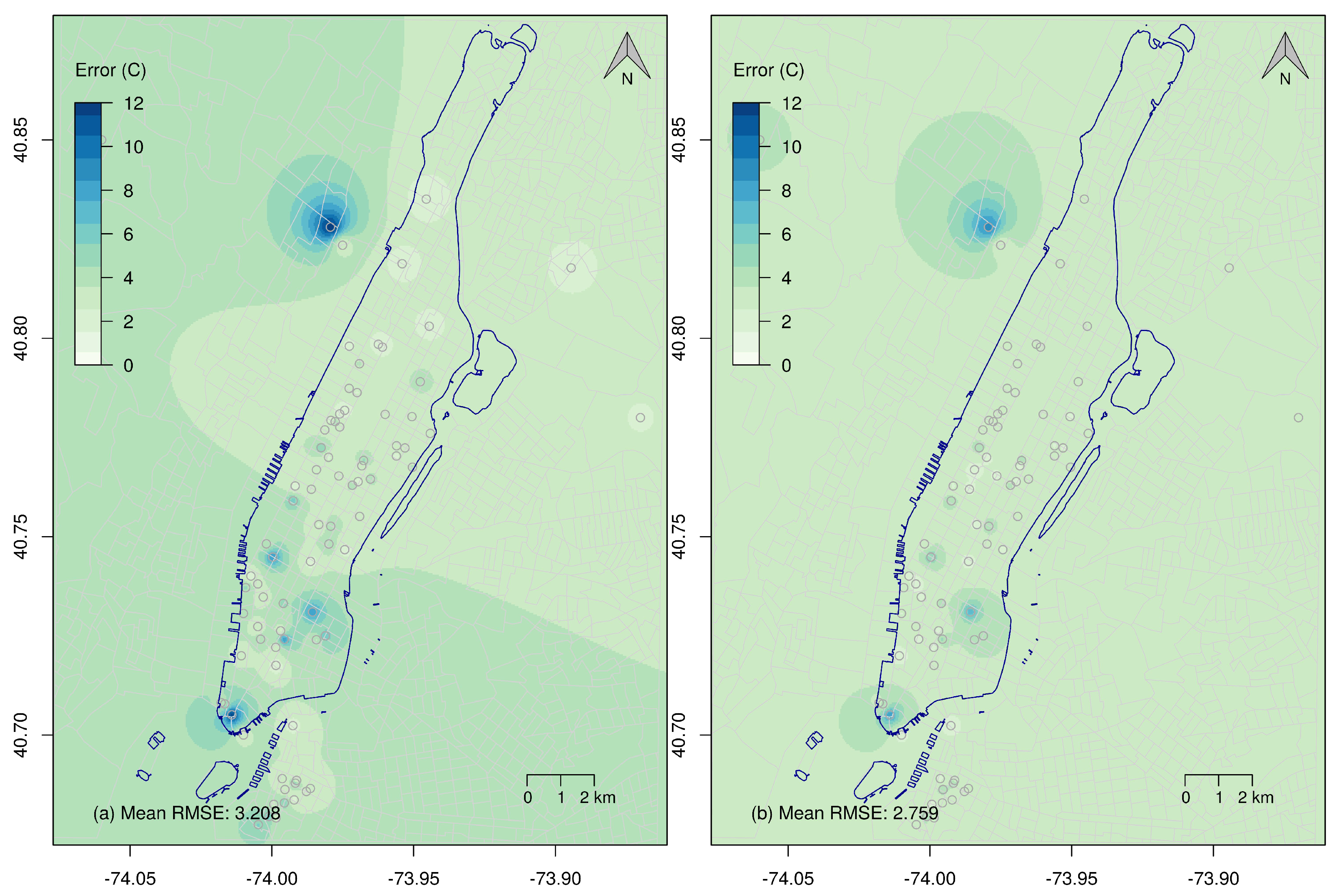
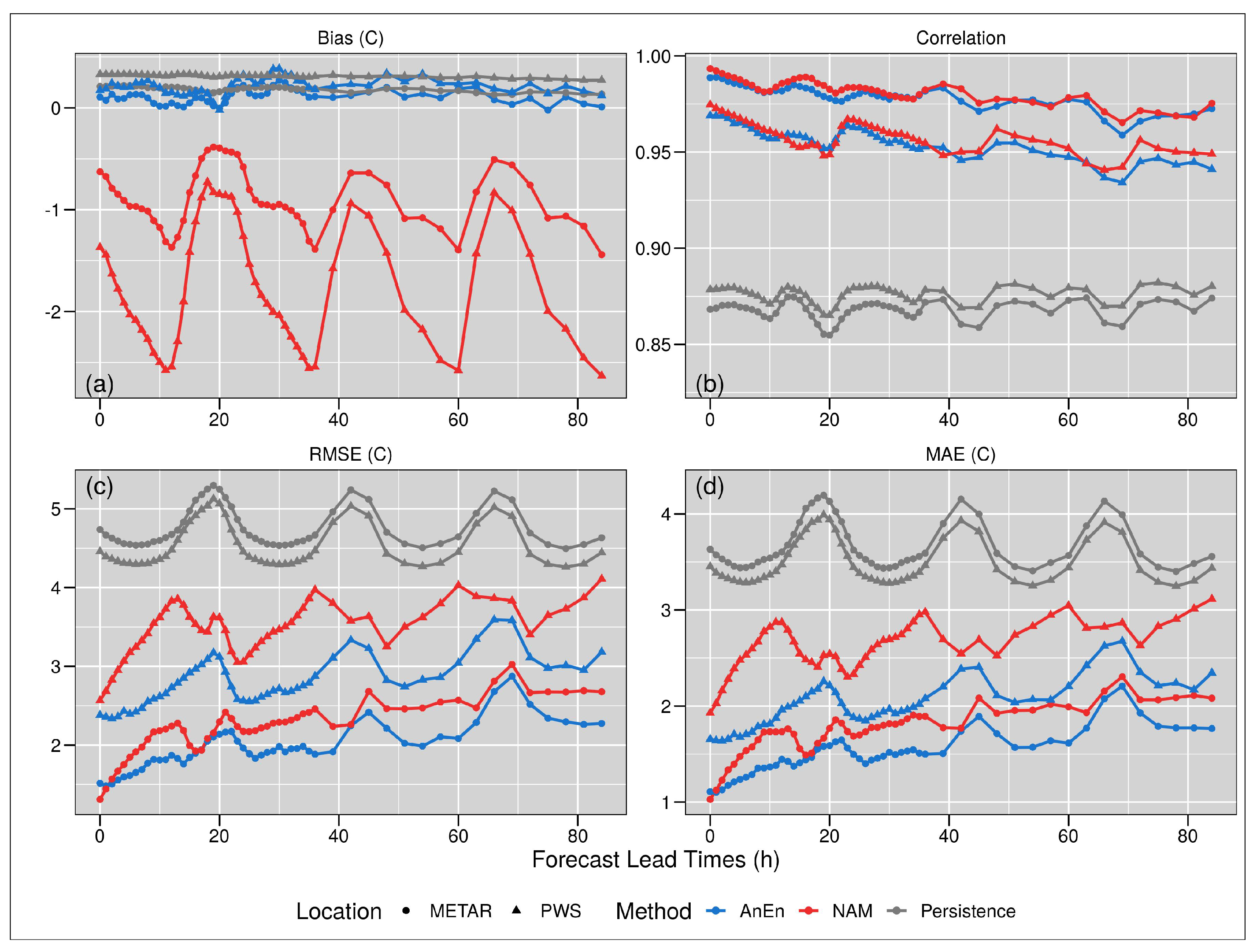
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Corburn, J. Cities, climate change and urban heat island mitigation: Localising global environmental science. Urban Stud. 2009, 46, 413–427. [Google Scholar] [CrossRef]
- Oppenheimer, M.; Campos, M.; Warren, R.; Birkmann, J.; Luber, G.; O’Neill, B.; Takahashi, K. Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Chapter Emergent Risks and Key Vulnerabilities; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Nazrul Islam, S.; Winkel, J. Climate Change and Social Inequality; DESA Working Paper No. 152; UN: New York, NY, USA, 2017. [Google Scholar]
- Redon, E.; Lemonsu, A.; Masson, V. An urban trees parameterization for modeling microclimatic variables and thermal comfort conditions at street level with the Town Energy Balance model (TEB-SURFEX v8.0). Geosci. Model Dev. 2020, 13, 385–399. [Google Scholar] [CrossRef] [Green Version]
- Susca, T.; Gaffin, S.; Dell’Osso, G. Positive effects of vegetation: Urban heat island and green roofs. Environ. Pollut. 2011, 159, 2119–2126. [Google Scholar] [CrossRef] [PubMed]
- Rizwan, A.M.; Dennis, L.Y.; Liu, C. A review on the generation, determination and mitigation of Urban Heat Island. J. Environ. Sci. 2008, 20, 120–128. [Google Scholar] [CrossRef]
- Canada Minister of Health. Adapting to Extreme Heat Events: Guidelines for Assessing Health Vulnerability; Publications Health Canada: Ottawa, ON, Canada, 2011; ISBN 978-1-100-18659-7.
- Li, H.; Meier, F.; Lee, X.; Chakraborty, T.; Liu, J.; Schaap, M.; Sodoudi, S. Interaction between urban heat island and urban pollution island during summer in Berlin. Sci. Total Environ. 2018, 636, 818–828. [Google Scholar] [CrossRef] [PubMed]
- Salvati, A.; Coch Roura, H.; Cecere, C. Assessing the urban heat island and its energy impact on residential buildings in Mediterranean climate: Barcelona case study. Energy Build. 2017, 146, 38–54. [Google Scholar] [CrossRef] [Green Version]
- Barsugli, J.J.; Guentchev, G.; Horton, R.M.; Wood, A.; Mearns, L.O.; Liang, X.Z.; Winkler, J.A.; Dixon, K.; Hayhoe, K.; Rood, R.B.; et al. The Practitioner’s Dilemma: How to Assess the Credibility of Downscaled Climate Projections. Eos Trans. Am. Geophys. Union 2013, 94, 424–425. [Google Scholar] [CrossRef] [Green Version]
- Trzaska, S.; Schnarr, E. A Review of Downscaling Methods for Climate Change Projections; United States Agency for International Development: Washington, DC, USA, 2014.
- Lanzante, J.R.; Dixon, K.W.; Nath, M.J.; Whitlock, C.E.; Adams-Smith, D. Some Pitfalls in Statistical Downscaling of Future Climate. Bull. Am. Meteorol. Soc. 2018, 99, 791–803. [Google Scholar] [CrossRef]
- Pinto, J.O.; Monaghan, A.J.; Delle Monache, L.; Vanvyve, E.; Rife, D.L. Regional Assessment of Sampling Techniques for More Efficient Dynamical Climate Downscaling. J. Clim. 2014, 27, 1524–1538. [Google Scholar] [CrossRef]
- Keller, J.D.; Delle Monache, L.; Alessandrini, S. Statistical Downscaling of a High-Resolution Precipitation Reanalysis Using the Analog Ensemble Method. J. Appl. Meteorol. Climatol. 2017, 56, 2081–2095. [Google Scholar] [CrossRef]
- Goodchild, M. Citizens as Sensors: The World of Volunteered Geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef] [Green Version]
- Schnebele, E.; Cervone, G.; Waters, N. Road assessment after flood events using non-authoritative data. Nat. Hazards Earth Syst. Sci. 2014, 14, 1007–1015. [Google Scholar] [CrossRef] [Green Version]
- Sui, D.; Goodchild, M. The convergence of GIS and social media: Challenges for GIScience. Int. J. Geogr. Inf. Sci. 2011, 25, 1737–1748. [Google Scholar] [CrossRef]
- Sui, D.; Elwood, S.; Goodchild, M. Crowdsourcing Geographic Knowledge: Volunteered Geographic Information (VGI) in Theory and Practice; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Oxendine, C.E.; Schnebele, E.; Cervone, G.; Waters, N. Fusing non-authoritative data to improve situational awareness in emergencies. In Proceedings of the ISCRAM 2014 Conference Proceedings—11th International Conference on Information Systems for Crisis Response and Management, University Park, PA, USA, 18–21 May 2014; pp. 762–766. [Google Scholar]
- Delle Monache, L.; Eckel, F.A.; Rife, D.L.; Nagarajan, B.; Searight, K. Probabilistic Weather Prediction with an Analog Ensemble. Mon. Weather Rev. 2013, 141, 3498–3516. [Google Scholar] [CrossRef] [Green Version]
- Alessandrini, S.; Davò, F.; Sperati, S.; Benini, M.; Delle Monache, L. Comparison of the economic impact of different wind power forecast systems for producers. Adv. Sci. Res. 2014, 11, 49–53. [Google Scholar] [CrossRef] [Green Version]
- National Centers for Environmental Prediction; National Weather Service; NOAA; U.S. Department of Commerce. NCEP North American Mesoscale (NAM) 12 km Analysis; University Corporation for Atmospheric Research: Boulder, CO, USA, 2015. [CrossRef]
- Junk, C.; Delle Monache, L.; Alessandrini, S.; Cervone, G.; von Bremen, L. Predictor-weighting strategies for probabilistic wind power forecasting with an analog ensemble. Meteorol. Z. 2015, 24, 361–379. [Google Scholar] [CrossRef]
- Hu, W.; Cervone, G.; Clemente-Harding, L.; Calovi, M. Parallel Analog Ensemble. Zenodo 2019. [Google Scholar] [CrossRef]
- Clemente-Harding, L.; Cervone, G.; Monache, L.D.; Alessandrini, S. Optimal Predictor Weighting with an Analog Ensemble. 2020; Unpublished. [Google Scholar]
- Cai, L.; Zhu, Y. The Challenges of Data Quality and Data Quality Assessment in the Big Data Era. Data Sci. J. 2015, 14, 2. [Google Scholar] [CrossRef]
- Herman, G.R.; Schumacher, R.S. Extreme Precipitation in Models: An Evaluation. Weather Forecast. 2016, 31, 1853–1879. [Google Scholar] [CrossRef]
- Coniglio, M.C.; Elmore, K.L.; Kain, J.S.; Weiss, S.J.; Xue, M.; Weisman, M.L. Evaluation of WRF Model Output for Severe Weather Forecasting from the 2008 NOAA Hazardous Weather Testbed Spring Experiment. Weather Forecast. 2010, 25, 408–427. [Google Scholar] [CrossRef]
- Delle Monache, L.; Nipen, T.; Liu, Y.; Roux, G.; Stull, R. Kalman Filter and Analog Schemes to Postprocess Numerical Weather Predictions. Mon. Weather Rev. 2011, 139, 3554–3570. [Google Scholar] [CrossRef] [Green Version]
- Alessandrini, S.; Delle Monache, L.; Sperati, S.; Cervone, G. An analog ensemble for short-term probabilistic solar power forecast. Appl. Energy 2015, 157, 95–110. [Google Scholar] [CrossRef] [Green Version]
- Alessandrini, S.; Monache, L.D.; Sperati, S.; Nissen, J. A novel application of an analog ensemble for short-term wind power forecasting. Renew. Energy 2015, 76, 768–781. [Google Scholar] [CrossRef]
- Zhang, J.; Draxl, C.; Hopson, T.; Monache, L.D.; Vanvyve, E.; Hodge, B.M. Comparison of numerical weather prediction based deterministic and probabilistic wind resource assessment methods. Appl. Energy 2015, 156, 528–541. [Google Scholar] [CrossRef] [Green Version]
- Davò, F.; Alessandrini, S.; Sperati, S.; Monache, L.D.; Airoldi, D.; Vespucci, M.T. Post-processing techniques and principal component analysis for regional wind power and solar irradiance forecasting. Sol. Energy 2016, 134, 327–338. [Google Scholar] [CrossRef] [Green Version]
- Vanvyve, E.; Delle Monache, L.; Monaghan, A.J.; Pinto, J.O. Wind resource estimates with an analog ensemble approach. Renew. Energy 2015, 74, 761–773. [Google Scholar] [CrossRef]
- Cervone, G.; Schnebele, E.; Waters, N.; Moccaldi, M.; Sicignano, R. Using Social Media and Satellite Data for Damage Assessment in Urban Areas During Emergencies. In Seeing Cities Through Big Data: Research, Methods and Applications in Urban Informatics; Springer International Publishing: Cham, Switzerland, 2017; pp. 443–457. [Google Scholar] [CrossRef]
- Djalalova, I.; Delle Monache, L.; Wilczak, J. PM 2.5 analog forecast and Kalman filter post-processing for the Community Multiscale Air Quality (CMAQ) model. Atmos. Environ. 2015, 108, 76–87. [Google Scholar] [CrossRef]
- Cervone, G.; Clemente-Harding, L.; Alessandrini, S.; Monache, L.D. Short-term photovoltaic power forecasting using Artificial Neural Networks and an Analog Ensemble. Renew. Energy 2017, 108, 274–286. [Google Scholar] [CrossRef] [Green Version]
- Hopson, T.M.; Webster, P.J. A 1–10-Day Ensemble Forecasting Scheme for the Major River Basins of Bangladesh: Forecasting Severe Floods of 2003–07. J. Hydrometeorol. 2010, 11, 618–641. [Google Scholar] [CrossRef]
- Eckel, F.A.; Delle Monache, L. A Hybrid NWP–Analog Ensemble. Mon. Weather Rev. 2016, 144, 897–911. [Google Scholar] [CrossRef]
- Delle Monache, L. Probabilistic Predictions and Downscaling with an Analog Ensemble for Weather, Renewable Energy, Air Quality, and Hurricane Intensity. In AGU Fall Meeting Abstracts; AGU: Washington, DC, USA, 2015; Volume 2015, p. A21E-0185. [Google Scholar]
- Delle Monache, L.; Shahriari, M.; Cervone, G. Using Analog Ensemble to generate spatially downscaled probabilistic wind power forecasts. In AGU Fall Meeting Abstracts; AGU: Washington, DC, USA, 2017; Volume 2017, p. GC24F-06. [Google Scholar]
- Klausner, Z.; Kaplan, H.; Fattal, E. The similar days method for predicting near surface wind vectors. Meteorol. Appl. 2009, 16, 569–579. [Google Scholar] [CrossRef]
- Giebel, G.; Brownsword, R.; Kariniotakis, G.; Denhard, M.; Draxl, C. The State-of-the-Art in Short-Term Prediction of Wind Power: A Literature Overview, 2nd ed.; ANEMOS.plus: Queens, NY, USA, 2011. [Google Scholar] [CrossRef]
- Alessandrini, S.; Sperati, S.; Delle Monache, L. Improving the Analog Ensemble Wind Speed Forecasts for Rare Events. Mon. Weather Rev. 2019, 147, 2677–2692. [Google Scholar] [CrossRef]
- NOAA. State of the Climate: Global Climate Report for Annual 2020; ANNO: Washington, DC, USA, 2021.
- Ji, F.; Wu, Z.; Huang, J.; Chassignet, E.P. Evolution of land surface air temperature trend. Nat. Clim. Chang. 2014, 4, 462–466. [Google Scholar] [CrossRef]
- Lanza, K.; Stone, B. Climate adaptation in cities: What trees are suitable for urban heat management? Landsc. Urban Plan. 2016, 153, 74–82. [Google Scholar] [CrossRef]
- Stone, B. The City and the Coming Climate: Climate Change and the Places We Live; Cambridge University Press: Cambridge, MA, USA, 2012. [Google Scholar]




| Parameter | Abbreviation | Vertical Level | Weight |
|---|---|---|---|
| wind speed | WSPD | 10 mASL | 0.1 |
| wind direction | WDIR | 10 mASL | 0.1 |
| Temperature | TMP | Surface | 0.4 |
| Relative humidity | RH | 10 mASL | 0.4 |
| Station Type | Metric | 95% CI | Lead Time (h) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | |||
| Official METARs stations | Bias | Lower | 0.023 | 0.05 | −0.048 | −0.043 | 0.123 | 0.167 | 0.016 | 0.012 | 0.086 |
| Upper | 0.186 | 0.224 | 0.142 | 0.173 | 0.324 | 0.374 | 0.207 | 0.234 | 0.315 | ||
| Correlation | Lower | 0.987 | 0.983 | 0.98 | 0.978 | 0.977 | 0.975 | 0.98 | 0.974 | 0.971 | |
| Upper | 0.99 | 0.986 | 0.983 | 0.983 | 0.981 | 0.98 | 0.983 | 0.979 | 0.976 | ||
| RMSE | Lower | 1.413 | 1.577 | 1.77 | 1.935 | 1.863 | 1.873 | 1.792 | 2.146 | 2.108 | |
| Upper | 1.598 | 1.722 | 1.953 | 2.151 | 2.052 | 2.071 | 1.959 | 2.338 | 2.311 | ||
| MAE | Lower | 1.052 | 1.205 | 1.379 | 1.482 | 1.43 | 1.452 | 1.434 | 1.672 | 1.641 | |
| Upper | 1.161 | 1.314 | 1.506 | 1.623 | 1.568 | 1.586 | 1.562 | 1.815 | 1.786 | ||
| PWS stations | Bias | Lower | 0.139 | 0.21 | 0.116 | 0.103 | 0.292 | 0.345 | 0.142 | 0.184 | 0.304 |
| Upper | 0.205 | 0.279 | 0.19 | 0.185 | 0.363 | 0.423 | 0.221 | 0.276 | 0.376 | ||
| Correlation | Lower | 0.968 | 0.962 | 0.957 | 0.952 | 0.962 | 0.953 | 0.951 | 0.944 | 0.953 | |
| Upper | 0.97 | 0.965 | 0.96 | 0.956 | 0.964 | 0.956 | 0.954 | 0.948 | 0.956 | ||
| RMSE | Lower | 2.334 | 2.374 | 2.683 | 3.02 | 2.524 | 2.668 | 2.822 | 3.272 | 2.782 | |
| Upper | 2.418 | 2.467 | 2.774 | 3.152 | 2.6 | 2.758 | 2.924 | 3.394 | 2.862 | ||
| MAE | Lower | 1.634 | 1.681 | 1.936 | 2.148 | 1.857 | 1.943 | 2.053 | 2.351 | 2.085 | |
| Upper | 1.68 | 1.729 | 1.99 | 2.208 | 1.906 | 1.992 | 2.106 | 2.419 | 2.135 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calovi, M.; Hu, W.; Cervone, G.; Delle Monache, L. NAM-NMM Temperature Downscaling Using Personal Weather Stations to Study Urban Heat Hazards. GeoHazards 2021, 2, 257-276. https://doi.org/10.3390/geohazards2030014
Calovi M, Hu W, Cervone G, Delle Monache L. NAM-NMM Temperature Downscaling Using Personal Weather Stations to Study Urban Heat Hazards. GeoHazards. 2021; 2(3):257-276. https://doi.org/10.3390/geohazards2030014
Chicago/Turabian StyleCalovi, Martina, Weiming Hu, Guido Cervone, and Luca Delle Monache. 2021. "NAM-NMM Temperature Downscaling Using Personal Weather Stations to Study Urban Heat Hazards" GeoHazards 2, no. 3: 257-276. https://doi.org/10.3390/geohazards2030014
APA StyleCalovi, M., Hu, W., Cervone, G., & Delle Monache, L. (2021). NAM-NMM Temperature Downscaling Using Personal Weather Stations to Study Urban Heat Hazards. GeoHazards, 2(3), 257-276. https://doi.org/10.3390/geohazards2030014







