Remote Prediction of Soybean Yield Using UAV-Based Hyperspectral Imaging and Machine Learning Models
Abstract
1. Introduction
2. Materials and Methods
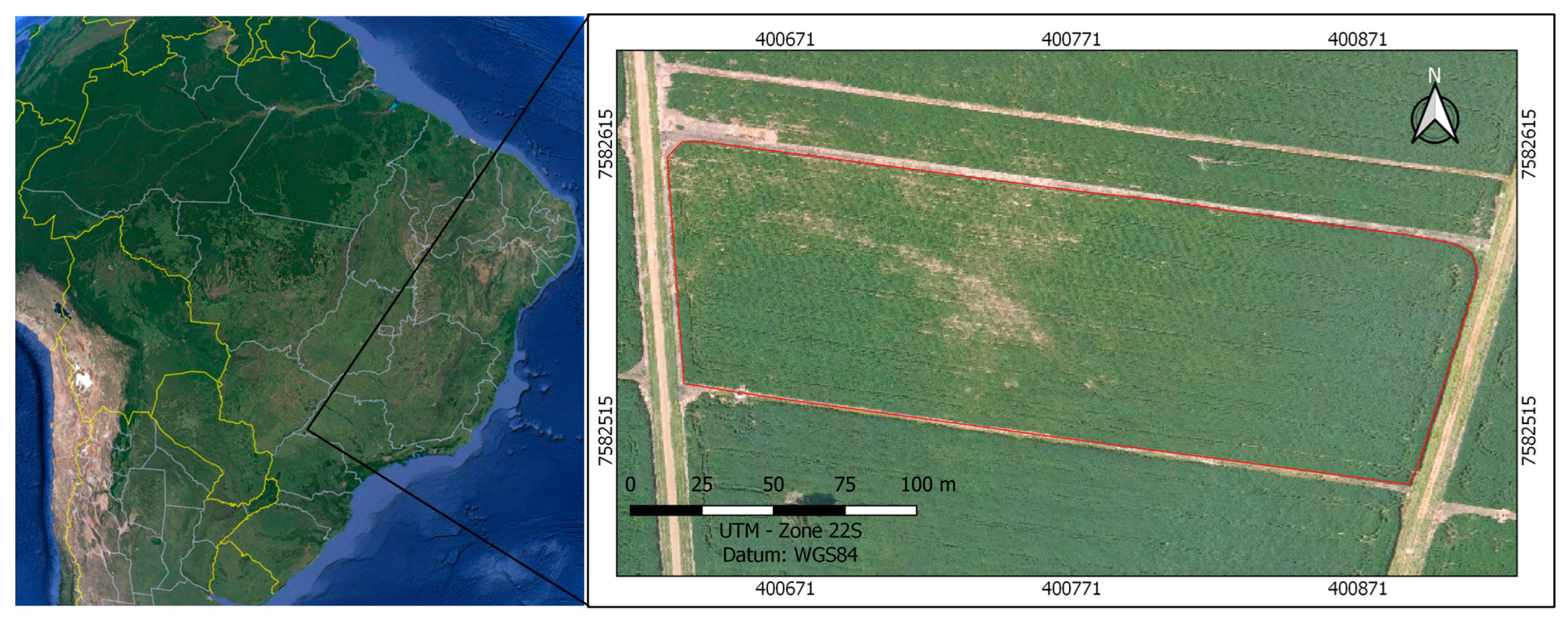
2.1. Study Area and Soybean Planting
2.2. Methodology
2.2.1. Image Acquisition with UAV Platform
2.2.2. Photogrammetric Processing for 3D Model Generation
2.2.3. Vegetation Indices Derived from the Hyperspectral Images
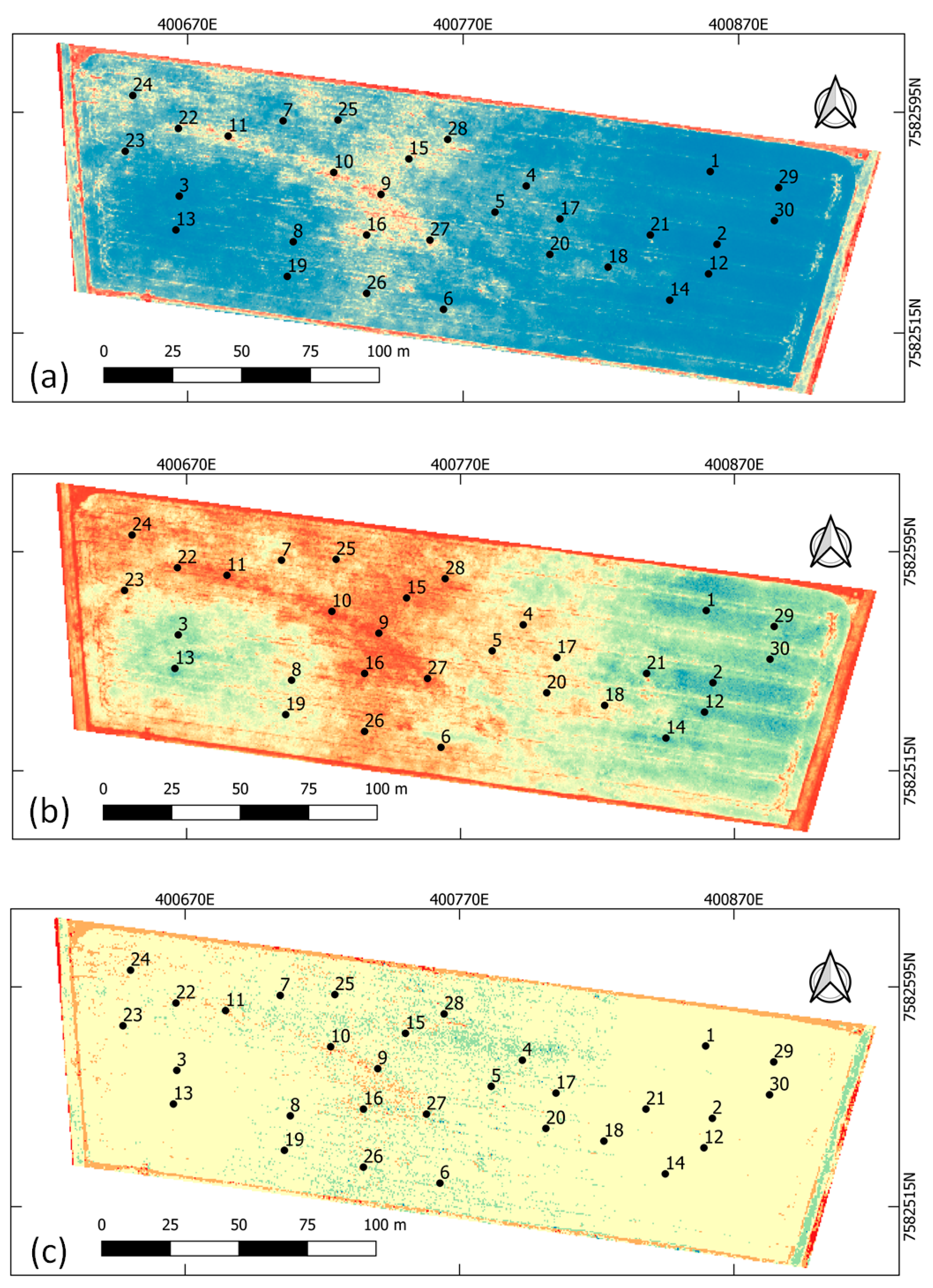
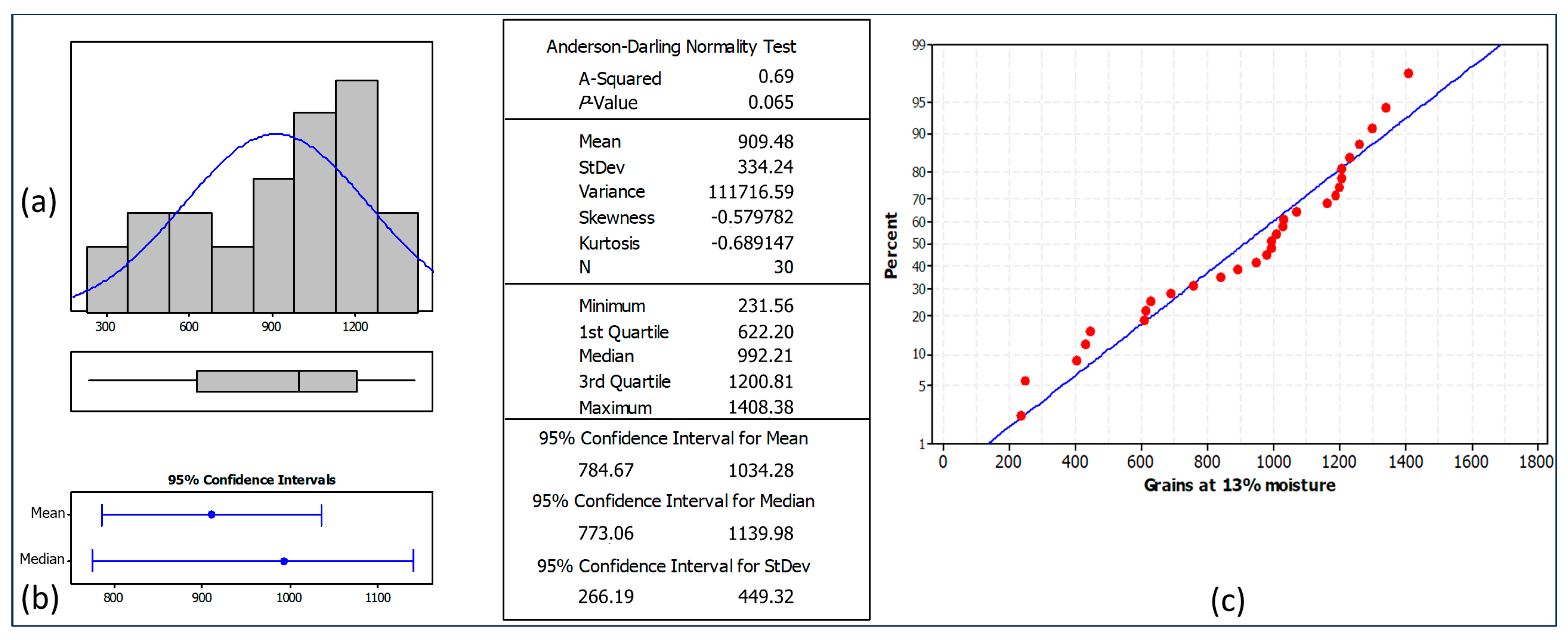
2.2.4. Crop Sample Collection
2.2.5. Prediction Models
2.3. Performance Assessment
3. Results
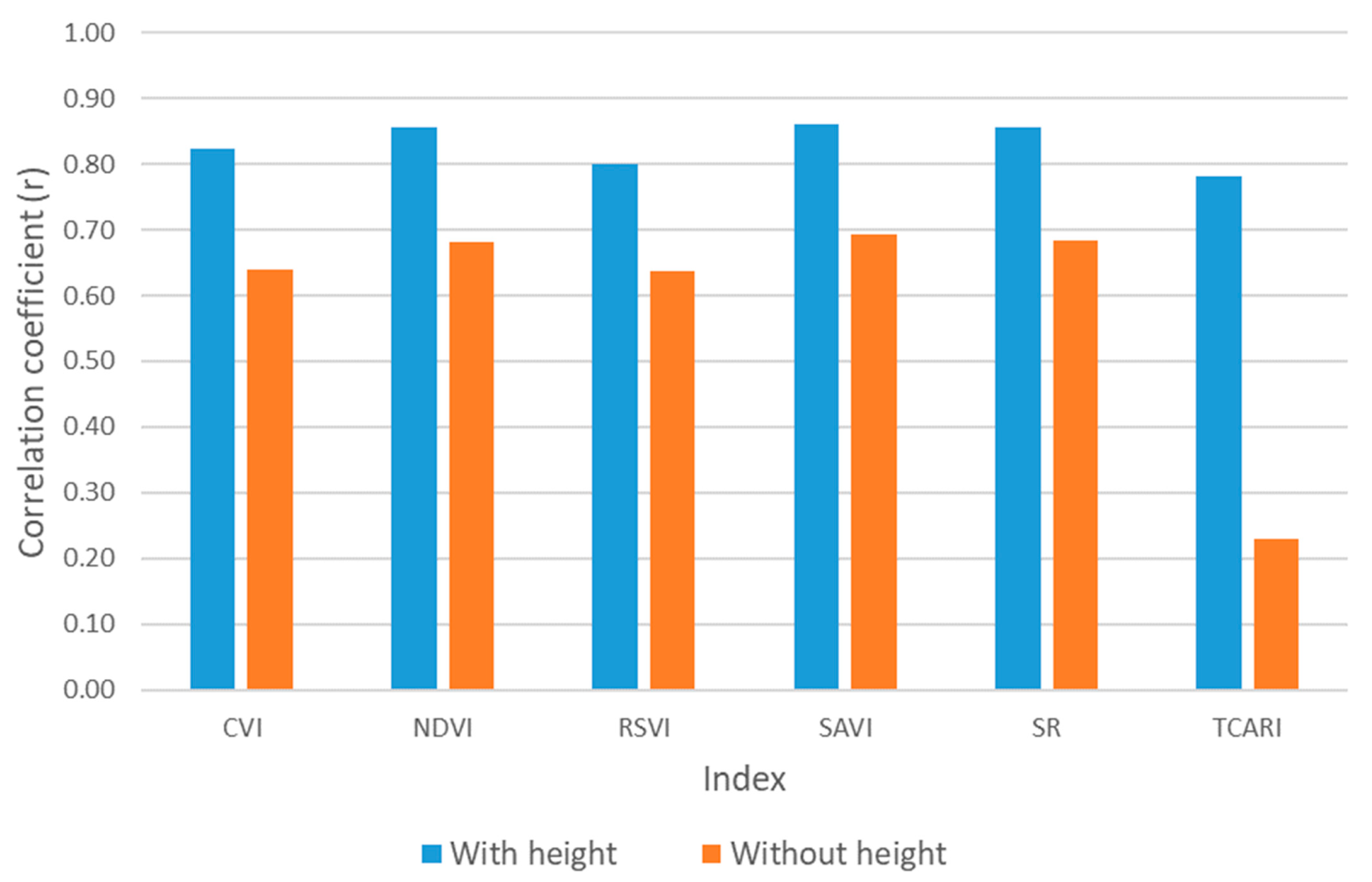
3.1. Machine Learning Estimators for Soybean Yield Productivity
3.2. Soybean Productivity Map and Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- USDA (United States Department of Agriculture) World Agricultural Production; Foreign Agricultural Service. Circular Series WAP 2-20: USA. 2020. Available online: https://apps.fas.usda.gov/PSDOnline/Circulars/2020/02/production.pdf (accessed on 2 September 2024).
- da Silva, E.E.; Baio, F.H.R.; Teodoro, L.P.R.; da Silva, C.A., Jr.; Borges, R.S.; Teodoro, P.E. UAV-Multispectral and Vegetation Indices in Soybean Grain Yield Prediction Based on in Situ Observation. Remote Sens. Appl. Soc. Environ. 2020, 18, 100318. [Google Scholar] [CrossRef]
- Wei, M.C.F.; Molin, J.P. Soybean Yield Estimation and Its Components: A Linear Regression Approach. Agriculture 2020, 10, 348. [Google Scholar] [CrossRef]
- Banerjee, B.P.; Spangenberg, G.; Kant, S. Fusion of Spectral and Structural Information from Aerial Images for Improved Biomass Estimation. Remote Sens. 2020, 12, 3164. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Hartling, S.; Esposito, F.; Fritschi, F.B. Soybean Yield Prediction from UAV Using Multimodal Data Fusion and Deep Learning. Remote Sens. Environ. 2020, 237, 111599. [Google Scholar] [CrossRef]
- Parmley, K.A.; Higgins, R.H.; Ganapathysubramanian, B.; Sarkar, S.; Singh, A.K. Machine Learning Approach for Prescriptive Plant Breeding. Sci. Rep. 2019, 9, 17132. [Google Scholar] [CrossRef]
- de Siqueira, D.A.B.; Vaz, C.M.P.; da Silva, F.S.; Ferreira, E.J.; Speranza, E.A.; Franchini, J.C.; Galbieri, R.; Belot, J.L.; de Souza, M.; Perina, F.J.; et al. Estimating Cotton Yield in the Brazilian Cerrado Using Linear Regression Models from MODIS Vegetation Index Time Series. AgriEngineering 2024, 6, 947–961. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Feng, L.; Du, Q.; Runge, T. Combining Multi-Source Data and Machine Learning Approaches to Predict Winter Wheat Yield in the Conterminous United States. Remote Sens. 2020, 12, 1232. [Google Scholar] [CrossRef]
- Zhao, Y.; Potgieter, A.B.; Zhang, M.; Wu, B.; Hammer, G.L. Predicting Wheat Yield at the Field Scale by Combining High-Resolution Sentinel-2 Satellite Imagery and Crop Modelling. Remote Sens. 2020, 12, 1024. [Google Scholar] [CrossRef]
- Gumma, M.K.; Nukala, R.M.; Panjala, P.; Bellam, P.K.; Gajjala, S.; Dubey, S.K.; Sehgal, V.K.; Mohammed, I.; Deevi, K.C. Optimizing Crop Yield Estimation through Geospatial Technology: A Comparative Analysis of a Semi-Physical Model, Crop Simulation, and Machine Learning Algorithms. AgriEngineering 2024, 6, 786–802. [Google Scholar] [CrossRef]
- Gao, F.; Anderson, M.; Daughtry, C.; Karnieli, A.; Hively, D.; Kustas, W. A Within-Season Approach for Detecting Early Growth Stages in Corn and Soybean Using High Temporal and Spatial Resolution Imagery. Remote Sens. Environ. 2020, 242, 111752. [Google Scholar] [CrossRef]
- Ramos, A.P.M.; Osco, L.P.; Furuya, D.E.G.; Gonçalves, W.N.; Santana, D.C.; Teodoro, L.P.R.; da Silva, C.A., Jr.; Capristo-Silva, G.F.; Li, J.; Baio, F.H.R.; et al. A Random Forest Ranking Approach to Predict Yield in Maize with Uav-Based Vegetation Spectral Indices. Comput. Electron. Agric. 2020, 178, 105791. [Google Scholar] [CrossRef]
- dos Silva, F.D.S.; Peixoto, I.C.; Costa, R.L.; Gomes, H.B.; Gomes, H.B.; Cabral Júnior, J.B.; de Araújo, R.M.; Herdies, D.L. Predictive Potential of Maize Yield in the Mesoregions of Northeast Brazil. AgriEngineering 2024, 6, 881–907. [Google Scholar] [CrossRef]
- Eugenio, F.C.; Grohs, M.; Venancio, L.P.; Schuh, M.; Bottega, E.L.; Ruoso, R.; Schons, C.; Mallmann, C.L.; Badin, T.L.; Fernandes, P. Estimation of Soybean Yield from Machine Learning Techniques and Multispectral RPAS Imagery. Remote Sens. Appl. Soc. Environ. 2020, 20, 100397. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, J.; Yang, G.; Liu, J.; Cao, J.; Li, C.; Zhao, X.; Gai, J. Establishment of Plot-Yield Prediction Models in Soy-bean Breeding Programs Using UAV-Based Hyperspectral Remote Sensing. Remote Sens. 2019, 11, 2752. [Google Scholar] [CrossRef]
- de Queiroz Otone, J.D.; de Theodoro, G.F.; Santana, D.C.; Teodoro, L.P.R.; de Oliveira, J.T.; de Oliveira, I.C.; da Silva Junior, C.A.; Teodoro, P.E.; Baio, F.H.R. Hyperspectral Response of the Soybean Crop as a Function of Target Spot (Corynespora Cassi-icola) Using Machine Learning to Classify Severity Levels. AgriEngineering 2024, 6, 330–343. [Google Scholar] [CrossRef]
- Fehr, W.R.; Caviness, C.E. Stages of Soybean Development; Iowa State University of Science and Technology: Ames, IA, USA, 1977; Volume 87. [Google Scholar]
- Ma, B.L.; Dwyer, L.M.; Costa, C.; Cober, E.R.; Morrison, M.J. Early Prediction of Soybean Yield from Canopy Reflectance Measurements. Agron. J. 2001, 93, 1227–1234. [Google Scholar] [CrossRef]
- Luo, S.; Liu, W.; Zhang, Y.; Wang, C.; Xi, X.; Nie, S.; Ma, D.; Lin, Y.; Zhou, G. Maize and Soybean Heights Estimation from Unmanned Aerial Vehicle (UAV) LiDAR Data. Comput. Electron. Agric. 2021, 182, 106005. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-Based Plant Height from Crop Surface Models, Visible, and near Infrared Vegetation Indices for Biomass Monitoring in Barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Geipel, J.; Link, J.; Claupein, W. Combined Spectral and Spatial Modeling of Corn Yield Based on Aerial Images and Crop Surface Models Acquired with an Unmanned Aircraft System. Remote Sens. 2014, 6, 10335–10355. [Google Scholar] [CrossRef]
- Yin, X.; McClure, M.A.; Jaja, N.; Tyler, D.D.; Hayes, R.M. In-Season Prediction of Corn Yield Using Plant Height under Major Production Systems. Agron. J. 2011, 103, 923–929. [Google Scholar] [CrossRef]
- Yu, N.; Li, L.; Schmitz, N.; Tian, L.F.; Greenberg, J.A.; Diers, B.W. Development of Methods to Improve Soybean Yield Estimation and Predict Plant Maturity with an Unmanned Aerial Vehicle Based Platform. Remote Sens. Environ. 2016, 187, 91–101. [Google Scholar] [CrossRef]
- Senop Ltd. Available online: http://senop.fi/en/optronics-hyperspectral (accessed on 20 October 2018).
- Oliveira, R.A.; Tommaselli, A.M.G.; Honkavaara, E. Geometric Calibration of a Hyperspectral Frame Camera. Photogramm. Rec. 2016, 31, 325–347. [Google Scholar] [CrossRef]
- Tommaselli, A.M.G.; Santos, L.D.; Oliveira, R.A.; Berveglieri, A.; Imai, N.N.; Honkavaara, E. Refining the Interior Orienta-tion of a Hyperspectral Frame Camera with Preliminary Bands Co-Registration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2097–2106. [Google Scholar] [CrossRef]
- Berveglieri, A.; Tommaselli, A.M.G.; Santos, L.D.; Honkavaara, E. Bundle Adjustment of a Time-Sequential Spectral Cam-era Using Polynomial Models. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9252–9263. [Google Scholar] [CrossRef]
- Rapidlasso GmbH. LAStools—Fast Tools to Catch Reality. Available online: http://rapidlasso.com/LAStools (accessed on 4 March 2020).
- Patrício, D.I.; Rieder, R. Computer Vision and Artificial Intelligence in Precision Agriculture for Grain Crops: A Systematic Review. Comput. Electron. Agric. 2018, 153, 69–81. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with Erts; NASA Special Publication: Washington, DC, USA, 1974; Volume 351, p. 309.
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated Narrow-Band Vegetation Indices for Prediction of Crop Chlorophyll Content for Application to Precision Agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Merton, R. Monitoring Community Hysteresis Using Spectral Shift Analysis and the Red-Edge Vegetation Stress Index. In Proceedings of the Seventh Annual JPL Airborne Earth Science Workshop, Pasadena, CA, USA, 12–16 January 1998; JPL: Pasadena, CA, USA, 1998; pp. 12–16. [Google Scholar]
- Vincini, M.; Frazzi, E.; D’Alessio, P. A Broad-Band Leaf Chlorophyll Vegetation Index at the Canopy Scale. Precis. Agricult. 2008, 9, 303–319. [Google Scholar] [CrossRef]
- Larson, R.; Farber, B. Elementary Statistics: Picturing the World, 6th ed.; Pearson Education, Inc.: Boston, MA, USA, 2015. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Heung, B.; Bulmer, C.E.; Schmidt, M.G. Predictive Soil Parent Material Mapping at a Regional-Scale: A Random Forest Approach. Geoderma 2014, 214–215, 141–154. [Google Scholar] [CrossRef]
- Li, Z.; Xin, X.; Tang, H.; Yang, F.; Chen, B.; Zhang, B. Estimating Grassland LAI Using the Random Forests Approach and Landsat Imagery in the Meadow Steppe of Hulunber, China. J. Integr. Agric. 2017, 16, 286–297. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Drummond, S.T.; Sudduth, K.A.; Joshi, A.; Birrell, S.J.; Kitchen, N.R. Statistical and Neural Methods for Site–Specific Yield Prediction. Trans. ASAE 2003, 46, 5. [Google Scholar] [CrossRef]
- Lee, H.; Wang, J.; Leblon, B. Using Linear Regression, Random Forests, and Support Vector Machine with Unmanned Aeri-al Vehicle Multispectral Images to Predict Canopy Nitrogen Weight in Corn. Remote Sens. 2020, 12, 2071. [Google Scholar] [CrossRef]






| Description | Specification |
|---|---|
| Camera model | Rikola FPI2015 |
| Nominal focal length | 9 mm |
| Pixel size | 5.5 μm |
| Image size | 1017 × 648 pixels |
| Sensors | 2 CMOS |
| Spectral range | 500–900 nm (spectral step 1 nm) |
| Spectral resolution | 10 nm—FWHM (full width at half maximum) |
| Weight | <700 g |
| 1st Sensor | 2nd Sensor | ||
|---|---|---|---|
| Band Position | λ (nm) | Band Position | λ (nm) |
| 1 | 509.35 | 11 | 654.21 |
| 2 | 522.47 | 12 | 663.02 |
| 3 | 538.12 | 13 | 672.61 |
| 4 | 552.91 | 14 | 684.10 |
| 5 | 566.29 | 15 | 691.90 |
| 6 | 581.33 | 16 | 701.27 |
| 7 | 591.90 | 17 | 712.06 |
| 8 | 606.36 | 18 | 723.16 |
| 9 | 620.22 | 19 | 731.22 |
| 10 | 633.41 | 20 | 741.37 |
| 21 | 751.06 | ||
| 22 | 771.87 | ||
| 23 | 790.30 | ||
| 24 | 810.46 | ||
| 25 | 829.39 | ||
| Parameter | FPI Camera |
|---|---|
| Flying height | 160 m |
| Forward and side overlap | 80% and 60% |
| Number of flying strips | 2 |
| Flying speed | 4 m/s |
| Integration time | 5 ms |
| Vegetation Index | Full Form | Formulation with the Adopted Bands | Reference |
|---|---|---|---|
| NDVI | Normalised difference vegetation index | (NIR810 − R672)/(NIR810 + R672) | [30] |
| SR | Simple ratio index | NIR810/R672 | [31] |
| TCARI | Transformed chlorophyll absorption in the reflectance index | 3 × [(RE701−R672) − 0.2(RE701−G552) × (RE701/R672)] | [32] |
| SAVI | Soil-adjusted vegetation index | (NIR810 − R672)/(NIR810 + R672 + 0.5) × (1 + 0.5) | [33] |
| RSVI | Red-edge stress vegetation index | [(RE723 + RE751)/2] − RE731 | [34] |
| CVI | Chlorophyll vegetation index | NIR829 × [R663/(G566)2] | [35] |
| Predictor Variables | Most Significant Attributes (in Descending Order) * | r | MAE | RMSE | RAE (%) | RRSE (%) |
|---|---|---|---|---|---|---|
| 25 bands | 25 22 23 17 15 14 12 11 9 8 7 5 4 | 0.77 | 0.01 | 0.01 | 57.56 | 63.57 |
| 25 bands + height | 25 22 23 17 15 14 12 11 9 8 7 5 4 | 0.77 | 0.01 | 0.01 | 56.07 | 60.89 |
| 6 indices | SAVI RSVI CVI TCARI SR | 0.79 | 0.01 | 0.01 | 57.56 | 63.57 |
| 6 indices + height | SAVI RSVI CVI TCARI SR | 0.79 | 0.01 | 0.01 | 56.07 | 60.89 |
| 25 bands + 6 indices | 25 24 22 23 21 20 16 15 14 10 9 8 5 4 3 1 SAVI TCARI SR NDVI | 0.79 | 0.01 | 0.01 | 55.65 | 62.14 |
| 25 bands + 6 indices + height | 25 24 22 23 21 20 16 15 14 10 9 8 5 4 3 1 SAVI TCARI SR NDVI | 0.79 | 0.01 | 0.01 | 55.65 | 62.14 |
| Predictor Variables | r | MAE | RMSE | RAE (%) | RRSE (%) |
|---|---|---|---|---|---|
| 25 bands | 0.83 | 0.01 | 0.01 | 48.89 | 56.27 |
| 25 bands + height | 0.89 | 0.01 | 0.01 | 40.11 | 45.73 |
| 6 indices | 0.81 | 0.01 | 0.01 | 52.87 | 59.30 |
| 6 indices + height | 0.88 | 0.01 | 0.01 | 42.44 | 47.60 |
| 25 bands + 6 indices | 0.84 | 0.01 | 0.01 | 47.41 | 54.93 |
| 25 bands + 6 indices + height | 0.88 | 0.01 | 0.01 | 40.95 | 46.74 |
| Predictor Variables | r | MAE | RMSE | RAE (%) | RRSE (%) |
|---|---|---|---|---|---|
| 4 bands | 0.84 | 0.01 | 0.01 | 47.36 | 53.91 |
| 4 bands + NDVI + SR | 0.83 | 0.01 | 0.01 | 47.90 | 55.27 |
| 4 bands + height | 0.91 | 0.01 | 0.01 | 35.13 | 40.96 |
| 4 bands + SR + height | 0.90 | 0.01 | 0.01 | 37.11 | 42.99 |
| 4 bands + NDVI + height | 0.91 | 0.01 | 0.01 | 36.32 | 41.83 |
| 4 bands + SR + NDVI + height | 0.90 | 0.01 | 0.01 | 37.67 | 43.54 |
| Prediction Technique | Net Weight (kg) in the Total Area | Productivity (kg/ha) | Difference (kg) [Estimated − Collected] |
|---|---|---|---|
| Grains harvested and weighted (reference) | 4982 | 2085 | – |
| Sample mean | 4830 | 2021 | −152 (3.1%) |
| MLR model | 4847 | 2027 | −135 (2.8%) |
| RF model | 5058 | 2116 | 76 (1.5%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berveglieri, A.; Imai, N.N.; Watanabe, F.S.Y.; Tommaselli, A.M.G.; Ederli, G.M.P.; de Araújo, F.F.; Lupatini, G.C.; Honkavaara, E. Remote Prediction of Soybean Yield Using UAV-Based Hyperspectral Imaging and Machine Learning Models. AgriEngineering 2024, 6, 3242-3260. https://doi.org/10.3390/agriengineering6030185
Berveglieri A, Imai NN, Watanabe FSY, Tommaselli AMG, Ederli GMP, de Araújo FF, Lupatini GC, Honkavaara E. Remote Prediction of Soybean Yield Using UAV-Based Hyperspectral Imaging and Machine Learning Models. AgriEngineering. 2024; 6(3):3242-3260. https://doi.org/10.3390/agriengineering6030185
Chicago/Turabian StyleBerveglieri, Adilson, Nilton Nobuhiro Imai, Fernanda Sayuri Yoshino Watanabe, Antonio Maria Garcia Tommaselli, Glória Maria Padovani Ederli, Fábio Fernandes de Araújo, Gelci Carlos Lupatini, and Eija Honkavaara. 2024. "Remote Prediction of Soybean Yield Using UAV-Based Hyperspectral Imaging and Machine Learning Models" AgriEngineering 6, no. 3: 3242-3260. https://doi.org/10.3390/agriengineering6030185
APA StyleBerveglieri, A., Imai, N. N., Watanabe, F. S. Y., Tommaselli, A. M. G., Ederli, G. M. P., de Araújo, F. F., Lupatini, G. C., & Honkavaara, E. (2024). Remote Prediction of Soybean Yield Using UAV-Based Hyperspectral Imaging and Machine Learning Models. AgriEngineering, 6(3), 3242-3260. https://doi.org/10.3390/agriengineering6030185







