Spatial-Temporal Dynamics of Water Resources in Seasonally Dry Tropical Forest: Causes and Vegetation Response
Abstract
1. Introduction
2. Materials and Methods
2.1. Characterization of the Study Area
2.2. Sampling and Data Collection
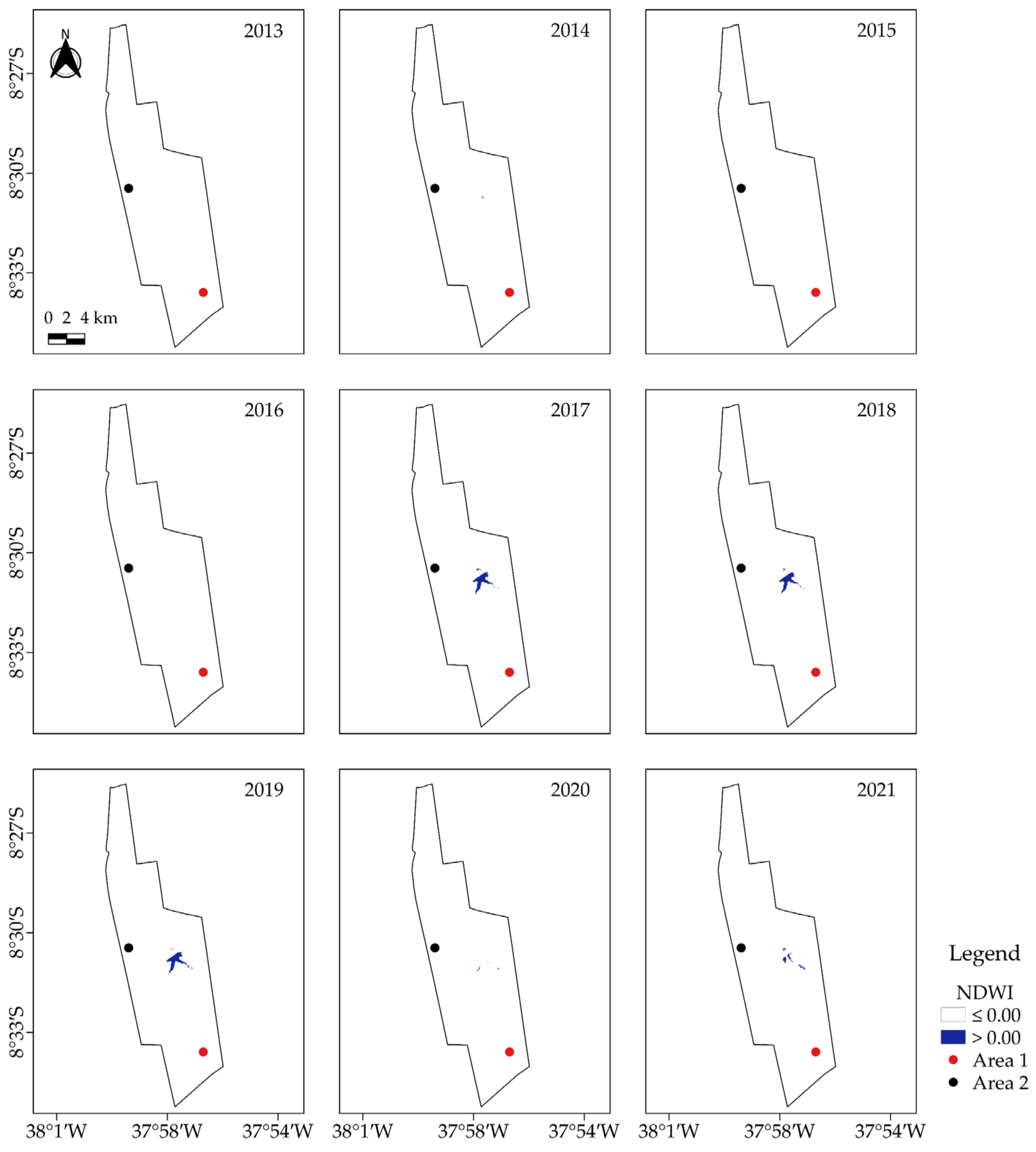
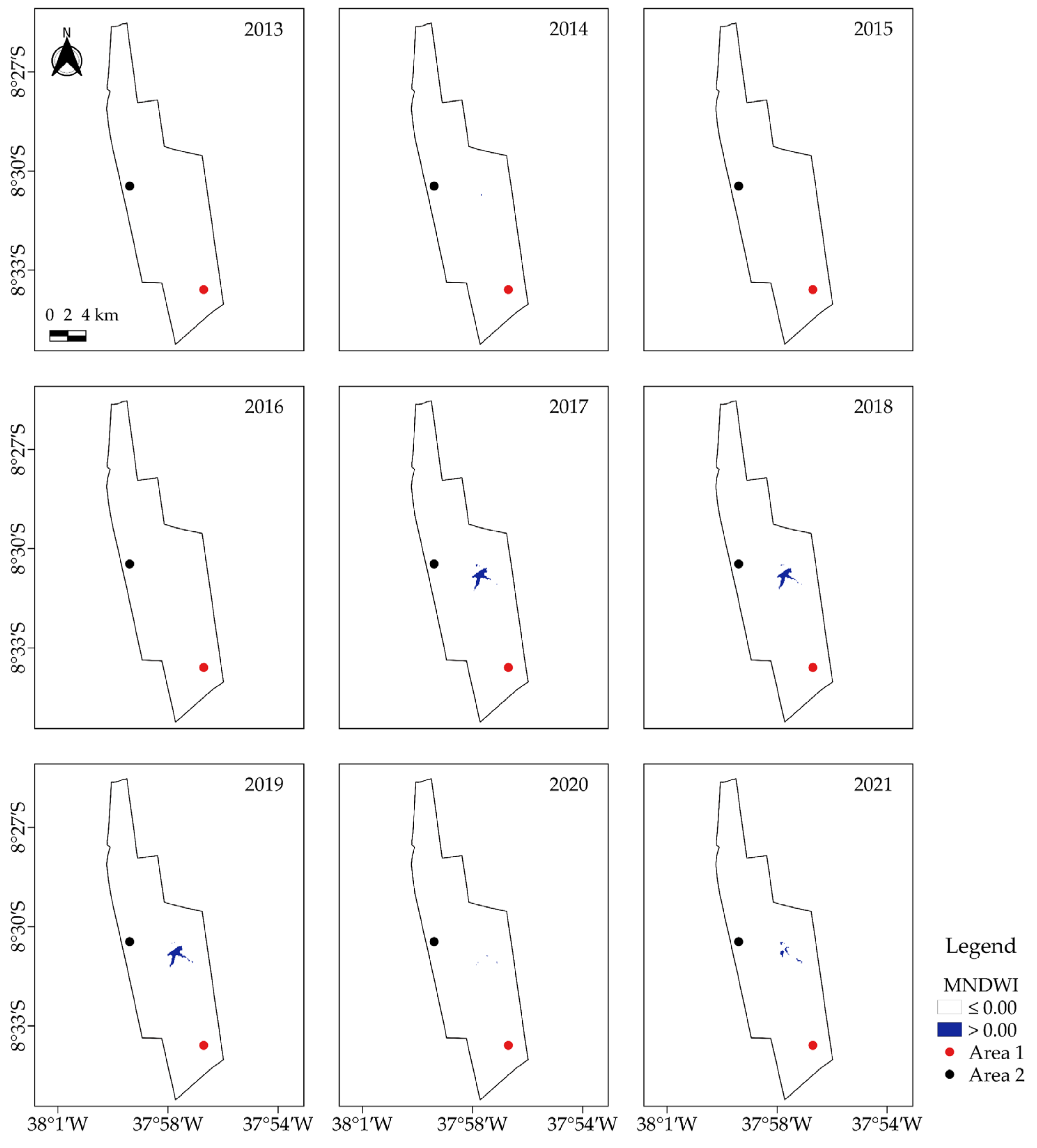
2.3. Characterization of Vegetation Cover via Geoprocessed Vegetation and Water Indices in Google Earth Engine (GEE)
- rNIR1—reflects radiation in the near infrared range;
- rRED—reflects radiation in the red range.
- rNIR1—reflects radiation in the near infrared range;
- rGREEN—reflects radiation in the green range.
- rNIR1—reflects radiation in the near infrared range;
- rSWIR—reflects radiation in the short-wave infrared range.
- rGREEN—reflects radiation in the green range
- rSWIR—reflects radiation in the short-wave infrared range.
2.4. Statistical Analyses
2.4.1. Analysis of Tree Community Dynamics
2.4.2. Boxplot Analysis
2.4.3. Trend Analysis
- n—the number of data points;
- xj and xi—refer to each of the measurements at different time steps i and j, with i ≠ j;
- sgn(xj − xi)—defined by Equation (6).
- n—the data set number;
- t—the number of data with repeated values in a given group;
- q—the number of groups containing repeated values.
2.4.4. Regression Analysis
2.4.5. Principal Component Analysis
2.4.6. Principal Component Regression (PCR)
- Y—biomass (kg), basal area (m2·ha−1), and number of trees;
- β0—intercept on the Y-axis;
- βi—slope of the i-th explanatory variable;
- k—number of explanatory variables;
- ε—random error.
3. Results and Discussion
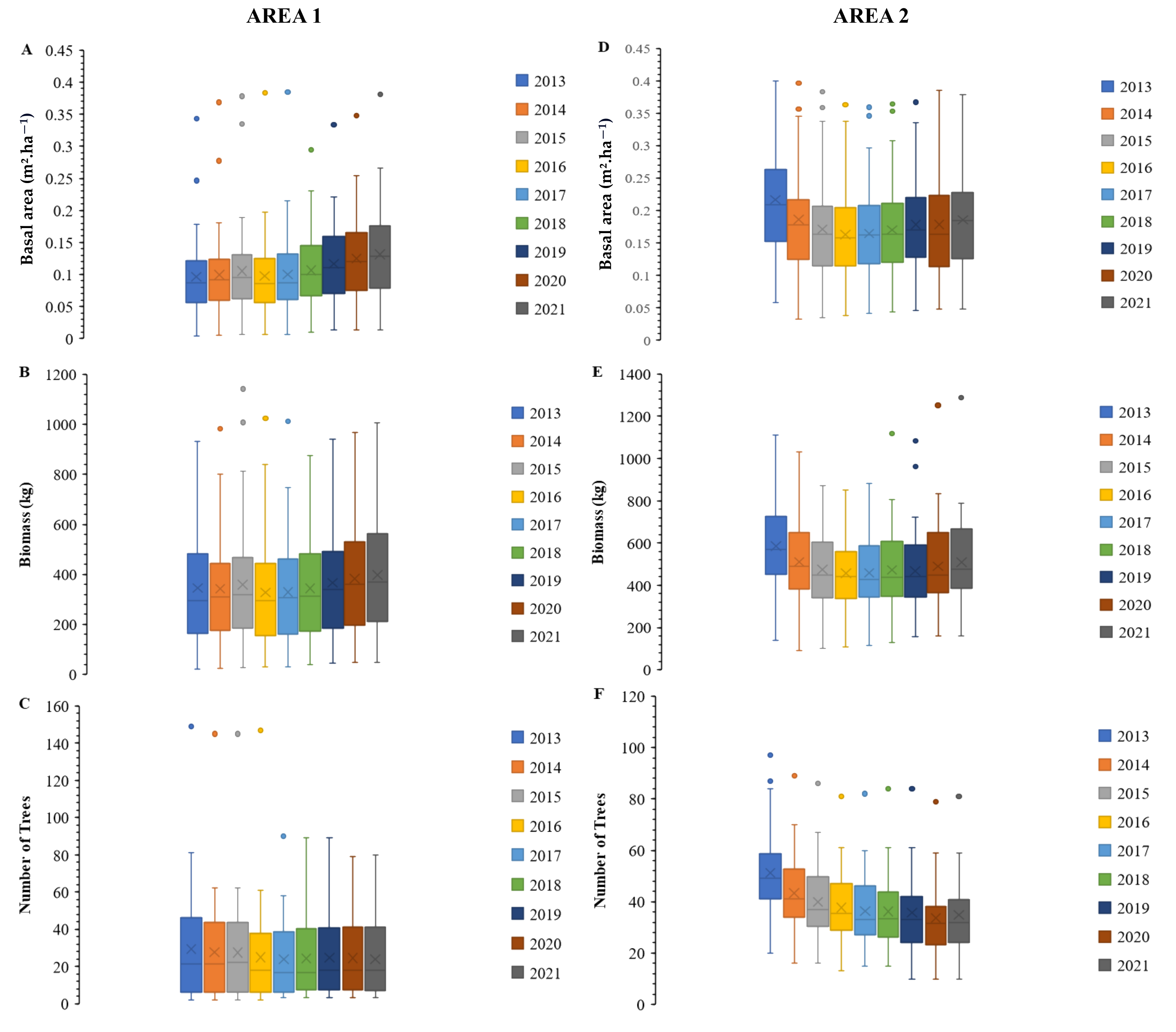
3.1. Dynamics of Tree Vegetation
3.2. Analysis of Vegetation and Water Indices
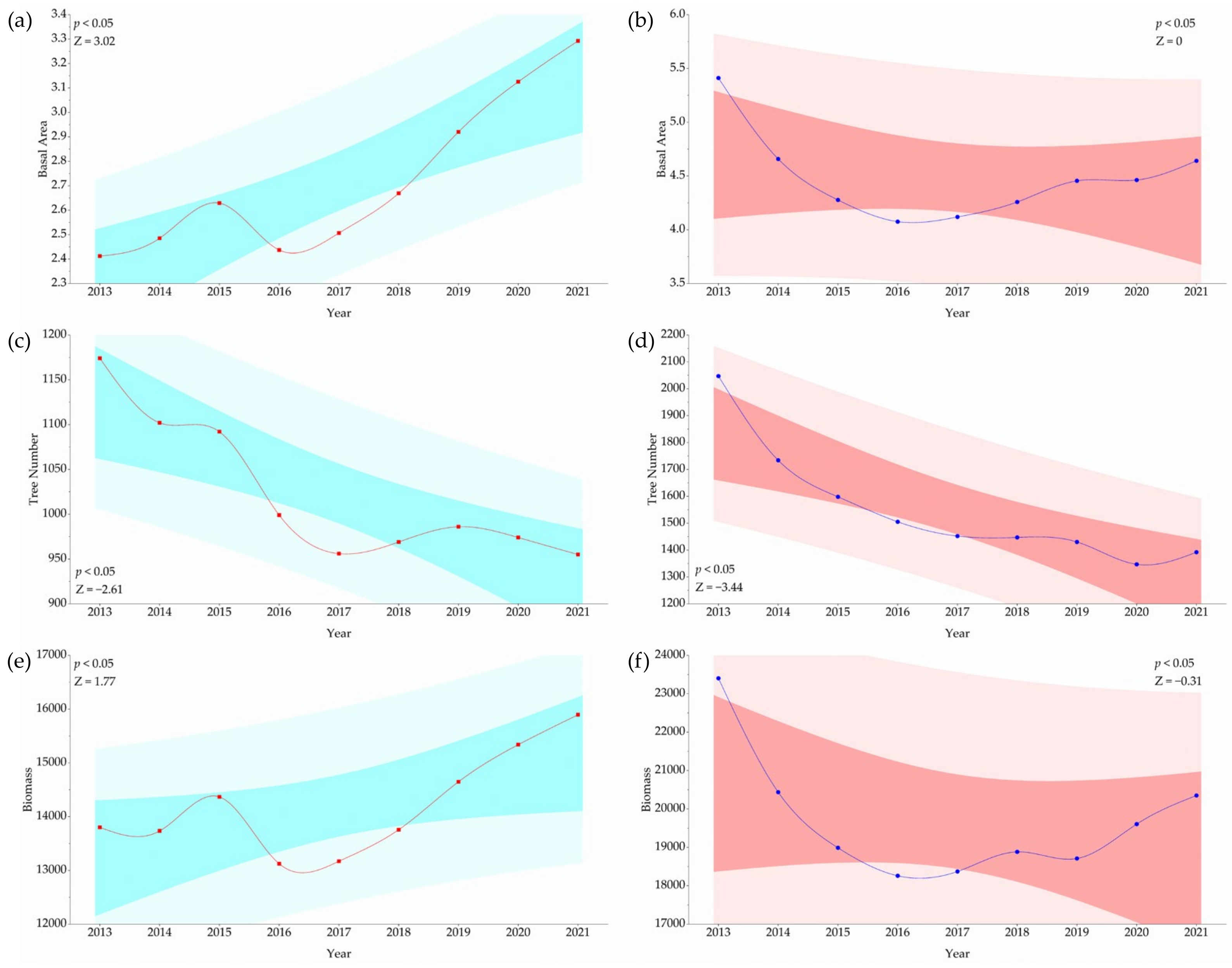
3.3. Mann–Kendall Trend Analysis of Field Parameters and Indices Analyzed
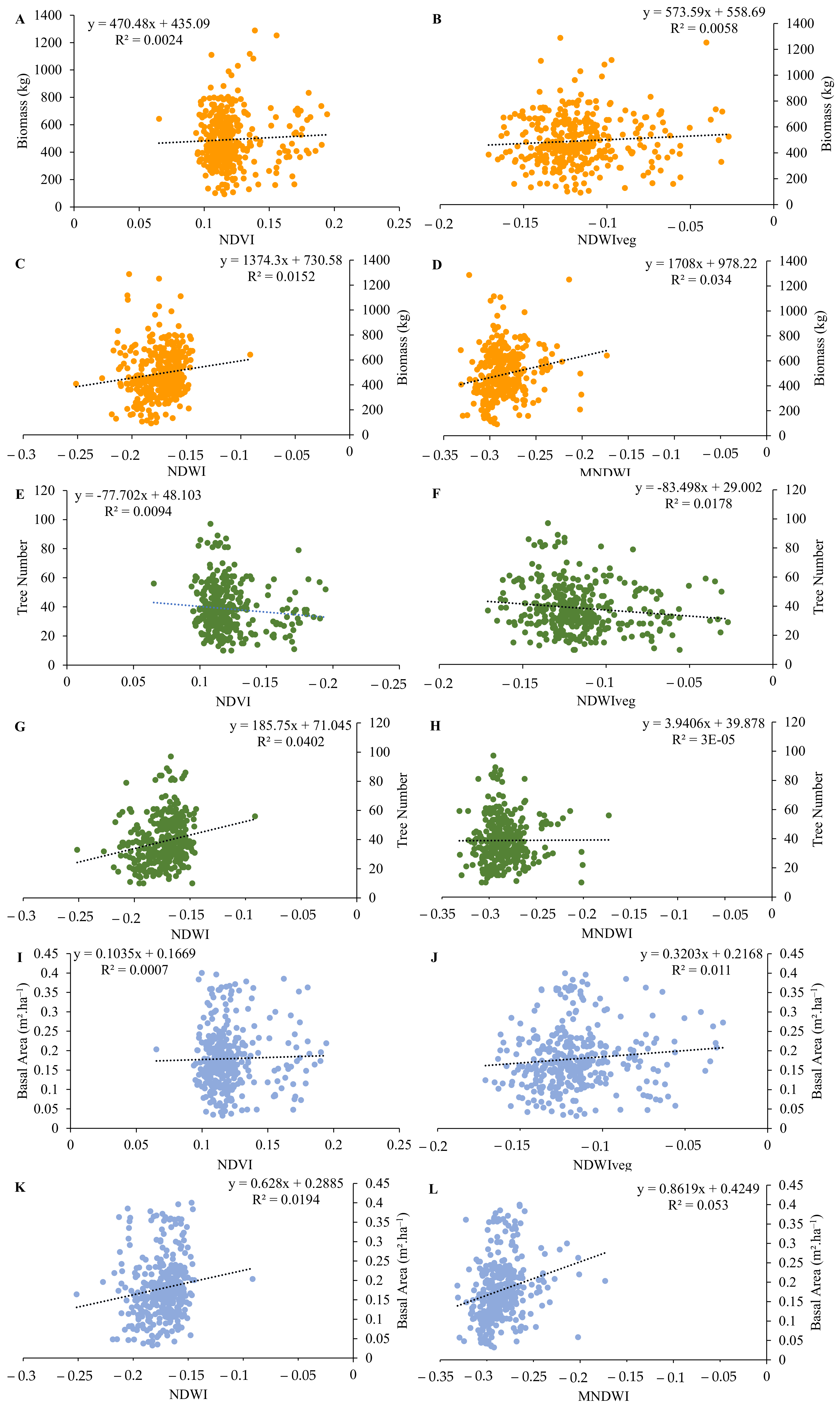
3.4. Regression Analysis
3.5. Principal Component Analysis (PCA)
3.5.1. Principal Component Regression (PCR)
Area 1
Area 2
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miles, L.; Newton, A.C.; DeFries, R.S.; Ravilious, C.; May, I.; Blyth, S.; Kapos, V.; Gordon, J.E. A Global Overview of the Conservation Status of Tropical Dry Forests. J. Biogeogr. 2006, 33, 491–505. [Google Scholar] [CrossRef]
- Siyum, Z.G. Tropical Dry Forest Dynamics in the Context of Climate Change: Syntheses of Drivers, Gaps, and Management Perspectives. Ecol. Process 2020, 9, 25. [Google Scholar] [CrossRef]
- Aguilar-Peralta, J.S.; González-Rodríguez, A.; Maldonado-López, Y.; Fagundes, M.; Faria, M.L.; Ávila-Cabadilla, L.D.; Álvarez-Añorve, M.Y.; Cuevas-Reyes, P. Contrasting Patterns of Morphology, Fluctuating Asymmetry and Leaf Herbivory in Three Plant Species of Different Successional Stages of a Tropical Dry Forest. Trees 2020, 34, 1075–1086. [Google Scholar] [CrossRef]
- FAO World Ecozones. Available online: http://foris.fao.org/static/data/fra2010/ecozones2010.jpg (accessed on 24 May 2024).
- Dionisio, L.F.S.; Schwartz, G.; Mazzei, L.; Lopes, J.d.C.; dos Santos, G.G.A.; Oliveira, F.d.A. Mortality of Stocking Commercial Trees after Reduced Impact Logging in Eastern Amazonia. For. Ecol. Manag. 2017, 401, 1–7. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, X.; Wang, K.; Ciais, P.; Tang, S.; Jin, L.; Li, L.; Piao, S. Responses of Vegetation Greenness and Carbon Cycle to Extreme Droughts in China. Agric. For. Meteorol. 2021, 298–299, 108307. [Google Scholar] [CrossRef]
- Senf, C.; Sebald, J.; Seidl, R. Increasing Canopy Mortality Affects the Future Demographic Structure of Europe’s Forests. One Earth 2021, 4, 749–755. [Google Scholar] [CrossRef]
- Bauman, D.; Fortunel, C.; Delhaye, G.; Malhi, Y.; Cernusak, L.A.; Bentley, L.P.; Rifai, S.W.; Aguirre-Gutiérrez, J.; Menor, I.O.; Phillips, O.L.; et al. Tropical Tree Mortality Has Increased with Rising Atmospheric Water Stress. Nature 2022, 608, 528–533. [Google Scholar] [CrossRef] [PubMed]
- Chazdon, R.L.; Guariguata, M.R. Natural Regeneration as a Tool for Large-scale Forest Restoration in the Tropics: Prospects and Challenges. Biotropica 2016, 48, 716–730. [Google Scholar] [CrossRef]
- Ferreira, M.B.; Bakke, I.A.; Bakke, O.A.; Sousa, G.G.D.; Silva Henrique, G.D.; Brito, G.F.D.; Batista, A.W.; Dantas, É.C.D.O.; de Sousa, A.N.; Ferreira, W.C.; et al. Distribution of Thornless Mimosa Tenuiflora, Piptadenia Stipulacea and Cnidoscolus Quercifolius in a Seasonally Dry Tropical Forest Remnant. For. Trees Livelihoods 2023, 32, 189–206. [Google Scholar] [CrossRef]
- Marin, A.; dos Santos, D.M.M.; Banzatto, D.A.; Ferraudo, A.S. Germinação de Sementes de Guandu Sob Efeito Da Disponibilidade Hídrica e de Doses Subletais de Alumínio. Bragantia 2004, 63, 13–24. [Google Scholar] [CrossRef]
- Reis, R.C.R.; Dantas, B.F.; Pelacani, C.R. Mobilization of Reserves and Germination of Seeds of Erythrina Velutina Willd. (Leguminosae-Papilionoideae) under Different Osmotic Potentials. Rev. Bras. Sementes 2012, 34, 580–588. [Google Scholar] [CrossRef]
- Fettig, C.J.; Mortenson, L.A.; Bulaon, B.M.; Foulk, P.B. Tree Mortality Following Drought in the Central and Southern Sierra Nevada, California, U.S. For. Ecol. Manag. 2019, 432, 164–178. [Google Scholar] [CrossRef]
- Dantas, B.F.; Moura, M.S.B.; Pelacani, C.R.; Angelotti, F.; Taura, T.A.; Oliveira, G.M.; Bispo, J.S.; Matias, J.R.; Silva, F.F.S.; Pritchard, H.W.; et al. Rainfall, Not Soil Temperature, Will Limit the Seed Germination of Dry Forest Species with Climate Change. Oecologia 2020, 192, 529–541. [Google Scholar] [CrossRef] [PubMed]
- Pettorelli, N.; Laurance, W.F.; O’Brien, T.G.; Wegmann, M.; Nagendra, H.; Turner, W. Satellite Remote Sensing for Applied Ecologists: Opportunities and Challenges. J. Appl. Ecol. 2014, 51, 839–848. [Google Scholar] [CrossRef]
- Skidmore, A.K.; Pettorelli, N.; Coops, N.C.; Geller, G.N.; Hansen, M.; Lucas, R.; Mücher, C.A.; O’Connor, B.; Paganini, M.; Pereira, H.M.; et al. Environmental Science: Agree on Biodiversity Metrics to Track from Space. Nature 2015, 523, 403–405. [Google Scholar] [CrossRef] [PubMed]
- Merchant, J.W. Remote Sensing of the Environment: An Earth Resource Perspective. Cartogr. Geogr. Inf. Sci. 2000, 27, 311. [Google Scholar]
- Stych, P.; Lastovicka, J.; Hladky, R.; Paluba, D. Evaluation of the Influence of Disturbances on Forest Vegetation Using the Time Series of Landsat Data: A Comparison Study of the Low Tatras and Sumava National Parks. ISPRS Int. J. Geoinf. 2019, 8, 71. [Google Scholar] [CrossRef]
- Lastovicka, J.; Svec, P.; Paluba, D.; Kobliuk, N.; Svoboda, J.; Hladky, R.; Stych, P. Sentinel-2 Data in an Evaluation of the Impact of the Disturbances on Forest Vegetation. Remote Sens. 2020, 12, 1914. [Google Scholar] [CrossRef]
- Silva, M.V.D.; Pandorfi, H.; Lopes, P.M.O.; Silva, J.L.B.D.; Almeida, G.L.P.D.; Silva, D.A.D.O.; Santos, A.D.; Rodrigues, J.A.D.M.; Batista, P.H.D.; Jardim, A.M.D.R.F. Pilot Monitoring of Caatinga Spatial-Temporal Dynamics through the Action of Agriculture and Livestock in the Brazilian Semiarid. Remote Sens. Appl. 2020, 19, 100353. [Google Scholar] [CrossRef]
- Gao, B. NDWI—A Normalized Difference Water Index for Remote Sensing of Vegetation Liquid Water from Space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- McFEETERS, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- da Silva, J.L.B.; Moura, G.B.d.A.; da Silva, M.V.; de Oliveira-Júnior, J.F.; Jardim, A.M.d.R.F.; Refati, D.C.; Lima, R.d.C.C.; de Carvalho, A.A.; Ferreira, M.B.; de Brito, J.I.B.; et al. Environmental Degradation of Vegetation Cover and Water Bodies in the Semiarid Region of the Brazilian Northeast via Cloud Geoprocessing Techniques Applied to Orbital Data. J. S. Am. Earth Sci. 2023, 121, 104164. [Google Scholar] [CrossRef]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to Enhance Open Water Features in Remotely Sensed Imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Abdolalizadeh, Z.; Ghorbani, A.; Mostafazadeh, R.; Moameri, M. Rangeland Canopy Cover Estimation Using Landsat OLI Data and Vegetation Indices in Sabalan Rangelands, Iran. Arab. J. Geosci. 2020, 13, 245. [Google Scholar] [CrossRef]
- Guerini Filho, M.; Kuplich, T.M.; Quadros, F.L.F. Estimating Natural Grassland Biomass by Vegetation Indices Using Sentinel 2 Remote Sensing Data. Int. J. Remote Sens. 2020, 41, 2861–2876. [Google Scholar] [CrossRef]
- Marques, J.M.; Marques, M.A.M. As Componentes Principais No Descarte de Variáveis Em Um Modelo de Regressão Múltipla. Revista FAE 2005, 8, 93–101. [Google Scholar]
- Keithley, R.B.; Mark Wightman, R.; Heien, M.L. Multivariate Concentration Determination Using Principal Component Regression with Residual Analysis. TrAC Trends Anal. Chem. 2009, 28, 1127–1136. [Google Scholar] [CrossRef] [PubMed]
- Supriyadi, E. Perbandingan Metode Partial Least Square (PLS) Dan Principal Component Regression (PCR) Untuk Mengatasi Multikolinearitas Pada Model Regresi Linear Berganda. Unnes J. Math. 2017, 6, 117–128. [Google Scholar]
- Köppen, W. Das geographische System der Klimate. In Handbuck der Klimatologie Bd. 1; Köppen, W., Geiger, R., Eds.; Teil C. Gebrüder Bornträger: Stuttgart, Berlin, 1936. [Google Scholar]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
- da Costa Júnior, D.S.; Ferreira, R.L.C.; da Silva, J.A.A.; da Silva, A.F.; Pessoa, M.M.d.L. Dinâmica de Crescimento de Uma Floresta Tropical Sazonalmente Seca No Semiárido Brasileiro. Ciência Florest. 2022, 32, 1594–1616. [Google Scholar] [CrossRef]
- Embrapa Sistema Brasileiro de Classificação de Solos. Available online: https://ainfo.cnptia.embrapa.br/digital/bitstream/item/199517/1/SiBCS-2018-ISBN-9788570358004.pdf (accessed on 22 May 2024).
- IBGE. Manual Técnico Da Vegetação Brasileira, 2nd ed.; Instituto Brasileiro de Geografia e Estatística: Rio de Janeiro, Brazil, 2012. [Google Scholar]
- da Silva, M.V.; Pandorfi, H.; de Oliveira-Júnior, J.F.; da Silva, J.L.B.; de Almeida, G.L.P.; Montenegro, A.A.d.A.; Mesquita, M.; Ferreira, M.B.; Santana, T.C.; Marinho, G.T.B.; et al. Remote Sensing Techniques via Google Earth Engine for Land Degradation Assessment in the Brazilian Semiarid Region, Brazil. J. S. Am. Earth Sci. 2022, 120, 104061. [Google Scholar] [CrossRef]
- GEE—Google Earth Engine. A Planetary-Scale Platform for Earth Science Data & Analysis. 2022. Available online: https://earthengine.google.com/ (accessed on 25 May 2023).
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; Technical Report; 1973. Available online: https://ntrs.nasa.gov/citations/19740022555 (accessed on 15 April 2023).
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Gasparri, N.I.; Parmuchi, M.G.; Bono, J.; Karszenbaum, H.; Montenegro, C.L. Assessing Multi-Temporal Landsat 7 ETM+ Images for Estimating above-Ground Biomass in Subtropical Dry Forests of Argentina. J. Arid. Environ. 2010, 74, 1262–1270. [Google Scholar] [CrossRef]
- Dalla Lana, M.; Caraciolo Ferreira, R.L.; Aleixo da Silva, J.A.; Pereira Duda, G.; Lins e Silva Brandão, C.F.; Da Silva, A.F. Biomass Equations for Caatinga Species. Nativa 2018, 6, 517. [Google Scholar] [CrossRef]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Zald, H.S.J. Large-Area Mapping of Canadian Boreal Forest Cover, Height, Biomass and Other Structural Attributes Using Landsat Composites and Lidar Plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Kaiser, H.F. The Varimax Criterion for Analytic Rotation in Factor Analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 6 February 2023).
- Oliveira, C.P.; Ferreira, R.L.C.; Silva, J.A.A.; Lima, R.B.; Silva, E.A.; Silva, A.F.; Lucena, J.D.S.; Santos, N.A.T.; Lopes, I.J.C.; Pessoa, M.M.L.; et al. Modeling and Spatialization of Biomass and Carbon Stock Using LiDAR Metrics in Tropical Dry Forest, Brazil. Forests 2021, 12, 473. [Google Scholar] [CrossRef]
- Taiz, L.; Zeiger, E.; Møller, I.M.; Murphy, A. Fisiologia e Desenvolvimento Vegetal; Artmed Editora: Porto Alegre, Brazil, 2017; ISBN 8582713673. [Google Scholar]
- Marengo, J.A.; Alves, L.M.; Alvala, R.C.S.; Cunha, A.P.; Brito, S.; Moraes, O.L.L. Climatic Characteristics of the 2010–2016 Drought in the Semiarid Northeast Brazil Region. An. Acad. Bras. Cienc. 2018, 90, 1973–1985. [Google Scholar] [CrossRef]
- Silva da Costa Júnior, D.; Luiz Caraciolo Ferreira, R.; Antônio Aleixo da Silva, J.; De Gois, G.; Maria de Lima Pessoa, M.; Sousa da Silva, V. Variabilidade Ambiental No Município de Ibimirim, Estado de Pernambuco, Brasil. Rev. Bras. De Climatol. 2022, 31, 565–610. [Google Scholar] [CrossRef]
- Dale, V.H.; Joyce, L.A.; McNulty, S.; Neilson, R.P.; Ayres, M.P.; Flannigan, M.D.; Hanson, P.J.; Irland, L.C.; Lugo, A.E.; Peterson, C.J.; et al. Climate Change and Forest Disturbances: Climate Change Can Affect Forests by Altering the Frequency, Intensity, Duration, and Timing of Fire, Drought, Introduced Species, Insect and Pathogen Outbreaks, Hurricanes, Windstorms, Ice Storms, or Landslides. Bioscience 2001, 51, 723–734. [Google Scholar] [CrossRef]
- Toillon, J.; Fichot, R.; Dallé, E.; Berthelot, A.; Brignolas, F.; Marron, N. Planting Density Affects Growth and Water-Use Efficiency Depending on Site in Populus Deltoides×P. Nigra. For. Ecol. Manag. 2013, 304, 345–354. [Google Scholar] [CrossRef]
- Xue, H.; Han, Y.; Li, Y.; Wang, G.; Feng, L.; Fan, Z.; Du, W.; Yang, B.; Cao, C.; Mao, S. Spatial Distribution of Light Interception by Different Plant Population Densities and Its Relationship with Yield. Field Crops Res. 2015, 184, 17–27. [Google Scholar] [CrossRef]
- Pereira Júnior, L.R.; Andrade, E.M.D.; Palácio, H.A.d.Q.; Raymer, P.C.L.; Ribeiro Filho, J.C.; Pereira, F.J.S. Carbon Stocks in a Tropical Dry Forest in Brazil. Rev. Ciência Agronômica 2016, 47. [Google Scholar] [CrossRef]
- Spannl, S.; Volland, F.; Pucha, D.; Peters, T.; Cueva, E.; Bräuning, A. Climate Variability, Tree Increment Patterns and ENSO-Related Carbon Sequestration Reduction of the Tropical Dry Forest Species Loxopterygium huasango of Southern Ecuador. Trees 2016, 30, 1245–1258. [Google Scholar] [CrossRef]
- Anderegg, W.R.L.; Kane, J.M.; Anderegg, L.D.L. Consequences of Widespread Tree Mortality Triggered by Drought and Temperature Stress. Nat. Clim. Change 2013, 3, 30–36. [Google Scholar] [CrossRef]
- McDowell, N.G.; Allen, C.D. Darcy’s Law Predicts Widespread Forest Mortality under Climate Warming. Nat. Clim. Change 2015, 5, 669–672. [Google Scholar] [CrossRef]
- Campos, D.A.; Andrade, E.M.; Castanho, A.D.A.; Feitosa, R.C.; Palácio, H.Q.A. Biomass Dynamics in a Fragment of Brazilian Tropical Forest (Caatinga) over Consecutive Dry Years. Appl. Sci. 2020, 10, 7813. [Google Scholar] [CrossRef]
- Marengo, J.A.; Galdos, M.V.; Challinor, A.; Cunha, A.P.; Marin, F.R.; Vianna, M.d.S.; Alvala, R.C.S.; Alves, L.M.; Moraes, O.L.; Bender, F. Drought in Northeast Brazil: A Review of Agricultural and Policy Adaptation Options for Food Security. Clim. Resil. Sustain. 2022, 1, e17. [Google Scholar] [CrossRef]
- Souza Nascimento, C.E.; Tabarelli, M.; da Silva, C.A.D.; Leal, I.R.; de Souza Tavares, W.; Serrão, J.E.; Zanuncio, J.C. The Introduced Tree Prosopis Juliflora Is a Serious Threat to Native Species of the Brazilian Caatinga Vegetation. Sci. Total Environ. 2014, 481, 108–113. [Google Scholar] [CrossRef]
- Albano, C.M.; McGwire, K.C.; Hausner, M.B.; McEvoy, D.J.; Morton, C.G.; Huntington, J.L. Drought Sensitivity and Trends of Riparian Vegetation Vigor in Nevada, USA (1985–2018). Remote Sens. 2020, 12, 1362. [Google Scholar] [CrossRef]
- Oliveira-Júnior, J.F.; Shah, M.; Abbas, A.; Correia Filho, W.L.F.; da Silva Junior, C.A.; de Barros Santiago, D.; Teodoro, P.E.; Mendes, D.; de Souza, A.; Aviv-Sharon, E.; et al. Spatiotemporal Analysis of Fire Foci and Environmental Degradation in the Biomes of Northeastern Brazil. Sustainability 2022, 14, 6935. [Google Scholar] [CrossRef]
- Cunha, A.P.M.; Alvalá, R.C.; Nobre, C.A.; Carvalho, M.A. Monitoring Vegetative Drought Dynamics in the Brazilian Semiarid Region. Agric. For. Meteorol. 2015, 214–215, 494–505. [Google Scholar] [CrossRef]
- Barbosa, H.A.; Huete, A.R.; Baethgen, W.E. A 20-Year Study of NDVI Variability over the Northeast Region of Brazil. J. Arid. Environ. 2006, 67, 288–307. [Google Scholar] [CrossRef]
- Rodrigues, J.A.D.M.; Lopes, P.M.O.; Silva, J.L.B.D.; Araújo, H.L.; Silva, M.V.D.; Santos, A.D.; Moura, G.B.D.A. Spatial-Temporal Dynamics of Caatinga Vegetation Cover by Remote Sensing in the Brazilian Semiarid Region. Dyna 2020, 87, 109–117. [Google Scholar] [CrossRef]
- Marengo, J.A.; Torres, R.R.; Alves, L.M. Drought in Northeast Brazil—Past, Present, and Future. Theor. Appl. Climatol. 2017, 129, 1189–1200. [Google Scholar] [CrossRef]
- Batista, P.H.D.; de Almeida, G.L.P.; da Silva, J.L.B.; Lins, F.A.C.; da Silva, M.V.; Cordeiro Junior, J.J.F. Hydro-Physical Properties of Soil and Pasture Vegetation Coverage under Animal Trampling. Rev. Bras. Eng. Agrícola Ambient. 2020, 24, 854–860. [Google Scholar] [CrossRef]
- dos Santos, A.; Oliveira Lopes, P.M.; da Silva, M.V.; Maniçoba da Rosa Ferraz Jardim, A.; Barbosa de Albuquerque Moura, G.; Siqueira Tavares Fernandes, G.; de Oliveira Silva, D.A.; Bezerra da Silva, J.L.; de Moraes Rodrigues, J.A.; Araújo Silva, E.; et al. Causes and Consequences of Seasonal Changes in the Water Flow of the São Francisco River in the Semiarid of Brazil. Environ. Sustain. Indic. 2020, 8, 100084. [Google Scholar] [CrossRef]
- David, R.M.; Rosser, N.J.; Donoghue, D.N.M. Remote Sensing for Monitoring Tropical Dryland Forests: A Review of Current Research, Knowledge Gaps and Future Directions for Southern Africa. Environ. Res. Commun. 2022, 4, 042001. [Google Scholar] [CrossRef]
- INPE Condições Atuais Do ENOS: Enfraquecimento Do La Niña e Início de Condições de Neutralidade. Available online: http://enos.cptec.inpe.br/ (accessed on 21 March 2024).
- de Oliveira-Júnior, J.F.; de Gois, G.; Silva, I.J.d.L.; de Oliveira Souza, E.; Jardim, A.M.d.R.F.; da Silva, M.V.; Shah, M.; Jamjareegulgarn, P. Wet and Dry Periods in the State of Alagoas (Northeast Brazil) via Standardized Precipitation Index. J. Atmos. Sol. Terr. Phys. 2021, 224, 105746. [Google Scholar] [CrossRef]
- Lopes, A.B.; Andreoli, R.V.; Souza, R.A.F.; Cerón, W.L.; Kayano, M.T.; Canchala, T.; de Moraes, D.S. Multiyear La Niña Effects on the Precipitation in South America. Int. J. Climatol. 2022, 42, 9567–9582. [Google Scholar] [CrossRef]
- da Silva, A.S.A.; Barreto, I.D.d.C.; Cunha-Filho, M.; Menezes, R.S.C.; Stosic, B.; Stosic, T. Spatial and Temporal Variability of Precipitation Complexity in Northeast Brazil. Sustainability 2022, 14, 13467. [Google Scholar] [CrossRef]
- Cunha, A.P.M.A.; Zeri, M.; Deusdará Leal, K.; Costa, L.; Cuartas, L.A.; Marengo, J.A.; Tomasella, J.; Vieira, R.M.; Barbosa, A.A.; Cunningham, C.; et al. Extreme Drought Events over Brazil from 2011 to 2019. Atmosphere 2019, 10, 642. [Google Scholar] [CrossRef]
- De Medeiros, F.J.; de Oliveira, C.P.; Gomes, R.D.S.; Da Silva, M.L.; Cabral Júnior, J.B. Hydrometeorological Conditions in the Semiarid and East Coast Regions of Northeast Brazil in the 2012–2017 Period. An. Acad. Bras. Cienc. 2021, 93. [Google Scholar] [CrossRef]
- Silva, T.R.B.F.; dos Santos, C.A.C.; Silva, D.J.F.; Santos, C.A.G.; da Silva, R.M.; de Brito, J.I.B. Climate Indices-Based Analysis of Rainfall Spatiotemporal Variability in Pernambuco State, Brazil. Water 2022, 14, 2190. [Google Scholar] [CrossRef]
- Titolo, A. Use of Time-Series NDWI to Monitor Emerging Archaeological Sites: Case Studies from Iraqi Artificial Reservoirs. Remote Sens. 2021, 13, 786. [Google Scholar] [CrossRef]
- Meira Junior, M.S.; Pinto, J.R.R.; Ramos, N.O.; Miguel, E.P.; Gaspar, R.O.; Phillips, O.L. The Impact of Long Dry Periods on the Aboveground Biomass in a Tropical Forest: 20 Years of Monitoring. Carbon. Balance Manag. 2020, 15, 12. [Google Scholar] [CrossRef]
- Mitchell, P.J.; O’Grady, A.P.; Tissue, D.T.; White, D.A.; Ottenschlaeger, M.L.; Pinkard, E.A. Drought Response Strategies Define the Relative Contributions of Hydraulic Dysfunction and Carbohydrate Depletion during Tree Mortality. New Phytol. 2013, 197, 862–872. [Google Scholar] [CrossRef]
- de Barros Santiago, D.; Correia Filho, W.L.F.; de Oliveira-Júnior, J.F.; da Silva Junior, C.A. Mathematical Modeling and Use of Orbital Products in the Environmental Degradation of the Araripe Forest in the Brazilian Northeast. Model. Earth Syst. Environ. 2019, 5, 1429–1441. [Google Scholar] [CrossRef]
- Serrano, J.; Shahidian, S.; Marques da Silva, J. Evaluation of Normalized Difference Water Index as a Tool for Monitoring Pasture Seasonal and Inter-Annual Variability in a Mediterranean Agro-Silvo-Pastoral System. Water 2019, 11, 62. [Google Scholar] [CrossRef]
- Melo, M.V.N.D.; Oliveira, M.E.G.D.; Almeida, G.L.P.D.; Gomes, N.F.; Montalvo Morales, K.R.; Santana, T.C.; Silva, P.C.; Moraes, A.S.; Pandorfi, H.; Silva, M.V.d. Spatiotemporal Characterization of Land Cover and Degradation in the Agreste Region of Pernambuco, Brazil, Using Cloud Geoprocessing on Google Earth Engine. Remote Sens. Appl. 2022, 26, 100756. [Google Scholar] [CrossRef]
- Pandorfi, H.; Sobrinho, A.T.; Oliveira, V.S.; Guiselini, C.; Almeida, G.L.P.; Oliveira, M.E.G.; Melo, M.V.N.; Silva, M.V. Prediction of an Occupational Comfort Index for Agricultural Tractor Operation in Sugarcane Cultivation. Sugar Tech 2023, 25, 630–637. [Google Scholar] [CrossRef]
- da Silva, M.V.; Pandorfi, H.; de Almeida, G.L.P.; de Lima, R.P.; dos Santos, A.; Jardim, A.M.d.R.F.; Rolim, M.M.; da Silva, J.L.B.; Batista, P.H.D.; da Silva, R.A.B.; et al. Spatio-Temporal Monitoring of Soil and Plant Indicators under Forage Cactus Cultivation by Geoprocessing in Brazilian Semi-Arid Region. J. S. Am. Earth Sci. 2021, 107, 103155. [Google Scholar] [CrossRef]
- Farooq, T.; Wu, W.; Tigabu, M.; Ma, X.; He, Z.; Rashid, M.; Gilani, M.; Wu, P. Growth, Biomass Production and Root Development of Chinese Fir in Relation to Initial Planting Density. Forests 2019, 10, 236. [Google Scholar] [CrossRef]
- Sajad, S.; Haq, S.M.; Yaqoob, U.; Calixto, E.S.; Hassan, M. Tree Composition and Standing Biomass in Forests of the Northern Part of Kashmir Himalaya. Vegetos 2021, 34, 857–866. [Google Scholar] [CrossRef]






| Species | Equations | R2aj | Sxy% |
|---|---|---|---|
| Anadenanthera colubrina var. cebil (Griseb.) Altschul | = 48.7255x [1 − exp(−0.1435*d)]2.4096 | 0.89 | 20.69 |
| Aspidosperma pyrifolium Mart. | = 0.7858x(d2xh)0.4550 | 0.75 | 26.64 |
| Bauhinia cheilantha (Bong.) Steud. | = 0.0669x(d2.2115)x(h0.8155) | 0.97 | 12.09 |
| Cnidoscolus quercifolius Pohl | = 0.6064x(d1.4216) | 0.82 | 25.51 |
| Croton heliotropiifolius Kunth | = 0.1868x(d1.2764)x(h0.9401) | 0.76 | 18.96 |
| Mimosa ophthalmocentra Mart. ex Benth. | ln = 1.1118 + 1.7371xln(d) − 0.9536xln(h) | 0.89 | 9.04 |
| Mimosa tenuiflora (Willd.) Poir. | = 0.5084x(d1.7121) | 0.94 | 16.79 |
| Cenostigma bracteosum (Tul.) Gagnon & G.P. Lewis | = 6.6205 + 0.0341x(d2xh) | 0.85 | 23.40 |
| Equação Geral | ln = −1.2884 + 1.6102xln(d) + 0.4343xln(h) | 0.85 | 23.46 |
| Kaiser–Meyer–Olkin (KMO) | Adequacy of Data |
|---|---|
| <0.5 | Not adequate |
| 0.5 to 0.6 | Weak |
| 0.6 to 0.69 | Mediocre |
| 0.7 to 0.79 | Middling |
| 0.8 to 1.0 | Adequate |
| >1.0 | Excellent |
| Sphericity Test | Area 1 | Sphericity Test | Area 2 | ||
|---|---|---|---|---|---|
| KMO | 0.721 | KMO | 0.732 | ||
| Test de Bartlett | Chi-square | 4773.292 | Test de Bartlett | Chi-square | 4685.68 |
| GL | 21 | GL | 21 | ||
| Significance | <0.01 | Significance | <0.01 | ||
| Component | Area 1 | Area 2 | ||||
|---|---|---|---|---|---|---|
| Initial Eigenvalues | % Cumulative | Initial Eigenvalues | % Cumulative | |||
| Eigenvalue | % of Variance | Eigenvalue | % of Variance | |||
| 1 | 2.70 | 38.52 | 38.52 | 2.57 | 36.72 | 36.72 |
| 2 | 2.06 | 29.37 | 67.89 | 2.29 | 32.68 | 69.40 |
| 3 | 1.62 | 23.15 | 91.04 | 1.26 | 17.97 | 87.37 |
| 4 | 0.45 | 6.39 | 97.43 | 0.66 | 9.49 | 96.86 |
| 5 | 0.13 | 1.86 | 99.30 | 0.13 | 1.83 | 98.69 |
| 6 | 0.05 | 0.71 | 100.00 | 0.09 | 1.31 | 100.00 |
| Variables | Components | |||||
|---|---|---|---|---|---|---|
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | |
| Basal Area | 0.85 | 0.27 | −0.18 | −0.39 | 0.03 | 0.13 |
| Tree Number | 0.73 | 0.35 | −0.26 | 0.52 | −0.05 | 0.06 |
| Biomass | 0.89 | 0.35 | −0.20 | −0.11 | −0.02 | −0.17 |
| MNDWI | 0.25 | 0.29 | 0.92 | 0.03 | 0.02 | 0.00 |
| NDWIveg | 0.50 | −0.45 | 0.73 | 0.00 | −0.13 | 0.00 |
| NDWI | −0.26 | 0.89 | 0.32 | 0.05 | 0.19 | 0.00 |
| NDVI | 0.51 | −0.81 | 0.01 | 0.11 | 0.27 | −0.01 |
| Basal Area | |||||
|---|---|---|---|---|---|
| Component | r | R2 | p-Value | Error | Regression p-Value |
| PC1 | 0.84 | 0.73 | <0.01 | 0.03 | <0.01 |
| PC2 | 0.27 | 0.07 | <0.01 | 0.06 | <0.01 |
| PC3 | 0.18 | 0.03 | <0.01 | 0.07 | <0.01 |
| Tree Number | |||||
| PC1 | 0.73 | 0.53 | <0.01 | 15.96 | <0.01 |
| PC2 | 0.35 | 0.12 | <0.01 | 21.91 | <0.01 |
| PC3 | 0.26 | 0.07 | <0.01 | 22.59 | <0.01 |
| Biomass | |||||
| PC1 | 0.89 | 0.80 | <0.01 | 101.49 | <0.01 |
| PC2 | 0.35 | 0.13 | <0.01 | 209.73 | <0.01 |
| PC3 | 0.20 | 0.04 | <0.01 | 219.90 | <0.01 |
| Basal Area | |||||
|---|---|---|---|---|---|
| Font | DF | SS | MS | F-Value | p-Value |
| Regression | 2 | 0.06 | 0.03 | 7.14 | 0.001 |
| Residue | 357 | 1.54 | 0 | – | – |
| Total | 359 | 1.6 | – | – | – |
| Model predictors | Constant (β0) | NDWIveg (β1) | NDVI (β2) | R2 | r |
| 0.095 | 0.237 | 0.328 | 0.04 | 0.2 | |
| Multiple regression | Basal Area = 0.095 + (0.237*NDWIveg) + (0.328*NDVI) | ||||
| Tree Number | |||||
| Font | DF | SS | MS | F-value | p-value |
| Regression | 2 | 3941.22 | 1970.61 | 3.67 | 0.027 |
| Residue | 357 | 191,840.75 | 537.37 | – | – |
| Total | 359 | 195,781.98 | – | – | – |
| Model predictors | Constant (β0) | NDWIveg (β1) | NDVI (β2) | R2 | r |
| −4.239 | −68.431 | 161.028 | 0.02 | 0.14 | |
| Multiple regression | Tree Number = −4.239 − (68.431*NDWIveg) + (161.028*NDVI) | ||||
| Biomass | |||||
| Font | DF | SS | MS | F-value | p-value |
| Regression | 2 | 490,779.3 | 245,389.65 | 5.01 | 0.007 |
| Residue | 357 | 17,502,392.4 | 49,026.31 | – | – |
| Total | 359 | 1,799,3171.7 | – | – | – |
| Model predictors | Constant (β0) | NDWIveg (β1) | NDVI (β2) | R2 | r |
| 331.024 | 722.696 | 873.497 | 0.02 | 0.17 | |
| Multiple regression | Biomass = 331.024 + (722.696*NDWIveg) + (873.497*NDVI) | ||||
| Variables | Components | |||||
|---|---|---|---|---|---|---|
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | |
| Basal_Area | 0.01 | 0.82 | −0.08 | −0.54 | 0.18 | −0.02 |
| Tree_Number | −0.25 | 0.68 | −0.34 | 0.59 | 0.14 | −0.03 |
| Biomass | −0.03 | 0.93 | −0.26 | −0.05 | −0.27 | 0.01 |
| MNDWI | 0.44 | 0.44 | 0.77 | 0.14 | 0.00 | 0.01 |
| NDWI_veg | 0.92 | 0.20 | 0.29 | 0.09 | 0.00 | −0.10 |
| NDWI | −0.78 | 0.26 | 0.54 | 0.04 | 0.01 | 0.16 |
| NDVI | 0.92 | 0.01 | −0.30 | 0.03 | 0.03 | 0.23 |
| Basal Area | |||||
|---|---|---|---|---|---|
| Component | r | R2 | p-Value | Error | Regression p-Value |
| PC1 | 0.01 | 0.00 | 0.824 | 0.08 | 0.824 |
| PC2 | 0.82 | 0.67 | <0.01 | 0.04 | <0.01 |
| PC3 | 0.08 | 0.01 | 0.144 | 0.08 | 0.144 |
| Tree Number | |||||
| PC1 | 0.25 | 0.06 | <0.01 | 15.23 | <0.01 |
| PC2 | 0.68 | 0.46 | <0.01 | 11.57 | <0.01 |
| PC3 | 0.34 | 0.12 | <0.01 | 14.75 | <0.01 |
| Biomass | |||||
| PC1 | 0.03 | 0.00 | 0.539 | 189.04 | 0.539 |
| PC2 | 0.93 | 0.86 | <0.01 | 71.58 | <0.01 |
| PC3 | 0.26 | 0.07 | <0.01 | 182.70 | <0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, M.B.; Ferreira, R.L.C.; da Silva, J.A.A.; de Lima, R.B.; Silva, E.A.; de Sousa, A.N.; De La Cruz, D.B.C.; da Silva, M.V. Spatial-Temporal Dynamics of Water Resources in Seasonally Dry Tropical Forest: Causes and Vegetation Response. AgriEngineering 2024, 6, 2526-2552. https://doi.org/10.3390/agriengineering6030148
Ferreira MB, Ferreira RLC, da Silva JAA, de Lima RB, Silva EA, de Sousa AN, De La Cruz DBC, da Silva MV. Spatial-Temporal Dynamics of Water Resources in Seasonally Dry Tropical Forest: Causes and Vegetation Response. AgriEngineering. 2024; 6(3):2526-2552. https://doi.org/10.3390/agriengineering6030148
Chicago/Turabian StyleFerreira, Maria Beatriz, Rinaldo Luiz Caraciolo Ferreira, Jose Antonio Aleixo da Silva, Robson Borges de Lima, Emanuel Araújo Silva, Alex Nascimento de Sousa, Doris Bianca Crispin De La Cruz, and Marcos Vinícius da Silva. 2024. "Spatial-Temporal Dynamics of Water Resources in Seasonally Dry Tropical Forest: Causes and Vegetation Response" AgriEngineering 6, no. 3: 2526-2552. https://doi.org/10.3390/agriengineering6030148
APA StyleFerreira, M. B., Ferreira, R. L. C., da Silva, J. A. A., de Lima, R. B., Silva, E. A., de Sousa, A. N., De La Cruz, D. B. C., & da Silva, M. V. (2024). Spatial-Temporal Dynamics of Water Resources in Seasonally Dry Tropical Forest: Causes and Vegetation Response. AgriEngineering, 6(3), 2526-2552. https://doi.org/10.3390/agriengineering6030148









