Abstract
The paper presents an analysis the spatial distribution of turbulent kinetic energy (TKE) for bolt fishways, including the impact of additional spillway slots and fixed channel development. The research was done for two models, each containing a different arrangement of slots. The presented results of research for bolt fishways were obtained as an effect of laboratory tests. The measurements were done for three components of instant flow velocity magnitude (speed). Analysis of the results was done for a 3D flow structure using Matlab software. In the case of bolt fishways, significant differences were noted for the method of velocity and TKE distribution, in reference to research comprising channels with biological development. It was stated that a reason for this is the flexible development of the channel. The occurrence of extreme TKE values in the chamber (pool) is strictly associated with the characteristics of interaction zones between various flow structures. It was also stated that the lower the parapet of the slot’s spillway shelf is in the fishway’s partition, the higher TKE could be expected just downstream of the section. These establishments may be important for the designing process in the case of fish passes of various types of construction.
1. Introduction
The occurrence of turbulent phenomena in the flow of rivers remains a determining element for the biology of fish (construction and shape of body and fins), different behavior for particular fish species, and the construction of fish passes [1]. In the case of a migrating fish, turbulence in rivers may form a specific signpost, as well as a barrier [2]. The behavior and swimming abilities of fish depend on the features of turbulent parameters, which affect the fish.
If whirl structures transform in a synchronized way in the flow, fish adapt the way they move. In such conditions of the turbulent flow it was noted that fish use less energy [3]. On the other hand, the production of impulsive, temporary and chaotic whirl structures results in an increased use of energy by migrating fish [4,5]. Lacey et al. [6] state that an element hampering swimming for fish is the lack of one dominating frequency in flows. Costa et al. [7] established that the conditions of flow and the behavior of fish are related to the channel’s development (type of deflectors). Extreme values of hydrodynamic parameters not always result in higher physiological parameters for fish or in increased movement frequencies for examined fish. A reduced physiological reaction and reduced frequencies of fish body’s movement are observed in cases when fish swim with a greater use of drifting within the flow area. This is an effect of fish using whirl structures more often in the case of swimming. A high swimming cost is observed at increased flows. Nonetheless, low flows may be used by fish to optimize fish behavior (swimming) during feeding.
Therefore, in order to design a fish pass properly, one shall focus on analyzing the impact of channel development (channel’s geometry and its development, as well as its flexibility) on the turbulent conditions inside. Such a detailed analysis shall allow for recording a scheme of turbulent flow parameters’ distribution and for their conscious reproduction in designed facilities.
One has focused in this paper on analyzing the turbulent kinetic energy (TKE) in the bolt fishway. TKE is one of the most important turbulence measures, which contributes to the increase of energy volume needed by fish to overcome an obstacle [5,8]. TKE directly affects the ability to overcome the current by fish [2,9].
TKE distribution shall be specified for the area of main flow and the whirl area, as well as the boundary zones for those two areas. The research is to indicate the impact of additional spillway slots (level of shelves’ parapets) within a flexible development of the channel on the distribution of TKE within a slot’s section and within the fishway’s chamber (pool). The research was performed for two models of different arrangement (location in the section) of the main slot and of two additional spillway slots. The bolt fishway contains partitions made of cylindrical elements. Elements of various heights are placed within a partition’s line and all together remain a partition separating further chambers. Due to the stiffness and shape, the bolt elements act as stiff tree trunks in the channel. As a consequence, in order to provide a more complex analysis, the presented research was compared to research concerning various forms of channel development, including fixed and flexible vegetation.
Dimensions of trunks and branches within the examined flow are directly associated with transformation of kinetic energy for the average movement. A trace formed after those elements has vertically even values of TKE [10,11]. The presence of biological development within the channel affects the effective reduction of the whirl structure’s size in the flow, which in turn results in a significant increase of energy dispersion for the stream flow (i.e., dissipation), but it does not contribute to the increase of turbulent kinetic energy. The share of vertical turbulence’s intensity in kinetic energy decreases gradually towards the bottom [12].
In the case of research concerning the development of channels with grass, Nepf and Vivoni [13] proved that vertical lines of velocities for filling of the chamber (H), which is equal to the level of plants’ crest (h), have maximum values at the channel’s bottom, and velocity is reduced above, up to the level of the water-table. The TKE analysis is presented using a normalized parameter of: √TKE/U, where U is the mean value of velocity at the spot. Distribution of normalized TKE values—at filling H/h = 1—has even vertical values. At the surface the TKE value is slightly higher than at the bottom. The level of maximum velocity in vertical alignment (i.e., inflection of the velocity diagram) does not overlap the vertical curvature of the normalized TKE value. A distribution mechanism for the velocity and normalized TKE is significantly changed, when the water-table rises over the crest of plants (grass). The maximum TKE at filling H/h = 1.25 occurs at the plant bowl. It is a spot of negative inflection of the TKE diagram, and TKE is reduced up to the water-table over the plant bowl. Along with the increase of H/h proportion from 1.25 to 2.75, the occurrence level for normalized TKE is decreased towards the bottom. In case of the analyzed flows the normalized TKE—after reaching the maximum value at an elevation below the plant bowl—is significantly reduced. The TKE distribution for filling higher than the crest of plants has a similar variability profile. In the case of flows of H/h > 1.25, velocity—from the bottom to the elevation of maximum TKE—is slightly reduced (with local maximum at the bottom). It is correlated with the increase of normalized TKE values. At H/h > 1.25 the maximum normalized TKE occurs at the level of positive inflection of the velocity diagram. Over the elevation of maximum TKE, the flow velocities rapidly increase. This is accompanied by a reduction of normalized TKE. In the case of H/h = 2.75 the positive increase of velocity values occurs until reaching the maximum for the vertical line at the level of about H/h = 2. Over that point the velocity is slightly reduced until reaching the water-table. In distribution of TKE it is reflected in evening of TKE values within a vertical line. It is a zone, where a minimum for that parameter occurs within the vertical line. In the case of all of the flows, where H/h reaches a value from 1.25 to 2.75, the flow velocity and the normalized TKE do not have any rapid value leaps at the level of plant bowl’s crest. Generally, the higher the H/h proportion is, the higher the initial value of normalized TKE at the bottom would be.
In the case of research where vegetation was modelled using fixed and flexible cylinders, it was established that the distribution of velocities and TKE is not fixed at the flow depth [14]. They reach the maximum at the bottom and depend on the structure of vegetation development. The other maximum of values in the main flow area is reached by TKE at the surface, as an effect of secondary current occurrence. Locally, TKE maximum values were also recorded in zones containing biological development, in the vicinity of vegetation, and in the areas of interaction as a derivative of strong clash between water masses having different flow character.
As showed by Baki et al. [15], the use of cylinders in the channel of a fish pass is also associated with the specific vertical distribution of TKE. Behind the flowing cylinder, a significant reduction in the TKE value was seen, with the level of its occurrence moving down the cylinders as the height of its water depth in the channel increased. As in the case of Schnauder [14], maximum TKE values were recorded in the bottom zone and at the water surface.
Research done by Sukhodolov et al. [16], which analyzed the 3D turbulent flow structure in fields between the groynes, proved that velocities raised towards the surface of free-flowing water within the range of measurement vertical lines’ levels of 0.1 < Z/H < 0.5 (Z is a coordinate of the spot within the measurement vertical line [m]; H is a filling depth for the measurement channel [m]). Furthermore, over the range of 0.5 < Z/H < 1 the level of water gauge (0.1 ÷ 0.6) Z/H shows a dependence trend described in a universal function provided by Nezu and Nakagawa [17]. Furthermore, in case of the channel’s filling level in the range of (0.6 ÷ 1.0) Z/H the TKE values increase along with the level. A reason for that situation was determined as actions of developed horizontal turbulent structures and impact of wind on the unconstrained flow surface. Those two additional sources of turbulent kinetic energy provide the amount of energy comparable to turbulent kinetic energy produced by the friction of the water flow mass in the river-bed.
Research on the distribution of TKE within plant development, where various heights of plant bowl were considered in reference to the channel’s filling [18], is also important. Studies have proven that in channels with flexible vegetation grown, the maximum TKE values occur at the bottom (inside of the plant area (body)). Assuming the constant filling for the channel, one shall state that the lower the vegetation is, the higher the maximum TKE rate would be. Comparing the channel without vegetation and the channel with vegetation of 20% filling level, a leap of the TKE value was noted by 81%. Therefore, the presence of plants in the channel is a direct reason for the increase of TKE within the flow area. In the case of plant development within the channel reaching about 50% of filling, velocity profiles and TKE are quite even within vertical lines. If the height of plants decreases in reference to filling, an average current—flowing in the direction opposite to the direction of flow in the channel without development—is noted within the area of plants and at some level over their crest. That current is located towards the wave propagation direction, and it may be generated by interaction between the wave speed and the resistance of the plant bowl. For the purpose of generating a significant average current, the relation of the inducing wave (Aw) and spacing of momentum (S) shall exceed a value of 1 [18,19,20]. The stronger the average current is (at the lower plant crest), the higher TKW in the plant area would be and the stronger the increase of longitudinal velocity in the channel over the plant development and over the area of average current’s flow would be. Along with the increase of the average current’s strength, its flow area also increases. It is interesting that more flexible plant meadows generate TKE having lower value, but flow structures and related intensified TKE fields within plant areas are maintained for a longer time. Stiffer meadows generate higher TKE, but flow structures and area of high TKE values are dispersed faster.
While analyzing mechanisms of TKE distribution in bolt fishways, it shall be especially considered, if establishments made by the scientists mentioned above may be applied to structures used for fish migration. These studies complement the analysis of the spatial effect of the flow structure on the TKE distributions in the bolt fishway [21].
2. Materials and Methods
2.1. Description of the Model
The name of the structure—bolt fishway—is associated with the applied cross-barriers in the facility’s channel. Cross-partitions are made of linearly placed cylindrical bolt elements of various heights, thus separating the consecutive chambers of the fish pass. The cylinders are assembled on spindles and they may be rotated. The cross-section of bolt elements—getting narrower with height—allows for the formation of diverse flow conditions in the fish pass. Bolt elements are assembled on steel spindles, and this is why the bolt element may be rotated and therefore the hydraulic conditions in the facility may be regulated on the object’s use stage.
The research was done based upon two laboratory models—A and B. A prototype of the solution is model A, which reflects basic assumptions for the construction. Model B remains a modification of model A, which includes the moving of 1 bolt, and therefore moving the axis of partition for the main slot and for two smaller spillway slots.
For the purpose of the model the bolt elements were developed while keeping a linear (geometric) scale of 1:5. The model was developed as a series of 8 chambers. The measurement chamber was located in the central part of the model. A drop of the bottom was 2.0%. Maximum filling of the model’s chambers was 22 cm, and minimum one—20 cm. The test flow corresponding with the flow probability criterion according to Froude was 38 L/s. Those elements were made of wet wood. Models A and B were develop in a scale, for which the width (B) of chambers was 0.8 m, and the length (L) of a single chamber was 1.20 m. Bolt elements in the laboratory model had the following parameters: (biggest) height of 26 cm; (small) height of 12 cm; (medium) height of 16 cm. The cross-dimension was reduced to 12.8 cm for the longer diameter, and to 10.4 cm for the shorter diameter. The bottom was mapped by using small rocks of 1–2 cm fraction, fixed to the substrate with glue. Moreover, the bottom was covered with loose quartz sand in order to observe the sand sedimentation. Before commencing the main part of the measurements, small fractions of sand were washed out of the model so that the bottom structure (from tiny sedimentary sand) did not affect the results of the obtained tests.
Basic assumptions on bolt fishway’s geometry in the actual scale are as follows: channel width 4 m, length of a single chamber—6 m, long drop of the bottom 2%. The designed actual flow was 2.14 m3/s, at the maximum filling of the chambers to a height of 1.10 m. Width of the main migration slot is 0.8 m. Bolt elements have the following dimensions (in the object’s actual scale): biggest bolt elements—height 1.3 m; small bolt elements—height 0.6 m; average bolt elements—height 0.8 m.
2.2. Measurements
Eleven sections were developed during the research of the model’s scale (the location of the section is longitudinal spacing between measurements points): section r—0.00 m (1) it is a bolt at the inlet to the measurement chamber; section a—0.15 m (2); section b—0.25m (3); section bb—0.35 m (4); section c—0.55 m (5); section cc—0.70 m (6); section d—0.85 m (7); section dd—1.00 m (8); section ddd—1.05 m (9); section ee—1.10 m (10); section rr—1.20 m (11), in accordance with Figure 1e. Eleven sections were developed during the research, 18 measurement vertical lines each, in accordance with Figure 1a,c.
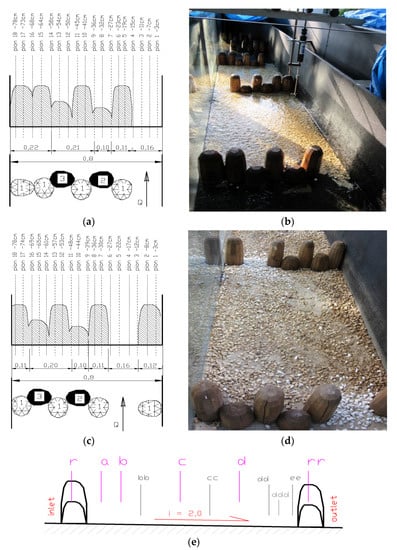
Figure 1.
Construction of models: (a): measurement vertical lines for model A—view from the top, from the side of inlet to the chamber; (b): model A—view from the bottom, from the side of outlet from the chamber; (c) measurement vertical lines for model B—view from the top, from the side of inlet to the chamber; (d) model B—view from the bottom, from the side of outlet from the chamber; (e) location of cross sections in the measuring chamber.
Measurements were done in sections for variable number of measurement levels. The number of levels resulted from a distance between the section and the inlet bolt and from its filling with water. Each time the levels of water in sections were checked using a needle water gauge, and then further measurement levels were established, maximally every 2 cm—starting from the lowest one at the level of 1 cm over the channel’s bottom. The essential number of measurement levels—as results from the global grid for the chamber—was:
- -
- for sections: r, a, b, bb—10 levels;
- -
- for sections: c, cc—11 levels;
- -
- for sections: d, dd, ddd, ee, rr—12 levels.
Additional spots were measured individually for each section below and over the level of spillway shelves in the inlet bolt partition (total of four additional measuring spots in each vertical line). In total the measurements were done for over 2000 spots in each of research variants.
Due to the fact that a distance between the measurement cell and the probe’s head is 5 cm, there were huge difficulties in measuring the final three spots placed at a level of 0 cm, 2 cm, and 4 cm underneath the surface of the water. Due to the requirements of Matlab, which was used to develop the results, one has decided to additionally measure those spots. Spots on a level of 4 cm underneath the surface of water (16cm above the bottom) were measured by placement of the probe at an angle. It was enabled by a rotary handle fixing the probe. Then the flow was increased, and the measurement of the same spot was repeated, but this time at the vertical alignment of the probe. After analyzing the results, it was established that the difference in values of average directional velocities and in their standard deviations is not more than 3% of the value. Therefore, it was assumed that geometry of the bolt affects the flow parameters more than the distance between the measurement spot and the surface of water. Spots placed on a depth of 0 cm and 2 cm below the water table at filling of up to 22 cm were additionally measured at the increased flow. It is important that the increase of flow (up to a height of 25 cm) did not cause flooding of the bolt chamber (height of bolt elements is 26 cm). This is why the stream’s flow character in the model was kept. Active opening in the bolt’s section was not modified at the additionally measured spots, because those levels were placed above the highest parapet of additional spillway slots.
For the purpose of tests three-dimensional acoustic Doppler velocimeter SonTek 16 MHz MicroADV (Xylem Inc., Rye Brook, NY, USA) was applied. The frequency of the measurements was 25 Hz. The length of the measurement at a single spot, measured using a probe, was established through preliminary tests for several spots located within the main flow and within the whirl area. From the collected data, it was established that the value of the second moment stabilizes quite early, and it is usually a series corresponding to a 90 s measurement. The exceptions are the spots located within the area of intensive whirls, where the relative stabilization of the measurement was achieved after 300 s. The average value of the velocity for the bolt section in the area of the main flow was stabilized after a duration of 180 s at most. For the whirl area underneath the bolt, regardless of the level of the spot, the minimum required measurement time was 300 s. Therefore, 300 s was adopted as the minimum time for the performance of essential measurements.
WinADV 32 software (version 2.012) was used as a filtration tool, and two types of filters were used: the acceleration method by Goring and Nikora (phase-spatial method) and the minimum SNR (Signal-to-Noise Ratio) rate method (filter of minimum correlation rate). The minimum threshold value for the SNR rate should amount to five. Both of the series produced a similar quantity of good data, which remained within 82–97%.
2.3. Methods of Analysis
In the case of the hydraulic analysis of fish passes, it becomes important to refer to features and characteristics of turbulent flow. Among the basic motion characteristics for liquid, turbulent kinetic energy (TKE) (sometimes marked as “k”) shall be distinguished. Therefore, a mathematic formula for turbulent kinetic energy is as follows [22]:
where vx’, vy’, vz’ are longitudinal, transversal and vertical velocity fluctuations, respectively.
The TKE grossing-up factor amounted to 5.08. In case of this publication the results were informed in an actual scale. The presented results of research for the bolt fishway were obtained due to laboratory tests done on a physical model provided by the laboratory of the Technical University of Wrocław. The research was done using Matlab software.
3. Results
3.1. Model A
The case of the Model A is shown in Figure 2 (spatial distribution) and in Figure 3 and Figure 4 (analysis of selected vertical measurement profiles). The TKE profiles in Figure 3 and Figure 4 show the directional values of the TKE components. This is to demonstrate the importance of the directional TKE values in the mean TKE value discussed in this paper.
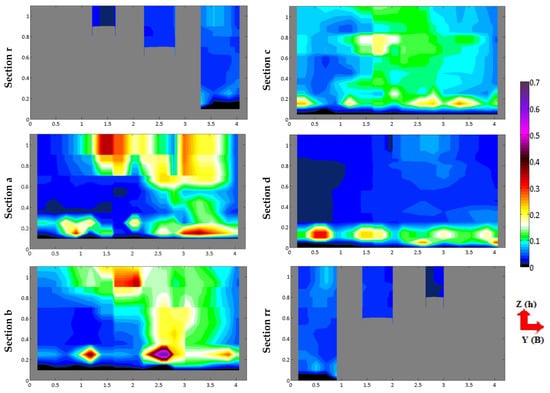
Figure 2.
Spatial distributions of TKE [m2/s2] for sections: r, a, b, c, d, rr; dimensions on the axes (m). MODEL A.

Figure 3.
Summary of exemplary vertical lines for directional velocities and speed (average water flow velocity) (m/s) and of corresponding TKE (m2/s2) and normalized TKE (—) within main flow area. MODEL A.
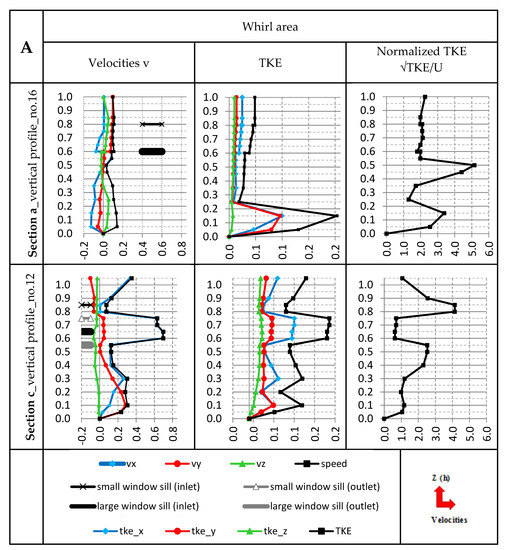
Figure 4.
Summary of exemplary vertical lines for directional velocities and speed (average water flow velocity) (m/s) and of corresponding TKE (m2/s2) and normalized TKE (—) within whirl area. MODEL A.
The partition’s section provides low TKE values. At the bottom—up to the level of 5 cm—TKE reaches the value of 0.002 m2/s2. The velocity rate at this level is also small, maximally up to 0.022 m/s. The normalized TKE provides a positive peak in that place, i.e., a rapid growth of value to the rate of 1.88. Above 5 cm a huge peak of average velocity is recorded in vertical velocity lines, which reaches quite equal values within the vertical lines. The maximum velocity is recorded at the level of 15 cm over the bottom, and it amounts to 1.52 m/s. Over that spot, velocity undergoes a gradual reduction to the rate of 1.2 m/s at the surface. It is important that at elevations of spillway shelves for smaller slots there is a negative leap of velocity values. It is reflected in the TKE distribution, as along with the increase of spots’ levels within vertical lines, that TKE rises towards the water surface. The local TKE minimum occurs at the level of maximum flow velocity, and it amounts to 0.035 m2/s2. In the case of TKE, levels of shelves, where the negative leap of velocity values occur, are the levels of the positive peak for that parameter’s values. Over the elevation of the last shelf TKE is stabilized and reaches the maximum of 0.08 m2/s2 for the vertical line.
In section a, the slot’s opening is shaded with fields of high TKE values. The highest mean values in vertical lines are reached by TKE within the area of main stream’s flow. The maximum of TKE values occur at the bottom. The maximum reaches the values of up to 0.30 m2/s2 and occurs about 10 cm over the channel’s bottom.
On higher levels—along with reduction of velocity magnitude—TKE is also reduced, to the level of up to 0.08 m2/s2. However, just below the elevation of additional spillway shelves TKE again raises to the level of 0.20 m2/s2, and after a peak of values at the elevation of shelf it reaches its 2nd maximum of 0.21 m2/s2 within the vertical line. Over the parapet of the lower shelf TKE again reduces its value until reaching the level of the higher parapet of the 2nd additional spillway slot. At the elevation of the 2nd parapet there is another peak of values reaching 0.2 m2/s2. Over the final parapet—up to the water-table—there is a small reduction reaching the rate of 0.19 m2/s2. An important observation refers to the fact that a positive increase of TKE values is coupled with a negative increase of mean velocity’s values within vertical lines. And positive peaks of TKE occur along with negative peaks of mean velocity’s values. The normalized TKE has two positive peaks—at the bottom and at the elevation of the lower spillway parapet. A different correlation of dependence between velocity and TKE occurs there. The maximum velocity at the level of 35 cm from the bottom is a level where the minimum of normalized TKE occurs. The occurrence of minimum velocity values within vertical lines underneath elevation of the lowest spillway shelf remains a zone of maximum values for the normalized TKE.
A huge area of low TKE—0.02 m2/s2—occurs within the whirl area underneath the bolt. An exception is present in areas neighboring spillway openings of additional slots. The highest increase of TKE takes place at the smallest slot and it reaches up to 0.3 m2/s2. It is important that there is no distinct trend for TKE in zones having different flow specificity. The areas of increased turbulence, which have raised TKE, occur both in the top flow area, as well in the isolated zone, where it forms quite tight field of high values.
In case of section b, located in a distance of 0.25 m (1.25 in the actual scale) from the bolt a division of TKE values due to the water flow’s way starts to be noticeable. Higher TKE values—about 0.10 m2/s2, on average—occur in the top flow zone. The area, where huge whirls are formed, are the vertical lines with mean TKE value at the level of 0.02–0.05 m2/s2. Local maximum values occur at the bottom, and in the main flow’s area they amount to about 0.25 m2/s2, and in the whirl area—to about 0.40 m2/s2.
However, one may see in that section fields of high TKE values located at the boundary between the main area and the isolated area. The mean TKE values within vertical lines for those location is 0.2 m2/s2. At the bottom of the boundary one may see the extremum of TKE values of 0.7 m2/s2. It is here that whirl structures are being fed by the main flow’s area. The feeding is provided by a current having the direction compliant with the main flow. A field of high TKE values for the boundary is kept up to elevation of the bottom parapet of the bigger spillway slot. Over that zone TKE is reduced to the range of 0.1–0.15 m2/s2, while keeping quite even values within vertical lines, until reaching the surface of water. The other field of high TKE is present over the elevation of the smaller slot’s shelf in a space between spillway windows. Its value reaches the level of 0.35 m2/s2.
Section c remains a zone of high dispersion for higher TKE values of 0.1 m2/s2, on average. The area of higher TKE values covers the main flow, as well as the whirl area. However, one may see a reduction of TKE to the level of 0.05–0.08 m2/s2 in the whirl area, on the channel’s wall side. Extreme values occur at the bottom, but they are much lower than 0.25 m2/s2. The section proves the occurrence of an additional field of TKE reaching the level of up to 0.3 m2/s2. This is a spot where a huge whirl is present. The area of the main flow on the channel’s wall side provides TKE values in the range of 0.07–0.08 m2/s2.
The analysis of measurement vertical lines proved reversed correlation between the TKE raise and the value of average velocities for the greater number of vertical lines. At the level, where maximum velocities occur at the bottom (20 cm from the bottom), the recorded TKE reaches local minimum values. Usually, TKE decreases at zones, where velocity increases. An exception is the area between elevations of spillway shelves for additional slots. Velocities and TKE increase there. However, the increase of velocity within vertical lines of the main flow is relatively small and one cannot discuss evening of the values. A much smaller impact of shelves on the analyzed distribution was noted in that case, there are no distinct peaks—both: in case of mean velocity, as well as TKE.
The impact of the spillway shelves is kept within the whirl zone. The vertical line of velocities is specified by an increase of average velocities starting from the bottom up to the level of 20 cm over the bottom, where the minimum TKE values occur. Over that spot the velocity is slightly reduced, and it is stabilized afterwards within the vertical line until reaching elevation of the lower spillway shelf. The mean velocity rises over that elevation. Impact of elevations of shelves at the inlet bolt and at the outlet bolt may be seen in section c. Over the elevation of the higher outlet (bottom) of the bolt’s slot, the velocity’s value drops from 0.45 to 0.1 m/s. Variability of velocities within vertical lines reflects in TKE values, because at the level between the shelves—where velocity increases—the TKE is reduced from 0.077 to 0.068 m2/s2. An additional peak of the normalized TKE occurs at the level of 0.9 m from the bottom, and local minimum for average velocity occurs there.
TKE values undergo significant reduction in section D, whereas they are slightly higher in the main flow’s zone, and they remain within a range of 0.03–0.05 m2/s2. The whirl zone provides values in a range of 0.005–0.02 m2/s2. Section d is specified by the repeatable local extreme TKE values, but they are present at the bottom only. The highest value of 0.3 m2/s2 occurs within a current flowing against the direction of the main flow in the fishway’s chamber. The remaining local bottom extreme values —with a maximum value of up to 0.2 m2/s2—occur in both the main flow’s zone as well as in the whirl area.
3.2. Model B
The case of the Model A is shown in Figure 5 (spatial distribution) and in Figure 6 and Figure 7 (analysis of selected vertical measurement profiles). The TKE profiles in Figure 6 and Figure 7 show the directional values of the TKE components. This is to demonstrate the importance of the directional TKE values in the mean TKE value discussed in this paper.
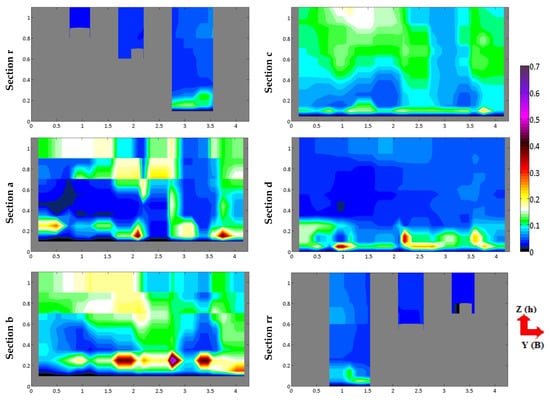
Figure 5.
Spatial distributions of TKE [m2/s2] for sections: r, a, b, c, d, rr; dimensions on the axes (m). MODEL B.
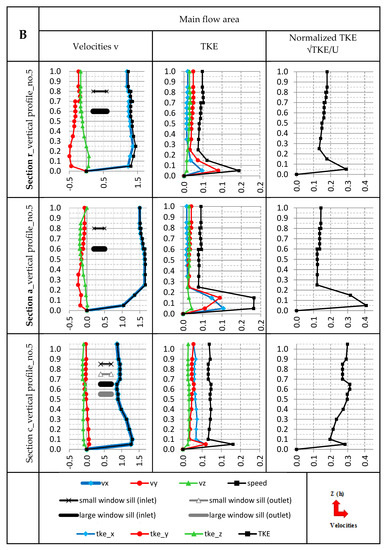
Figure 6.
Summary of exemplary vertical lines for directional velocities and speed (average water flow velocity) (m/s) and of corresponding TKE (m2/s2) and normalized TKE (—) within main flow area. MODEL B.
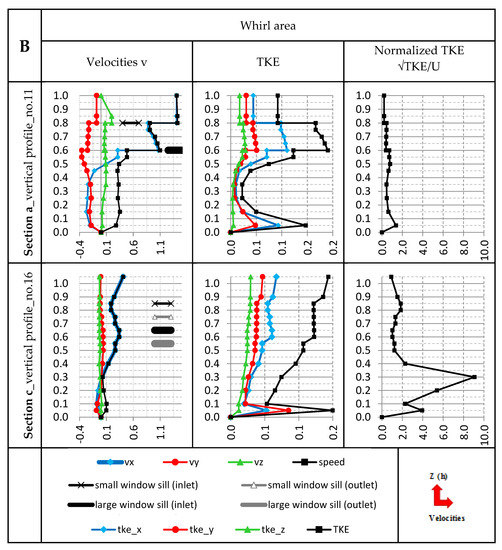
Figure 7.
Summary of exemplary vertical lines for directional velocities and speed (average water flow velocity) (m/s) and of corresponding TKE (m2/s2) and normalized TKE (—) within whirl area. MODEL B.
A spatial analysis of TKE values proved that the flow in model B has lower TKE values. One may distinguish areas of the main flow and whirl areas in case of almost all of the sections. Although local minimums occur in the whirl area, the flow within the main flow’s area provides lower values within vertical lines than the whirl zones.
The distribution of mean velocities and TKE within vertical lines in this section of the bolt is slightly different than in the case of model A. The velocity rises just at the bottom and reaches the maximum on the level of 25 cm. The highest TKE values in the section occur at the bottom and they amount to about 0.14 m2/s2. On the level where velocity reaches its maximum value, TKE (also the normalized TKE) reaches its minimum amounting to 0.035 m2/s2. Along with a minor reduction of mean velocity values, an increase of TKE values is recorded over that spot.
Vertical lines of those values, bolt’s section and section a do not provide such a high vulnerability to elevation of shelves, as in case of model A. In case of the main flow in section a, velocity grows from the bottom to elevation of 0.25 m, where it reaches the maximum of 1.7 m/s. The minimum value of TKE is recorded in the same location within the vertical line, and it is 0.04 m2/s2. Over that spot the velocity is reduced along with the increase of level, and TKE slightly rises.
Interestingly, within the vertical lines for velocities, the elevations of additional spillway shelves are not clearly distinguished, but they may be seen within the vertical lines for TKE—especially the shelf of the bigger slot. An additional peak of TKE values occurs at its elevation. Vertical lines located within the whirl area are much more vulnerable to the impact of spillway shelves. A reverse correlation between the increase of average velocities and TKE may be observed in that zone.
This is particularly noticeable below the parapet of the bigger spillway slot, where the velocity gets reduced and TKE raises. Positive peaks of mean velocity values and, importantly, positive peaks of TKE are recorded at both elevations of the spillway shelves’ parapets. The highest extreme values for TKE in section a are located at boundaries of whirl zones (on both sides of the flow’s main slot), at the bottom. They amount to up to 0.4 m2/s2. The raise of TKE values within boundary vertical lines between the main area and the whirl zones on both sides of the slot is also clear.
TKE grows in that place to the value of 0.15 m2/s2. Except for the listed ones, one may also set out relatively huge fields of high TKE values, which are located in vicinity of openings for smaller spillway slots. In those locations TKE reaches maximum values of 0.20 m2/s2. The whirl area below the elevation of spillway shelves is a place where minimum TKE values occur within the entire chamber. Their value is about 0.01 m2/s2. Those are areas where huge whirl structures occur.
Section b provides higher TKE values than in case of section a. One may observe here a greater impact of spillway shelves’ elevations, which has been recorded also for the distribution of TKE values in the area of main flow as a positive peak of TKE values. A positive peak of TKE was also recorded in the whirl area above the elevation of each and every additional spillway shelf. A significant difference is the fact that extreme values occurring at the bottom are this time present in some distance from the bottom (at a level of about 10 cm). In that case they are much higher than in section a, and they even reach values of up to 0.6 m2/s2. Extreme values occur in both the main flow’s area as well as in the whirl areas. Furthermore, in spots where the greatest whirls occur, the TKE value is higher than in section a, and it reaches the range of 0.02–0.08 m2/s2.
In section c velocities are not so even within vertical lines in terms of their value. The highest velocities occur within a space from the bottom to the elevation of the lowest parapet of the inlet bolt. Along with the drop of velocity values within vertical lines’ level, TKE proves a trend of a positive increase. The extreme value of velocity on a level of 10 cm from the bottom overlaps with the minimum TKE value for the vertical line, which is 0.07 m2/s2. Just underneath the elevation of the lowest spillway shelf’s parapet, there is an area of the lowest velocities within the main flow’s vertical lines, which overlaps with the area of maximum TKE reaching the value of 0.075 m2/s2. Above the elevation of the bottom parapet there is a positive peak of velocity values within the main section, and at the same time there is a negative peak of TKE values. Above the elevation of the highest parapet (of the smaller slot) a reverse dependence occurs, i.e., a peak of velocity is negative, and of TKE—positive.
The lack of even values for velocity and TKE was observed within the whirl area. A reverse correlation of dependence for velocity and normalized TKE was observed, what not always corresponds with the same dependence at comparing vertical lines for velocities and TKE (without normalization). Spatial analysis for section c proves a significant reduction of high TKE fields. The greatest field with TKE = 0.15 m2/s2 is present at the surface zone of the whirl area above elevation of spillway shelves’ parapets. Moreover, local extreme values occur just at the bottom in all flow areas. Their maximum value is 0.2 m2/s2. One may note diversity of occurrence levels for maximum TKE values within bottom areas in the following sections. It is most likely an effect of overlapping two factors—long drop of the bottom and spatial structure of turbulence. However, one shall note that vertical lines with the lowest TKE occur in the zone of the main flow. In the case of the whirl zone, a significant stratification of TKE values may be seen. Vertical lines within the whirl area—from the water-table to elevations of spillway shelves—have higher TKE—from 0.10 to 0.15 m2/s2, on average. However, below that location, area of very low TKE occurs—0.02–0.08 m2/s2. It is important to state that in case of section c there are no stable huge whirls. In the spot of the lowest TKE within the whirl area stable whirl structures placed underneath the bolt are fed by a back current. The top part of the whirl area remains a space, where the flow gets uniformed and the water flows out of the whirl area towards the migration slot.
Section d is an area of highly reduced average TKE value—0.01–0.05 m2/s2; however, there is no distinct diversification of whirl areas and areas of the main flow in terms of the obtained values. Area of higher TKE occurs at the bottom. Local maximum values even reach the rate of up to 0.35–0.4 m2/s2. It seems important that extreme values occur in both: the main flow’s zone, as well as in whirl zones. There is no uniformed trend for TKE distribution, which may be assigned to the areas of particular way of the water stream’s flow. Therefore, there neither are stable whirl structures nor feeding areas for those structures within that section.
A section of the outlet bolt rr provides values and features for dependence between velocity and TKE as in case of the inlet bolt. A difference is related to the filling for the section only.
4. Discussion
A hydraulic analysis proved the compliance for the dependence between the velocity and the normalized TKE value, as obtained by Nepf and Vivoni [13], for the bigger part of spots within the measurement vertical lines for both of the models. It was however stated that areas where a dependence of negative correlation between the increase of average velocity and normalized TKE are present. It was established that those areas are located in spots, where positive or negative peaks of average velocities occur (a negative peak is a rapid negative leap of velocity). For example, in the case of the presented vertical line for section c of model A (Figure 4), within the whirl area—at an elevation of 20 cm above the bottom—there is a negative peak of average velocity. A diagram shows that somehow “a dent in the diagram” occurs in that spot. The area of such a deviation for the increase of velocity is an area where a negative correlation between the average velocities and normalized TKE is not met. Therefore, the rises and drops of normalized TKE values are directly proportional, and have the same direction of value change as the average velocity. An analysis of directional features proved that the change most often occurs in a dominating direction of the flow, usually a longitudinal one or a cross one, depending on the location of the measurement vertical line. An important feature for the analyzed vertical lines is also their shape, i.e., vertical lines for velocities and TKE are smoothened for researches containing flexible development. It means that changes to the value of parameters run while keeping a fixed proportion of values between the consecutive measurement spots. In the case of the research on bolt fishways one may see that the vertical lines for values of parameters are quite angular (lacerated) in shape, what means that changes to the value are relatively rapid. The occurrence of spillway shelves additionally implements an element of value leap at shelves’ elevations. The occurrence of peaks for velocities and TKE additionally strengthens the visual effect of breaking a value curve for particular parameters down.
It shall be stated that a TKE analysis using TKE normalization only is an incorrect method for assessment of turbulent flow’s features. Normalization presents the dependence between the velocity and the TKE without provision of information stating which qualitative change appeared in the flow, i.e., if the increase of normalized TKE results from the peak of TKE or from the drop of average velocities in the given spot. For example, in section of the bolt (r) in model A (Figure 3) the normalized TKE provides a huge peak in the bottom zone. This might suggest the occurrence of unfavorable conditions for fish migration in that area. However, such a high peak results from the fact that in that spot the average flow value is getting close to zero and amounts to 0.022 m/s. Nonetheless, TKE is also very low and amounts to 0.002 m2/s2. A proportion between those values shall provide a huge value. However, it is a favorable zone fish migration because of low velocities value, which is a critical element to limited nature of migration.
Just as in case of model A, an analysis of measurement vertical lines in model B proves observations done by Schnauder et al. [14] and Baki et al. [15]. Within a chamber of model A and of model B extreme TKE values are located at the bottom mainly, and they reach high values especially in feeding areas for whirl zones (Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7). This feeding is provided by longitudinal and secondary currents. Their occurrence often provides extreme values for bottom stress. Extreme values and fields of TKE are visible in interaction areas for flow fields having a different hydraulic specificity in case of both of the models. Maximum TKE in whirl areas—shown in the top part of vertical lines in both of the models—is associated with the occurrence of interaction between longitudinal currents and back currents within whirl structures (Figure 4 Section c; Figure 7 Section a). They remain a result of the impact of additional spillway shelves on the structure.
Similar to the Baki et al. [15] study, a reduction in the value of TKE is visible behind the bolt elements. The level (height) of TKE reduction is strictly connected with the height of the bolt element (with the height of parapet of the additional spillway slot). The higher the surface of water in relation to the bolt crest (apex), the stronger the reduction (Figure 7, section a). The reduction of TKE is much more noticeable in the whirl area. In the area of main flow, this trend has also been noted. The reduction of TKE depend on distance the cross-section from the baffle, the nearer the cross-section is located, the stronger the reduction of TKE (section “a” in Figure 3 and Figure 7).
The appearance of additional spillway slots significantly interferes with the TKE distribution. But the process is different for both models. In model A, where the flow path is more heavily meandering, in the main flow area, the described reduction is limited. Under the level of the elevation of the bottom parapet of the bigger spillway slot there is a significant increase in the value of TKEs and a positive jump in the value TKE above their level. In the whirl area, the reduction TKE is maintained to the level of the bottom parapet of the bigger spillway slot, and above the height of the bottom parapet of the bigger spillway slot there is a significant positive jump of the TKE value. In model B, where the migration slots are located more linearly, the reduction of the TKE value is maintained to the level of bottom parapet of the bigger spillway slot, above bottom which there is a positive jump of the TKE value. In the whirl area (Figure 7-section a), the TKE reduction is inhibited. Under the level of bottom parapet of the bigger spillway slot there is a rapid increase in TKE and a large positive increase above the parapet of the bigger spillway slot, which resembles the mechanism of TKE distribution observed in the area of the main flow in model A. The occurrence of spillway shelves affects the flow structure in such a strong way that, in the case of both models of the bolt fishway, observations done by Sukhodolov et al. [16] are not confirmed.
In the case of this research an analogy was found in the case of a study of flows including various levels of plant bowl in the channel [18]. An analysis of the spatial distribution of TKE proved that just underneath huge additional spillway slots (section a in both of the models) higher TKE values were recorded at the bottom than in the case of an analogous area just behind the small spillway slots (Section a in Figure 2 and Figure 5). This means that the lower the parapet of the slot’s spillway shelf is, the higher TKE would be expected in the bottom area just downstream of the section. This rule is provided only within section a of both models. In the case of further sections (b–d) the rule is not observed due to a very complicated spatial structure of the flow, and to related mutual interactions between flow structures affecting the obtained TKE value. The distribution of TKE occurring in the top part of the flow is also not confirmed in further tests.
Fields of TKE seen in bolt fishways reach significantly high values at smaller slots (Section a in Figure 2 and Figure 5). It is a result of the smaller size of the stream flowing out from the smaller slot; thus, it is weaker and broken down faster. This rule may be seen in the case of both of the models.
5. Conclusions
A hydraulic analysis done for both of the models proved major energy diversification for accommodation of the stream in fishways’ chambers. The highest TKE values in huge areas were noted in model A, where the main flow’s stream runs along strongly meandering route. More linear arrangement of main migration slots caused reduction of values and decrease of the reach of higher TKE occurrence areas in the chamber. The paper succeeded in finding a dependence between the increase of mean velocities and TKE, what may significantly affect shaping of hydraulics for fishways just on the stage of designing.
A reason for the deviation between the results of other research in the case of mean velocities and TKE is considered as stiffness (or flexibility) of the fishway’s channel development. It is a feature of development strongly affecting the turbulence structure, which is subsequently reflected in values of particular parameters and their spatial distribution within the analyzed flow. It was also established that the bolt’s geometry and location of measurement vertical lines referring to the bolt’s section have the strongest impact on changes to the value of velocity and TKE.
In the case of chambers in model A and in model B, the maximum TKE values are mainly located at the bottom, and significantly high values are reached in areas of feeding the whirl zones with water (by longitudinal currents and secondary currents). Their occurrence often provides extreme values of bottom stress. The highest TKE values may be observed in areas of interaction between flow structures in case of both of the models. The maximum TKE—observed in top parts of vertical lines in both of the models—in the whirl area is associated with the occurrence of back currents within whirl structures. They remain a result of additional spillway shelves’ impact on the structure. The lower the parapet of the slot’s spillway shelf is, the higher TKE would be expected in the bottom area just below the section.
Stiff development (deflectors) in channels is observable in the form of bolts influencing the appearance of TKE reduction areas, clearly visible just behind the bolts. Its magnitude and the position at the height of the profiles is determined by the height of the bolt and its proportion to the surface of water level.
To summarise, the low bolt elements are to be expected: higher TKE values in the bottom zone and proportionally stronger TKE reductions at the height of these rafters than in the zones behind the high bolts. These establishments may be crucial for the designing process of fishways of various construction types, as well as for other open channels provided with fixed or flexible (biological) development.
This paper—in reference to the article on the impact of spatial structure on the flow [21]—proves that the analysis of flow in a bolt fishway, performed for a horizontal, flat section of flow characteristics only, is insufficient. Lots of information on the shaping of TKE distribution mechanisms are visible, just at observing a 3D flow structure. One shall therefore also consider the distribution of flow features for vertical cross-sections for the direction of the main stream’s flow. This is a consequence of the fact that the flow in bolt fishways is three-dimensional. This is a result of not only the geometry of the migration slot and of the bolt partition, but also the stiffness of development inside the fishway’s channel, as proven in the paper. Therefore, the provision of an analysis of hydraulics without any flow directions provides incomplete, often false results.
Author Contributions
Conceptualization: M.P.; Data curation: M.P.; Formal analysis: M.P.; Funding acquisition: T.H.; Investigation: M.P.; Methodology: M.P.; Software: M.P.; Supervision: T.H.; Visualization: M.P.; Writing—original draft, M.P.; Writing—review & editing, T.H.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Castro-Santos, T.; Cotel, A.J.; Webb, P.W. Fishway evaluations for better bioengineering–an integrative approach. Am. Fish. Soc. Symp. 2009, 69, 557–575. [Google Scholar]
- Puzdrowska, M. Application of numerical methods in the design and analysis of fish pass efficiency. Tech. Trans. Environ. Eng. 2013, 110, 99–109. [Google Scholar]
- Liao, J.C.; Beal, D.N.; Lauder, G.V.; Triantafyllou, M.S. Fish exploiting vortices decrease muscle activity. Science 2003, 302, 1566–1569. [Google Scholar] [CrossRef] [PubMed]
- Enders, E.C.; Boisclair, D.; Roy, A.G. The Effect of Turbulence on the Cost of Swimming for Juvenile Atlantic Salmon. Can. J. Fish. Aquat. Sci. 2003, 60, 1149–1160. [Google Scholar] [CrossRef]
- Tritico, H.M.; Cotel, A.J. The effects of turbulent eddies on the stability and critical swimming speed of creek chub (Semotilus atromaculatus). J. Exp. Biol. 2010, 213, 2284–2293. [Google Scholar] [CrossRef] [PubMed]
- Lacey, R.W.J.; Neary, V.S.; Liao, J.C.; Enders, E.C.; Tritico, H.M. The IPOS framework: Linking fish swimming performance in altered flows from laboratory experiments to rivers. River Res. Appl. 2011, 28, 429–443. [Google Scholar] [CrossRef]
- Costa, M.J.; Fuentes-Perez, J.F.; Boavida, I.; Tuhtan, J.A.; Pinheiro, A.N. Fish under pressure: Examining behavioural responses of Iberian barbel under simulated hydropeaking with instream structures. PLoS ONE 2019, 14, e0211115. [Google Scholar] [CrossRef] [PubMed]
- Enders, E.C.; Buffin-Bélanger, T.; Boisclair, D.; Roy, A.G. The feeding behaviour of juvenile Atlantic salmon in relation to turbulent flow. J. Fish Biol. 2005, 66, 242–253. [Google Scholar] [CrossRef]
- Odeh, M.; Noreika, J.F.; Haro, A.; Maynard, A.; Castro-Santos, T. Evaluation of the Effects of Turbulence on the Behavior of Migratory Fish; Oak Ridge National Laboratory (ORNL): Oak Ridge, TN, USA; US Geological Survey (USGS): Portland, OR, USA, 2002; pp. 1–55.
- Nepf, H.M.; Sullivan, J.A.; Zavistoski, R.A. A model for diffusion within an emergentp lant canopy. Limnol. Oceanogr. 1997, 42, 1735–1745. [Google Scholar] [CrossRef]
- Nepf, H.M. Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour. Res. 1999, 35, 479–489. [Google Scholar] [CrossRef]
- Grinvald, D.I.; Nikora, V.I. The Turbulence of Rivers (in Russian); Hydrometeoizdat: Leningrad, Russia, 1988. [Google Scholar]
- Nepf, H.M.; Vivoni, E.R. Flow structure in depth-limited, vegetated flow. J. Geophys. Res. 2000, 105, 28547–28557. [Google Scholar] [CrossRef]
- Schnauder, I. Strömungsstruktur und Impulsaustausch in Gegliederten Gerinnen mit Vorlandvegetation; Mitteilungen des Instituts für Wasserwirtschaft und Kulturtechnik der Universität Karlsruhe (TH) mit ″Theodor-Rehbock-Wasserbaulaboratorium″; Inst. für Wasserwirtschaft und Kulturtechnik, Bibliothek: Karlsruhe, Deutschland, 2004; Volume 224. [Google Scholar]
- Baki, A.B.M.; Zhu, D.Z.; Rajaratnam, N. Turbulence Characteristics in a Rock-Ramp-Type Fish Pass. J. Hydraul. Eng. 2015, 141, 2. [Google Scholar] [CrossRef]
- Sukhodolov, A.; Engelhardt, C.; Krüger, A.; Bungartz, H. Case study: Turbulent flow and sediment distributions in a groyne field. J. Hydraul. Eng. 2004, 130, 1–9. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H. Turbulence in Open-Channel Flows; IAHR Monograph: Balkema, Rotterdam, 1993. [Google Scholar]
- Zhang, Y.; Tang, C.; Nepf, H. Turbulent kinetic energy in submerged model canopies under oscillatory flow. Water Resour. Res. 2018, 54, 1734–1750. [Google Scholar] [CrossRef]
- Luhar, M.; Coutu, S.; Infantes, E.; Fox, S.; Nepf, H. Wave-induced velocities inside a model seagrass bed. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Abdolahpour, M.; Hambleton, M.; Ghisalberti, M. The wave-driven current in coastal canopies. J. Geophys. Res. Oceans 2017, 122, 3660–3674. [Google Scholar] [CrossRef]
- Puzdrowska, M.; Heese, T. Detailed Research on the Turbulent Kinetic Energy’s Distribution in Fishways in Reference to the Bolt Fishway. Fluids 2019, 4, 64. [Google Scholar] [CrossRef]
- Velasco, D.; Bateman, A.; Redondo, J.M.; Demedina, V. An open channel flow experimental and theoretical study of resistance and turbulent characterization over flexible vegetated linings Flow. Turbul. Combust. 2003, 70, 69–88. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).