Multi-Type Structural Damage Image Segmentation via Dual-Stage Optimization-Based Few-Shot Learning
Highlights
- A dual-stage optimization framework with internal segmentation model and ex-ternal meta-learning machine is proposed for structural damage recognition using only a few images.
- The effectiveness and necessity are validated by comparative experiments with directly training semantic segmentation models, and the generalization ability for unseen damage category is also verified.
- The results indicate that the underlying image features of multi-type structural damage can be accurately learned by the proposed method via small data as prior knowledge to enhance the transferability and adaptability.
- It provides a promising solution to accomplish image-based damage recognition with high accuracy and robustness for the intelligent inspection of civil infra-structure in smart cities.
Abstract
1. Introduction
2. Methodology
2.1. Problem Definition
2.2. Dual-Stage Optimization-Based Few-Shot Learning (DOFSL)
- (1)
- Multiple meta-tasks are generated by randomly sampling with replacement from the training set and disordered to form meta-batches for the latter model optimization;
- (2)
- Each task inside a meta-batch is individually fed into the internal semantic segmentation network, in which the support set is utilized to update model parameters in the internal optimization stage, and the query set is adopted to compute the prediction loss by the updated model;
- (3)
- The external optimization stage for the meta-learning machine is performed based on all the query losses inside a meta-batch, which is concretized as updating the initial network parameters. Following this manner, the internal semantic segmentation model learns universal prior knowledge among various damage categories from the training meta-tasks and transfers it to the test tasks.
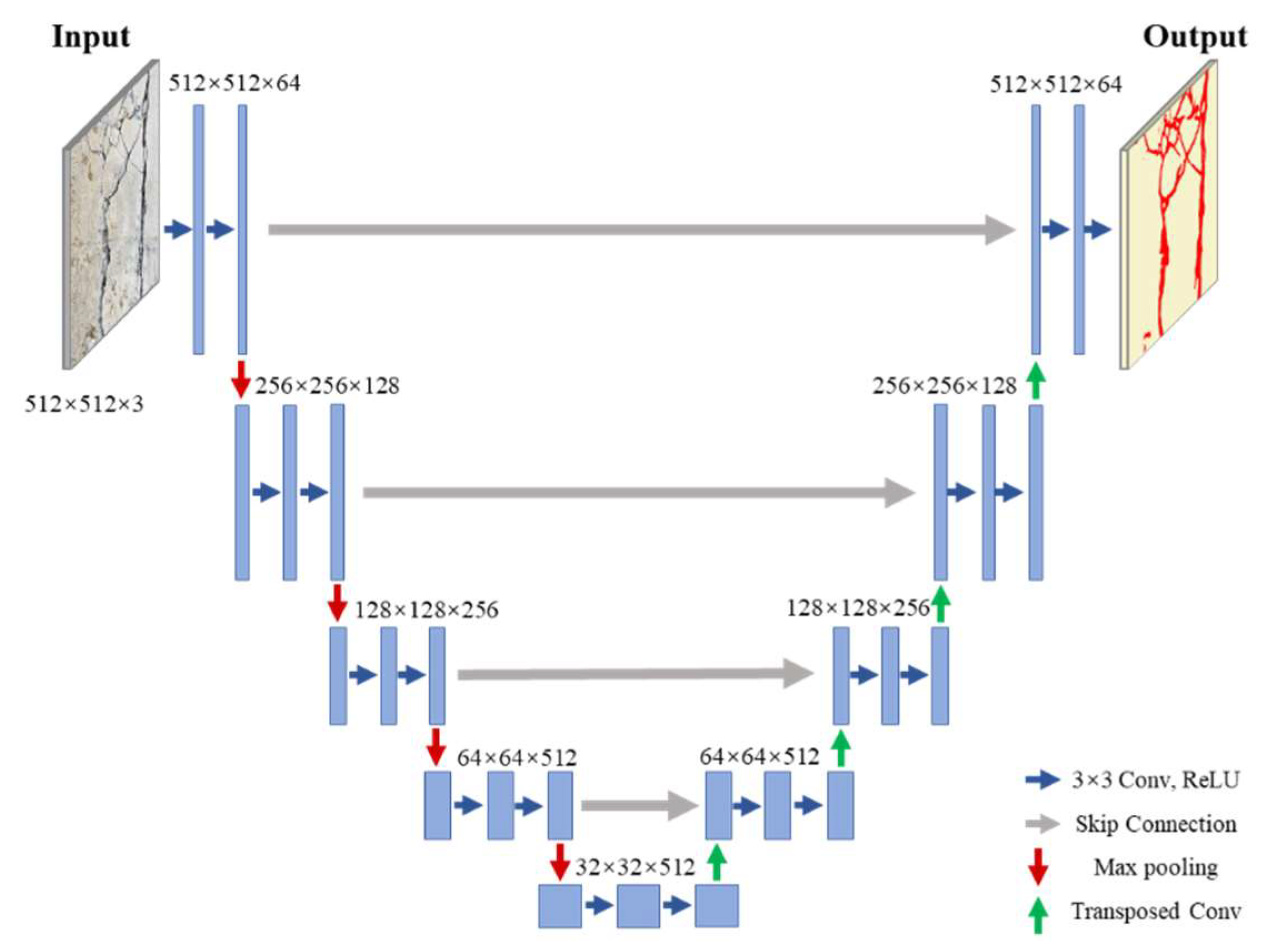
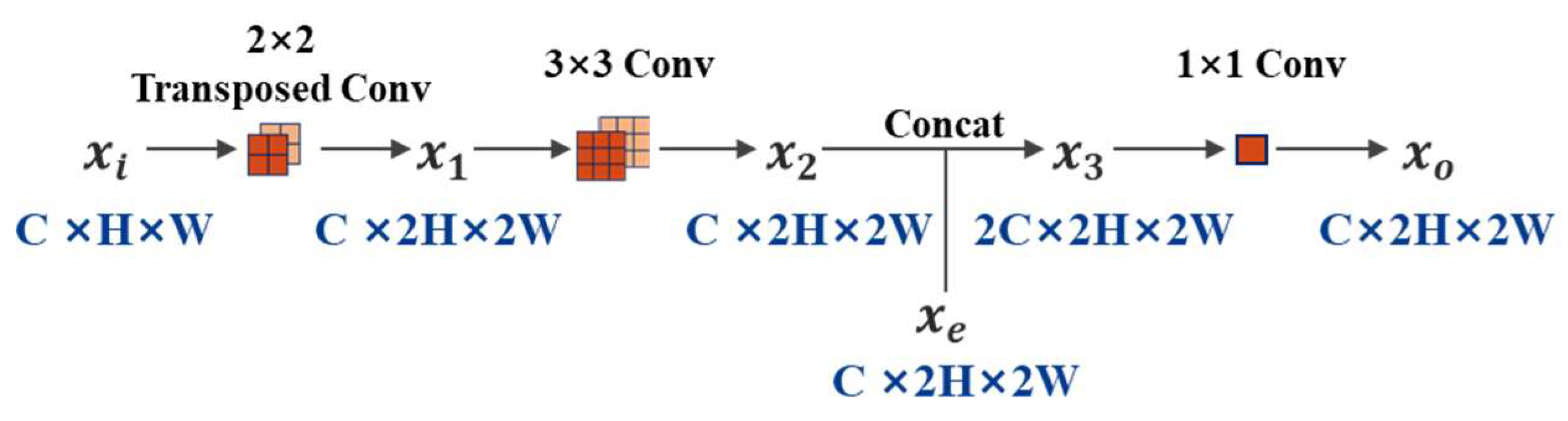
2.3. Internal Model Structure for Semantic Segmentation of Multi-Type Structural Damage
3. Implementation Details
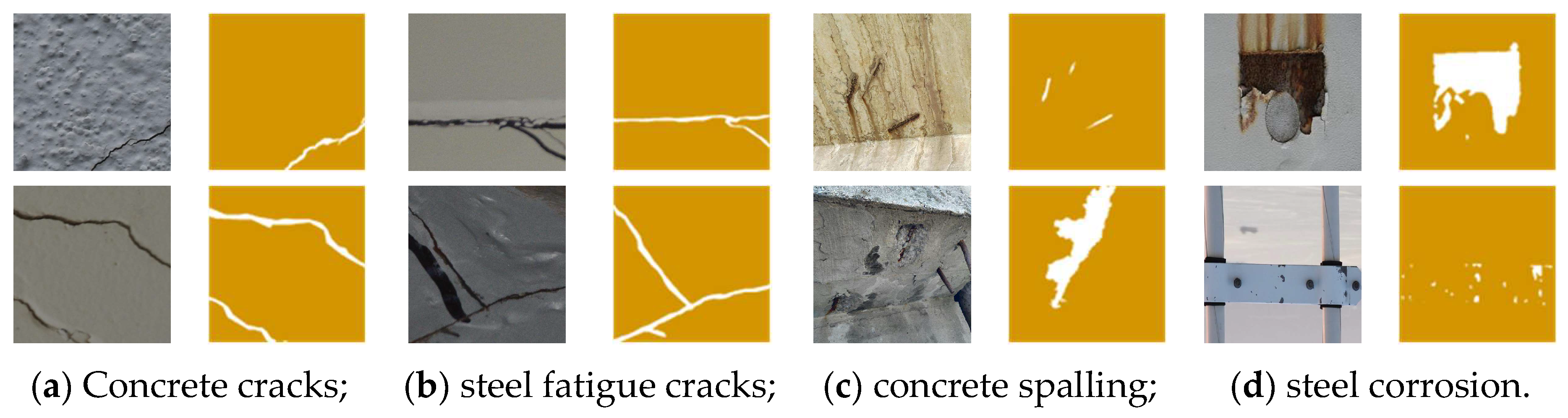
3.1. Multi-Type Structural Damage Image Dataset
3.2. Training Hyperparameter Configurations
3.3. Specifications of Training Loss Function and Test Evaluation Metrics
4. Results and Discussion
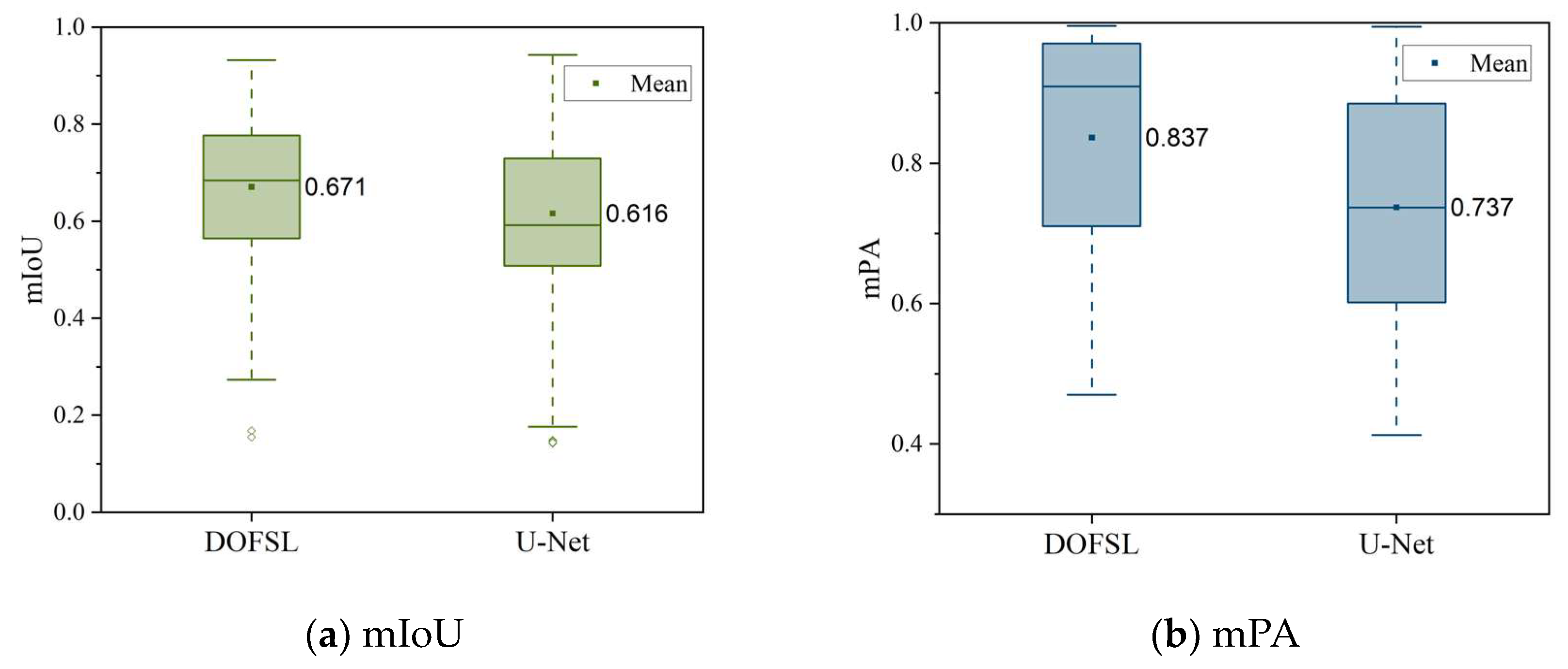
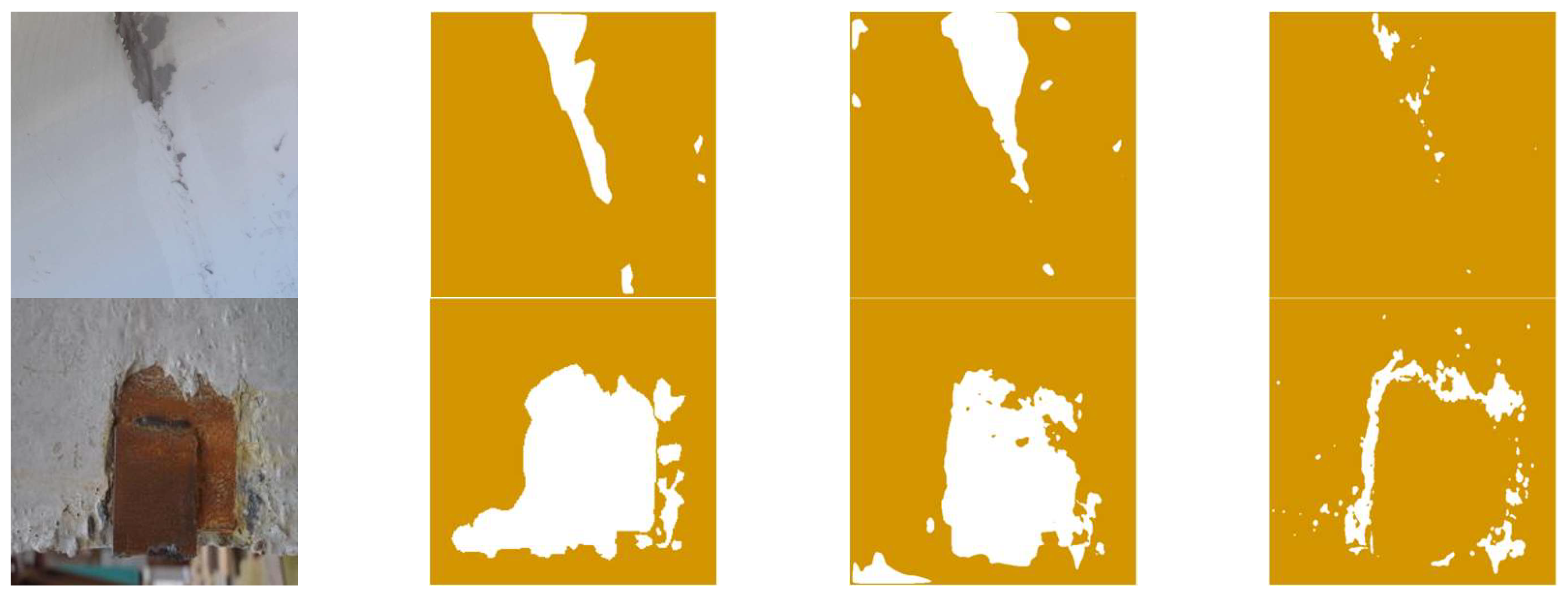
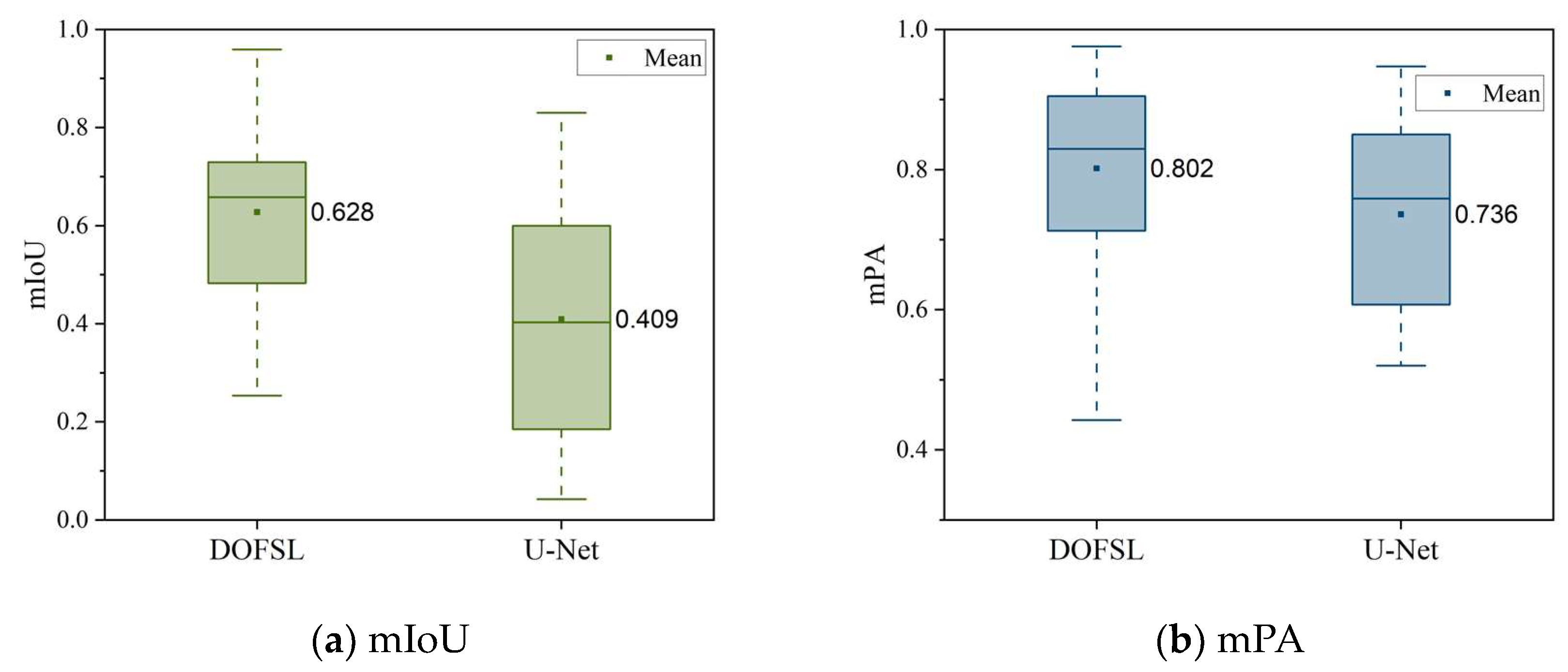
4.1. Test Results for Multi-Type Structural Damage Segmentation
4.2. Validation of Generalization Ability for Unseen Structural Damage Category
4.3. Ablation Studies for Individual-Type Damage Segmentation
5. Conclusions
- (1)
- The dual-stage optimization-based few-shot learning framework is established containing the internal network optimization stage based on meta-task and the external meta-learning-machine optimization based on meta-batch. The mathematical formulation of few-shot learning-based multi-type structural damage segmentation is formed exclusively relying on limited supervised images.
- (2)
- Comparative experiments are conducted to verify the effectiveness and necessity of the proposed dual-stage optimization-based few-shot learning method using the multi-type structural damage image set including concrete cracks, steel fatigue cracks, concrete spalling, and steel corrosion. The results indicate that compared with the original image segmentation model, the proposed DOFSL achieves an average increase in mIoU and mPA of 5.5% and 10.0%, respectively.
- (3)
- Furthermore, ablation studies for individual damage types and new damage categories are implemented to validate the model stability, generalization capacity, and universal applicability of the proposed DOFSL method for semantic segmentation of arbitrary structural damage categories. The quantitative analysis results achieve a significant improvement in average mIoU and mPA of 21.9% and 6.6% for unseen damage in the training dataset.
6. Future Directions
- (1)
- Incorporating geometric constraints, such as curvature shapes and boundary condition features, can promote the robustness and accuracy of image segmentation [49,50]. These constraints can provide supplementary contextual information, facilitating model training to understand input images, predict structural damage, and avoid reliance on extensive labeled data.
- (2)
- Network integration and modular design can be adopted to simplify network structures and reduce network complexity and training difficulty. Separate modules are designed and individually optimized for specific damage types, and they are subsequently integrated to the initial shared network to process and analyze multi-type structural damage using ensemble deep convolutional neural network models [51].
- (3)
- Leveraging transfer learning and domain adaptation techniques can significantly improve the model performance for multi-type damage recognition, particularly when training samples are limited. The transferable knowledge is adaptively involved and optimized in specific fields, which enhances the generalization ability under different application scenes and damage scenarios [52].
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ali, A.; Sandhu, T.Y.; Usman, M. Ambient vibration testing of a pedestrian bridge using low-cost accelerometers for SHM applications. Smart Cities 2019, 2, 20–30. [Google Scholar] [CrossRef]
- Liu, Y.; Cho, S.; Spencer, B.F., Jr.; Fan, J. Automated assessment of cracks on concrete surfaces using adaptive digital image processing. Smart Struct. Syst. 2014, 14, 719–741. [Google Scholar] [CrossRef]
- Zakeri, H.; Nejad, F.M.; Fahimifar, A. Image based techniques for crack detection, classification and quantification in asphalt pavement: A review. Arch. Comput. Methods Eng. 2017, 24, 935–977. [Google Scholar] [CrossRef]
- Adhikari, R.S.; Moselhi, O.; Bagchi, A. Image-based retrieval of concrete crack properties for bridge inspection. Autom. Constr. 2014, 39, 180–194. [Google Scholar] [CrossRef]
- Luo, Q.; Ge, B.; Tian, Q. A fast adaptive crack detection algorithm based on a double-edge extraction operator of FSM. Constr. Build. Mater. 2019, 204, 244–254. [Google Scholar] [CrossRef]
- German, S.; Brilakis, I.; DesRoches, R. Rapid entropy-based detection and properties measurement of concrete spalling with machine vision for post-earthquake safety assessments. Adv. Eng. Inform. 2012, 26, 846–858. [Google Scholar] [CrossRef]
- Paal, S.G.; Jeon, J.S.; Brilakis, I.; DesRoches, R. Automated damage index estimation of reinforced concrete columns for post-earthquake evaluations. J. Struct. Eng. 2015, 141, 04014228. [Google Scholar] [CrossRef]
- Figueiredo, E.; Park, G.; Farrar, C.R.; Worden, K.; Figueiras, J. Machine learning algorithms for damage detection under operational and environmental variability. Struct. Health Monit. 2011, 10, 559–572. [Google Scholar] [CrossRef]
- Hsieh, Y.A.; Tsai, Y.J. Machine learning for crack detection: Review and model performance comparison. J. Comput. Civ. Eng. 2020, 34, 04020038. [Google Scholar] [CrossRef]
- Morgenthal, G.; Hallermann, N.; Kersten, J.; Taraben, J.; Debus, P.; Helmrich, M.; Rodehorst, V. Framework for automated UAS-based structural condition assessment of bridges. Autom. Constr. 2019, 97, 77–95. [Google Scholar] [CrossRef]
- Rafiei, M.H.; Adeli, H. A novel unsupervised deep learning model for global and local health condition assessment of structures. Eng. Struct. 2018, 156, 598–607. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, J.; Yuan, J. mCENTRIST: A multi-channel feature generation mechanism for scene categorization. IEEE Trans. Image Process. 2013, 23, 823–836. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, B.; Su, H.; Li, W.; Wang, L. Land-use scene classification using multi-scale completed local binary patterns. Signal Image Video Process. 2016, 10, 745–752. [Google Scholar] [CrossRef]
- Spencer, B.F., Jr.; Hoskere, V.; Narazaki, Y. Advances in computer vision-based civil infrastructure inspection and monitoring. Engineering 2019, 5, 199–222. [Google Scholar] [CrossRef]
- Cha, Y.J.; Choi, W.; Suh, G.; Mahmoudkhani, S.; Büyüköztürk, O. Autonomous structural visual inspection using region-based deep learning for detecting multiple damage types. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 731–747. [Google Scholar] [CrossRef]
- Kantsepolsky, B.; Aviv, I. Sensors in Civil Engineering: From Existing Gaps to Quantum Opportunities. Smart Cities 2024, 7, 277–301. [Google Scholar] [CrossRef]
- Dong, C.Z.; Catbas, F.N. A review of computer vision-based structural health monitoring at local and global levels. Struct. Health Monit. 2021, 20, 692–743. [Google Scholar] [CrossRef]
- Shirzad-Ghaleroudkhani, N.; Gül, M. An enhanced inverse filtering methodology for drive-by frequency identification of bridges using smartphones in real-life conditions. Smart Cities 2021, 4, 499–513. [Google Scholar] [CrossRef]
- Sun, L.; Shang, Z.; Xia, Y.; Bhowmick, S.; Nagarajaiah, S. Review of bridge structural health monitoring aided by big data and artificial intelligence: From condition assessment to damage detection. J. Struct. Eng. 2020, 146, 04020073. [Google Scholar] [CrossRef]
- Bao, Y.; Li, H. Machine learning paradigm for structural health monitoring. Struct. Health Monit. 2021, 20, 1353–1372. [Google Scholar] [CrossRef]
- Modarres, C.; Astorga, N.; Droguett, E.L.; Meruane, V. Convolutional neural networks for automated damage recognition and damage type identification. Struct. Control. Health Monit. 2018, 25, e2230. [Google Scholar] [CrossRef]
- Gao, Y.; Mosalam, K.M. Deep transfer learning for image-based structural damage recognition. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 748–768. [Google Scholar] [CrossRef]
- Gulgec, N.S.; Takáč, M.; Pakzad, S.N. Convolutional neural network approach for robust structural damage detection and localization. J. Comput. Civ. Eng. 2019, 33, 04019005. [Google Scholar] [CrossRef]
- Zhang, C.; Chang, C.C.; Jamshidi, M. Concrete bridge surface damage detection using a single-stage detector. Comput.-Aided Civ. Infrastruct. Eng. 2020, 35, 389–409. [Google Scholar] [CrossRef]
- Zhou, Q.; Ding, S.; Qing, G.; Hu, J. UAV vision detection method for crane surface cracks based on Faster R-CNN and image segmentation. J. Civ. Struct. Health Monit. 2022, 12, 845–855. [Google Scholar] [CrossRef]
- Shokri, P.; Shahbazi, M.; Nielsen, J. Semantic Segmentation and 3D Reconstruction of Concrete Cracks. Remote Sens. 2022, 14, 5793. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, K.C.; Fei, Y.; Liu, Y.; Chen, C.; Yang, G.; Li, J.; Yang, E.; Qiu, S. Automated pixel-level pavement crack detection on 3D asphalt surfaces with a recurrent neural network. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 213–229. [Google Scholar] [CrossRef]
- Zhao, J.; Hu, F.; Qiao, W.; Zhai, W.; Xu, Y.; Bao, Y.; Li, H. A modified U-Net for crack segmentation by Self-Attention-Self-Adaption neuron and random elastic deformation. Smart Struct. Syst. 2022, 29, 1–16. [Google Scholar]
- Xu, Y.; Fan, Y.; Li, H. Lightweight semantic segmentation of complex structural damage recognition for actual bridges. Struct. Health Monit. 2023, 22, 3250–3269. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L. Dual attention deep learning network for automatic steel surface defect segmentation. Comput.-Aided Civ. Infrastruct. Eng. 2021, 37, 1468–1487. [Google Scholar] [CrossRef]
- Cui, X.; Wang, Q.; Li, S.; Dai, J.; Xie, C.; Duan, Y.; Wang, J. Deep learning for intelligent identification of concrete wind-erosion damage. Autom. Constr. 2022, 141, 104427. [Google Scholar] [CrossRef]
- Xu, J.; Gui, C.; Han, Q. Recognition of rust grade and rust ratio of steel structures based on ensembled convolutional neural network. Comput.-Aided Civ. Infrastruct. Eng. 2020, 35, 1160–1174. [Google Scholar] [CrossRef]
- Li, D.; Xie, Q.; Gong, X.; Yu, Z.; Xu, J.; Sun, Y.; Wang, J. Automatic defect detection of metro tunnel surfaces using a vision-based inspection system. Adv. Eng. Inform. 2021, 47, 101206. [Google Scholar] [CrossRef]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. Adv. Neural Inf. Process. Syst. 2017, 4080–4090. [Google Scholar]
- Fort, S. Gaussian prototypical networks for few-shot learning on omniglot. arXiv 2017, arXiv:1708.02735. [Google Scholar]
- Ji, Z.; Chai, X.; Yu, Y.; Pang, Y.; Zhang, Z. Improved prototypical networks for few-shot learning. Pattern Recognit. Lett. 2020, 140, 81–87. [Google Scholar] [CrossRef]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Nichol, A.; Schulman, J. Reptile: A scalable meta learning algorithm. arXiv 2018, arXiv:1803.02999. [Google Scholar]
- Sun, Q.; Liu, Y.; Chua, T.S.; Schiele, B. Meta-transfer learning for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 403–412. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Mehrotra, A.; Dukkipati, A. Generative adversarial residual pair-wise networks for one shot learning. arXiv 2017, arXiv:1703.08033. [Google Scholar]
- Rezende, D.; Danihelka, I.; Gregor, K.; Wierstra, D. One-shot generalization in deep generative models. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 1521–1529. [Google Scholar]
- Guo, J.; Wang, Q.; Li, Y.; Liu, P. Façade defects classification from imbalanced dataset using meta learning-based convolutional neural network. Comput.-Aided Civ. Infrastruct. Eng. 2020, 35, 1403–1418. [Google Scholar] [CrossRef]
- Dong, H.; Song, K.; Wang, Q.; Yan, Y.; Jiang, P. Deep metric learning-based for multi-target few-shot pavement distress Classification. IEEE Trans. Ind. Inform. 2021, 18, 1801–1810. [Google Scholar] [CrossRef]
- Xu, Y.; Bao, Y.; Zhang, Y.; Li, H. Attribute-based structural damage identification by few-shot meta learning with inter-class knowledge transfer. Struct. Health Monit. 2021, 20, 1494–1517. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, Q.; Guo, J.; Lu, N. Few-shot classification of façade defects based on extensible classifier and contrastive learning. Autom. Constr. 2022, 141, 104381. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Part III 18. pp. 234–241. [Google Scholar]
- Sudre, C.H.; Li, W.; Vercauteren, T.; Ourselin, S.; Jorge Cardoso, M. Generalised dice overlap as a deep learning loss function for highly unbalanced segmentations. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support: Third International Workshop, DLMIA 2017, and 7th International Workshop, Held in Conjunction with MICCAI, Québec City, QC, Canada, 14 September 2017; Proceedings 3. pp. 240–248. [Google Scholar]
- Wang, Y.; Jing, X.; Xu, Y.; Cui, L.; Zhang, Q.; Li, H. Geometry-guided semantic segmentation for post-earthquake buildings using optical remote sensing images. Earthq. Eng. Struct. Dyn. 2023, 52, 3392–3413. [Google Scholar] [CrossRef]
- Wang, Y.; Jing, X.; Cui, L.; Zhang, C.; Xu, Y.; Yuan, J.; Zhang, Q. Geometric consistency enhanced deep convolutional encoder-decoder for urban seismic damage assessment by UAV images. Eng. Struct. 2023, 286, 116132. [Google Scholar] [CrossRef]
- Barkhordari, M.S.; Armaghani, D.J.; Asteris, P.G. Structural damage identification using ensemble deep convolutional neural network models. Comput. Model. Eng. Sci. 2023, 134, 835–855. [Google Scholar] [CrossRef]
- Xu, Y.; Fan, Y.; Bao, Y.; Li, H. Few-shot learning for structural health diagnosis of civil infrastructure. Adv. Eng. Inform. 2024, 62, 102650. [Google Scholar] [CrossRef]






| Damage Category | Model | Average mIoU | Average mPA | |
|---|---|---|---|---|
| Concrete cracks | Original U-Net | 100 | 72.7% | 83.7% |
| Original U-Net | 200 | 77.1% | 84.2% | |
| Proposed DOFSL | 100 | 81.4% | 91.5% | |
| Proposed DOFSL | 200 | 81.5% | 89.7% | |
| Steel fatigue cracks | Original U-Net | 100 | 68.2% | 73.5% |
| Original U-Net | 200 | 68.5% | 81.3% | |
| Proposed DOFSL | 100 | 75.5% | 81.1% | |
| Proposed DOFSL | 200 | 73.4% | 80.9% | |
| Concrete spalling | Original U-Net | 100 | 58.0% | 68.2% |
| Original U-Net | 200 | 59.9% | 76.3% | |
| Proposed DOFSL | 100 | 62.3% | 74.8% | |
| Proposed DOFSL | 200 | 64.8% | 78.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, J.; Fan, Y.; Zhao, X.; Zhou, Q.; Xu, Y. Multi-Type Structural Damage Image Segmentation via Dual-Stage Optimization-Based Few-Shot Learning. Smart Cities 2024, 7, 1888-1906. https://doi.org/10.3390/smartcities7040074
Zhong J, Fan Y, Zhao X, Zhou Q, Xu Y. Multi-Type Structural Damage Image Segmentation via Dual-Stage Optimization-Based Few-Shot Learning. Smart Cities. 2024; 7(4):1888-1906. https://doi.org/10.3390/smartcities7040074
Chicago/Turabian StyleZhong, Jiwei, Yunlei Fan, Xungang Zhao, Qiang Zhou, and Yang Xu. 2024. "Multi-Type Structural Damage Image Segmentation via Dual-Stage Optimization-Based Few-Shot Learning" Smart Cities 7, no. 4: 1888-1906. https://doi.org/10.3390/smartcities7040074
APA StyleZhong, J., Fan, Y., Zhao, X., Zhou, Q., & Xu, Y. (2024). Multi-Type Structural Damage Image Segmentation via Dual-Stage Optimization-Based Few-Shot Learning. Smart Cities, 7(4), 1888-1906. https://doi.org/10.3390/smartcities7040074






