Integration of Smart City Technologies with Advanced Predictive Analytics for Geotechnical Investigations

Highlights

What are the main findings?

• Ensemble learning methods proved superior in accurately predicting the depth of bearing layers critical to urban infrastructure, improving geotechnical predictions and urban planning.
• The integration of smart technologies and predictive analytics significantly improved the accuracy of geotechnical investigations, facilitating the development of smart cities by providing advanced tools for real-time data analysis and geographic mapping.

What are the implications of the main finding?

• The success of ensemble learning in accurately predicting the depth of bearing layers can lead to more reliable urban planning and infrastructure development, reducing the risks associated with building on unstable ground.
• By using advanced predictive analytics, smart city technologies can significantly improve the resilience and sustainability of urban environments, leading to better preparedness for environmental challenges and disasters.

Abstract

This paper addresses challenges and solutions in urban development and infrastructure resilience, particularly in the context of Japan’s rapidly urbanizing landscape. It explores the integration of smart city concepts to combat land subsidence and liquefaction, phenomena highlighted by the 2011 Great East Japan Earthquake. Additionally, it examines the current situation and lack of geoinformation and communication technology in the concept of smart cities in Japan. Consequently, this study employs advanced technologies, including smart sensing and predictive analytics through kriging and ensemble learning, with the objective of enhancing the precision of geotechnical investigations and urban planning. By analyzing data in Setagaya, Tokyo, it develops predictive models to accurately determine the depth of bearing layers that are critical to urban infrastructure. The results demonstrate the superiority of ensemble learning in predicting the depth of bearing layers. Two methods have been developed to predict undetected geographic data and prepare ground reality and digital smart maps for the construction industry to build smart cities. This study is useful for real-time analysis of existing data, for the government to make new urban plans, for construction companies to conduct risk assessments before doing their jobs, and for individuals to obtain real-time geographic data and hazard warnings through mobile phones and other means in the future. To the best of our knowledge, this is the first instance of predictive analysis of geographic information being conducted through geographic information, big data technology, machine learning, integrated learning, and artificial intelligence.

1. Introduction

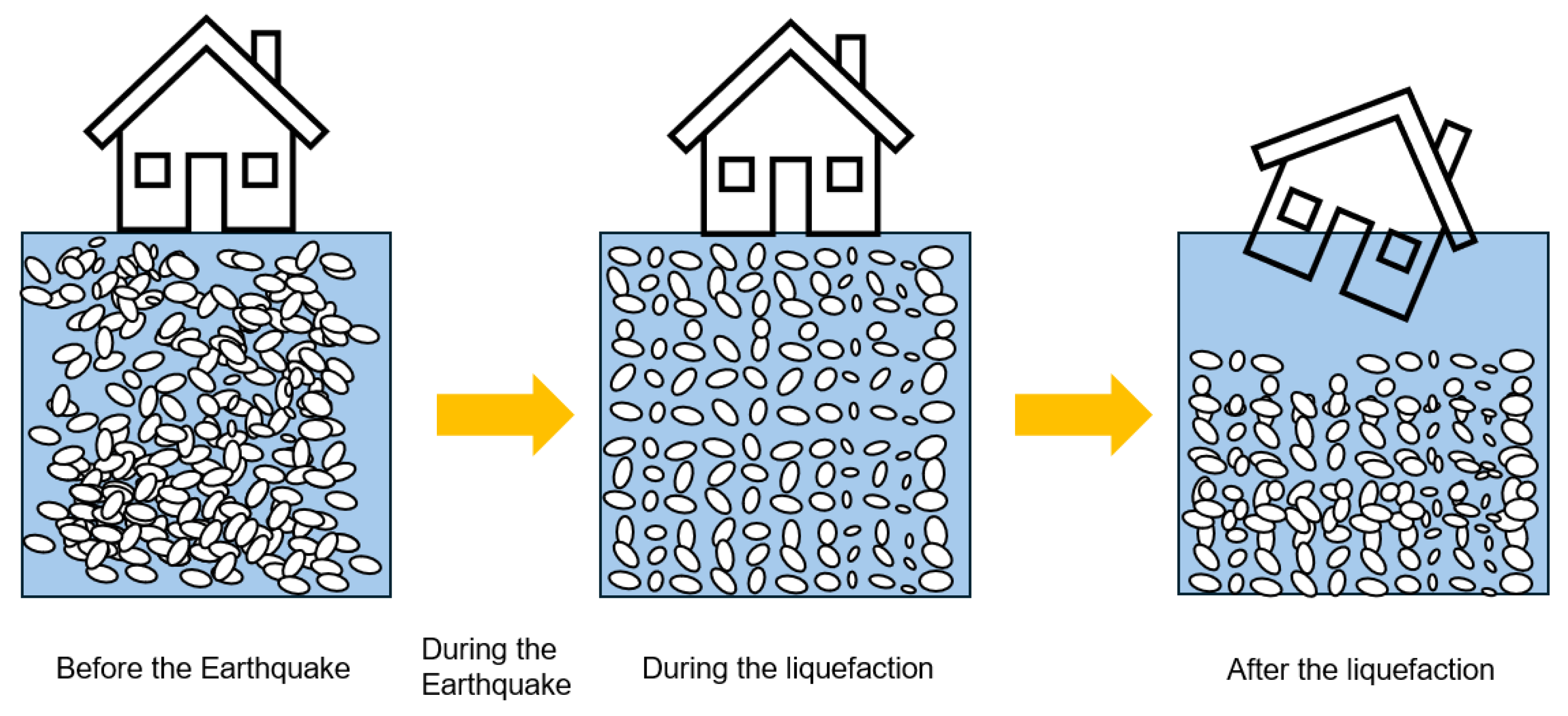
Japan’s urban landscape, characterized by rapid urbanization and cutting-edge technological advances, is at the forefront of addressing complex challenges in the construction and infrastructure sectors. In Japan, the significant structural damage often caused by the settlement or tilting of structures, due to the liquefaction of saturated sandy soils during large earthquakes, has long been a major concern in the field of geotechnical engineering, as shown in Figure 1. The lateral ground spreading (Dh) due to liquefaction-induced lateral spreading can occur on both gently sloping ground and fairly level ground with free face (e.g., river or stream bank). Past earthquakes had devastating effects on infrastructure due to lateral spread. Hence, the effectiveness of the available approaches for designing civil engineering structures in areas prone to liquefaction-induced lateral spreading is directly linked to the Dh value [1]. This phenomenon, which can have serious consequences, was particularly documented in a seminal study [2,3,4,5]. The sudden instability of the ground during such events can lead to the catastrophic destruction of buildings and infrastructures, resulting in significant economic losses as well as the tragic loss of human life. This critical issue was further highlighted in [6,7]. These concerns have led to a significant increase in the study and development of activities aimed at improving liquefaction resistance and developing other mitigation methods. This focus was particularly highlighted by the groundbreaking work of [8,9], which contributed to a better understanding of these challenges [10].

In response to these pressing issues, the concept of smart cities emerges. The smart city aims at developing more scientifically, managing more efficiently, and living a better life. It is supported by information technology and communication technology, and through transparent and sufficient information acquisition, extensive and safe information transmission, and effective and scientific information processing, improving urban operation efficiency, improving public service levels, and forming a new form of city built on the basis of a low-carbon urban ecosystem. With the rapid development of science and technology and the advent of the information society, smart cities have become a new direction for urban planning in the future, as a key strategy that combines the resilience of smart buildings and the precision of smart sensing technologies. Smart buildings, using advanced materials and structural designs, can withstand the damaging effects of subsidence and liquefaction, thereby ensuring the integrity and durability of infrastructure assets. In addition, the use of smart sensing technologies is revolutionizing the process of monitoring and assessing geotechnical risks. Seamlessly integrated into the urban fabric, these sensors provide continuous, real-time data on critical factors such as ground movement and moisture levels, which are essential for maintaining soil stability. In addition, the integration of smart grids and infrastructure strengthens the resilience of urban spaces by optimizing the distribution of resources and energy. This harmonious integration ensures the continued operation of essential services in the aftermath of a disaster, facilitating rapid recovery. The collaborative functioning of smart grids, infrastructure, and sensing technologies promotes a proactive approach to disaster management and mitigation, moving from reactive measures to preventive strategies.

Despite continued advances in monitoring and mitigation technologies for liquefaction and subsidence, significant limitations remain. Challenges related to site availability, time, funding, and physical constraints underscore the need for groundbreaking approaches. Traditional empirical methods, while widely used, lack the precision and reliability required for robust risk management. In this light, the fields of geostatistics and machine learning emerge as promising areas for improving predictive accuracy and understanding of geotechnical phenomena. Techniques such as kriging [11,12], a sophisticated interpolation tool, and ensemble learning [13,14], which enhances prediction through algorithmic diversity, are at the forefront of spatial and temporal data analysis.

This study aims to transcend conventional geotechnical investigation technologies by harnessing the dynamic potential of smart technologies. It seeks to refine the prediction of unknown soil points or areas with unprecedented accuracy using existing datasets. By combining kriging and ensemble learning with the innovative application of smart buildings, sensing technologies, and infrastructure, the study proposes a holistic approach to address the problems of subsidence and liquefaction in Japan.

The Initial concept of a smart city has been recognized as a framework that builds on advances in information and communication technology (ICT) to address the challenges of urbanization. In a broader context, the vision of smart cities, underpinned by intelligent infrastructure and data-driven insights, heralds a new era of urban development. People are increasingly engaging with smart city platforms in multiple ways (e.g., mobile devices, connected cars, and smart homes). However, the development of smart city frameworks has not fully matured to take advantage of new and emerging data-driven technologies. The advancement of new technologies such as big data, artificial intelligence (AI), machine learning, deep learning, and the Internet of Things (IoT) will further shape the smart city framework and revolutionize different sectors of smart cities [15,16]. Geoinformation and communication technology (GeoICT) [17] is another emerging field that is increasingly being used to promote urban sustainability and smart cities. GeoICT is of great importance for the implementation of ICT, which includes geographic information science and systems in smart cities to support analysis and decision making. Geospatial data and geographic information are essential components for building smart cities in a fundamental way that maps the physical world into a virtual environment as a reference framework. In the digital city era, digital maps and geospatial databases have long been integrated into government workflows for land management, urban planning, and transportation. People have expected Geographic Information System (GIS) to be more powerful, not only as an archiving and data management tool, but also as a spatial model to support decision making in smart cities. Successful applications have been developed in private and public organizations by using GIS as a platform for data integration, a system for geospatial analysis, and a collection of models for visualization and decision making [18].

As Japan’s population declines and ages, various social problems are becoming more serious, including the intensification of natural disasters and the spread of COVID-19. Under the Vision for a Digital Garden City Nation, the Government of Japan aims to realize a “fulfilled life” (well-being) by solving social problems and enhancing regional charm through the use of digital technology, while capitalizing on the uniqueness of each region. In this context, smart city initiatives aimed at improving well-being are finally entering the implementation stage across the country. According to the Bureau of Digital Services in Japan, only three of Tokyo’s 23 wards, Sumida, Itabashi, and Minato, have so far vigorously promoted smart cities. In addition, through the existing data integration platforms in Japan, the current situation only uses sensors and other real-time data collection. Therefore, how to manage, analyze, and predict the large amount of geotechnical information collected by numerous sensors in the cloud computing environment to achieve GeoICT is an urgent issue to promote smart city management.

This study aims to go beyond conventional geotechnical investigation technologies by exploiting the dynamic potential of smart technologies. It attempts to refine the prediction of unknown soil points or areas with unprecedented accuracy using existing datasets. By combining kriging and ensemble learning with the innovative application of smart buildings, sensing technologies, and infrastructure, the study proposes a holistic approach to the problems of subsidence and liquefaction in Japan, which will be used to facilitate urban modeling and decision making.

2. Overview of Predictive Analytics for Bearing Layer Depth

In the field of urban development and smart city planning, the intricate interplay between geotechnical engineering and urban infrastructure is of paramount importance. This paper reports on a comprehensive study conducted in Setagaya, Tokyo, focusing on the prediction of the depth of the bearing layer—a critical factor in the foundation and stability of urban structures. By applying sophisticated methods such as kriging and ensemble learning, the study utilizes data from 433 geotechnical surveys and provides insights into optimizing construction processes in the context of smart cities.

The foundation of this study is the use of data from the standard penetration test and the mini-ram sounding test. Introduced in 1951, the standard penetration test has become a staple of soil investigation methods due to its proven applicability to Japanese soil types (excluding special soils). The test was originally designed to determine the relative density of cohesionless soils, but its use has been extended to include the design of foundations by determining the load and the required embedment of piles into the bearing strata. The standard penetration test is performed by the use of the cable percussion drilling rig and its accessories [19], quickly gained popularity for its effectiveness in evaluating soil suitability for buildings, condominiums, and other civil structures. Complementing this, the mini-ram sounding test uses half the impact energy of the automatic ram sounding test, providing an alternative dynamic penetration testing method.

A key aspect of soil mechanics is the calculation of the pressure on the bearing layer, which decreases with depth until it reaches a point where it becomes negligible. This critical depth, beyond which the pressure can be ignored, defines the bearing layer—a key concept in pile foundation design. Soil selection for the bearing layer is stringent, with viscous soils with low compressibility, silty soils, and medium-density or dense sands favored due to their superior bearing properties. The study underscores the importance of selecting the appropriate soil type to ensure the stability and longevity of urban infrastructure, a principle that is increasingly relevant in the context of smart cities, where efficiency and sustainability are paramount.

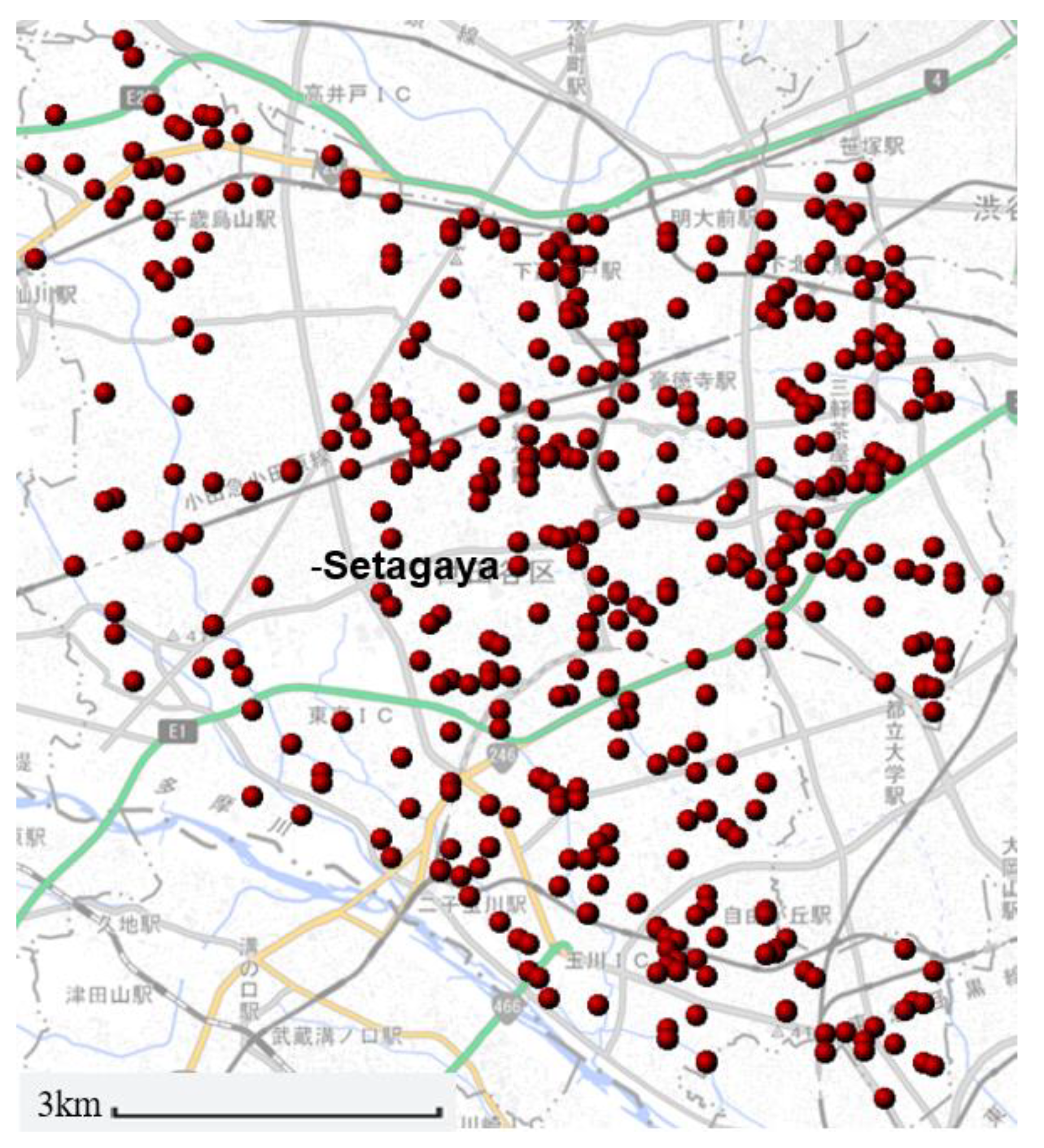
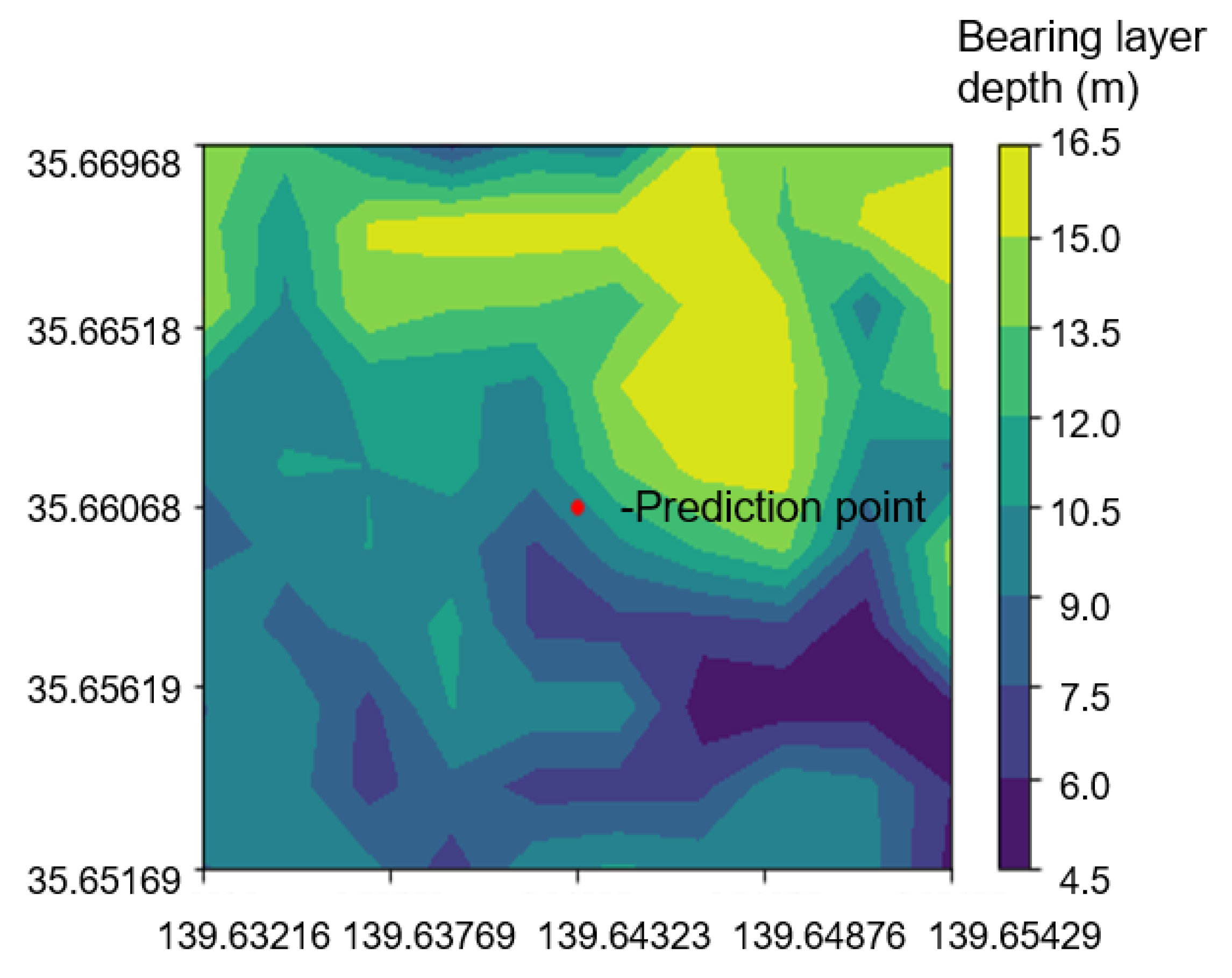
The methodology of this study involved the construction of a predictive model based on the results of geotechnical surveys at 433 locations within Setagaya, Tokyo. The 433 locations are shown in Figure 2. The specific latitude and longitude used are available from the authors upon reasonable request. The model identifies layers with an N value of 50 or more that extend more than 2 m as indicating the presence of a bearing layer. In general, soil with an N value of 20 or more or rock is desirable as a foundation bearing layer. When the N value is between 30 and 50, it can be said that the layer is suitable as the foundation ground for civil engineering and building structures. If the N value is 50 or more, it can be judged to be very solid. It is a good bearing layer that can withstand even large structures, such as high-rise condominiums. 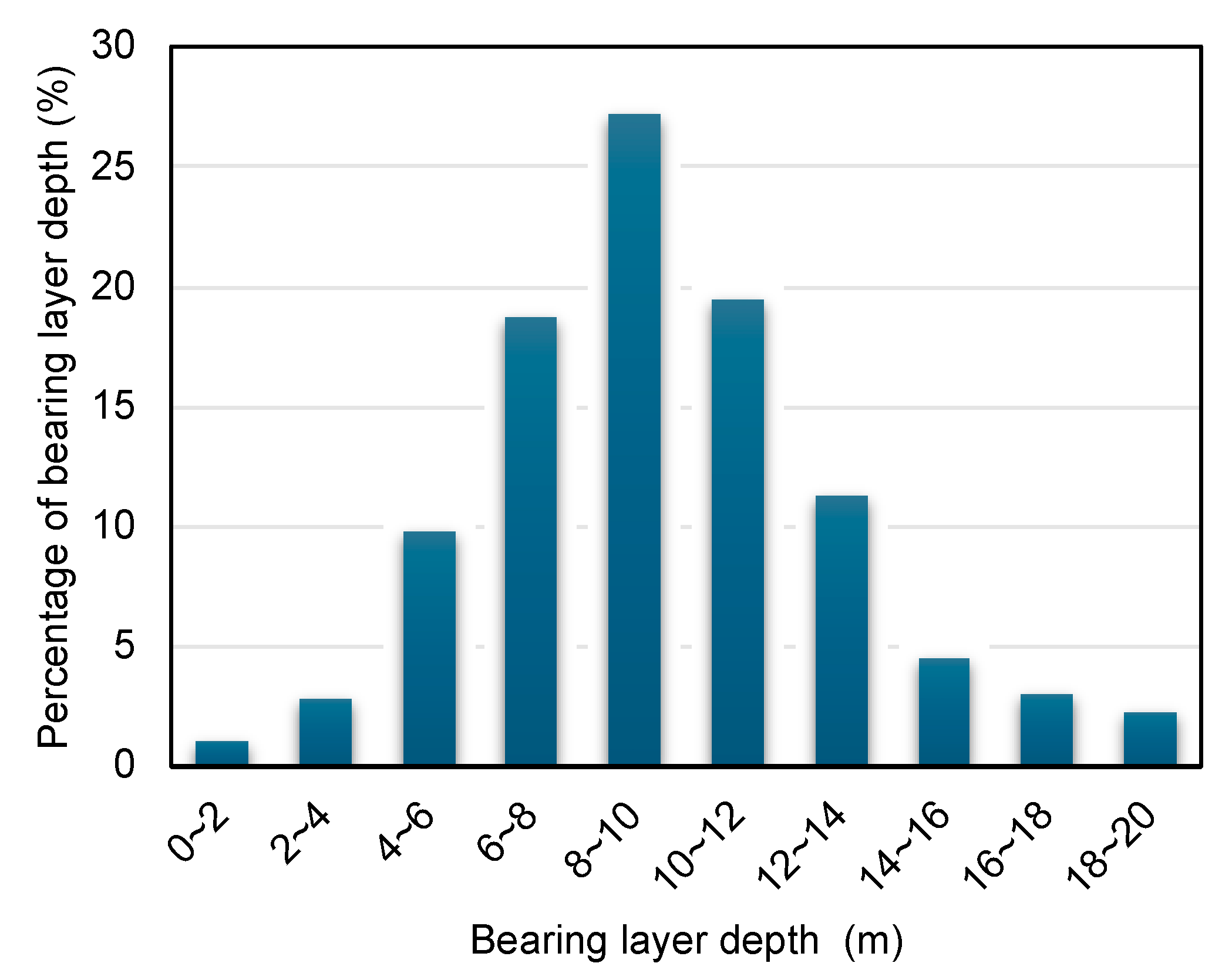Therefore, in this study, if the N value is greater than 50 or more within the range of more than 3 m in a row, it is called the bearing layer [20]. Notably, the study introduces “bearing layer depth A” as a standardized measure, adjusting for elevation differences by subtracting elevation from all bearing layer depths. Elevation is mainly used to refer to the height above the Earth’s surface, and is also called altitude above sea level, since the mean sea level is 0. This adjustment allows for more accurate comparison and analysis across sites, thereby increasing the reliability of predictions. The figures and tables presented in the paper, such as Figure 3 and Figure 4 and

Table 1. Data conditions used in predicting bearing layer depth for Setagaya, Tokyo.

	Area (km2)	Number of Data (pcs)	Data Density (pcs/km2)	Standard Deviation of Data
Setagaya	58.1	433	7.46	9.53

, detail the statistical analysis and data used to make the predictions for Setagaya, Tokyo. The data of longitude, latitude, and bearing layer depth come from the actual data provided by the company, and the elevation comes from the Japan Geographical Institute map.

Table 2. Differences in target variable used by two methods.

Case	Target Variable	Actual Value of Target Variable
Case1	Bearing layer depth A	Bearing layer depth—Elevation
Case2	Bearing layer depth	Bearing layer depth

details the difference in the target variable used by two methods. These visual aids not only illustrate the methodology and results, but also serve as a valuable reference for future studies and applications in urban planning and smart city development.

In the broader context of smart cities, the implications of this study are many. Using advanced predictive models, urban planners and engineers can more accurately assess the suitability of sites for development and optimize the design and placement of buildings, infrastructure, and public utilities. This proactive approach to urban development aligns with the principles of smart cities, which emphasize the use of technology and data to improve the efficiency, sustainability, and resilience of urban environments. In addition, the study’s focus on the depth of the bearing layer aligns with the growing interest in sustainable building practices. By ensuring that urban structures are built on solid foundations, cities can reduce the risk of structural failure, minimize maintenance costs, and extend the life of buildings and infrastructure. This not only contributes to the economic viability of urban projects, but also supports the environmental and social pillars of sustainability.

The study presented in this paper provides valuable insights into the prediction of bearing layer depth in Setagaya, Tokyo, and demonstrates the potential of kriging and ensemble learning methods in improving urban construction practices. As cities worldwide strive to become smarter and more sustainable, the integration of geotechnical engineering principles with advanced predictive analytics will play a critical role in shaping the urban landscapes of the future.

3. Models Used in Predictive Analysis

In the rapidly evolving landscape of urban development, smart cities have emerged as a beacon of innovation, using technology to improve infrastructure, sustainability, and living conditions. The new generation of information technology represented by the mobile Internet can promote the gradual formation of a smart city. A critical aspect of this transformation lies in the careful design and construction of urban infrastructure, where the stability and safety of buildings depend on the accurate prediction of geotechnical properties, such as the depth of the bearing layer. This study explores the application of advanced predictive analytics, specifically kriging and ensemble learning, to predict the bearing layer depth in Setagaya, Tokyo, using a dataset of 433 data points.

Kriging, a geostatistical method named after South African engineer D.G. Krige, provides a sophisticated approach to spatial interpolation. By incorporating the geographic coordinates of the data points, this method makes it possible to create a spatial model that predicts the depth of the bearing layer at various locations in Setagaya, Tokyo. The essence of kriging lies in its ability to provide not only an estimate, but also a measure of the uncertainty of the estimate, making it invaluable for urban planning in smart cities, where risk assessment is critical. Ordinary kriging is by far the most popular method, partly because it is robust with respect to departures from the underlying assumptions [21].

Ensemble learning, on the other hand, uses multiple machine learning algorithms to produce weakly predictive results based on features extracted through a variety of projections on the data and fuse the results with various voting mechanisms to achieve a better performance than that obtained by any constituent algorithm alone [22]. By aggregating predictions from different models, ensemble learning reduces the likelihood of overfitting and increases the robustness of the prediction. In this study, ensemble learning used the same input variables, latitude and longitude, to predict bearing layer depth, illustrating the method’s versatility and power in handling complex urban datasets.

The comparative analysis of the two methods, kriging and ensemble learning, focused on the prediction accuracy against measured values and the mean prediction error at validation points. Such an evaluation is critical in urban planning contexts, where the accuracy of predicting geotechnical properties directly impacts the feasibility, safety, and cost-effectiveness of construction projects.

Smart cities, with their emphasis on data-driven decision making, will benefit significantly from advances in predictive analytics, as demonstrated in this study. In addition, the horizontal analysis between Case 1 (kriging) and Case 2 (ensemble learning) provided insights into the suitability of each method for urban geotechnical prediction;

Table 3. Explanatory variables and target variable used in two cases.

Case	Explanatory Variables	Target Variable
Case 1	Bearing layer depth A	Bearing layer depth A
	Latitude
	Longitude
Case 2	Bearing layer depth	Bearing layer depth
	Latitude
	Longitude
	Elevation

details the differences between Case 1 and Case 2. This analysis is not only academic, but has practical implications for urban developers, engineers, and policy makers involved in smart city projects. The method that exhibits higher accuracy and lower average error can inform more reliable geotechnical investigation protocols, contributing to safer and more sustainable urban environments. Bagging is conducted with spiders (Anaconda 3).

The implications of this study extend beyond the boundaries of Setagaya, Tokyo or even Tokyo. As cities around the world strive to become smarter by integrating technology into every facet of urban life, the methods validated by this study provide a blueprint for using predictive analytics in urban planning. By accurately predicting the depth of bearing layers, city planners can optimize the location and design of buildings and infrastructure, mitigate risks associated with soil instability, and ensure the long-term resilience of urban developments. This study exemplifies the synergy between geotechnical engineering and smart city concepts and highlights the potential of kriging and ensemble learning to improve urban infrastructure projects. As smart cities continue to evolve, the use of data-driven methodologies will be paramount in addressing the complex challenges of urban development, ensuring that cities become not only smarter, but also safer and more sustainable for future generations.

3.1. Kriging

Smart cities represent the pinnacle of urban planning and development, where technology, data, and efficient resource management converge to create environments that are sustainable, livable, and technologically advanced. At the heart of smart cities is the need for accurate, reliable data about the urban landscape, its resources, and the environment. Geostatistics provides a powerful toolkit for analyzing and predicting variables across space and time, which is essential for the complex task of urban planning and management in smart cities.

Kriging comes from the earth sciences and has been progressively developed since the 1950s along with the discipline called geostatistics [23]. Using geology data, researchers established geology models primarily based on statistical methods, which produced geostatistics [24,25]. In land resource inventories, kriging and its variants have been widely recognized as primary spatial interpolation technologies from the 1970s. In the 1990s, with the emergence of GIS and remote sensing technologies, soil surveyors became interested in using exhaustively mapped secondary variables to directly map soil variables. The first applications were based on the use of simple linear regression models between terrain attribute maps and soil parameters. In the next phase, the predictors were extended to a set of environmental variables and remote sensing images [26,27]. This evolution reflects a broader trend toward comprehensive, data-driven approaches to urban planning and resource management. By enabling precise mapping of soil variables, terrain attributes, and other environmental factors, kriging facilitates the detailed, accurate modeling of urban spaces that is essential for smart city development.

In this study, ordinary kriging is utilized, which imposes constraints on weighting and can relatively express spatial random fields. The method predicts the bearing layer depth. The research in [28] defines a functional random variable as a random variable taking values in a space of functions [29]. In this paper, at a certain point $x$, the estimated value of the target value $\hat{\mathrm{w}}(x)$ is generally the measured value at n points $x_i$ around it. It is given as the weighted average of $\hat{\mathrm{w}}(x)$ ($i$ = 1, 2, ⋯, $n$), as shown in Equation (1) [30,31].

$$\hat{\mathrm{w}}(x)={\sum }_{i=1}^n{b}_i\mathrm{w}\left(x_i\right)$$

(1)

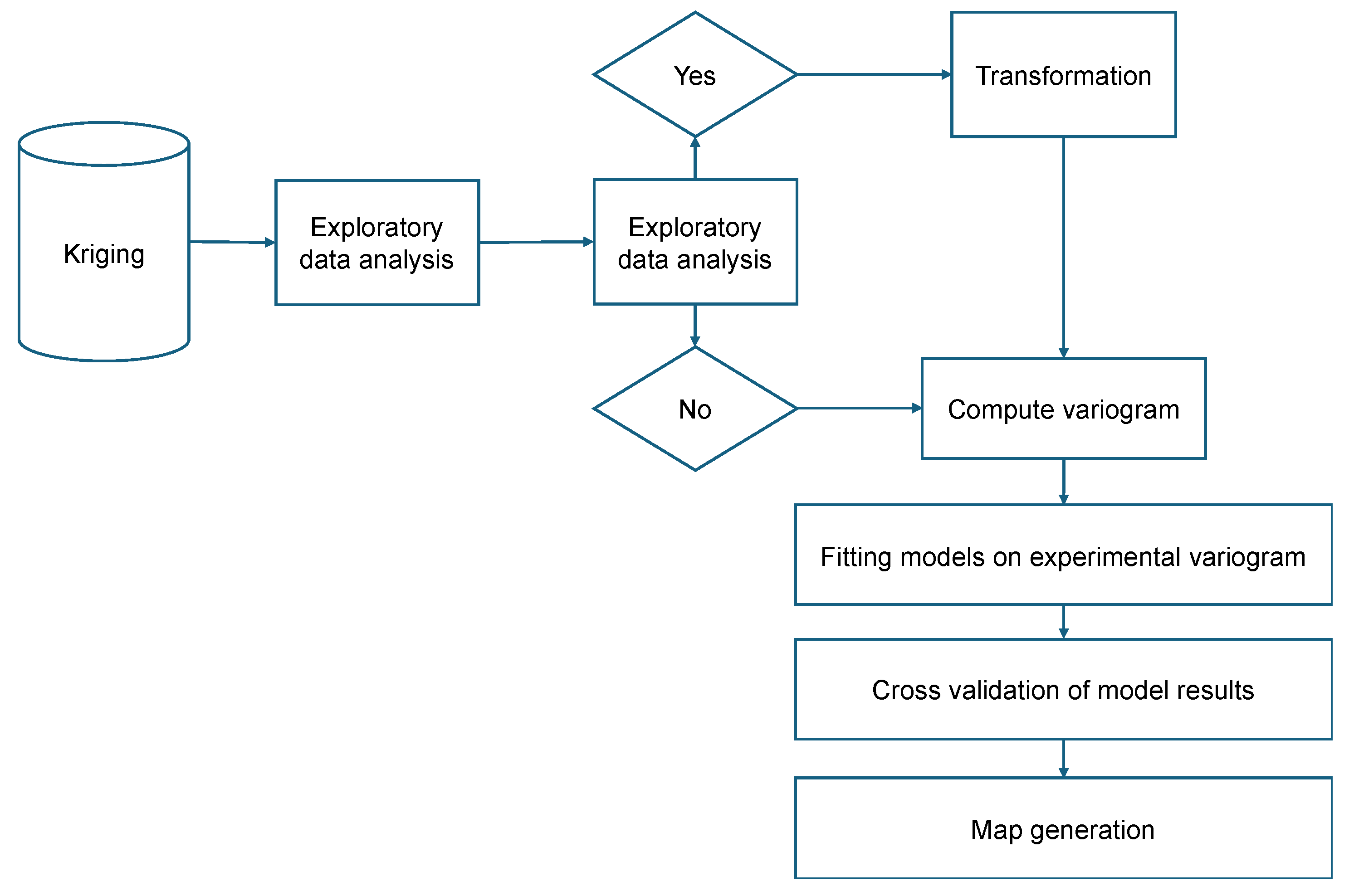
The ordinary kriging used in this study is an example of integrating geostatistical methods with smart city technologies. By imposing constraints on the weighting and expression of spatial random fields, ordinary kriging allows for the accurate prediction of bearing layer depths, a critical factor in urban infrastructure development. The transformation of latitude and longitude data into Transverse Mercator coordinates for kriging prediction exemplifies the methodological precision required for smart city planning. The orthogonal UTM coordinate system, by representing the spherical Earth in a planar view, ensures accurate distance representation, essential for the meticulous design and layout of urban infrastructure [32]. The kriging procedure is depicted in Figure 5.

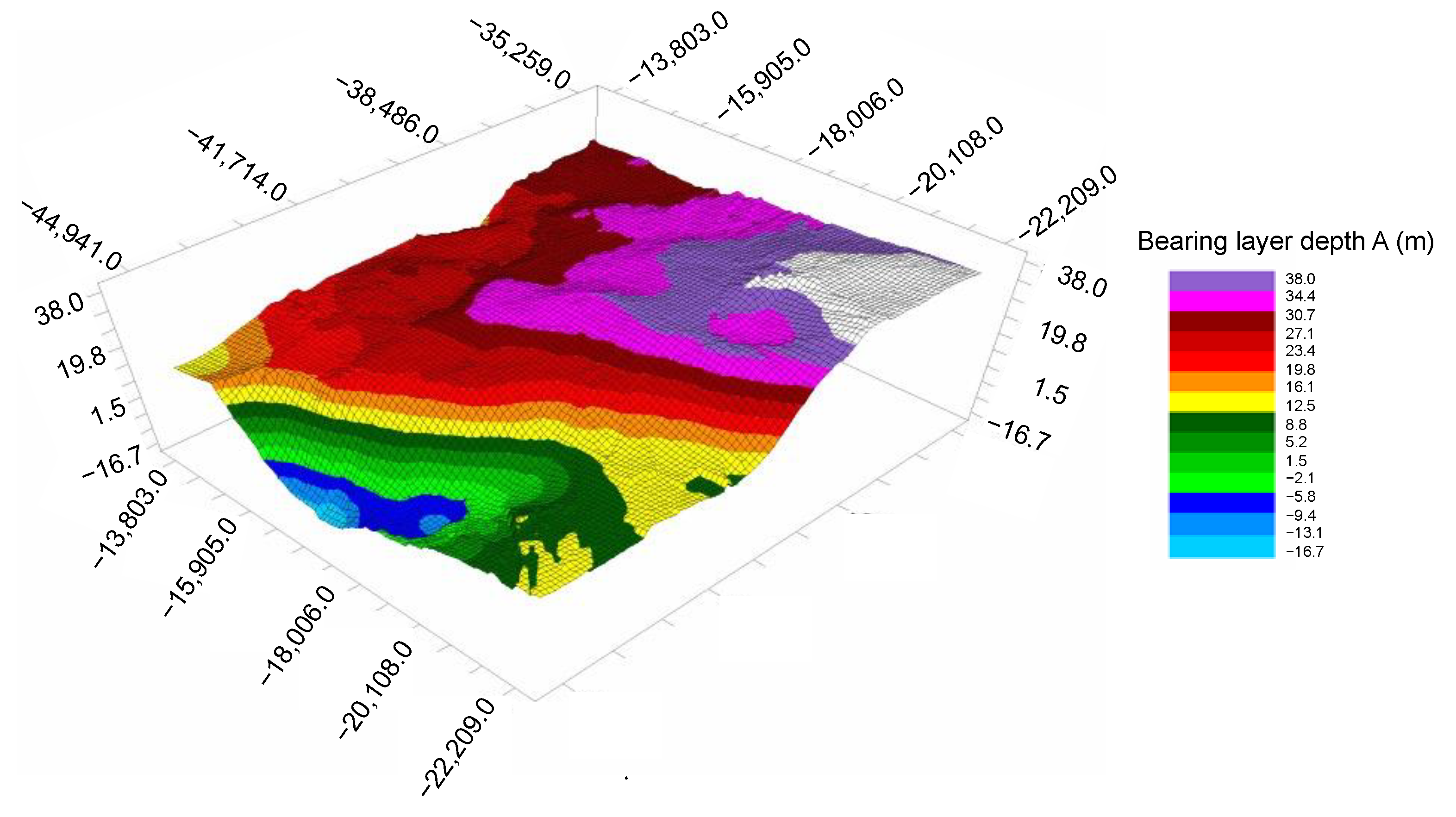
The application of kriging to the prediction of bearing layer depth illustrates the utility of the method in a smart city context. By converting geographic data to UTM coordinates and incorporating elevation conditions, this study demonstrates how geostatistical predictions can inform urban infrastructure development. The resulting three-dimensional map of the predicted distribution of bearing layer depth provides a fundamental tool for planners and engineers to make informed decisions in the construction of buildings, roads, and other critical infrastructure components.

The impact of accurate geostatistical predictions extends beyond infrastructure development to include environmental management, resource allocation, and emergency response planning. In smart cities, where efficiency and sustainability are paramount, the ability to accurately predict environmental and spatial variables is invaluable. It informs the deployment of resources, the management of environmental challenges, and the planning of future development with an unprecedented level of precision and foresight.

The integration of geostatistics, and kriging in particular, into the fabric of smart cities represents a significant advancement in urban planning and management. By enabling accurate spatial predictions and analysis, these methods provide the data-driven foundation necessary for the efficient, sustainable development of urban environments. As smart cities continue to evolve, the role of geostatistical methods will undoubtedly expand, driving innovation in urban planning, infrastructure development, and environmental management. The case study presented in this analysis, focusing on the prediction of bearing layer depth, exemplifies the practical applications and potential of kriging in the context of smart cities, underscoring its importance in the quest for more livable, technologically advanced urban spaces.

3.2. Ensemble Learning

Ensemble learning methods utilize a variety of machine learning algorithms that aim to produce weakly predictive results through a variety of data projections. These results are then aggregated using various voting mechanisms to outperform the performance achievable by each individual algorithm [33]. This strategy can be broadly categorized into three different types. Among them, our study highlights the use of the bagging method due to its effectiveness and simplicity.

The bagging technique, a cornerstone of ensemble learning, involves generating multiple subsets of the original training dataset through random sampling. These subsets are then used to train basic models in parallel, and their outputs are integrated to form a comprehensive predictive model [34]. Bagging is characterized by its simple, yet powerful approach of combining multiple basic learners to construct a highly accurate predictive model [35].

The procedural essence of bagging is illustrated in Figure 6, which shows the use of decision trees for each bagging-derived data segment. In addition, a decision tree diagram is shown in Figure 7, highlighting the structural foundation of the method. Prior to actual model assembly, hyperparameter optimization is meticulously performed, identifying the optimal model configuration that achieves peak accuracy with 91 decision trees. Decision tree is the most commonly used algorithm because of its ease of implementation and because it is easier to understand compared to other classification algorithms [36,37].

Building a predictive forest by bagging involves several key steps. First, “sample data” are generated by randomly selecting from the training dataset, allowing for data reuse across different samples. Among the 433 data, 70% are used for training and 30% are used for verification. Next, 91 decision trees are cultivated using the sample data, and their predictions are averaged to derive the final prediction. This averaging process follows Equation (2). The values of the hyperparameters are shown in

Table 4. The values of tuned hyperparameters of bagging in Case 2.

Hyperparameters	Value
N_esimators	91
Max_depth	1
Max_features	None

.

$$\mathrm{Y}=\frac{1}{N}\sum _{n=1}^N{X}_n$$

(2)

where $\mathrm{Y}$ is the predicted value of the forest, $X_n$ is the prediction of an individual decision tree, and $N$ is the total number of decision trees.

Cross-validation is a data resampling method used to assess the generalization ability of predictive models and to prevent overfitting [38,39]. This study uses k-fold cross-validation to examine the performance of the model built with certain data test. The k value used in this k-fold cross-validation is 10, with the review of 433 data test as testing data and using 10-fold cross-validation so that the prediction will be repeated 10 times [40]. As depicted in Figure 8, testing data are randomly extracted, while the remaining data are divided into training and validation sets.

In smart cities, the implications of using ensemble learning, particularly the bagging technique, are profound. By harnessing the collective intelligence of multiple predictive models, city officials can achieve unprecedented accuracy in predicting and managing citywide systems. Whether optimizing traffic flow, improving energy efficiency, or enhancing public safety, the strategic application of ensemble learning paves the way for smarter, more responsive urban environments. As smart cities continue to evolve, the integration of advanced ensemble learning techniques will play a critical role in shaping their future. By bridging the gap between complex data patterns and actionable insights, ensemble learning is a testament to the transformative power of machine learning in the quest for more livable, efficient, and sustainable urban landscapes.

4. Results and Discussion

In the context of smart city development, the integration of advanced spatial analysis techniques can significantly improve urban planning and management. This study focuses on two case studies in Setagaya, Tokyo, where the kriging method and the bagging algorithm are used to predict the distribution of bearing layers, a critical factor in urban infrastructure development. The accuracy and effectiveness of these methods are crucial for smart city applications, including urban planning, environmental monitoring, and infrastructure management.

4.1. Results of Cases 1 and 2

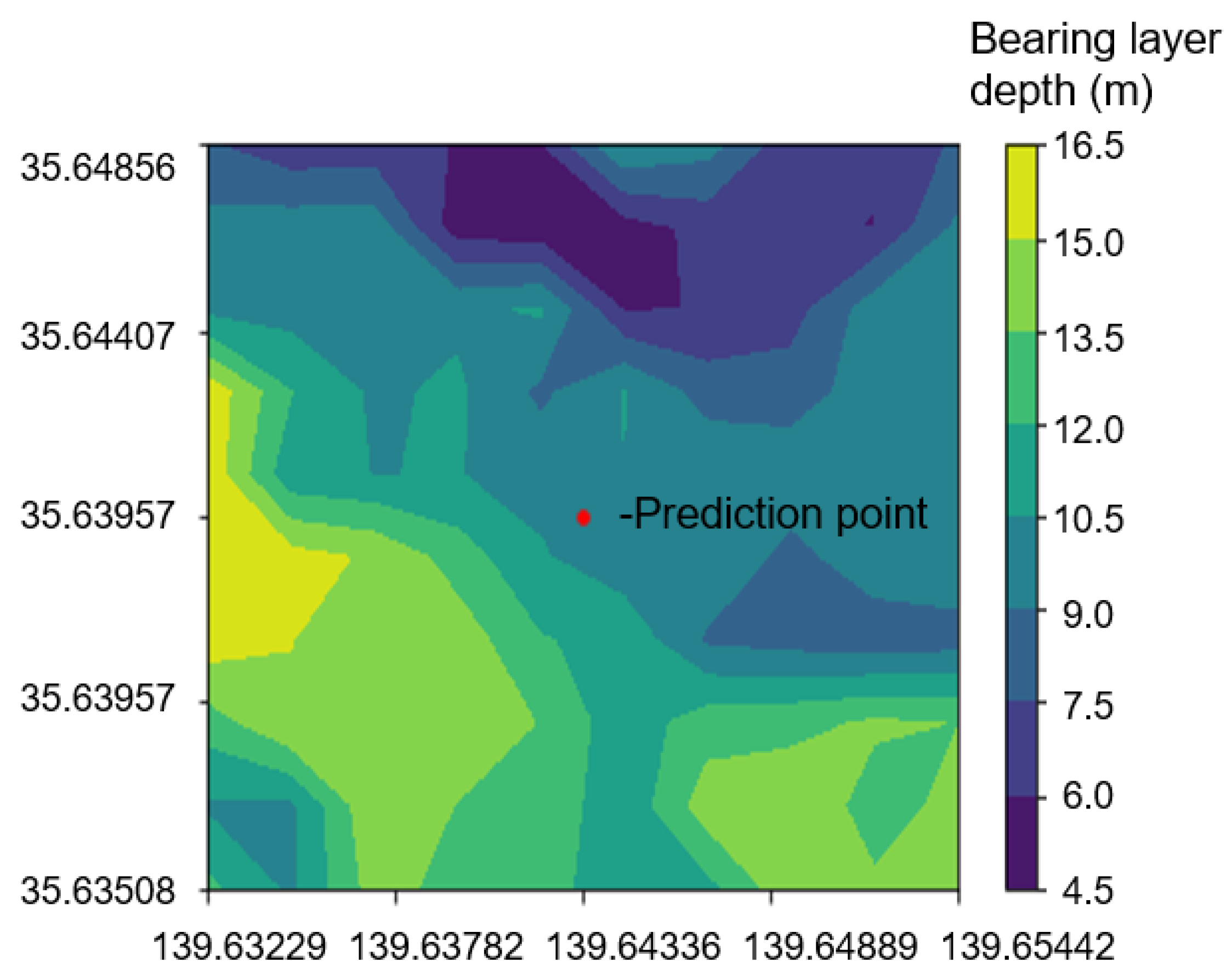
In the first case study, the kriging method, a geostatistical technique, was used to predict the distribution of bearing layers at 10 locations in Setagaya, Tokyo. Actual measurements at these locations provided a basis for evaluating the accuracy of the predictions, with error values calculated between the predicted and actual values. The results, detailed in

Table 5. Average error of prediction of bearing layer depth for ten locations in Case 1.

Prediction Location	Error (m)
1	1.46
2	1.78
3	1.33
4	4.88
5	3.23
6	3.3
7	2.15
8	7.13
9	3.53
10	2.63
Average error (m)	3.14

, underscore the accuracy of the method in spatial prediction. Figure 9 illustrates the distribution of bearing layers, providing a visual representation of the predicted values over the area. To understand the relationship between data density and prediction error, we calculated the correlation coefficient ($r$) using Equation (3).

$$r=\frac{s_{xy}}{s_x\times s_y}=\frac{\frac{1}{n}\sum _{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\frac{1}{n}\sum _{i=1}^n{(x_i-\overline{x})}^2}\times \sqrt{\frac{1}{n}\sum _{i=1}^n{(y_i-\overline{y})}^2}}$$

(3)

where $r$ is the correlation coefficient between $x$ and $y$, $s_{xy}$ is the covariance of $x$ and $y$, $s_x$ is the standard deviation of $x$, $s_y$ is the standard deviation of $y$, $n$ is the total number of data, $x_i$ and $y_i$ are the value of $i$th data, respectively, $\overline{x}$ is the average of $x$, and $\overline{y}$ is the average of $y$ [41].

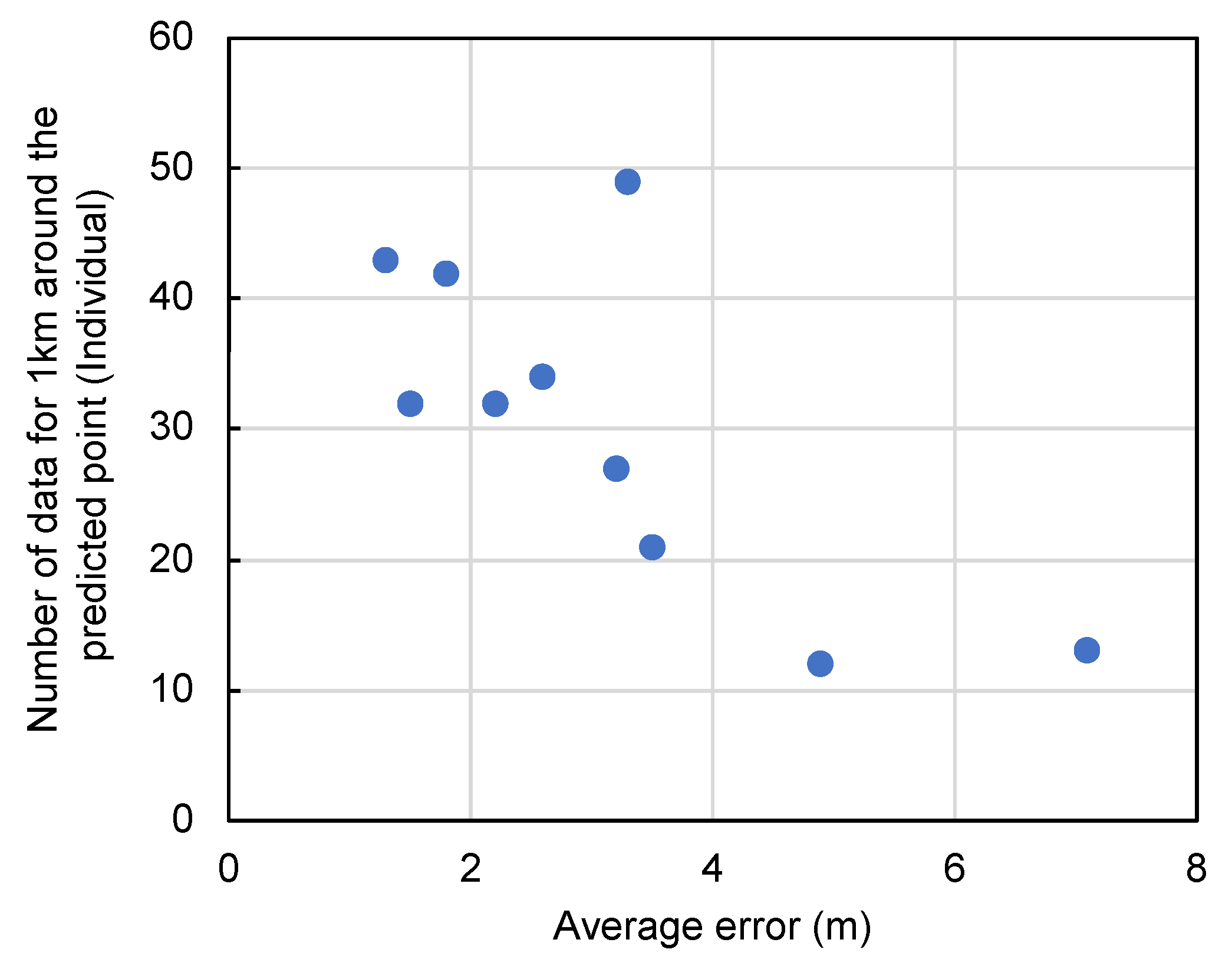
This statistical analysis revealed a correlation coefficient of −0.62, indicating a moderate inverse relationship between data density and error. This finding suggests that areas with denser data points tend to have lower prediction errors, highlighting the importance of data quality and quantity in spatial analysis. The proximity of data points to the prediction location plays a critical role, with more neighboring data points contributing to higher accuracy. Thus, the quantity of data existing within a 1 km radius (as depicted in

Table 6. Comparison of amount of data within 1 km with ten prediction locations as center in Setagaya, Tokyo.

Prediction Location	Error (m)	Within 1 km Surrounding Area Amount of Data (Individual)
1	1.46	32
2	1.78	42
3	1.33	43
4	4.88	12
5	3.23	27
6	3.3	49
7	2.15	32
8	7.13	13
9	3.53.	21
10	2.63	34
Average error (m)	3.14

) is reassessed. This principle is visualized in Figure 10 and Figure 11, which show the data density around a given point and the correlation between density and error, respectively.

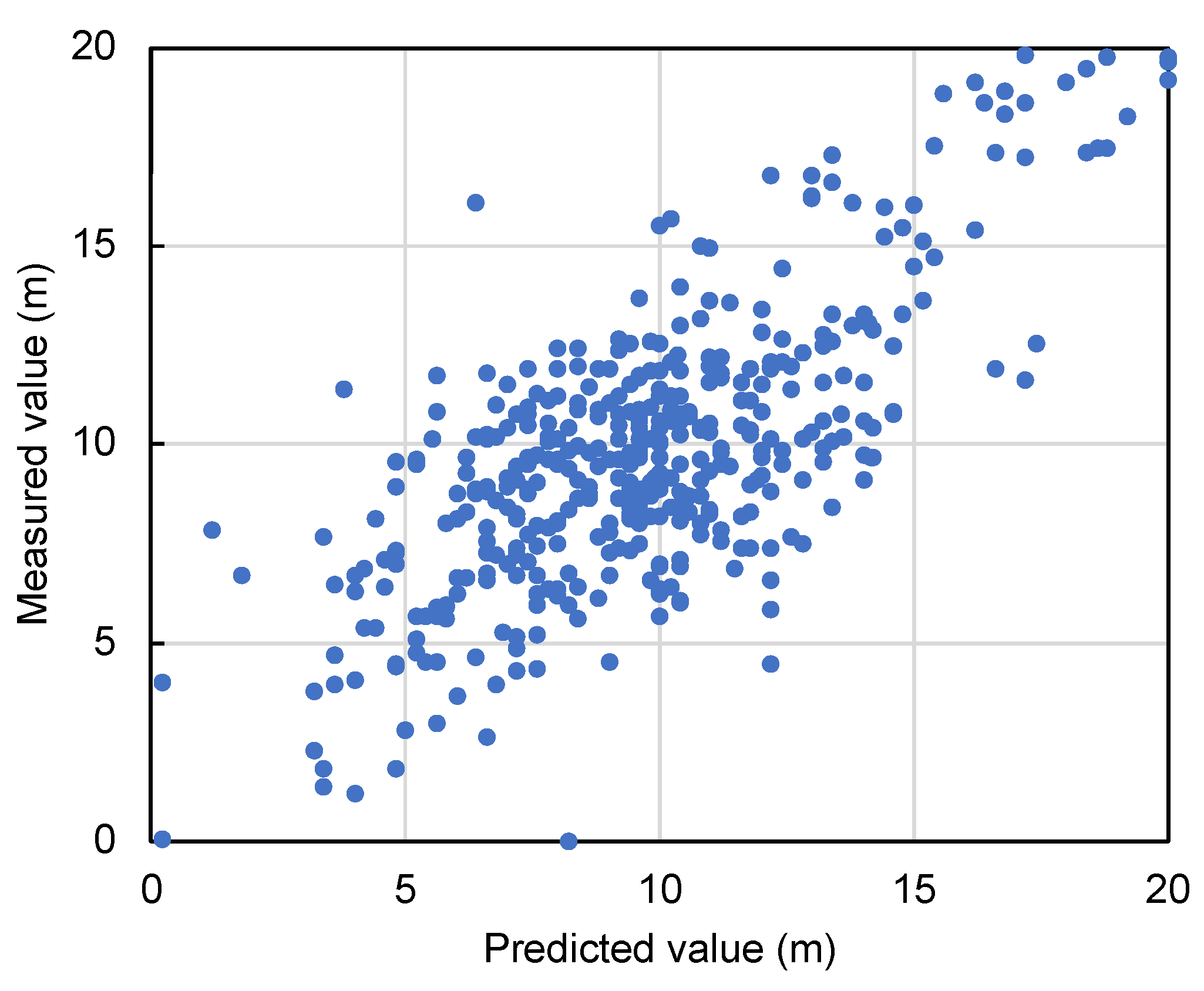
The second case study advances the application of machine learning through the bagging algorithm by incorporating multiple predictors such as latitude, longitude, and elevation along with geotechnical data from 433 locations. This ensemble learning method aims to improve the prediction accuracy of bearing layer depths, a critical component in urban infrastructure planning. The error analysis shown in

Table 7. Average error of prediction of bearing layer depth for ten locations in Case 2.

Prediction Location	Error (m)
1	0.75
2	0.53
3	3.41
4	1.95
5	0.09
6	0.22
7	0.02
8	0.1
9	0.26
10	1.26
Average error (m)	0.86

and the prediction accuracy shown in Figure 12 demonstrate the effectiveness of the bagging method. The proximity of the data points to the diagonal in Figure 12 indicates high accuracy, with an average error value of 0.86 m, demonstrating the potential of machine learning to improve urban planning processes.

4.2. Comparison of Average Error Values for Kriging and Ensemble Learning

In the context of the advancement of smart cities, the implementation of accurate and efficient predictive modeling techniques is crucial for the development and maintenance of urban infrastructure. As smart cities leverage data and technology to improve the efficiency of services and meet the needs of residents, the accuracy of predictive models such as kriging and ensemble learning, especially bagging, is critical for planning and operational efficiency. This analysis focuses on comparing the average error values for kriging and bagging methods used to predict the depth of the bearing layer in Setagaya, Tokyo, providing insights into their suitability for smart city applications.

The prediction results for both the kriging and bagging methods are meticulously documented in

Table 8. Kriging method and bagging prediction results of bearing layer depth.

	Error of Case 1 (Kriging)	Error of Case 2 (Bagging)
1	1.46	0.75
2	1.78	0.53
3	1.33	3.41
4	4.88	1.95
5	3.23	0.09
6	3.3	0.22
7	2.15	0.02
8	7.13	0.1
9	3.53.	0.26
10	2.63	1.26
Mean error (m)	3.14	0.86
MAE	3.14	0.86
MSE	12.7	1.8
RMSE	3.56	1.34

, which shows that the prediction model using bagging outperforms kriging in terms of accuracy. And it used three matrices, MAE, MSE, and RMSE, to evaluate the prediction accuracy of the models in Cases 1 and 2. MAE is the average of the absolute values of the errors, while MSE is a metric that represents the average squared difference between the predicted values and the actual values in a dataset. The lower the MSE, the better a model fits a dataset. RMSE is a metric that represents the square root of the average squared difference between the predicted values and the actual values in a dataset. The lower the RMSE, the better a model fits a dataset. According to these matrices, it can be concluded that the prediction model built using bagging is higher. This discrepancy in performance prompts a deeper analysis of the advantages and disadvantages of each method, particularly in the context of their application in smart city planning and development.

The kriging method, although widely used for its interpolation capabilities, has several limitations:

(1)

Sensitivity to the number and distribution of data points: The performance of kriging is highly dependent on the availability and spatial arrangement of sampling points. A sparse or uneven distribution can significantly affect the model’s interpolation accuracy.

(2)

Error increases with interpolation distance: As the distance over which interpolation is performed increases, the potential for error accumulation increases, potentially limiting the effectiveness of the method over larger areas.

(3)

Over-smoothing in the presence of spatial variability: Kriging can over-smooth data and fail to capture subtle but important variations across terrain surfaces, which is critical for accurate urban planning in smart cities.

These limitations highlight the need for a dense, uniformly distributed dataset when using kriging for predictive modeling in urban areas. However, the case of Setagaya, Tokyo illustrates the challenges that arise when the data are sparse and unevenly distributed at the depth of the bearing layer, which leads to compromised prediction accuracy with the kriging method.

Conversely, bagging has several advantages that are well-suited to the needs of predictive modeling in smart cities:

(1)

Strong resistance to noise: The method’s inherent robustness to noisy data, due to random sampling and optimal feature selection, enhances its reliability in urban data analysis.

(2)

Parallel computing capability: Bagging’s design allows for independent training of basic learners, facilitating parallel processing that can significantly speed up the model training process—a critical factor in the fast-paced environment of smart city development.

(3)

Applicability to High-Dimensional Data: Without the need for feature selection, bagging’s ability to process high-dimensional data makes it particularly suitable for the complex datasets typical of urban environments.

(4)

Insensitivity to missing features: The method’s tolerance for missing data points ensures that predictive models remain effective even when datasets are incomplete, a common occurrence in urban data collection.

Given these advantages, bagging emerges as a more suitable method for predicting bearing layer depth in smart cities, where data complexity, dimensionality, and quality can vary widely. The higher accuracy of bagging in predicting the bearing layer depth in Setagaya, Tokyo underscores its potential to enhance the predictive modeling capabilities of smart cities, ensuring more informed decision making and efficient urban management.

The comparison between kriging and bagging in the context of predicting bearing layer depth in Setagaya, Tokyo reveals significant differences in performance, with bagging showing superior accuracy. This finding suggests that ensemble learning methods, such as bagging, hold promise for improving the data analysis framework of smart cities. By leveraging these advanced predictive models, smart cities can optimize their infrastructure and services, ultimately improving the quality of life for their residents.

4.3. The Relationship between Geological Information Prediction and Smart Cities

The construction of GeoICT requires the availability of both above-ground and underground spatio-temporal data resources. In addition, a big data platform requires three-dimensional underground spatial data and the quantity, quality, and spatio-temporal distribution of various natural resource elements to support natural resource management needs. Urban geology involves the study of urban underground space, resources, environment, disasters, ecology, and other factors. It uses geological theory and technical methods to conduct comprehensive analysis and evaluation, determine the status of urban natural resources, evaluate the resource and environmental carrying capacity of urban development, and serve as a basis for urban planning, construction, and operation management.

In this study, the geological data and results generated by the geological survey in Setagaya were collected, processed, verified, and stored in a “data center”. The two technologies were comprehensively used for prediction, and three-dimensional visual prediction results were obtained. Both case studies contribute to the concept of smart cities by providing methods for accurate urban mapping and planning, as shown in Figure 13 and Figure 14. The ability to accurately predict the subsurface is of inestimable value for infrastructure development, risk management, and environmental protection in urban areas. The accuracy of spatial predictions has a direct impact on urban planning, infrastructure development, and environmental management. By leveraging accurate data and advanced analytical technologies, cities can optimize resource allocation, mitigate risks associated with urban development, and improve sustainability.

The goal of smart cities is not only to improve predictive accuracy, but also to facilitate real-time monitoring and management of the urban environment. In accordance with the requirements of urban economic development, professional geological applications are customized and developed to provide geological information services. These services support the development planning of urban underground space resources, the delineation of urban production, living, and ecological space, and the site selection of major urban projects. As shown in Figure 15, geological information is integrated into the core processes of urban planning, construction, and management as a key component of smart cities. The main challenge in establishing this process is the availability of comprehensive data, but it is not feasible to measure all data points. Consequently, in order to obtain all the data, it is essential to predict the location intelligence of unknown points. Therefore, this study is of paramount importance to obtain a complete data center. In addition, machine learning can improve the resilience of infrastructure in smart cities in a number of ways. These include:

(1)

Predictive maintenance: Machine learning models analyze sensor data to predict equipment failures and prevent outages.

(2)

Risk assessment: Machine learning algorithms assess risks associated with natural disasters, climate change, and aging infrastructure.

(3)

Early warning systems: Machine learning-based systems can detect anomalies (such as structural damage) and issue timely warnings.

Recognizing the critical role of machine learning in infrastructure resilience is paramount to creating more livable, sustainable, and efficient cities. In the future, the integration of more sophisticated machine learning algorithms and the incorporation of additional variables such as soil composition, water table levels, and urban density could further refine predictions. It is paramount that government agencies, research institutions, and technology companies work together to advance smart city initiatives. By sharing data, expertise, and resources, stakeholders can drive innovation and develop more resilient, sustainable, and livable urban environments. The application of kriging and bagging algorithms in Setagaya, Tokyo demonstrates the value of advanced spatial analytics in the context of smart cities. These case studies provide insights into the potential of geostatistical and machine learning techniques to improve urban planning, infrastructure development, and environmental management. As cities around the world strive to become smarter and more sustainable, the integration of these techniques will be paramount in shaping the urban landscape of the future.

5. Conclusions

Smart cities represent the pinnacle of urban development and innovation, integrating technology into the fabric of urban planning and management to create more efficient, sustainable, and livable communities. At the heart of smart city advancements is the critical role of predictive analytics, which uses data to predict future scenarios and inform decision-making processes. This study explores the development and establishment of a highly accurate prediction method for unknown points or areas in new territory, demonstrating the potential of smart cities to harness data for urban improvement.

The effectiveness of this prediction was validated using two sophisticated methods, kriging and ensemble learning, applied to data derived from ground survey results. The study achieved remarkable results, highlighting the capabilities of these methods in urban context applications, particularly in smart cities. Here is a detailed look at the results and their implications for smart cities:

(1)

The study demonstrated highly accurate predictions of bearing layer depth by learning critical geographic and geological variables such as “latitude”, “longitude”, “elevation”, and “bearing layer depth”. This accuracy is critical for smart cities, where understanding the geotechnical properties of the ground can significantly impact infrastructure development, from building construction to transportation network design.

(2)

Kriging analysis revealed a strong correlation between the size of the dataset used to create the prediction map and the accuracy of the predictions. This finding is particularly relevant to smart cities, as it underscores the importance of comprehensive data collection and analysis in improving prediction accuracy, thereby facilitating better urban planning and management.

(3)

The study found that when predicting geotechnical survey results using bagging, a technique in ensemble learning, the small variation in the bearing layer depth of the training data significantly affected the accuracy of the predictions. For smart cities, this finding suggests that even small discrepancies in data can affect the results of predictive models, emphasizing the need for accurate data collection and processing.

(4)

A comparative analysis between kriging and bagging showed that for the same amount of training data, the prediction model for bearing layer depth was more accurate when bagging was used. This finding provides valuable guidance to smart city planners and developers in selecting the most effective predictive models for their projects to ensure optimal outcomes.

This study suggests areas for future improvement to further enhance the accuracy of predictions that are critical to the development and management of smart cities:

(1)

The study used a Gaussian semi-variogram in kriging, which assumes a gradual increase in predicted values. However, kriging offers several models, including spherical, exponential, and linear. Future research should quantitatively determine which prediction model achieves the highest accuracy by considering these other models.

(2)

For ensemble learning, the study suggests considering more influencing factors and identifying the impact each factor has on prediction accuracy. By creating new models that incorporate a broader range of variables, the data analysis platform can further improve predictive accuracy.

(3)

While promoting the precision of prediction models, the corresponding software is formed to promote the active use of data by all people, hoping to use data to solve problems and realize a data-driven society.