Abstract
Efficient energy management is crucial for optimizing greenhouse (GH) operations and promoting sustainability. This paper presents a novel multi-objective optimization approach tailored for GH energy management, aiming to minimize grid energy consumption while maximizing battery state of charge (SOC) within a specified time frame. The optimization problem integrates decision variables such as network power, battery power, and battery energy, subject to constraints based on battery capacity and initial energy, along with minimum and maximum energy from the battery storage system. Through the comparison of a smart energy management system (EMS) with traditional optimization algorithms, the study evaluates its efficiency. Key hyperparameters essential for the optimization problem, including plateau time, prediction time, and optimization time, are determined using the ellipse optimization method. Treating the GH as a microgrid, the analysis encompasses energy management indicators and loads. A simulation conducted via Simulink in MATLAB software (R2021b) demonstrates a significant enhancement, with the smart EMS achieving a more than 50% reduction in the objective function compared to conventional EMS. Moreover, the EMS exhibits robust performance across variations in the load power and irradiation profile. Under partial shading conditions, the EMS maintains adaptability, with a maximum objective function increase of 0.35553%. Aligning the output power of photovoltaic (PV) systems with real-world conditions further validates the EMS’s effectiveness in practical scenarios. The findings underscore the efficiency of the smart EMS in optimizing energy consumption within GH environments, offering promising avenues for sustainable energy management practices. This research contributes to advancing energy optimization strategies in agricultural settings, thereby fostering resource efficiency and environmental stewardship.
1. Introduction
1.1. Background and Motivations
Integrating renewable energy sources (RESs) such as photovoltaic (PV), wind, and battery storage into small- and medium-scale power systems can have various advantages as they can reduce energy costs and help prevent service disruptions [1,2]. One of the structures in which RES can be used is GHs. GH agriculture plays a pivotal role in sustaining food production by providing a controlled environment for optimal plant growth. However, the energy-intensive nature of GH operations poses a significant challenge, prompting the exploration of innovative approaches to enhance energy efficiency. The quest for sustainable solutions has led researchers to investigate the integration of RESs and advanced energy management systems (EMSs) [3]. In this regard, this paper contributes to this discourse by proposing a smart EMS designed to optimize the utilization of solar energy in GH environments.
The rising global demand for food, coupled with the imperative to reduce the environmental impact of agriculture, has intensified efforts to make GH operations more sustainable. Energy consumption in GHs, largely derived from conventional power grids, is a major contributor to operational costs and carbon footprints. As a response to this challenge, there has been a growing interest in harnessing RESs, such as solar energy, to power GH facilities [4]. Efficient utilization of RESs necessitates sophisticated EMSs to balance supply and demand, considering the intermittent nature of energy needs in GH environments. Figure 1 shows a schematic of integrating RESs into a smart GH [5].
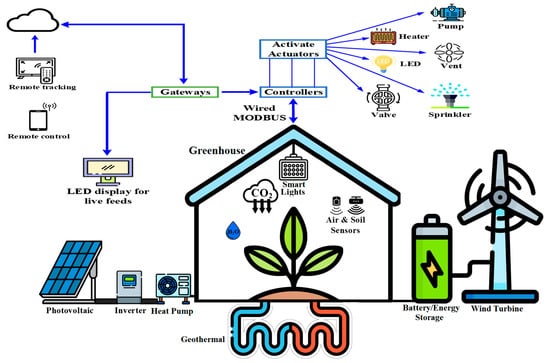
Figure 1.
A schematic of integrating RESs in a smart GH.
1.2. Literature Review of Energy Management in GHs
Previous studies have explored various aspects of energy management in GHs, with an emphasis on integrating RESs. Notable works by authors such as Smith et al. [6] and Wang et al. [7] have investigated the potential of geothermal energy in GH applications, highlighting its advantages in terms of sustainability and cost-effectiveness. However, the optimization of energy consumption through smart systems in conjunction with geothermal energy remains an underexplored area.
In the domain of EMS, traditional optimization algorithms have been employed to enhance energy efficiency in different settings. Nevertheless, the application of smart EMSs, incorporating machine learning and predictive algorithms, is gaining attention for its potential to adapt to dynamic environmental conditions. Studies by Li et al. [8] and Chen et al. [9] showcase the effectiveness of smart EMS in various energy optimization scenarios, motivating our exploration of its application in the GH context.
GH agriculture, a crucial component of global food production, faces the challenge of optimizing energy consumption for sustainability and efficiency. The integration of smart EMSs and optimization strategies emerges as a promising solution, offering several advantages over traditional approaches [5]. These can be classified in the following ways:
- Enhancing Resource Utilization and Adaptability: Smart EMSs in GH operations offer precise control over resource utilization, aligning energy consumption with actual needs. This ensures that resources, including electricity and heating, are employed efficiently, minimizing waste and reducing operational costs. Additionally, one of the key advantages of smart systems lies in their ability to adapt dynamically to changing environmental conditions. Utilizing real-time data and predictive algorithms, these systems adjust energy usage based on factors such as temperature, humidity, and sunlight, optimizing GH operations under varying circumstances [10,11].
- Optimized Crop Growth and Yield: Smart EMSs contributes to optimized crop growth by tailoring environmental conditions to the specific needs of plants. Studies by Li et al. [12] emphasize the positive impact of smart systems on crop yield, as they provide precise control over factors like temperature, light, and CO2 levels.
- Reduction in Environmental Footprint: By unnecessary energy consumption and utilizing RESs, smart EMSs contribute to a reduced environmental footprint. The integration of RESs, such as solar power, aligns with sustainability goals, mitigating the ecological impact of GH operations [13,14].
- Cost Savings and Economic Viability: Smart EMSs offer economic advantages by optimizing energy use and reducing dependency on external energy sources. These systems contribute to significant cost savings over time, making GH operations more economically viable and financially sustainable [15,16].
- Mitigation of Energy Price Volatility: The integration of optimization strategies provides a level of independence from external energy grids, mitigating the impact of energy price volatility. This is particularly crucial for GH operators, as it ensures stable and predictable energy costs, contributing to long-term financial planning [17].
- Real-Time Monitoring and Control: Smart systems enable real-time monitoring and control of energy usage, allowing GH operators to respond promptly to fluctuations in demand or unforeseen events. This proactive approach enhances overall system resilience and reliability, crucial for the continuous and uninterrupted functioning of GH facilities [18].
- Integration of Machine Learning for Predictive Analysis: Machine learning algorithms, integrated into smart EMSs, offer the capability for predictive analysis. By learning from historical data and environmental patterns, these systems can anticipate future energy requirements, optimizing energy distribution and storage within the GH [19].
- Improved Operational Efficiency: The precise control afforded by smart systems translates into improved operational efficiency. Through the automation of energy-intensive processes, such as heating and cooling, these systems reduce manual intervention, allowing GH operators to focus on strategic decision-making and crop management [10,20].
- Technological Innovation and Industry Leadership: GH operators adopting smart EMSs position themselves as industry leaders in technological innovation. By embracing cutting-edge solutions, these operators contribute to the advancement of sustainable agricultural practices and set a benchmark for others in the sector [21].
Considering the presented problems, we can provide four important questions to address in this paper, as follows:
- How can the integration of solar energy be optimized to reduce dependence on conventional power grids and enhance the overall environmental sustainability of greenhouse operations?
- What are the key advantages and potential challenges associated with the implementation of a smart EMS in the context of greenhouse energy optimization, particularly in comparison to traditional optimization approaches?
- How can the identification and optimization of hyperparameters, such as plateau time, prediction time, and optimization time during a day, contribute to the adaptability and efficiency of a smart EMSs for greenhouse energy management?
- What are the specific findings or quantitative metrics that support the claim of improved energy consumption and operational efficiency achieved through the proposed multi-objective optimization approach tailored for greenhouse energy management?
To address the above-mentioned issues, overall, our paper bridges the gap in the existing literature by proposing a multi-objective optimization approach specifically tailored for GH energy management, incorporating solar energy and utilizing a smart EMS. The subsequent sections detail the methodology, present simulation results, and offer a comprehensive analysis of the proposed system’s efficiency in comparison to traditional optimization approaches.
1.3. Motivation and Main Contributions
The main motivations of this paper are driven by several key factors:
- Multi-Objective Optimization for GH Energy Management: This paper presents an innovative multi-objective optimization method aimed at concurrently minimizing grid energy consumption and maximizing the SOC of a battery within a specified period. This approach ensures comprehensive and efficient utilization of energy resources in GH operations.
- Integration of Solar Energy: A significant contribution lies in the integration of solar energy as a primary source within the proposed EMS. By harnessing the constant and sustainable nature of solar energy, the system aims to reduce dependence on conventional power grids, thereby enhancing the overall environmental sustainability of GH operations.
- Smart EMS: This paper introduces and assesses the effectiveness of a smart EMS in the context of GH energy optimization. This involves the use of advanced algorithms, including machine learning and predictive analytics, to adaptively manage energy consumption based on dynamic environmental conditions. This sets it apart from traditional optimization approaches and contributes to more intelligent and responsive EMSs.
- Identification and Optimization of Hyperparameters: This study identifies and optimizes crucial hyperparameters essential for the success of the proposed EMS. Parameters such as the plateau time, prediction time, and optimization time during a day are determined using the ellipse optimization method. This optimization process enhances the adaptability and efficiency of the system, ensuring optimal performance under varying conditions.
Also, the primary contributions of this paper include the following:
- Simplifying the objective function and restricting the decision variables to independent ones.
- Defining the hyperparameters and determining their optimal values.
- Accounting for uncertainty in the predicted values of Ppv and load power.
- Incorporating natural effects such as partial shading.
- Updating the advanced predicted Ppv throughout the day.
In summary, this paper aims to deal with various practical aspects of the problem to ensure that the provided solution is usable, effective, and implementable in real-world scenarios. The paper addresses the challenges of GH energy management through a multi-faceted approach, incorporating multi-objective optimization, solar energy integration, smart EMSs with advanced algorithms, and the identification and optimization of key hyperparameters. The overarching goal is to promote holistic and sustainable practices in GH operations while maximizing energy efficiency.
1.4. Paper Structure
2. Problem Definition and Methodology
Efficient energy management in GH operations is of paramount importance in the context of modern agriculture and environmental sustainability. As global populations continue to burgeon, the demand for food rises, underscoring the critical role played by GH agriculture in ensuring food security [22]. However, the conventional energy-intensive practices within GHs pose significant challenges, both economically and ecologically.
Effective energy consumption management is pivotal for mitigating operational costs and reducing the environmental impact associated with conventional power sources. GH operators are confronted with the need to strike a delicate balance between sustaining optimal plant growth and minimizing energy-related expenditures. The imperative to transition towards sustainable practices has led to a surge in research focused on integrating RESs into GH operations [23].
This paper addresses this imperative by proposing a smart EMS specifically designed for GH environments. The integration of solar energy, known for its reliability, is a key facet of this endeavor. By presenting a multi-objective optimization approach, this paper seeks to minimize reliance on external grids, maximize battery storage efficiency, and enhance the overall environmental sustainability of GH operations. The significance of this research lies in its potential to revolutionize energy consumption practices within GHs, fostering a more economically viable and ecologically responsible approach to agricultural production. In the following, we present an optimal strategy to address these issues.
Throughout the article, we use the terms “solar energy” and “PV”. Solar energy refers to energy derived from the sun in a general sense, while PV specifically refers to the technology that converts sunlight into electricity. In our study, we use these terms interchangeably to cover both the overall concept of solar energy and the specific use of PV technology.
2.1. Objective Function for Multi-Objective Optimization
In order to provide an energy optimization method for the GH, our primary goal in terms of efficiency is to minimize the cost incurred from grid power while simultaneously maximizing the value SOC for the battery at the end of the day. It reflects the dual goal of reducing dependence on external energy sources and optimizing battery storage within the GH. Battery SOC is obtained using Equation (1) [24].
, the battery SOC, is defined as the ratio of the current battery energy, , to the battery capacity, . This equation maintains the balance between energy storage and the total capacity of the battery. We can also consider battery energy and power constraints using Equation (2).
where and also represent the minimum and maximum of battery energy, respectively. Additionally, and denote the minimum and maximum battery power, respectively.
These constraints ensure that the battery energy and power remain within the permissible range defined by its minimum and maximum capacity. It considers both the initial energy of the battery and the limits imposed by the storage system.
2.2. Energy Management System (EMS)
Depending on the scope of management, EMSs exist at various tiers including buildings, houses, and factories. As shown in Table 1, they can be connected to models composed of EMSs at different levels and degrees of efficiency [25].

Table 1.
EMS levels.
An EMS is a comprehensive framework that monitors, controls, and optimizes energy consumption and production in various contexts. It combines hardware, software, and processes to efficiently use energy resources while maintaining operational conditions. The main goal is to reduce energy costs and environmental impacts and improve system performance [26,27]. EMSs can be traditional or smart, with a growing demand for intelligent approaches as systems become more electrified. Traditional systems rely on static policies and lack real-time information, while the goal is to move towards more intelligent EMSs with dynamic policies, incorporating factors like demand forecasts and electricity prices through optimization-based methods and utilizing real-time data for automated operations [28]. Notably, these practices are already established in utilities, where strategies are employed to dictate power plant operations based on demand and pricing. This paradigm can be seamlessly extrapolated to smaller systems, including microgrids, and its applicability spans across diverse domains. The goal of smart EMSs is to have a system that continuously monitors the energy demand and how the system reacts to that demand. This helps to optimize the entire system [29]. This optimization can achieve various goals like saving energy, reducing emissions, and cutting costs. This continuous process works like a loop—it keeps happening over and over again. Figure 2 depicts various EMS approaches. On the left-hand side, the traditional EMS is presented.
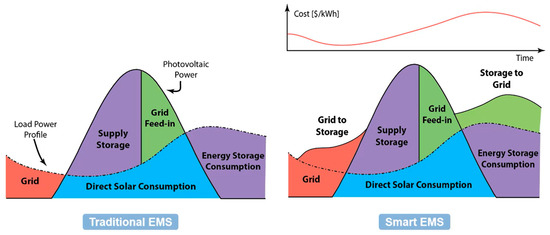
Figure 2.
EMS logic in traditional and smart stats [30].
The diagram illustrates the load power profile, represented by a dotted line, along with the input of PV power. The load profile exhibits its peak during the afternoon and evening when individuals are likely returning home. At the apex of the load power, we observe the PV power input, particularly on sunnier days when solar energy is most abundant. The distinct shaded regions showcase the traditional heuristic approach to energy management. During the early morning, energy derived from the grid is employed. As the load remains minimal, solar energy is harnessed directly while simultaneously charging the energy storage. At a specific juncture, a transition is made to channel surplus energy back into the grid. In the evening, the stored energy can be utilized. The smart approach is depicted on the right-hand side. It also considers costs. For instance, when prices are low, the grid is also utilized for storing energy, and, at a later point, the shift from storage to the grid occurs when prices become higher.
In this paper, we focus on optimizing an EMS for a microgrid configuration. The microgrid comprises PV arrays and battery systems interconnected with multiple residences and the terrestrial grid. We assume the presence of previously designed power electronic systems, with the EMS operating at a higher level, taking a holistic system-wide perspective. To achieve optimization, we employ a decision algorithm that leverages predictions and forecasts to determine when to store or draw power, when to utilize the external grid, and how to optimize energy utilization. This optimization process takes into account various system limitations and aims to provide an optimal strategy for the collective utilization of all these components within the microgrid.
The overarching control logic plays a crucial role in orchestrating the entire system, serving as the core of the EMS. This orchestration ensures efficient and coordinated operation of the microgrid components to achieve optimal energy utilization [31]. In order to improve the optimization strategy, we employ smart EMS optimization formulation for improved efficiency. To enhance the optimization strategy, we employ a smart EMS optimization formulation to achieve heightened efficiency. The primary objective is the minimization of grid power costs while simultaneously maximizing the final SOC of the battery using Equation (3).
where , , and indicate the power of the PV array, battery, and load, respectively, and is a weighting parameter. Moreover, there exist some constraints, one of which pertains to maintaining a balanced load, as below:
The decision variables should be independent of each other, and the value of one variable should not affect the value of another variable. The number of decision variables should be kept to a minimum to reduce the complexity of the problem. Ignoring independent variables decreases the accuracy of the EMS algorithm and considering dependent variables increases computation volume and time. and are dependent. On the other hand, can be calculated using (4). Since we use fixed profiles for and at each optimization time, we can have as follows:
that minimizes will minimize
Considering energy is the cumulative sum of power consumption or generation over a specific period, we can express energy of the battery as
Using Equations (1) and (7), we can rewrite the as follows:
So, that minimizes will minimize using Equation (8). Removing the constant part, we arrive at the following:
It is obvious that that minimizes will minimize given in (9). So, the optimization problem can be expressed as follows:
The optimization problem finds the decision variables for the prediction horizon, , while assuming that the decision variables remain constant for the duration of . The optimization process is repeated at intervals of optimization time, . The hyperparameters are , , and .
Since the problem is high-dimensional, some numerical methods such as Bayesian optimization incur significant computational costs to solve optimization problem (10) to calculate the decision variable at each time instant. The following MATLAB commands are utilized to optimize decision variables, resulting in nearly identical outcomes:
- -
- “fmincon”: used to find the minimum of a constrained nonlinear multivariable function.
- -
- “fminimax”: employed to solve a minimax constraint problem.
- -
- “solve”: utilized to address optimization problems or equation problems.
is variable and is equal to the rest of the day, since the cost of grid power is highest during the last hours of the day. It is obvious that .
The Bayesian method is used to optimize and using the “bayesopt” MATLAB command. The Bayesian method is a powerful numerical optimization technique that facilitates efficient exploration of the search space, taking advantage of promising areas while also taking into consideration uncertainty and prior knowledge.
To compare the effectiveness of the proposed smart strategy, the traditional EMS algorithm is shown in Figure 3. Also, Figure 4 shows how a smart EMS works. Over 24 h, optimization is repeated every . At each optimization time instant (ti), the grid power cost is minimized for time interval . The calculated optimal value for battery power is used for each ti, and battery power will remain constant during the next optimization time instant to calculate the SOC. For each optimization, the SOC at the optimization time instant (ti) is known.
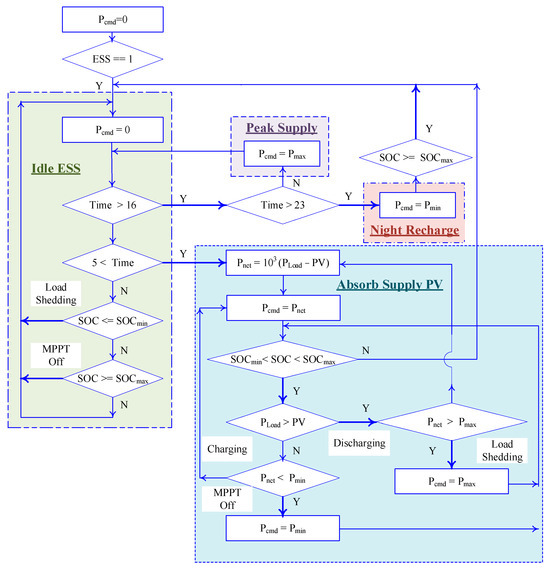
Figure 3.
Traditional EMS algorithm.
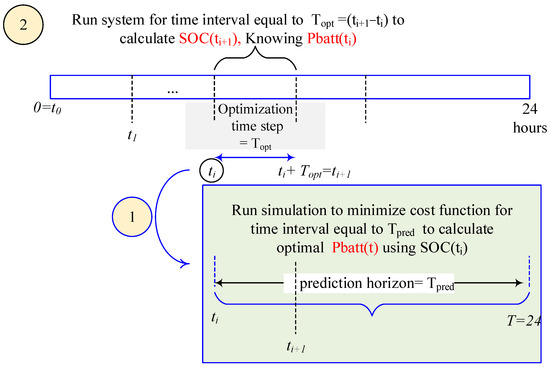
Figure 4.
Smart EMS procedure.
3. Simulation Results
To show the simulation results, we present and compare two modes of smart energy management and traffic energy management. Figure 5 displays the implemented EMS approaches for GHs in Simulink. As we already mentioned, by considering energy management indicators and loads, we can consider the GH as a microgrid. A straightforward microgrid system has been constructed within Simulink. This model serves the purpose of observing how the system behaves when considering both the traditional and optimization-based EMS approaches. The objective is to make a comparison between these two techniques. The model encompasses a load variable that symbolizes residential homes. Additionally, a fixed load has been incorporated, which remains constant over time, resembling the fundamental load. Furthermore, the model comprises a solar array, which functions as an input and can adopt distinct irradiance patterns. These patterns, corresponding to clear and cloudy days, can be observed in Figure 6.
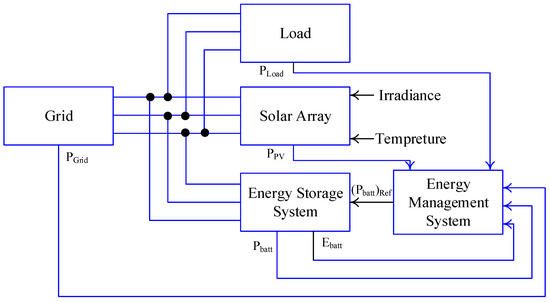
Figure 5.
Implementing EMS approaches for GHs in Simulink.
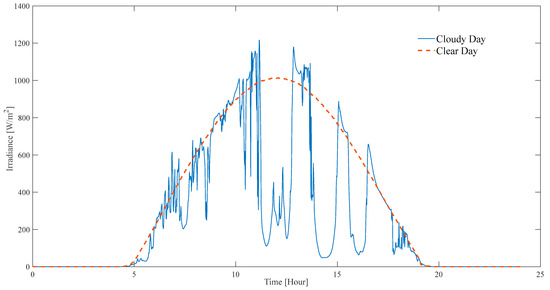
Figure 6.
Comparison of irradiance profile on a clear and cloudy day.
Figure 7 displays the load profile of the study case, and Figure 8 illustrates the variations in grid power costs based on different values of the prediction horizon, , and optimization time, . This reaffirms the significance of optimizing these hyperparameters. It is evident that extending the prediction horizon imposes a heavier computational burden. However, given that the highest costs occur during the final hours of the day, it is imperative to encompass this period within to ensure the reliability of the predictions. Hence, prediction horizon () is considered as a variable parameter, equals to the rest of the day. As a consequence, is initially longer at the beginning of the day and gradually shortens as time progresses.
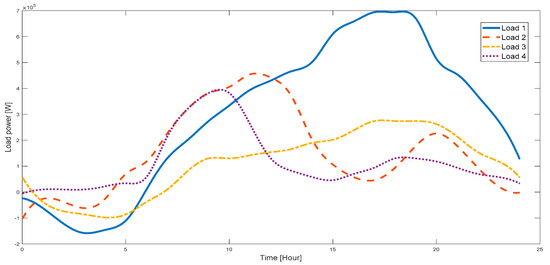
Figure 7.
Load profiles of the study case.
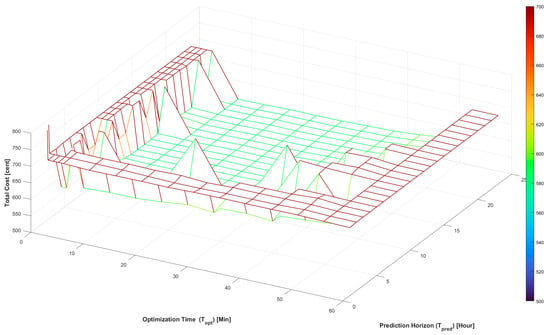
Figure 8.
Impact of prediction horizon and optimization time on grid power costs.
In Figure 9, we present a comprehensive illustration of various parameters within the microgrid environment, including microgrid voltage, PV output, battery status, grid power, and load power.
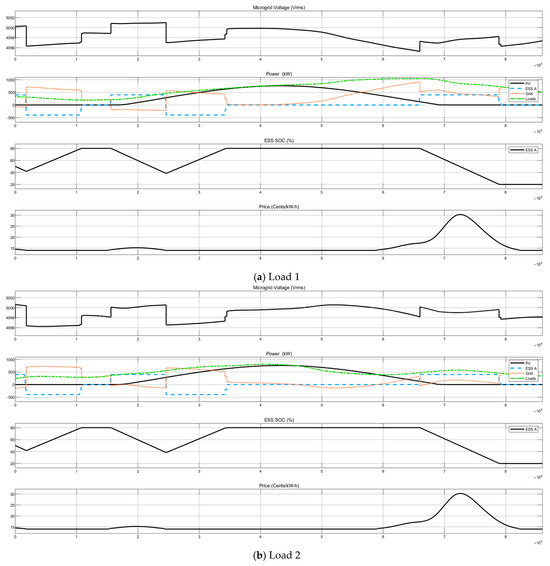

Figure 9.
Simulation results for different load profiles using smart EMS.
Figure 9 depicts the SOC of the battery and the grid power cost across the day for different load profiles, utilizing the smart EMS. By employing two different traditional intelligent modes, we can effectively compare the results against the smart EMS approach. To facilitate comparison, Table 2 outlines the simulation numerical results for both traditional and smart EMS methodologies. The data clearly indicate a remarkable achievement: a reduction of more than 50% in the objective function with the implementation of the smart EMS. This reduction signifies a significant enhancement in the smart EMS approach’s capability to minimize grid power costs while simultaneously endeavoring to maximize the SOC of the battery by day’s end. The comparison underscores the efficacy of the smart EMS in optimizing energy consumption within GH environments. It highlights the system’s ability to adapt and respond dynamically to varying load profiles, environmental conditions, and operational requirements, thereby enhancing overall energy efficiency and resource utilization within the GH setting. These findings reaffirm the value and potential of the smart EMS approach in addressing the complex challenges associated with energy management in agricultural contexts. They provide a solid foundation for future research and practical implementation of sustainable energy solutions in GH environments, contributing to the advancement of resource-efficient and environmentally conscious practices in agricultural production.

Table 2.
Comparing simulation results for traditional and smart EMS.
To resemble real-world scenarios more closely, a tolerance of 10% for the load power and irradiation profile has been incorporated, as illustrated in Figure 10. Table 3 shows the numerical results. and are considered 5 min. The numerical results show that, despite variations in the load power and irradiation profile, the objective function remains relatively stable. This observation confirms the robust performance of the suggested EMS.
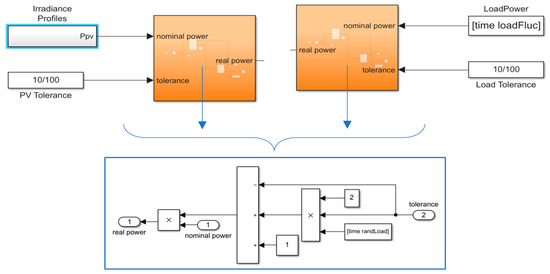
Figure 10.
Irradiance and load power with 10% tolerance.

Table 3.
Simulation result for irradiance and load power with 10% tolerance.
Repeating the simulation considering partial shading for 30 min starting at 11 a.m., as shown in Figure 11, the simulation results are given in Table 4. The simulation results indicate that partial shading increases the objective function of 0.35553%. This negligible increase demonstrates the effective response of the suggested EMS to natural events like partial shading, highlighting its adaptability and resilience.
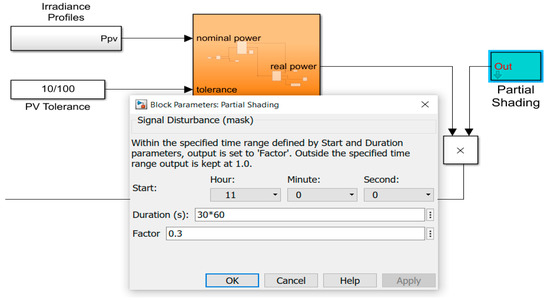
Figure 11.
Partial shading at 11 a.m. for 30 min.

Table 4.
Simulation result for partial shading at 11 a.m. for 30 min.
As expected, with the reduction in PV power, there is an increase in the summation of the grid, and battery power is increased to satisfy the power balance. Figure 12 compares how PV, battery, grid, load power, and SOC of the battery change with and without partial shading for Load 2.
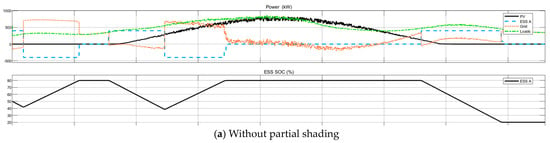
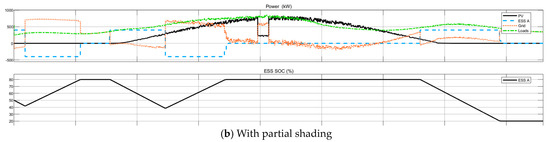
Figure 12.
Comparing power and SOC with (a) and without (b) partial shading for Load 2.
Initial forecasting for irradiance and temperature is utilized to predict photovoltaic power (Ppv). Since forecasting is not always precise, three different cases are considered, as follows:
- Case 1: Ppv prediction is almost correct. For optimization, initial Ppv prediction is used.
- Case 2: Ppv prediction is not correct. For optimization, initial Ppv prediction is used.
- Case 3: Ppv prediction is not correct. For optimization, updated Ppv prediction is used.
It is assumed that, at 11 a.m., the PV power prediction is updated; its value decreased to 70% of its initial prediction. Simulation numerical results for different cases for different values of optimization time are compared in Table 5. Battery power changes for Cases 1, 2, and 3 are depicted in Figure 13, Figure 14 and Figure 15. The simulation results underscore the significance of updating the forecasting of Ppv in influencing the objective function. This updating process is critical for aligning with real-world conditions and attaining optimal results. Additionally, the simulation results illustrate the importance of the optimal selection of the optimization time step in impacting both the value of the objective function and the execution time.

Table 5.
Simulation result for different optimization times.
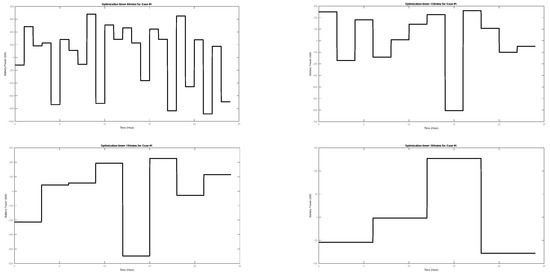
Figure 13.
Battery power for different optimization times when Ppv prediction is almost correct (Case 1).
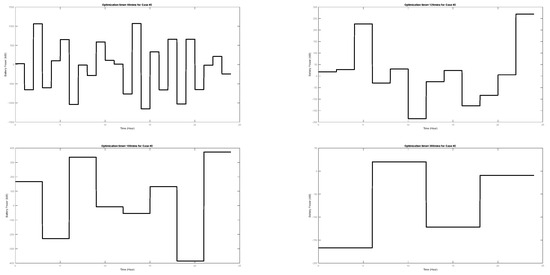
Figure 14.
Battery power for different optimization times when Ppv prediction is not correct and initial Ppv prediction is used (Case 2).
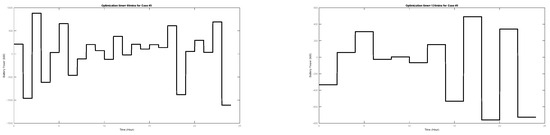

Figure 15.
Battery power for different optimization times when Ppv prediction is not correct and updated Ppv prediction is used (Case 3).
It is evident that the longer the optimization time step, the shorter the execution time. However, as illustrated in Table 5, there is no consistent or general trend observed between the optimization time step and the objective function (). Although, in Case 1, increasing the optimization time step results in a decrease in f_obj, this trend does not hold true for Cases 2 and 3. Surprisingly, for an optimization time step of 180 min, is minimized, underscoring the significance of optimizing the optimization time step.
4. Discussion
The optimization problem finds the decision variables for the prediction horizon, , using MATLAB commands such as “solve”, while assuming that the decision variables remain constant for the duration of . The optimization process is repeated at intervals of the optimization time, . is a variable illustrating the rest of the day. “Bayesopt” in MATLAB is used to optimize and .
The simulation results demonstrate a substantial improvement, with the smart EMS achieving over a 50% decrease in the objective function compared to the traditional EMS. This notable enhancement validates the efficacy of the proposed approach in minimizing grid power costs while maximizing the battery’s state of charge (SOC) by day’s end. Furthermore, the robustness of the smart EMS is evident in its consistent performance across variations in load power and irradiation profiles, indicating its resilience to environmental factors.
Additionally, the inclusion of partial shading scenarios reveals a negligible increase of only 0.35553% in the objective function, highlighting the adaptability of the smart EMS to natural events. This adaptability is crucial for ensuring reliable energy management under changing conditions.
Moreover, the simulation results emphasize the importance of updating the forecasting of PV power, as it significantly influences the objective function. This underscores the necessity of aligning predictions with real-world conditions to achieve optimal results. Furthermore, the optimal selection of the optimization time step is shown to impact both the objective function value and execution time, emphasizing the need for careful parameter optimization.
Table 6 shows a comparison between the current work and three other similar articles in the field of optimization and energy management in greenhouses, highlighting the advantages of our article over them. This comparison demonstrates the unique contributions and advantages of our paper over other articles in the field, particularly in terms of the significant decrease in the objective function achieved by our smart energy management system and its adaptability to environmental factors.

Table 6.
A comparison between this paper and three other similar articles.
In summary, the simulation results validate the effectiveness of the proposed smart EMS in optimizing energy consumption within greenhouse environments. The robust performance, adaptability to environmental factors, and sensitivity to parameter selection underscore the practical utility of the smart EMS in real-world scenarios, contributing to more efficient and sustainable energy management practices.
5. Conclusions
In conclusion, this paper delves into the pivotal realm of agricultural greenhouse (GH) energy management, offering a comprehensive solution through the integration of renewable energy resources (RESs) and the implementation of a smart energy management system (EMS). The escalating global demand for food production necessitates a paradigm shift toward sustainable and efficient practices within GH agriculture. The proposed multi-objective optimization approach, centered on minimizing grid energy consumption while maximizing battery state of charge (SOC), represents a significant advancement. By introducing solar energy as a primary source and employing a smart EMS, the study addresses the dual challenges of reducing operational costs and mitigating the environmental impact associated with conventional energy sources.
The significance of this research extends beyond theoretical advancements, offering tangible benefits to GH operators and the environment. The identified hyperparameters, optimized through the ellipse optimization method, contribute to the adaptability and efficiency of the smart EMS.
Comparison with traditional optimization algorithms underscores the efficiency of the proposed smart EMS, reaffirming its potential to revolutionize GH energy management. As the agricultural sector grapples with the imperative of sustainability, this research catalyzes the adoption of innovative and eco-friendly practices, paving the way for a more resilient and efficient future in GH agriculture.
Future research directions may involve exploring advanced optimization techniques to improve the performance of the smart EMS further. Additionally, investigating the integration of other renewable energy sources like wind or geothermal energy could be beneficial. Field studies validating the effectiveness of the proposed solution in real-world GH environments could also be pursued. These efforts would contribute to ongoing initiatives aimed at optimizing energy management practices and fostering sustainability in agriculture.
Author Contributions
Conceptualization, F.J. and M.G.; methodology, F.J., M.G. and M.M.; software, F.J. and M.G.; validation, F.J., M.G., M.M., Z.W. and R.P.; formal analysis, F.J., M.G. and M.M.; investigation, F.J., M.G., M.M., Z.W. and R.P.; resources, F.J., M.G., M.M., Z.W. and R.P.; data curation, F.J., M.G., M.M., Z.W. and R.P.; writing—original draft preparation, F.J. and M.G.; writing—review and editing, F.J. and M.G.; visualization, F.J., M.G., M.M., Z.W. and R.P.; supervision, M.M., Z.W. and R.P.; project administration, M.M., Z.W. and R.P.; funding acquisition, M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This project was funded by Mitacs Accelerate Program, partnered with the Petroleum Technology Research Centre (PTRC) in Regina, SK, Canada, project ID: IT29866.
Data Availability Statement
Data will be made available upon request.
Acknowledgments
The natural language artificial intelligence, ChatGPT (Version 3.5, OpenAI), was employed in this process. This AI tool, renowned for its proficiency in language tasks, has been instrumental in meticulously polishing the language of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jamshidi, F.; Salehizadeh, M.R.; Yazdani, R.; Azzopardi, B.; Jately, V. An Improved Sliding Mode Controller for MPP Tracking of Photovoltaics. Energies 2023, 16, 2473. [Google Scholar] [CrossRef]
- Fathi, M.; Ghiasi, M. Optimal DG Placement to Find Optimal Voltage Profile Considering Minimum DG Investment Cost in Smart Neighborhood. Smart Cities 2019, 2, 328–344. [Google Scholar] [CrossRef]
- Kolagar, M. Adherence to urban agriculture in order to reach sustainable cities; a BWM–WASPAS approach. Smart Cities 2019, 2, 31–45. [Google Scholar] [CrossRef]
- Anser, M.K.; Khan, M.A.; Nassani, A.A.; Aldakhil, A.M.; Hinh Voo, X.; Zaman, K. Relationship of environment with technological innovation, carbon pricing, renewable energy, and global food production. Econ. Innov. New Technol. 2021, 30, 807–842. [Google Scholar] [CrossRef]
- Ghiasi, M.; Wang, Z.; Mehrandezh, M.; Paranjape, R. A Systematic Review of Optimal and Practical Methods in Design, Construction, Control, Energy Management and Operation of Smart Greenhouses. IEEE Access 2024, 12, 2830–2853. [Google Scholar] [CrossRef]
- Smith, D.; Taylor-Curran, H.; Barkwith, A.; Thomas, R.L.; Kirk, K.; Hannis, S.; Shorter, K.; Walker-Verkuil, K. Applying ground gas and gas flux monitoring techniques to low-enthalpy, shallow geothermal energy exploration. Geothermics 2021, 97, 102251. [Google Scholar] [CrossRef]
- Wang, K.; Yuan, B.; Ji, G.; Wu, X. A comprehensive review of geothermal energy extraction and utilization in oilfields. J. Pet. Sci. Eng. 2018, 168, 465–477. [Google Scholar] [CrossRef]
- Li, X.; Wang, S. Energy management and operational control methods for grid battery energy storage systems. CSEE J. Power Energy Syst. 2019, 7, 1026–1040. [Google Scholar]
- Chen, C.; Nelson, H.; Xu, X.; Bonilla, G.; Jones, N. Beyond technology adoption: Examining home energy management systems, energy burdens and climate change perceptions during COVID-19 pandemic. Renew. Sustain. Energy Rev. 2021, 145, 111066. [Google Scholar] [CrossRef]
- Park, D.-H.; Park, J.-W. Wireless sensor network-based greenhouse environment monitoring and automatic control system for dew condensation prevention. Sensors 2011, 11, 3640–3651. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, L.; Li, Y.; Li, D. Model predictive control and its application in agriculture: A review. Comput. Electron. Agric. 2018, 151, 104–117. [Google Scholar] [CrossRef]
- Sofwan, A.; Sumardi, S.; Ahmada, A.I.; Ibrahim, I.; Budiraharjo, K.; Karno, K. Smart greetthings: Smart greenhouse based on Internet of Things for environmental engineering. In Proceedings of the 2020 International Conference on Smart Technology and Applications (ICoSTA), Surabaya, Indonesia, 20 February 2020; pp. 1–5. [Google Scholar]
- Cuce, E.; Harjunowibowo, D.; Cuce, P.M. Renewable and sustainable energy saving strategies for greenhouse systems: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 64, 34–59. [Google Scholar] [CrossRef]
- Ghiasi, M.; Dehghani, M.; Niknam, T.; Siano, P.; Haes Alhelou, H. A Detailed Analysis of the Barriers of Using Renewable Energies and Their Roles in Sustainable Development in Iran. In Handbook of Smart Energy Systems; Fathi, M., Zio, E., Pardalos, P.M., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 1–24. [Google Scholar]
- Tzounis, A.; Katsoulas, N.; Bartzanas, T.; Kittas, C. Internet of Things in agriculture, recent advances and future challenges. Biosyst. Eng. 2017, 164, 31–48. [Google Scholar] [CrossRef]
- Ghiasi, M.; Ahmed, F.; Paranjape, R.; Wang, Z.; Mehrandezh, M. A Comparative Analysis for Control of Heating and Cooling Systems of a Real Office Building with TRNSYS. In Proceedings of the 2023 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Regina, SK, Canada, 24–27 September 2023; pp. 1–6. [Google Scholar]
- Karimi, H.; Jadid, S.; Hasanzadeh, S. Optimal-sustainable multi-energy management of microgrid systems considering integration of renewable energy resources: A multi-layer four-objective optimization. Sustain. Prod. Consum. 2023, 36, 126–138. [Google Scholar] [CrossRef]
- Bersani, C.; Ouammi, A.; Sacile, R.; Zero, E. Model predictive control of smart greenhouses as the path towards near zero energy consumption. Energies 2020, 13, 3647. [Google Scholar] [CrossRef]
- Cai, W.; Wen, X.; Tu, Q. Designing an intelligent greenhouse monitoring system based on the Internet of Things. Appl. Ecol. Environ. Res. 2019, 17, 8449–8464. [Google Scholar] [CrossRef]
- Ghiasi, M.; Wang, Z.; Mehrandezh, M.; Jalilian, S.; Ghadimi, N. Evolution of smart grids towards the Internet of energy: Concept and essential components for deep decarbonisation. IET Smart Grid 2023, 6, 86–102. [Google Scholar] [CrossRef]
- Mellit, A.; Benghanem, M.; Herrak, O.; Messalaoui, A. Design of a novel remote monitoring system for smart greenhouses using the internet of things and deep convolutional neural networks. Energies 2021, 14, 5045. [Google Scholar] [CrossRef]
- Rajabzadeh, M.; Fatorachian, H. Modelling Factors Influencing IoT Adoption: With a Focus on Agricultural Logistics Operations. Smart Cities 2023, 6, 3266–3296. [Google Scholar] [CrossRef]
- Ghiasi, M.; Wang, Z.; Mehrandezh, M.; Paranjape, R. Integrating Solar-Collector and Biomass Heating Systems for Sustainable Greenhouse Agriculture. In Proceedings of the IEEE International Conference on Energy Technologies for Future Grids (IEEE ETFG 2023), Wollongong, Australia, 3–6 December 2023. [Google Scholar]
- Hoang, K.D.; Lee, H.-H. State of Charge Balancing for Distributed Battery Units Based on Adaptive Virtual Power Rating in a DC Microgrid. J. Electr. Eng. Technol. 2020, 15, 2121–2131. [Google Scholar] [CrossRef]
- Aziz, M.; Oda, T.; Mitani, T.; Watanabe, Y.; Kashiwagi, T. Utilization of electric vehicles and their used batteries for peak-load shifting. Energies 2015, 8, 3720–3738. [Google Scholar] [CrossRef]
- Yu, D.; Zhang, T.; He, G.; Nojavan, S.; Jermsittiparsert, K.; Ghadimi, N. Energy management of wind-PV-storage-grid based large electricity consumer using robust optimization technique. J. Energy Storage 2020, 27, 101054. [Google Scholar] [CrossRef]
- Molla, T.; Khan, B.; Moges, B.; Alhelou, H.H.; Zamani, R.; Siano, P. Integrated optimization of smart home appliances with cost-effective energy management system. CSEE J. Power Energy Syst. 2019, 5, 249–258. [Google Scholar] [CrossRef]
- Slob, N.; Hurst, W. Digital Twins and Industry 4.0 Technologies for Agricultural Greenhouses. Smart Cities 2022, 5, 1179–1192. [Google Scholar] [CrossRef]
- Gonzalez-Gil, P.; Martinez, J.A.; Skarmeta, A. A Prosumer-Oriented, Interoperable, Modular and Secure Smart Home Energy Management System Architecture. Smart Cities 2022, 5, 1054–1078. [Google Scholar] [CrossRef]
- Mathworks. Microgrid System Development and Analysis. 2023. Available online: https://www.mathworks.com/videos/series/microgrid-system-development-and-analysis.html (accessed on 25 March 2024).
- Ghadimi, N.; Yasoubi, E.; Akbari, E.; Sabzalian, M.H.; Alkhazaleh, H.A.; Ghadamyari, M. SqueezeNet for the forecasting of the energy demand using a combined version of the sewing training-based optimization algorithm. Heliyon 2023, 9, e16827. [Google Scholar] [CrossRef] [PubMed]
- Ziapour, B.M.; Hashtroudi, A. Performance study of an enhanced solar greenhouse combined with the phase change material using genetic algorithm optimization method. Appl. Therm. Eng. 2017, 110, 253–264. [Google Scholar] [CrossRef]
- Adetoro, S.A.; Olatomiwa, L.; Tsado, J.; Dauda, S.M. A comparative analysis of the performance of multiple meta-heuristic algorithms in sizing hybrid energy systems connected to an unreliable grid. e-Prime-Adv. Electr. Eng. Electron. Energy 2023, 4, 100140. [Google Scholar] [CrossRef]
- Adesanya, M.A.; Na, W.-H.; Rabiu, A.; Ogunlowo, Q.O.; Akpenpuun, T.D.; Rasheed, A.; Yoon, Y.-C.; Lee, H.-W. TRNSYS simulation and experimental validation of internal temperature and heating demand in a glass greenhouse. Sustainability 2022, 14, 8283. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).