1. Introduction
Fifth generation (5G) communication systems and beyond play a crucial role in the development and improvement of smart cities by enabling seamless connectivity to support a wide range of applications [
1]. A common backbone to almost all aspects of smart cities relates to reliable and prompt data transmission. In fact, 5G networks can support a very large number of users and thus facilitate the proliferation of Internet of Things (IoT) applications such as infrastructure and environment monitoring, and enhanced healthcare solutions [
2,
3]. Moreover, 5G represents a leap in terms of increased capacity and throughput allowing for large amounts of data transfer, which is critical for traffic management [
4] and real-time public safety and surveillance [
5,
6]. Finally, the latency and high speed of 5G systems make them essential for the operation of autonomous vehicles in smart cities [
7,
8].
The design of wireless infrastructure for 5G systems involves several aspects related to networking, data transmission and radiofrequency (RF) electronics. This paper focuses on performance enhancement of the RF transmitters found in base stations, and more specifically on the compensation of nonlinear distortions exhibited by the power amplifier (PA). In fact, 5G systems impose increasingly rigid requirements on the performance of the radio frequency front-end of the transmitters, and more specifically the RF power amplifier. From a performance perspective, linearity and power efficiency are two antagonist but critically important requirements. While using linear amplifiers can easily address the linearity issue, the need for operating the power amplifier in a power efficient mode calls for a trade-off between linearity and efficiency. Such trade-off is commonly addressed by designing high-efficiency nonlinear power amplifiers and compensating for their nonlinearity by means of linearization techniques [
9].
Predistortion, and more specifically baseband digital predistortion, is widely adopted for the linearization of base station power amplifiers. This consists of implementing, in the baseband digital domain, a nonlinear function that is complementary to that of the amplifier being linearized such that the cascade made of the predistorter and the amplifier operates as a linear amplification system. Even though digital predistortion is often perceived as a mature linearization technology, several improvements are continuously needed to address the specificities of emerging wireless standards and the evolving requirements that these impose. Recently, several researchers have addressed the challenges in digital predistortion systems. These include the linearization of millimeter-wave power amplifiers [
10], the reduction of the computational complexity associated with delay estimation algorithm [
11], and the computational stability of low sampling rate systems [
12]. Furthermore, neural networks are gaining popularity, and have recently been reported for bandwidth, power and carrier configuration resilient predistorters [
13], multi-input multi-output (MIMO) beamforming applications [
14], 5G radio over fiber applications [
15] and 6G dynamic spectrum aggregation [
16]. Through all recent work, a common issue can be clearly identified. The design of digital predistorters for modern applications has to address two major concerns: the accurate characterization of the amplifier’s nonlinear behavior, and the perfect match between the predistortion function and the amplifier’s nonlinearity [
9].
The observation bandwidth of the feedback path used to acquire the amplifier’s output signal is becoming a design bottleneck due to the use of wideband signals in modern applications with up to 100 MHz in 5G sub-6 GHz frequency band and up to 400 MHz in the 5G millimeter wave frequency range (above 24 GHz). The main concern is that, due to spectrum regrowth, the signal at the output of the PA typically has up to five times the bandwidth of the signal being transmitted. This spectral regrowth is directly caused by the nonlinearity of the power amplifier. Therefore, the sampling rate of the analog to digital converter (ADC) in the feedback path of predistortion systems needs to accommodate such wide bandwidths. Recently, several research efforts have focused on the reduction of the required bandwidth of the feedback path, also referred to as the observation bandwidth, in order to enable the predistortion of power amplifiers driven by wideband signals using architectures with observation bandwidths that are less than five times that of the transmitted signal [
17,
18,
19,
20,
21,
22,
23]. In [
17], a sub-band decomposition technique is proposed to divide the signal spectrum into different ranges to be processed separately. These ranges are overlapping in the frequency domain due to the nature of decomposition filters. Compensating for this overlap and ensuring signal reconstruction once the predistortion function is applied typically requires significant computational overhead. In [
18], extended correction bandwidth is achieved while using analog to digital converters operating at a reduced sampling rate. However, this leads to a significant hardware overhead by requiring two feedback paths as well as the use of an analog predistortion function. The bandlimited DPD system proposed in [
19] uses a relaxed sampling rate and does not add significant computational overhead. The main drawback in this technique is that the correction bandwidth of the digital predistorter is identical to the observation bandwidth of the feedback path. This issue was addressed in [
20,
21] where a correction bandwidth larger than the observation bandwidth was reported. However, this was achieved at the expense of complex signal spectral extrapolation technique [
20] and hardware overhead [
21]. The authors in [
22] proposed a low-complexity technique to extend the correction bandwidth of digital predistortion system through the use of a synthetic test signal. This made this technique valuable for laboratory experiments but not useful for field deployed systems. A two-box DPD system with extended correction bandwidth was proposed for an LTE-A power amplifier [
24]. This predistortion system uses a bank of look-up tables (LUT)-based memoryless predistortion functions that are pre-calculated from offline measurements, which represents a limitation.
Accordingly, previously reported techniques suffer either from a degradation in the correction bandwidth due to the limitation of the observation bandwidth, or a significant computational/hardware complexity overhead in order to maintain the correction bandwidth while operating the DPD feedback path at a relaxed sampling rate. This represents a major limitation in state-of-the-art work. Hence, a low-complexity digital predistortion technique in which a reduced sampling rate can be used without limiting the correction bandwidth is needed.
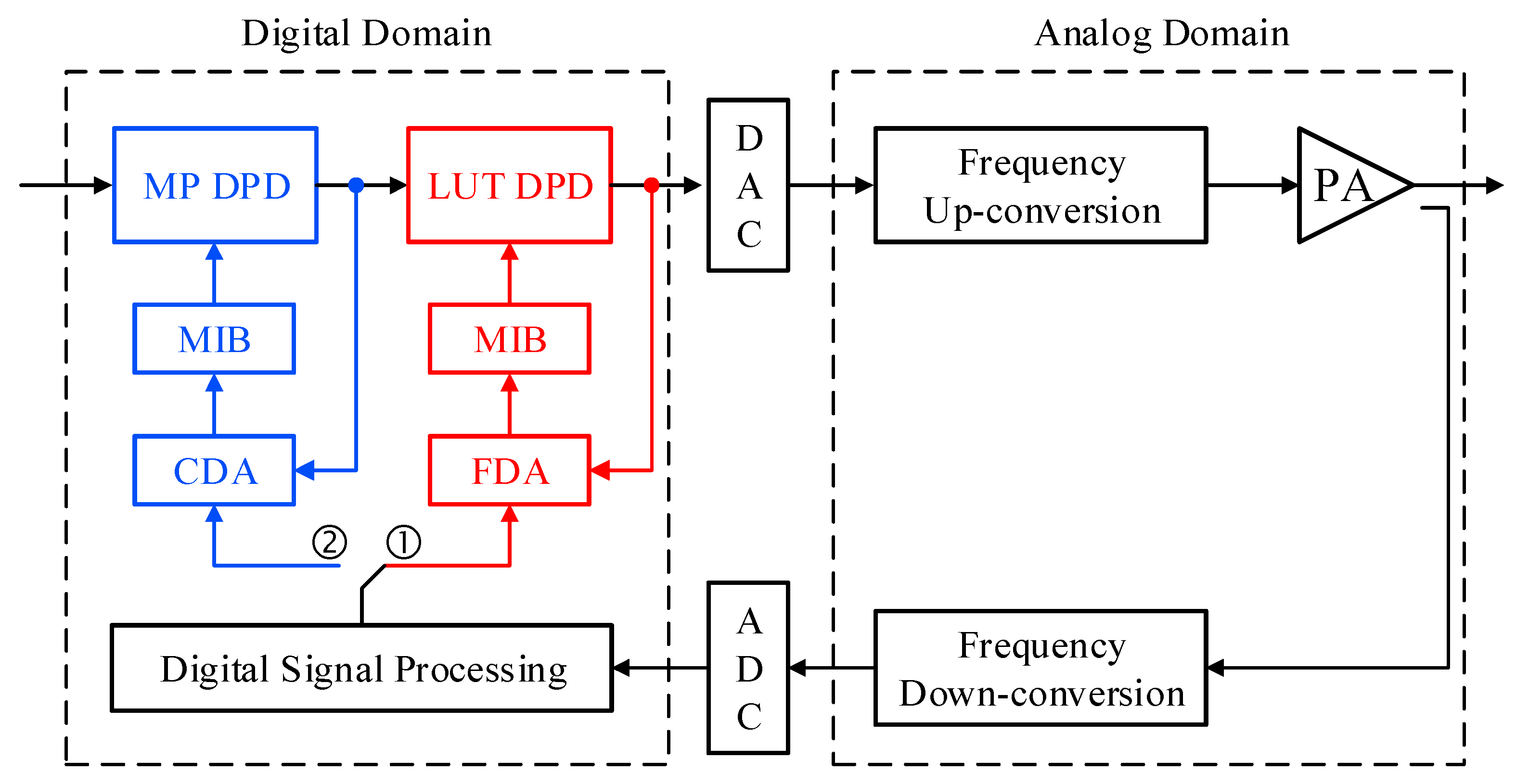
In this paper, a sequential digital predistorter (S-DPD) system built using a twin nonlinear two-box (TNTB) predistorter able to achieve an extended correction bandwidth is proposed. The proposed predistorter system contrasts with previously reported TNTB predistorters [
23,
24] in several major aspects. Firstly, the predistortion function is identified in two sequential steps: two consecutive characterizations using reduced feedback bandwidth are used to derive the static predistortion sub-function implemented as a memoryless look-up table, and then the dynamic nonlinear sub-function implemented as a memory polynomial (MP). Secondly, the S-DPD system does not require any hardware overhead to implement the predistortion function. Indeed, only a single standard feedback loop is needed to derive the predistortion function since the sequential characterization is performed within the digital domain. Thirdly, the computational complexity associated with the proposed S-DPD system is reduced by adopting a coarse delay estimation and alignment algorithm while calculating the coefficients of the memory polynomial sub-function of the predistorter and alleviating the need for data de-embedding when identifying the second predistortion sub-function. Finally, extended correction bandwidth is achieved without the need for offline characterization of the static nonlinearity of the device under test (DUT). In fact, the use of static predistortion function derived from offline measurements (as reported in prior work) represents a significant drawback for several reasons. First, there is a need to pre-calculate a large set of memoryless predistortion functions that would take into account the variation of the operating conditions of the PA mainly due to the variations of the average power as well as the signal statistics. Secondly, the PA is likely to experience long-term drifts of the bias point, operating temperature, etc. While some of these changes (such as bias drifts) are unobservable, their impact on the DPD performance translates into a degradation of the adjacent channel leakage ratio. Taking into account the signal variations as well as the operating conditions, variations will require an unrealistically large set of LUTs to be pre-built offline. Moreover, from an implementation point of view, there is a need to determine which of the memoryless LUTs needs to be applied as the static predistortion function. This requires an additional processing block that would select the most suitable LUT predistorter based on the knowledge of the signal characteristics, operating conditions, etc.
Accordingly, the novelty in the proposed predistorter is related to the following aspects:
First, the predistortion function is performed in a sequential manner through two distinct characterization steps.
Second, a single characterization hardware loop is used for both characterization steps.
Third, a relaxed sampling rate is used in the feedback path for acquisition of the power amplifier’s output.
Fourth, the computational complexity overhead due to the proposed technique is minimized through the use of coarse delay alignment when identifying the second predistortion sub-function.
Fifth, the use of sequential identification process minimizes the computational complexity associated with the signal reconstruction to a simple re-sampling operation.
The above-mentioned five aspects cohesively allow for substantial improvements in digital predistortion systems that makes it possible to achieve satisfactory linearity performance over a correction bandwidth much larger than the observation bandwidth of the feedback path without the computational and hardware complexity drawbacks observed in previously reported work.
In
Section 2, the proposed S-DPD system is introduced and thoroughly discussed. In
Section 3, the S-DPD system is applied for the linearization of an inverse Class-F power amplifier prototype. The computational complexity reduction through coarse delay alignment is investigated in
Section 4. The conclusions are reported in
Section 5.
3. Performance Assessment of the Proposed Digital Predistortion System
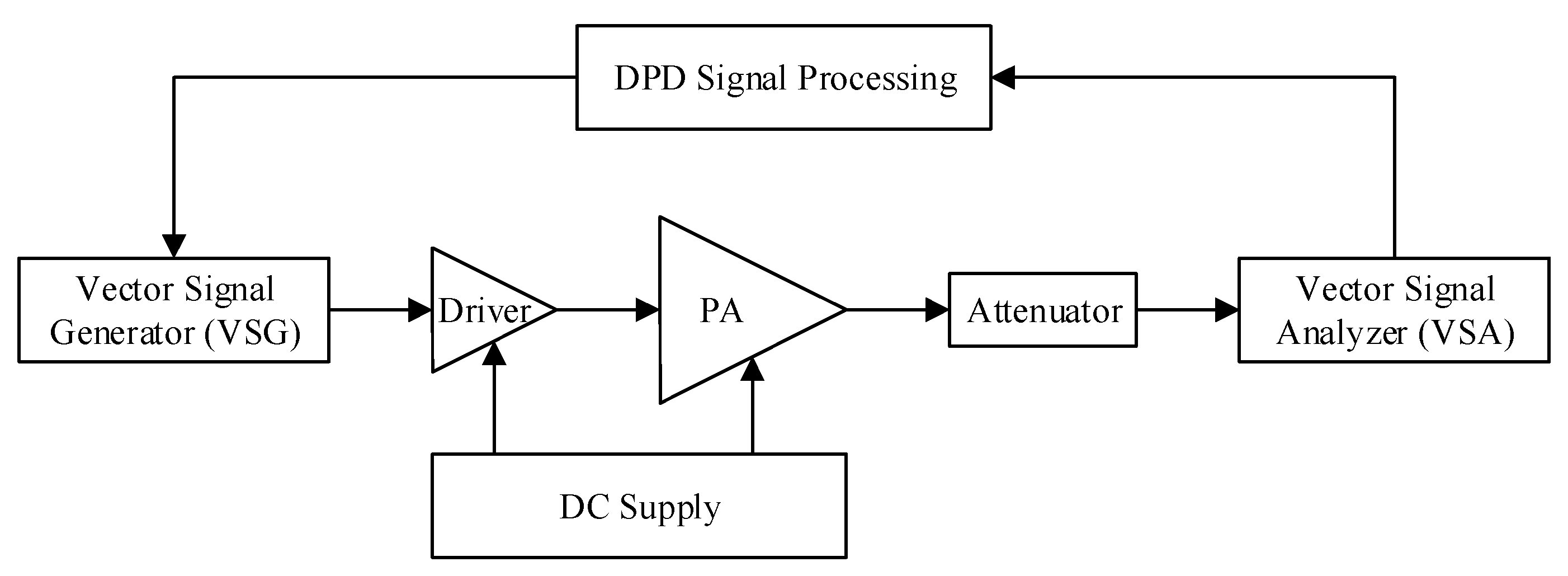
For the experimental validation of the proposed DPD, an inverse Class-F power amplifier operating around 900 MHz was used. The functional block diagram of the experimental setup is reported in
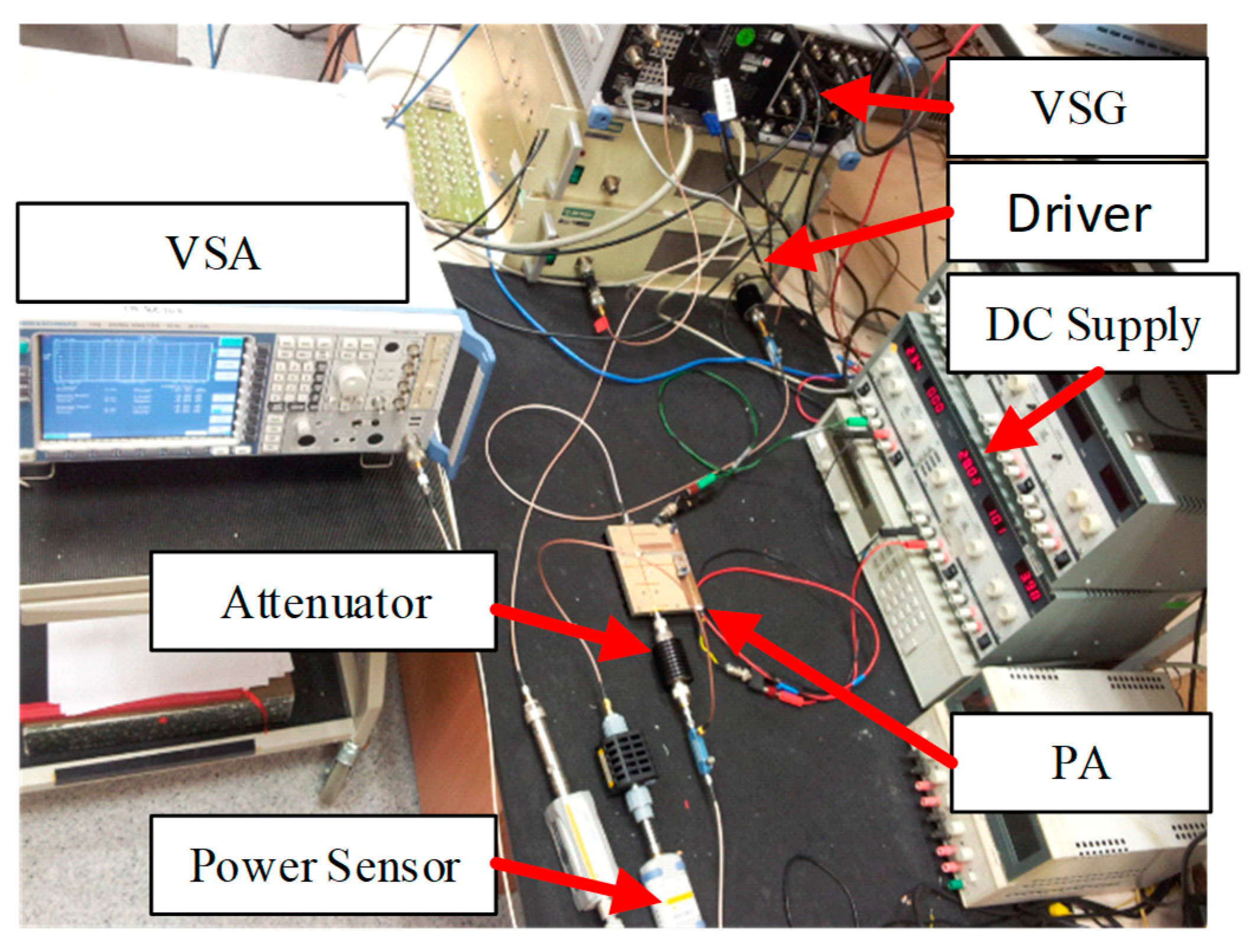
Figure 6. The DPD signal processing unit includes the functionalities related to time delay alignment, DPD function identification and predistortion of the input signal. The baseband digital waveform at the output of the DPD signal processing unit is fed into the vector signal generator (VSG) which implements the digital to analog conversion and the frequency up-conversion. The signal at the output of the VSG is pre-amplified using a driver before being applied at the input of the main power amplifier. The signal at the output of the power amplifier is first attenuated and then fed into the vector signal analyzer (VSA). The VSA performs the frequency down-conversion, the analog to digital conversion, and the demodulation of the signal. The resulting digital waveform corresponding to the PA’s output signal is used by the DPD signal processing block to synthesize the predistortion function. A photograph of the experimental setup is presented in
Figure 7.
The PA was driven by a test signal having a bandwidth of 20 MHz. This bandwidth is largest that can be handled by the available experimental setup. The output signal was acquired at various sampling rates using the vector signal analyzer. The sampling rates used were 100 MSa/s, 50 MSa/s, 40 MSa/s, 30 MSa/s and 25 MSa/s. The in-phase and quadrature components of the baseband input signal
and the in-phase and quadrature components of the baseband output signal
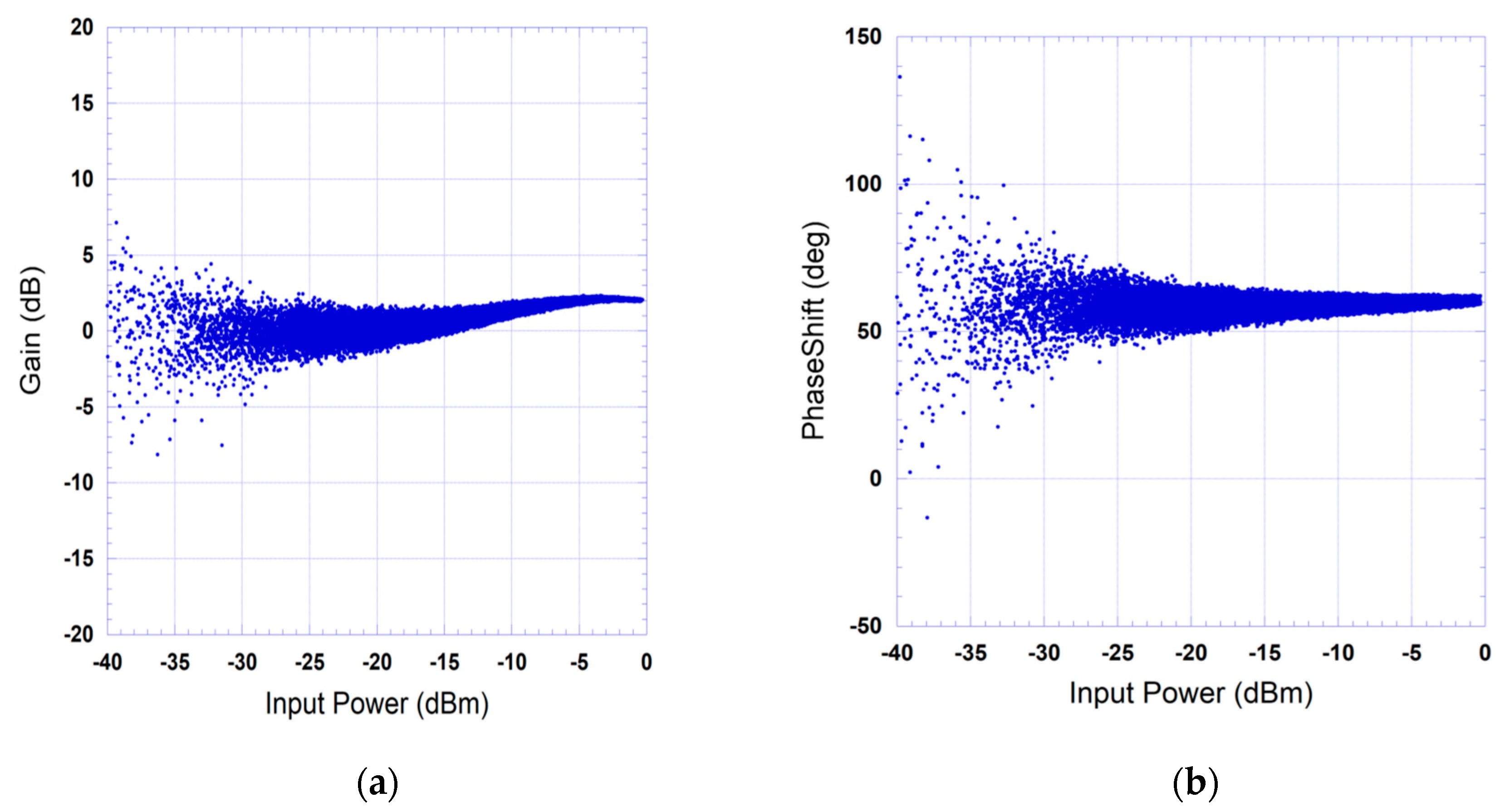
were used to compute the instantaneous complex gain of the device under test and derive its AM/AM (amplitude-modulation to amplitude-modulation) and AM/PM (amplitude-modulation to phase-modulation) characteristics. The AM/AM and AM/PM characteristics represent the magnitude and the phase of the complex instantaneous gain, respectively. The measured AM/AM and AM/PM characteristics of the device under test derived from the 100 MSa/s sampling rate data acquisition are presented in
Figure 8.
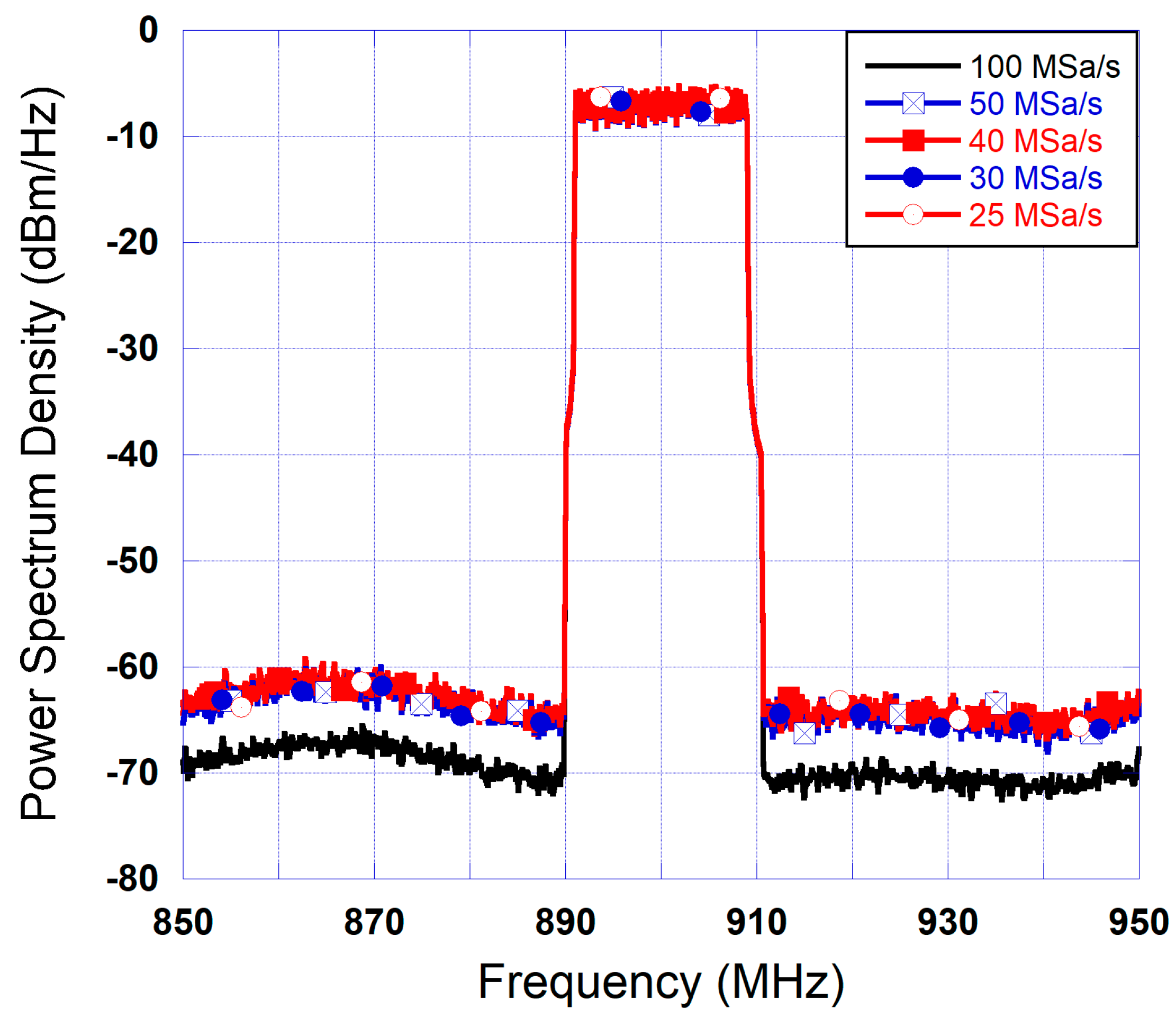
Then, the five acquisitions of the DUT’s output signal were performed using sampling rates of 100 MSa/s, 50 MSa/s, 40 MSa/s, 30 MSa/s and 25 MSa/s. In these tests, since the input waveform has a sampling rate of 100 MSa/s, acquisitions performed at lower sampling rates required the use of a resampling step in order to up-sample the acquired output signal to the same 100 MSa/s rate as the input signal. This resampling step is accomplished before performing the time delay estimation and alignment as well as the predistortion function synthesis. From each of the five acquired output signals, a memoryless look-up table was built. All predistorters were derived from the measured input and output data using the same exponentially weighted moving average algorithm for the LUT DPD synthesis. These LUT-based DPDs were then used to linearize the power amplifier when driven by the 20 MHz input signal. The spectra obtained at the output of the linearized power amplifier are reported in
Figure 9 for all the memoryless predistorters along with the output spectra without linearization. This figure shows that the LUT derived from the measured output signal at 100 MSa/s leads to the best linearization performance. However, residual distortions can be seen in this spectrum. This is expected since the DUT exhibits memory effects, and therefore a memoryless DPD will not be able to fully compensate for the DUT’s distortions.
Moreover, considering the spectra (of
Figure 9) corresponding to DPDs derived from lower sampling rates, additional performance degradation is observed. This performance deterioration is more pronounced as the sampling rate decreases. This is anticipated since a more accurate reconstruction of the output signal waveform sampled at 100 MSa/s will translate into a more accurate model of the DUT, and hence a more optimal memoryless LUT. However, even though the performances of the DPDs derived from low-sampling-rate data acquisitions are not as good as the one derived from 100 MSa/s measurement, they lead to noticeable spectrum regrowth cancellation ranging from 10 dB to 20 dB for the 25 MSa/s and the 50 MSa/s data acquisitions, respectively. More importantly, this spectrum regrowth cancellation reduces the bandwidth of the signal at the output of the device under test, which will reduce the impact of the limited observation bandwidth on the performance of the DPD. Accordingly, the use of the low-sampling-rate data acquisitions for the synthesis of the second predistortion sub-function (the memory polynomial block) is anticipated to further enhance the capabilities of the predistorter.
The last step in the validation of the proposed S-DPD system is to assess the performance of the complete two-box DPD for each value of the sampling rates used in the signal observation path. First, the benchmark data corresponding to a data acquisition at sampling rate of 100 MSa/s was used to determine the required dimensions for the memory polynomial block of the two-box DPD. The memory polynomial predistortion function is given by
where
and
are the input and the output of the MP function, respectively.
are the complex-valued model coefficients.
and
represent the memory polynomial’s nonlinearity order and memory depth, respectively.
For the considered DUT, it was found that the MP sub-function needed to have a nonlinearity order and a memory depth . This setting (nonlinearity order and memory depth) of the MP sub-function was kept the same for all MP sub-functions derived from the under-sampled output waveforms. For each acquisition, a new set of coefficients was calculated.
For the 25 MSa/s data acquisition, the signal at the output of the amplifier linearized using the memoryless LUT derived from the same sampling rate was used along with the LUT’s input signal to build the memory polynomial sub-function of the predistorter. This sub-function, also derived from data acquired at 25 MSa/s, aims at linearizing the cascade made of the LUT predistorter and the power amplifier. The same test was repeated for the 30 MSa/s, 40 MSa/s and 50 MSa/s acquisitions as well as the 100 MSa/s benchmark. The spectra obtained at the output of the power amplifier following the use of the cascade made of the memory polynomial and the LUT DPDs are reported in
Figure 10 for all considered sampling rates. This figure clearly shows that the use of the proposed sequential DPD technique can result in excellent linearization without performance deteriorations as the sampling rate is reduced by a factor of four from 100 MSa/s to 25 MSa/s. This is mainly due to the fact that despite the imperfections of the LUT DPD, it still reduces the bandwidth of the partly linearized output signal, and the fact that the MP DPD is derived to linearize the cascade made of the LUT and DUT in a second iteration.
4. Complexity Reduction through Coarse Delay Alignment
In order to further reduce the computational complexity associated with the identification of the memory polynomial coefficients, coarse delay alignment algorithm was used to time-align the input and output waveforms prior to the identification of the memory polynomial predistortion function. The main reason is that fine-delay alignment is a computationally extensive process. In fact, delay alignment with a resolution where is the sampling period of the two signals to be time-aligned typically requires up-sampling the signals by a factor , performing delay estimation and alignment often using cross-correlation technique, and then down-sampling the waveforms by a factor of back to their original sampling rate. Therefore, using a delay resolution equal to the signal’s sampling rate will eliminate the need for the signal up-sampling and down-sampling processes in the delay estimation and alignment and hence reduce the computational complexity associated with this process.
For the experimental validation of the coarse delay alignment, the identification of the LUT sub-function was not modified, and a fine delay alignment was used in that step. However, a coarse delay alignment algorithm was adopted for the MP DPD identification.
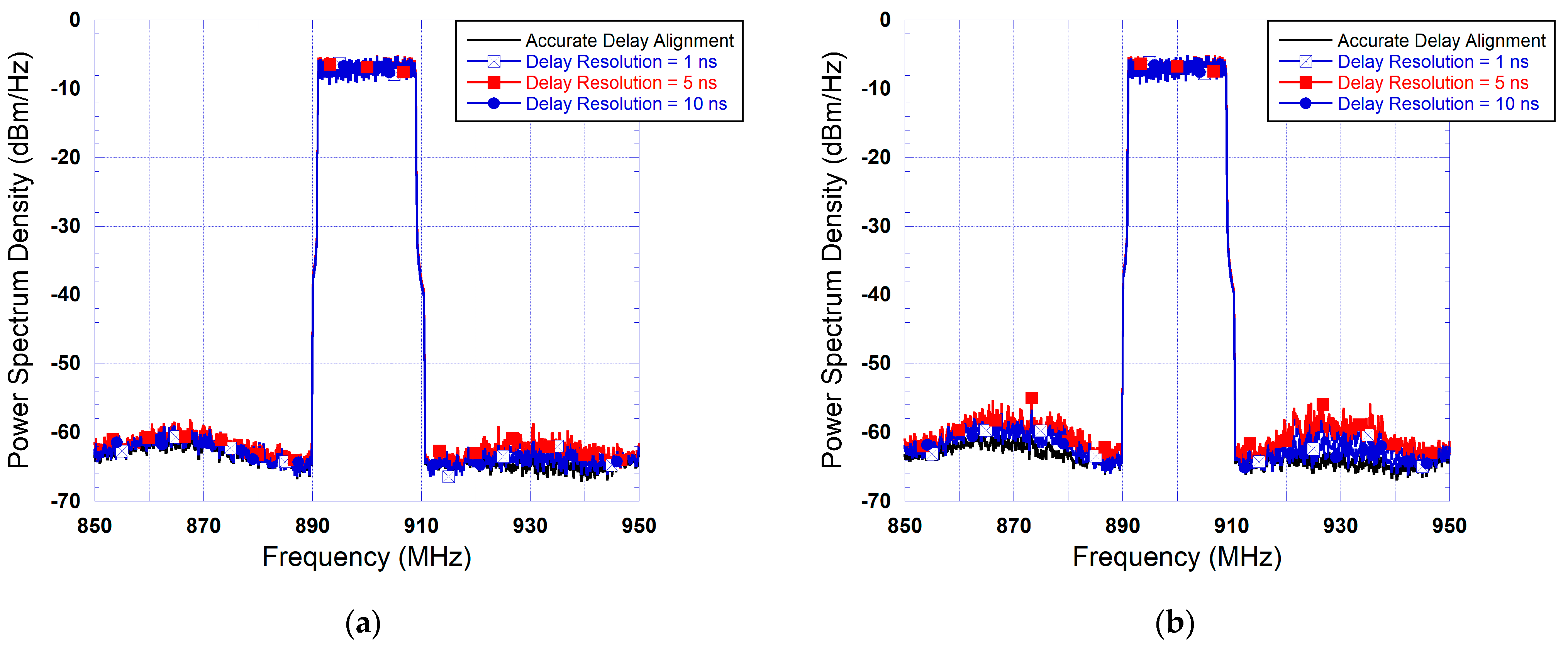
To assess the impact of the delay misalignment caused by the limited delay resolution of the coarse alignment, three delay resolutions were considered. These are 1 ns, 5 ns and 10 ns, which correspond to , and , where is the sampling period of the 100 MSa/s input signal. Moreover, a reference memory polynomial DPD derived from accurate delay estimation and alignment was used as a benchmark.
The effects of the coarse delay alignment are depicted in the plots of
Figure 11. For conciseness, this figure only includes the results corresponding to 50 MSa/s and 25 MSa/s rates in the feedback path. Comparable results have been obtained for the 40 MSa/s and 30 MSa/s cases. The results of
Figure 11 show that the impact of limited delay resolution is slightly more pronounced for the signal acquisition performed at 25 MSa/s than the one performed at 50 MSa/s. Most importantly, these results clearly demonstrate that a delay resolution of up to 10 ns, which corresponds to one sample, does not have a significant impact on the sequential DPD performance. Hence, delay estimation and alignment for the MP DPD identification can be performed with low complexity algorithms that do not require sub-sample resolution without compromising the performance of the S-DPD.