A Day Ahead Demand Schedule Strategy for Optimal Operation of Microgrid with Uncertainty
Abstract
1. Introduction
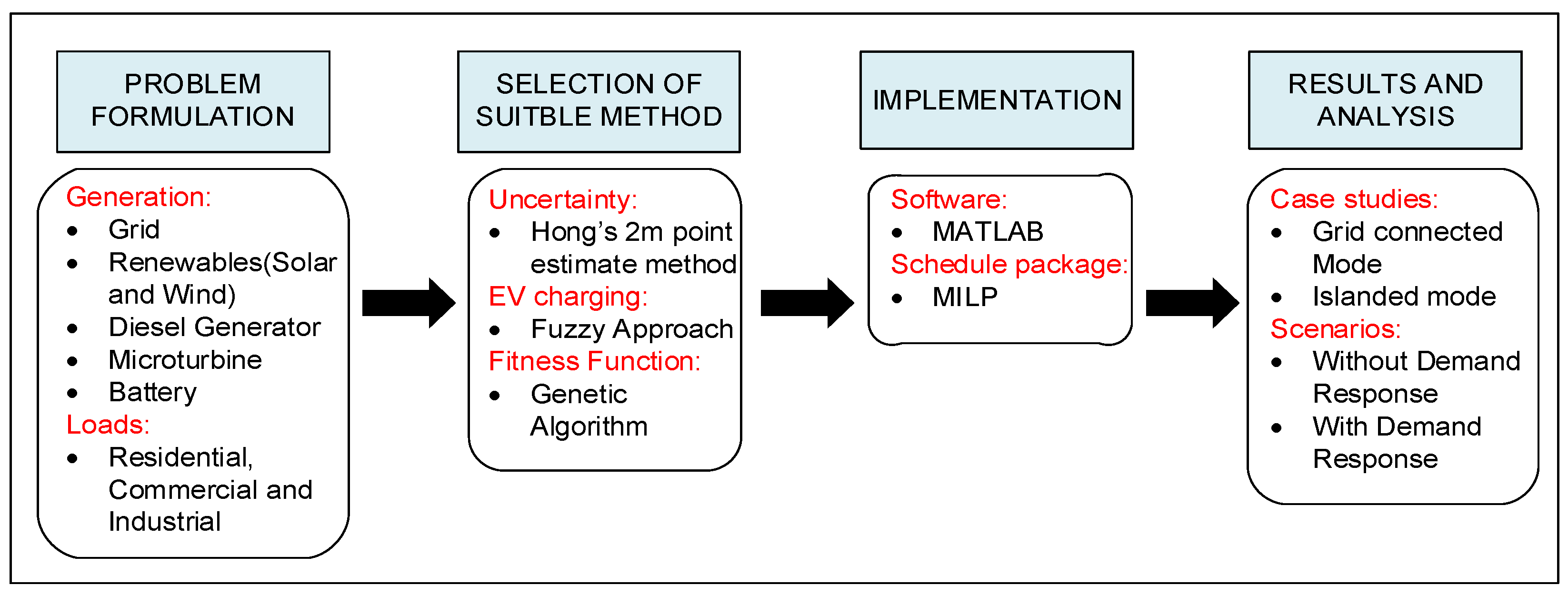
2. Methodology
2.1. Problem Formulation
2.2. Fitness Function
2.3. Hong’s Two Point 2 m Estimate Method
2.4. Fuzzy Approach for EVs Fleets Scheduling
2.5. Multi Objective Genetic Algorithm
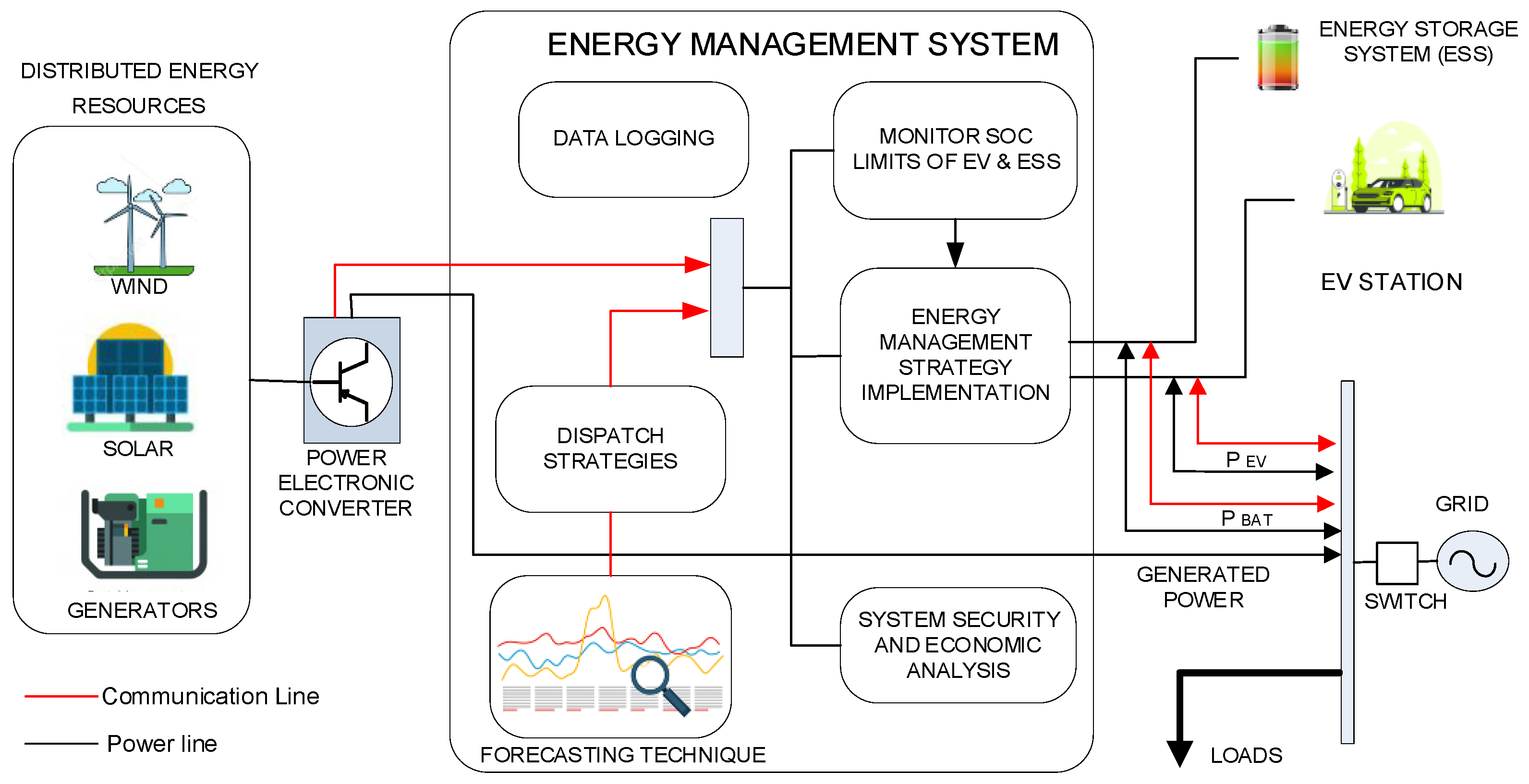
3. Proposed Strategy
- Step 1: Set the values of the GA algorithm; population size at 100, variables 24, crossover and mutation are 30, crossover and mutation probabilities are 0.8 and 0.2, define lower and upper limits are 0 and 0.3, respectively. Selection of new chromosomes is by tournament and fitness scaling is linear rank-based scaling.
- Step 2: Randomly generate the initial position with the population within the feasible range.
- Step 3: Implement Hong’s 2 m method for the uncertain variable and formulate the location and weights.
- Step 4: Repeat for all uncertain variables l.
- Step 5: Calculate the first and second moments for the deterministic scheduling with constraints (2)–(11).
- Step 6: Obtain the updated best chromosomes with moments of the cost function.
- Step 7: Assign a new population from the parent chromosomes through reproduction.
- Step 8: Update the population with mutation and crossover function with their characteristics.
- Step 9: Obtain the updated new solution through tournament selection.
- Step 10: Repeat steps 3 to 5.
- Step 11: Update the population with fitness scaling.
- Step 12: Repeat steps 3 to 5 for the expected cost function from the 2 m method.
- Step 13: The best subjected to the elitism of a random generation population.
- Step 14: Objective fitness is obtained by repeating steps 3 to 5.
- Step 15: Go to step 6 and repeat until the maximum number of iterations.
4. Results
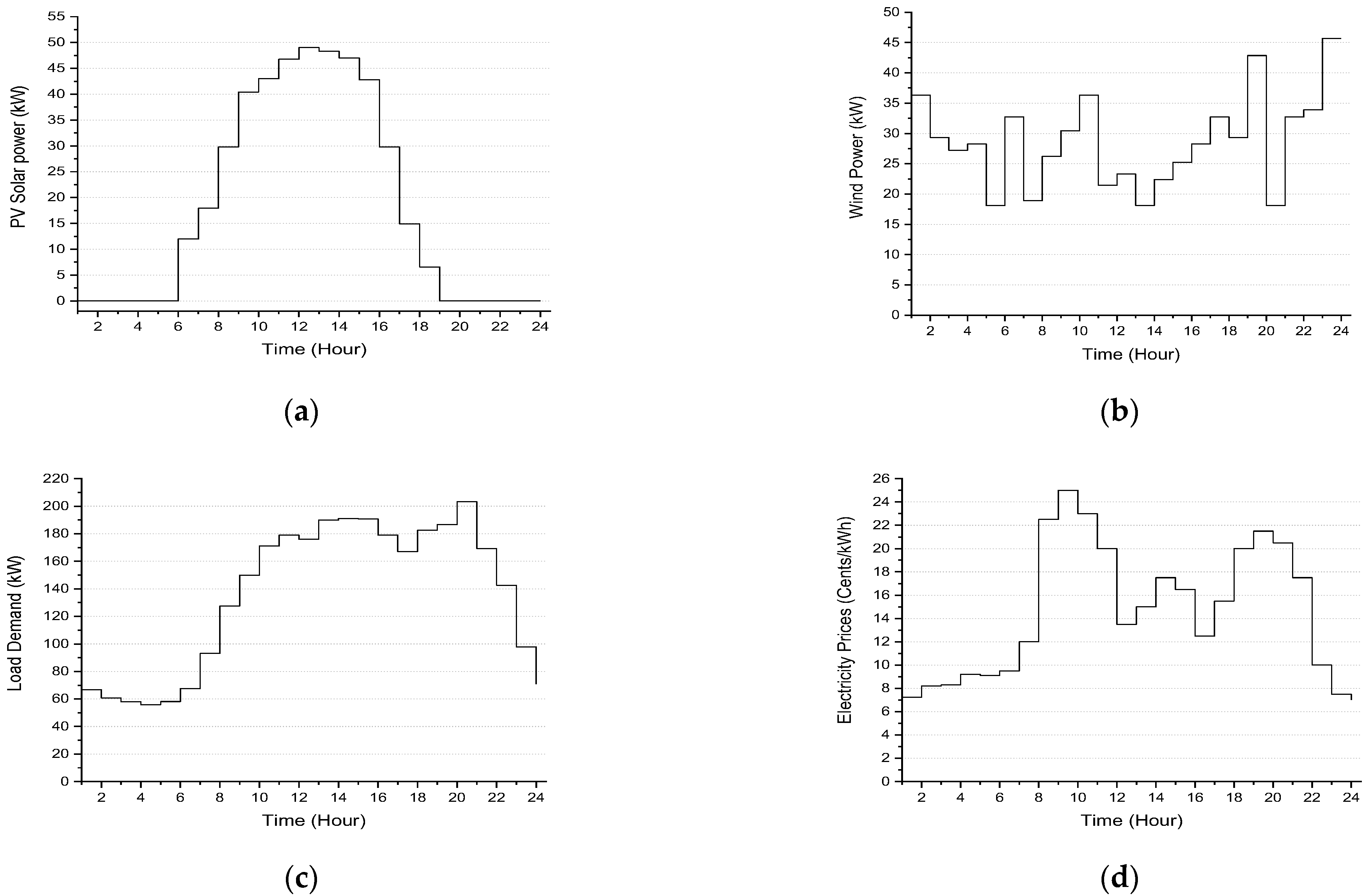
4.1. Test System
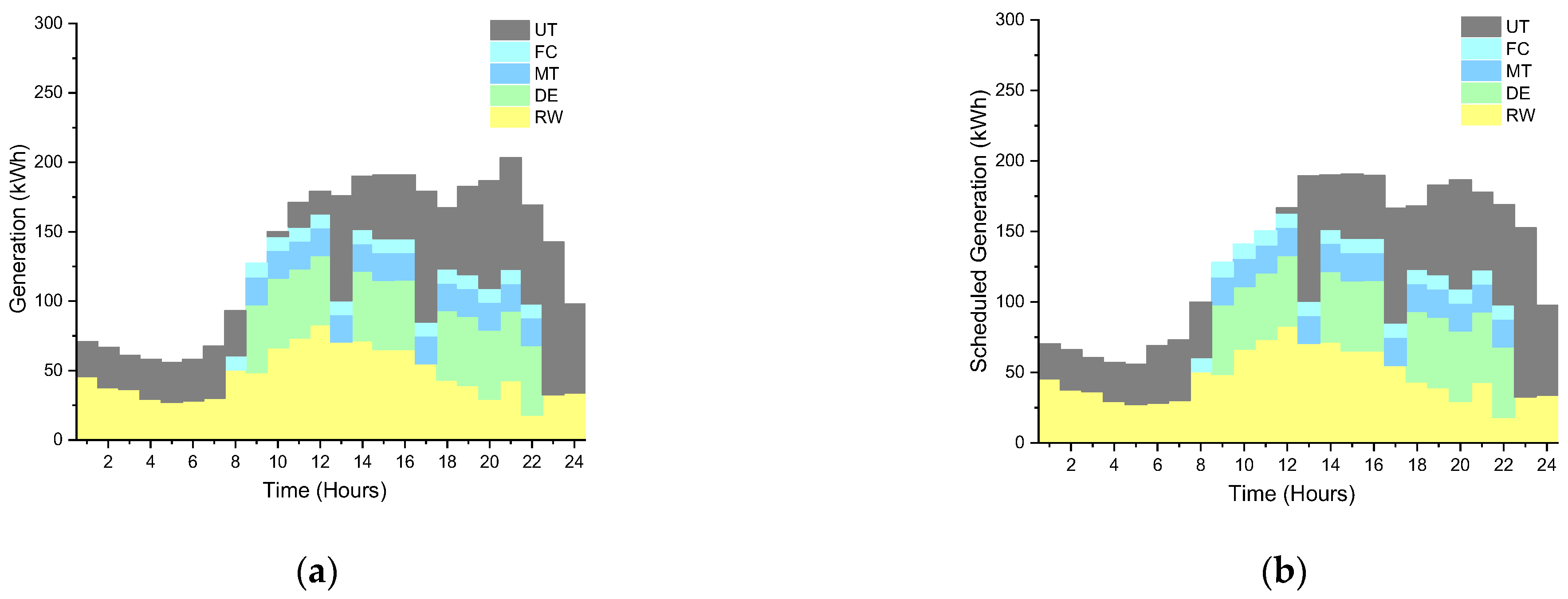
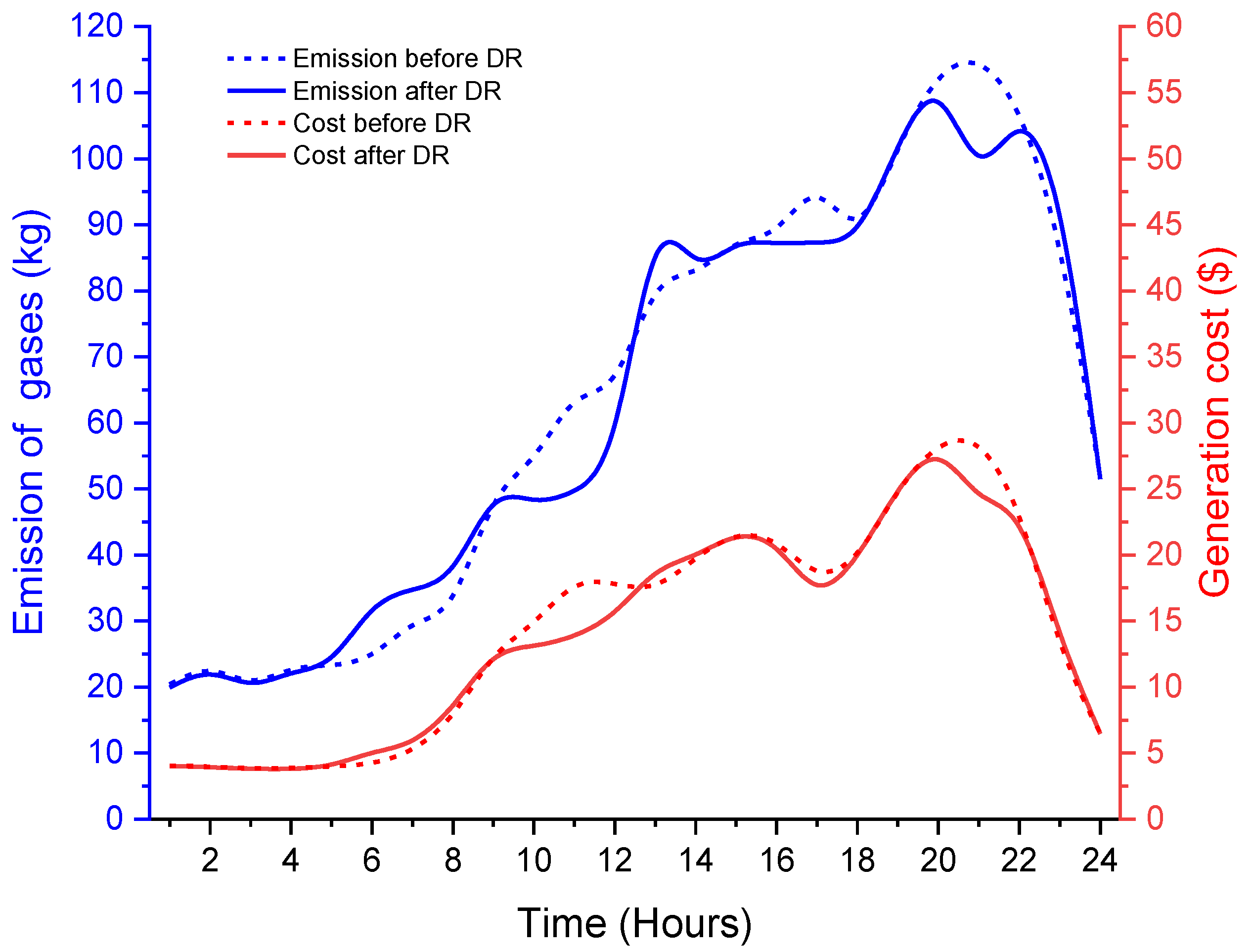
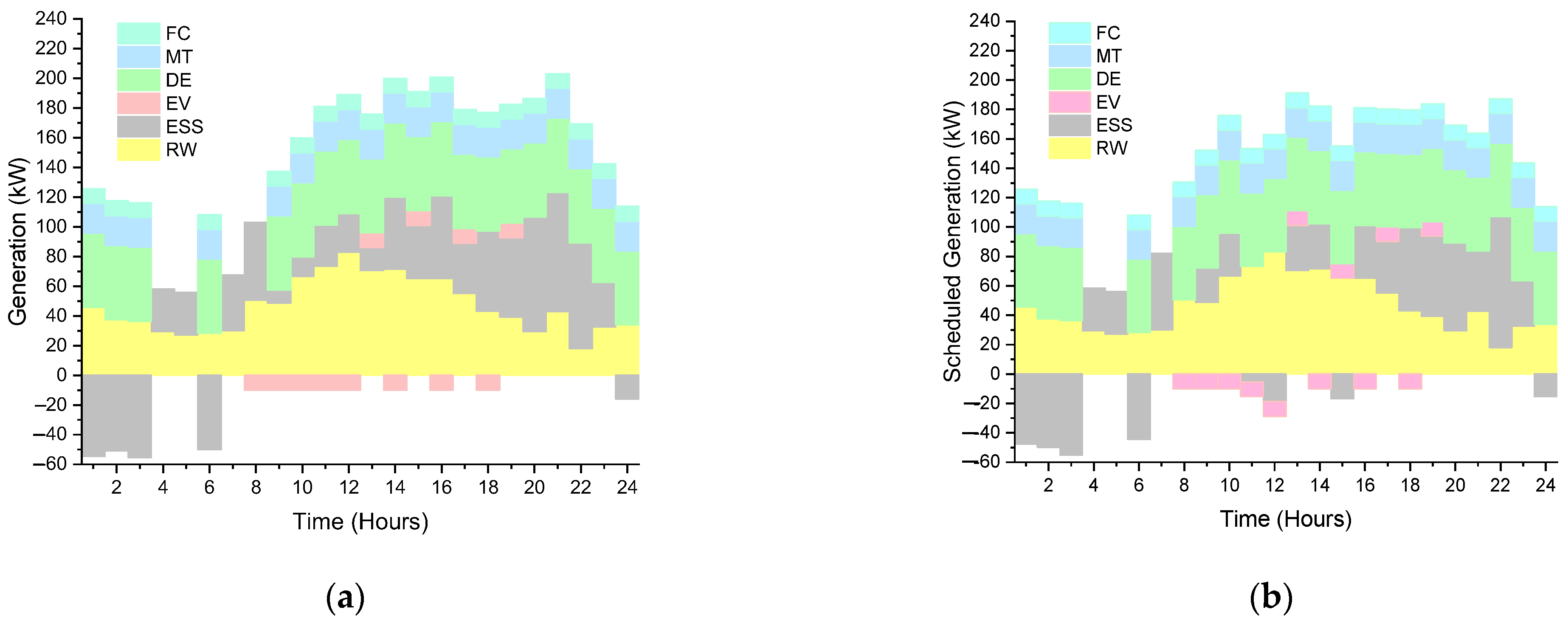
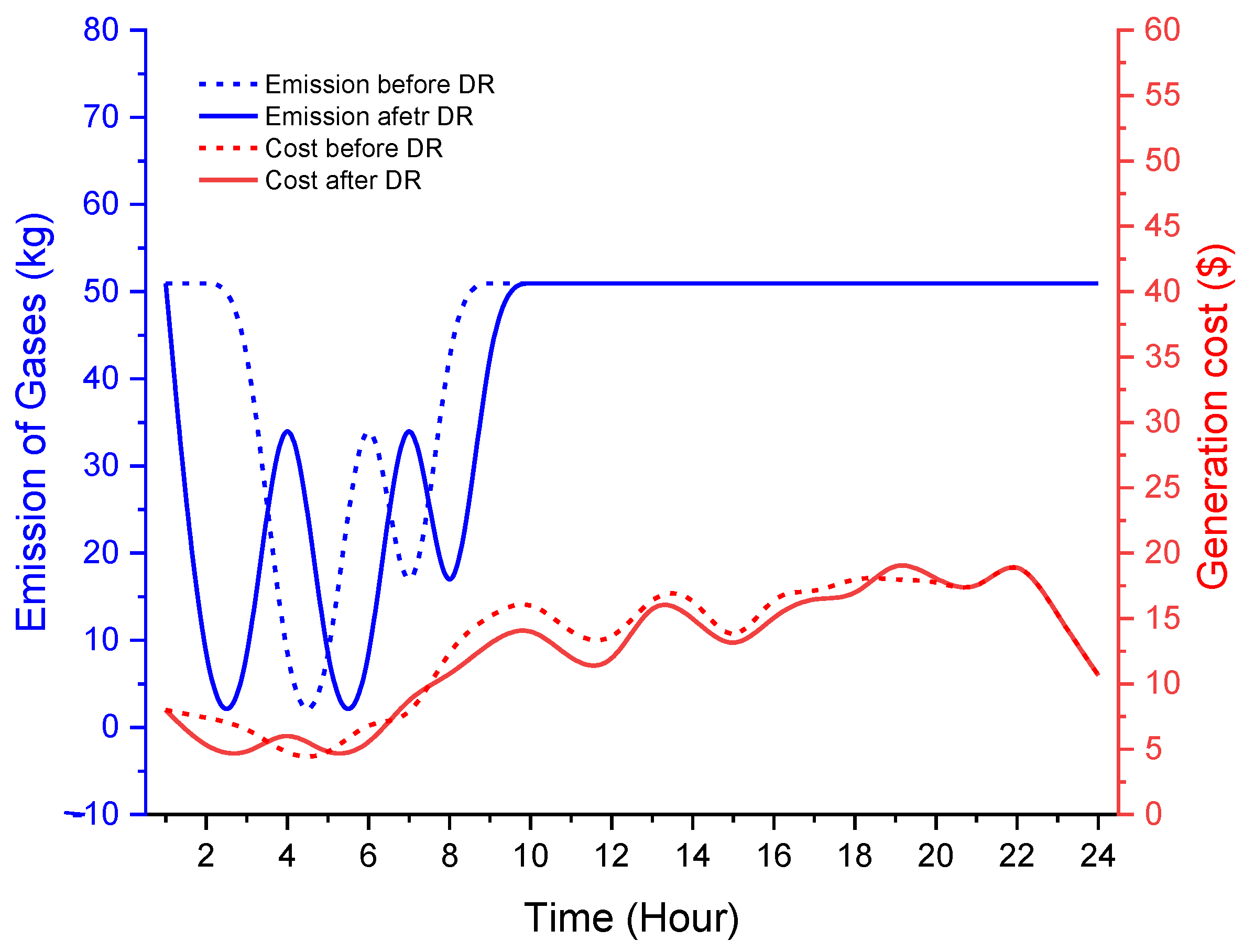
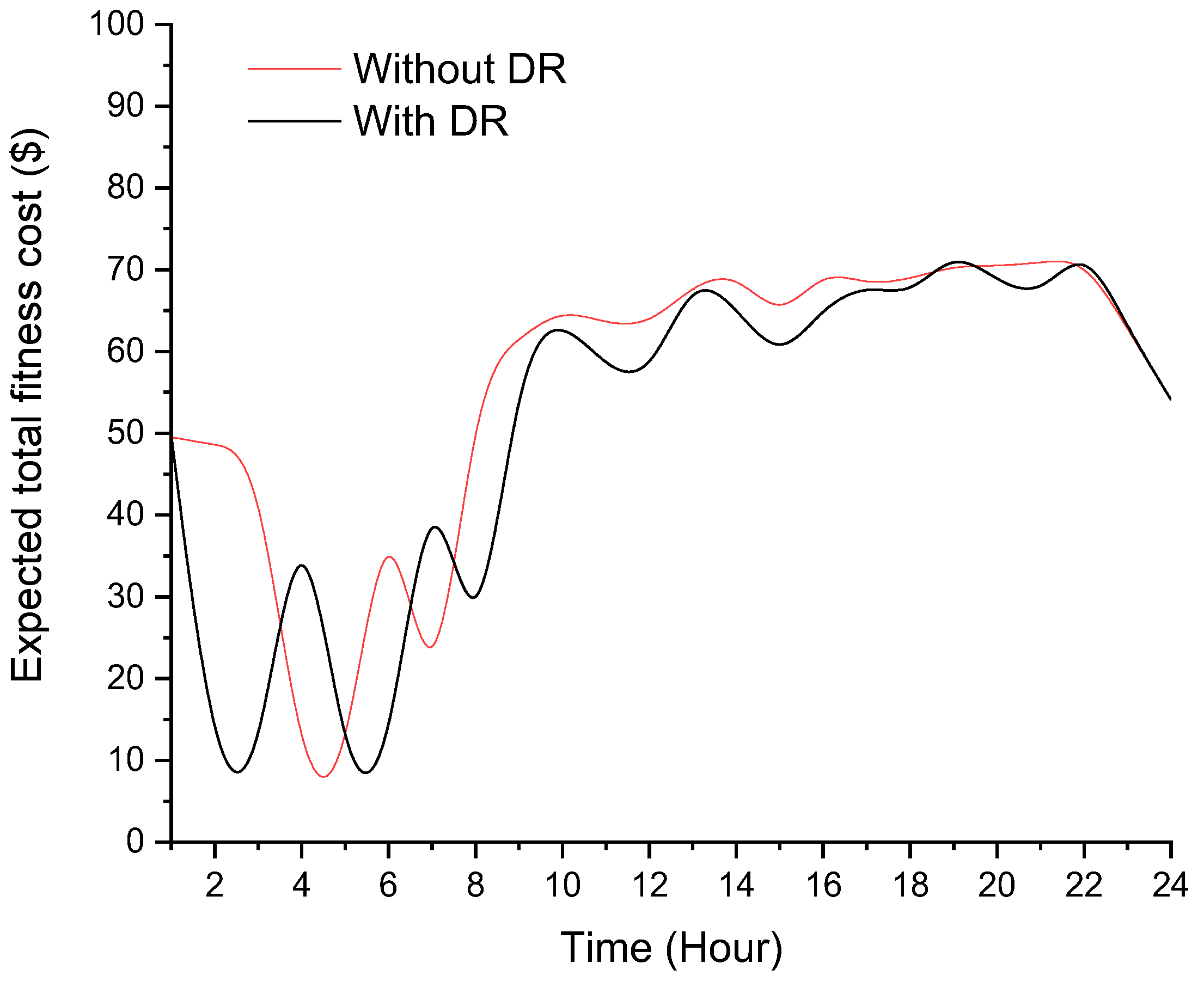
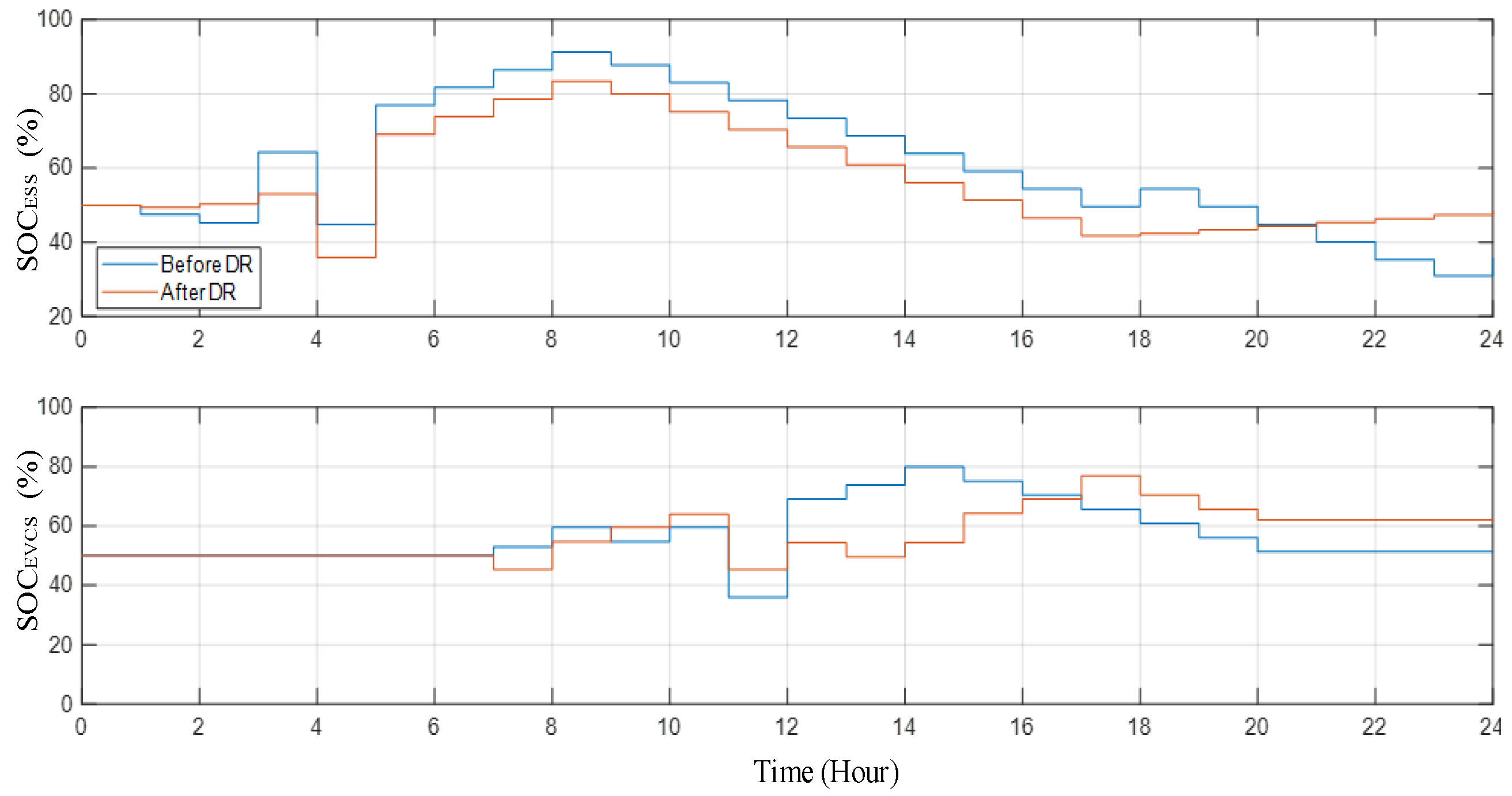
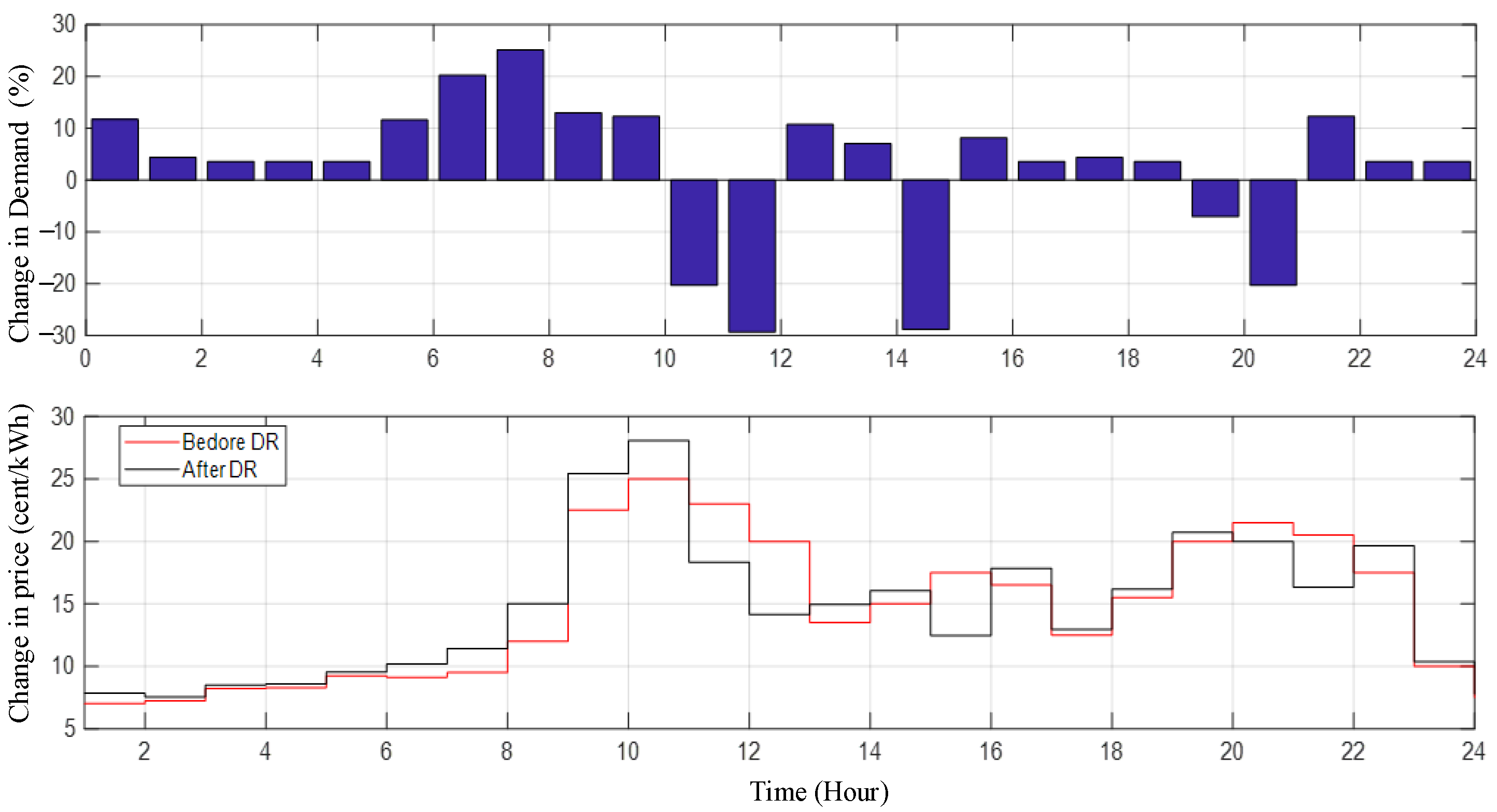
4.2. Analysis
4.3. Discussion and Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Power loss at time “t”, kW. | |
| Grid utility power at time “t”, kW. | |
| Solar and Wind power at time “t”, kW. | |
| Fuel based power output at time “t”, kW. | |
| Power of distributed generators at time “t”, kW. | |
| Power demand shift at “t”, kW. | |
| Power of demand response, kW. | |
| Irradiance of the PV in W/m2, irradiance (1000 W/m2). | |
| State of charge at time “t” (%). | |
| state of charge of combined station at time “t”. | |
| State of charge of EV at time “t”. | |
| Temperature (25 °C), PV temperature (°C). | |
| Voltage profile at time “t” | |
| Wind speed, cut-in, cut-off, rated wind speeds(m/s). | |
| Weights of the kth concentration. | |
| Charging and discharge efficiency | |
| Efficiency of EV power exchange during grid to vehicle and vice versa | |
| Scale and shape of Weibull distribution | |
| Mean and standard deviation for normal distribution. | |
| Weights of the objective function | |
| Controllable load ratio | |
| Fraction of shifted load | |
| Uncertain parameter | |
| Mean of the concentration | |
| Standard location of the concentration | |
| Standard deviation of the moment | |
| skewness | |
| DE | Diesel Generator |
| ESS | Energy storage system |
| EV | Electric Vehicle |
| EVCS | Electric vehicle charging station |
| FC | Fuel cell |
| MT | Micro turbine |
| NP | Nondeterministic polynomial time |
| PV | Photo voltaic |
| SD | Standard deviation |
| WT | Wind turbine |
| a, b | Shape parameters for beta distribution. |
| Generator cost coefficients. | |
| Battery capacity, Wh | |
| Cg,t | Operating cost of system at time “t”. |
| ELRt | Expected load remaining (kW). |
| ETPt | Electricity Price (cents) at hour “t”. |
| Es,t | Emission of pollutants at time “t”. |
| Icharge | Charge consumed, A. |
| k | Manufacturer’s temperature power coefficient W/°C. |
| Total time (24 h) | |
| Number of generator units. | |
| Number of emissions generating units. | |
| Number of electric vehicles at charging station. | |
| Rated PV power at time “t”. | |
| Maximum wind power output (kW). | |
| Fuel based generators output, kW. | |
| Power of ith generator at time “t”, kW. | |
| Power of energy storage systems at “t”, kW. | |
| Pcharge,t, Pdischarge,t | Charging and discharging power at “t”, kW. |
| EV power at charging station at time “t”, kW. | |
| Microgrid power at “t”, kW | |
| Electricity demand of the system. |
References
- Hussain, A.; Bui, V.-H.; Kim, H.-M. Microgrids as a resilience resource and strategies used by microgrids for enhancing resilience. Appl. Energy 2019, 240, 56–72. [Google Scholar] [CrossRef]
- Lee, J.; An, M.; Kim, Y.; Seo, J.-I. Optimal Allocation for Electric Vehicle Charging Stations. Energies 2021, 14, 5781. [Google Scholar] [CrossRef]
- Mojumder, M.R.H.; Ahmed Antara, F.; Hasanuzzaman, M.; Alamri, B.; Alsharef, M. Electric Vehicle-to-Grid (V2G) Technologies: Impact on the Power Grid and Battery. Sustainability 2022, 14, 13856. [Google Scholar] [CrossRef]
- Tehrani, K.; Simde, D.; Fozing, J.; Jamshidi, M. A 3D design of small hybrid farm for microgrids. In Proceedings of the 2022 World Automation Congress (WAC), San Antonio, TX, USA, 11–15 October 2022; pp. 1–6. [Google Scholar]
- Moradi, H.; Esfahanian, M.; Abtahi, A.; Zilouchian, A. Optimization and energy management of a standalone hybrid microgrid in the presence of battery storage system. Energy 2018, 147, 226–238. [Google Scholar] [CrossRef]
- Kanakadhurga, D.; Prabaharan, N. Demand side management in microgrid: A critical review of key issues and recent trends. Renew. Sustain. Energy Rev. 2022, 156, 111915. [Google Scholar] [CrossRef]
- Raju, A.R.; Sandeep, V. Optimal reconfiguration of balanced and unbalanced distribution systems using firefly algorithm. Int. J. Emerg. Electr. Power Syst. 2021, 23, 317–328. [Google Scholar]
- Yetis, Y.; Tehrani, K.; Jamshidi, M. Wind Speed Forecasting Using Machine Learning Approach Based on Meteorological Data-A Case Study. Energy Environ. Res. 2022, 12, 11–25. [Google Scholar] [CrossRef]
- Dakanalis, M.; Kanellos, F.D. Efficient Model for Accurate Assessment of Frequency Support by Large Populations of Plug-in Electric Vehicles. Inventions 2021, 6, 89. [Google Scholar] [CrossRef]
- Arabali, A.; Ghofrani, M.; Etezadi-Amoli, M.; Fadali, M.S.; Baghzouz, Y. Genetic-Algorithm-Based Optimization Approach for Energy Management. IEEE Trans. Power Deliv. 2013, 28, 162–170. [Google Scholar] [CrossRef]
- Tung, Y.; Yen, B. Hydrosystems Engineering Uncertainty Analysis; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Alonso-Travesset, À.; Martín, H.; Coronas, S.; de la Hoz, J. Optimization Models under Uncertainty in Distributed Generation Systems: A Review. Energies 2022, 15, 1932. [Google Scholar] [CrossRef]
- Gonzalez-Gil, P.; Martinez, J.A.; Skarmeta, A. A Prosumer-Oriented, Interoperable, Modular and Secure Smart Home Energy Management System Architecture. Smart Cities 2022, 5, 53. [Google Scholar] [CrossRef]
- Jasiński, J.; Kozakiewicz, M.; Sołtysik, M. The Effectiveness of Energy Cooperatives Operating on the Capacity Market. Energies 2021, 14, 3226. [Google Scholar] [CrossRef]
- Yu, Z.-X.; Li, M.-S.; Xu, Y.-P.; Aslam, S.; Li, Y.-K. Techno-Economic Planning and Operation of the Microgrid Considering Real-Time Pricing Demand Response Program. Energies 2021, 14, 4597. [Google Scholar] [CrossRef]
- Ebeed, M.; Shady, H.E.; Aleem, A. Chapter 1—Overview of Uncertainties in Modern Power Systems: Uncertainty Models and Methods, Uncertainties in Modern Power Systems; Academic Press: Cambridge, MA, USA, 2021; pp. 1–34. [Google Scholar]
- Sarda, J.S.; Lee, K.; Patel, H.; Patel, N.; Patel, D. Energy Management System of Microgrid using Optimization Approach. IFAC-PapersOnLine 2022, 55, 280–284. [Google Scholar] [CrossRef]
- Khalid, A.; Javaid, N.; Mateen, A.; Ilahi, M.; Saba, T.; Rehman, A. Enhanced Time-of-Use Electricity Price Rate Using Game Theory. Electronics 2019, 8, 48. [Google Scholar] [CrossRef]
- Sołtysik, M.; Kozakiewicz, M.; Jasiński, J. Improvement of Operating Efficiency of Energy Cooperatives with the Use of “Crypto-Coin Mining”. Energies 2022, 15, 8061. [Google Scholar] [CrossRef]
- Hassan, M.A.S.; Assad, U.; Farooq, U.; Kabir, A.; Khan, M.Z.; Bukhari, S.S.H.; Jaffri, Z.A.; Oláh, J.; Popp, J. Dynamic Price-Based Demand Response through Linear Regression for Microgrids with Renewable Energy Resources. Energies 2022, 15, 1385. [Google Scholar] [CrossRef]
- Zhou, B.; Zou, J.; Chung, C.Y.; Wang, H.; Liu, N.; Voropai, N.; Xu, D. Multi-microgrid Energy Management Systems: Architecture, Communication, and Scheduling Strategies. J. Mod. Power Syst. Clean Energy 2021, 9, 463–476. [Google Scholar] [CrossRef]
- Kaluthanthrige, R.; Rajapakse, A.D. Demand response integrated day-ahead energy management strategy for remote off-grid hybrid renewable energy systems. Int. J. Electr. Power Energy Syst. 2021, 129, 106731. [Google Scholar] [CrossRef]
- Sanguesa, J.A.; Torres-Sanz, V.; Garrido, P.; Martinez, F.J.; Marquez-Barja, J.M. A Review on Electric Vehicles: Technologies and Challenges. Smart Cities 2021, 4, 22. [Google Scholar] [CrossRef]
- Battula, A.R.; Vuddanti, S.; Salkuti, S.R. Review of Energy Management System Approaches in Microgrids. Energies 2021, 14, 5459. [Google Scholar] [CrossRef]
- Mohseni-Bonab, S.M.; Rabiee, A. Optimal reactive power dispatch: A review, and a new stochastic voltage stability constrained multi-objective model at the presence of uncertain wind power generation. IET Gener. Transm. Distrib. 2017, 11, 815–829. [Google Scholar] [CrossRef]
- Atwa, Y.M.; El-Saadany, E.F.; Salama, M.M.A.; Seethapathy, R.; Assam, M.; Conti, S. Adequacy evaluation of distribution system including wind/solar DG during different modes of operation. IEEE Trans. Power Syst. 2011, 26, 1945–1952. [Google Scholar] [CrossRef]
- Boglou, V.; Karavas, C.-S.; Arvanitis, K.; Karlis, A. A Fuzzy Energy Management Strategy for the Coordination of Electric Vehicle Charging in Low Voltage Distribution Grids. Energies 2020, 13, 3709. [Google Scholar] [CrossRef]
- Tayarani, H.; Jahangir, H.; Nadafiansh Ahamabadi, R.; Aliakbar Golkar, M.; Ahmadian, A.; Elkamel, A. Optimal Charging of Plug-In Electric Vehicle: Considering Travel Behavior Uncertainties and Battery Degradation. Appl. Sci. 2019, 9, 3420. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Carli, R.; Dotoli, M. Robust day-ahead energy scheduling of a smart residential user under uncertainty. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 935–940. [Google Scholar]
- Pothireddy, K.M.R.; Vuddanti, S.; Salkuti, S.R. Impact of Demand Response on Optimal Sizing of Distributed Generation and Customer Tariff. Energies 2022, 15, 190. [Google Scholar] [CrossRef]
- Hossain, F.A.; Rokonuzzaman, M.; Amin, N.; Zhang, J.; Mishu, M.K.; Tan, W.-S.; Islam, M.R.; Roy, R.B. Probabilistic Load Flow–Based Optimal Placement and Sizing of Distributed Generators. Energies 2021, 14, 7857. [Google Scholar] [CrossRef]
- Raju, B.A.; Sandeep, V. A chance constraint microgrid energy management with phase balancing using electric vehicle demand aggregation. Energy Sources Part A Recover. Util. Environ. Eff. 2023, 45, 111–139. [Google Scholar] [CrossRef]
- Leonori, S.; Paschero, M.; Mascioli, F.M.F.; Rizzi, A. Optimization strategies for Microgrid energy management systems by Genetic Algorithms. Appl. Soft Comput. 2020, 86, 105903. [Google Scholar] [CrossRef]
- Melhem, F.Y.; Grunder, O.; Hammoudan, Z.; Moubayed, N. Energy Management in Electrical Smart Grid Environment Using Robust Optimization Algorithm. IEEE Trans. Ind. Appl. 2018, 54, 2714–2726. [Google Scholar] [CrossRef]
- Papathanassiou, S.; Hatziargyriou, N.; Strunz, K. A benchmark low voltage microgrid network. In Proceedings of the CIGRE Symposium: Power Systems with Dispersed Generation, CIGRE, Athens, Greece, 13–16 April 2005; pp. 1–8. [Google Scholar]
- Murty, V.V.S.N.; Kumar, A. Multi-objective energy management in microgrids with hybrid energy sources and battery energy storage systems. Prot. Control Mod. Power Syst. 2020, 5, 2. [Google Scholar] [CrossRef]
- Zhuang, Z.; Zheng, X.; Chen, Z.; Jin, T.; Li, Z. Load Forecast of Electric Vehicle Charging Station Considering Multi-Source Information and User Decision Modification. Energies 2022, 15, 7021. [Google Scholar] [CrossRef]
- ComEd. Day-Ahead Hourly Prices for February 3, 2023. Available online: https://hourlypricing.comed.com/live-prices/day-ahead-prices/ (accessed on 10 March 2022).
- Mohammadi, S.; Mozafari, B.; Soleymani, S. Optimal operation management of microgrids using the point estimate method and firefly algorithm while considering uncertainty. Turk. J. Electr. Eng. Comput. Sci. 2014, 22, 735–753. [Google Scholar] [CrossRef]




| Residential Devices | Expected Schedule | Commercial Devices | Expected Schedule | Industrial Devices | Expected Schedule |
|---|---|---|---|---|---|
| Dryer | 18:10–19:20 | Water dispenser | 9:00–9:30 | Water | 16:00–20:00 |
| Dishwasher | 20:10–22:10 | Auxiliary Fans | 10:00–18:30 | Welding | 08:00–13:00 |
| Washing machine | 17:20–18:00 | Secondary Lights | 18:00–22:00 | Kettle | 15:00–21:00 |
| Oven | 18:30–18:40 | Oven | 12:10–12:20; 12:30–12:40 | Auxiliary Fans | 10:00–16:00 |
| Vacuum cleaner | 19:30–20:00 | Dryer | 14.00–15:00 | Arc Furnace | 12:00–18:00 |
| kettle | 19:00–19:10 | Coffee maker | 11:00–11:10 | Induction motor | 15:00–21:00 |
| Coffee maker | 7:00–7:40 | Kettle | 14:00–14:10 | DC motor | 13:00–15:00 |
| Steam iron | 17:40–17:50 |
| Initial Variables | Values |
|---|---|
| Population size | 100 |
| Variables | 24 |
| Crossover and crossover probabilities | 30, 0.8 |
| Mutation and mutation probabilities | 30, 0.2 |
| Selection of new chromosomes | Tournament |
| Fitness scaling | Linear rank-based |
| No | TYPE | Power (kW) | Cost (cent/kWh) | Emission (g/kWh) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Start/Running | ai | bi | ci | CO2 | SO2 | NOx | ||
| 1 | PV (1) | 0 | 100 | 0/5 | - | - | - | - | - | - |
| 2 | WT (2) | 0 | 50 | 0/5 | - | - | - | - | - | - |
| 3 | DE (1) | 0 | 50 | 3/3 | 0.00104 | 0.0304 | 1.3 | 697 | 0.22 | 0.5 |
| 4 | MT (1) | 0 | 20 | 2/3 | 0.00051 | 0.0397 | 0.4 | 670 | 0.0036 | 0.186 |
| 5 | FC (1) | 0 | 10 | 1.5/3 | 0.00024 | 0.0297 | 0.38 | 441 | 0.0022 | 0.0136 |
| 6 | BT (4) | −25 | 25 | 0/5 | - | - | - | - | - | - |
| 7 | EV | −10 | 10 | 0/5 | - | - | - | - | - | - |
| 8 | GRID | ~ | ~ | - | - | - | - | 884 | 1.8 | 1.6 |
| Case Studies | Grid Connected | Islanded Mode | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenarios | without DR | with DR | without DR | with DR | |||||
| Objectives | Mean | SD | Mean | SD | Mean | SD | Mean | SD | |
| Total cost of operation, USD | 343.33 | 13.52 | 332.86 | 12.35 | 314.53 | 9.25 | 297.67 | 10.23 | 314.53 |
| Total power loss, kWh | 140.61 | 14.12 | 138.24 | 16.21 | 140.61 | 11.21 | 127.03 | 8.21 | 140.61 |
| Emission, kg | 1533.64 | 120.44 | 1506.02 | 22.02 | 1069 | 63.01 | 967.16 | 44.21 | 1069 |
| Fitness function cost, USD | 1717.91 | 11.698 | 1506.02 | 18.26 | 1681.85 | 13.25 | 1363.33 | 15.21 | 1681.85 |
| Method [36] | Method [39] | Monte Carlo | Proposed | |
|---|---|---|---|---|
| Expected operation cost (USD) | 343 | 335 | 328 | 332 |
| Standard deviation | 13.24 | 12.15 | 12.85 | 12.63 |
| Mean Time (s) | 0.138 | 0.131 | 38.21 | 0.144 |
| Cases with DR | Method | Objective Function Cost (USD) | Total Cost (USD) | Total Emission (kg) | Total Power Loss (kW) | Convergence (Iterations) |
|---|---|---|---|---|---|---|
| Grid-connected mode | GA | 1710.24 | 332.32 | 1506.98 | 138.08 | 150 |
| PSO | 1721.85 | 365.19 | 1537.71 | 141.57 | 180 | |
| FFA | 1796.69 | 345.76 | 1512.64 | 139.11 | 160 | |
| Islanded mode | GA | 1363.33 | 297.67 | 967.16 | 127.03 | 120 |
| PSO | 1396.26 | 358.59 | 924.65 | 129.37 | 180 | |
| FFA | 1365.79 | 387.23 | 835.87 | 127.88 | 230 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Battula, A.R.; Vuddanti, S.; Salkuti, S.R. A Day Ahead Demand Schedule Strategy for Optimal Operation of Microgrid with Uncertainty. Smart Cities 2023, 6, 491-509. https://doi.org/10.3390/smartcities6010023
Battula AR, Vuddanti S, Salkuti SR. A Day Ahead Demand Schedule Strategy for Optimal Operation of Microgrid with Uncertainty. Smart Cities. 2023; 6(1):491-509. https://doi.org/10.3390/smartcities6010023
Chicago/Turabian StyleBattula, Amrutha Raju, Sandeep Vuddanti, and Surender Reddy Salkuti. 2023. "A Day Ahead Demand Schedule Strategy for Optimal Operation of Microgrid with Uncertainty" Smart Cities 6, no. 1: 491-509. https://doi.org/10.3390/smartcities6010023
APA StyleBattula, A. R., Vuddanti, S., & Salkuti, S. R. (2023). A Day Ahead Demand Schedule Strategy for Optimal Operation of Microgrid with Uncertainty. Smart Cities, 6(1), 491-509. https://doi.org/10.3390/smartcities6010023








