Power Quality Analysis by H-Bridge DSTATCOM Control by Icosθ and ESRF SOGI-FLL Methods for Different Industrial Loads
Abstract
1. Introduction
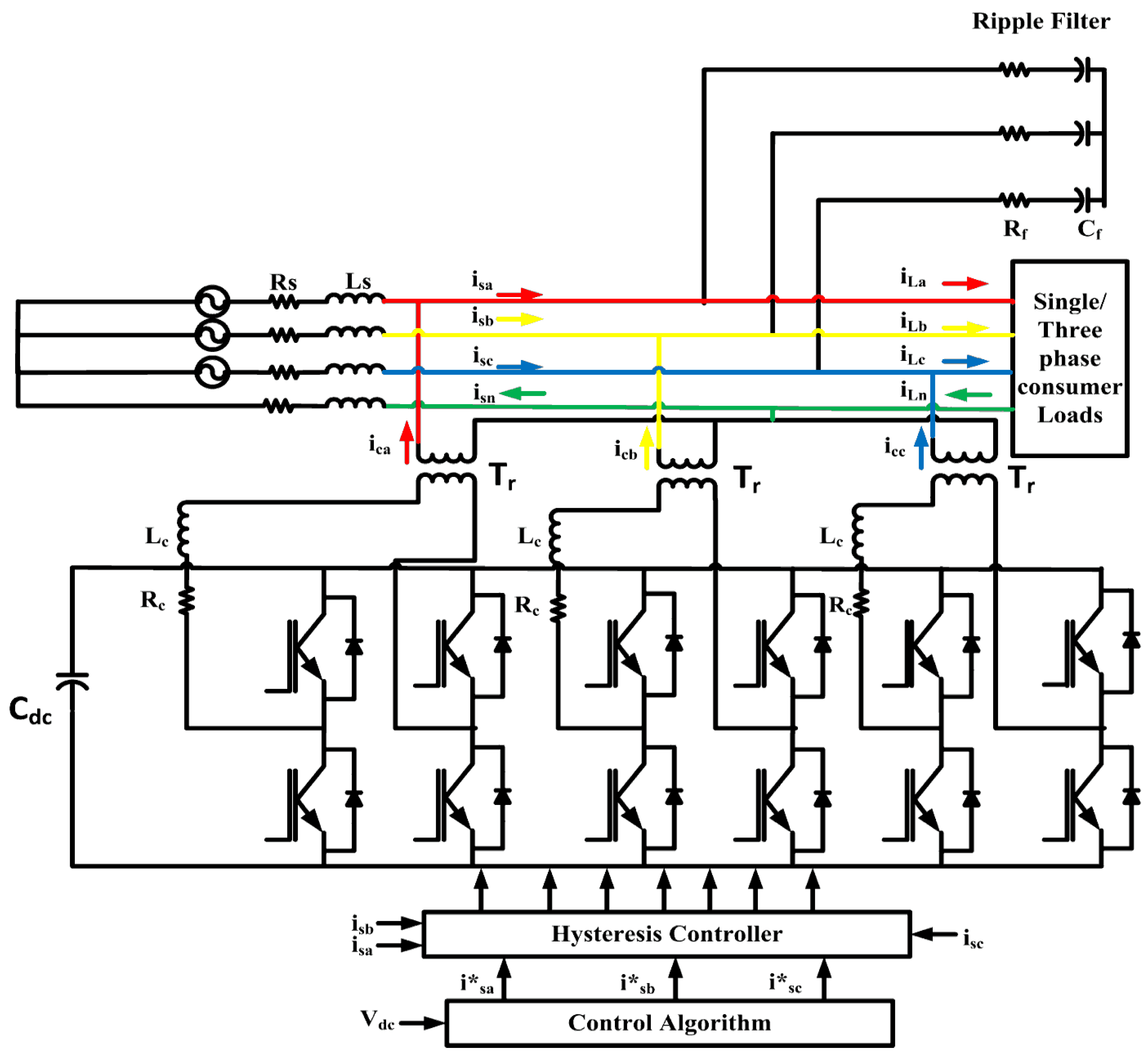
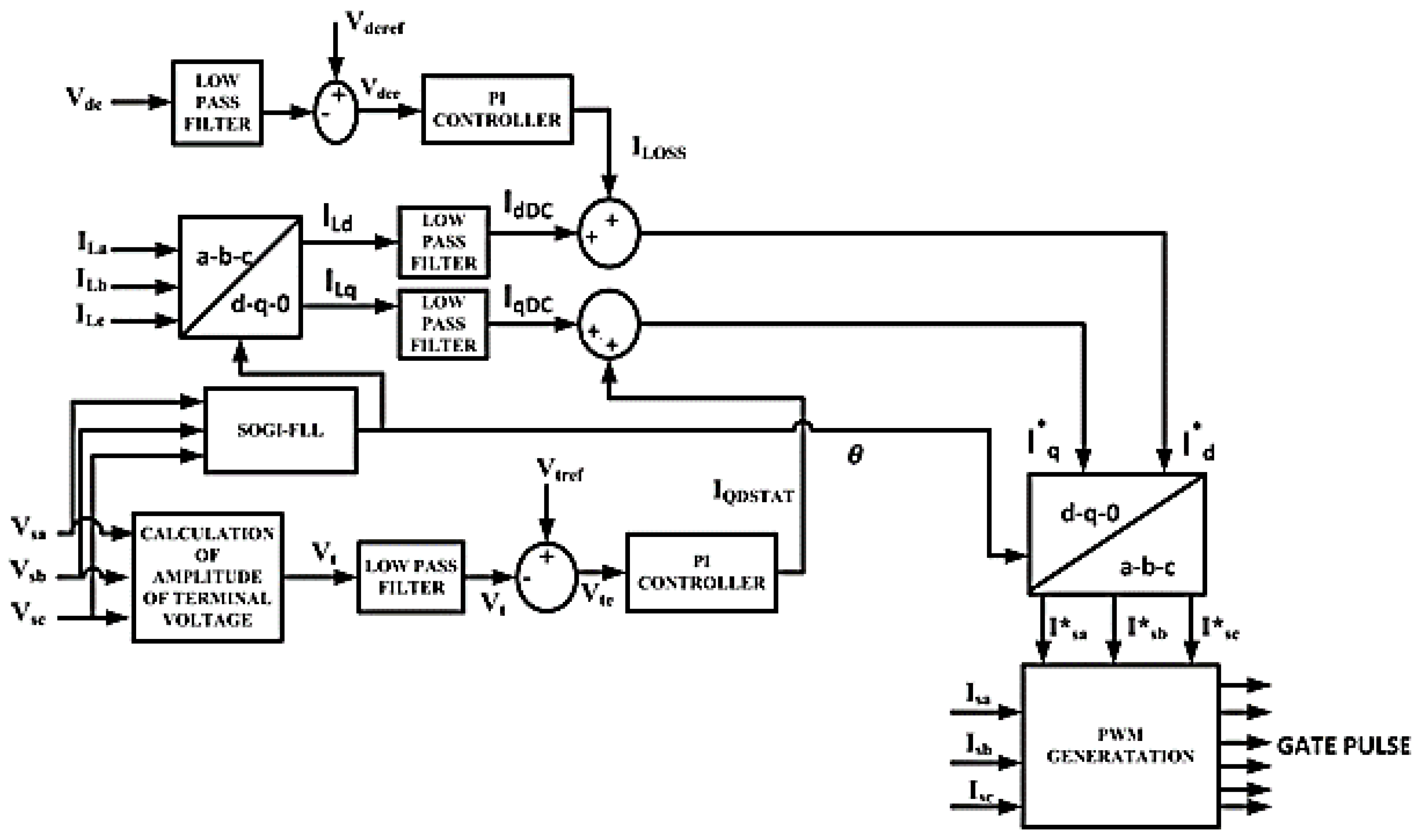
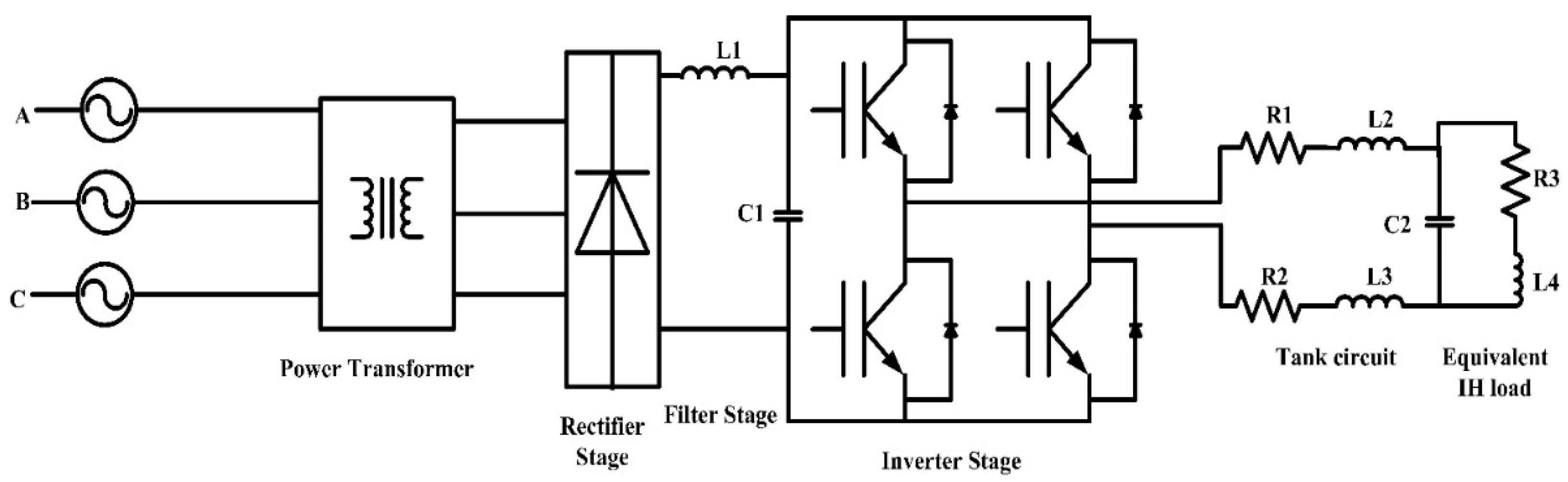
2. Distribution Static Compensator (DSTATCOM)
3. Control Algorithms
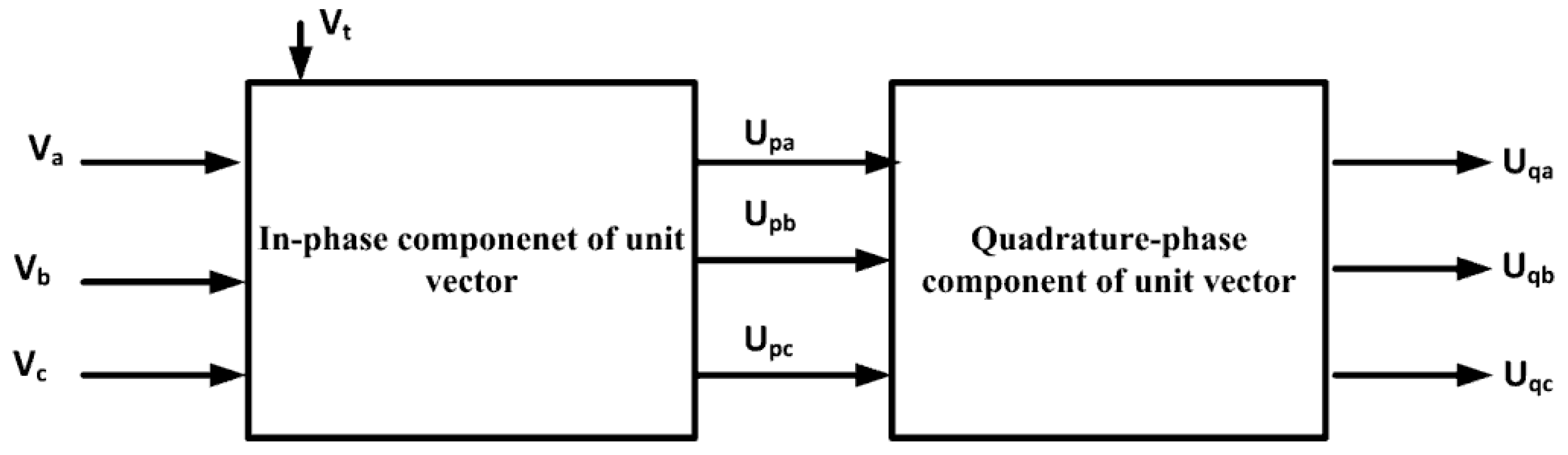
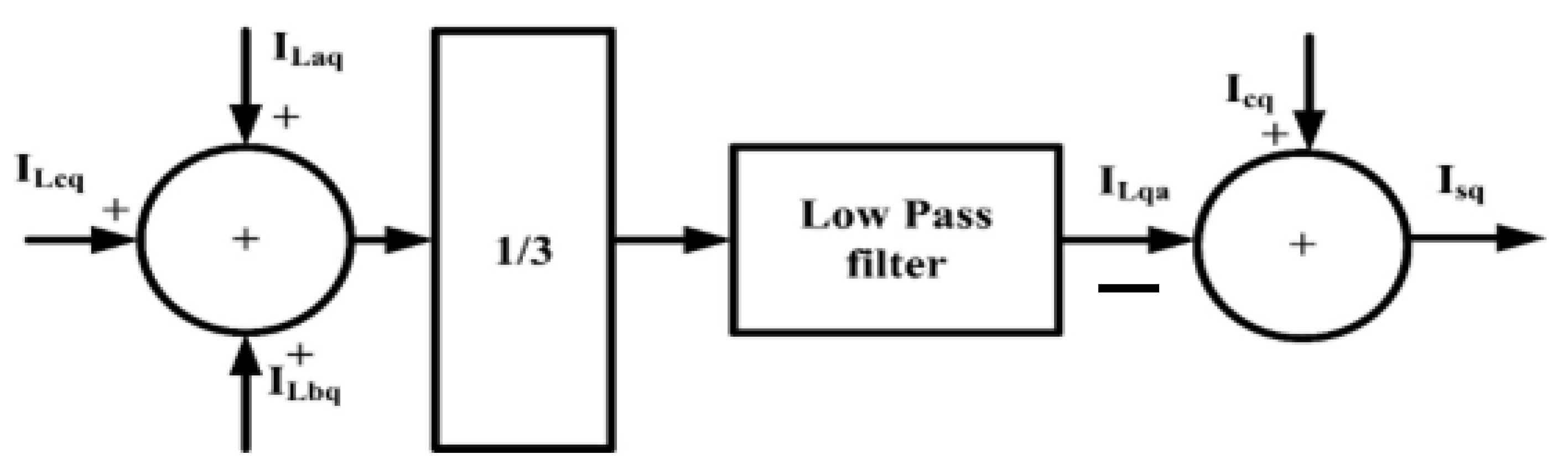
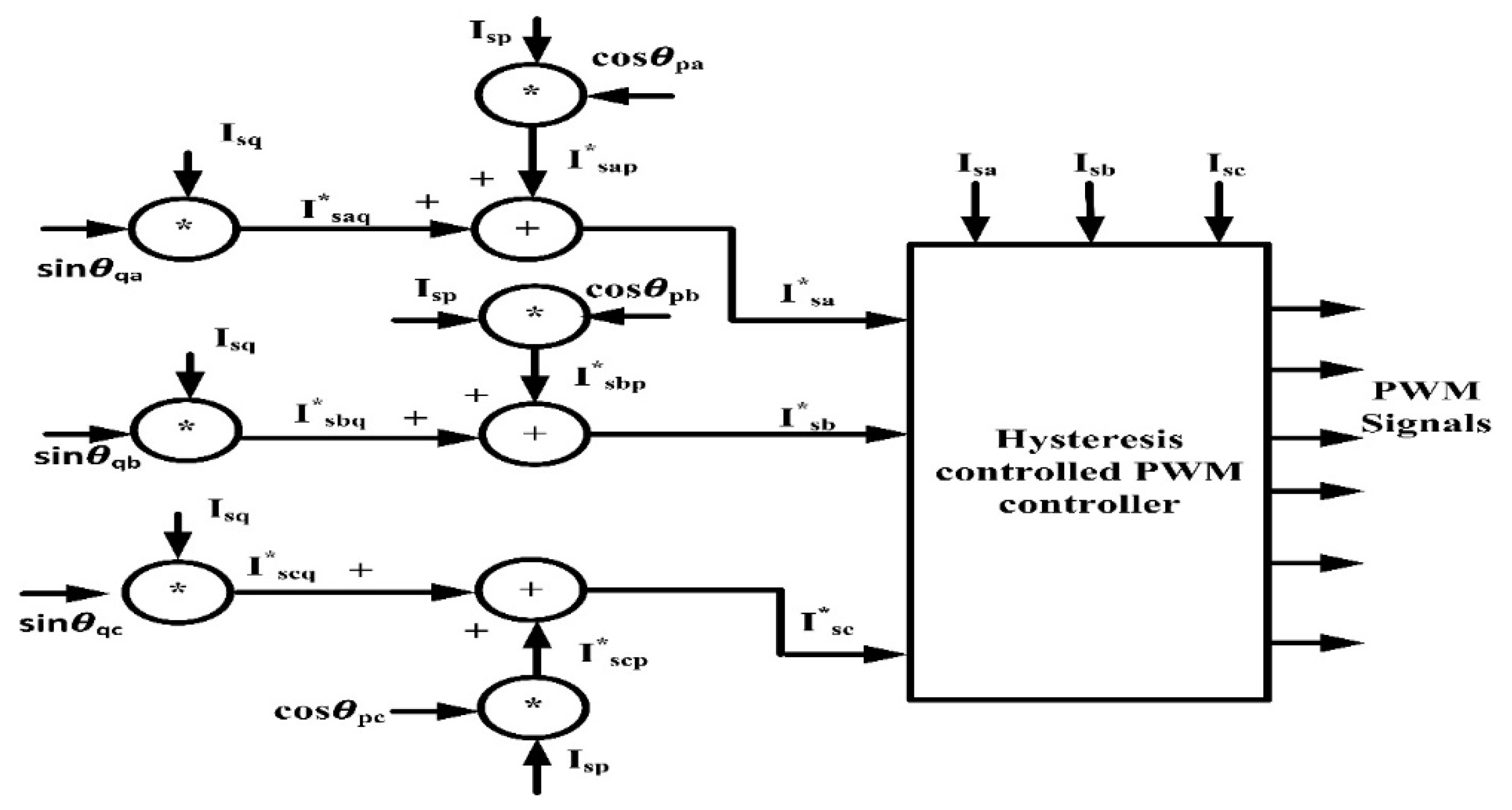
3.1. Icosθ Controller
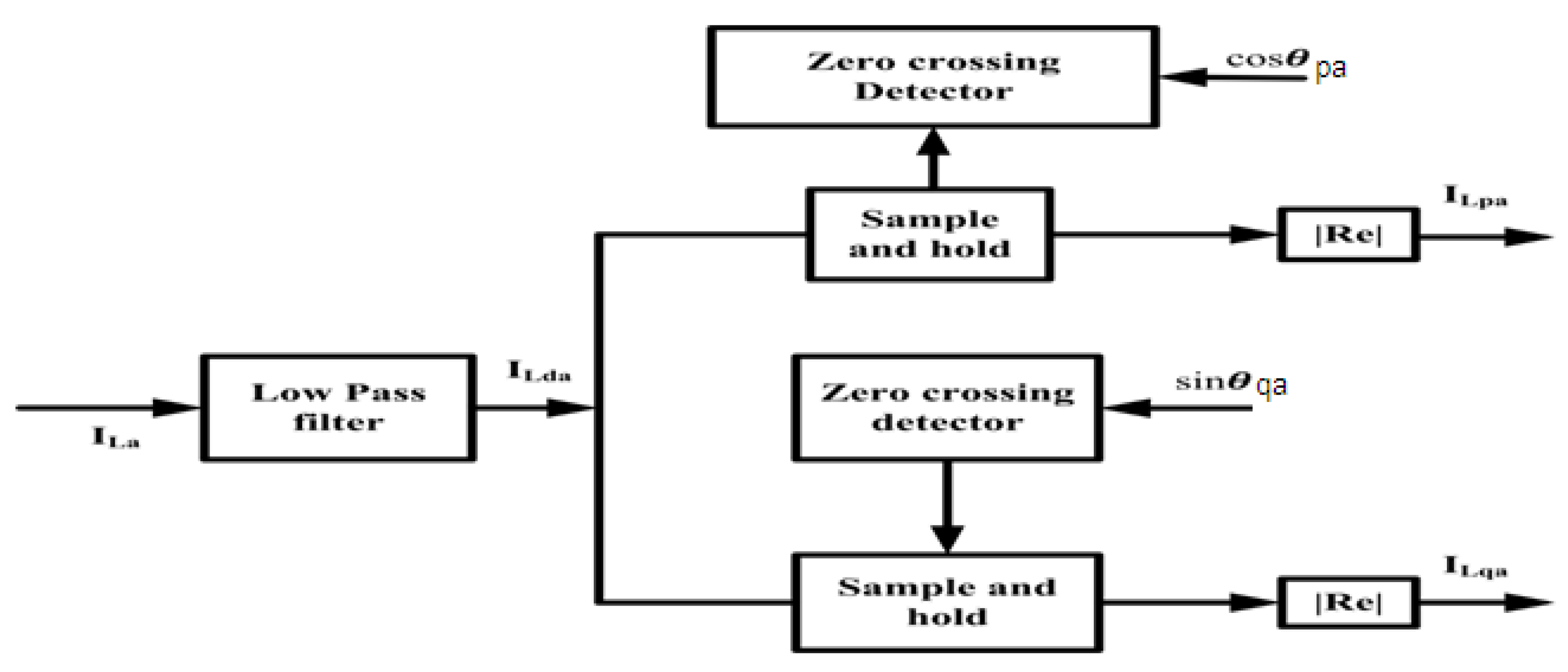
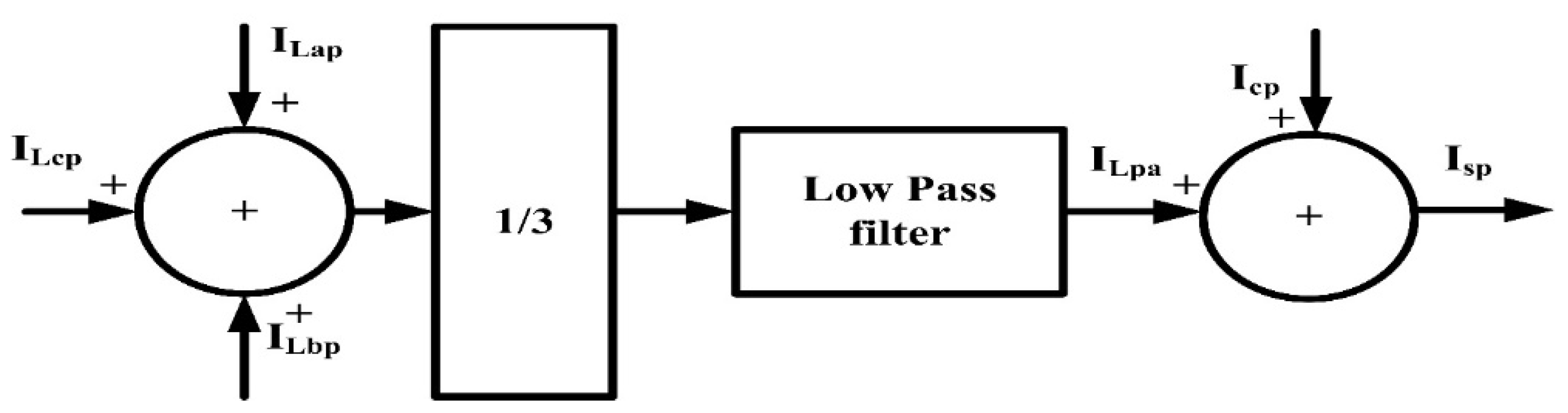
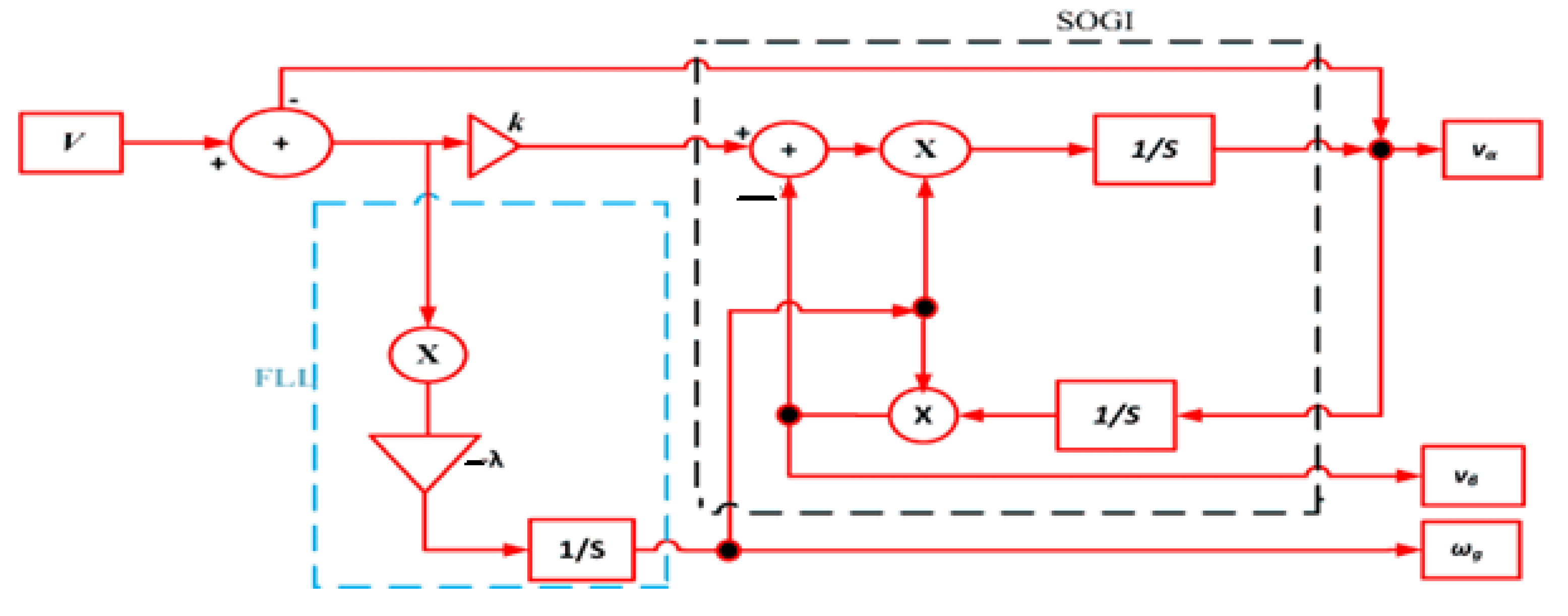
3.2. Enhanced SRF SOGI-FLL
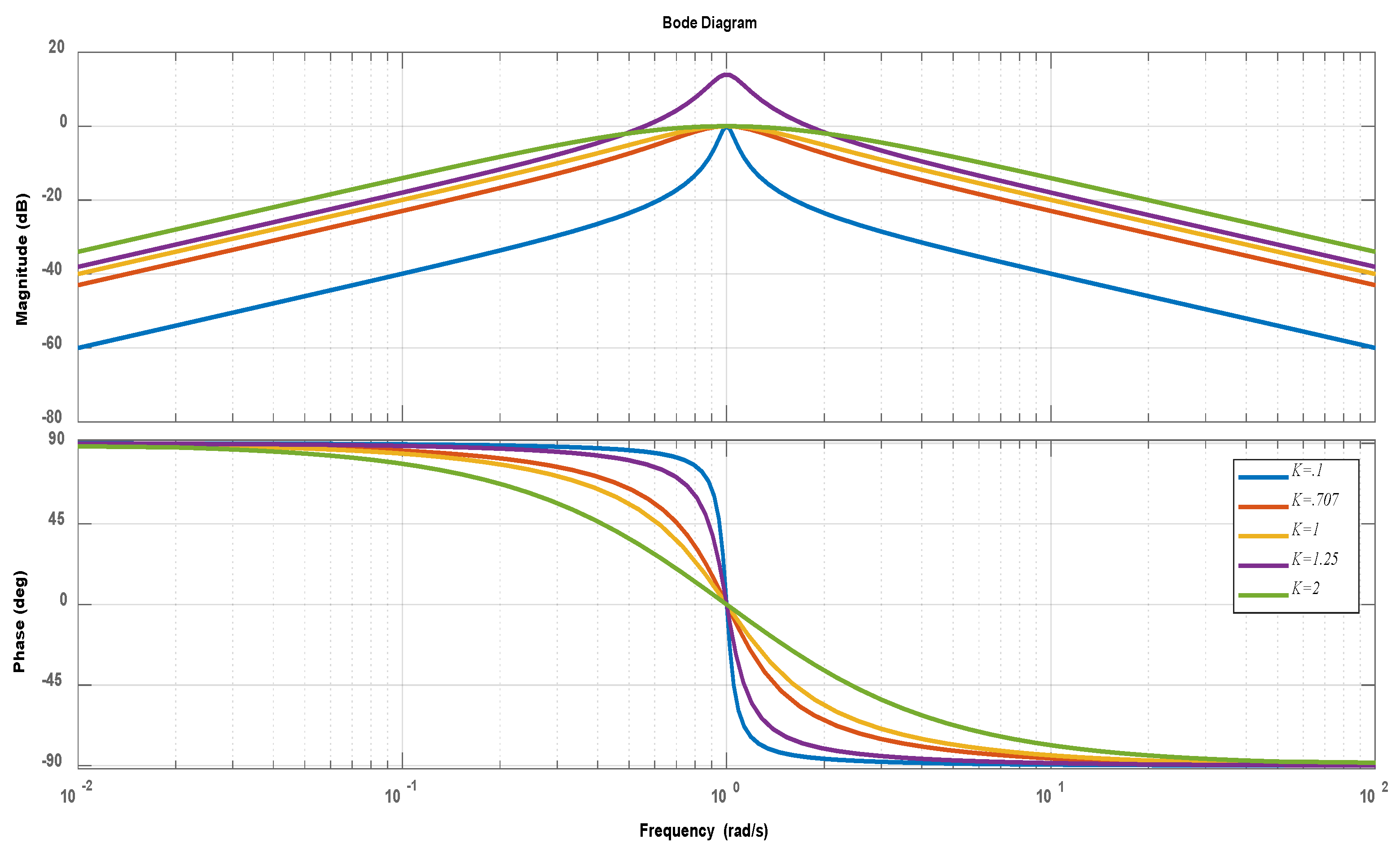
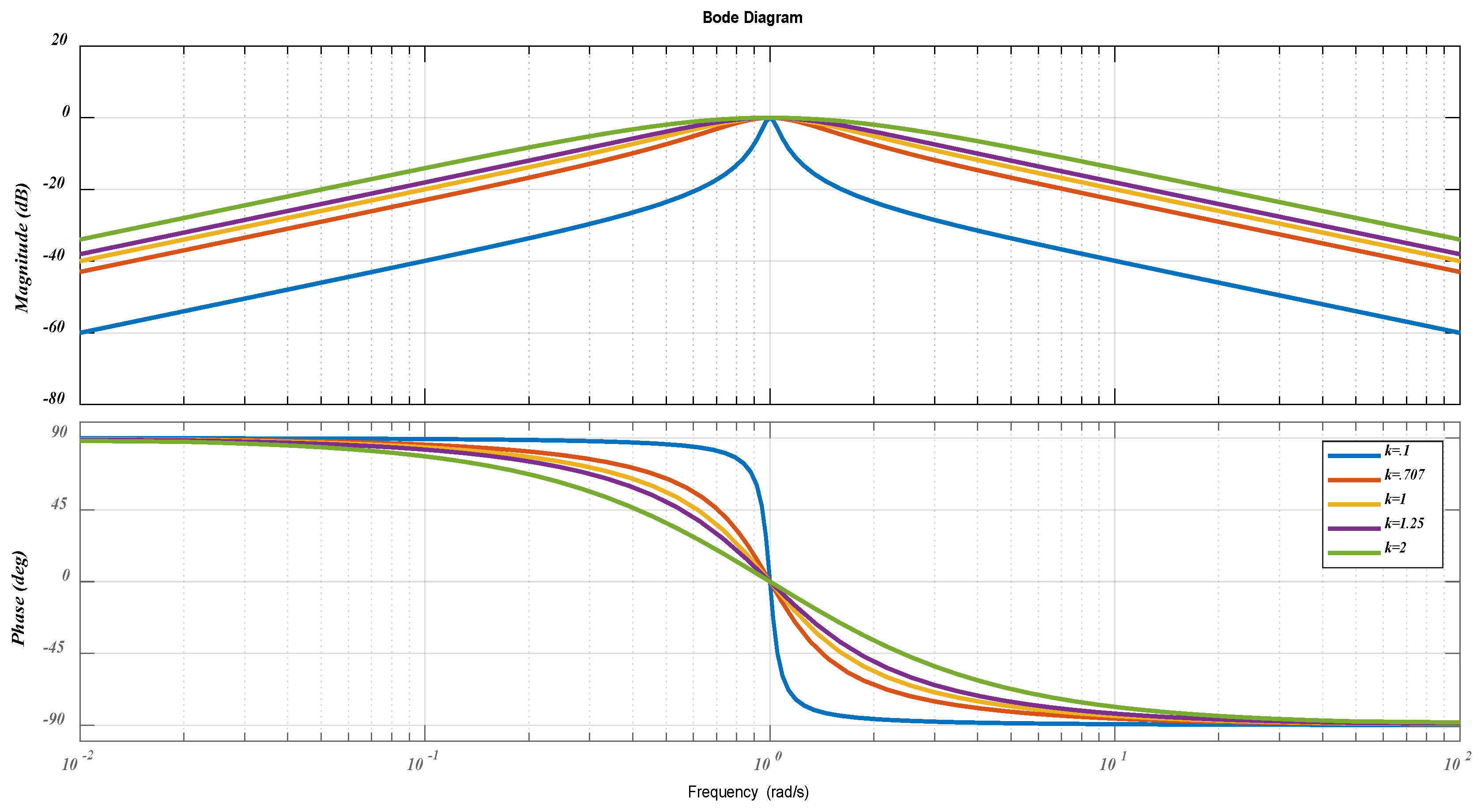
3.2.1. Dynamics of SOGI-FLL
3.2.2. Mathematical Modeling of Standard SOGI-FLL
3.2.3. Modeling of Tuning Parameters [35]
4. Non-Linear Loads
4.1. Non-Linear Load of the Voltage Source and Current Source Form
4.2. Induction Heating-Based Non-Linear Load
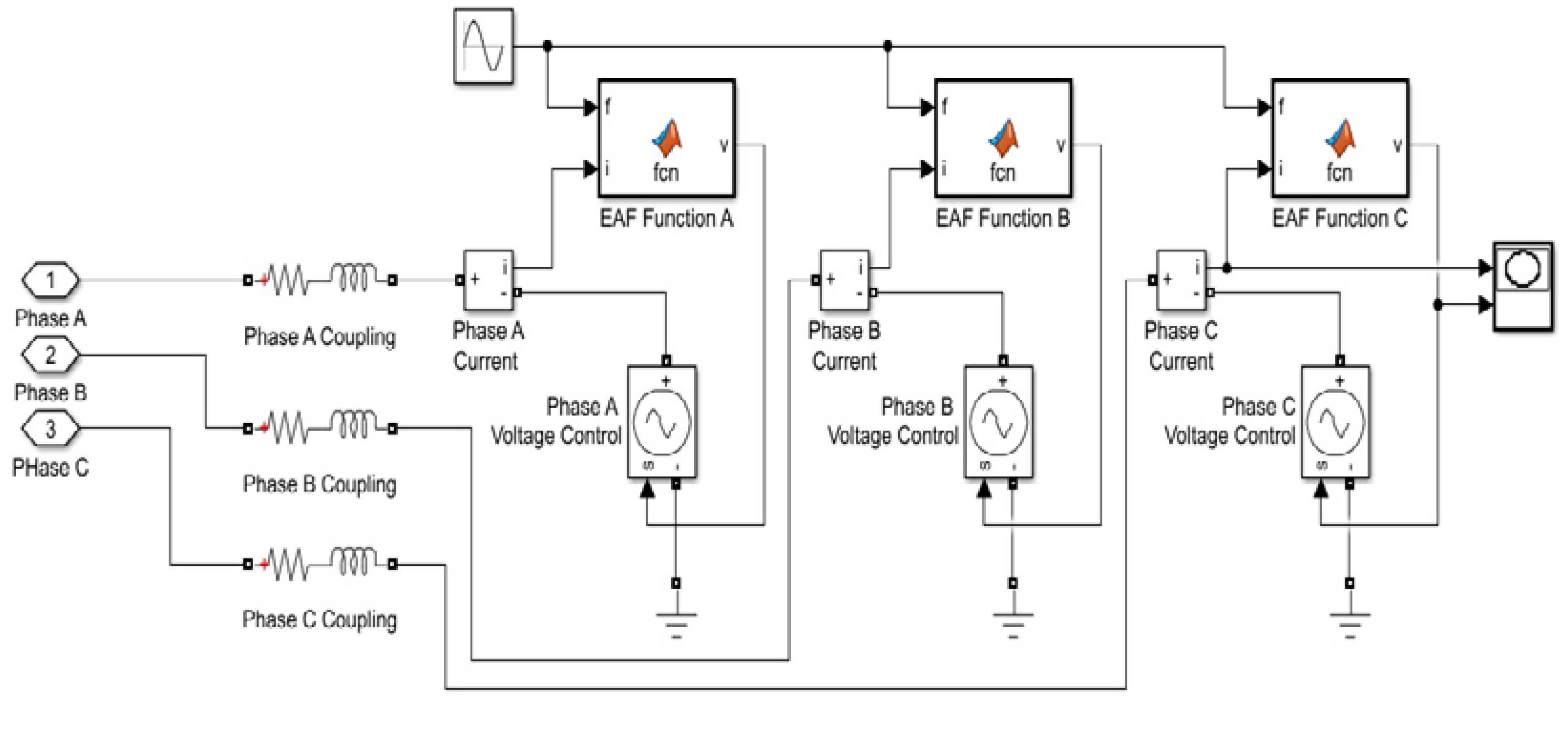
4.3. Electric Arc Furnace Type Non-Linear Load
5. Analyses of Results
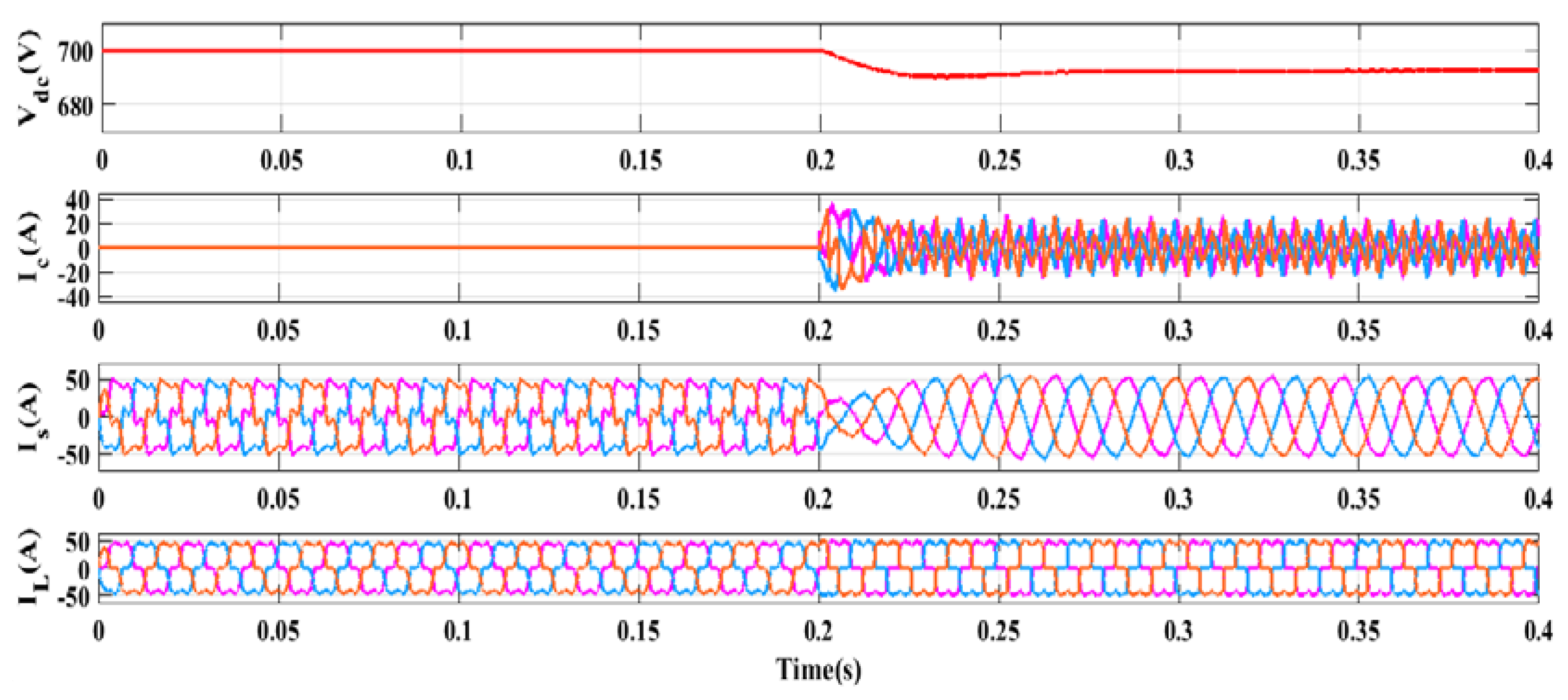
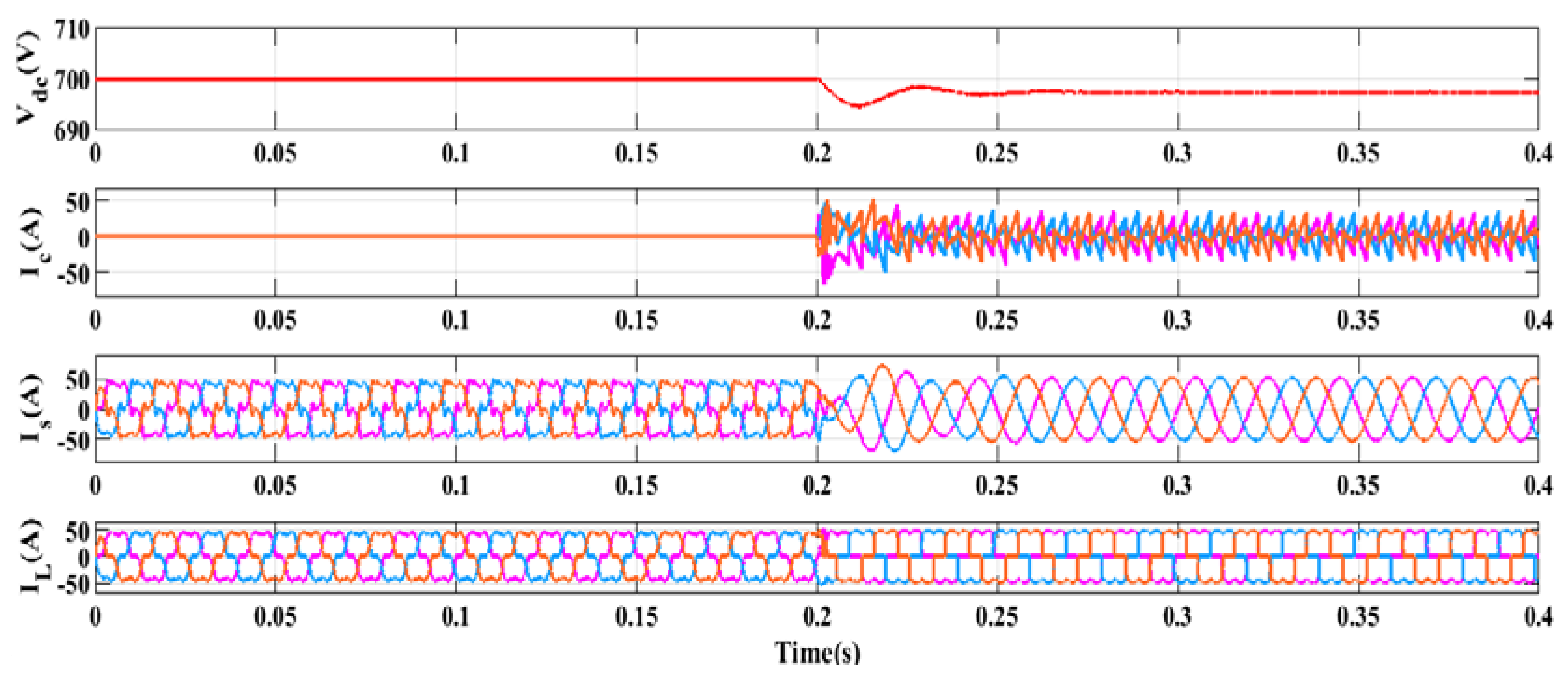
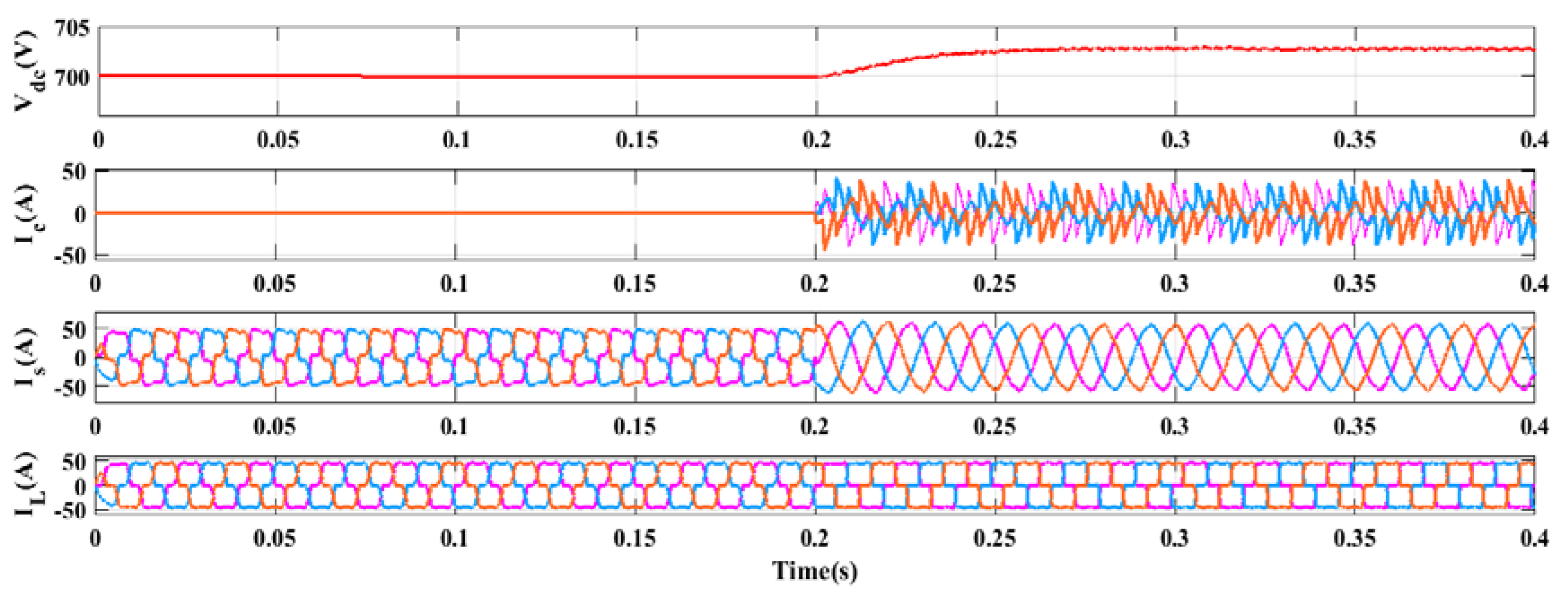
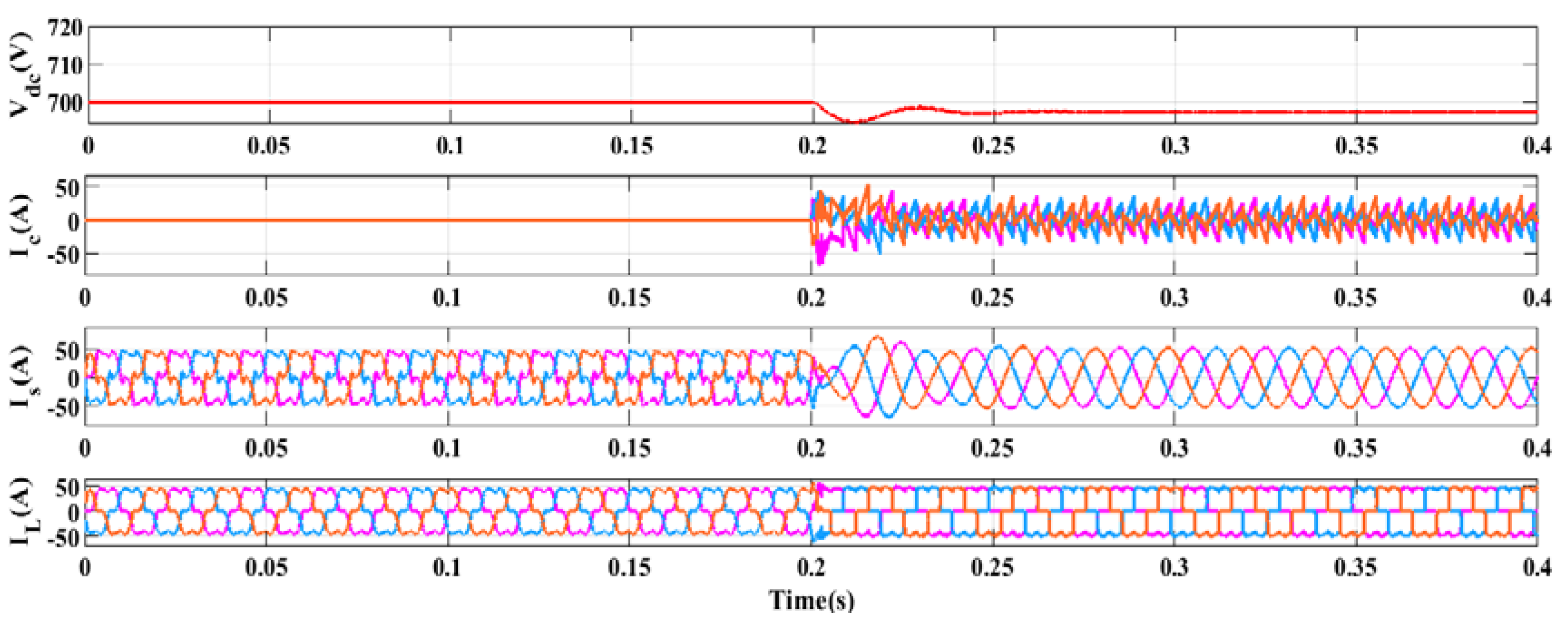
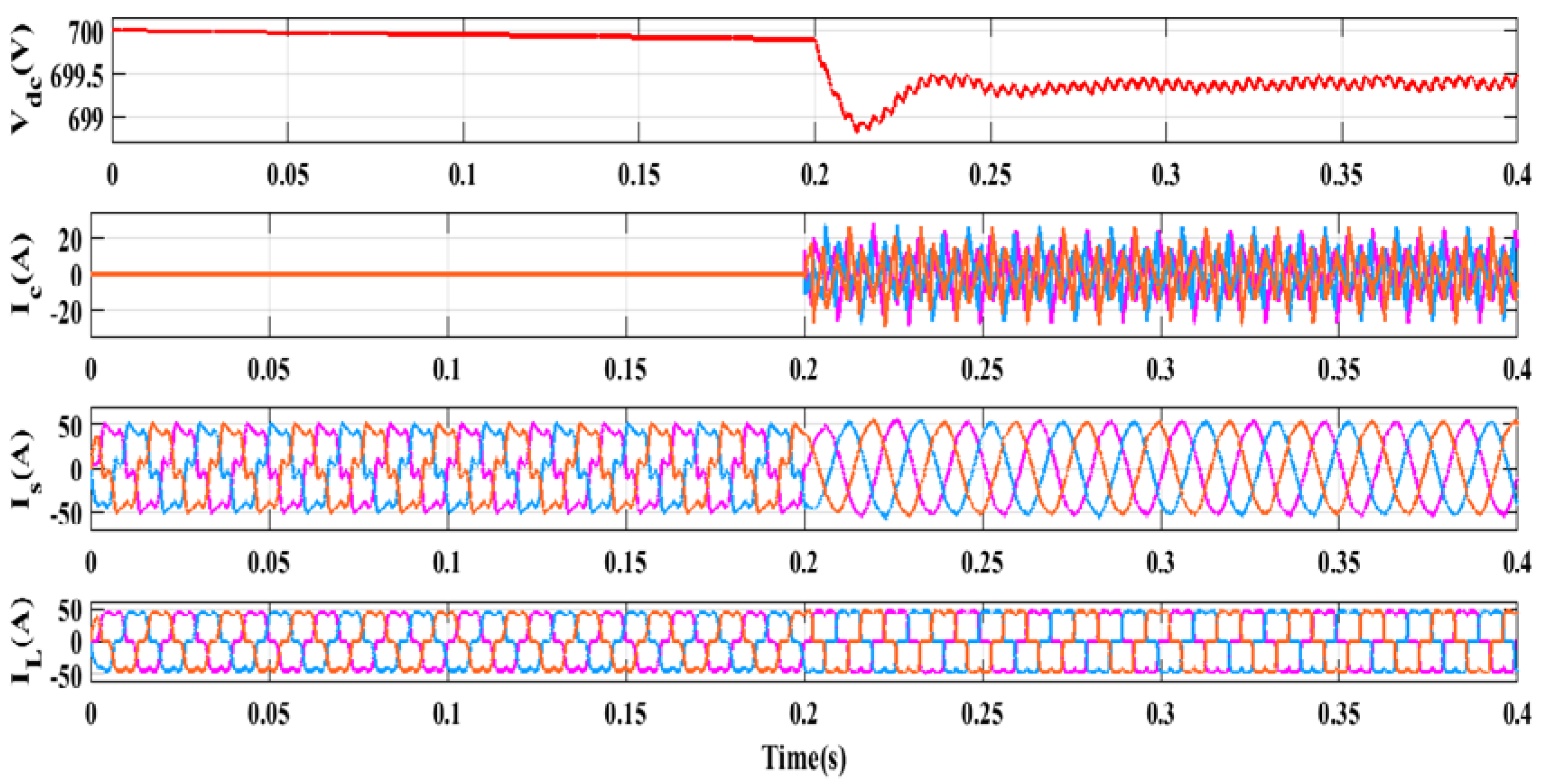
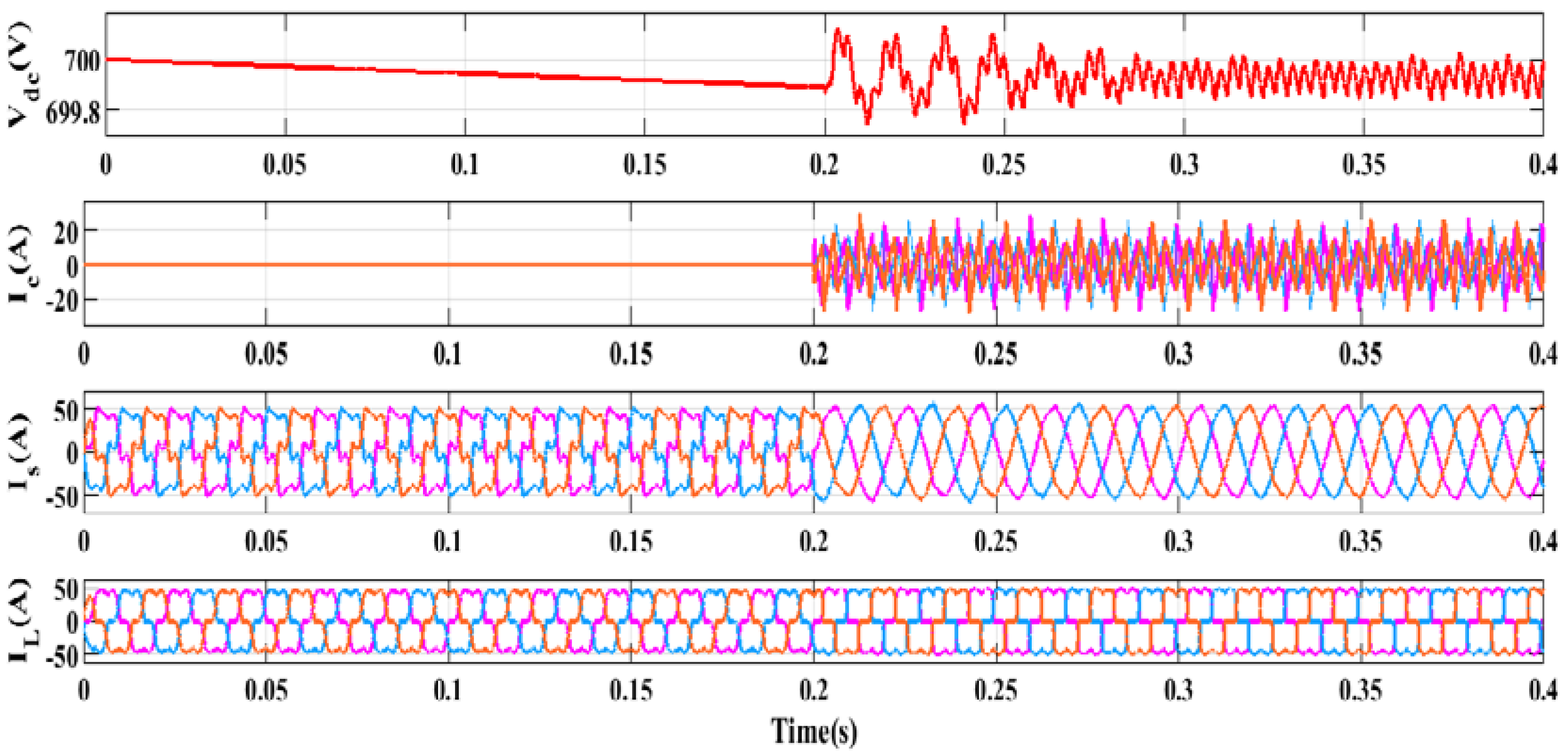
5.1. Performances Investigation under Voltage Source-Based Non-Linear Load
5.2. Performances Investigation under Current Source-Based Non-Linear Load
5.3. Performances Investigation under Induction Heating-Based Non-Linear Load
5.4. Performances Investigation under Electric Arc Furnace-Based Non-Linear Load
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghosh, A.; Ledwich, G. Power Quality Enhancement Using Custom Power Devices; Kluwer: London, UK, 2002. [Google Scholar]
- Dugan, R.C.; Mc Granaghan, M.F.; Santoso, S.; Beaty, H.W. Electric Power Systems Quality; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Thentral, T.T.; Palanisamy, R.; Usha, S.; Bajaj, M.; Zawbaa, H.M.; Kamel, S. Analysis of Power Quality issues of different types of household applications. Energy Rep. 2022, 8, 5370–5386. [Google Scholar] [CrossRef]
- Fuchs, E.F.; Masoum, M.A.S. Power Quality in Power Systems and Electrical Machines; Elsevier: London, UK, 2008. [Google Scholar]
- Myneni, H.; Kumar, G.S. Simple algorithm for current and voltage control of LCL DSTATCOM for power quality improvement. IET Gener. Transm. Distrib. 2019, 13, 423–434. [Google Scholar] [CrossRef]
- Chittora, P.; Singh, A.; Singh, M. Simple and efficient control of DSTATCOM in three phase four wire polluted grid system using MCCF-SOGI based controller, IET Gener. Transm. Distrib. 2018, 12, 1213–1222. [Google Scholar] [CrossRef]
- Singh, B.; Chandra, A.; Al-Haddad, K. Power Quality: Problems and Mitigation Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Mariscotti, A. Harmonic and Supraharmonic Emissions of Plug-In Electric Vehicle Chargers. Smart Cities 2022, 5, 496–521. [Google Scholar] [CrossRef]
- Milešević, B.; Uglešić, I.; Filipović-Grčić, B. Power quality analysis in electric traction system with three-phase induction motors. Electr. Power Syst. Res. 2016, 138, 172–179. [Google Scholar] [CrossRef]
- Singh, B.; Bhuvaneswari, G.; Garg, V. 24-Pulse AC-DC Converter for Power Quality Improvement in Vector Controlled Induction Motor Drives. Electr. Power Compon. Syst. 2006, 34, 1077–1098. [Google Scholar] [CrossRef]
- Cespedes, M.; Sun, J. Impedance modelling and analysis of grid-connected voltage-source converters. IEEE Trans. Power Electron. 2014, 29, 1254–1261. [Google Scholar] [CrossRef]
- Malathi, S.; Jayachandran, J. FPGA implementation of NN based LMS–LMF control algorithm in DSTATCOM for power quality improvement. Control. Eng. Pract. 2020, 98, 104378. [Google Scholar] [CrossRef]
- Qasim, M.; Kanjiya, P.; Khadkikar, V. Optimal current harmonic extractor based on unified ADALINEs for shunt active power filters. IEEE Trans. Power Electron. 2014, 29, 6383–6393. [Google Scholar] [CrossRef]
- Latran, M.B.; Teke, A.; Yoldaş, Y. Mitigation of power quality problems using distribution static synchronous compensator: A comprehensive review. IET Power Electron. 2015, 8, 1312–1328. [Google Scholar] [CrossRef]
- Bouafia, S.; Benaissa, A.; Barkat, S.; Bouzidi, M. Second order sliding mode control of three level four leg DSTATCOM based on instantaneous symmetrical component theory. Energy Syst. 2018, 9, 79–111. [Google Scholar] [CrossRef]
- Mangaraj, M.; Panda, A.K. Performance analysis of DSTATCOM employing various control algorithms. IET Gener. Transm. Distrib. 2017, 11, 2643–2653. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, N.; Akella, A.K. A Simulation Based Case Study for Control of DSTATCOM. ISA Trans. 2014, 53, 767–775. [Google Scholar] [CrossRef] [PubMed]
- Nunes, W.T.; Encarnação, L.F.; Aredes, M. An Improved Asymmetric Cascaded Multilevel D–STATCOM with Enhanced Hybrid Modulation. Electronics 2015, 4, 311–328. [Google Scholar] [CrossRef]
- Shahgholian, G.; Azimi, Z. Analysis and Design of a DSTATCOM Based on Sliding Mode Control Strategy for Improvement of Voltage Sag in Distribution Systems. Electronics 2016, 5, 41. [Google Scholar] [CrossRef]
- Irfan, M.M.; Rangarajan, S.S.; Collins, E.R.; Senjyu, T. Enhancing the Power Quality of the Grid Interactive Solar Photovoltaic-Electric Vehicle System. World Electr. Veh. J. 2021, 12, 98. [Google Scholar] [CrossRef]
- Satish, R.; Vaisakh, K.; Abdelaziz, A.Y.; El-Shahat, A. A Novel Three-Phase Harmonic Power Flow Algorithm for Unbalanced Radial Distribution Networks with the Presence of D-STATCOM Devices. Electronics 2021, 10, 2663. [Google Scholar] [CrossRef]
- Alshareef, S.M. Analyzing and Mitigating the Impacts of Integrating Fast-Charging Stations on the Power Quality in Electric Power Distribution Systems. Sustainability 2022, 14, 5595. [Google Scholar] [CrossRef]
- Mora-Burbano, J.A.; Fonseca-Díaz, C.D.; Montoya, O.D. Application of the SSA for Optimal Reactive Power Compensation in Radial and Meshed Distribution Using D-STATCOMs. Algorithms 2022, 15, 345. [Google Scholar] [CrossRef]
- Irfan, M.M.; Malaji, S.; Patsa, C.; Rangarajan, S.S.; Hussain, S.M.S. Control of DSTATCOM Using ANN-BP Algorithm for the Grid Connected Wind Energy System. Energies 2022, 15, 6988. [Google Scholar] [CrossRef]
- Chen, J.-H.; Tan, K.-H.; Lee, Y.-D. Intelligent Controlled DSTATCOM for Power Quality Enhancement. Energies 2022, 15, 4017. [Google Scholar] [CrossRef]
- Dash, A.; Bagarty, D.P.; Hota, P.K.; Sahu, M.K.; Hazra, T.; Behera, S.; Behera, A.K.; Behera, S.; Nayak, A.K.; Mohapatra, S.B.; et al. Grid-Tied Distribution Static Synchronous Compensator for Power Quality Enhancement Using Combined-Step-Size Real-Coefficient Improved Proportionate Affine Projection Sign Algorithm. Energies 2022, 15, 197. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C.; Abusorrah, A.M.; Al-Turki, Y. Modeling, tuning, and performance comparison of advanced second-order generalized integrator-based FLLs. IEEE Trans. Power Electron. 2018, 33, 10229–10239. [Google Scholar] [CrossRef]
- Duarte, S.N.; Souza, B.C.; Almeida, P.M.; Araujo, L.R.; Barbosa, P.G. Control algorithm for DSTATCOM to compensate consumer generated negative and zero sequence voltage unbalance. Int. J. Electr. Power Energy Syst. 2019, 120, 105957. [Google Scholar] [CrossRef]
- Penthia, T.; Panda, A.K.; Mangaraj, M. Experimental Validation of ADALINE Least Mean Square Algorithm in a Three-Phase Four-Wire DSTATCOM to Enhance Power Quality. Electr. Power Compon. Syst. 2020, 48, 769–780. [Google Scholar] [CrossRef]
- Jampana, B.; Veramalla, R.; Askani, J. Performance of four-leg VSC based DSTATCOM using single phase PQ theory. J. Inst. Eng. India Ser. B 2017, 98, 65–76. [Google Scholar] [CrossRef]
- Raveendra, N.; Madhusudhan, V.; Jaya Laxmi, A. RFLSA control scheme for power quality disturbances mitigation in DSTATCOM with n-level inverter connected power systems. Energy Syst. 2020, 11, 753–788. [Google Scholar] [CrossRef]
- Singh, B.; Kandpal, M.; Hussain, I. Control of grid tied smart PV-DSTATCOM system using an adaptive technique. IEEE Trans. Smart Grid 2018, 9, 3986–3993. [Google Scholar] [CrossRef]
- Puranik, V.; Arya, S.R. SOGI-FLL based adaptive filter for DSTATCOM under variable supply frequency. J. Inst. Eng. India Ser. B 2017, 98, 423–431. [Google Scholar] [CrossRef]
- Punna, S.; Mailugundla, R.; Salkuti, S.R. Design, Analysis and Implementation of Bidirectional DC–DC Converters for HESS in DC Microgrid Applications. Smart Cities 2022, 5, 433–454. [Google Scholar] [CrossRef]
- Zou, Z.X.; Liserre, M. Modeling phase-locked loop-based synchronization in grid-interfaced converter. IEEE Trans. Energy Convers. 2019, 35, 394–404. [Google Scholar] [CrossRef]
- Saggu, T.S.; Singh, L.; Gill, B. Harmonics Mitigation in a Steel Industry using eleven level Cascaded Multilevel Inverter based Dstatcom. Can. J. Electr. Comput. Eng. 2017, 40, 110–115. [Google Scholar] [CrossRef]
- Bhonsle, D.C.; Kelkar, R.B. Analyzing power quality issue in electric arc furnace by modeling. Energy 2016, 115, 830–839. [Google Scholar] [CrossRef]
- Noroozi, M.; Haghjoo, F.; Javadi, H.; Zolghadri, M.R. Power quality improvement in single-phase transformerless semi-quasi-Z-source inverters for off-grid photovoltaic systems. Int. J. Electr. Power Energy Syst. 2023, 145, 108703. [Google Scholar] [CrossRef]
- IEEE. Recommended Practice and Requirements for Harmonic Control in Electric Power Systems—Redline. In IEEE Std 519-2014 (Revision of IEEE Std 519-1992)—Redline; IEEE: Piscataway, NJ, USA, 2014; pp. 1–213. [Google Scholar]
- Hemalatha, R.; Ramasamy, M. Microprocessor and PI controller based three phase CHBMLI based DSTATCOM for THD mitigation using hybrid control technique. Microprocess. Microsystem. 2020, 76, 103093. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| SOGI gain | |
| FLL gain | |
| Frequency | 50 Hz |
| Nominal angular frequency | rad/s |
| Non-Linear Loads | Parameter Used in the Simulation | Application | Power Quality Issues |
| Voltage source-based | , = 5 μF | Household appliances, switched-mode power supply (SMPS) | Harmonics, power factor deterioration, reactive power burden |
| Current source-based | 0.002 H, | Electric motor, industrial load | Current harmonics, power factor deterioration, reactive power burden |
| Induction heating-based | 0.002 H 0.006 H 0.008 H 0.003 H = 5 μF = 2.5 μF | Steel industries, cooking induction heater | Unbalanced phases, reactive power burden, harmonics |
| Electric Arc Furnace | = 360 V m = 0.2 = 0.4 = 200 V C = 23,000 D = 5000 | Welding industries, heavy engineering industries | Flicker, voltage fluctuation, harmonics |
| DSTATCOM | = 0.0004 H = 9000 μF | Power quality issues’ mitigation | |
| Source/Grid | = 415 V
= 0.001 = 0.002 H |
| Non-Linear Load | Harmonic Order (Uncompensated Mode) | Control Algorithm | Harmonic Order (Compensated Mode) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 3rd | 5th | 7th | 9th | 3rd | 5th | 7th | 9th | ||
| Voltage source | 4.12% | 6.23% | 2.23% | 1.5% | Icosθ | 2.32% | 1.18% | 0.98% | 0.63% |
| SOGI-FLL | 2.10% | 1.02% | 0.78% | 0.63% | |||||
| Current source | 3.25% | 5.32% | 2.01% | 1.9% | Icosθ | 2.01% | 1.23% | 0.69% | 0.25% |
| SOGI-FLL | 1.98% | 1.25% | 0.32% | 0.21% | |||||
| Induction furnace | 5.72% | 3.12% | 2.03% | 1.02% | Icosθ | 2.15% | 0.96% | 1.78% | 0.89% |
| SOGI-FLL | 2.89% | 1.06% | 1.54% | 0.26% | |||||
| Arc furnace | 6.89% | 4.07% | 2.30% | 1.87% | Icosθ | 2.96% | 1.23% | 0.75% | 0.23% |
| SOGI-FLL | 1.56% | 1.25% | 0.89% | 0.45% | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islavatu, S.; Kumar, P.; Kumar, A.; Salkuti, S.R. Power Quality Analysis by H-Bridge DSTATCOM Control by Icosθ and ESRF SOGI-FLL Methods for Different Industrial Loads. Smart Cities 2022, 5, 1590-1610. https://doi.org/10.3390/smartcities5040081
Islavatu S, Kumar P, Kumar A, Salkuti SR. Power Quality Analysis by H-Bridge DSTATCOM Control by Icosθ and ESRF SOGI-FLL Methods for Different Industrial Loads. Smart Cities. 2022; 5(4):1590-1610. https://doi.org/10.3390/smartcities5040081
Chicago/Turabian StyleIslavatu, Srikanth, Pradeep Kumar, Amit Kumar, and Surender Reddy Salkuti. 2022. "Power Quality Analysis by H-Bridge DSTATCOM Control by Icosθ and ESRF SOGI-FLL Methods for Different Industrial Loads" Smart Cities 5, no. 4: 1590-1610. https://doi.org/10.3390/smartcities5040081
APA StyleIslavatu, S., Kumar, P., Kumar, A., & Salkuti, S. R. (2022). Power Quality Analysis by H-Bridge DSTATCOM Control by Icosθ and ESRF SOGI-FLL Methods for Different Industrial Loads. Smart Cities, 5(4), 1590-1610. https://doi.org/10.3390/smartcities5040081







