Utilizing Computational Modelling to Bridge the Gap between In Vivo and In Vitro Degradation Rates for Mg-xGd Implants
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Calibration Data
2.2. Peridynamic Model and Implementation
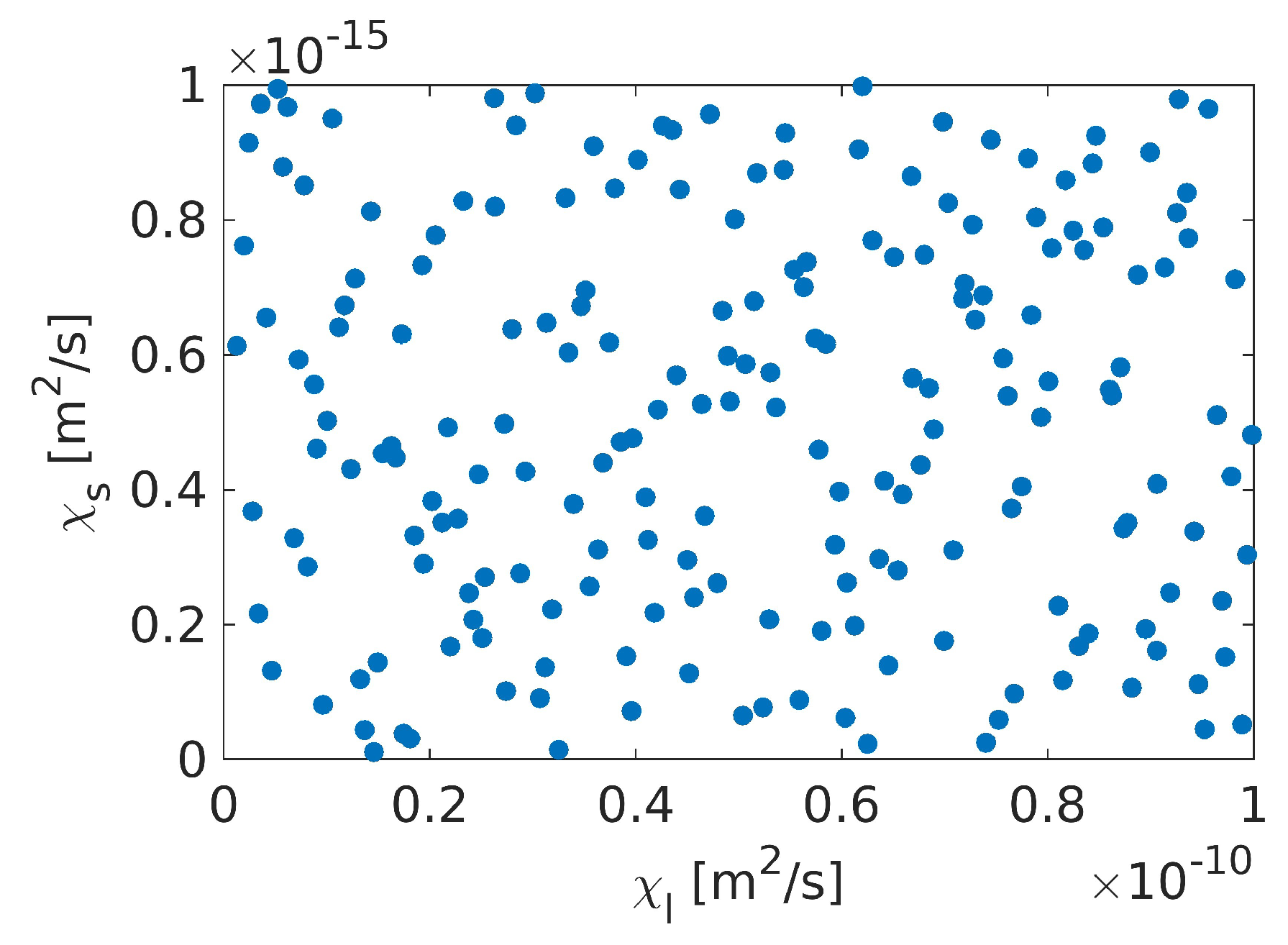
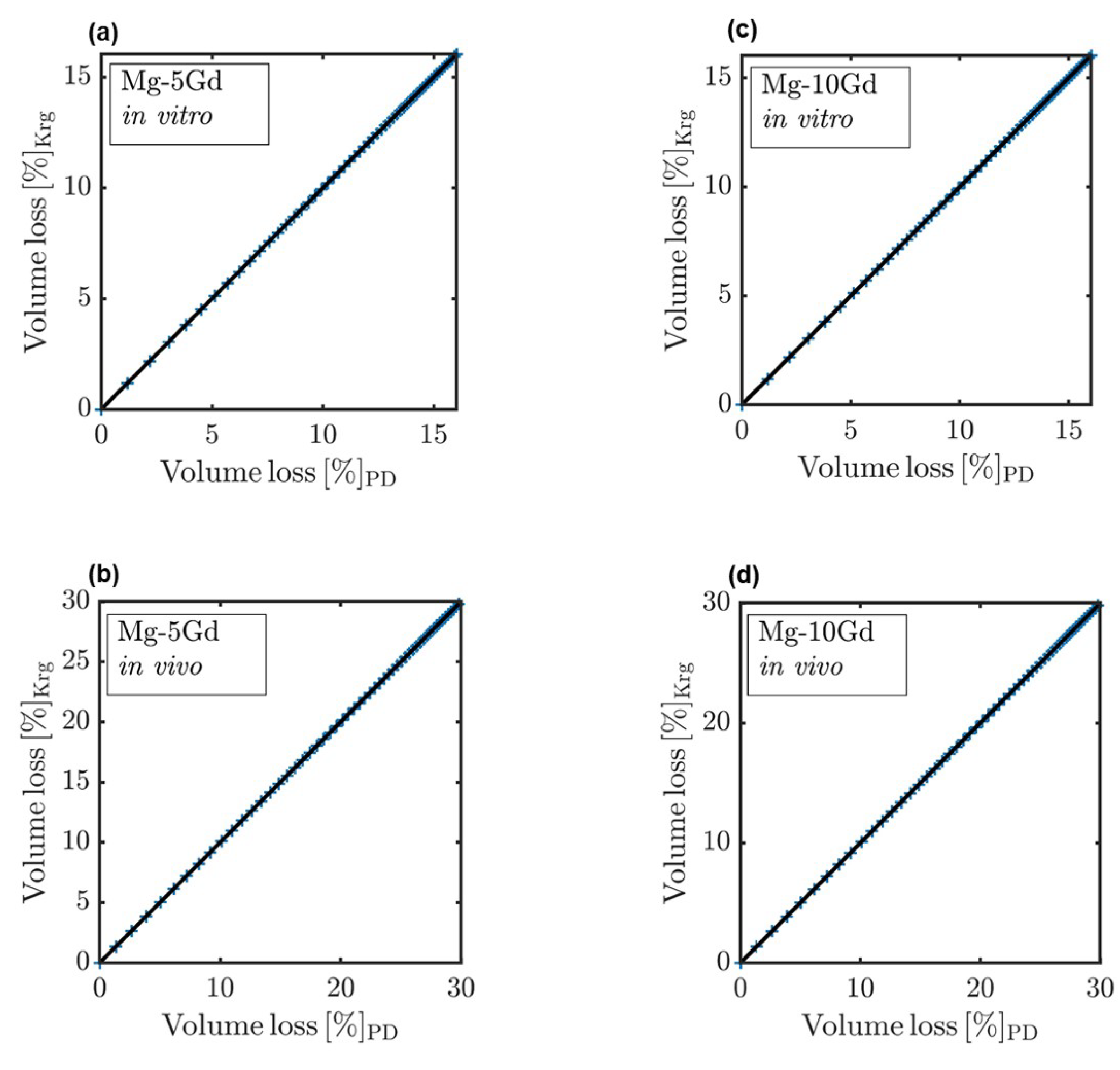
2.3. Kriging-Based Surrogate Model and Implementation
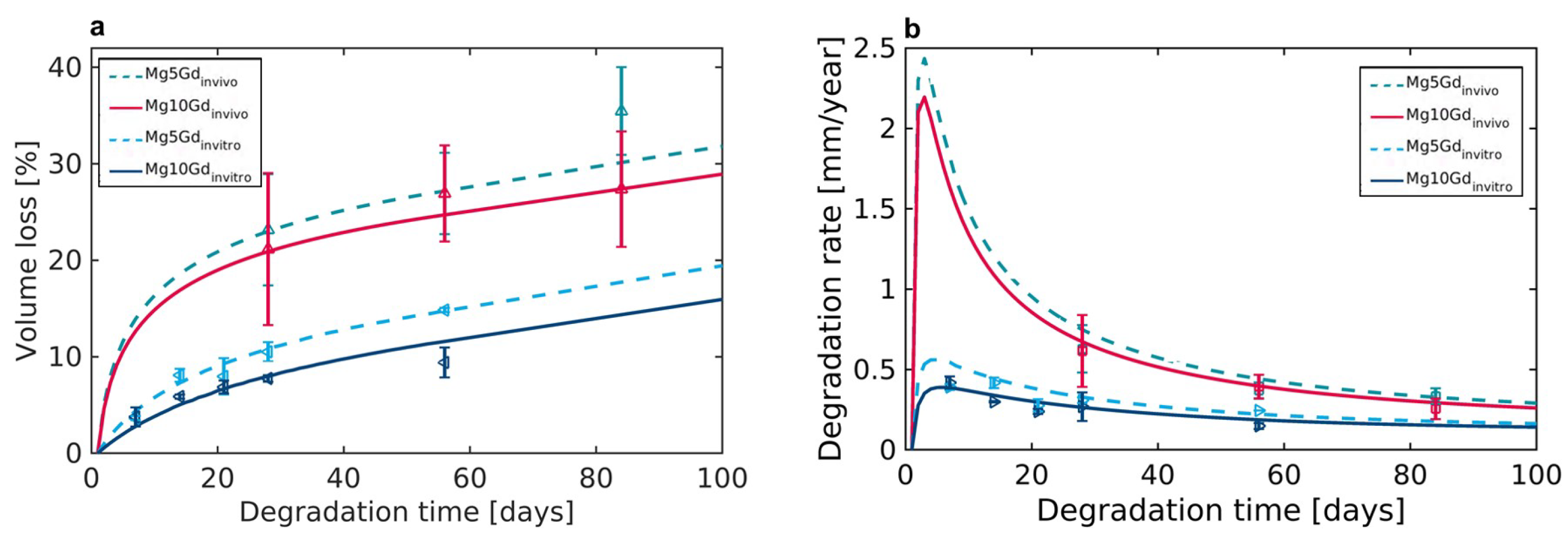
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gonzalez, J.; Hou, R.Q.; Nidadavolu, E.P.S.; Willumeit-Römer, R.; Feyerabend, F. Magnesium degradation under physiological conditions—Best practice. Bioact. Mater. 2018, 3, 174–185. [Google Scholar] [CrossRef] [PubMed]
- Luthringer, B.; Feyerabend, F.; Willumeit, R. Magnesium-Based Implants: A Mini-Review. Magnes. Res. 2014, 27, 142–154. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Cockerill, I.; Zheng, Y.; Tang, L.; Qin, Y.X.; Zhu, D. Biofunctionalization of metallic implants by calcium phosphate coatings. Bioact. Mater. 2019, 4, 196–206. [Google Scholar] [CrossRef]
- Myrissa, A.; Agha, N.A.; Lu, Y.; Martinelli, E.; Eichler, J.; Szakács, G.; Kleinhans, C.; Willumeit-Römer, R.; Schäfer, U.; Weinberg, A.M. In vitro and in vivo comparison of binary Mg alloys and pure Mg. Mater. Sci. Eng. C 2016, 61, 865–874. [Google Scholar] [CrossRef]
- Willumeit-Römer, R.; Bruns, S.; Helmholz, H.; Krüger, D.; Wiese, B.; Galli, S.; Moosmann, J.; Zeller-Plumhoff, B. The Comparability of In Vitro and In Vivo Experiments for Degradable Mg Implants; Springer International Publishing: Cham, Switzerland, 2022; pp. 9–16. [Google Scholar]
- Negrescu, A.M.; Necula, M.G.; Costache, M.; Cimpean, A. In vitro and in vivo biological performance of Mg-based bone implants. Rev. Biol. Biomed. Sci. 2020, 3, 11–41. [Google Scholar] [CrossRef]
- Sanchez, A.H.M.; Luthringer, B.J.C.; Feyerabend, F.; Willumeit, R. Mg and Mg alloys: How comparable are in vitro and in vivo corrosion rates? A review. Acta Biomater. 2015, 13, 16–31. [Google Scholar] [CrossRef]
- Krüger, D.; Galli, S.; Zeller-Plumhoff, B.; Wieland, D.F.; Peruzzi, N.; Wiese, B.; Heuser, P.; Moosmann, J.; Wennerberg, A.; Willumeit-Römer, R. High-resolution ex vivo analysis of the degradation and osseointegration of Mg-xGd implant screws in 3D. Bioact. Mater. 2022, 13, 37–52. [Google Scholar] [CrossRef]
- Kokubo, T.; Takadama, H. How useful is SBF in predicting in vivo bone bioactivity? Biomaterials 2006, 27, 2907–2915. [Google Scholar] [CrossRef]
- Zheng, Y.F.; Gu, X.N.; Witte, F. Biodegradable metals. Mater. Sci. Eng. R Rep. 2014, 77, 1–34. [Google Scholar] [CrossRef]
- Amukarimi, S.; Mozafari, M. Biodegradable magnesium-based biomaterials: An overview of challenges and opportunities. MedComm 2021, 2, 123–144. [Google Scholar] [CrossRef]
- Zeller-Plumhoff, B.; AlBaraghtheh, T.; Höche, D.; Willumeit-Römer, R. Computational modelling of magnesium degradation in simulated body fluid under physiological conditions. J. Magnes. Alloys 2022, 10, 965–978. [Google Scholar] [CrossRef]
- Grogan, J.A.; Leen, S.B.; McHugh, P.E. A physical corrosion model for bioabsorbable metal stents. Acta Biomater. 2014, 10, 2313–2322. [Google Scholar] [CrossRef] [PubMed]
- Hermann, A.; Shojaei, A.; Steglich, D.; Höche, D.; Zeller-Plumhoff, B.; Cyron, C.J. Combining peridynamic and finite element simulations to capture the corrosion of degradable bone implants and to predict their residual strength. Int. J. Mech. Sci. 2022, 220, 107143. [Google Scholar] [CrossRef]
- Deshpande, K.B. Numerical modeling of micro-galvanic corrosion. Electrochim. Acta 2011, 56, 1737–1745. [Google Scholar] [CrossRef]
- Chen, Z.; Bobaru, F. Peridynamic modeling of pitting corrosion damage. J. Mech. Phys. Solids 2015, 78, 352–381. [Google Scholar] [CrossRef]
- Marvi-Mashhadi, M.; Ali, W.; Li, M.; González, C.; LLorca, J. Simulation of corrosion and mechanical degradation of additively manufactured Mg scaffolds in simulated body fluid. J. Mech. Behav. Biomed. Mater. 2022, 126, 104881. [Google Scholar] [CrossRef] [PubMed]
- Boland, E.L.; Shine, R.; Kelly, N.; Sweeney, C.A.; McHugh, P.E. A Review of Material Degradation Modelling for the Analysis and Design of Bioabsorbable Stents. Ann. Biomed. Eng. 2016, 44, 341–356. [Google Scholar] [CrossRef] [PubMed]
- Albaraghtheh, T.; Willumeit-Römer, R.; Zeller-Plumhoff, B. In silico studies of magnesium-based implants: A review of the current stage and challenges. J. Magnes. Alloys 2022, 10, 2968–2996. [Google Scholar] [CrossRef]
- Abdallah, M.; Joplin, A.; Elahinia, M.; Ibrahim, H. Corrosion Modeling of Magnesium and Its Alloys for Biomedical Applications: Review. Corros. Mater. Degrad. 2020, 1, 219–248. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, X.; Yan, Y. A novel pathway for the preparation of Mg metal from magnesia. J. Magnes. Alloys 2021, 10, 2847–2856. [Google Scholar] [CrossRef]
- Sanz-Herrera, J.A.; Reina-Romo, E.; Boccaccini, A.R. In silico design of magnesium implants: Macroscopic modeling. J. Mech. Behav. Biomed. Mater. 2018, 79, 181–188. [Google Scholar] [CrossRef] [PubMed]
- Gartzke, A.K.; Julmi, S.; Klose, C.; Waselau, A.C.; Meyer-Lindenberg, A.; Maier, H.J.; Besdo, S.; Wriggers, P. A simulation model for the degradation of magnesium-based bone implants. J. Mech. Behav. Biomed. Mater. 2020, 101, 103411. [Google Scholar] [CrossRef] [PubMed]
- Shojaei, A.; Hermann, A.; Seleson, P.; Cyron, C.J. Dirichlet absorbing boundary conditions for classical and peridynamic diffusion-type models. Comput. Mech. 2020, 66, 773–793. [Google Scholar] [CrossRef]
- Jafarzadeh, S.; Chen, Z.; Bobaru, F. Peridynamic Modeling of Repassivation in Pitting Corrosion of Stainless Steel. Corrosion 2018, 74, 393–414. [Google Scholar] [CrossRef]
- Jafarzadeh, S.; Chen, Z.; Bobaru, F. Peridynamic Modeling of Intergranular Corrosion Damage. J. Electrochem. Soc. 2018, 165, C362–C374. [Google Scholar] [CrossRef]
- Jafarzadeh, S.; Chen, Z.; Bobaru, F. Computational modeling of pitting corrosion. Corros. Rev. 2019, 37, 419–439. [Google Scholar] [CrossRef]
- Chen, Z.; Jafarzadeh, S.; Zhao, J.; Bobaru, F. A coupled mechano-chemical peridynamic model for pit-to-crack transition in stress-corrosion cracking. J. Mech. Phys. Solids 2021, 146, 104203. [Google Scholar] [CrossRef]
- Zhao, J.; Jafarzadeh, S.; Rahmani, M.; Chen, Z.; Kim, Y.R.; Bobaru, F. A peridynamic model for galvanic corrosion and fracture. Electrochim. Acta 2021, 391, 138968. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, J.; Wang, R. Basic Framework and Main Methods of Uncertainty Quantification. Math. Probl. Eng. 2020, 2020, 6068203. [Google Scholar] [CrossRef]
- Sudret, B.; Marelli, S.; Wiart, J. Surrogate Models for Uncertainty Quantification: An Overview. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017. [Google Scholar] [CrossRef]
- Wu, X.; Wang, C.; Kozlowski, T. Kriging-Based Surrogate Models for Uncertainty Quantification and Sensitivity Analysis. In Proceedings of the International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, Jeju, Republic of Korea, 16–20 April 2017. [Google Scholar]
- Wang, K.; Wang, Y.; Yue, X.; Cai, W. Multiphysics modeling and uncertainty quantification of tribocorrosion in aluminum alloys. Corros. Sci. 2021, 178, 109095. [Google Scholar] [CrossRef]
- Liu, Y.; Li, L.; Zhao, S.; Song, S. A global surrogate model technique based on principal component analysis and Kriging for uncertainty propagation of dynamic systems. Reliab. Eng. Syst. Saf. 2021, 207, 107365. [Google Scholar] [CrossRef]
- Bhosekar, A.; Ierapetritou, M. Advances in surrogate based modeling, feasibility analysis, and optimization: A review. Comput. Chem. Eng. 2018, 108, 250–267. [Google Scholar] [CrossRef]
- Fuhg, J.N.; Fau, A.; Nackenhorst, U. State-of-the-Art and Comparative Review of Adaptive Sampling Methods for Kriging. Arch. Comput. Methods Eng. 2021, 28, 2689–2747. [Google Scholar] [CrossRef]
- Cole, D.A.; Christianson, R.B.; Gramacy, R.B. Locally induced Gaussian processes for large-scale simulation experiments. Stat. Comput. 2021, 31, 33. [Google Scholar] [CrossRef]
- Krüger, D.; Zeller-Plumhoff, B.; Wiese, B.; Yi, S.; Zuber, M.; Wieland, D.C.; Moosmann, J.; Willumeit-Römer, R. Assessing the microstructure and in vitro degradation behavior of Mg-xGd screw implants using µCT. J. Magnes. Alloys 2021, 9, 2207–2222. [Google Scholar] [CrossRef]
- Zeller-Plumhoff, B.; Tolnai, D.; Wolff, M.; Greving, I.; Hort, N.; Willumeit-Römer, R. Utilizing Synchrotron Radiation for the Characterization of Biodegradable Magnesium Alloys-From Alloy Development to the Application as Implant Material. Adv. Eng. Mater. 2021, 23, 2100197. [Google Scholar] [CrossRef]
- Gießgen, T.; Mittelbach, A.; Höche, D.; Zheludkevich, M.; Kainer, K.U. Enhanced predictive corrosion modeling with implicit corrosion products. Mater. Corros. 2019, 70, 2247–2255. [Google Scholar] [CrossRef]
- Shojaei, A.; Hermann, A.; Cyron, C.J.; Seleson, P.; Silling, S.A. A hybrid meshfree discretization to improve the numerical performance of peridynamic models. Comput. Methods Appl. Mech. Eng. 2022, 391, 114544. [Google Scholar] [CrossRef]
- Cheng, K.; Lu, Z.; Ling, C.; Zhou, S. Surrogate-assisted global sensitivity analysis: An overview. Struct. Multidiscip. Optim. 2020, 61, 1187–1213. [Google Scholar] [CrossRef]
- Wang, C.; Duan, Q.; Tong, C.H.; Di, Z.; Gong, W. A GUI platform for uncertainty quantification of complex dynamical models. Environ. Model. Softw. 2016, 76, 1–12. [Google Scholar] [CrossRef]
- Zhao, L.; Choi, K.; Lee, I. Metamodeling Method Using Dynamic Kriging for Design Optimization. AIAA J. 2011, 49, 2034–2046. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. UQLab: A Framework for Uncertainty Quantification in Matlab. In Vulnerability, Uncertainty, and Risk; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 2554–2563. [Google Scholar] [CrossRef]

| In Vitro | In Vivo | |||
|---|---|---|---|---|
| Mg-5Gd | Mg-10Gd | Mg-5Gd | Mg-10Gd | |
| [m/s] | ||||
| [m/s] | ||||
| MAE | 0.03 | 0.08 | 0.31 | 0.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Baraghtheh, T.; Hermann, A.; Shojaei, A.; Willumeit-Römer, R.; Cyron, C.J.; Zeller-Plumhoff, B. Utilizing Computational Modelling to Bridge the Gap between In Vivo and In Vitro Degradation Rates for Mg-xGd Implants. Corros. Mater. Degrad. 2023, 4, 274-283. https://doi.org/10.3390/cmd4020014
Al Baraghtheh T, Hermann A, Shojaei A, Willumeit-Römer R, Cyron CJ, Zeller-Plumhoff B. Utilizing Computational Modelling to Bridge the Gap between In Vivo and In Vitro Degradation Rates for Mg-xGd Implants. Corrosion and Materials Degradation. 2023; 4(2):274-283. https://doi.org/10.3390/cmd4020014
Chicago/Turabian StyleAl Baraghtheh, Tamadur, Alexander Hermann, Arman Shojaei, Regine Willumeit-Römer, Christian J. Cyron, and Berit Zeller-Plumhoff. 2023. "Utilizing Computational Modelling to Bridge the Gap between In Vivo and In Vitro Degradation Rates for Mg-xGd Implants" Corrosion and Materials Degradation 4, no. 2: 274-283. https://doi.org/10.3390/cmd4020014
APA StyleAl Baraghtheh, T., Hermann, A., Shojaei, A., Willumeit-Römer, R., Cyron, C. J., & Zeller-Plumhoff, B. (2023). Utilizing Computational Modelling to Bridge the Gap between In Vivo and In Vitro Degradation Rates for Mg-xGd Implants. Corrosion and Materials Degradation, 4(2), 274-283. https://doi.org/10.3390/cmd4020014






