Statistical Treatments of Chloride Threshold and Corrosion Propagation Rate
Abstract
1. Introduction
1.1. Previous Results on Chloride Threshold
1.1.1. Laboratory Results
1.1.2. Real Structures
1.2. Previous Results on Corrosion Rate
2. Materials and Methods
2.1. Chloride Threshold
2.2. Corrosion Rate Determination
3. Results
3.1. Chloride Theshold
3.1.1. Laboratory Results
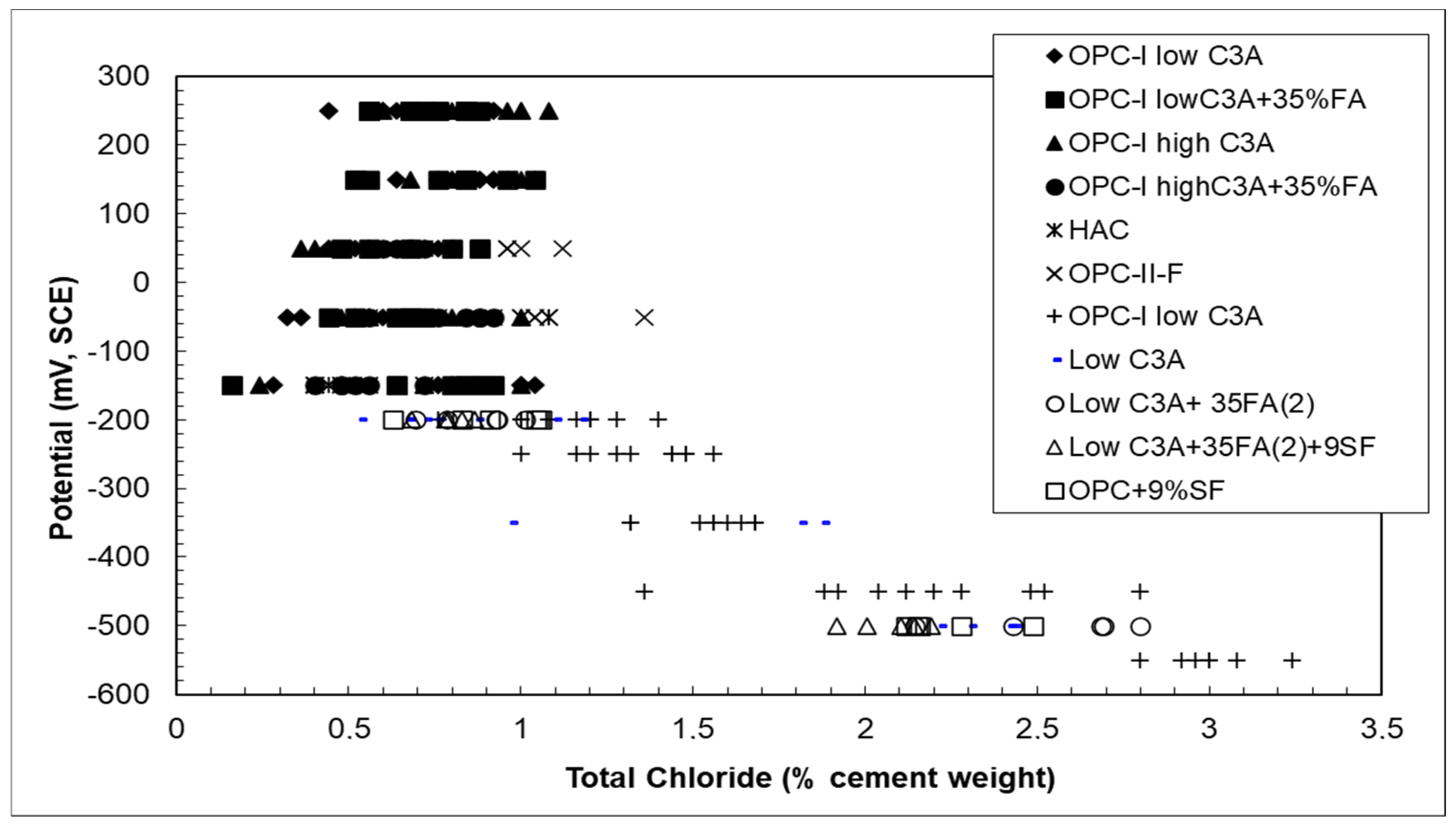
3.1.2. Results from Real Structures of Chloride Threshold
3.2. Corrosion Rates
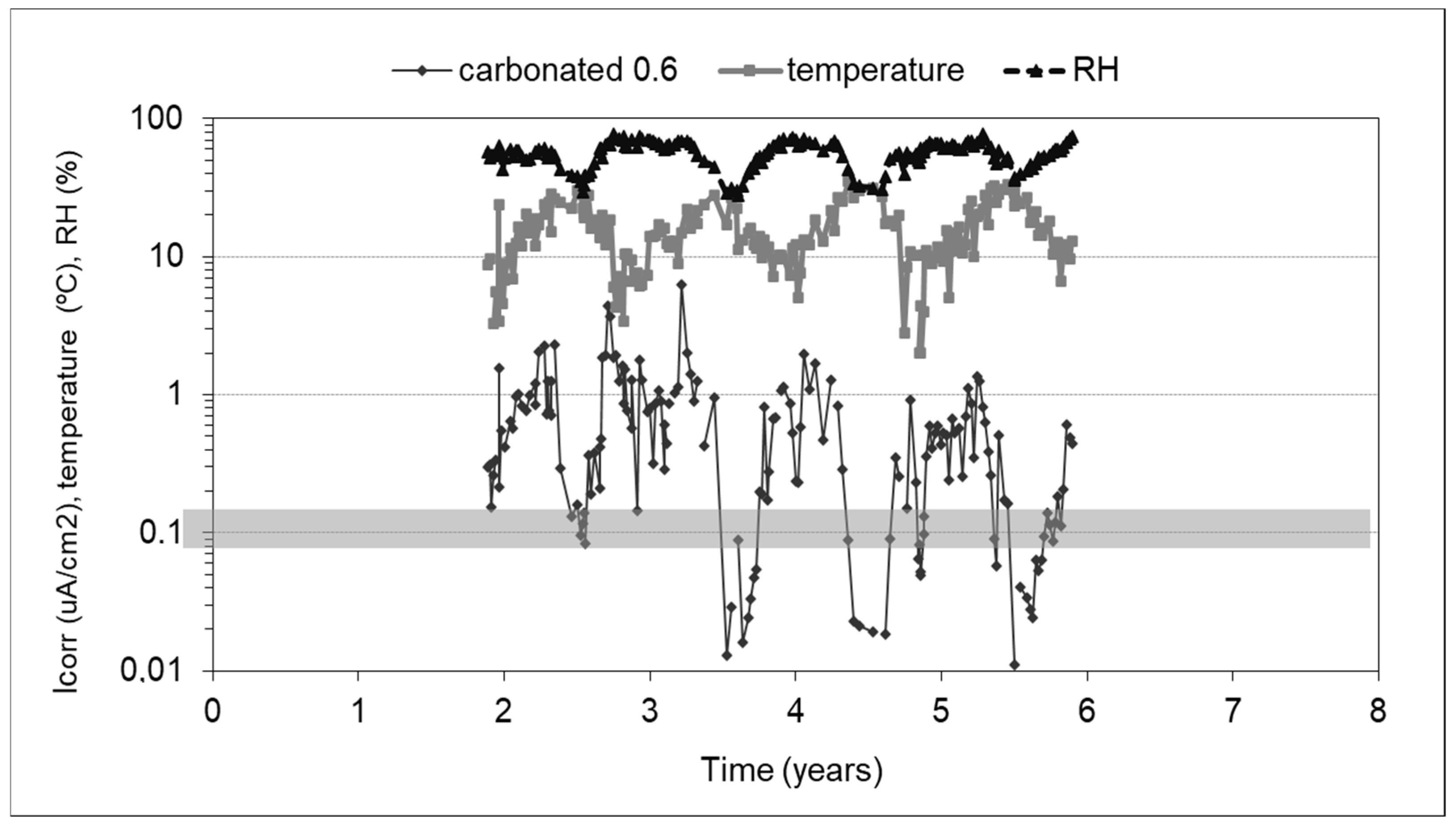
3.2.1. Laboratory Results. Temporal Variation
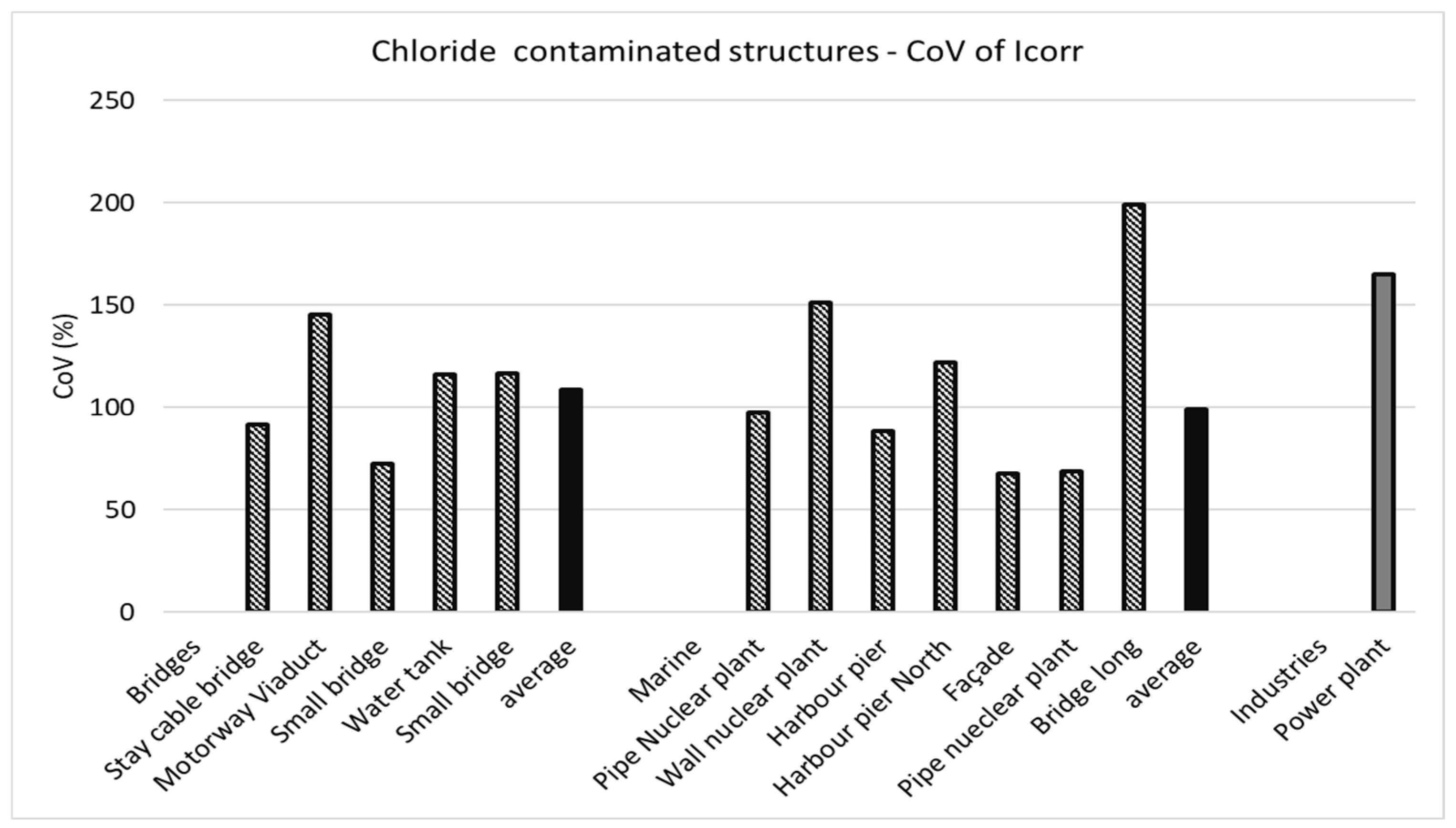
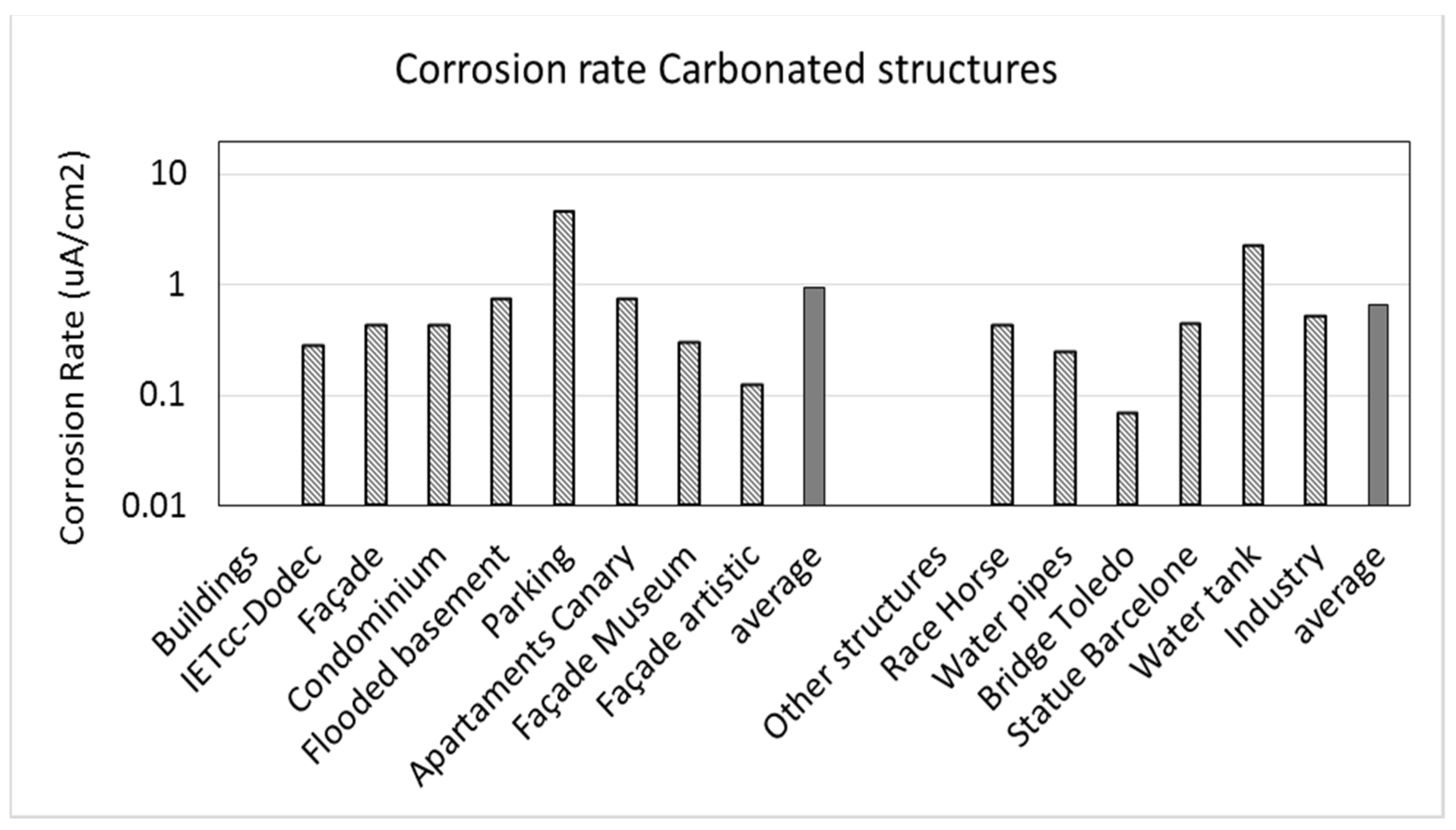
3.2.2. Results from Real Structures of Corrosion Rates
4. Discussion
4.1. Chloride Threshold
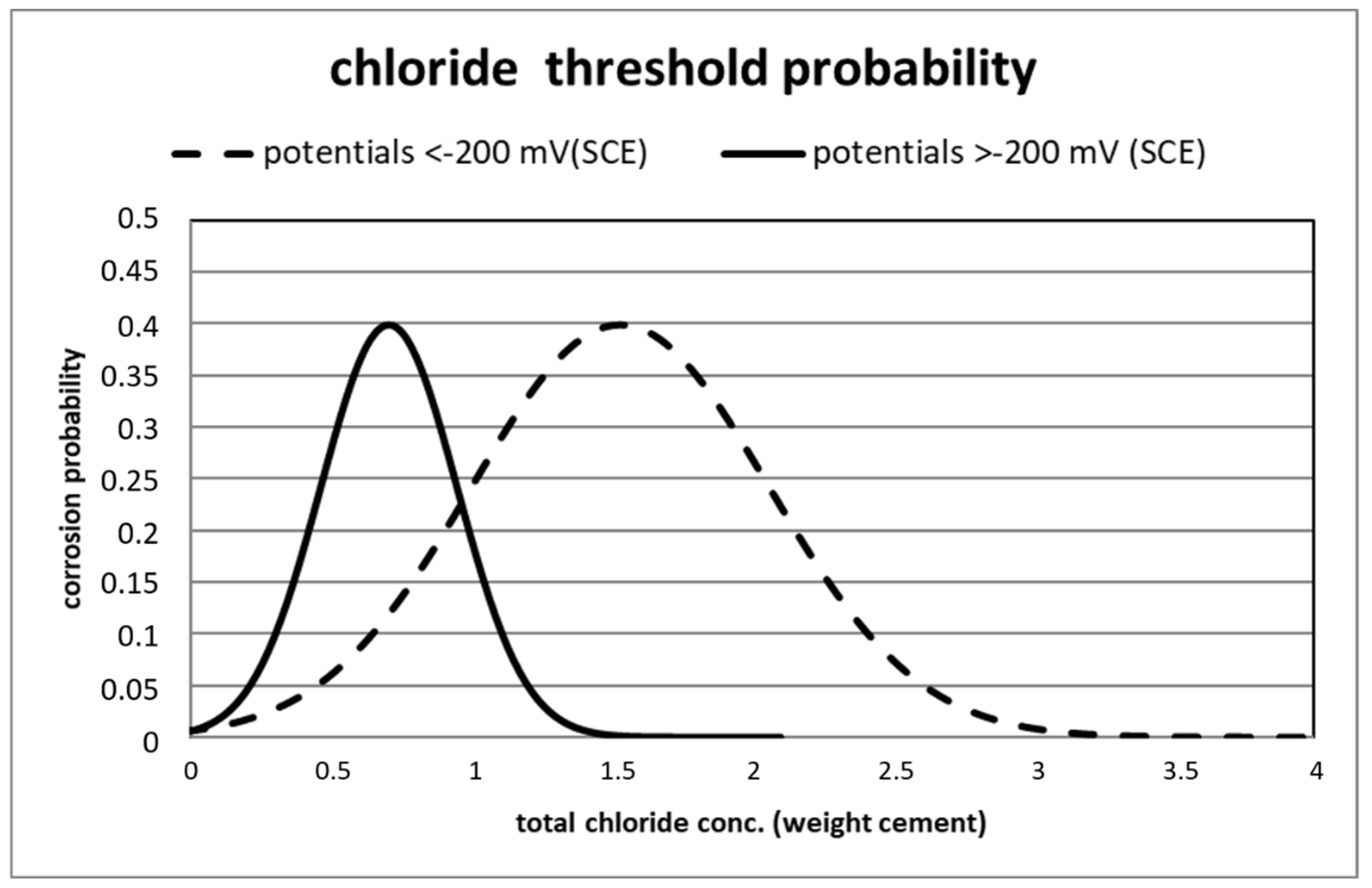
4.1.1. Statistical Characterization
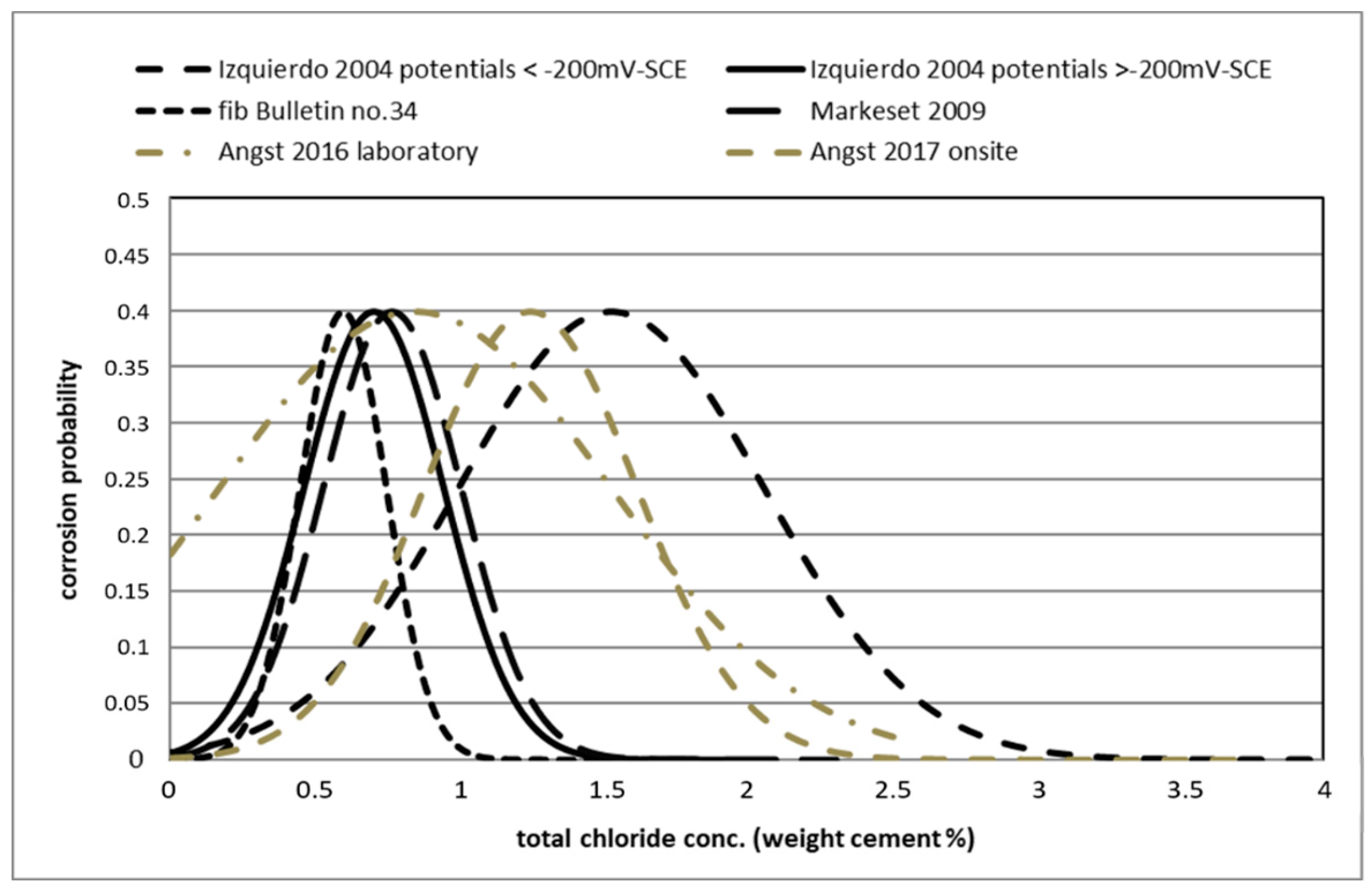
4.1.2. Results from Real Structures of Chloride Threshold
4.2. Chloride Threshold Values for Design of New Structures and Assessment of Existing Ones
- -
- The “consequences of corrosion (failure);
- -
- The importance of the structure;
- -
- Whether or not the structural element or zone is accessible for inspection;
- -
- The exposure class;
- -
- Whether previous testing is feasible or similar concrete has been already characterized.
4.3. Ccorrosion Rate
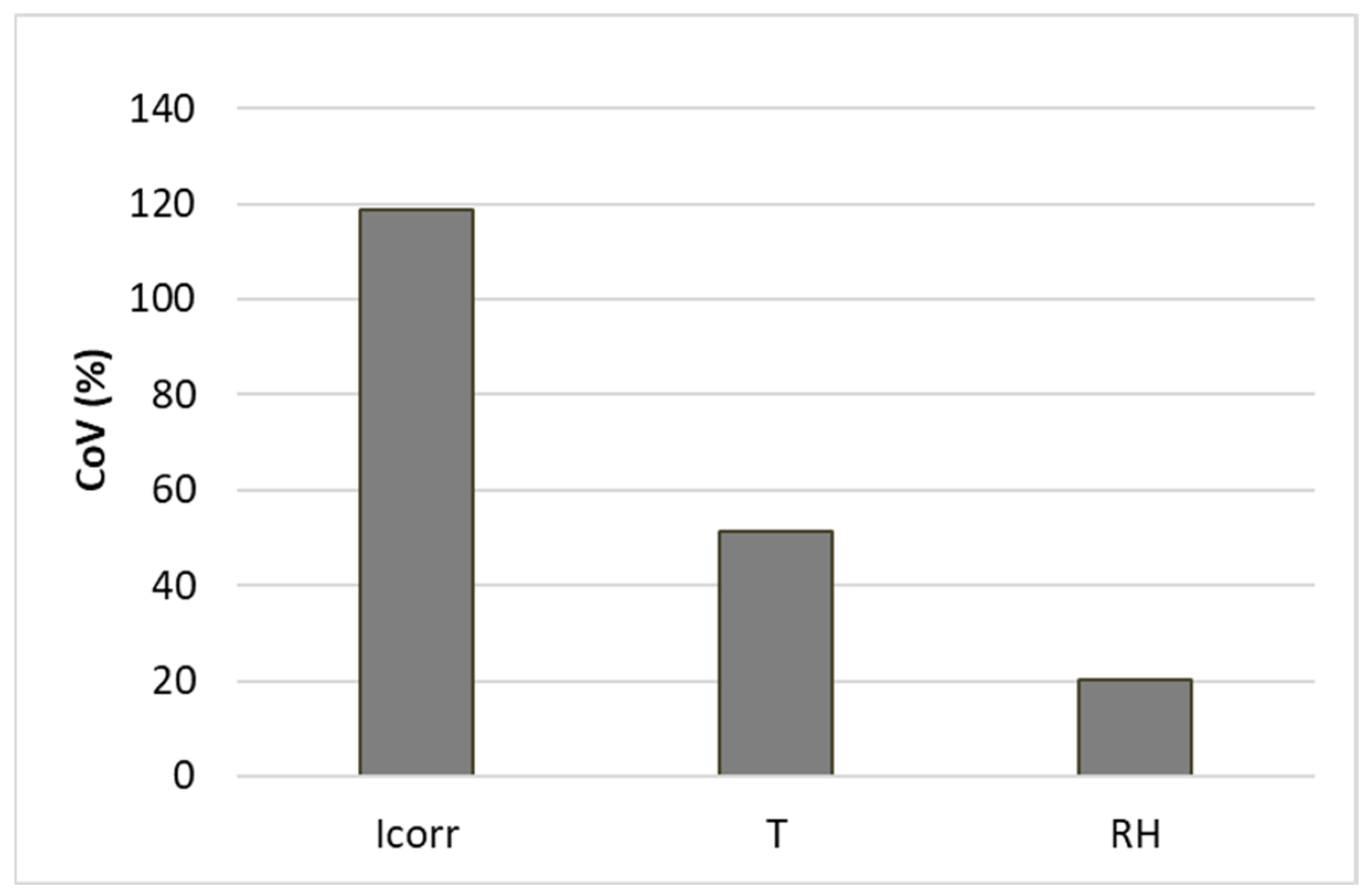
4.3.1. Uncertainty of Corrosion Rate Due to Climatic Seasons
4.3.2. Statistical Distributions of Corrosion Rates in Real Structures
- -
- All the cases correspond to structures where corrosion has been already detected and then they are representative, not of the whole population of structures, but of those with signs of corrosion;
- -
- The selection of measurement zones was made by choosing only one zone where corrosion is likely not yet produced, and several zones where the corrosion was evident. Then, the number of places measured with no corrosion are smaller than those corroding, although some apparently corroding have shown values below the limit of 0.1–0.2 μA/cm2.
4.3.3. Statistical Distribution of Corrosion Rates Valid for Design and Assessment
5. Conclusions
- Several statistical distributions of chloride threshold have been compared, deducing that each structure may present a different one, but all within the range of chloride concentration until around 3–3.5% by cement weight;
- As the data found on site by [5] with a distribution of an averaged value of 0.77% of total chlorides by weight of cement were very similar to those of [15] in the laboratory with an averaged value of 0.7%, such distribution can be considered as universally representing the most conservative probability of corrosion in structures exposed to the atmosphere. The total range in these more conservative distributions was from 0.1–0.2% by weight of cement to around 1.5%;
- Another distribution with a higher averaged value was also found by [15] for potentials more cathodic than −200 mVSCE, which could represent wet/submerged structures, and that gives as corrosion threshold an averaged value of 1.53% by weight of cement. The range of possible threshold values is higher until around 3%;
- For practical engineering use, the codes are deterministic and the values given as chloride threshold are in the safer limit of the distribution indicated for the maximum chloride amount in the concrete mix components. For probabilistic calculations related to service life prediction, the selection of a threshold value should be made attending at: (a) the “consequences of corrosion (failure), (b) the importance of the structure, (c) whether the structural element or zone is accessible or not for inspection, (d) the exposure class and (e) whether previous testing is feasible or similar concrete has been already characterized.
- The data were collected in corroding structures and then represented the probability of corrosion rate values, assuming that the measurements made in the non corroding zones are fewer than the number of measurements in the corroding zones;
- An average value of 0.526 μA/cm2 was found for the carbonated structures and of 0.89 μA/cm2 for those containing chlorides;
- The variation found depends not only on the spatial variation, but also of the temporal evolution produced by the climatic seasons;
- The spatial variation is very much dependent on the contamination and humidity distribution in each element and in the whole structure. In its interpretation, the number of data measured in the corroding and non corroding zones must be taken into account;
- The temporal variation is influenced by the regime of raining and temperature due to the climatic conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kropp, J. Relations between transport characteristics and Durability. Chapter 5. RILEM Report no.5. In Performance Criteria for Concrete Durability; Kropp, J., Hilsdorf, H.K., Eds.; E&FN SPON: London, UK, 1995. [Google Scholar]
- Xia, Y.; Chen, B.; Zhou, X.; Xu, Y. Field monitoring and numerical analysis of Tsing Ma Suspension Bridge temperature behavior. Struct. Control Heath Monit. 2013, 20, 560–575. [Google Scholar] [CrossRef]
- Tuutti, K. Corrosion of Steel in Concrete; Swedish Cement and Concrete Institute (CBI) n° 4-82: Stockholm, Sweden, 1982. [Google Scholar]
- Andrade, C.; Castillo, A. Evolution of reinforcement corrosion due to climatic variations. Mater. Corros. 2003, 54, 379–386. [Google Scholar] [CrossRef]
- Markeset, G. Critical chloride content and its influence on service life predictions. Mater. Corros. 2009, 60, 8593–8596. [Google Scholar] [CrossRef]
- Fluge, F. Marine chlorides—A probabilistic approach to derive provisions for EN 206-1. In Proceedings of the 3rd DuraNet Workshop, Tromsø, Norway, 10–12 June 2001. [Google Scholar]
- Helland, S.; Aarstein, R.; Maage, M. In-field performance of North Sea offshore platforms with regard to chloride resistance. Struct. Concr. 2010, 11, 15–24. [Google Scholar] [CrossRef]
- Angst, U.; Wagner, M.; Elsener, B.; Leemann, A.; Nygaard, P.V. Method to Determine the Critical Chloride Content of Existing Reinforced Concrete Structures; Swiss Federal Roads Office: Berne, Switzerland, 2016.
- Angst, U.; Elsener, B. The size effect in corrosion greatly influences the predicted life span of concrete infrastructures. Sci. Adv. 2017, 3. [Google Scholar] [CrossRef] [PubMed]
- fib Bulletin no. 34 Model Code for Service Life Design. 2006. Available online: https://www.fib-international.org/publications/fib-bulletins/model-code-for-service-life-design-pdf-detail.html (accessed on 6 October 2022).
- fib Model Code for Concrete Structures 2010; Fédération Internationale du Béton: Lausanne, Switzerland, 2013.
- Hausmann, D.A. A probability model for steel corrosion in concrete. Mater. Perform. 1996, 37, 64–68. [Google Scholar]
- Everett, L.H.; Treadaway, K.W.J. Deterioration due to Corrosion inReinforced Concrete. IP12/80 Monograph-Building Research Establishment-Garston-Watford, WD2 7JR. 1980, pp. 4–8. Available online: https://trid.trb.org/view/165106 (accessed on 6 October 2022).
- Alonso, C.; Andrade, C.; Castellote, M.; Castro, P. Chloride threshold values to depassivate reinforcing bars embedded in a standardized OPC mortar. Cem. Concr. Res. 2000, 30, 1047–1055. [Google Scholar] [CrossRef]
- Izquierdo, D.; Alonso, C.; Andrade, C.; Castellote, M. Potentiostatic determination of chloride threshold values for rebar depassivation. Exp. Stat. Study-Electrochim. Acta 2004, 49, 2731–2739. [Google Scholar] [CrossRef]
- Pourbaix, M. Significance of protection potential in pitting and intergranular corrosion. Corrosion 1970, 26, 431–438. [Google Scholar] [CrossRef]
- Breit, W. Kritischer korrosionsauslösender Chloridgehalt—Neuere Untersuchungsergebnisse (Teil 2). Beton 1998, 8, 511. [Google Scholar]
- DuraCrete Project Final Technical Report Brite EuRam Project BE95-1347, Probabilistic Performance Based Durability Design of Concrete Structures. Report TG4/B Statistical Quantification, Onset of Corrosion. 2000. Available online: https://cordis.europa.eu/project/id/BRPR950132 (accessed on 6 October 2022).
- Ghelen, C. Probability-Based Service Life Design of Reinforced Concrete Structures-Reliability Studies for Prevention of Reinforcement Corrosion (Probabilistische Lebensdauerbemessung von Stahlbetonbauwerken–Zuverlässigkeitsbetrachtungen zur Wirksamen Vermeidung von Bewehrungskorrosion. Ph.D. Thesis, RWTH Aachen, Aachen, Germany, 2000. [Google Scholar]
- Ferreira, R.M. Probability-Based Durability Analysis of Concrete Structures in Marine Environment. Ph.D. Thesis, University of Minho, Braga, Portugal, 2004. [Google Scholar]
- Angst, U. Predicting the time to corrosion initiation in reinforced concrete structures exposed to chlorides. Cem. Concr. Res. 2019, 115, 559–567. [Google Scholar] [CrossRef]
- Andrade, C. Modelling the concrete-real environment interaction to predict service life. Struct. Concr. 2015, 16, 159–160. [Google Scholar] [CrossRef]
- Castellote, M.; Andrade, C. Analysis of total chloride content. RILEM Recommendation of TC-178-Testing and modelling chloride penetration in concrete. Mater. Struct. 2002, 35, 583–585. [Google Scholar]
- Castellote, M.; Andrade, C. Analysis of water soluble chloride content in concrete. RILEM Recommendation of TC-178-Testing and modelling chloride penetration in concrete. Mater. Struct. 2002, 35, 586–588. [Google Scholar]
- Andrade, C.; González, J.A. Quantitative measurements of corrosion rate of reinforcing steels embedded in concrete using polarization resistance measurements. Werkst. Und Korros. 1978, 29, 515. [Google Scholar] [CrossRef]
- Feliú, S.; González, J.A.; Feliú, S., Jr.; Andrade, C. Confinement of the electrical signal or in-situ measurement of Polarization Resistance in Reinforced concrete. ACI Mater. J. 1990, 87, 457. [Google Scholar]
- Rodriguez, J.; Ortega, L.M.; Garcia, A.M.; Johansson, L.; Petterson, K. On site corrosion rate measurements in concrete structures using a device developed under the EUREKA project EU-401. In Proceedings of the Conference Concrete Across Borders, Odense, Denmark, June 1995; pp. 215–226. [Google Scholar]
- Andrade, C.; Rebolledo, N.; Morales, J.A. Surface Inhibitors for the Non-Invasive treatment of Corroded Structures. In Proceedings of the XIV DBMC—14th International Conference on Durability of Building Materials and Components, Ghent, Belgium, 29–31 May 2017. [Google Scholar]
- CONTECVET. Manual for the Evaluation of Structures Affected by Reinforcement Corrosion, DG Enterprise, CEC 2001. Available online: https://www.ietcc.csic.es/wp-content/uploads/1989/02/manual_contecvet.pdf (accessed on 6 October 2022).
- Andrade, C.; Alonso, C.; Gulikers, J.; Polder, R.; Cigna, R.; Vennesland, Ø.; Salta, M.; Raharinaivo, A.; Elsener, B. RILEM TC 154-EMC: Electrochemical Techniques for Measuring Metallic Corrosion. Recommendations Test methods for on-site corrosion rate measurement of steel reinforcement in concrete by means of the polarization resistance method. Mater. Struct. 2004, 37, 623–643. [Google Scholar] [CrossRef]




| Literature Source | Statistical Distribution | Average Value % by Cement Weight | Coefficient of Variation (%) | |
|---|---|---|---|---|
| fib Bulletin no. 34 | Beta | 0.6 | 31.00 | |
| Markeset 2009 | Log-normal | 0.77 | 32.46 | |
| Izquierdo et al. 2004 | >−200mV (atmospheric) | normal | 0.7 | 28.57 |
| <−200mV (submerged) | Log-normal | 1.53 | 34.64 | |
| Type of Contamination | Probability | Averaged Corrosion Rate | Coefficient of Variation |
|---|---|---|---|
| carbonation | 75% | 0.526 μA/cm2 | 177.30% |
| chlorides | 80% | 0.89 μA/cm2 | 221.86% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrade, C.; Izquierdo, D. Statistical Treatments of Chloride Threshold and Corrosion Propagation Rate. Corros. Mater. Degrad. 2022, 3, 598-611. https://doi.org/10.3390/cmd3040032
Andrade C, Izquierdo D. Statistical Treatments of Chloride Threshold and Corrosion Propagation Rate. Corrosion and Materials Degradation. 2022; 3(4):598-611. https://doi.org/10.3390/cmd3040032
Chicago/Turabian StyleAndrade, Carmen, and David Izquierdo. 2022. "Statistical Treatments of Chloride Threshold and Corrosion Propagation Rate" Corrosion and Materials Degradation 3, no. 4: 598-611. https://doi.org/10.3390/cmd3040032
APA StyleAndrade, C., & Izquierdo, D. (2022). Statistical Treatments of Chloride Threshold and Corrosion Propagation Rate. Corrosion and Materials Degradation, 3(4), 598-611. https://doi.org/10.3390/cmd3040032








