Abstract
Inundation maps that show water depths that occur in the event of a flood are essential for protection. Especially information on timings is crucial. Creating a dynamic inundation map with depth data in temporal resolution is a major challenge and is not possible with physical models, as these are too slow for real-time predictions. To provide a dynamic inundation map in real-time, we developed a data-driven multi-step inundation forecast system for fluvial flood events. The forecast system is based on a convolutional neural network (CNN), feature-informed dense layers, and a recursive connection from the predicted inundation at timestep t as a new input for timestep t + 1. The forecast system takes a hydrograph as input, cuts it at desired timesteps (t), and outputs the respective inundation for each timestep, concluding in a dynamic inundation map with a temporal resolution (t). The prediction shows a Critical Success Index (CSI) of over 90%, an average Root Mean Square Error (RMSE) of 0.07, 0.12, and 0.15 for the next 6 h, 12 h, and 24 h, respectively, and an individual RMSE value below 0.3 m, for all test datasets when compared with the results from a physically based model.
1. Introduction
Extreme weather events pose major challenges for humanity. Especially due to climate change, such events are likely to occur more often in the future [1,2]. In this context, flood events are one of the most common natural disasters and lead to the highest damages among all possible natural catastrophes [3]. In recent years, flood management has evolved from traditional structural measures to include non-structural measures such as early warning and forecast systems [4]. Such systems are of great interest to protect the population and infrastructures as well as to prevent or mitigate economic damage [5].
Flood forecasting is typically conducted by rainfall-runoff modeling, providing information about the impending hydrograph. Once a specific discharge threshold value is reached, a flood warning is communicated. In addition to this hydrological forecast, the impact of the impending hydrograph on a possible inundation and its extent is essential information [6]. The inundation extent is commonly provided by a map, showing spatially distributed water depths in the respective study site, helping to quickly identify dangerous regions and allowing, for example, the optimization of rescue routes [7].
Such inundation maps are produced by hydrodynamic modeling using physically based models, which solve the shallow water equations for given water input based on numerical schemes. The advantage of these models lies in the consideration of a detailed spatial resolution (e.g., solving on a grid of 4 by 4 m) and thus in high-resolution spatially distributed water depths.
However, their disadvantage lies in long calculation times. The numerical schemes that solve the equations require timesteps of seconds, resulting in an enormous amount of calculations [7,8,9]. To speed up these calculation times, recent studies have developed numerical solvers for the shallow water equation that can make use of Graphical Processing Units (GPUs) [10,11,12]. Although the run times could be reduced by a factor of 15 in some cases [12,13], they are still not suitable in the context of real-time forecasting, especially if the inundation model has to be run multiple times in the context of uncertainty estimation or in the case of a changing input when new timesteps are available [7,9].
To consider inundation extent and depth in the context of forecasting despite the long calculation times of physically based models, nowadays, some authorities use one pre-simulated static flood map for a specific return period (e.g., 100 years) or, in rare cases, a complete database of pre-simulated flood events [6]. This is undoubtedly an improvement, but above all, it improves flood preparedness in advance of an event. Static maps based on a synthetic return period are not able to describe the inundation of a real event. Operational early warning requires real-time forecasts and especially information about the times (e.g., what will the situation be like in 3 or 6 h). Considering a temporal resolution of the flood event could significantly improve flood and early warning management, as time strongly influences decision making. Such information about time could be achieved by a dynamic inundation map, which shows the respective inundation for several timesteps. Nevertheless, providing a dynamic inundation map remains a great challenge.
Due to the excessive computing times of physically based models for real-time predictions, other approaches are being researched. Crotti et al. (2019), for example, have developed an inundation forecast framework based on a database with multiple pre-simulated inundation maps, where the similarity of the input data is used to select the most likely inundation map [6]. Along with inundation mapping, flood susceptibility mapping based on flood-influencing factors has also gained more attention in recent years, where spatial geographical data [14] and even social media data [15] are used to generate a map that shows the susceptibility towards inundation and flooding.
Besides these approaches, data-driven applications have gained importance in the research community in recent years. Data-driven models, as the name suggests, rely on datasets and attempt to establish a relationship between a set of input and corresponding output data [16]. They offer very good computational efficiency and originate from the fields of statistical modeling, artificial intelligence, and machine learning. Data-driven models are, for example, applied in computer vision tasks in the field of medical engineering [17] or object detection [18].
To make use of the benefit, in the field of flood forecasting, data-driven approaches are applied in multiple studies to predict the flood hydrograph [19,20] or to replace physically based models and to generate flood inundation maps [7,9,21,22,23,24,25,26,27,28,29]. Recent advances in data-driven flood forecasting models aim to incorporate multiple uncertainty sources within the input data [20,28] and physical laws [19].
The generation of inundation maps, showing the maximum water level occurring during a flood event, is presented for pluvial events in a study by Berkhahn et al. (2019) [21] and for fluvial events by Lin et al. (2020) [22]. Both authors used artificial neural networks (ANNs) and a supervised learning strategy with pre-simulated physically based scenarios. The output resolutions of the ANNs match the grid resolution of the physically based models, and after successful training, the ANNs were able to replace the physically based model. However, both studies did not consider a temporal variation of the inundation, outputting a single (maximum) water depth. Follow-up studies focused on the improvement of the data-driven model architecture, applying convolutional neural networks (CNNs) following an image-to-image translation strategy for a single part of the catchment [26] or for the total catchment in multiple parts presented as subcatchments [24,25,27]. CNNs are specialized data-driven models for handling structured grid data, and, in contrast to ANNs, they take into account the information of their neighboring cells for the prediction of one cell. This improved the forecast quality and made CNNs the standard procedure. For further improvement, some studies added additional geographical information (GIS) data into the model, like elevation or slope [24,25]. This approach improved the prediction quality but made training on a standard computer nearly impossible. Besides that, these studies did not consider the temporal resolution of the inundation. To address the issue of training on a standard computer while keeping the idea of integrating further knowledge into the network via additional datasets, Schmid and Leandro (2023) developed a feature-informed network for the prediction of fluvial flooding extents [7]. This approach made it possible to integrate information about the distance for each cell to be predicted to a river into the network without providing the network with additional datasets. This strategy improved the forecast but did also not consider the temporal resolution of the flood event.
An approach for incorporating temporal resolution with the prediction for fluvial flood events is presented by Lin et al. (2020) [23]. The authors used separate ANNs for the timesteps 3, 6, 9, and 12 h, and each ANN was trained with hydrographs up to this timestep. This configuration allowed the integration of a time, but for each timestep, a separate ANN has to be set up and trained. Furthermore, no CNNs were used, and the inundation is only dependent on the discharge. Another approach for pluvial flooding is presented by Burrichter et al. (2023), where the output of the data-driven model is the complete time sequence [29]. However, the complete time sequence is not always feasible, especially at the beginning of an event. To resolve these issues, Berkhahn and Neuweiler (2024) developed a data-driven inundation model with a spatial and temporal resolution for pluvial flooding [9]. The authors applied a recursive modeling architecture, which is also often used in multiple studies in the fields of multi-step time series forecasting [28,30,31]. These recursive structures feed the prediction from the precious timestep back and use it as new input. Thus, the prediction of the next timestep is influenced by some current input and the output of the previous timestep. This data-driven model showed promising results but did not consider the inclusion of additional knowledge into the data-driven model to improve the forecast.
The present study builds on the described knowledge and methods and aims to develop a data-driven multi-step flood inundation forecast system for fluvial events to provide a dynamic inundation map for the respective study site in real time. To ensure high prediction quality for both spatial and temporal dimensions, the forecast system is implemented with a recursive connection, but unlike other studies, we follow the idea of a feature-informed network to further integrate additional knowledge into the forecast system.
2. Materials and Methods
2.1. General Overview
Like other studies [7,9,21,22,23,25,26], we applied a supervised learning strategy using pre-simulated physically based inundation scenarios as true and, therefore, desired inundation values to achieve the aim of developing a multi-step forecast system for real-time prediction. In this case, a supervised strategy ensures better prediction quality since the model has a clear desired target value. Once the optimization is finished, the data-driven model is able to replace the physically based model by providing a dynamic inundation map in real time. Figure 1 describes the general workflow for the development, which consists of three blocks: (I) the operational design, (II) data-driven modeling, and (III) the physically based modeling. By following this workflow, a data-driven multi-step forecast system can be developed for any study area.
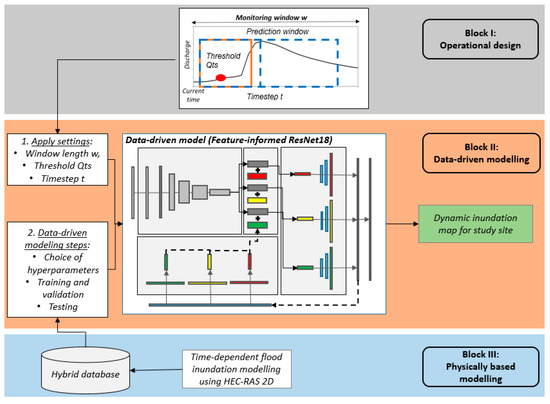
Figure 1.
Workflow for the development of a data-driven multi-step forecast system.
The first block deals with the operational design. A specific time period is defined within a monitoring window . Within this window, a future/predicted hydrograph is listed, which forms the basic input for the inundation forecast later. The length of this window is also the maximum lead time for the multi-step forecast. The hydrograph within this window moves with a specific timestep towards the current time. As the inundation forecast does not have to be carried out continuously, a threshold value can be set for the start of the forecast. These three parameters (length of the window , timestep , and threshold ) provide the operational settings for the forecast system. Once a forecast is started, for each possible timestep within the window, the respective inundation map will be generated. It is worth mentioning that the operating design must be defined in advance but can be adapted to meet the requirements of the application in any study area. In this study, the length of the forecasting window is set to 24 h, the discharge threshold is set to 25 m3/s, and the timestep is set to 1 h. A detailed description of the forecast strategy is presented in Section 2.2.
The second block deals with the data-driven modeling (block II). In this, the architecture of the model itself is set, and the operational settings from block I (monitoring window length , discharge threshold , and the timestep ) are applied to the model. Afterward, the hyperparameters of the models are set, and training, validation, and testing are carried out in this part. We follow an image-to-image approach [7,9,26] since this allows the use of a convolutional neural network, and, additionally, we apply a feature-informed strategy since the integration of additional knowledge into the network has been proven beneficial [7]. Furthermore, we add a recursive feedback connection from the predicted inundation of the previous timestep as an additional new input besides the hydrograph. The final developed forecast system is able to produce a dynamic inundation map for the maximum lead time (length of the forecast window) with a temporal resolution of timestep . Section 2.3 presents further details about the model structure and choice of hyperparameters as well as the complete data-driven modeling approach.
The third block deals with physical modeling. Since we aim to replace the physical-based model with a data-driven model, it is necessary to generate a database, which is used for setting up the data-driven model later. Therefore, different discharge events are simulated with a two-dimensional (2D) inundation model to gain physical-based inundation maps. Here, the 2D-inundation model must output these maps at the same timestep as in the operational design. In general, any database that contains hydrographs and respective inundation maps can be used for development. In this study, we used a hybrid database generated by Crotti et al. [6], where the hydrological model LARSIM (Large Area Runoff Simulation Model) [32] was used to generate the discharge scenarios, and the hydrodynamic model HEC-RAS 2D (Hydrologic Engineering Center—River Analysis System, Davis, CA, USA) [33] to obtain the corresponding inundation map. This database was also used by Schmid and Leandro [7] for the development of a feature-informed data-driven model to predict the maximum inundation extent. A detailed description of the database and the physical-based modeling is presented in Section 2.4.
2.2. Operational Design
The operational design builds the frame around the forecast system and is controlled by three parameters: (i) the monitoring window , (ii) the timestep , and (iii) the discharge threshold value . These parameters will be applied later to the data-driven model. We would like to mention that these parameters are user-defined and need to be set beforehand; however, by introducing them, the methodology is customizable and, therefore, easy to transfer for the development of a forecast system in other study areas. A maximum prediction lead time is decided by the length of the monitoring window , in which the future hydrograph is listed from the current time ( towards the maximum prediction lead time and end of the monitoring window ). Once time evolves, the hydrograph moves with a specific timestep towards the current. also gives the temporal resolution of the dynamic inundation map later. The third parameter, the threshold , is responsible for starting an inundation forecast. Figure 2a shows these parameters for an event.
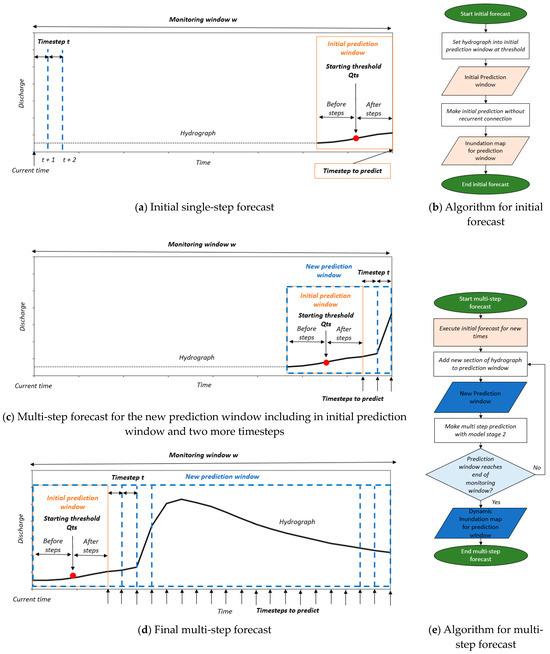
Figure 2.
Visual presentation of the forecast system in an operational mode. (a) Representation of a monitoring window once the discharge threshold value is reached for the first time and an initial single-step forecast is carried out; (b) algorithm that is necessary to carry out the initial forecast; (c) the monitoring window once two more timesteps after the initial single-step forecast are available and a multi-step forecast is carried out for the new prediction window; (d) the monitoring window once the initial prediction window reaches the current time, which marks the final forecast; (e) algorithm that is necessary to carry out the multi-step forecast.
Once the discharge threshold is reached, the inundation forecast is started. If the threshold is reached for the first time, the inundation is still multiple steps ahead, and only the last timesteps of the hydrograph in the monitoring window are responsible for the incoming inundation. Therefore, an initial single-step forecast is carried out (Figure 2a), and an initial prediction window is set three timesteps before and after the discharge threshold value are taken into the prediction window (visualized by the orange box in Figure 2a). This is necessary for obtaining the shape of the hydrograph. The rest of the hydrograph (timesteps before the initial prediction window) is neglected (shown by the dotted points in Figure 2b). Afterward, the initial prediction window is used to carry out the first inundation forecast. Since this inundation is only influenced by the hydrograph itself, no inundation of the previous timestep is necessary. The initial single-step forecast outputs an inundation as a map occurring at the maximum lead time. Figure 2b shows the algorithm behind the initial forecast.
Once time passes by, new timesteps of the hydrograph are available, and the event comes closer to the current time (visualized in Figure 2c). Now, it is important to also know how the inundation will behave over time. At this stage, the multi-step forecast is started, and a first dynamic inundation map can be generated. The time of reaching the discharge threshold value can be identified again, and the initial prediction window (orange) can be set, now only closer to the current time. Since the shape of the hydrograph normally also changes once new timesteps are available, the initial prediction window is forecasted again following the initial forecast. Afterward, the initial prediction window is extended by every newly available timestep. This new prediction window (visualized by the blue box in Figure 2c) is used to forecast the new timesteps via consideration of recursive connections.
This multi-step forecast is carried out until the new prediction window is at the current time of the monitoring window , concluding with a dynamic inundation map, starting with the initial forecast, and adding more inundation maps with the timely resolution until the maximum lead time is reached (shown in Figure 2d). The necessary algorithm and its steps for running a multi-step forecast are listed in Figure 2e. An overall algorithm for running the forecast system in operational mode is provided in Figure 3. This algorithm describes the application of the forecast system for real-world implementation.
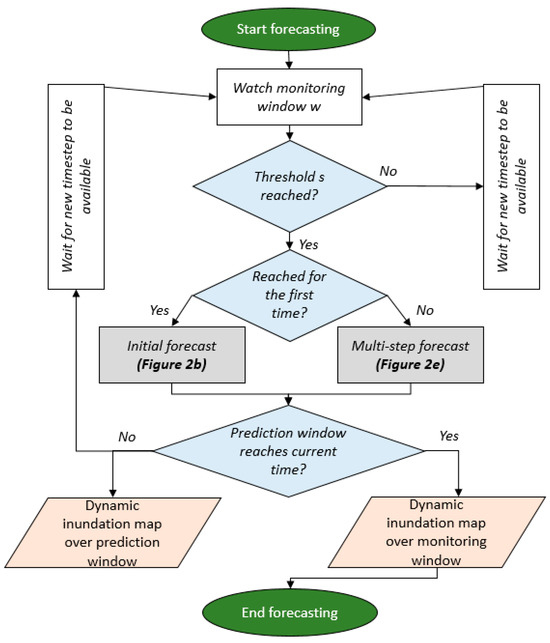
Figure 3.
Algorithm for running the forecast system.
2.3. The Data-Driven Modeling
The data-driven modeling part is responsible for generating the dynamic inundation map in real time. We applied the image-to-image translation strategy following a feature-informed architecture.
2.3.1. Architecture
The data-driven modeling approach to enable time-dependent predictions presented herein builds upon the work of the authors on feature-informed architecture [7]. The feature-informed architecture combines a convolutional neural network with feature-informed dense layers, in which the additional information of the distance to the river for each cell to be predicted is integrated.
To address the challenge of providing time-dependent multi-step predictions, this architecture is enhanced with a recursive connection in which the predictions of the feature-informed path are fed back as a new input; thus, the prediction of timestep t is dependent on the input of the hydrograph and its own prediction of t − 1. Figure 4 shows this architecture. The architecture can mainly be split into three different parts: (i) convolution, (ii) feature-informed paths, and (iii) recursive feature-informed paths. Each part will be explained in the following paragraphs.
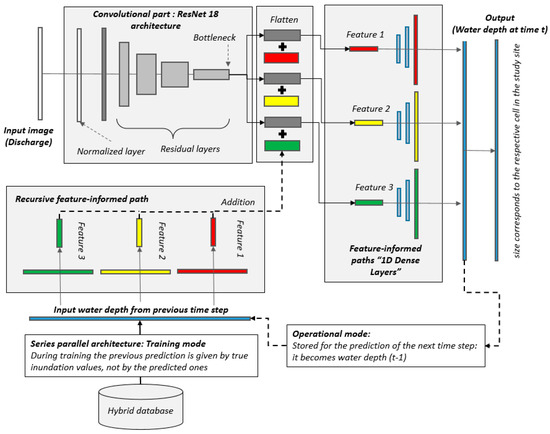
Figure 4.
The architecture of the data-driven model. The recursive connection is represented with the dotted black line and is activated only in the operational mode, whereas during training, it is replaced by the true inundation values.
The convolution part consists of a residual convolutional network with 18 layers and is responsible for taking the input hydrograph as an image. This adjustment from the original residual network 50 (ResNet50) from Schmid and Leandro 2023 [7] was re-adjusted to minimize the computational amount. Convolutional networks (CNNs) are specifically designed for handling structured grid-like data, such as images. They have demonstrated widespread success in a range of computer vision tasks, like image classification, object detection, and image segmentation [34,35]. The fundamental concept behind CNNs lies in their utilization of multiple convolutional layers. A convolutional layer applies learnable filters (also known as kernels, a smaller matrix with the respective kernel size) to the input image. Each filter/kernel slides over the image, conducting element-wise multiplication and summation, resulting in a feature map. The primary aim of this process and the resultant feature map is to identify and retain local patterns, characteristics, and attributes of the image. A mathematical description of this process is given by Equation (1) [34]:
where is the respective value at index ( in the th output feature map, k refers to the number of filters applied, c is the number of channels of the input image, is the size of the kernel, is the kernel and respective value at index ( while iterates over the input channels of the provided image, is the input image and the respective value at the position in the channel , and the stride is the step size at which the kernel moves over the image. After such a convolutional operation, batch normalization (Equations (2) and (3)) is applied to the produced feature maps, where is the normalized activation, is the input, is the mean of the batch, is the variance, is a small constant for stability, and are learnable scales and shift parameters, respectively, and is the output of the batch normalization.
Batch normalization is performed because it accelerates training, reduces overfitting, stabilizes gradients, and makes the network more robust [36]. An activation function, which is responsible for determining the importance of information passed through the network, is applied to the output of the batch normalization. We applied the rectified linear activation function (ReLU). It is a piecewise linear function that will output the input directly if it is positive; otherwise, it will output zero. The ReLu function is commonly used in data-driven modeling [9,37].
These three steps can be summarized into a convolutional block; thus, the output of a convolutional block can be described as follows (Equation (4)), where is the output of a single block; the activation function; the batch normalization, produced by Equations (2) and (3); and the feature map, produced by the convolutional operation from Equation (1).
After one convolutional block, four residual blocks follow. A residual block always contains two convolutional blocks and a skip connection that adds the original input back to the output of this block. The skip connection forces the network to learn the difference (residual) that is left over when you subtract input from output, allowing it to refine features effectively [37]. Mathematically, the residual block can be described as follows (Equation (4)), where is the output of the residual block, is the input to the block, represents the residual mapping to be learned by the layers in the block, and are the weights/values in the kernel of the layer, which is responsible for the generation of the feature maps.
After the last residual block, the extracted feature maps are stored in the flattened layer. This layer can be interpreted as compressed and dense information from the input, and it generates a one-dimensional vector. Afterward, the feature-informed part follows.
The feature-informed part is responsible for rebuilding the image and translating it into the inundation map. Each path represents a feature, which should be integrated into the network. The paths consist of three dense layers, which hold a specific number of neurons in it. One neuron can be described as follows (Equation (6)), where is the output of a dense layer, the input to the dense layer, and an added bias.
In this study, we applied the ReLu activation function until the last dense layer, in which we applied a linear activation function. This is also a common strategy [9,21,28]. The output size from the feature-informed dense layers matches exactly the number of cells to be predicted within the study area. After the feature-informed path, the first inundation map for the timestep t is produced. This map is outputted, and, if a multi-step prediction is aimed, this map is provided to the recursive part. If it is the first prediction, no time resolution for the inundation is necessary, since the inundation will take place at the end of the monitoring window/max lead time.
The recursive part stores the prediction from the last timestep and serves as a memory. Once more, it feeds the information through one feature-informed dense layer with the size of the flattened layer and mathematically adds the information to this layer. Thus, at this stage, the model is thereby influenced by the information of the hydrograph at the time , which runs in the convolutional part, and the inundation from , which was processed through the feature-informed paths, allowing the model to perform multi-timestep into the future.
2.3.2. Hyperparameter and Optimization
Before the data-driven model is optimized in the training process, the hyperparameters need to be set. The term hyperparameter covers all parameters/settings within the data-driven structure that are not trainable. Since this type of data-driven model has already proven suitable for flood prediction [7], in this study, we only made the filters of the convolution part and the number of neurons in the recursive paths variable, as we changed the architecture from the ResNet50 of Schmid and Leandro (2023) [7] to a ResNet18 and added the recursive connection. Additionally, we considered in the recursive connection the inundation only from the previous timestep . Taking more timesteps () into account might sound reasonable, but it makes training on a standard computer impossible.
To ensure the high prediction quality of the forecast system, the prediction of the data-driven model should match the physically based inundation map as closely as possible. This agreement between prediction and true values is measured by the loss function (LF). We applied the mean squared error (MSE) (Equation (7)) as LF, where the true values are given by the physically based model, is the prediction value of the data-driven model, and is the number of samples.
During the training process, the weights in the data-driven model are adjusted so that a minimum value of the LF is found by the optimization algorithm. This is carried out by iterating over the number of epochs. In each epoch, the model sees all training data once and tries to improve the prediction performance. Since our model features a recursive connection and the output is dependent on its own prediction, we had to find a training strategy. To still make use of the common optimization algorithms, the recursive connection is cut during training and replaced with the true inundation from the previous timestep provided by the physically based model. This is known as series-parallel architecture. Only in the operational forecasting mode the recursive connection is re-installed. This is also visualized in Figure 4. Such a strategy is also applied in multiple other studies [9,28,31,38]. Furthermore, this is beneficial since the network and weights are trained on true values and the prediction error of each timestep is not carried on.
For optimization, we used the Adam algorithm [39]. Adam is a stochastic gradient descent algorithm that incorporates momentum to past gradients into account, which supports avoiding becoming stuck in a local minimum. Besides this training optimization algorithm, we applied the workflow for the optimization of the feature-informed architecture developed by the authors [7]. This workflow consists of two separate algorithms. The first algorithm trains the total data-driven model. The second algorithm takes the previously trained model, freezes all trainable weights, and then starts an iterative retraining loop around the feature paths. In each iteration, the weights in the respective feature path are unfrozen and retrained. This retraining strategy ensures that the weights in each feature path are optimized to describe the flood depths and characteristics of this path in the best possible way. For more details on the optimization algorithm, please refer to [7]. Furthermore, all input data for the model are scaled between 0 and 1 as a preprocessing step. This improves the prediction quality as well. It is a standard approach in many other studies [21,28].
2.3.3. Evaluation Criteria
Evaluating flood prediction of data-driven models is critical since, in real cases, scenario decisions will be based on the predictions. The outcome of the forecast system is an inundation map, which shows the water depths within the study area. These water depths are typically provided in certain classes, and only cells that are higher than 0.05 m are highlighted, indicating cells below 0.05 m as safe areas. Therefore, we applied the Critical Success Index (CSI) as the first evaluation criterion. The CSI indicates that an alarm is given if a certain limit value is reached; thus, we set the limit to 0.05 m to assess the quality of the inundation extent. Such a limit is also used in Löwe et al. (2021) [24].
Equation (8) presents the calculation of the CSI, where refers to the number of correct positive predictions (values classified correctly into the classes below and above the limit), refers to the number of positive events that were missed by the model (water-depth predictions, which should be higher than 0.05 m but are less), and refers to the number of false positive predictions (water-depth predictions, which should be less than 0.05 m but are higher). An optimal value of 100% would indicate a perfect prediction/classification around the limit value.
Furthermore, to assess the prediction quality of the forecast system, the root mean squared error (RMSE) (Equation (9)) is used. The true values hereby are taken as the results from the physical-based hydrodynamic model, while the predicted values are provided by the developed forecast system. The small accounts for the number of predictions. The RMSE is used because the results are intuitive to interpret, as the error value has the same units as the water level. An optimal score of 0 would indicate a perfect agreement between prediction and true values. We also apply a threshold value, which should be reached to assure high prediction quality [7]. The threshold is set to 0.05 m, which can be interpreted as a water depth error of around 5 cm.
To summarize the evaluation, we assess the performance of the multi-step forecast system in three different ways:
- For all values within a test dataset, the CSI is calculated.
- For each cell, the RMSE value is calculated. This concludes with a map showing the spatial distribution of the prediction error.
- For each timestep in the monitoring window (t1, t2, t3, …, tn), an average RMSE error (Equation (10)) is calculated, where is the respective RMSE of a cell and refers to the number of cells in the study site. The lead-time prediction error is given by the following equation:
2.4. Physical-Based Modeling and Dataset for Training, Validation, and Testing
A hybrid database was used for the development of the multi-step inundation forecast system. The database was generated by Crotti et al. (2019) [6] and consists of 270 different scenarios, where each scenario includes discharges of the three rivers and corresponding inundation maps. One-half of the database (135) consists of synthetic events, where the authors applied the hydrological model LARSIM (Large Area Runoff Simulation Model) [32] on rainfall return periods provided by the German Meteorological Services Deutscher Wetterdienst (DWD) KOSTRA (Koordinierte Starkniederschlags Regionalisierungs Auswertungen) to generate the discharge hydrographs at the inflow location of the three rivers. The other half (135) consists of real-life-based events, where the authors applied a rescaling process to individual observed discharge events from time series analyses to higher return periods so that flooding in the study site occurred. The hydrographs have an hourly resolution and were then used as boundary conditions for two-dimensional inundation modeling using the hydrodynamic model HEC-RAS 2D [33] to obtain respective inundation maps. The maps have a spatial resolution of 4 m × 4 m, resulting in approximately 500,000 cells for the whole study site and a timely resolution of one hour. We would like to state that hydrodynamic modeling was not our focus. For details regarding the generation or validation of the 2D inundation model, please refer to Bhola et al. (2018) [40] or Crotti et al. (2019) [6]. The database was already used for multiple studies [22,23,28]. Besides this database, the three observed events from the years 2005, 2006, and 2013 were additionally used to test the developed forecast system on observed events.
The database was randomly split into three subsets of training (70%), validation (15%), and testing data (15%). The validation subset was used to gain an unbiased evaluation of the model during fitting and hyperparameter tuning, while the test dataset was used to provide an unbiased evaluation of the final model. Since we followed an image-to-image approach, the discharges had to be converted into images. We used a tensor with the size 14 × 14 × 3. Each of the three rivers was represented within its own channel, while the first timestep of the hydrographs was placed in the first position of the image matrix (1, 1), the second timestep in the second one (1, 2), and so on.
3. Study Area
We implemented our developed methodology in the study area Kulmbach (Figure 5). The area has a size of about 12 km2 and is located in the federal state of Bavaria, Germany. The catchment area has a flow direction from northeast to southwest. Three main rivers flow through the area, namely the Schorgast, the White Main, and the Red Main. The first two flow into the study area in the northeast, while the Red Main enters in the southern part and, unlike the other rivers, flows only briefly through the area. The northeastern part is narrow and surrounded by hills, while in the western part, the catchment area becomes wider and merges into floodplains.
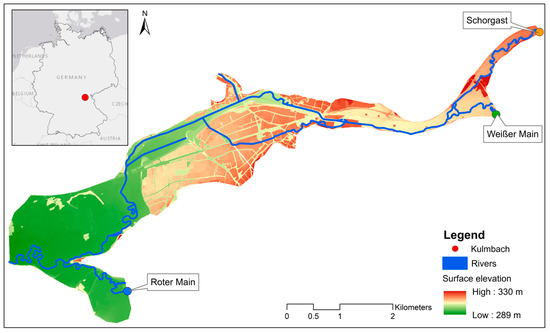
Figure 5.
The study area: Kulmbach. The subplot in the upper left shows the location of Kulmbach within Germany.
The soil consists of gravels and sands with a higher proportion of fine material originating from stream or river deposits ranging from the Pleistocene to the Holocene [41]. This mixture forms a porous aquifer. The city center is located in the central part of the catchment area and is home to 27,000 people [22]. Depending on the discharge of the three rivers, the study area can become flooded and pose a threat to its residents. In the years 2005, 2006, and 2013, the study area was heavily flooded, which led to an investigation of flood protection measures for the city. As feature information for the data-driven model, we applied the distance to the river of each cell and grouped them into three groups: cells with a distance of a maximum of 150 m, a maximum of 400 m, and more than 400 m.
4. Results
4.1. Operational Design
Since the study area is influenced by three rivers, we had to implement these rivers into the monitoring window . For the sake of demonstrating our methodology, we applied a monitoring window of 24 h and a discharge threshold of 19 m3/s, as inundation typically starts at this value. Since the resolution of the hydrographs from the hybrid database was one hour, the choice to set the timestep also to one hour is reasonable. As previously mentioned above, for the first forecast, the initial prediction window consists of three timesteps before and after the threshold; hence, the initial forecast accounts for 6 h. This configuration takes 19 timesteps to predict the final forecast in (the next 6 h as the initial forecast, following t + 7, t + 8, t + 9, …t + 24). The model was trained and tested on an NVIDIA Quadro M4000 graphics card with a memory of 8 GB. Such a card (or similar) is found commonly in many PCs. Python 3.9 and TensorFlow 2.6 were used for the development of the multi-step forecast system.
4.2. Hyperparameter and Optimization
We considered the filters in the convolutional part and the neurons in the recursive paths variable hyperparameters, and, thus, we performed a sensitivity analysis on these hyperparameters (the filter and neurons). To decide on the final model configuration, we relied on the validation results of this configuration and checked if the threshold (RMSE of 0.05 m) was reached. Table 1 shows the tested configurations, and Table 2 shows the evaluation and results of the sensitivity analysis for these configurations. Since configuration 2 showed the best validation performance and reached the threshold, we decided on this one.

Table 1.
Tested configurations for the number of filters in the convolutional part of the model.

Table 2.
Training and validation results of the three different configurations.
4.3. Performance Evaluation of the Forecast System
The forecast system was tested with the test dataset, including 35 events from the hybrid database. Additionally, three observed events from the years 2005, 2006, and 2013 were also used for testing. Since, in our case, the hydrographs are not changing over time, all tests were performed over the entire monitoring window. The prediction of one dynamic inundation map over the monitoring window was carried out within 47 s instead of the hours required by the physically based model, achieving the aim of real-time prediction.
As already mentioned, the performance of the forecast system was evaluated in three different ways: the calculation of the CSI with a limit value of 0.05 m, the calculation of the average RMSE value for each timestep and event, and the calculation of the spatial distribution of the prediction error. Section 4.3.1 presents the CSI values, Section 4.3.2 shows the overall performance and lead time prediction error, and Section 4.3.3 shows exemplarily the observed event from the year 2006, the inundation maps, and spatial error distribution.
4.3.1. Critical Success Index (CSI)
Table 3 shows the CSI values for all values in all timesteps to predict. For prediction purposes, we also took a look at the CSI values for each respective timestep. It turned out that there is no real difference between the respective timesteps, and, therefore, the CSI value for all timesteps is a sensible and meaningful approach. It can be seen that the CSI is always above 90%, meaning that, more or less, all cells are classified correctly in cells with water higher than 0.05 m (which can be interpreted as flooded areas) and safe cells (water depth < 0.05). Regarding this evaluation criteria, the forecast system delivers very good results and achieves the aimed high prediction quality.

Table 3.
Critical Success Index (CSI) in percentage for the test datasets over all timesteps.
4.3.2. Overall Performance and Lead Time Prediction Error
Figure 6 shows the average RMSE values for these test datasets plotted over the entire monitoring window, concluding with a prediction error for each timestep. It can be seen that all sets have an RMSE for the first 6 h below 0.07 m, which can be interpreted as an average water depth error below 7 cm over the entire study site. This error increases over time since the prediction error from t − 1 is carried on for each timestep. Nevertheless, even after 12 h, the error is still acceptable and around 0.08 m and 0.12 m. Except for the observed event from 2013, the worst predictions are at 24 h. At this stage, the error ranges from 0.1 m to 0.14 m. Overall, the prediction errors are good and always below 0.15 m.
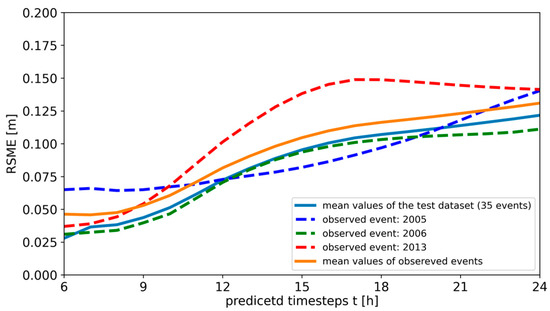
Figure 6.
Average RMSE prediction errors for the test datasets over the timesteps to predict.
4.3.3. Inundation Maps and Spatial Prediction Error Distribution
The evaluation of the forecast system for three timesteps (6 h, 12 h, and 24 h) of the observed events from the year 2006 is presented in Figure 7, Figure 8 and Figure 9, where Figure part (a) shows the used section of the hydrographs within the monitoring window, part (b) the respective predicted inundation map, (c) the true inundation, and part (d) the RMSE value of the respective cells. It is clearly visible that all predicted inundation maps are very similar to the true inundation maps, which were calculated by HEC-RAS 2D. Furthermore, the RMSE map shows that most of the respective cells have very small RMSE values.
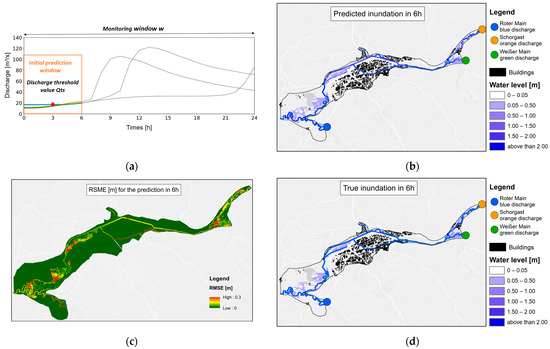
Figure 7.
Visualization of the prediction for the next 6 h of the observed event from 2006. (a) Hydrographs within the monitoring window w, dotted timesteps are not used for the initial forecast, the orange box represents the initial prediction window, and the red dot represents the discharge threshold Qts; (b) predicted inundation map; (c) true inundation for this timestep; (d) spatially distributed RMSE prediction error.
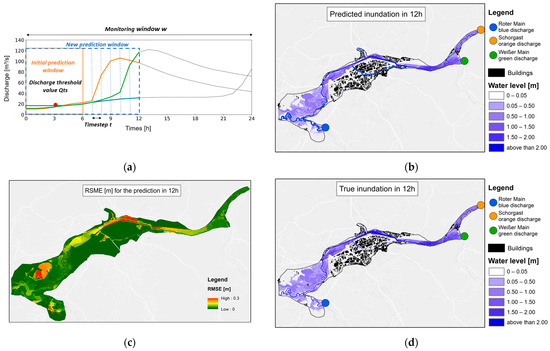
Figure 8.
Visualization of a multi-step prediction for the next 12 h of the observed event from 2006. (a) Hydrographs within the monitoring window w, dotted timesteps are not used for the forecast, the orange box represents the initial prediction window, the red dot represents the discharge threshold Qts, and the blue box represents the new prediction window including the timesteps t (visualized by the thin blue lines); (b) predicted inundation map; (c) spatially distributed RMSE prediction error; (d) true inundation for this timestep.
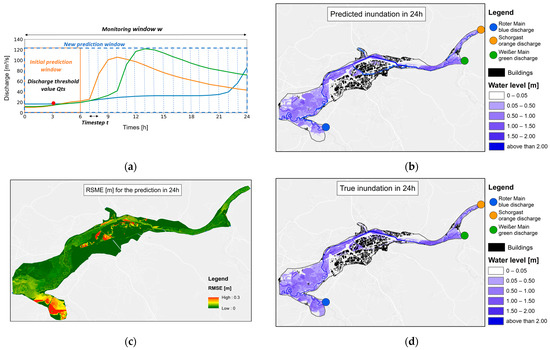
Figure 9.
Visualization of a multi-step prediction for the next 24 h of the observed event from 2006. (a) Hydrographs within the monitoring window w, dotted timesteps are not used for the forecast, the orange box represents the initial prediction window, the red dot represents the discharge threshold Qts, and the blue box represents the new prediction window including the timesteps t (visualized by the thin blue lines); (b) predicted inundation map; (c) spatially distributed RMSE prediction error; (d) true inundation for this timestep.
5. Discussion
5.1. Operational Design
Since we focused on the development of the data-driven model and implemented our method for the sake of demonstration based on the available dataset, no critical statement on the implementation of the operational design can be made. However, we would like to mention that the operational design is extremely flexible; thus, any requirement for any study area can be implemented. For a longer lead time prediction, the monitoring window just needs to be increased. If someone aims for a higher temporal resolution, the timestep within the monitoring window can be lower. Thus, our method is clearly beneficial for the implementation of real-world applications.
5.2. Hyperparameters and Optimization
In this study, the number of filters and number of neurons in the recursive feature path were considered flexible hyperparameters. Table 1 shows the tested configurations, while Table 2 shows the validation results of these configurations. The three configurations add more parameters (filters/neurons) to the model. In general, each additional parameter in a data-driven model increases the number of parameters that need to be learned during training. This leads to higher computational requirements during both training and inference phases, which can be a problem, especially for resource-constrained environments. Nevertheless, we were able to train all of these configurations and could investigate adding more parameters.
Adding more parameters also increases the model’s capacity to memorize the training data, which can lead to overfitting. Overfitting occurs when the model performs well on the training data but fails to generalize to unseen data. This is exactly what happened while using configuration 3. From Table 2, a better training accuracy can be seen, while the validation accuracy becomes worse in comparison to the other configurations. This affirmed us to take configuration 2, since in comparison to configuration 1, it had better validation accuracy.
The training and validation results for configuration 2 shown in Table 2 are very good. This indicates the effectiveness, firstly, of the feature-informed architecture and, secondly, of the optimizing workflow (retraining each path) as well as the omission of the recursive path and training only on the true flooding values. We would also like to mention that the recurve path, which is used in the operational forecasting mode, allows the integration of updating procedures. For example, real-time measurements taken at the study site could be integrated to update the predicted inundation map before the map is fed back into the model. This circumstance is also beneficial for real-world applications.
5.3. Performance Evaluation of the Forecast System
5.3.1. Critical Success Index (CSI)
Table 3 shows the results of the CSI evaluation, where the limit value is considered to be 0.05 m. This threshold is also critical since values of this magnitude are typically not visualized in flood maps. The table shows that all test data reach values of over 90%. This very high performance originates from the feature-informed architecture and the recursive informed loop, which also maintains the feature information for the next input. The high values across the test datasets indicate that the predictive model performs very well in classifying cells correctly in flooded cells (cells with water depth higher than 0.05 m) and safe cells (water depth < 0.05 m); thus, the model is highly accurate in predicting the flooding extent. This also indicates that the forecast system has achieved its goal of providing high-quality predictions of water depth. Stakeholders and decision-makers can have confidence in using the forecast system to make decisions based on the flooding extent.
5.3.2. Overall Performance and Lead Time Prediction Error
Figure 6 shows the average prediction quality as RMSE for each timestep to predict. All timesteps have RMSE values below 0.15 m, which indicates high prediction quality. Of course, the overall prediction becomes worse over the prediction timesteps and reaches a maximum in general at 24 h, since the new predictions also include the prediction error of the previous timestep fed back via the recursive path. Nevertheless, the feature-informed recursive path is able to integrate the inundation from the previous timestep in a satisfactory manner. One could argue that an hourly flood map (new map every hour) is not suitable for decision making in case of an emergency, but this resolution also keeps the uncertainty within the maps low and ensures that there are no bigger jumps in the inundations. For practical reasons, the timestep for a communicated map could be set to a higher interval (for example, 3 h).
The observed event for the year 2005 performs the worst at the beginning. The reason for this is that the available discharge data for this event already start higher than the threshold value of 25 m3/s. The results of the observed event from 2013 are the worst in total since this event is so different from the training dataset. Either expanding the training set or splitting the features in the informed layers into more categories are possible strategies.
5.3.3. Inundation Maps and Spatial Prediction Error Distribution
Figure 7, Figure 8 and Figure 9 show inundation for the timesteps 6, 12, and 24 h for the observed event in 2006. The inundation maps in figure parts (b and d) show no real visual difference from the true inundation maps from the HEC-RAS 2D model. This shows that the data-driven approach is a real alternative to the physically based model. Part (c) of these figures also shows the spatially distributed prediction error as RMSE. It can be seen that the predictions have an RMSE below 0.3 m, meaning that the prediction error is never worse than 30 cm. In Figure 9c, it can be seen that the southwestern part of the study area has the worst predictions. This is due to the fact that the hydrograph at this entry point is rising, while the other two are falling. Such a scenario is not covered within the training data. Expanding the training data would be an appropriate approach to deal with this issue.
Lin et al. (2020) [23] also developed a multi-step prediction model for this study area using the same dataset. However, the authors of this study only applied forecasts for the next 3, 6, 9, and 12 h with a network without a recursive path. For the observed event from 2006, they concluded that 89.63% and 82.40% of the predicted values had an RMSE below 0.3 m for the timesteps t = 6 h and t = 12 h, respectively. Hereby, the recursive and informed strategy of our approach shows its benefit since all predicted values for all timesteps have RMSE values below 0.3 m.
5.4. Limitations and Outlook
It should be mentioned that for running our multi-step inundation forecast, at least one hydrograph is required; otherwise, no forecast is possible. This hydrograph must be predicted in advance, and, thus, it also has to be mentioned that all of the uncertainties and data quality issues, which come hand in hand with the hydrograph, are also transferred into the data-driven model, leading to potentially poor performance. Furthermore, since the forecast system is trained on the hydrodynamic HEC-RAS 2D model results, all sources of uncertainty within this model are also transferred into the data-driven model. Nevertheless, HEC-RAS 2D is considered to be state of the art for the generation of inundation maps.
Also, if the forecast system has to be implemented within a different study area, the database for training, validation, and testing has to be generated beforehand by running a physically based model, and training has to be performed again, since the data-driven model is validated only to this specific study area. However, to date, there is no data-driven model available that can be transferred into a new study while keeping high prediction quality without retraining. Future research should investigate strategies for optimizing transferability.
In this study, we applied a monitoring window of 24 h; thus, it allows only discharge time series for the next 24 h. Longer series require a longer monitoring window. Nevertheless, this could be achieved with the current architecture by adjusting the parameters of the operational design and a re-training process. Additionally, in the current configuration of the data-driven multi-step forecast system, the predictions have to be stopped once the event reaches the current time. Further research should investigate strategies for also providing predictions during the event.
6. Conclusions
This study presented the development of a data-driven multi-step inundation forecast system for fluvial flood events, which provides a dynamic inundation map. The forecast system is set up over a monitoring window, where a hydrograph is listed. Once the hydrograph reaches a certain pre-defined discharge threshold, the inundation prediction is started. Therefore, the timesteps of the hydrograph responsible for the inundation are used as input for the data-driven model. The data-driven model consists of a convolutional neural network with the architecture of a residual network (ResNet18), feature-informed dense layers, and a recursive path. For the first prediction, the recursive path is not used. The recursive path is added once more timesteps of the hydrograph are relevant for the inundation. This path allows the model to predict multiple steps into the future. This procedure outputs a dynamic inundation map over the entire monitoring window. The temporal resolution of the dynamic inundation map is given the timestep at which the hydrograph is updated, and the maximum lead time is dependent on the length of the monitoring window. Test results show very high prediction quality; for example, for the next 6 h, 12 h, and 24 h, RMSE values of 0.07 m, 0.12 m, and 0.15 m are, respectively, reached. Furthermore, the predictions are performed within seconds, making the forecast system capable of real-time predictions in comparison to traditional physically based models. Unlike other studies, our data-driven model combines the recursive path with the input of additional knowledge about flooding into the data-driven model by the use of the feature-informed architecture. This led to high prediction quality even for multiple timesteps into the future. Additionally, the algorithm for running the whole forecast system is designed from an operation point of view; thus, it can be transferable to other real-world applications.
Author Contributions
Conceptualization, F.S.; methodology, F.S.; software, F.S.; validation, F.S.; data curation, F.S.; writing—original draft preparation, F.S.; writing—review and editing, J.L.; visualization, F.S.; supervision, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented in this paper has been carried out as part of the HiOS project (Hinweiskarte Oberflächenabfluss und Sturzflut) funded by the Bayerisches Staatsministerium für Umwelt und Verbraucherschutz (StMUV) [Bavarian State Ministry of the Environment and Consumer Protection] (69-0270-92086/2017) and supervised by the Bayerisches Landesamt für Umwelt (LfU) [Bavarian Environment Agency].
Data Availability Statement
The datasets generated for this study are available upon request to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Arnell, N.W.; Lloyd-Hughes, B. The Global-Scale Impacts of Climate Change on Water Resources and Flooding under New Climate and Socio-Economic Scenarios. Clim. Chang. 2014, 122, 127–140. [Google Scholar] [CrossRef]
- Calvin, K.; Dasgupta, D.; Krinner, G.; Mukherji, A.; Thorne, P.W.; Trisos, C.; Romero, J.; Aldunce, P.; Barrett, K.; Blanco, G.; et al. IPCC, 2023: Climate Change 2023: Synthesis Report. In Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; First Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2023. [Google Scholar]
- Swiss RE Institute Sigma. Natural Catastrophes in 2021: The Floodgates Are Open. Available online: https://www.swissre.com/institute/research/sigma-research/sigma-2022-01.html (accessed on 11 September 2024).
- Kuller, M.; Schoenholzer, K.; Lienert, J. Creating Effective Flood Warnings: A Framework from a Critical Review. J. Hydrol. 2021, 602, 126708. [Google Scholar] [CrossRef]
- Rözer, V.; Peche, A.; Berkhahn, S.; Feng, Y.; Fuchs, L.; Graf, T.; Haberlandt, U.; Kreibich, H.; Sämann, R.; Sester, M.; et al. Impact-Based Forecasting for Pluvial Floods. Earth’s Futur. 2021, 9, 2020EF001851. [Google Scholar] [CrossRef]
- Crotti, G.; Leandro, J.; Bhola, P.K. A 2D Real-Time Flood Forecast Framework Based on a Hybrid Historical and Synthetic Runoff Database. Water 2019, 12, 114. [Google Scholar] [CrossRef]
- Schmid, F.; Leandro, J. A Feature-Informed Data-Driven Approach for Predicting Maximum Flood Inundation Extends. Geosciences 2023, 13, 384. [Google Scholar] [CrossRef]
- Henonin, J.; Russo, B.; Mark, O.; Gourbesville, P. Real-Time Urban Flood Forecasting and Modelling–a State of the Art. J. Hydroinformatics 2013, 15, 717–736. [Google Scholar] [CrossRef]
- Berkhahn, S.; Neuweiler, I. Data Driven Real-Time Prediction of Urban Floods with Spatial and Temporal Distribution. J. Hydrol. X 2024, 22, 100167. [Google Scholar] [CrossRef]
- Sanders, B.F.; Schubert, J.E.; Detwiler, R.L. ParBreZo: A Parallel, Unstructured Grid, Godunov-Type, Shallow-Water Code for High-Resolution Flood Inundation Modeling at the Regional Scale. Adv. Water Resour. 2010, 33, 1456–1467. [Google Scholar] [CrossRef]
- Delestre, O.; Darboux, F.; James, F.; Lucas, C.; Laguerre, C.; Cordier, S. FullSWOF: Full Shallow-Water Equations for Overland Flow. J. Open Source Softw. 2017, 2, 448. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Sharif, M.B.; Kalyanapu, A.; Ghafoor, S.K.; Dullo, T.T.; Gangrade, S.; Kao, S.-C.; Norman, M.R.; Evans, K.J. TRITON: A Multi-GPU Open Source 2D Hydrodynamic Flood Model. Environ. Model. Softw. 2021, 141, 105034. [Google Scholar] [CrossRef]
- Hou, J.; Kang, Y.; Hu, C.; Tong, Y.; Pan, B.; Xia, J. A GPU-Based Numerical Model Coupling Hydrodynamical and Morphological Processes. Int. J. Sediment Res. 2020, 35, 386–394. [Google Scholar] [CrossRef]
- Seleem, O.; Ayzel, G.; De Souza, A.C.T.; Bronstert, A.; Heistermann, M. Towards Urban Flood Susceptibility Mapping Using Data-Driven Models in Berlin, Germany. Geomat. Nat. Hazards Risk 2022, 13, 1640–1662. [Google Scholar] [CrossRef]
- Li, Y.; Martinis, S.; Wieland, M. Urban Flood Mapping with an Active Self-Learning Convolutional Neural Network Based on TerraSAR-X Intensity and Interferometric Coherence. ISPRS J. Photogramm. Remote Sens. 2019, 152, 178–191. [Google Scholar] [CrossRef]
- Solomatine, D.; See, L.M.; Abrahart, R.J. Data-Driven Modelling: Concepts, Approaches and Experiences. Water Science and Technology Library. In Practical Hydroinformatics; Abrahart, R.J., See, L.M., Solomatine, D.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 68, pp. 17–30. ISBN 978-3-540-79880-4. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Liu, C.; Tao, Y.; Liang, J.; Li, K.; Chen, Y. Object Detection Based on YOLO Network. In Proceedings of the 2018 IEEE 4th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 14–16 December 2018; pp. 799–803. [Google Scholar]
- Shao, P.; Feng, J.; Lu, J.; Zhang, P.; Zou, C. Data-Driven and Knowledge-Guided Denoising Diffusion Model for Flood Forecasting. Expert Syst. Appl. 2024, 244, 122908. [Google Scholar] [CrossRef]
- Xu, C.; Zhong, P.; Zhu, F.; Xu, B.; Wang, Y.; Yang, L.; Wang, S.; Xu, S. A Hybrid Model Coupling Process-Driven and Data-Driven Models for Improved Real-Time Flood Forecasting. J. Hydrol. 2024, 638, 131494. [Google Scholar] [CrossRef]
- Berkhahn, S. An Ensemble Neural Network Model for Real-Time Prediction of Urban Floods. J. Hydrol. 2019, 575, 743–754. [Google Scholar] [CrossRef]
- Lin, Q.; Leandro, J.; Wu, W.; Bhola, P.; Disse, M. Prediction of Maximum Flood Inundation Extents with Resilient Backpropagation Neural Network: Case Study of Kulmbach. Front. Earth Sci. 2020, 8, 332. [Google Scholar] [CrossRef]
- Lin, Q.; Leandro, J.; Gerber, S.; Disse, M. Multistep Flood Inundation Forecasts with Resilient Backpropagation Neural Networks: Kulmbach Case Study. Water 2020, 12, 3568. [Google Scholar] [CrossRef]
- Löwe, R.; Böhm, J.; Jensen, D.G.; Leandro, J.; Rasmussen, S.H. U-FLOOD–Topographic Deep Learning for Predicting Urban Pluvial Flood Water Depth. J. Hydrol. 2021, 603, 126898. [Google Scholar] [CrossRef]
- Guo, Z.; Leitão, J.P.; Simões, N.E.; Moosavi, V. Data-driven Flood Emulation: Speeding up Urban Flood Predictions by Deep Convolutional Neural Networks. J. Flood Risk Manag. 2021, 14, e12684. [Google Scholar] [CrossRef]
- Hofmann, J.; Schüttrumpf, H. floodGAN: Using Deep Adversarial Learning to Predict Pluvial Flooding in Real Time. Water 2021, 13, 2255. [Google Scholar] [CrossRef]
- Guo, Z.; Moosavi, V.; Leitão, J.P. Data-Driven Rapid Flood Prediction Mapping with Catchment Generalizability. J. Hydrol. 2022, 609, 127726. [Google Scholar] [CrossRef]
- Schmid, F.; Leandro, J. An Ensemble Data-Driven Approach for Incorporating Uncertainty in the Forecasting of Stormwater Sewer Surcharge. Urban Water J. 2023, 20, 1140–1156. [Google Scholar] [CrossRef]
- Burrichter, B.; Hofmann, J.; Koltermann da Silva, J.; Niemann, A.; Quirmbach, M. A Spatiotemporal Deep Learning Approach for Urban Pluvial Flood Forecasting with Multi-Source Data. Water 2023, 15, 1760. [Google Scholar] [CrossRef]
- Chiang, Y.-M.; Chang, L.-C.; Tsai, M.-J.; Wang, Y.-F.; Chang, F.-J. Dynamic Neural Networks for Real-Time Water Level Predictions of Sewerage Systems-Covering Gauged and Ungauged Sites. Hydrol. Earth Syst. Sci. 2010, 11, 1309–1319. [Google Scholar] [CrossRef]
- Chang, F.-J.; Chen, P.-A.; Lu, Y.-R.; Huang, E.; Chang, K.-Y. Real-Time Multi-Step-Ahead Water Level Forecasting by Recurrent Neural Networks for Urban Flood Control. J. Hydrol. 2014, 517, 836–846. [Google Scholar] [CrossRef]
- Ludwig, K.; Bremicker, M. The Water Balance Model LARSIM-Design, Content and Applications. In Freiburger Schriften zur Hydrologie; Institut für Hydrologie: Amsterdam, The Netherlands, 2006; p. 22. [Google Scholar]
- US Army Corps of Engineers. H.E.C. HEC-RAS River Analysis System-2D Modeling Users Manual, Version 5.0; US Army Corps of Engineers: Davis, CA, USA, 2016.
- O’Shea, K.; Nash, R. An Introduction to Convolutional Neural Networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6999–7019. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Wunsch, A.; Liesch, T.; Broda, S. Forecasting Groundwater Levels Using Nonlinear Autoregressive Networks with Exogenous Input (NARX). J. Hydrol. 2018, 567, 743–758. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Bhola, P.K. Dynamic Flood Inundation Forecasting in Real-Time Including Associated Uncertainties for Operational Flood Risk Management. Ph.D. Dissertation, TU München, München, Germany, 2019. [Google Scholar]
- Landsamt für Umwelt (LfU). Hydrogeologische Karte. Available online: https://www.lfu.bayern.de/geologie/hydrogeologie_karten_daten/hk50/index.htm (accessed on 11 September 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).