Abstract
Since cryptocurrencies are among the most extensively traded financial instruments globally, predicting their price has become a crucial topic for investors. Our dataset, which includes fluctuations in Bitcoin’s hourly prices from 15 May 2018 to 19 January 2024, was gathered from Crypto Data Download. It is made up of over 50,000 hourly data points that provide a detailed view of the price behavior of Bitcoin over a five-year period. In this study, we used potent algorithms, including gradient descent, attention mechanisms, long short-term memory (LSTM), and artificial neural networks (ANNs). Furthermore, to estimate the price of Bitcoin, we first merged two deep learning algorithms, LSTM and attention mechanisms, and then combined LSTM-Attention with gradient-specific optimization to increase our model’s performance. Then we integrated ANN-LSTM and included gradient-specific optimization for the same reason. Our results show that the hybrid model with gradient-specific optimization can be used to anticipate Bitcoin values with better accuracy. Indeed, the hybrid model combines the best features of both approaches, and gradient-specific optimization improves predictive performance through frequent analysis of pricing data changes.
1. Introduction
Over the past few years, technological progress and the advent of digital transformation imply a paradigm shift in various industries, including the business sector [1]. The rapid progress of digital transformation has undeniably sparked the emergence of fintech (financial technology). These innovations are considered by many to be among the most important developments in the financial sector. Also, the financial landscape is facing a revolution owing to digital solutions, which are challenging and revolutionizing age-old techniques and practices that have held their ground for a long time.
Moreover, fintech, in fact, provides a broad spectrum of services. These include mobile banking, digital wallets, peer-to-peer payment systems, e-insurance, e-payments, and even cryptocurrencies like Bitcoin.
The cryptocurrencies that have taken the world by storm are a relatively complex form of exchange medium. With Bitcoin being the first form of this development, the heterogeneous nature of these cryptocurrencies has made it difficult to ascertain a proper method of prediction of the prices of these currencies using conventional econometric or even deep learning models, which have been employed to predict trends in other exchange mediums. Madan et al. [2] used various machine learning methodologies, such as generalized linear models and random forest, to address the Bitcoin prediction challenge. Jiang, X. [3] proposed deep learning methods in order to predict the Bitcoin price. His study shows that long short-term memory (LSTM) provides the best prediction.
In addition, cryptocurrencies can undergo fast and remarkable cost variances over short periods, making them an especially hazardous speculation. This instability is driven by an assortment of variables, including counting theoretical exchanges, advertising estimations, and outside occasions. Another particular characteristic of cryptocurrency markets is their ceaseless 24/7 exchanging. Not at all like conventional stock markets that have settled exchanging hours, advanced resources can be bought and sold at any time, and predicting the price of any digital financial asset is considered one of the most challenging tasks, which makes it difficult for investors to stay well-informed due to their instability. Our study contributes to the existing literature by proposing novel approaches for Bitcoin price prediction using network models and high-frequency data. We employ a network-based method to capture the interdependencies and relationships between different cryptocurrencies and market variables. Additionally, we utilize high-frequency data to capture rapid price fluctuations and market dynamics. Our approach provides a more comprehensive and accurate prediction of Bitcoin prices, addressing the limitations of previous models. The first model integrates long short-term memory (LSTM) and attention mechanisms that allow sequence learning and optimization to take place. Gradient-aware optimization has been introduced to improve the model’s ability to make better forecasts and make informed trading decisions. The second model combines ANN-LSTM with gradient-aware optimization to improve its forecasting and trading decision-making capabilities. These models stand out because they use sophisticated techniques that allow them to adapt to the conditions of the ever-changing Bitcoin market. These models are a helpful tool for participants in the currency trading industry because of their adaptive characteristics, which allow them to maintain a constant in a variety of market conditions. In fact, predicting the price of this volatile asset is challenging due to its reliance on various external factors. The dataset in question contains information regarding cryptocurrencies that is dynamic and subject to change as the world transforms and develops. The search results shed light on the dynamic nature of Bitcoin data, such as changing market dynamics, constant updates to cryptocurrency temporal data, and an examination of cryptocurrency rates of return.
Moreover, the effects of social media play an impressive part. A single tweet or news report can send cryptocurrency costs taking off or falling. This lively relationship between social media and cryptocurrency markets incorporates an extra layer of complexity.
In recent years, deep learning techniques have been applied to time series forecasting, especially in popular real-world application areas such as cryptocurrencies, due to the market’s instability and dynamism. The majority of these models employ advanced deep learning strategies based on long short-term memory (LSTM), attention mechanisms, gradient-based optimization techniques, and so many others.
Actually, deep learning models have shown superior performance in predicting cryptocurrency prices compared with traditional machine learning models. Together, these devices offer a powerful system and well-suited data for exploring the complex and highly volatile cryptocurrency landscape (Sun et al. [4]). Hence, analysts have committed critical effort to progressing time series estimating models, investigating different combinations to distinguish the most successful approach for price forecasts. As it stands now, investing or even setting exchange rates for cryptocurrencies is a gamble.
In point of fact, our models stand out because they use sophisticated techniques that allow them to adapt to the conditions of the ever-changing Bitcoin market. These models are a helpful tool for participants in the currency trading industry because of their adaptive characteristic, which allows them to maintain a constant in a variety of market conditions.
The paper is organized as follows. In Section 2, we conduct a literature assessment of the market under consideration, investigating the methods used to estimate cryptocurrency values. Section 3 describes the methods for estimating Bitcoin prices as well as the research contributions. Section 4 presents our methodology. Section 5 discusses the research findings. In Section 6, we describe the results of this study. Finally, Section 7 will conclude the paper.
2. Literature Review
The trading and exchanging of cryptocurrencies across the globe have increased significantly over the last decade. This upsurge has pushed their market value to hundreds of billions of dollars globally. In January 2021, this figure reached an impressive USD 1 trillion [5]. In financial market modeling, accurate forecasting and investment choices depend on having a solid grasp of the dynamics of asset prices, entry points, and market behavior. An attempt was made to build upon the Tramontana et al. model by Gu, E. G. [6]. They built a new two-dimensional discontinuous piecewise linear (PWL) map with three branches, as well as trend followers that adhere to the most recent price trend, to power their financial market model.
Forecasting digital currencies’ worth is a challenge, as they are volatile and have unique systems. The prices keep changing due to emerging technologies with no clear future monetary value, according to analysts. Media and investors have recently taken notice of Bitcoin. However, it can be difficult to estimate the prices of Bitcoin and other cryptocurrencies because they are too volatile and complicated in nature. Earlier findings propose that deep learning algorithms can boost accuracy in forecasting cryptocurrency values by uncovering intricate patterns in complex and dynamic datasets. Through these techniques, behaviors or movements within unstable cryptocurrency markets can be identified. In order to have a better prediction with good accuracy, Bangroo et al. [7] used different machine learning algorithms like random forest regressor and gradient boosting regressor to predict cryptocurrencies like Bitcoin, XRP, Ethereum, and Stellar. Xiaolei et al. [4] proposed three models: SVM, RF model, and light gradient boosting machine to forecast the price of the cryptocurrency market. Lahmiri et al. [8] presented two deep learning methods, a deep learning neural network (DLNN) and generalized regression neural networks (GRNNs), to forecast the price of Bitcoin. Modi, Parth Daxesh, et al. [9] investigated the use of deep neural networks, specifically a shallow bidirectional-LSTM (Bi-LSTM) model, to forecast daily closing prices for Bitcoin. Also, in their research work, Tripathi, B., & Sharma, R. K. [10] explore how to model Bitcoin values using deep learning, Bayesian optimization, and signal processing techniques. Chen, J. [11] focused on the prediction of Bitcoin prices using deep learning algorithms, such as CNN, LSTM, and GRU.
Additionally, in their revolutionary study, Zhou et at. [12] focus on deep learning within the financial markets and offer perceptive details regarding the potential applications of deep learning techniques for Bitcoin returns.
Our findings build on previous research using deep learning approaches to estimate the price of Bitcoin and other cryptocurrencies. Indeed, various deep learning models have been used over the previous five years, and they have shown to be the finest technology for forecasting cryptocurrency prices. Kristjanpoller and Minutolo’s [13] research has significant advanced the area by introducing a hybrid MLP neural network-GARCH model for predicting Bitcoin price volatility. In their work, they conducted a comprehensive assessment of multiple GARCH models and discovered the benefits of combining linear and nonlinear models for better forecasting of Bitcoin price volatility. Also, Nakano et al. [14] used an MLP neural network to estimate Bitcoin returns based on a variety of technical indications.
Further, in 2023, Akila et al. [15] recommended LSTM networks, a deep learning technique to forecast prices of cryptocurrencies. Their method consisted of using historical price data and technical indicators as input to the LSTM model. This decision was prompted by LSTM’s ability to identify underlying patterns and trends in data. It was revealed by the outcomes that LSTM uses significantly and effectively predicted future cryptocurrency prices. Moreover, Gurgul, V. et al. [16] integrate their method with recent research on artificial intelligence risk measurement and safe artificial intelligence, emphasizing the significance of considering both financial and textual data when projecting cryptocurrency prices. This is especially important for investors, traders, and politicians, who rely on accurate forecasts to make sound judgments.
One of the foremost important and decentralized cryptocurrencies is Bitcoin, which was presented by Satoshi Nakamoto [17] on 31 October 2008. Also, we can find another notable study by Liu et al. [18] focused on Bitcoin. Building on the advancements in deep learning for cryptocurrency price prediction, they used a separate deep learning technique, stacked denoising autoencoders (SDAEs), to forecast Bitcoin’s price. SDAE outperformed other models in forecasting the price of Bitcoin in both the directional and level prediction.
Furthermore, deep learning algorithms have achieved great advances in past research, producing excellent results in a variety of domains such as image-to-language conversion, speech recognition, and computer vision. According to research, combining deep learning algorithms results in the lowest anticipated mistakes. For example, Patel et al. [19] proposed a hybrid cryptocurrency prediction system based on LSTM and GRU in their study. The results demonstrate great price accuracy, and the combination of LSTM and GRU can be used to predict the prices of multiple cryptocurrencies (Monero, Litecoin, and Bitcoin). In the same context, a range of hybrid deep learning techniques are employed for estimating cryptocurrency prices, combining the strengths of different deep learning models to produce better predictable results.
A variety of hybrid approaches have been utilized in order to achieve better performance. For example, the combination of a convolutional neural Network (CNN) and stacked gated recurrent unit (GRU) suggested by Kang et al. [20] was evaluated on three different cryptocurrency datasets including Bitcoin, Ethereum, and Ripple.
In addition, Petrovic et al. [21] proposed a novel combined method to predict the price that is based on hybrid machine learning and the swarm intelligence approach, combining the power of both techniques. In a similar vein, in their study, Li et al. [22] proposed a novel data decomposition-based hybrid bidirectional deep learning model for forecasting the daily price change in the Bitcoin market. Results show that the model outperforms other benchmark models such as econometric models, machine learning models, and deep learning models. Likewise, Li et al. [23] conducted a study on the Bitcoin price forecasting method based on a CNN-LSTM hybrid neural network model. The findings demonstrate that the proposed model performs well in forecasting Bitcoin.
Along the same lines, Zahouani and Boubaker [24] investigated the efficacy of several mixed forecasting models to predict daily oil prices, including ANN-LSTM, CNN-LSTM, BRNN-LSTM, and LSTM-Attention. The investigation shows that the hybrid LSTM-Attention model beats other hybrid models in terms of accuracy, with the lowest error rate.
Our study seeks to increase the forecast accuracy by introducing extra optimization and a refining algorithm into hybrid models. Our goal is to improve prediction accuracy and ensure reliable results.
3. Proposed Algorithms
3.1. Long Short-Term Memory (LSTM)
Long short-term memory (LSTM) networks are a type of deep learning technique and a refined version of the recurrent neural network (RNN). LSTM has been employed in prediction tasks such as forecasting cryptocurrency prices, including Ethereum, Litecoin, and particularly for Bitcoin (Livieris, Ioannis E., et al. [25]). Its utility encompasses activities related to time series and sequential prediction issues like machine translation and speech recognition. The fundamental component of LSTM is the memory module, and the other components are three gates: input gate, output gate, and forget gate.
Calculation formula is:
where is the input at time t, is the hidden state at time t, is the cell state at time t, is the sigmoid function, and tanh is the hyperbolic tangent function.
3.2. Artificial Neural Network (ANN)
Artificial neurons, also called ANNs, are AI tools enabling robots to simulate human cognitive abilities. The application of ANN as a powerful AI computing tool is manifest in fields like telecommunications, material research, health care, neurology, and finance (Hong et al. [26]). It is referred to as an algorithm for classification and regression problems by ANN. The output layer collects information from the input layers of the ANN through its hidden layers.
A neural network may include three layers. The first one is the input layer, where the activity of input units represents raw data delivered to the network. The second layer is the hidden layer, which controls the activities of each hidden unit. The number of hidden layers, as well as the activities of the input units and the weights assigned to their interactions with the hidden units, can vary. Finally, the output layer’s behavior is determined by both the activity of the hidden units and the weights between the hidden and output units.
3.3. Attention Mechanisms
Attention mechanisms are a crucial component of deep learning models and have been proven to be effective in various sectors.
In medical image analysis, Li, Xiang, et al. [27] have examined deep learning models to investigate inter-spatial information and improve the accuracy of image classification and segmentation. And in the area of cryptocurrency price forecasting, Yazhini, V., et al. [28] combined attention mechanisms with long short-term memory, bidirectional-LSTM, and gated recurrent unit models to anticipate the future closing price of Bitcoin and Ethereum.
Several recent publications have demonstrated how attention mechanisms can boost the predictive ability of deep learning models of virtual currency prices. In addition, attention mechanisms allow models to focus on specific areas of input or output data, resulting in improved performance for tasks such as machine translation, sentiment analysis, and time series prediction. In fact, they can help deep learning models focus on relevant data in order to improve their accuracy and efficiency.
3.4. Gradient Descent
Gradient descent is used widely as an optimization method to train machine learning models and neural networks. It reduces discrepancies between predicted and actual outcomes and could be combined with deep learning algorithms like LSTM to enhance prediction precision (Elsayed et al. [29]). In fact, gradient descent is based on a convex function that can be thought of as finding the lowest point within a linear curve by moving along its steepest slope direction. The technique updates model parameters depending on the estimated gradient, providing the ability for the model to learn and become better over time. It is similar to estimating the line of best fit in linear regression.
Additionally, the selection of an appropriate gradient descent type plays a significant part in the training process of machine learning in the domain and relies on some key things like dataset size, jamming, and stability, as well as hyperparameters. Furthermore, there are three different gradient descent learning algorithms: batch gradient descent (BGD), stochastic gradient descent (SGD) and mini-batch gradient descent. BGD is characterized by traditional methodology that produces a stable error gradient and convergence; it is also suitable for smaller datasets that can fit into memory. On the contrary, stochastic gradient descent (SGD) repeats a training epoch for every instance in the dataset, modifying the parameters of each individual sample at a time, and hence it is suitable for larger datasets. Lastly, mini-batch gradient descent combines ideas from both BGD as well as SGD. This kind balances the speed of SGD with the computational efficiency of BGD.
- ❖
- Batch Gradient Descent
The mathematical expression of batch gradient descent is:
where:
θ denotes the parameters under optimization.
ƞ is the learning rate that determines the step size in the parameter space.
is a cost function that evaluates the model’s performance.
represents the gradient of the cost function with respect to the parameters.
- ❖
- Stochastic Gradient Descent (SGD)
The mathematical expression of stochastic gradient descent (SGD) is:
where:
denotes the parameters under optimization.
ƞ is the learning rate that determines the step size in the parameter space.
is the cost function that measures the model’s performance for a specific training example .
denotes the gradient of the cost function with respect to the parameters for a specific training example.
- ❖
- Mini-Batch Gradient Descent
The mathematical expression of mini-batch gradient descent is:
where:
denotes the parameters under optimization.
ƞ is the learning rate that determines the step size in the parameter space.
is the cost function that measures the model’s performance for a mini-batch of training examples .
denotes the gradient of the cost function with respect to the parameters for a mini-batch of training examples.
4. Methodology
4.1. Dataset
This paper delves into a robust dataset obtained from a reputable platform called Crypto Data Download and focuses on Bitcoin’s hourly price movements from 15 May 2018 to 19 January 2024, and it contains approximately 50,000 hourly data points and provides a detailed snapshot of Bitcoin price behavior over five years. We split our data into training and testing sets to evaluate the performance of our model. We purposefully started our sample in 2018 for a number of reasons. Among these are the early stages of the global health crisis, which had an impact on financial markets, including cryptocurrency markets. The COVID-19 pandemic in 2018 caused a global economic catastrophe that resulted in exceptionally high market volatility and trading in various asset classes, including Bitcoin.
Figure 1 illustrates the fluctuations in the price of Bitcoin over time, using an hourly time scale on the x-axis and the corresponding values of price on the y-axis. This visual representation enables us to interpret the data’s behavior.
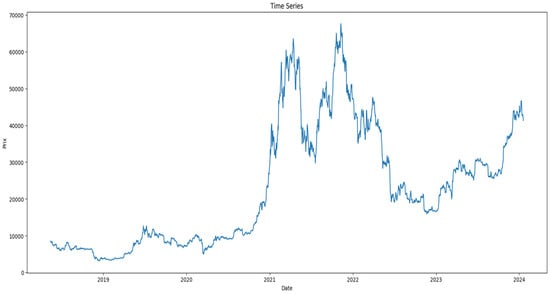
Figure 1.
Time series plot for Bitcoin price.
4.2. Model Evaluation Metrics
Model evaluation is important to assess the effectiveness of a model in the early stages of research and also plays a role in model monitoring. In this study, we evaluated model performance using three common evaluation metrics used in machine learning and predicting tasks to determine the model’s predictive efficacy: mean absolute error (MAE), mean squared error (MSE), and mean absolute percentage error (MAPE).
where N is the quantity of data to be assessed, is the ith true value, and is the ith forecast value. The degree of variation between the expected and actual values is shown by the MAE, MSE, and MAPE. The prediction’s accuracy increases with decreasing values of MAE, MSE, and MAPE.
Similarly, to compare the prediction accuracy of two competing forecasts defined by DM, we use the Diebold and Mariano (1999) [30] test. This test verifies the null hypothesis that the expected differential loss is zero, or , when the loss differential , using a loss function linked to each prediction’s forecast inaccuracy. The two loss functions are computed as follows:
and
where are two forecasts for t = 1, 2, …, T. The loss function is often either an absolute error loss or squared error loss function. The hypotheses of interest are presented as follows:
where h ≥ 1 is the forecast horizon. The DM test has a standard normal-limiting distribution under the null hypothesis.
5. Numerical Results
5.1. ANN-LSTM Model
This part focuses on applying the hybrid ANN-LSTM model, using each algorithm outlined in Section 3. The hybrid technique seeks to forecast Bitcoin’s hourly price. Table 1 displays the projected and actual values for the most recent 20 observations.

Table 1.
Observed and forecasted values using the hybrid model ANN-LSTM.
Figure 2 compares the supplied and actual values for the ANN LSTM model, providing a straightforward evaluation of its performance across 400 observations. In order to evaluate the model’s effectiveness, three performance metrics were used: mean square error (MSE), mean absolute error (MAE), and mean absolute percentage error (MAPE). Table 2 displays the MSE, MAE, and MAPE values to demonstrate how well the hybrid model predicts.
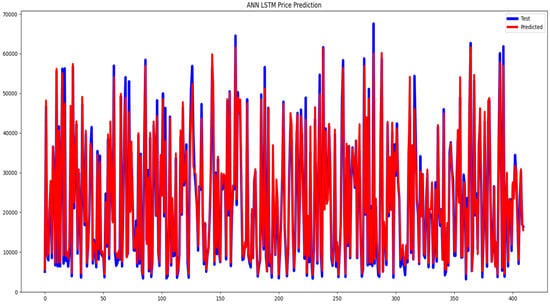
Figure 2.
ANN-LSTM price prediction.

Table 2.
Evaluation metrics results of ANN-LSTM model.
Figure 3 depicts how the model’s performance has increased with time. As the number of epochs increases, the loss lowers, indicating that the model is becoming more accurate in its predictions.
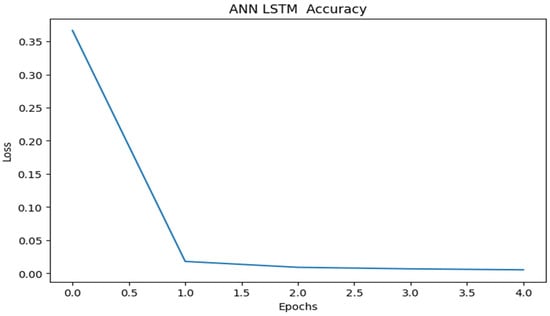
Figure 3.
ANN-LSTM accuracy.
The model’s overall accuracy is 99.46%.
5.2. ANN-LSTM with Gradient Specific Optimization
The section focuses on using a hybrid ANN LSTM model with gradient-specific optimization to estimate Bitcoin’s hourly price, with better predictions to improve the model’s performance. Table 3 shows the gradient variations and ANN-LSTM levels for the 10 most recent data points.

Table 3.
Gradient-specific optimization variations and ANN-LSTM values.
Figure 4 depicts the actual results for the ANN LSTM model in forecasting Bitcoin’s hourly price, allowing for obvious evaluations of its performance across 400 observations and demonstrating market volatility and variations. And Figure 5 demonstrates the gradient variation in projecting Bitcoin’s hourly prices using 400 datasets.
Figure 4.
Presentation of ANN-LSTM graph.
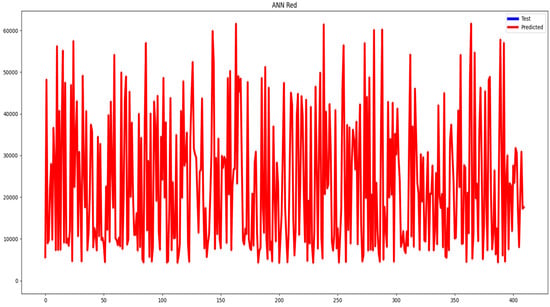
Figure 5.
Presentation of the gradient variation graph.
To directly compare the model’s performance with the gradient-specific optimization, Figure 6 displays both the curve of ANN-LSTM values and the curve of gradient variations, allowing for obvious observations of higher precision.
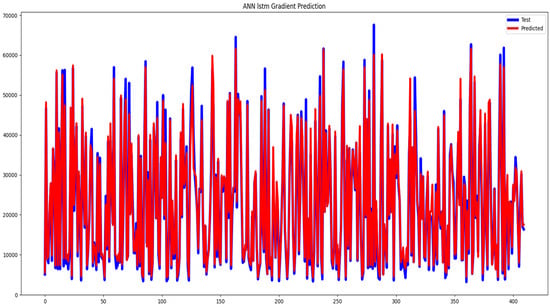
Figure 6.
Presentation of the ANN-LSTM with gradient variation graph.
5.3. LSTM-Attention Model
This chapter emphasizes using a hybrid LSTM-Attention model, which was presented in Section 3, to forecast the hourly price of Bitcoin. Table 4 shows the projected and real values for the latest 20 observations.

Table 4.
Observed and forecasted values using the hybrid model LSTM-Attention.
Figure 7 contrasts the given and actual values for the LSTM-Attention model, allowing for a clear evaluation of its performance over 200 observations. To evaluate the effectiveness of the LSTM-Attention model, this study used three performance evaluation metrics: mean square error (MSE), mean absolute error (MAE), and mean absolute percentage error (MAPE). Table 5 shows the hybrid model’s accuracy in projecting outcomes for MSE, MAE, and MAPE.
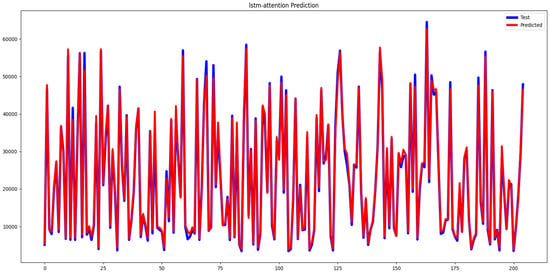
Figure 7.
LSTM-Attention price prediction.

Table 5.
Evaluation metrics results of LSTM-Attention model.
A lower MSE suggests better accuracy in prediction. A lower MAPE suggests better accuracy. And the DM statistic of 4.253 is a measure of the difference in forecast accuracy between two competing models or approaches.
Figure 8 shows how the model’s performance has improved over time. As the number of epochs increases, the loss decreases, showing that the model is becoming more accurate in its predictions. The model’s overall accuracy of 99.84% reflects its outstanding performance in properly predicting outcomes.
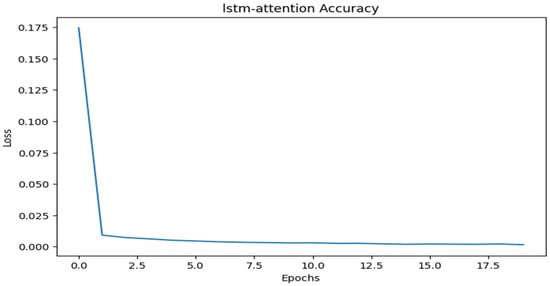
Figure 8.
LSTM-Attention accuracy.
5.4. LSTM-Attention with Gradient Specific Optimization
The section focuses on applying the hybrid LSTM-Attention model with gradient-specific optimization to forecast Bitcoin’s hourly price. Table 6 illustrates the gradient variations and LSTM-Attention values for the most recent ten observations.

Table 6.
Gradient-specific optimization variations and LSTM-Attention values.
Figure 9 shows the real results for the LSTM-Attention model in forecasting Bitcoin’s hourly price, providing clear evaluations of its performance across 200 observations and displaying the market’s volatility and fluctuations. And Figure 10 depicts the gradient variation in forecasting Bitcoin’s hourly prices across 200 data points.
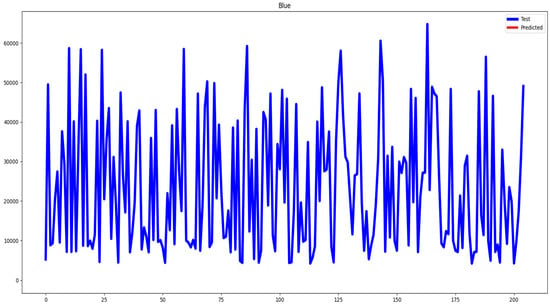
Figure 9.
Presentation of the LSTM-Attention graph.
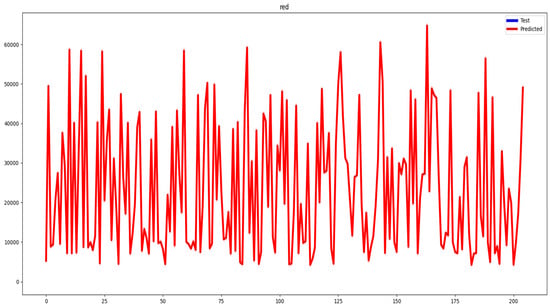
Figure 10.
Presentation of the gradient variation graph.
In Figure 11, the gradient-specific optimization curve and the LSTM Attention values curve are displayed side by side, enabling a direct comparison of the model’s performance and demonstrating improved accuracy.
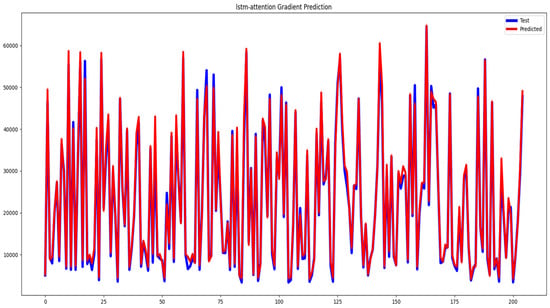
Figure 11.
Presentation of the LSTM-Attention with gradient variation graph.
6. Discussion
Our study discovered that hybrid deep learning techniques, such as LSTM-Attention, outperform ANN-LSTM at predicting cryptocurrencies like Bitcoin, as shown in Table 7. With the combination of LSTM and attention, we attained an accuracy of 99.84 percent. Furthermore, our findings suggest that, in this scenario, boosting optimization specificity can enhance forecasting accuracy, as illustrated in Figure 6 and Figure 11.

Table 7.
Evaluation metrics results of both models.
Deep learning approaches, such as LSTM-Attention, have shown potential in predicting Bitcoin prices due to their capacity to detect complicated patterns and correlations in data. Gradient-specific optimization is a strategy that uses gradient information gathered during the training process to optimize model parameters. Using this strategy allows the model to learn more efficiently and precisely, resulting in higher forecasting accuracy.
In summary, the LSTM-Attention hybrid model generally outperforms the ANN-LSTM hybrid model in terms of forecast accuracy, as evidenced by lower error metrics and a higher accuracy rate. Furthermore, the LSTM-Attention model shows a greater difference in forecast accuracy than the ANN-LSTM model, as evidenced by the higher DM statistic. A higher DM value of 4.253 indicates a substantial difference in forecast accuracy against the ANN-LSTM model.
7. Conclusions
Predicting Bitcoin values is a difficult task owing to numerous market variables. For this reason, recent advances in deep learning and artificial intelligence have yielded more accurate and reliable predictive models than formerly effective methods such as time series analysis or econometric modeling. Hybridization can increase the precision of predictions of Bitcoin prices by adopting mixed approaches to the use of these two modeling systems.
Firstly, as previously stated, we employed the LSTM with attention mechanism, followed by gradient-specific optimization, to enhance our predictions of Bitcoin prices over the last five years. Secondly, we merged the ANNs and LSTM and incorporated gradient-specific optimization. The findings show that LSTM-Attention with gradient-specific optimization performs well in Bitcoin forecasts, making it more appropriate for Bitcoin predictions, producing results that are very similar to reality when compared with the second model.
Therefore, our findings have major implications for investors, traders, and politicians, who rely on precise forecasting to make educated decisions. Although our hybrid LSTM-Attention model with gradient-specific optimization was quite successful, it is important to realize that no model is perfect. In some situations, the model may underperform or fail to appropriately anticipate cryptocurrencies. In fact, our models have a few limitations: they do not take into consideration sentiment analysis in the Bitcoin market, and they cannot measure the intensity of sentiment from text-based sources like social media platforms, which is why there is always opportunity for development in terms of forecast accuracy, prediction error reduction, and model robustness to changing market conditions. In the future, we want to increase the accuracy of forecasts by adding more models, adjusting hyperparameters, and improving hybrid models that are already in place. We need to have better forecasting models so that they can easily be relied upon. As a result, our goals are to increase forecast accuracy, produce trustworthy outcomes, and account for changes in the market.
Author Contributions
Conceptualization, A.L.; methodology, A.L.; software, A.L.; data curation, H.B.; writing—original draft, A.L.; visualization, H.B.; supervision, H.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rachinger, M.; Rauter, R.; Müller, C.; Vorraber, W.; Schirgi, E. Digitalization and its influence on business model innovation. J. Manuf. Technol. Manag. 2018, 30, 1143–1160. [Google Scholar] [CrossRef]
- Isaac, M.; Saluja, S.; Zhao, A. Automated Bitcoin Trading via Machine Learning Algorithms. 2015. Available online: http://cs229.stanford.edu/proj2014/Isaac%20Madan,%20Shaurya%20Saluja,%20Aojia%20Zhao,Automated%20Bitcoin%20Trading%20via%20Machine%20Learning%20Algorithms.pdf (accessed on 16 April 2024).
- Jiang, X. Bitcoin price prediction based on deep learning methods. J. Math. Financ. 2019, 10, 132–139. [Google Scholar] [CrossRef]
- Sun, X.; Liu, M.; Sima, Z. A novel cryptocurrency price trend forecasting model based on LightGBM. Financ. Res. Lett. 2020, 32, 101084. [Google Scholar] [CrossRef]
- Ortu, M.; Uras, N.; Conversano, C.; Bartolucci, S.; Destefanis, G. On technical trading and social media indicators for cryptocurrency price classification through deep learning. Expert Syst. Appl. 2022, 198, 116804. [Google Scholar] [CrossRef]
- Gu, E.G. On the Price Dynamics of a Two-Dimensional Financial Market Model with Entry Levels. Complexity 2020, 2020, 3654083. [Google Scholar] [CrossRef]
- Bangroo, R.; Gupta, U.; Sah, R.; Kumar, A. Cryptocurrency Price Prediction using Machine Learning Algorithm. In Proceedings of the 2022 10th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions) (ICRITO), Noida, India, 13–14 October 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S. Cryptocurrency forecasting with deep learning chaotic neural networks. Chaos Solitons Fractals 2019, 118, 35–40. [Google Scholar] [CrossRef]
- Modi, P.D.; Arshi, K.; Kunz, P.J.; Zoubir, A.M. A Data-driven Deep Learning Approach for Bitcoin Price Forecasting. In Proceedings of the 2023 24th International Conference on Digital Signal Processing (DSP), Rhodes, Greece, 11–13 June 2023; pp. 1–4. [Google Scholar]
- Tripathi, B.; Sharma, R.K. Modeling bitcoin prices using signal processing methods, bayesian optimization, and deep neural networks. Comput. Econ. 2023, 62, 1919–1945. [Google Scholar] [CrossRef] [PubMed]
- Chen, J. Analysis of bitcoin price prediction using machine learning. J. Risk Financ. Manag. 2023, 16, 51. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, H.; Long, H. Forecasting the equity premium: Do deep neural network models work? Mod. Financ. 2023, 1, 1–11. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Minutolo, M.C. A hybrid volatility forecasting framework integrating GARCH, artificial neural network, technical analysis and principal components analysis. Expert Syst. Appl. 2018, 109, 1–11. [Google Scholar] [CrossRef]
- Nakano, M.; Takahashi, A.; Takahashi, S. Bitcoin technical trading with artificial neural network. Phys. A Stat. Mech. Appl. 2018, 510, 587–609. [Google Scholar] [CrossRef]
- Akila, V.; Nitin, M.V.S.; Prasanth, I.; Reddy, S.; Kumar, A. A Cryptocurrency Price Prediction Model using Deep Learning. E3S Web Conf. 2023, 391, 01112. [Google Scholar]
- Gurgul, V.; Lessmann, S.; Härdle, W.K. Forecasting Cryptocurrency Prices Using Deep Learning: Integrating Financial, Blockchain, and Text Data. arXiv 2023, arXiv:2311.14759. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008. Available online: https://git.dhimmel.com/bitcoin-whitepaper/ (accessed on 20 August 2020).
- Liu, M.; Li, G.; Li, J.; Zhu, X.; Yao, Y. Forecasting the price of Bitcoin using deep learning. Financ. Res. Lett. 2021, 40, 101755. [Google Scholar] [CrossRef]
- Patel, M.M.; Tanwar, S.; Gupta, R.; Kumar, N. A deep learning-based cryptocurrency price prediction scheme for financial institutions. J. Inf. Secur. Appl. 2020, 55, 102583. [Google Scholar] [CrossRef]
- Kang, C.Y.; Lee, C.P.; Lim, K.M. Cryptocurrency Price Prediction with Convolutional Neural Network and Stacked Gated Recurrent Unit. Data 2022, 7, 149. [Google Scholar] [CrossRef]
- Petrovic, A.; Strumberger, I.; Bezdan, T.; Jassim, H.S.; Nassor, S.S. Cryptocurrency price prediction by using hybrid machine learning and beetle antennae search approach. In Proceedings of the 2021 29th Telecommunications Forum (TELFOR), Belgrade, Serbia, 23–24 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–4. [Google Scholar]
- Li, Y.; Jiang, S.; Li, X.; Wang, S. Hybrid data decomposition-based deep learning for bitcoin prediction and algorithm trading. Financ. Innov. 2022, 8, 31. [Google Scholar] [CrossRef]
- Li, Y.; Dai, W. Bitcoin price forecasting method based on CNN-LSTM hybrid neural network model. J. Eng. 2020, 2020, 344–347. [Google Scholar] [CrossRef]
- Zahouani, A.L.; Boubaker, H. Forecasting Crude Oil Price with Hybrid Approaches. Rev. Econ. Financ. 2023, 21, 564–576. [Google Scholar]
- Livieris, I.E.; Kiriakidou, N.; Stavroyiannis, S.; Pintelas, P. An advanced CNN-LSTM model for cryptocurrency forecasting. Electronics 2021, 10, 287. [Google Scholar] [CrossRef]
- Hong, Y.; Hou, B.; Jiang, H.; Zhang, J. Machine learning and artificial neural network accelerated computational discoveries in materials science. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020, 10, e1450. [Google Scholar] [CrossRef]
- Li, X.; Li, M.; Yan, P.; Li, G.; Jiang, Y.; Luo, H.; Yin, S. Deep learning attention mechanism in medical image analysis: Basics and beyonds. Int. J. Netw. Dyn. Intell. 2023, 2, 93–116. [Google Scholar] [CrossRef]
- Yazhini, V.; Nimal Madhu, M.; Premjith, B.; Gopalakrishnan, E.A. Deep Learning with Attention Mechanism for Cryptocurrency Price Forecasting. In Proceedings of the International Conference on Information, Communication and Computing Technology, New Delhi, India, 27 May 2023; Springer Nature: Singapore, 2023; pp. 471–484. [Google Scholar]
- Elsayed, S.; Thyssens, D.; Rashed, A.; Jomaa, H.S.; Schmidt-Thieme, L. Do we really need deep learning models for time series forecasting? arXiv 2021, arXiv:2101.02118. [Google Scholar]
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. In Business Cycles: Durations, Dynamics, and Forecasting; Princeton University Press: Princeton, NJ, USA, 1999; 387p. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).