1. Introduction
The Gutenberg–Richter law [
1] represents the building block of modern seismology, widely adopted by seismologists to describe the relationship between the magnitude and frequency of seismic events [
2]. The formulation of this law reads:
where
is the number of events of magnitude greater than the threshold
, and
and
(usually called “b-value”) are the two parameters that characterize the magnitude–frequency relation. The b-value regulates the frequency of smaller earthquakes relative to larger ones: the larger the b-value, the higher the frequency of smaller events.
Numerous studies demonstrate that the b-value relates to the differential stress of Earth’s crust: highly stressed zones, or faults, usually exhibit low b-values, whereas weakly stressed areas usually exhibit higher b-values [
3,
4,
5].
In a recent study, Gulia et al. [
6] show that during aftershock sequences the b-value measured nearby the mainshock’s fault tends to increase with respect to its “background” value. This increase occurring during aftershock sequences is a direct consequence of the decrease of the differential stress in the fault due to the mainshock; a similar increase in b-value is observed near patches that experienced the largest slip after the Tohoku 2011 earthquake [
4].
Nevertheless, a decrease in b-value on the mainshock’s fault can indicate that the strongest event of the sequence has not yet occurred, and thus this information could be useful to forecast future stronger earthquakes [
7].
For these reasons, analyzing the time series of the b-value can be a powerful tool to enhance seismologists’ forecasting capability.
Statistical methods that estimate this value rely on the probabilistic representation of the Gutenberg–Richter law, which interpret the b-value as the rate parameter of an exponential distribution [
8]. Currently, the widespread approach to estimate the b-value considers a fixed number of events, commonly in the range of 50 to 400 events [
7,
9]. However, since the earthquake rate can change very rapidly during a seismic sequence (and in general in any seismic catalogue), using a fixed number of events generally leads to time windows of unequal length. This unequal length leads to a difficult interpretation of the b-value time series. During a period of high seismic activity, e.g., the beginning of an aftershock sequence, more than 100 events can happen in few hours, while in a period of low seismic activity, e.g., the end of an aftershock sequence, a similar number of events can take up to a year to realize.
This paper introduces a robust statistical framework to compute the temporal variation of the b-value, avoiding the subjective choice of the number of events to use in the estimation. In addition, this framework allows proper consideration of the natural variability of the seismic rate. We adopt the weighted likelihood approach [
10,
11], previously used to compute the spatial variation of b-value [
12], to estimate the time variation of the parameter, along with the associated uncertainty. We test our model both on an Italian high-resolution catalogue of natural seismicity [
13], and on a global catalogue [
14,
15], and we evaluate the estimation accuracy against the classical fixed-number estimation approach.
2. Methods
Aki [
8] and Utsu [
16] show that the Gutenberg–Richter law corresponds to an exponential distribution, and the b-value can be estimated by the maximum likelihood (ML) approach as follows:
where
,
and
are the mean magnitude of events in the catalogue, the completeness magnitude, and the binning of the magnitude, respectively.
To capture the possible time-varying dynamic of the b-value, we propose to employ the weighted likelihood (WL) method of Hu and Zidek [
10]:
where
is the weighted log-likelihood,
is the probability density function (pdf) of an exponential distribution with rate parameter
,
, and
is the weight associated with the
i-th event with a magnitude
in the catalogue. Taroni et al. [
17] show that Equation (3) can be generalized to accommodate weights as follows:
The standard deviation of
also depends on the weights:
However, while Taroni et al. [
17] investigate the spatial variation of the b-value (e.g., across locations), here we place our focus on its variation over time. We devise a weighting scheme that depends on the time lag between the
i-th event, and the first event reported in the catalogue (
), ensuring
. Specifically, we consider the following exponential kernel:
with
being the forgetting parameter and
being a normalizing constant to ensure
. The parameter
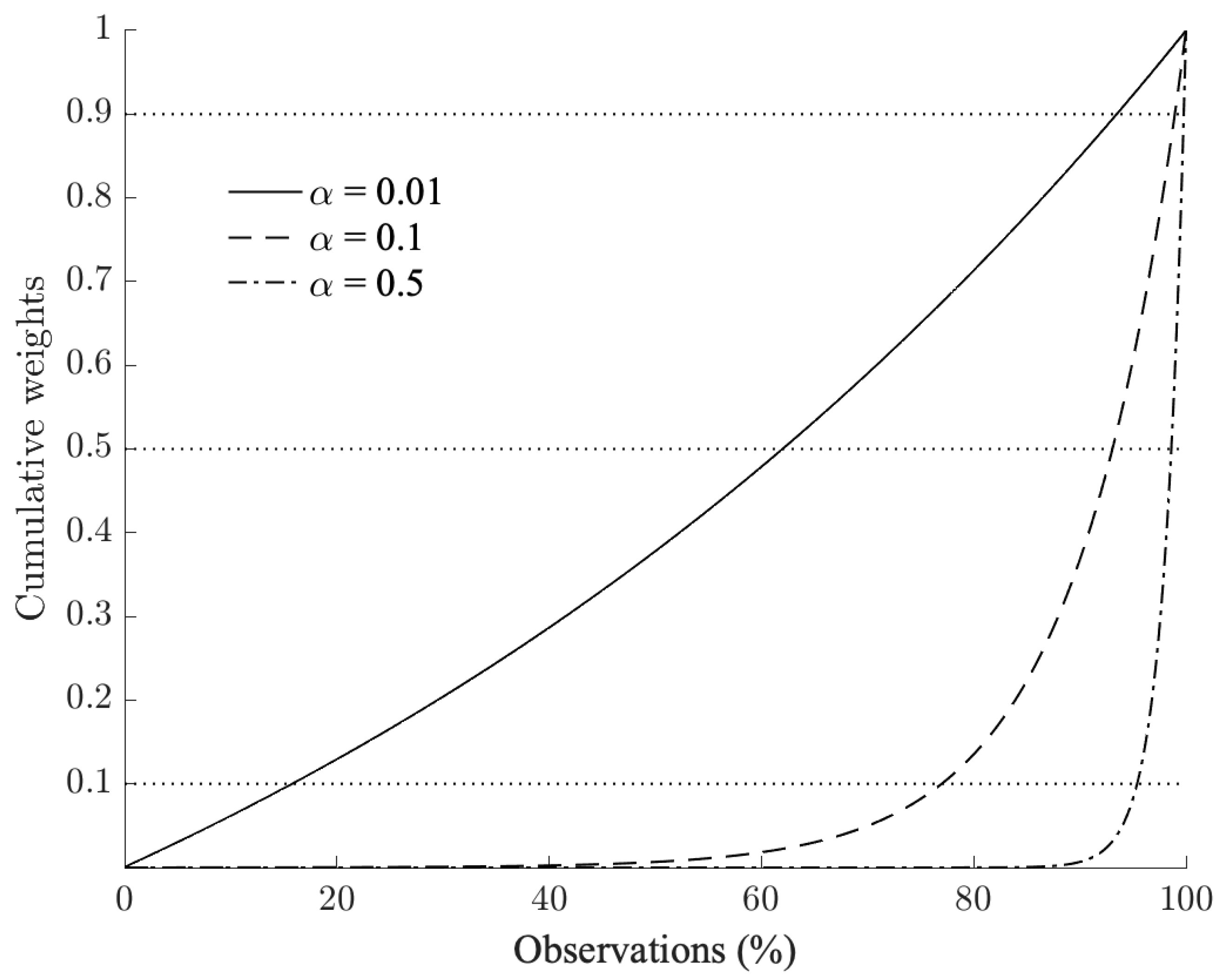
gauges the amount of past information that is relevant to estimate the weights. This forgetting factor regulates the steepness of the rate at which past information is discounted. To provide an intuition for this, in
Figure 1 we report the cumulative weights associated with different forgetting factors. As
increases, the relative weights associated with information far in the past decrease, suggesting that only recent events bear the relevant signal. For a forgetting factor of 0.01, almost 85% of past observations receive a cumulative weight greater than 0.1, while this reduces to only about 7% for
.
At this point, we can rewrite Equation (4) as:
The forgetting factor is estimated using a grid-search approach. That is, we generate a grid of plausible values for , i.e., = [, …,], with and , and we evaluate the log-likelihood of the model for each value. The optimal is found in the correspondence of the maximum of the log-likelihood function. We outlined that the value of also depends on the unit of measurement chosen for the time and on the total number of events in the catalogue.
Current methods rely on using a fixed number of the most recent observations to capture the evolution over time of the b-value, the so-called rolling window estimation. This approach, despite proving useful in several other disciplines, e.g., finance and economics [
18], imposes an equal weight on every observation in the estimation sample, which directly depends on the choice of the number of observations used. Thus, the validity of these results heavily hinges upon researchers’ inputs.
In contrast, the WL methodology posits a weighting scheme that assigns a weight to each available observation, and optimally sets the rate at which past information is discounted. Furthermore, the WL estimator accounts for unequally spaced observation, allowing events that occurred after long periods of quiet to receive higher weights.
We compare the performance between the WL approach and the rolling window estimation, considering several window sizes, through a pseudoprospective test. That is, we divide the catalogue into two subsamples of equal size, and we use the first to estimate the forgetting parameter
. In the second subsample, we use the weighting scheme obtained from the training sample to estimate the b-value. We compare this approach to several rolling window specifications by means of the Bayes Factor (BF), computed as the ratio of the predictive densities [
19]. These are calculated as the likelihood function (
) of each observation in the second subsample, where the b-value is estimated by optimally weighting all the preceding; similarly, for the rolling window approach, the log-likelihood function is computed using the b-value estimated on a fixed number of previous observations. Hence:
where
represents the set of magnitudes in the catalogue as in Equation (3),
and
are the b-values estimated with the weighted likelihood and rolling window methods, respectively. A BF > 1 provides statistical evidence in favor of the WL approach, while BF < 1 would suggest otherwise; Kass and Raftery [
20] propose a threshold approach to determine the strength of the evidence in favor of either statistical model.
3. Data
We applied our methodology to two different catalogues. The first one is a high-definition seismic catalogue concerning the central area of Italy (TABOO catalogue, Valoroso et al. 2017) [
13]; the catalogue contains natural seismicity observations for about 4.5 years, from 2010 to 2014. This dataset is particularly suitable to study the time variation of the b-value as the available events were small in magnitude, being the maximum magnitude of ML 3.81. In fact, strong events (e.g., earthquake with magnitude higher than 5.5) might lead to incompleteness problems in the first days of the associated aftershock sequences [
21,
22], and thus induce bias in the estimation of the b-value [
12,
23]. The completeness magnitude of the catalogue we used is ML 0.5 [
13], with 6453 events above the completeness threshold, as illustrated in
Figure 2a. Following Marzocchi et al. [
12], we verified the reliability of the completeness by testing the exponentiality of the magnitudes through a Lilliefors test [
24]. A completeness of 0.5 is strongly supported by the data, with a
p-value of 0.26.
The second catalogue we used is the global Centroid Moment Tensor catalogue (CMT, [
14,
15]). This catalogue contains worldwide events of stronger magnitude, from 1980 to 2019. We selected earthquakes with a minimum magnitude of Mw 5.5 [
3], and a maximum depth of 50 km, in the Tonga trench zone, one of the most active seismic areas in the world. We refrained from using the whole global catalogue to focus on temporal variations of the b-value in a particular region. As for the previous case, we verified the reliability of the completeness by testing the exponentiality of the magnitudes. The completeness of 5.5 is strongly supported by the data, with a
p-value of 0.17. This catalogue contains 1007 events above the completeness threshold, as illustrated in
Figure 2b. The high level of completeness, Mw 5.5, allowed us to evaluate our method with data robust to the incompleteness problems in the first days of the aftershock sequences (usually related to smaller events, i.e., <Mw 5.0).
4. Results
We initially applied our method to the TABOO catalogue. We used the first subset of the catalogue, containing the first half of the data, as a training sample, estimating a forgetting factor
(see
Figure 3a). We then used the testing sample, the second subsample, to forecast the evolution over time of the b-value, and to compare the forecasting performances against the rolling window method. As the number of events used for rolling window estimations ranged between 50 and 400, we used six different values to cover this range (50, 75, 100, 150, 200, 400). To assess the performances of the models, we computed the Bayes Factor as described in Equation (8), using the Bayes Factor thresholds of Kass and Raftery [
20], for which “strong evidence” is associated to
. Results are summarized in
Table 1. Four out of the six rolling windows we considered were significantly outperformed by the WL method, and in only one case the Bayes Factor provided weak evidence in favor of the competing benchmark.
In a similar fashion, we applied the WL method to the CMT catalogue, obtaining a forgetting factor
(see
Figure 3b). Again, the WL method delivered good performances, achieving a “strong evidence” for two out of the six rolling windows (see
Table 1).
5. Discussion
The results reported in
Table 1 highlight that the forecasting ability of the WL approach significantly and consistently outperforms classical, widespread methods by optimally choosing the amount of relevant information for estimating the b-value. In
Figure 4 and
Figure 5 we illustrate how different estimation methods give rise to different time series of b-values. For both the 100 events (upper panels) and the 200 events (lower panels) case, the relative time series present higher volatility with respect to the one generated by the weighted likelihood estimation. Based on these results, it is possible to suspect that a large share of the variation visible in the rolling window time series is attributable to the natural statistical fluctuations of the b-value. Therefore, the weighted likelihood estimation represents a robust estimation method, able to filter out the non-physical fluctuations of the signal.
To further validate our methodology, we also compared the weighted likelihood approach with the novel MUST-B estimator introduced by García-Hernández et al. [
25]. This estimator avoids subjective biases in the choice of the window size by taking the median values of different b-values estimated using rolling windows of different lengths. This method was successfully applied to the 2016–2017 central Italy seismic sequence; in our exercise, we retained the parameters’ values described in García-Hernández et al. [
25]. Bayes Factor values suggest that our methodology performed better than MUST-B, for both the TABOO (
), and the CMT (
) catalogues, respectively. It is, however, worth noting that tuning of the MUST-B approach refers to a single, different seismic sequence compared to the TABOO and CMT catalogues. A deeper investigation of the comparison between the WL and MUST-B is beyond the scope of this paper, and is left for future research avenues.
The TABOO catalogue that we used in our forecast exercise features a stable and time-independent magnitude of completeness of 0.5, with a maximum magnitude of 3.8.
The CMT catalogue, given its high threshold of completeness, Mw 5.5, is probably not affected by the incompleteness problems. For instrumental catalogues that contain strong events (i.e., events with a magnitude larger than 5.5) and with a relatively low magnitude of completeness (e.g., lower than 3.5), a proper estimation of such completeness is of paramount importance, in particular during aftershock sequences, and it strongly influences the b-value estimation [
23].
A future improvement of the WL method could be the inclusion of temporal variations of the magnitude of completeness, using the b-value estimation approach of Taroni [
26].