Photovoltaic Output Power Estimation and Baseline Prediction Approach for a Residential Distribution Network with Behind-the-Meter Systems
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Literature Review
- The net load is decoupled from PV output power and actual load precisely;
- To correct the deviation of the matched net load data, the relationship between PV output power and the solar irradiance, and the relationship between actual load and the temperature, are discovered and further formulated;
- The CBL is predicted based on the PV-load decoupling.
2. Problem Formulation
2.1. PV Output Decoupling
2.2. CBL Prediction
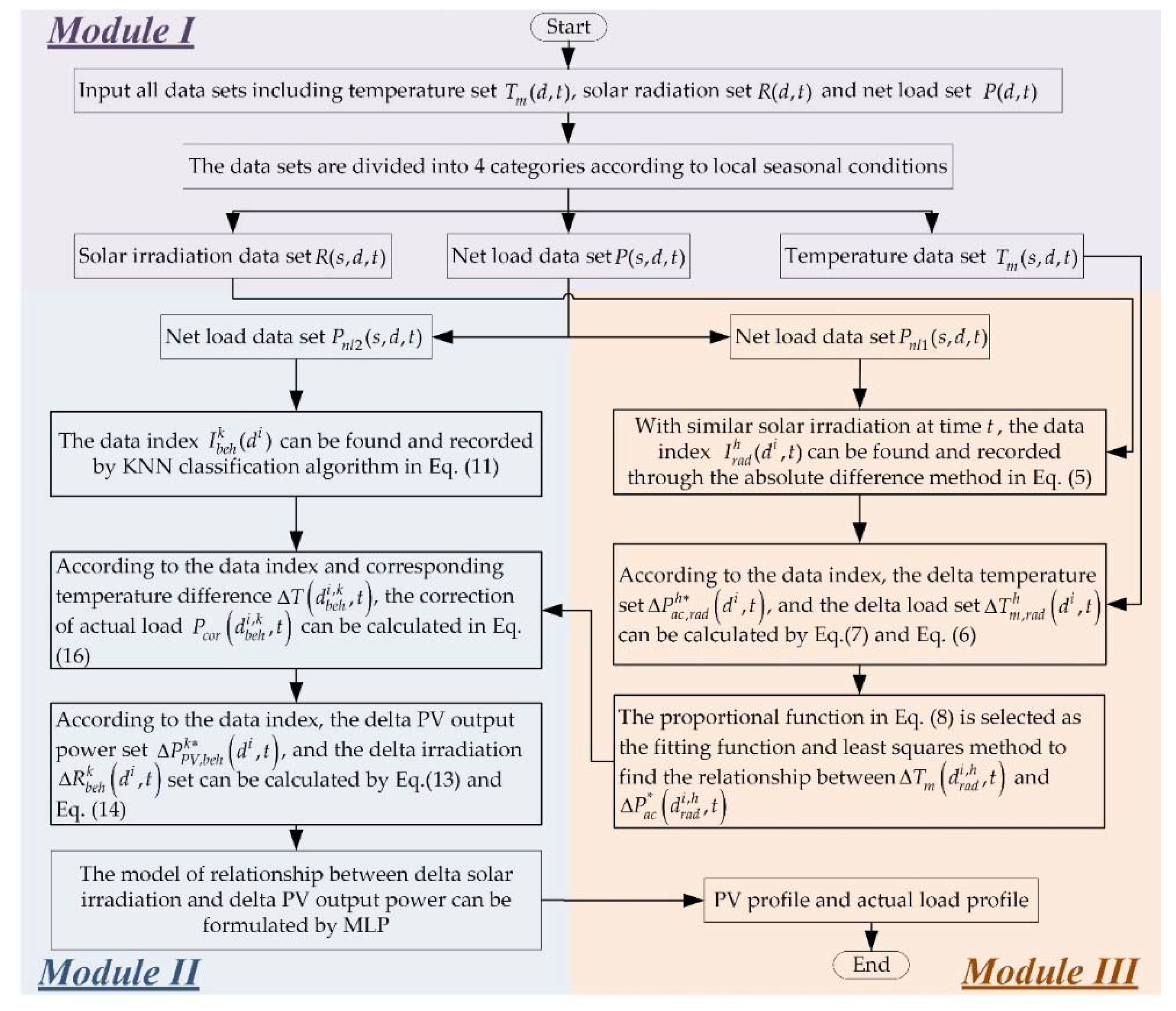
3. Methods
3.1. Data Set Division
3.2. Load Consumption Sensitivity Analysis
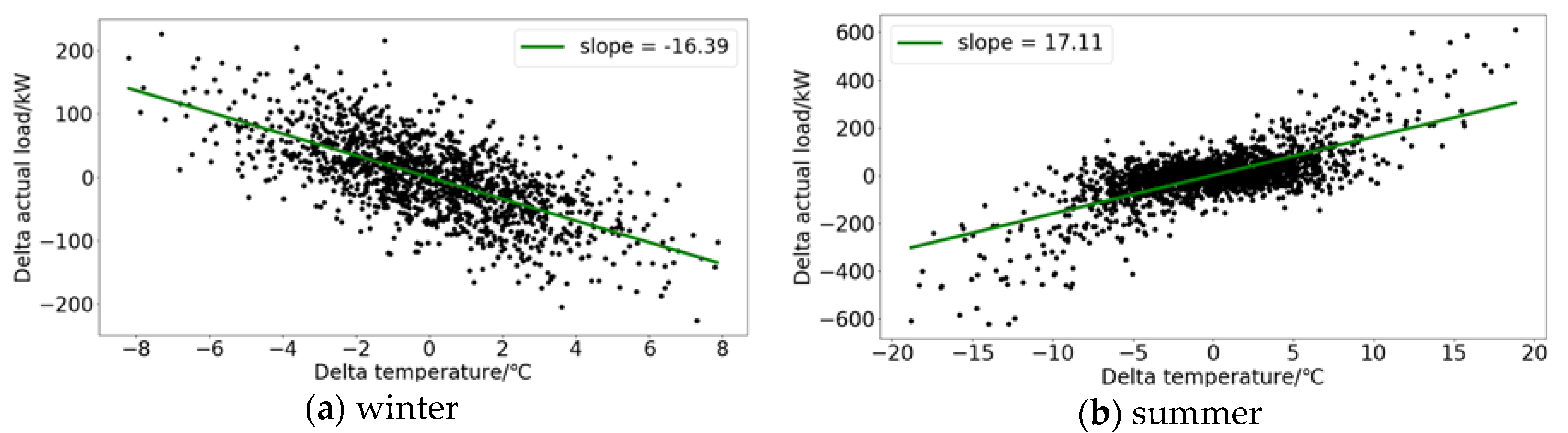
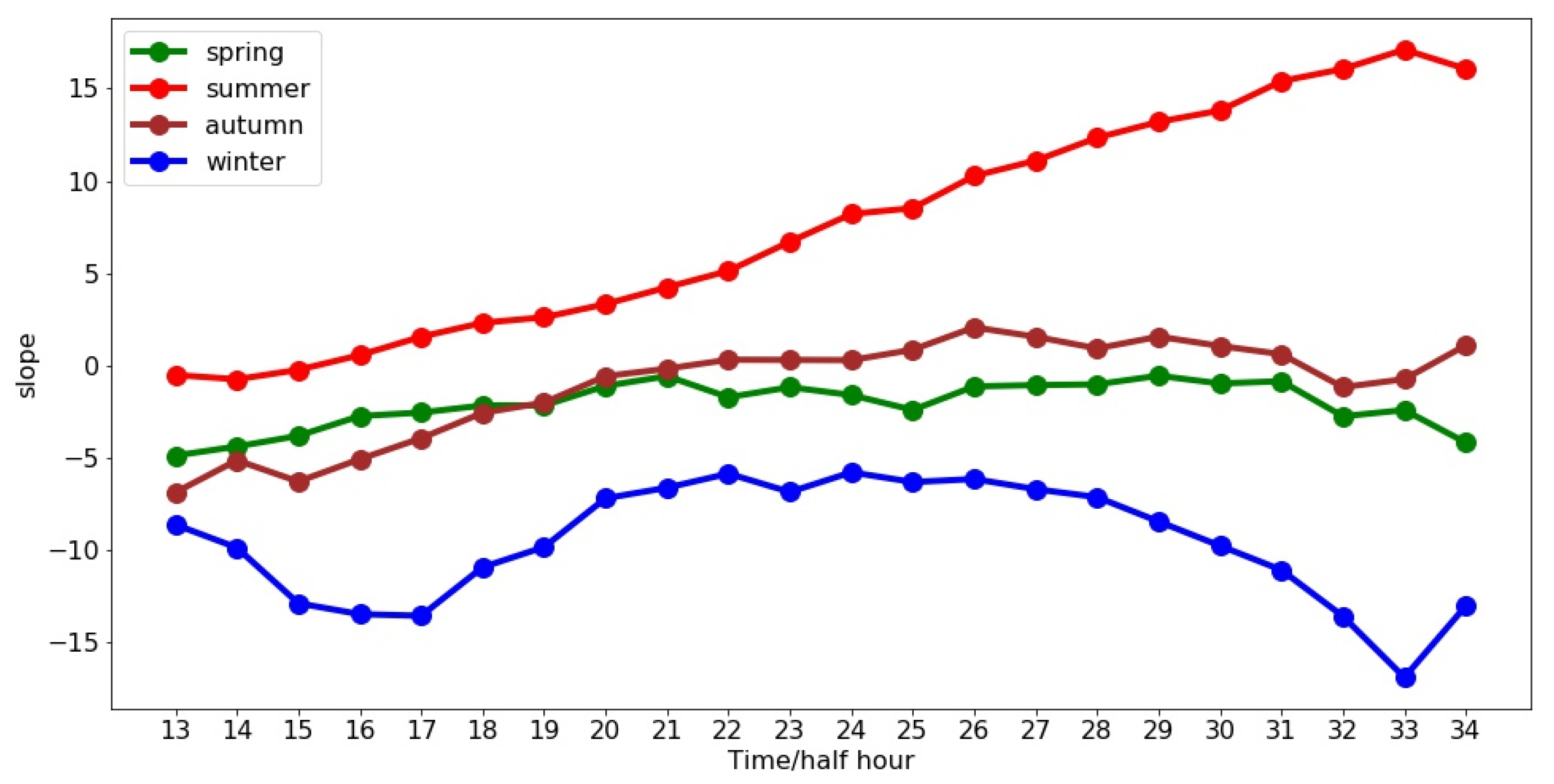
3.2.1. Correlation between Electricity Consumption and Temperature
3.2.2. Electricity Consumption Sensitivity Model
3.3. PV Output Power Sensitivity Analysis
3.3.1. PV Output Power Sensitivity Model
3.3.2. PV Output Power Sensitivity Model Based on Electricity Consumption Sensitivity Correction
3.3.3. Evaluation Index of the PV Output Power Estimation
3.4. CBL Prediction Model Construction
3.4.1. Direct Prediction Method
3.4.2. Prediction Method Based on PV Output Separation
3.4.3. Evaluation Index of CBL Prediction
4. Case Study
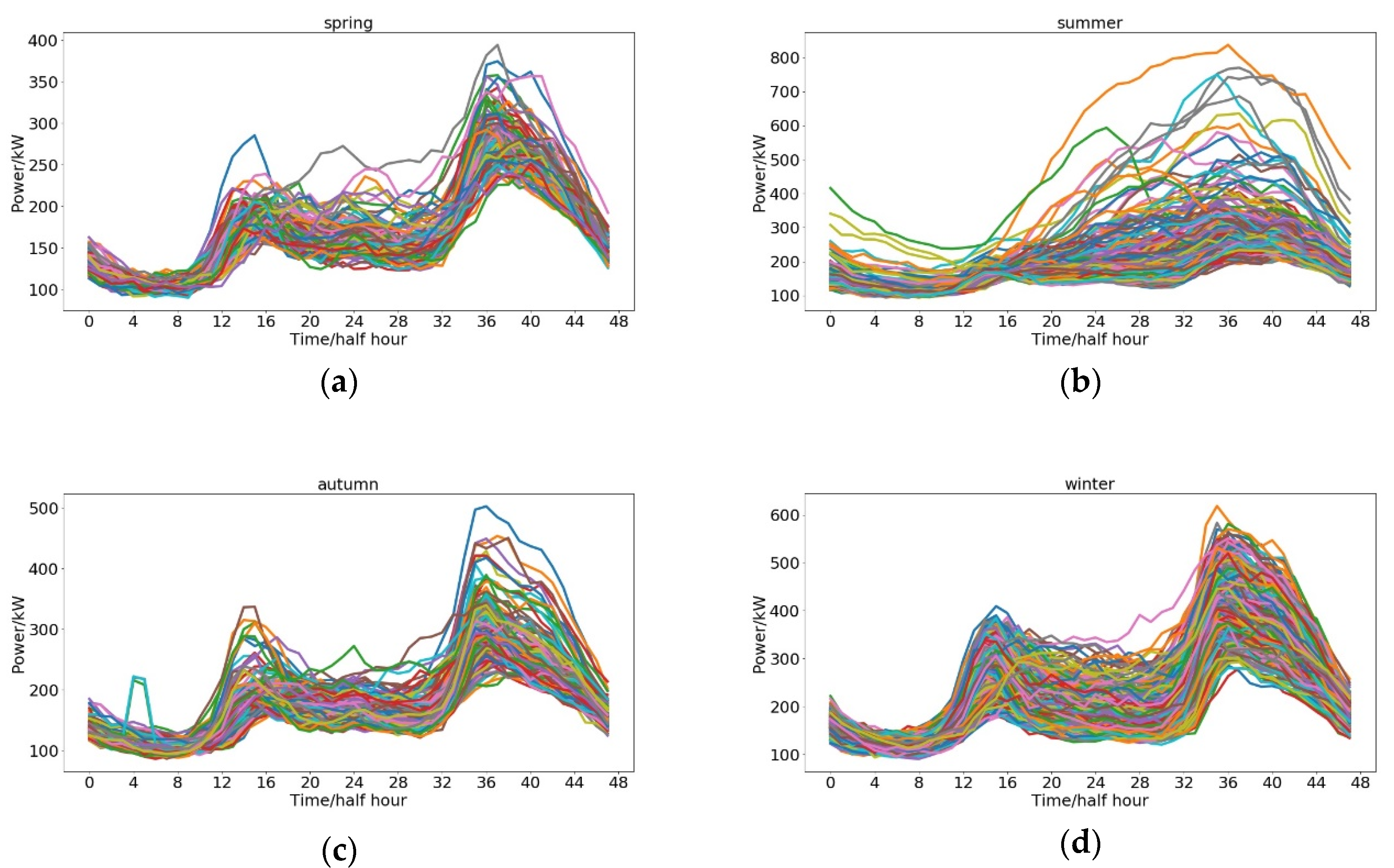
4.1. Experimental Data Set and Platform Description
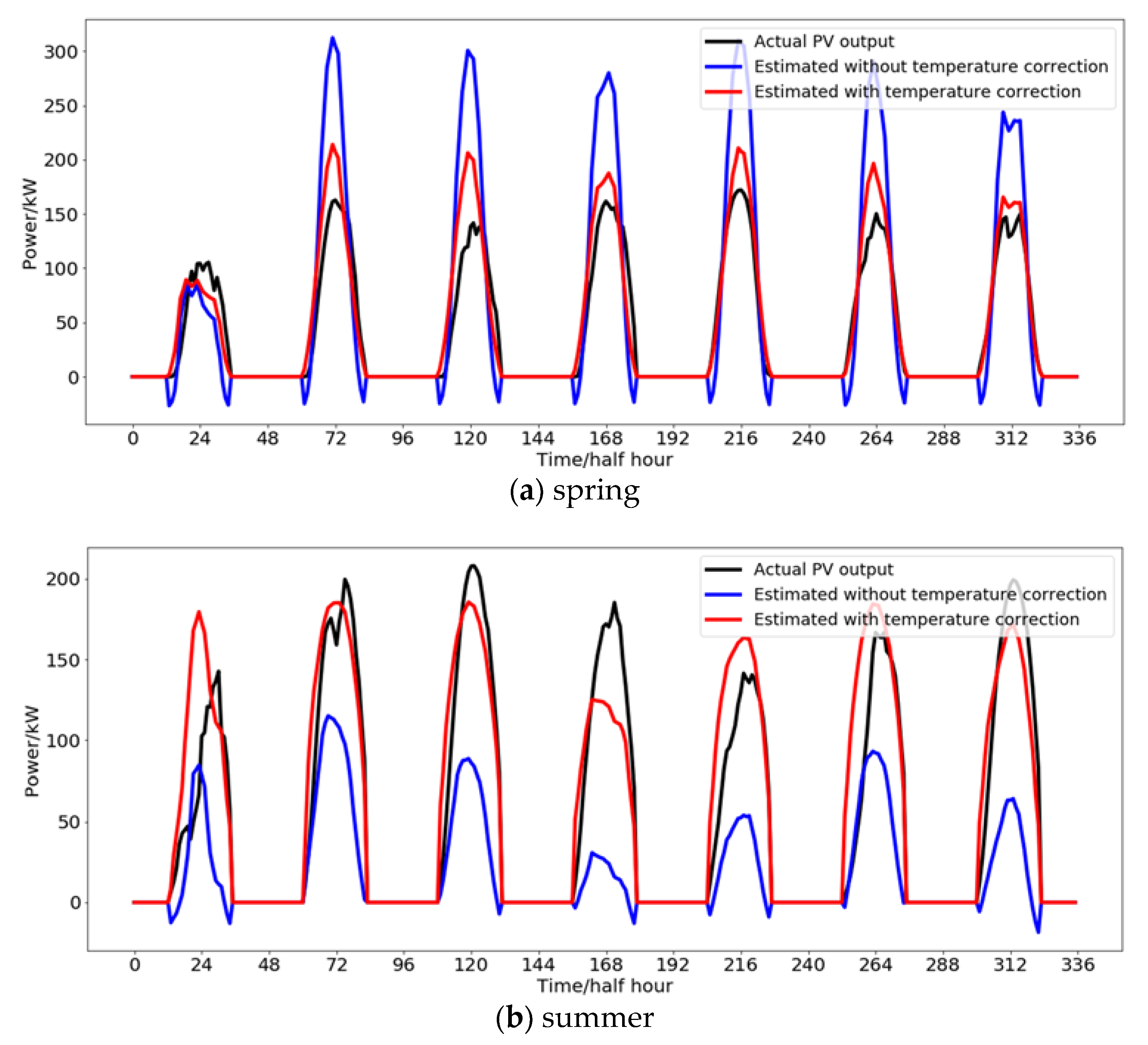
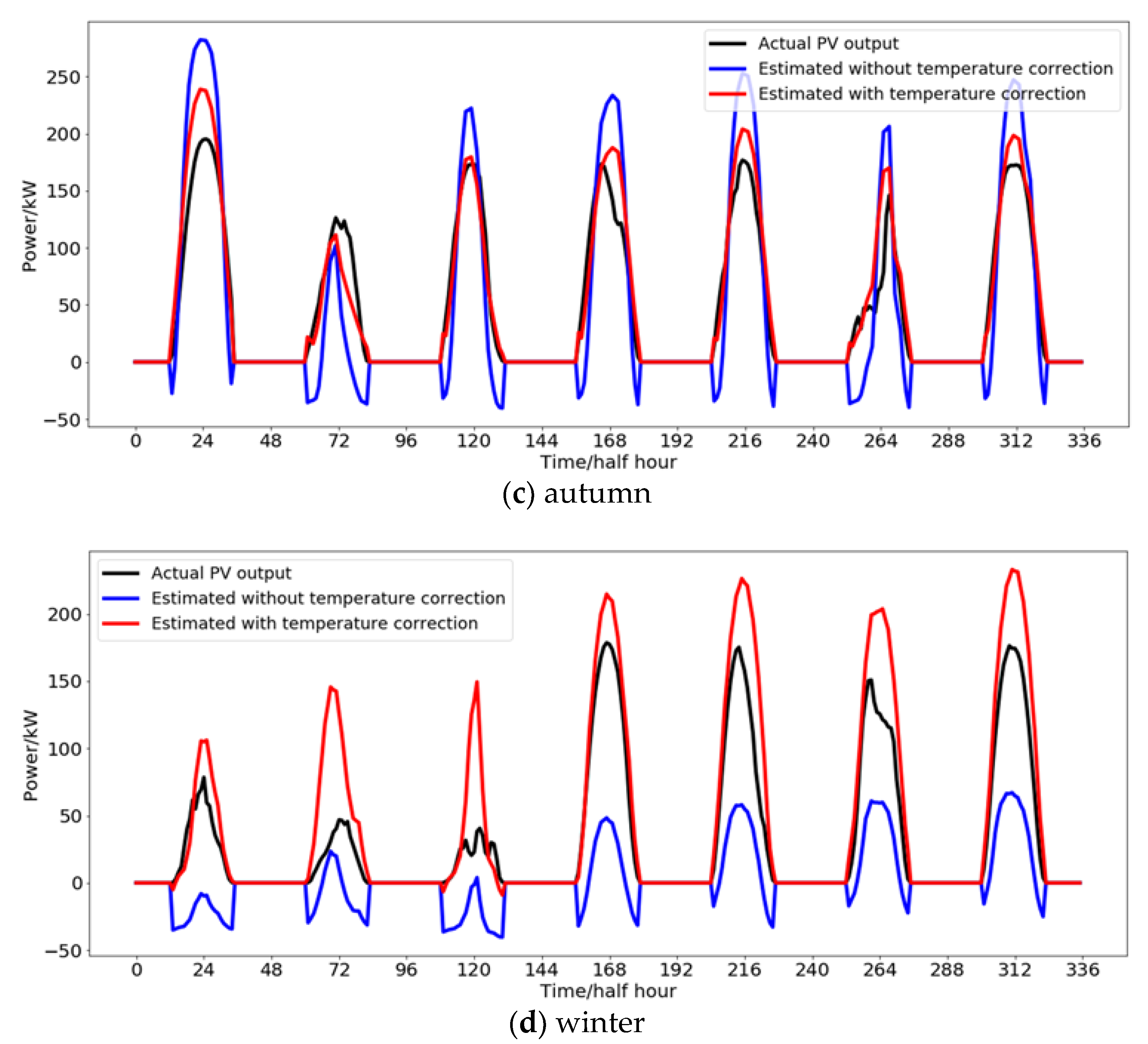
4.2. PV Output Power Curve Separation
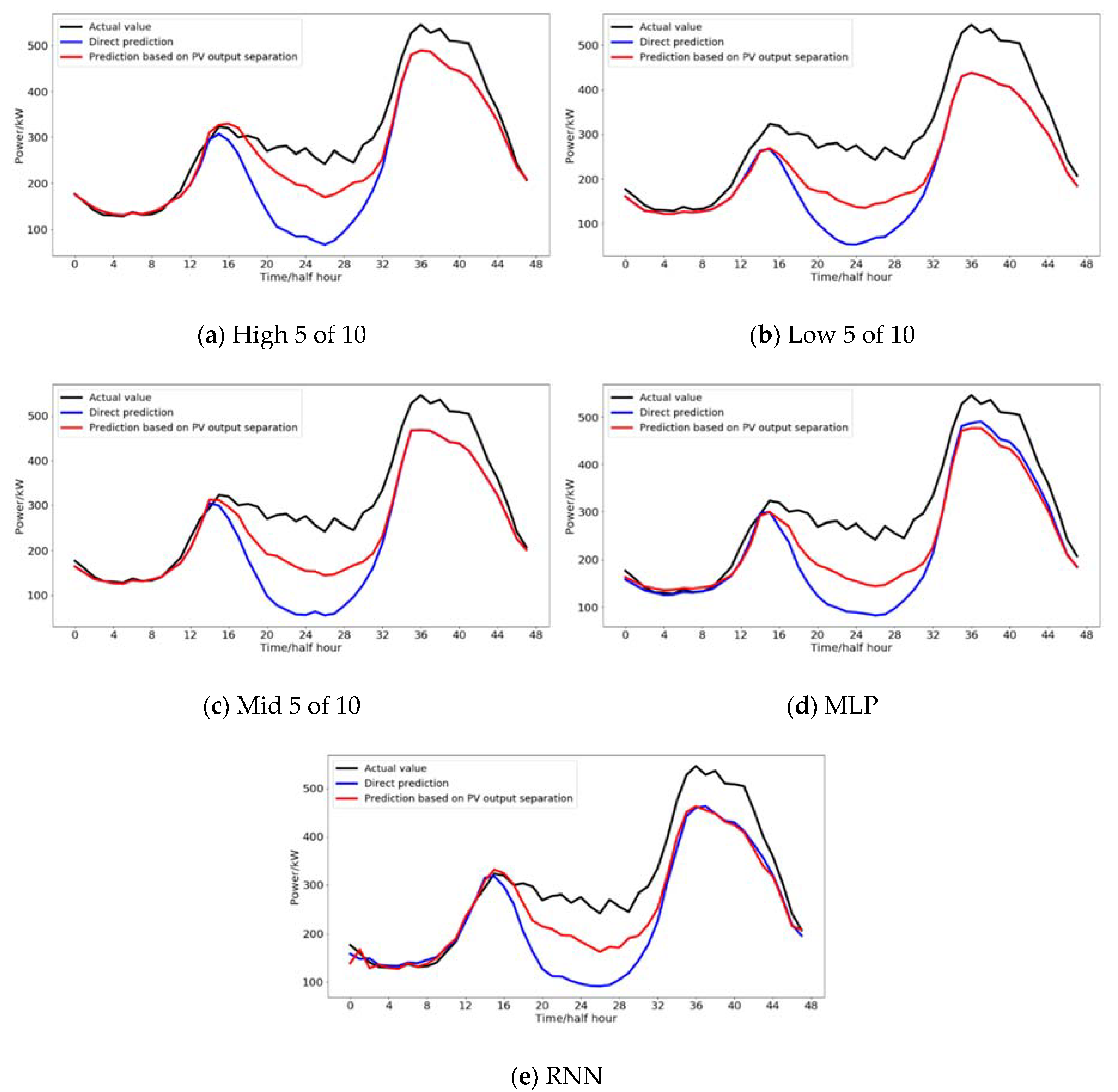
4.3. Results and Analysis of CBL Prediction
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |||
| BESS | Battery energy storage system | MLP | Multilayer perceptron |
| BL | Baseline | PV | Photovoltaic |
| BTM | Behind-the-meter | RAE | Relative absolute error |
| CBL | Customer baseline | ReLU | Rectified linear unit |
| DR | Demand response | RER | Relative error ratio |
| KNN | K nearest neighbor | RNN | Recurrent neural network |
| MAE | Mean absolute error | SCADA | Supervisory control and data acquisition |
| MAPE | Mean absolute percentage error | ||
| Variables | |||
| of day | Number of days in a season | ||
| of season | Aggregated actual load | ||
| of time | Average actual load | ||
| of time day | CBL prediction of actual load | ||
| of time day season | Actual load during the time period with solar irradiation | ||
| Approximate actual load difference | Correction of actual load difference | ||
| Set of approximate delta actual load according to the date match | Estimated value of the PV output power | ||
| Approximate PV output power difference | Aggregated net load | ||
| Correction of approximate PV output power difference | CBL prediction of net load | ||
| Set of approximate delta PV output according to the date match | Aggregated net load data during the time period with solar irradiation | ||
| Difference values between the solar irradiation of two days | Aggregated net load data during the time period without solar irradiation | ||
| Set of delta solar irradiation according to the date match | Aggregated PV output power | ||
| Set of solar irradiance difference between two days with similar solar irradiance | Estimated PV output power for CBL prediction | ||
| Temperature difference between two days | Real value of the PV output power | ||
| Set of delta temperature according to the date match | Pearson’s correlation coefficient | ||
| Euclidean distance | Solar irradiation | ||
| Time period with solar irradiation | Equivalent solar irradiation amplitude | ||
| Time period without solar irradiation | Daily relative absolute error of PV output power estimation | ||
| day | Label of season | ||
| Set of day record | Time | ||
| Recording set of the date of electricity consumption behavior similarity match | Time of sunrise | ||
| Recording set of the date of solar irradiation similarity match | Time of sunset | ||
| Number of the neighbors of KNN | Set of timestamp | ||
| Slope calculated by least squares method between delta temperature and delta actual load | Average temperature | ||
| MAE of the PV output power estimation | |||
References
- Wang, D.; Wu, R.; Li, X.; Lai, C.S.; Wu, X.; Wei, J.; Xu, Y.; Wu, W.; Lai, L.L. Two-stage optimal scheduling of air conditioning resources with high photovoltaic penetrations. J. Clean. Prod. 2019, 241, 118407. [Google Scholar] [CrossRef]
- Lai, C.S.; McCulloch, M.D. Levelized cost of electricity for solar photovoltaic and electrical energy storage. Appl. Energy 2017, 190, 191–203. [Google Scholar] [CrossRef]
- Zhao, Z.; Cheng, R.; Yan, B.; Zhang, J.; Zhang, Z.; Zhang, M.; Lai, L.L. A dynamic particles MPPT method for photovoltaic systems under partial shading conditions. Energy Convers. Manag. 2020, 220, 113070. [Google Scholar] [CrossRef]
- Renewables 2020 Global Status Report–REN21. Available online: https://www.ren21.net/gsr-2020/chapters/chapter_01/chapter_01/ (accessed on 15 August 2020).
- Lai, C.S.; Jia, Y.; Lai, L.L.; Xu, Z.; McCulloch, M.D.; Wong, K.P. A comprehensive review on large-scale photovoltaic system with applications of electrical energy storage. Renew. Sust. Energ. Rev. 2017, 78, 439–451. [Google Scholar] [CrossRef]
- Hou, Q.; Du, E.; Zhang, N.; Kang, C. Impact of high renewable penetration on the power system operation mode: A data-driven approach. IEEE Trans. Power Syst. 2020, 35, 731–741. [Google Scholar] [CrossRef]
- Xu, X.; Li, J.; Xu, Y.; Xu, Z.; Lai, C.S. A two-stage game-theoretic method for residential PV panels planning considering energy sharing mechanism. IEEE Trans. Power Syst. 2020, 35, 3562–3573. [Google Scholar] [CrossRef]
- Xu, X.; Jia, Y.; Xu, Y.; Xu, Z.; Chai, S.; Lai, C.S. A multi-agent reinforcement learning based data-driven method for home energy management. IEEE Trans Smart Grid. 2020, 11, 3201–3211. [Google Scholar] [CrossRef]
- Xu, X.; Li, J.; Xu, Z.; Zhao, J.; Lai, C.S. Enhancing photovoltaic hosting capacity-A stochastic approach to optimal planning of static var compensator devices in distribution networks. Appl. Energy 2019, 238, 952–962. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Xu, F.Y.; Cun, X.; Yan, M.; Yuan, H.; Wang, Y.; Lai, L.L. Power market load forecasting on neural network with beneficial correlated regularization. IEEE Trans. Industr. Inform. 2018, 14, 5050–5059. [Google Scholar] [CrossRef]
- Lai, C.S.; Mo, Z.; Wang, T.; Yuan, H.; Ng, W.W.Y.; Lai, L.L. Load forecasting based on deep neural network and historical data augmentation. IET Gener. Transm. Distrib. 2020. [Google Scholar] [CrossRef]
- Lai, C.S.; Locatelli, G.; Pimm, A.; Tao, Y.; Li, X.; Lai, L.L. A financial model for lithium-ion storage in a photovoltaic and biogas energy system. Appl. Energy 2019, 251, 113179. [Google Scholar] [CrossRef]
- Lai, C.S.; McCulloch, M.D. Sizing of stand-alone solar PV and storage system with anaerobic digestion biogas power plants. IEEE Trans. Ind. Electron. 2017, 64, 2112–2121. [Google Scholar] [CrossRef]
- Wu, X.; Lai, C.S.; Bai, C.C.; Lai, L.L.; Zhang, Q.; Liu, B. Optimal kernel ELM and variational mode decomposition for probabilistic PV power prediction. Energies 2020, 13, 3592. [Google Scholar] [CrossRef]
- Lai, C.S.; Jia, Y.; McCulloch, M.D.; Xu, Z. Daily clearness index profiles cluster analysis for photovoltaic system. IEEE Trans. Industr. Inform. 2017, 13, 2322–2332. [Google Scholar] [CrossRef]
- Siano, P. Demand response and smart grids—A survey. Renew. Sust. Energ. Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Shariatzadeh, F.; Mandal, P.; Srivastava, A.K. Demand response for sustainable energy systems: A review, application and implementation strategy. Renew. Sust. Energ. Rev. 2015, 45, 343–350. [Google Scholar] [CrossRef]
- Xu, F.Y.; Zhang, T.; Lai, L.L.; Zhou, H. Shifting boundary for price-based residential demand response and applications. Appl. Energy 2015, 146, 353–370. [Google Scholar] [CrossRef]
- Xu, F.; Huang, B.; Cun, X.; Wang, F.; Yuan, H.; Lai, L.L.; Vaccaro, A. Classifier economics of Semi-Intrusive Load Monitoring. Int. J. Electr. Power Energy Syst. 2018, 103, 224–232. [Google Scholar] [CrossRef]
- Wang, D.; Qiu, J.; Reedman, L.; Meng, K.; Lai, L.L. Two stage energy management for networked microgrids with high renewable penetrations. Appl. Energy 2018, 226, 39–48. [Google Scholar] [CrossRef]
- Zheng, J.; Lai, C.S.; Yuan, H.; Dong, Z.Y.; Meng, K.; Lai, L.L. Electricity plan recommender system with electrical instruction-based recovery. Energy 2020, 203, 117775. [Google Scholar] [CrossRef]
- Li, K.; Wang, F.; Mi, Z.; Fotuhi-Firuzabad, M.; Duić, N.; Wang, T. Capacity and output power estimation approach of individual behind-the-meter distributed photovoltaic system for demand response baseline estimation. Appl. Energy 2019, 253, 113595. [Google Scholar] [CrossRef]
- Wang, F.; Li, K.; Wang, X.; Jiang, L.; Ren, J.; Mi, Z.; Shafie-khah, M.; Catalão, J.P.S. A distributed PV system capacity estimation approach based on support vector machine with customer net load curve features. Energies 2018, 11, 1750. [Google Scholar] [CrossRef]
- Jazaeri, J.; Alpcan, T.; Gordon, R.; Brandao, M.; Hoban, T.; Seeling, C. Baseline methodologies for small scale residential demand response. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies Asia (ISGT-Asia), Melbourne, Australia, 28 November–1 December 2016. [Google Scholar]
- Zhang, X.; Grijalva, S. A data-driven approach for detection and estimation of residential PV installations. IEEE Trans. Smart Grid. 2016, 7, 2477–2485. [Google Scholar] [CrossRef]
- Shaker, H.; Manfre, D.; Zareipour, H. Forecasting the aggregated output of a large fleet of small behind-the-meter solar photovoltaic sites. Renew. Energy 2020, 147, 1861–1869. [Google Scholar] [CrossRef]
- Landelius, T.; Andersson, S.; Abrahamsson, R. Modelling and forecasting PV production in the absence of behind-the-meter measurements. Prog. Photovolt. Res. Appl. 2019, 27, 990–998. [Google Scholar] [CrossRef]
- Tazvinga, H.; Xia, X.; Zhang, J. Minimum cost solution of photovoltaic–diesel–battery hybrid power systems for remote consumers. Sol. Energy 2013, 96, 292–299. [Google Scholar] [CrossRef]
- Wu, K.; Zhou, H. A multi-agent-based energy-coordination control system for grid-connected large-scale wind-photovoltaic energy storage power-generation units. Sol. Energy 2014, 107, 245–259. [Google Scholar] [CrossRef]
- Kabir, F.; Yu, N.; Yao, W.; Yang, R.; Zhang, Y. Estimation of behind-the-meter solar generation by integrating physical with statistical models. In Proceedings of the 2019 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Beijing, China, 21–23 October 2019. [Google Scholar]
- Shaker, H.; Zareipour, H.; Wood, D. A data-driven approach for estimating the power generation of invisible solar sites. IEEE Trans. Smart Grid. 2016, 7, 2466–2476. [Google Scholar] [CrossRef]
- Cheung, C.M.; Zhong, W.; Xiong, C.; Srivastava, A.; Kannan, R.; Prasanna, V.K. Behind-the-meter solar generation disaggregation using consumer mixture models. In Proceedings of the 2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aalborg, Denmark, 29–31 October 2018. [Google Scholar]
- Cheung, C.M.; Kuppannagari, S.R.; Kannan, R.; Prasanna, V.K. Disaggregation of behind-the-meter solar generation in presence of energy storage resources. In Proceedings of the 2020 IEEE Conference on Technologies for Sustainability (SusTech), Santa Ana, CA, USA, 23–25 April 2020. [Google Scholar]
- Qiu, Y.; Kahn, M.E.; Xing, B. Quantifying the rebound effects of residential solar panel adoption. J. Environ. Econ. Manag. 2019, 96, 310–341. [Google Scholar] [CrossRef]
- Pouraltafi-kheljan, S.; Göl, M. Power generation nowcasting of the behind-the-meter photovoltaic systems. arXiv 2020, arXiv:2001.02157. [Google Scholar]
- Chen, Y.; Xu, P.; Chu, Y.; Li, W.; Wu, Y.; Ni, L.; Bao, Y.; Wang, K. Short-term electrical load forecasting using the Support Vector Regression (SVR) model to calculate the demand response baseline for office buildings. Appl. Energy 2017, 195, 659–670. [Google Scholar] [CrossRef]
- Wijaya, T.K.; Vasirani, M.; Aberer, K. When bias matters: An economic assessment of demand response baselines for residential customers. IEEE Trans. Smart Grid. 2014, 5, 1755–1763. [Google Scholar] [CrossRef]
- Wang, F.; Li, K.; Liu, C.; Mi, Z.; Shafie-Khah, M.; Catalão, J.P.S. Synchronous pattern matching principle-based residential demand response baseline estimation: Mechanism analysis and approach description. IEEE Trans. Smart Grid. 2018, 9, 6972–6985. [Google Scholar] [CrossRef]
- Park, S.; Ryu, S.; Choi, Y.; Kim, J.; Kim, H. Data-driven baseline estimation of residential buildings for demand response. Energies 2015, 8, 10239–10259. [Google Scholar] [CrossRef]
- Haas, R.; Auer, H.; Biermayr, P. The impact of consumer behavior on residential energy demand for space heating. Energy Build. 1998, 27, 195–205. [Google Scholar] [CrossRef]
- Hatton, L.; Charpentier, P.; Matzner-Lober, E. Statistical estimation of the residential baseline. IEEE Trans. Power Syst. 2016, 31, 1752–1759. [Google Scholar] [CrossRef]
- Wu, X.; Wu, R.; Wang, D.; Wei, J.; Li, X.; Lai, L.L.; Lai, C.S. Coordinated air conditioning resources scheduling with high photovoltaic penetrations. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018. [Google Scholar]
- Mu, Y.; Liu, X.; Wang, L. A Pearson’s correlation coefficient based decision tree and its parallel implementation. Inf. Sci. 2018, 435, 40–58. [Google Scholar] [CrossRef]
- Pinson, P.; Nielsen, H.A.; Madsen, H.; Nielsen, T.S. Local linear regression with adaptive orthogonal fitting for the wind power application. Stat. Comput. 2008, 18, 59–71. [Google Scholar] [CrossRef]
- Keller, J.M.; Gray, M.R.; Givens, J.A. A fuzzy k-nearest neighbor algorithm. IEEE Trans. Syst. Man Cybern. Syst. 1985, 15, 580–585. [Google Scholar] [CrossRef]
- Taud, H.; Mas, J.F. Multilayer Perceptron (MLP). In Geomatic Approaches for Modelling Land Change Scenarios; Springer: Berlin, Germany, 2018; pp. 451–455. [Google Scholar]
- Kim, J.; Moon, J.; Hwang, E.; Kang, P. Recurrent inception convolution neural network for multi short-term load forecasting. Energy Build. 2019, 194, 328–341. [Google Scholar] [CrossRef]
- Renewables.ninjia. Available online: https://www.renewables.ninja/ (accessed on 15 August 2020).

| Season | Label | Duration |
|---|---|---|
| Spring | 1 | Early September to end of October |
| Summer | 2 | Early November to end of March |
| Autumn | 3 | Early April to end of May |
| Winter | 4 | Early June to end of August |
| Baseline Estimation Model | Definition |
|---|---|
| High of | The average load of the highest consumption days within those non-DR days preceding the DR event days |
| Low of | The average load of the lowest consumption days within those non-DR days preceding the DR event days |
| Mid of | The average load of the middle consumption days within those non-DR days preceding the DR event days |
| Season | Without Temperature Correction | With Temperature Correction | ||
|---|---|---|---|---|
| MAE (kW) | RAE (%) | MAE (kW) | RAE (%) | |
| Spring | 56.47 | 62.21 | 27.79 | 30.61 |
| Summer | 70.25 | 78.42 | 30.76 | 34.34 |
| Autumn | 51.83 | 70.66 | 20.72 | 28.26 |
| Winter | 61.68 | 98.96 | 23.97 | 38.45 |
| CBL Prediction Methods | Direct Prediction | Prediction Based on PV Output Separation | ||||
|---|---|---|---|---|---|---|
| MAE (kW) | Bias (kW) | RER | MAE (kW) | Bias (kW) | RER | |
| High 5 of 10 | 73.46 | −51.16 | 78.07 | 65.56 | −45.44 | 79.34 |
| Low 5 of 10 | 118.53 | −115.00 | 79.28 | 102.05 | −98.16 | 63.11 |
| Mid 5 of 10 | 93.27 | −82.33 | 77.19 | 80.36 | −69.34 | 72.32 |
| MLP | 83.15 | −74.76 | 76.44 | 74.49 | −66.87 | 71.42 |
| RNN | 82.50 | −71.69 | 72.42 | 69.15 | −57.86 | 66.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, K.; Xie, C.; Lai, C.S.; Wang, D.; Lai, L.L. Photovoltaic Output Power Estimation and Baseline Prediction Approach for a Residential Distribution Network with Behind-the-Meter Systems. Forecasting 2020, 2, 470-487. https://doi.org/10.3390/forecast2040025
Pan K, Xie C, Lai CS, Wang D, Lai LL. Photovoltaic Output Power Estimation and Baseline Prediction Approach for a Residential Distribution Network with Behind-the-Meter Systems. Forecasting. 2020; 2(4):470-487. https://doi.org/10.3390/forecast2040025
Chicago/Turabian StylePan, Keda, Changhong Xie, Chun Sing Lai, Dongxiao Wang, and Loi Lei Lai. 2020. "Photovoltaic Output Power Estimation and Baseline Prediction Approach for a Residential Distribution Network with Behind-the-Meter Systems" Forecasting 2, no. 4: 470-487. https://doi.org/10.3390/forecast2040025
APA StylePan, K., Xie, C., Lai, C. S., Wang, D., & Lai, L. L. (2020). Photovoltaic Output Power Estimation and Baseline Prediction Approach for a Residential Distribution Network with Behind-the-Meter Systems. Forecasting, 2(4), 470-487. https://doi.org/10.3390/forecast2040025







