Rank-Based Control Charts Under Non-Overlapping Counting with Practical Applications in Logistics and Services

Abstract

In this article, we establish a constructive nonparametric scheme for monitoring the quality of services provided by a transportation company. The proposed methodology aims at achieving the diligent tracking of the underlying process and the swift detection of any potential malfunctions. The implementation of the new framework requires the construction of appropriate schemes, which follow the set-up of a Shewhart chart and are connected to ranks and multiple run decision criteria. The dispersion and the mean value of the run length distribution for the suggested distribution-free scheme are investigated for the special case $k=2$. For illustration purposes, a real-data logistics environment is discussed, whereas the proposed approach is applied for improving the quality of the provided services.

1. Introduction

Statistical process control is widely used to guarantee the quality of manufacturing procedures, wherein intrinsic variability persists despite rigorous maintenance and optimization. Control charts serve as diagnostic tools for isolating assignable sources of variation. Once the process transitions into a nonconforming or undesirable state, an effective monitoring framework must promptly detect the shift and generate an out-of-control signal.

It is well established that the majority of monitoring schemes rely on distributional assumptions. Nevertheless, such assumptions are often violated in practical applications. To address this limitation while preserving the conventional structure of classical control charts, a variety of monitoring alternatives appear in the literature already. These methods employ suitably selected nonparametric plotting statistics within the established frameworks of Shewhart-type, Exponentially Weighted Moving Average [1,2,3,4], or Cumulative Sum [5,6,7,8] schemes.

It is widely recognized that Shewhart-type control charts demonstrate strong performance given notable variations in the underlying distribution. Within such a context, a range of monitoring schemes grounded in rank-sum statistics have been developed and extensively investigated in the literature.

Indicatively, we can mention the distribution-free control charts, which exploit Wilcoxon-type rank-sum statistics and were discussed in [9]. A nonparametric control chart for the joint monitoring of the unknown location and scale parameters of the underlying distribution has been established in [10]. The aforementioned test statistic utilizes the Wilcoxon rank sum and the Ansari-Bradley methodology for location and scale, respectively. Additionally, Ref. [11] considered adding runs-rules to enhance the performance of the distribution-free Phase II Shewhart-type chart based on the common Mann–Whitney statistic being established in [11]. More recently, a family of distribution-free statistical tools which utilize alternative Wilcoxon-type rank sum plotting statistics is discussed in [12]. Moreover, Ref. [13] utilized the ranks from a larger amount of test observations and by the aid of that they managed to generalize the monitoring tools suggested by [8]. Further results on Nonparametric Statistical process control are offered by [14,15,16,17,18].

In the present work, we investigate distribution-free Shewhart monitoring tools which are related to Wilcoxon-type rank-sum plotting statistics under non-overlapping counting. The set-up of the scheme established by [9] is implemented, while the resulting monitoring framework is enhanced by applying multiple runs-rules. The main contribution of the present work refers to the simultaneous usage of rank-based statistics and multiple runs. To the best of our knowledge, this is the first instance of both techniques being applied simultaneously in the international literature. The main research motivation for developing the proposed non-parametric scheme is to improve the current monitoring schemes and offer an alternative statistical tool for supporting the underlying supply chain management strategy. It should be mentioned that the simultaneous implementation of rank-based statistics and multiple run rules (instead of the usual simple ones) constitutes a step forward for the research within the field of nonparametric statistical process control. It is evident that multiple run rules strengthen the underlying methodology and generalize the existing results. Indeed, the proposed class of control charts includes as special cases some of the monitoring schemes which have been already introduced in the literature. Moreover, since the new charts seem to be more capable of detecting possible distributional shifts in the underlying process, their implementation in practical situations could be strongly recommended. The particular argumentation will be confirmed by the results appeared in Section 3 and Section 4 of the present paper.

In Section 2, the general set-up of the suggested scheme is discussed in some detail, while closed formulae for calculating the mean and dispersion of the respective run length are delivered in Section 3. In Section 4, a real-life application based on logistics and transportation data is considered. Therein, the new monitoring framework is designed to keep track of the quality of the provided services. This specific example aims to highlight the usefulness of the proposed method in the field of Supply Chain Management, as well as its potential extensions to related areas such as operations management, logistics, inventory control and quality assurance.

The Discussion part concludes by presenting the strengths and weaknesses of the current work, while also proposing directions for upcoming investigations.

2. Control Charts Under Non-Overlapping Counting Based on Ranks

In the following lines, we introduce a family of improved control charts based on rank-sum statistics. The so-called non-overlapping counting strategy is also applied to make the scheme more effective in detecting out-of-control shifts. Within this framework, each run of same objects could not share any object with the next or the previous run. For instance, in the binary sequence 0011100010, we first have a run of two 0′s, then a run of three 1′s, a run of three 0′s, a run of one 0 and finally a run of one 1. We thus have five runs in that binary sequence. If we allow overlapping counting, then the second run of three 1′s in the above binary sequence can be regarded as two runs of two 1′s. The same holds true for the run of three 0′s which follow. On the other hand, if we use non-overlapping counting, then the second (third) run of three 1′s (0′s) can be regarded as a single run of 1′s (0’s) of length 3.

In the proposed nonparametric framework, control limits are defined based on reference observations. These data are obtained during periods of process stability, corresponding to instances when service provision meets the expected quality standards.

The resulting schemes are constructed by implementing the plotting statistics used by [9]. However, some improvements in their performance are accomplished by applying multiple run-type rules under a non-overlapping counting scenario.

The construction of the new monitoring schemes calls for a reference data set of m observations, say $X_1,X_2,\dots ,X_m$. These reference data have cumulative distribution function $F$, which is drawn from the process during periods of stability. We symbolize by $X_{i:m}$ the i-th smallest observation of the reference data set. Note that the control limits of the new schemes rely on suitably chosen values of the respective sample containing the ordered observations, e.g., $X_{1:m},X_{2:m},\dots ,X_{m:m}$.

To figure out whether the underlying operation remains under stability circumstances or not, test data sets with n observations, namely random variables $Y_1^h,Y_2^h,\dots ,Y_n^h$ having cumulative distribution function $G$, are then collected. It is noted that the sampling is accomplished in such a way so that test samples are all independent not only to each other but also to the reference data. In a more technical language, the detection of small or large modifications within the process, namely the diagnosis of distributional alterations.

To be more specific, the suggested monitoring tool relies on the ranks of appropriately chosen test observations, which are drawn from the process. Let us first denote by $Y_{1:n}^h,Y_{2:n}^h,\dots ,Y_{n:n}^h$ the ordered observations within the h-th test data set. Note that the integer-valued parameter $h$ ranges from 1 onwards. On the other hand, two specific order statistics from the reference sample, say $X_{a:m},X_{b:m}$, are used as control limits (LCL, UCL hereafter), where $1\le a<b\le m$. If $W_i^h$ corresponds to the sum of the ranks of those $Y_j^{\prime }s$ within the h-th test data set, which are greater than $X_{i-1:m}$ but less than $X_{i:m}$, the resulting plotted statistic is defined as

$$W^h={\sum }_{i=a+1}^b{W}_i^h.$$

(1)

For the proper implementation of (1), all ranks should not be computed within the separate samples but within the joint one.

Let $M_i^h$ be the amount of the observations ($Y_j^h)$ within the h-th test data set that are greater than the $\left(i-1\right)$-th smallest but smaller than the i-th smallest observation of the reference data set. Note that the index $i$ takes on values from 1 to $m$. We may readily observe that $W^h$ is determined by the aid of the following expression (see, e.g., [8])

$$W^h={\sum }_{i=a+1}^b{M}_i^h\left(i+{\sum }_{j=a+1}^{i-1}{M}_j^h\right)+{\sum }_{i=a+1}^b{M}_i^h(M_0^h-1)+{\displaystyle \frac{1}{2}}{\sum }_{i=a+1}^b{(M}_i^h+(M_i^h{)}^2),$$

(2)

where $M_0^h=\sum _{i=1}^a{M}_i^h$ is simply the amount of test data that are smaller than $X_{a:m}$. The random variable $W^h$ mentioned in (1) plays the role of the first plotting statistic. Furthermore, $R^h=R\left(Y_1^h,Y_2^h,\dots ,Y_n^h;X_{a:m}\right)$ expresses the amount of values within the h-th test data set which are smaller than the lower control limit. The h-th test sample is characterized as well-produced, whenever the following restrictions are not violated

$$W^h\le w \mathrm{and} R^h\le r_1.$$

(3)

Kindly note that parameters $w,r_1$ are related to the underlying design and take on only positive values.

Before presenting the methodological framework of the proposed monitoring schemes, we next illustrate a numerical example, wherein both plotting statistics $W^h,R^h$ are computed. Let us assume that a reference sample of size $m=10$ is available, e.g., the following data

2.1, 3.8, 1.7, 5.5, 3.2, 4.5, 7.7, 6.7, 1.8, 4.2

have been collected from the in-control process. Based on the reference data, we determine the control limits of the scheme as $X_{2:10}=1.8, X_{5:10}=3.8$. Afterwards, three test samples of size $n=5$ are drawn successively from the underlying process and the corresponding data are reported below

• Test sample 1: 3.4, 6.5, 8.7, 7.3, 3.1
• Test sample 2: 1.5, 5.6, 4.4, 2.0, 8.1
• Test sample 3: 7.0, 6.1, 3.7, 3.4, 3.3

Both test statistics of interest, namely $W^h,R^h$, can be calculated for each one of the three available test samples as follows

$$h=1: W^1={\sum }_{i=3}^5{W}_i^1=W_3^1+W_4^1+W_5^1=10,R^1=0$$

$$h=2: W^2={\sum }_{i=3}^5{W}_i^2=W_3^2+W_4^2+W_5^2=3,R^2=1$$

$$h=3: W^3={\sum }_{i=3}^5{W}_i^3=W_3^3+W_4^3+W_5^3=18,R^3=0.$$

In addition, we propose that the entire process, which is under monitoring, should be declared to be in- or out-of-control based on the occurrence of multiple runs. Every test sample obtained from the process results in either an in-control (IC) or an out-of-control (OOC) signal. Consequently, the monitoring scheme may be interpreted as a sequence of binary experiments with two possible outcomes. Within this framework, a multiple run ${MR}_{r,k}$ happens when the r-th streak of $k$ OOC results appears, with $r$ and $k$ being positive integers. In practice, the process is declared out-of-control once $k$ OOC results occur in a row for the r-th time, rather than the first (see, e.g., [19]).

The random variable that is of primary interest is the one which expresses the so-called waiting time till a multiple run ${MR}_{r,k}$ happens. In the literature, various enumeration strategies have been proposed for analyzing the distribution of the waiting time random variable described above. The classical approach to problems involving runs of fixed length is that introduced in [19]. Under this method, whenever k consecutive OOC signals occur, an OOC run of length k is registered, and the enumeration begins anew. It is evident that, within this framework, overlapping runs are not counted. In this study, we adopt this enumeration convention. It should be mentioned that this is the first time that the particular counting framework has been applied in a nonparametric setting of monitoring schemes. In previous works, some authors provided results regarding simple run rules and not the multiple ones applied in the present work.

The general set-up of the proposed family of alternative statistical tools follows the next levels.

Level 1. Collection of m reference data.

Level 2. Calculation of the control limits for the chart.

Level 3. Collection of test data set with n observations.

Level 4. Determination of plotting variables $W^h$ and $R^h$ by the aid of the available test data.

Level 5. Activation of a multiple run ${MR}_{r,k}$ criterion.

Level 6. Characterization of the process as good or bad utilizing plotting points and the ${MR}_{r,k}$ criterion.

Before we proceed to prove the main theoretical results for the proposed class of control charts, we should briefly note some details about the underlying monitoring statistics. In simple words, it is of some interest to figure out the way that the suggested chart generates a bad signal. Since the new scheme plots two values, e.g., the values of random variables $W^h$ and $R^h$, our initial job is to determine them for each test sample, which is drawn from the process. Within the suggested strategy, the $h$-th test data set is not characterized as OOC sample, if the conditions stated in (1) hold true. Under the proposed monitoring scheme ($NMC{C}_{r,k,a,b,w,r_1}$-chart, hereafter), the operation is characterized as a bad one whenever at least $r$ rows of $k$ undesirable products appear. That is whenever we observe $r$ rows of test data sets of length $k$, one condition (or even more conditions) included in (1) is not satisfied.

It is worth mentioning that the monitoring scheme introduced in [9] can be considered as a special case of the new nonparametric family proposed in the present manuscript. Indeed, if we assume that both design parameters $r,k$ take on values 1, the resulting monitoring scheme coincides with the one presented in [9].

3. Run Length Distribution of the Proposed $\mathit{N}\mathit{M}\mathit{C}{\mathit{C}}_{\mathit{r},\mathit{k},\mathit{a},\mathit{b},\mathit{w},{\mathit{r}}_1}$-Tools for $\mathit{k}=2$

We next provide some mathematical aspects of the suggested monitoring tools. In particular, two crucial attributes of the run length distribution for the proposed family of $NMC{C}_{r,k,a,b,w,r_1}$-charts are under investigation. Explicit expressions for determining the mean value and the dispersion with respect to $NMC{C}_{r,k,a,b,w,r_1}$-charts are delivered. Since the number of design parameters of the new charts is large, the practitioner is able to fulfill any specified criteria by appropriately configuring the parameter values.

The following result delivers closed formulae for the mean value and the dispersion of the $NMC{C}_{r,k,a,b,w,r_1}$-schemes for the special case $k=2$.

Proposition 1.

(i) The unconditional Average Run Length and the unconditional Variance of the Run Length of the $NMC{C}_{r,k,a,b,w,r_1}$-chart are given by

$$AR{L}_{r,k}=\int \int \dots {\int }_{0\le u_a\le u_{a+1}\le \dots \le u_b\le 1}{\displaystyle \frac{r\left(1-p^k\right)}{\left(1-p\right)p^k}}\times f_{a:b}\left(u_a,u_{a+1},\dots ,u_b\right){du}_a{du}_{a+1}\dots d{u}_b$$

(4)

and

$$V{RL}_{r,k}=\int \int \dots {\int }_{0\le u_a\le u_{a+1}\le \dots \le u_b\le 1}{\displaystyle \frac{r(1-\left(2k+1\right)\left(1-p\right)p^k-p^{2k+1})}{\left(\right(1-p)p^k{)}^2}}\times f_{a:b}\left(u_a,u_{a+1},\dots ,u_b\right){du}_a{du}_{a+1}\dots d{u}_b$$

(5)

correspondingly, while

$$p=1-q(G{F}^{-1}\left(u_a\right),G{F}^{-1}\left(u_{a+1}\right),\dots ,{GF}^{-1}\left(u_b\right);r_1)$$

and

$$\begin{gathered} q\left(v_a,v_{a+1},\dots ,v_b;r_1\right)=\sum _{\left(m_0,m_{a+1},\dots ,m_b\right)\in A}{\displaystyle \frac{n!}{m_0!\left(\prod _{j=a+1}^b{m}_j!\right)\left(n-m_0-\sum _{j=a+1}^b{m}_j\right)!}}{v}_a^{m_0} \\ \times \prod _{j=a+1}^b{\left(v_j-v_{j-1}\right)}^{m_j}{\left(1-v_b\right)}^{n-m_0-\sum _{j=a+1}^b{m}_j}, \end{gathered}$$

(6)

where A includes those integer values $(M_0,M_a,M_{a+1},\dots ,M_b)$which lead to the violation of one condition (or even more than one) mentioned in (3) and

$$f_{a:b}\left(u_a,u_{a+1},\dots ,u_b\right)={\displaystyle \frac{m!}{\left(a-1\right)!\left(m-b\right)!}}{u}_a^{a-1}{\left(1-u_b\right)}^{m-b},0\le u_a\le u_{a+1}\le \dots \le u_b\le 1.$$

(7)

corresponds to the joint density function of the random variables $u_a,u_{a+1},\dots ,u_b$.

Proof. 

We symbolize by $T_{r,k}$, the waiting time till the appearance of a bad indication, which is generated by the $NMC{C}_{r,k,a,b,w,r_1}$-chart. Note that $T_{r,k}$ corresponds to the run length of the underlying monitoring scheme. Because each test data set is regarded as independent of the others and of the reference data set, the quantity $T_{r,k}$ follows the negative binomial distribution of order $k$.

Given $X_{a:m}=x_a,X_{a+1:m}=x_{a+1},\dots ,X_{b:m}=x_b$, the quantity $T_{r,k}$ is actually the $r$-th convolution of the geometric distribution of order $k$. The probability generating function of $T_{r,k}$ can be expressed as

$$E\left(z^{T_{r,k}}\right)={\left(G\left(z\right)\right)}^r,$$

(8)

where $G\left(z\right)$ is simply the probability generating function of the random variable which expresses the waiting time till a run happens for the first time. In other words, if $p$ corresponds to the success probability of the aforementioned distribution, function $G\left(z\right)$ can be written as

$$G\left(z\right)={\displaystyle \frac{{\left(pz\right)}^k}{1-\left(1-p\right)zA\left(z\right)}},$$

(9)

where

$$A\left(z\right)={\displaystyle \frac{1-{\left(pz\right)}^k}{1-pz}}.$$

(10)

It is now readily deduced that, given the derivates $G^{\prime }\left(z\right)$, $G^{″}\left(z\right)$ of the cumulative density function, the conditional mean and dispersion of the random variable $T_{r,k}$ could be computed via the next expression

$$\begin{array}{ll}E\left(T_{r,k}\left|X_{a:m}=x_a,X_{a+1:m}=x_{a+1},\dots ,X_{b:m}=x_b\right.\right)& =r·G\prime \left(1\right)\\ & ={\displaystyle \frac{r\left(1-p^k\right)}{\left(1-p\right)p^k}}\end{array}$$

(11)

and

$$\begin{array}{ll}Var\left(T_{r,k}\left|X_{a:m}=x_a,X_{a+1:m}=x_{a+1},\dots ,X_{b:m}=x_b\right.\right)& =r·\left(G^{″}\left(1\right)+G^{\prime }\left(1\right)-{\left(G^{\prime }\left(1\right)\right)}^2\right)\\ & ={\displaystyle \frac{r(1-\left(2k+1\right)\left(1-p\right)p^k-p^{2k+1})}{\left(\right(1-p)p^k{)}^2}}\end{array}$$

(12)

correspondingly. Within the $NMC{C}_{r,k,a,b,w,r_1}$-statistical tool, the success probability p which is related to the previously mentioned geometric distribution of order $k$ expresses the possibility that one (or more than one) condition included in (3) has been violated. Nevertheless, the above-mentioned possibility can be written in terms of the next multiple sum (see [8])

$$\sum _{\mathbf{m}}{\displaystyle \frac{n!v_a^{m_0}\prod _{j=a+1}^b{\left(v_j-v_{j-1}\right)}^{m_j}{\left(1-v_b\right)}^{n-m_0-\sum _{j=a+1}^b{m}_j}}{m_0!\left(\prod _{j=a+1}^b{m}_j!\right)\left(n-m_0-\sum _{j=a+1}^b{m}_j\right)!}}$$

(13)

where in $\mathbf{m}=(m_0,m_{a+1},\dots ,m_b{)}^T$ is a vector which is determined in such a way so takes on values such that one (or more than one) condition included in (3) has not been met. Our next step is to substitute (13) in (11), (12) and the outcome we are looking for is delivered if we just average over the distribution of $X_{a:m},X_{a+1:m},\dots X_{b:m}$. □

Kindly note that for the case $k\ge 3$ explicit expressions for the quantities of interest are not available. Thus, a parallel application of the present methodology is not feasible. A potential alternative would be to estimate the necessary quantities via simulation.

Having at hand the results proved in Proposition 1, the unconditional ARL and dispersion of the random variable $T_{r,k}$ for the suggested statistical schemes under in-control circumstances are readily obtained by substituting $F=G$ in formulae proved previously. In other words, Formulae (4) and (5) offer a nice tool for representing and measuring the in-control performance of the proposed monitoring scheme.

Table 1. In-control ARL of $NMC{C}_{r,k,a,b,w,r_1}$-charts.

ARLo	Designs and ARL’s
	(m,n)	(r, k, a, b, w, r1)	Exact ARLin
370	(100,5)	(2, 4, 35, 37, 25, 2)	379.7
	(100,7)	(4, 6, 38, 40, 75, 2)	371.3
	(100,11)	(5, 5, 26, 28, 88, 3)	368.0
	(100,15)	(6, 4, 18, 20, 88, 3)	371.9
	(200,5)	(15, 2, 37, 39, 70, 2)	380.3
	(200,7)	(2, 3, 33, 35, 55, 2)	363.6
	(200,11)	(7, 3, 28, 30, 55, 3)	377.9
	(200,15)	(5, 3, 23, 25, 59, 4)	367.7
500	(100,5)	(1, 5, 38, 40, 75, 2)	490.5
	(100,7)	(11, 5, 38, 40, 75, 2)	492.4
	(100,11)	(5, 4, 21, 23, 84, 3)	502.6
	(100,15)	(2, 4, 15, 17, 88, 3)	506.0
	(200,5)	(16, 2, 35, 37, 70, 2)	497.3
	(200,7)	(3, 3, 35, 37, 70, 2)	494.0
	(200,11)	(3, 3, 26, 28, 55, 2)	497.5
	(200,15)	(8, 2, 17, 19, 58, 3)	494.1

provides some numerical evidence for the performance of the suggested scheme. More specifically, one may select from the designs displayed therein the appropriate one which leads to a pre-specified level of ARL-performance for the $NMC{C}_{r,k,a,b,w,r_1}$-control charts. Note that the most traditional values of the in-control ARLo for constructing a monitoring scheme are equal to 370 and 500. Thereof, we chose to follow the guidelines provided in the literature.

For instance, let us consider the case where we are able to draw $200$ reference data from the operation under in-control circumstances. Our next step is to collect successive test data sets with $n$ observations under the assumption that all of them are independent to each. What we are searching for is a control chart which gives an in-control ARL almost equal to 500. Given the above-mentioned numerical results, the requirement can be ensured by building a

• a $NMC{C}_{r,k,a,b,w,r_1}$-chart with design parameters $n=5,r=16,k=2,a=35,b=37,w=70, r_1=2$. This practically means that our choice is to draw test data sets with 5 observations, wherein the 35th and 37th smallest observations play the role of the control limits. The $NMC{C}_{r,k,a,b,w,r_1}$-chart, which has been now constructed, achieves an Average Run Length equal to 497.3, or
• a $NMC{C}_{r,k,a,b,w,r_1}$-chart with design parameters $n=7,r=3,k=3,a=35,b=37, w=70,r_1=2$. This practically means that our choice is to draw test data sets with 7 observations, wherein the 35th and 37th smallest observations play the role of the control limits. The $NMC{C}_{r,k,a,b,w,r_1}$-chart, which has been now constructed, achieves an Average Run Length equal to 494.0, or
• a $NMC{C}_{r,k,a,b,w,r_1}$-chart with design parameters $n=11,r=3,k=3,a=26,b=28,w=55,r_1=2$. This practically means that our choice is to draw test data sets with 11 observations, wherein the 26th and 28th smallest observations play the role of the control limits. The $NMC{C}_{r,k,a,b,w,r_1}$-chart, which has been now constructed, achieves an Average Run Length equal to 497.5, or
• a $NMC{C}_{r,k,a,b,w,r_1}$-chart with design parameters $n=15,r=8,k=2,a=17,b=19, w=58,r_1=3$. This practically means that our choice is to draw test data sets with 15 observations, wherein the 17th and 19th ordered reference observations play the role of the control limits. The $NMC{C}_{r,k,a,b,w,r_1}$-chart, which has been now constructed, achieves an Average Run Length equal to 494.91.

In order to implement the above-mentioned monitoring scheme, a large number of design parameters should be specified. Thereof, some guidelines could prove helpful to this direction. For instance, the practitioner is advised to collect a reference sample of large samples. That could provide more reliable representation of the in-control process. On the other hand, the size of test samples should be quite small. This is reasonable, since using large test samples may lead to a slower identification of process shifts, potentially resulting in the generation of defective products. In addition, with increasing parameter values $r,k$, the chart finds it progressively harder to trigger an alarm. In fact, for large parameter values $r,k$, fulfilling the criterion becomes substantially more difficult. Lower values of the aforementioned parameters should be chosen in situations where the manufactured products are costly, and defects would result in significant losses. The code in order to produce numerical or graphical results for the proposed schemes is available to the interested reader upon request.

A typical approach when comparing two different control charts is to use a common in-control average run length and then to examine their out-of-control average run length. To this direction, we next compare the proposed monitoring schemes with other established nonparametric control charts. Specifically, we examine well-known rank-based monitoring approaches and evaluate their out-of-control performance in relation to that of the proposed methods.

Table 2. ARL values of seven different control charts under the N(0,1) distribution.

Shift	New Chart	W-Shewhart Chart 1	W-Shewhart Chart 2	Wmin	MW	W-CUSUM	W-EWMA
0.0	498.11	473.51	501.92	501.66	502.48	498.64	502.94
0.25	72.85	77.44	93.12	100.82	428.03	333.45	321.52
0.50	14.25	19.87	21.88	25.59	292.77	107.19	103.15
1.00	3.26	3.27	3.46	3.52	86.57	13.04	14.29
1.50	1.32	1.32	1.33	1.33	28.52	6.25	7.52

presents a set of numerical comparisons between the newly proposed control charts and six existing distribution-free schemes. More specifically the new chart is compared to the W-Shewhart-chart 1 and the W-Shewhart-chart 2, which have been introduced by [20], the so-called W-CUSUM and W-EWMA control charts established by [21], to the Wmin-chart (see, [13]), as well as to the Mann–Whitney-based chart (MW chart hereafter) instituted by [12]. Note that the comparisons are made under the assumption that the underlying in-control process is normally distributed with parameters 0 and 1.

The design parameters of all competing schemes were appropriately selected so that the corresponding rules yield an in-control Average Run Length of approximately 500. Subsequently, the out-of-control ARL values were computed under specific mean shifts in the underlying distribution.

The results in Table 2 furnish numerical support for the superior performance of the proposed monitoring schemes over existing alternatives.

Indeed, the out-of-control ARL of the proposed chart is lower than that of the competing charts. In practical terms, this implies that the new charts are able to detect distributional shifts more rapidly than the alternative monitoring schemes.

As an illustration, under a distributional shift of 0.25 units, the proposed chart identifies the change within 72.85 plotting points, e.g., independent test samples, while the competing charts detect it at a noticeably slower rate. As we readily observe at the 2nd line of the above table, the W-Shewhart charts 1 and 2 attain an out-of-control performance equal to 77.44 and 93.12, respectively. On the other hand, the remaining competitors achieve even worse performance. In particular, W_min-chart realizes an ARL_out equal to 100.82, while the ARL_out for the MW-chart, the W-CUSUM and W-EWMA control charts correspond to 428.03, 333.45 and 321.52 plotting points.

As readily inferred from the above numerical investigation, the proposed schemes provide a competitive approach to monitoring the quality of the underlying process, regardless of the specific distribution governing it. In other words, the new control charts appear to detect potential shifts in the process distribution more quickly than their competitors in all examined cases. In addition, due to the flexibility of the proposed frameworks which allows us to determine appropriately their design parameters in order to reach the desired level of performance under any requirements, the practitioner seems to be able to choose a suitable design in every case.

4. An Illustrative Application in Industrial Environment

For illustration purposes, let us next implement the proposed monitoring framework to a real-life application. This application is related to logistics, transportation, and services management, specifically focusing on ride-hailing and delivery services. Data have been collected from a real-world database, which belongs to a food delivery company known for its delivery platform for food and merchandise. Two specific performance metrics have been reported for 150 days of platform operation to help assess and optimize operational efficiency and service quality. First of all, the system tracks the average time it takes for a service request (like a ride or a delivery) to be assigned to a driver or agent (response time, hereafter). This helps measure the efficiency of the service and how quickly customers are attended to. After each service is completed, customers provide feedback, which is then aggregated to give an average satisfaction score (customer satisfaction, hereafter). This reflects the quality of the service in terms of driver professionalism, timeliness, and overall customer experience. Each score is reported in a scale of 0 to 5.

By continuously tracking these metrics over extended periods (e.g., 175 days as shown in the data set), the company can identify patterns or areas needing improvement. For example, a high average response time might correlate with lower customer satisfaction, signaling that the company needs to optimize route planning, driver availability, or communication systems.

It goes without saying that an effective monitoring scheme based on non-parametric statistics could be proved to be really helpful for the company. This is justified by the fact that its implementation on response time and customer satisfaction scores can identify poor service delivery and provide protection to the company against low levels of customer satisfaction. The above-mentioned argument clearly defines the usefulness of the proposed framework and the necessity of developing this specific scientific methodology.

Table 3. Average response time (per day) and corresponding customer satisfaction score for 175 consecutive days.

8.8 4.4	9.5 4.0	9.0 4.8	9.2 4.6	8.2 4.4	9.1 3.9	9.2 4.5	8.1 3.9	7.9 4.8	8.8 4.2	9.0 4.4
9.0 4.1	9.2 4.7	9.4 4.7	8.0 4.7	9.0 3.8	9.0 3.7	9.1 4.7	9.4 4.3	9.0 4.5	9.3 4.4	8.8 4.4
9.2 4.1	9.4 4.4	9.1 4.0	8.0 3.8	7.9 4.7	9.5 4.5	9.2 4.2	9.4 3.8	8.0 4.3	8.5 4.8	9.5 4.7
9.6 4.6	9.1 4.5	9.0 3.9	9.4 4.5	8.0 4.1	7.6 4.6	9.5 4.6	8.8 4.7	9.1 4.5	9.8 3.7	9.7 3.9
8.7 4.0	7.7 4.8	9.2 4.1	9.5 4.7	9.1 4.6	15.1 3.6	7.8 3.7	9.4 4.4	10.5 4.1	9.3 4.4	11.8 4.3
12.9 4.6	11.7 3.3	7.3 3.8	7.9 4.7	9.4 4.3	13.5 4.2	11.8 4.1	9.2 4.1	8.1 3.7	11.5 3.6	8.7 4.1
14.8 3.8	13.8 4.2	9.3 4.3	14.5 4.3	9.4 3.6	7.5 4.7	8.5 3.4	10.2 4.2	15.1 4.4	7.9 4.8	9.4 4.5
9.1 3.9	8.8 4.3	8.2 3.6	9.2 4.1	9.4 4.5	8.7 4.2	9.3 4.3	9.4 3.4	12.6 4.3	8.9 3.7	17.5 4.1
9.4 4.1	8.4 4.2	11.5 4.9	8.1 3.6	18.6 3.4	18.0 4.7	14.5 4.2	9.4 4.1	12.0 4.6	14.8 4.1	7.1 4.7
13.9 4.4	9.3 3.6	8.5 4.3	8.7 4.9	9.2 4.2	9.2 4.1	8.4 3.7	14.2 4.3	9.3 3.4	8.0 4.1	9.4 4.1
8.7 3.9	9.9 4.2	8.6 3.5	8.2 3.4	8.0 4.1	11.8 3.5	9.2 4.1	9.3 3.4	9.2 4.0	11.1 4.6	15.3 4.3
8.5 4.6	8.7 4.0	9.2 4.2	13.6 4.6	9.3 4.6	8.2 4.3	9.2 3.9	8.2 3.6	9.3 4.0	15.0 4.4	8.8 4.6
8.5 4.5	17.1 3.4	9.3 4.3	9.3 3.5	9.3 3.9	8.5 4.2	8.6 4.1	8.9 4.2	17.2 3.3	9.1 4.3	9.1 3.6
8.8 3.4	8.8 4.2	9.3 4.3	9.4 4.0	8.8 3.6	9.2 4.7	8.4 4.3	17.7 4.1	9.1 3.4	8.5 4.2	9.3 4.1
17.6 3.6	18.9 3.4	8.5 4.4	14.0 4.2	9.4 4.1	15.5 4.1	16.9 4.0	17.7 3.6	9.3 4.5	8.6 3.3	7.8 3.7
8.9 4.1	9.4 4.2	9.3 4.0	8.9 4.1	8.5 3.9	8.8 3.4	18.0 3.5	9.3 3.6	9.2 4.1	9.1 4.0

displays the average response time (per day) for all the transportation services provided, along with the corresponding average customer satisfaction score. The reporting time period reflects a total of 175 working days.

It is evident that, during the first 7 weeks, e.g., for the first 49 days of the stated timeframe, the service operations functioned smoothly and aligned with the company’s established standards. Starting on Day 50, however, alterations in the company’s staffing led to interruptions in service delivery, and the quality manager noted that the transportation process no longer satisfied his criteria. Consequently, the information collected during Days 1 through 49 can be considered the baseline sample of size $m=49$, while the remaining 126 days are considered to be test data per week, namely these data are divided into samples of size $n=7$.

We aim to implement the suggested monitoring approach to determine if the disturbance observed from Day 50 onward can be identified through the use of the control chart. This particular choice appears appropriate, given that in such production processes, deviations from specifications can be quite large and thereof the EWMA- or CUSUM-type charts are best avoided.

We first monitor the Average Response times data. The design parameters of the proposed monitoring scheme are determined such that the in-control ARL of the resulting monitoring scheme to be equal to 370 (approximately). In fact, by assigning the following values to the remaining parameters

$$a=35,b=37,n=7,r_1=2,r=2,k=2,w=55$$

the tool which has been constructed includes two separate monitoring schemes and succeeds an in-control ARL-value equal to 360.3.

The abovementioned design indicates practically the following:

• a reference sample of size $m=49$ observations has been collected when the process is supposed to be in-control,
• the ordered observations at the 35th and 37th position of the reference sample, e.g., the observed values $X_{35:49},X_{37:49}$ are related to the control limits for the resulting charts (see also (1)–(3)),
• test samples of size $n=7$ observations are drawn from the process,
• the observed values for the plotting statistics are calculated for each test data set separately, meaning that the random variables $W^h,R^h$ are determined for each one among the 18 test samples.

It is noteworthy that the practitioner may select any alternative combination of parameter values in order to develop a suitable design that achieves the intended standard of process stability, e.g., $AR{L}_{in}=370$. However, we note that it is recommended to use a large reference sample size and a relatively small test sample size. This is justified by the fact that the first condition enables a reliable determination of the control limits, while the second facilitates the prompt detection of possible process shifts.

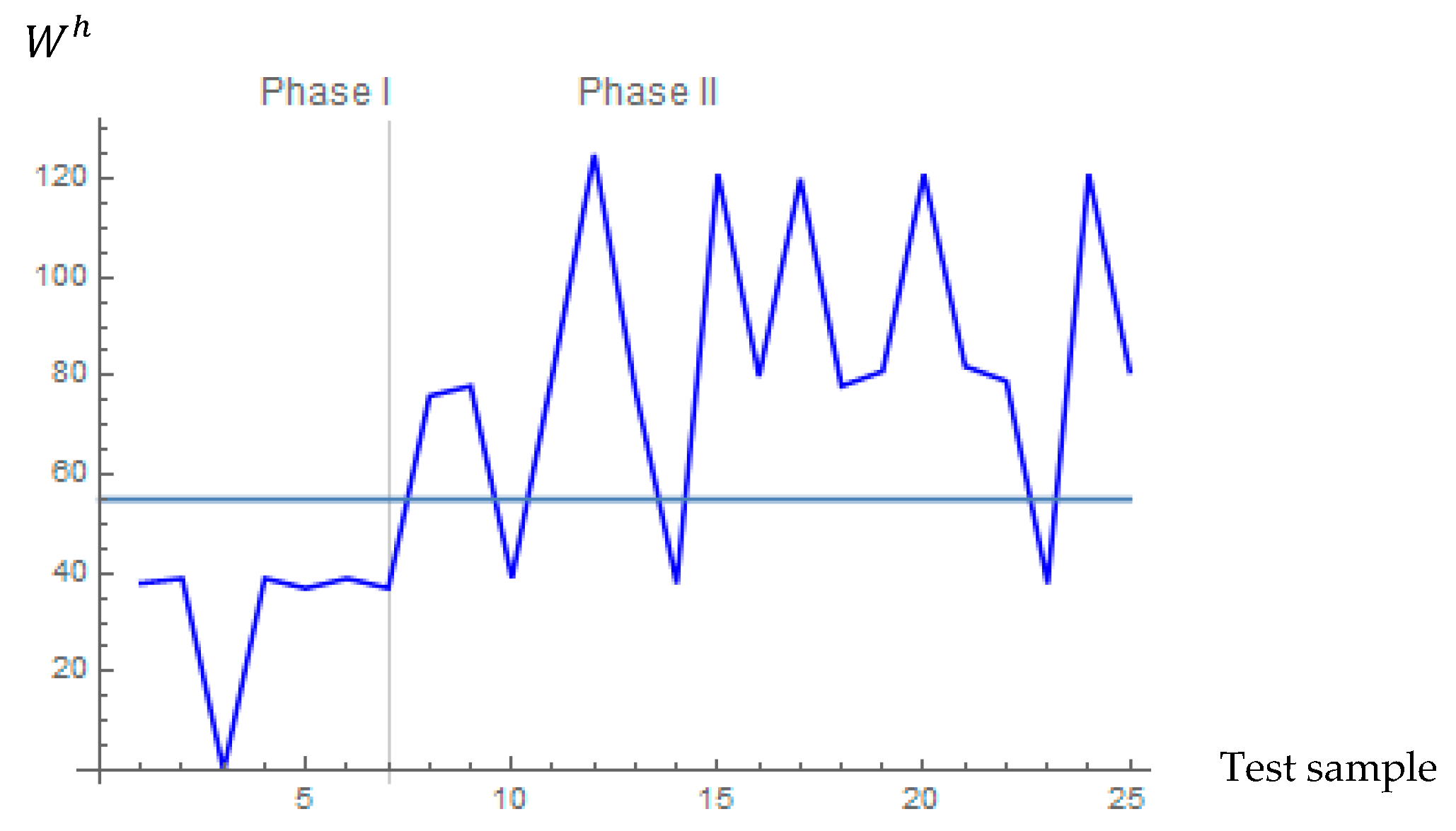
Afterwards, we construct two control charts for the Average Response times, which compose the proposed monitoring scheme for the available data. The constructed scheme is shown in both Figure 1 and Figure 2.

The $h$-th test sample produces a bad signal (or is characterized as OOC), if one (or more than one) condition among the ones stated below has not been met

$$W^h\le 55, R^h\le 2.$$

(14)

Note that every time that a plotting point is over the blue horizontal line, which expresses the corresponding control limit, we record a single undesirable product. In simpler words, each point on the chart corresponds to a distinct test sample. In particular, in Figure 1 each point depicts the value of $W^h$, whereas in Figure 2 each point illustrates the value of $R^h$. As long as the points in both charts remain within the displayed control limits, the process is considered to be in-control, and no intervention or alarm is required. However, when the multiple run ${MR}_{r,k}$ criterion is met, we declare that the process has shifted to an out-of-control state.

In more technical terms, under the proposed monitoring scheme the process is characterized as OOC whenever $r=2$ rows of $k=2$ undesired signals happen, or alternatively whenever $r=2$ rows of test data sets of length $k=2$ are present, wherein one or even more than one condition included in (14) has not been fulfilled. It goes without saying that Phase I data sets (Days 1 to 49 or equivalently samples 1 to 7) are not creating an OOC signal (as expected due to our knowledge that this period the process was operating well), the suggested distribution-free tool signals in the prospective phase (Day 50 onwards). More specifically, we observe that an out-of-control signal appears upon the 5th test sample (or 12th overall) since at that time 2 subsequences of 2 bad signals have already been reported.

From these findings, the quality manager can reasonably conclude that the workforce modifications within the factory indeed led to disturbances in the service process. Moreover, the conclusion that the assembly process no longer satisfies his expectations could also be drawn. It is worth highlighting that the monitoring scheme employed is able to rapidly identify the unfavorable shift in process conditions.

Furthermore, the suggested tool can also be applied for monitoring the available Customer Satisfaction Scores data. More precisely, our interest focuses now on the low entries of each cell in Table 2, namely on the 175 scores in the scale of 0-5 for the whole reporting time period. We first determine the design parameters for the suggested monitoring scheme such as the in-control ARL of the resulting monitoring scheme to be equal to 370 (approximately). Since we have already at hand that $m=49, n=7$, we assign the next values to the remaining parameters

$$a=5,b=7,r_1=2,r=2,k=2,$$

the resulting scheme, which includes two different control charts based on test statistics, attains an in-control ARL-value equal to 360.4. The design mentioned previously declares practically the next statements:

• a reference sample of size $m=49$ observations has been collected under the assumption that the operation runs well,
• the 5th and 7th smallest reference observation, e.g., the observed values $X_{5:49},X_{7:49}$ are related to the control limits for the resulting charts (see also (1)–(3)),
• test samples of size $n=7$ observations are drawn from the process,
• the observed values of plotting statistics are calculated separately for each test data set, which practically means that random variables $W^h,R^h$ are determined for each one of the 18 available test data sets.

Afterwards, we construct two control charts for the Customer Satisfaction Scores, which comprise the proposed monitoring scheme for the available data. The outcomes are presented in Figure 3 and Figure 4.

The $h$-th test sample produces a bad signal (or is characterized as OOC), if one or even more than one condition included below has not been met

$$W^h\le 34, R^h\le 2.$$

(15)

Each point on the above charts corresponds to a separate test sample based on the recorded values of the variable Customer Satisfaction Scores. More precisely, in Figure 3 each point displays the value of $W^h$, whereas in Figure 4 each point corresponds to the value of $R^h$. As long as the points in both charts remain within the respective control limits, the process is characterized as in-control. However, when the multiple run ${MR}_{r,k}$ criterion is met, we conclude that the process has shifted to an out-of-control state.

More technically speaking, under the proposed monitoring scheme the process is characterized as OOC whenever we observe $r=2$ rows of $k=2$ bad signals, which practically means that $r=2$ rows of test data sets of length $k=2$, wherein one or even more than one condition included in (14) has not been met. It is straightforward that Phase I data sets (Days 1 to 49 or equivalently samples 1 to 7) are not creating an OOC signal (as expected due to our knowledge that this period the process was operating well), the suggested distribution-free tool signals in the prospective time period (Day 50 onwards). To be specific, we observe that an out-of-control signal appears upon the 6th test data set (or 13th data set in case we start counting from the beginning of the process) since at that time 2 rows of 2 undesirable signals have already occurred. With the aid of the outcomes mentioned previously, the quality manager can figure out that his/her requirements are not met anymore.

5. Discussion

The present article offers a distribution-free control chart under non-overlapping counting. A well-known Wilcoxon-type rank-sum statistic is plotted, while a multiple run occurrence should be observed for an out-of-control signal to be produced.

A real-life application in a logistics environment is discussed, wherein the new approach is applied for improving the quality of the services provided. More precisely, the suggested family of distribution-free monitoring schemes are related to the common Wilcoxon-type statistics and at the same time a multiple run criterion is also activated. The monitoring statistics are related to reference ordered observations. The characterization of the process as either good or bad is accomplished by applying additional multiple run criteria. The run length for the suggested monitoring tool is investigated in some detail. The practitioner can choose from the designs provided in the tables of the previous sections the appropriate one for constructing the most suitable monitoring scheme for the underlying application.

It should be mentioned that two main limitations could be met when that practitioner attempts to apply the proposed monitoring scheme. The first one refers to the fact that a quite large reference sample is required for developing properly the corresponding control limits. It is evident that the proposed methodology could provide better results whenever a reference sample of large size has been collected. This is a particular limitation of the new monitoring schemes. Nevertheless, collecting a large reference sample is feasible, as this needs to be performed only once and during an in-control period of the underlying process.

The second drawback is related to complexity of the proposed technique, as it requires specifying a large number of design parameters. It is true that the practitioner should determine the values of many design parameters in order to construct a suitable control chart which achieves his/her requirements. However, the latter difficulty could be faced as a privilege at the same time, since it offers the practitioner the opportunity to choose the proper design among many available ones. Moreover, the guidelines given in previous sections could provide some help in this direction.

Throughout the lines of the paper, it is highlighted how the proposed control charts can be proved helpful in a logistics management environment. As a future potential, it could be reported that the implementation of additional or more complex scans/runs-type rules along with alternative distribution-free test statistics may result in even more effective monitoring schemes. In addition, further and deeper analysis could be provided to reduce the complexity of applying the proposed technique in practice and to highlight its usefulness in other related fields as well, such as inventory management, demand forecasting or operations management.