The Use of Double Poisson Regression for Count Data in Health and Life Science—A Narrative Review
Abstract
1. Introduction
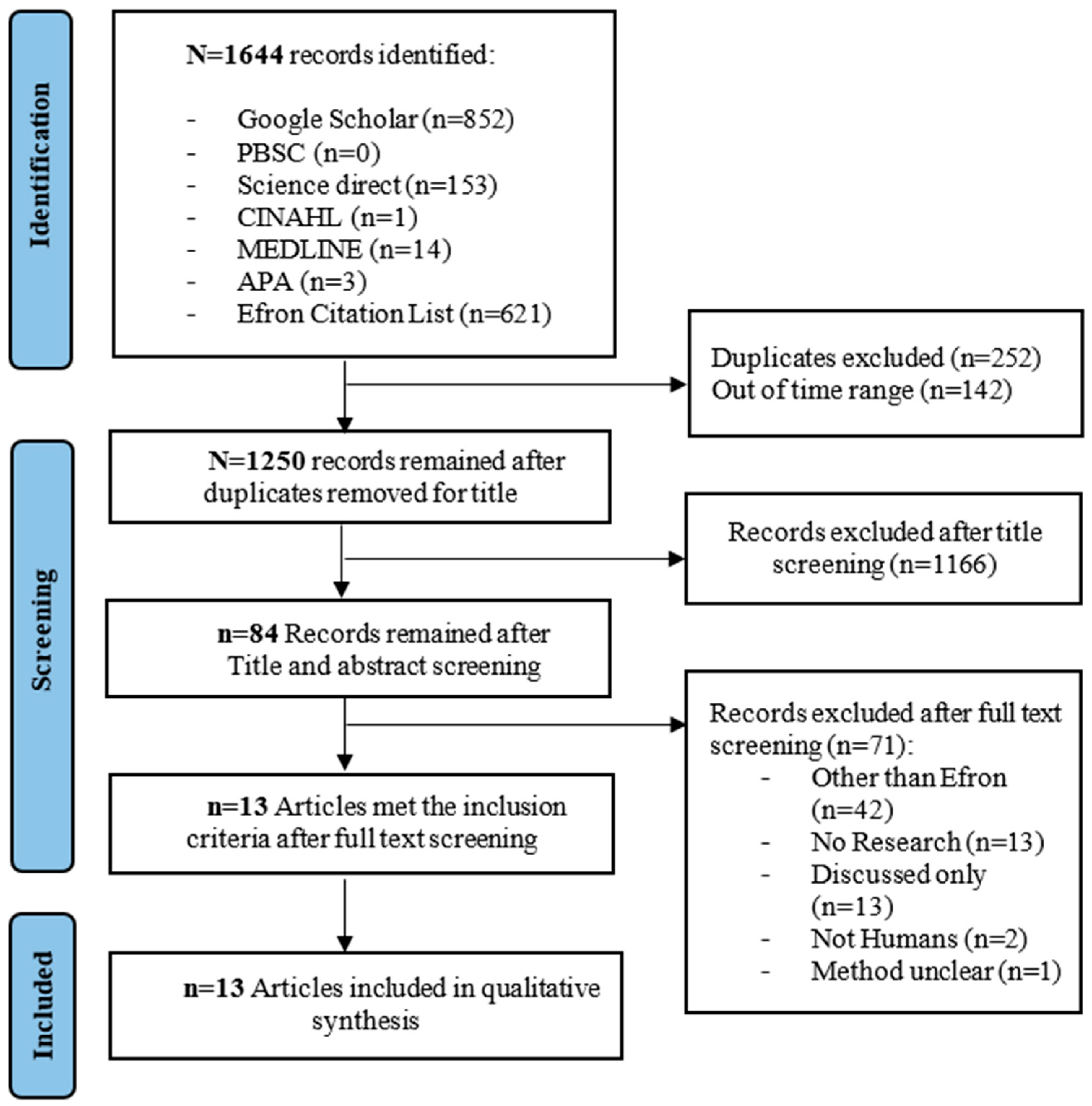
2. Materials and Methods
2.1. Inclusion and Exclusion Criteria
2.2. Search Strategy
2.3. Selection Strategy
2.4. Data Extraction
3. Results
Summary
| Author (Year), Country a | Area | Type of Study | Count Variable | Quality Criteria b | Type of Dispersion | Software |
|---|---|---|---|---|---|---|
| Aragon et al. (2016) [32], Brazil | Public Health | Ecological study | Snakebites | DIC | Under-dispersion | Open BUGS |
| de Andrade et al. (2021) [37], Brasil | Infectious diseases | Ecological study | Infectious diseases | AIC | Modeled Dispersion c | R/ GAMLSS |
| Giacomet et al. (2023) [38], Brazil | Infectious diseases | Ecological study | Infectious diseases | AIC | Over-dispersion | R/ GAMLSS |
| Gijbels & Prosdocimi (2011) [29], Italy | Obstetrics | Epidemiological study | Abortion Rate | AISE | Under-dispersion | R/ GAMLSS |
| Hu et al. (2023) [39], China | Sleep quality | Survey | PSQI | BIC | Modeled Dispersion c | R/ GAMLSS |
| Khoei et al. (2021) [43], Iran | Neonatology | Epidemiological study | Congenital malformations | DIC | Over-dispersion | Open BUGS |
| Nogueira et al. (2021) [33], Brazil | Diseases of the respiratory system | Observational study | Number of surgeries | Not reported | Over-dispersion | SAS |
| Nunes et al. (2021) [34], Brazil | Angioedema | Observational study | Angioedema attacks | Not reported | Not reported | Open BUGS |
| Orooji et al. (2022) [45], Iran | Cardio- logy | Epidemiological study | Number of vessels with stenosis | AIC | Under-dispersion | SAS |
| Phiri et al. (2016) [35], Malawi | Infectious diseases | RCT-Secondary analysis d | Co-occurrence of parasites | AIC and BIC | Over-dispersion | STATA |
| Quintero-Sarmiento et al. (2012) [31], Colombia | Mortality | Epidemiological study | Children < 5 years who died | AIC and BIC | Over-dispersion | Not reported |
| Rajalu et al. (2022) [41], India | Emergency medicine | Epidemiological study | Cases of traumatic brain injury | AIC | Over-dispersion | R/ GAMLSS |
| Schmidt et al. (2022) [42], Germany | Oral Health | Cohort study | Oral Health Score | Not reported | Over-dispersion | R/ GAMLSS |
4. Discussion
4.1. Limitations
4.2. Further Research
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ratna, M.B.; Khan, H.A.; Hossain, M.A. Modeling the number of children ever born in a household in Bangladesh using generalized Poisson regression. Ulab J. Sci. Eng. 2011, 3, 51–56. [Google Scholar]
- Winkelmann, R.; Zimmerman, K.F. Count data models for demographic data. Math. Popul. Stud. 1994, 4, 205–221. [Google Scholar] [CrossRef]
- Ghaznavi, C.; Kawashima, T.; Tanoue, Y.; Yoneoka, D.; Makiyama, K.; Sakamoto, H.; Ueda, P.; Akifumi, E.; Nomura, S. Changes in marriage, divorce and births during the COVID-19 pandemic in Japan. BMJ Glob. Health 2022, 7, e007866. [Google Scholar] [CrossRef]
- Loukas, K.; Karapiperis, D.; Feretzakis, G.; Verykios, V.S. Predicting football match results using a Poisson regression model. Appl. Sci. 2024, 14, 7230. [Google Scholar] [CrossRef]
- Maier, T.; Meister, D.; Trösch, S.; Wehrlin, J.P. Predicting biathlon shooting performance using machine learning. J. Sports Sci. 2018, 36, 2333–2339. [Google Scholar] [CrossRef]
- Pińskwar, I.; Choryński, A.; Graczyk, D. Good weather for a ride (or not?): How weather conditions impact road accidents—A case study from Wielkopolska (Poland). Int. J. Biometeorol. 2024, 68, 317–331. [Google Scholar] [CrossRef]
- Denis, T.; Lanfranchi, J. A new empirical model of the determinants of sickness and the choice between presenteeism and absence. Labour 2025, 39, 61–87. [Google Scholar] [CrossRef]
- Ostermann, T.; Appelbaum, S.; Baumgartner, S.; Rist, L.; Krüerke, D. Using merged cancer registry data for survival analysis in patients treated with integrative oncology: Conceptual framework and first results of a feasibility study. In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies, Online, 9–11 February 2022; Volume 5, pp. 463–468. [Google Scholar]
- Ondrick, C.W.; Griffiths, J.C. Fortran IV computer program for fitting observed count data to discrete distribution models of binomial, Poisson and negative binomial. In Kansas Geological Survey Computer Contribution 35; Merriam, D.F., Ed.; University of Kansas: Lawrence, KS, USA, 1969. [Google Scholar]
- Poisson, S.D. Recherches sur la Probabilité des Jugements en Matière Criminelle et en Matière Civile: Précédées des Règles Générales du Calcul des Probabilités; Bachelier: Paris, France, 1837. [Google Scholar]
- Coxe, S.; West, S.G.; Aiken, L.S. The analysis of count data: A gentle introduction to Poisson regression and its alternatives. J. Pers. Assess. 2009, 91, 121–136. [Google Scholar] [CrossRef]
- Palmer, A.; Losilla, J.M.; Vives, J.; Jiménez, R. Overdispersion in the Poisson regression model. Methodology 2007, 3, 89–99. [Google Scholar] [CrossRef]
- Yule, G.U. On the distribution of deaths with age when the causes of death act cumulatively, and similar frequency distributions. J. R. Stat. Soc. 1910, 73, 26–38. [Google Scholar] [CrossRef]
- Greenwood, M.; Yule, G.U. An inquiry into the nature of frequency distributions representative of multiple happenings with particular reference to the occurrence of multiple attacks of disease or repeated accidents. J. R. Stat. Soc. 1920, 83, 255–279. [Google Scholar] [CrossRef]
- Consul, P.C.; Jain, G.C. A generalization of the Poisson distribution. Technometrics 1973, 15, 791–799. [Google Scholar] [CrossRef]
- Consul, P.C.; Famoye, F. Maximum likelihood estimation for the generalized Poisson distribution when sample mean is larger than sample variance. Commun. Stat.–Theory Methods 1988, 17, 219–234. [Google Scholar] [CrossRef]
- Harris, T.; Yang, Z.; Hardin, J.W. Modeling underdispersed count data with generalized Poisson regression. Stata J. 2012, 12, 736–747. [Google Scholar] [CrossRef]
- Famoye, F. Restricted generalized Poisson regression model. Commun. Stat.—Theory Methods 1993, 22, 1335–1354. [Google Scholar] [CrossRef]
- Conway, R.W.; Maxwell, W.L. A queuing model with state dependent service rates. J. Ind. Eng. 1962, 12, 132–136. [Google Scholar]
- Shmueli, G.; Minka, T.P.; Kadane, J.B.; Borle, S.; Boatwright, P.B. A useful discrete distribution for fitting discrete data: Revival of the Conway–Maxwell–Poisson distribution. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2005, 54, 127–142. [Google Scholar] [CrossRef]
- Sellers, K.F.; Shmueli, G. A flexible regression model for count data. Ann. Appl. Stat. 2010, 4, 943–961. [Google Scholar] [CrossRef]
- Huang, A. Mean-Parametrized Conway–Maxwell–Poisson regression models for dispersed counts. Stat Model. 2017, 17, 359–380. [Google Scholar] [CrossRef]
- Efron, B. Double exponential families and their use in generalized linear regression. J. Am. Stat. Assoc. 1986, 81, 709–721. [Google Scholar] [CrossRef]
- Aragon, D.C.; Achcar, J.A.; Martinez, E.Z. Maximum likelihood and Bayesian estimators for the double Poisson distribution. J. Stat. Theory Pract. 2018, 12, 886–911. [Google Scholar] [CrossRef]
- Zou, Y.; Geedipally, S.R.; Lord, D. Evaluating the double Poisson generalized linear model. Accid. Anal. Prev. 2013, 59, 497–504. [Google Scholar] [CrossRef]
- Appelbaum, S.; Ostermann, T.; Konerding, U. Maximum likelihood estimation of parameters for double poisson regression: A simulation study. Comput. Stat. 2025, 1–39. [Google Scholar] [CrossRef]
- Siddaway, A.P.; Wood, A.M.; Hedges, L.V. How to do a systematic review: A best practice guide for conducting and reporting narrative reviews, meta-analyses, and meta-syntheses. Annu. Rev. Psychol. 2019, 70, 747–770. [Google Scholar] [CrossRef]
- Matthews, J.R. EBSCOhost. Libr. Technol. Rep. 1996, 32, 221–227. [Google Scholar]
- Gijbels, I.; Prosdocimi, I. Smooth estimation of mean and dispersion function in extended generalized additive models with application to Italian induced abortion data. J. Appl. Stat. 2011, 38, 2391–2411. [Google Scholar] [CrossRef]
- Gijbels, I.; Prosdocimi, I.; Claeskens, G. Nonparametric estimation of mean and dispersion functions in extended generalized linear models. Test 2010, 19, 580–608. [Google Scholar] [CrossRef]
- Quintero-Sarmiento, A.; Cepeda-Cuervo, E.; Núñez-Antón, V. Estimating infant mortality in Colombia: Some overdispersion modelling approaches. J. Appl. Stat. 2012, 39, 1011–1036. [Google Scholar] [CrossRef]
- Aragon, D.C.; Queiroz, J.A.M.D.; Martinez, E.Z. Incidence of snakebites from 2007 to 2014 in the State of São Paulo, Southeast Brazil, using a Bayesian time series model. Rev. Soc. Bras. Med. Trop. 2016, 49, 515–519. [Google Scholar] [CrossRef]
- Nogueira, R.L.; Küpper, D.S.; do Bonfim, C.M.; Aragon, D.C.; Damico, T.A.; Miura, C.S.; Passos, I.M.; Nogueira, M.L.; Rahal, P.; Valera, F.C. HPV genotype is a prognosticator for recurrence of respiratory papillomatosis in children. Clin. Otolaryngol. 2021, 46, 181–188. [Google Scholar] [CrossRef]
- Nunes, F.L.; Ferriani, M.P.; Moreno, A.S.; Langer, S.S.; Maia, L.S.; Ferraro, M.F.; Sarti, W.; de Bessa Junior, J.; Cunha, D.; Suffritti, C.; et al. Decreasing attacks and improving quality of life through a systematic management program for patients with hereditary angioedema. Int. Arch. Allergy Immunol. 2021, 182, 697–708. [Google Scholar] [CrossRef]
- Phiri, B.B.; Ngwira, B.; Kazembe, L.N. Analysing risk factors of co-occurrence of schistosomiasis haematobium and hookworm using bivariate regression models: Case study of Chikwawa, Malawi. Parasite Epidemiol. Control 2016, 1, 149–158. [Google Scholar]
- Rigby, R.A.; Stasinopoulos, M.D.; Heller, G.Z.; De Bastiani, F. Distributions for Modeling Location, Scale, and Shape: Using GAMLSS in R; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- De Andrade, H.L.P.; Arroyo, L.H.; Yamamura, M.; Ramos, A.C.V.; de Almeida Crispim, J.; Berra, T.Z.; Santos Neto, M.; Carvalho Pinto, I.; Palha, P.F.; Monroe, A.A.; et al. Social inequalities associated with the onset of tuberculosis in disease-prone territories in a city from northeastern Brazil. J. Infect. Dev. Ctries. 2021, 15, 1443–1452. [Google Scholar] [CrossRef]
- Giacomet, C.L.; Ramos, A.C.V.; Moura, H.S.D.; Berra, T.Z.; Alves, Y.M.; Delpino, F.M.; Farley, J.E.; Reynolds, N.R.; Bodini Alonso, J.; Teibo, T.K.A.; et al. A distributional regression approach to modeling the impact of structural and intermediary social determinants on communities burdened by tuberculosis in Eastern Amazonia–Brazil. Arch. Public Health 2023, 81, 135. [Google Scholar] [CrossRef]
- Hu, Y.; Duan, X.; Zhang, Z.; Lu, C.; Zhang, Y. Effects of adverse events and 12-week group step aerobics on sleep quality in Chinese adolescents. Children 2023, 10, 1253. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Rajalu, B.M.; Devi, B.I.; Shukla, D.P.; Shukla, L.; Jayan, M.; Prasad, K.; Jayarajan, D.; Kandasamy, A.; Murthy, P. Traumatic brain injury during COVID-19 pandemic—Time-series analysis of a natural experiment. BMJ Open 2022, 12, e052639. [Google Scholar] [CrossRef]
- Schmidt, J.; Vogel, M.; Poulain, T.; Kiess, W.; Hirsch, C.; Ziebolz, D.; Haak, R. Association of oral health conditions in adolescents with social factors and obesity. Int. J. Environ. Res. Public Health 2022, 19, 2905. [Google Scholar]
- Khoei, R.A.A.; Kazemnejad, A.; Eskandari, F.; Heidarzadeh, M. Analysis of infant congenital malformation data using the Bayesian count regression. Iran. Red Crescent Med. J. 2021, 23, e180. [Google Scholar]
- Green, J.A. Too many zeros and/or highly skewed? A tutorial on modelling health behaviour as count data with Poisson and negative binomial regression. Health Psychol. Behav. Med. 2021, 9, 436–455. [Google Scholar]
- Orooji, A.; Sahranavard, T.; Shakeri, M.T.; Tajfard, M.; Saffari, S.E. Application of the truncated zero-inflated double Poisson for determining of the effecting factors on the number of coronary artery stenosis. Comput. Math. Methods Med. 2022, 1, 5353539. [Google Scholar] [CrossRef] [PubMed]
- Stasinopoulos, D.M.; Rigby, R.A. Generalized additive models for location scale and shape (GAMLSS) in R. J. Stat. Softw. 2008, 23, 1–46. [Google Scholar]
- Stasinopoulos, M.D.; Kneib, T.; Klein, N.; Mayr, A.; Heller, G.Z. Generalized Additive Models for Location, Scale and Shape: A Distributional Regression Approach, with Applications; Cambridge University Press: Cambridge, UK, 2024; Volume 56. [Google Scholar]
- Carroll, R.; Lawson, A.B.; Faes, C.; Kirby, R.S.; Aregay, M.; Watjou, K. Comparing INLA and OpenBUGS for hierarchical Poisson modeling in disease mapping. Spat. Spatiotemporal Epidemiol. 2015, 14, 45–54. [Google Scholar]
- Akib, M.M.H.; Afroz, F.; Pal, B. Beyond averages: Dissecting urban-rural disparities in skilled antenatal care utilization in Bangladesh-a conway-maxwell-poisson regression analysis. BMC Pregnancy Childbirth 2025, 25, 119. [Google Scholar] [CrossRef]
- Hohberg, M.; Pütz, P.; Kneib, T. Treatment effects beyond the mean using distributional regression: Methods and guidance. PLoS ONE 2020, 15, e0226514. [Google Scholar] [CrossRef]
- Nogueira-Pileggi, V.; Achcar, M.C.; Carmona, F.; da Silva, A.C.; Aragon, D.C.; da Veiga Ued, F.; de Oliveira, M.M.; Fonseca, L.M.M.; Alves, L.G.; Bomfim, V.S.; et al. LioNeo project: A randomised double-blind clinical trial for nutrition of very-low-birth-weight infants. Br. J. Nutr. 2022, 128, 2490–2497. [Google Scholar]
- Sathyanarayana, S.; Mohanasundaram, T. Fit indices in structural equation modeling and confirmatory factor analysis: Reporting guidelines. Asian J. Econ. Bus. Account. 2024, 24, 561–577. [Google Scholar] [CrossRef]
- Sellers, K.F.; Morris, D.S. Underdispersion models: Models that are “under the radar”. Commun. Stat. Theory Methods 2017, 46, 12075–12086. [Google Scholar] [CrossRef]
- Lindsey, J.K.; Altham, P.M.E. Analysis of the human sex ratio by using overdispersion models. J. R. Stat. Soc. C Appl. Stat. 1998, 47, 149–157. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.Y.; Suchindran, C.M.; Pan, W.H. Using the overdispersed exponential family to estimate the distribution of usual daily intakes of people aged between 18 and 28 in Taiwan. Stat. Med. 2001, 20, 2337–2350. [Google Scholar] [CrossRef] [PubMed]
- King, G. Variance specification in event count models: From restrictive assumptions to a generalized estimator. Am. J. Political Sci. 1989, 33, 762–784. [Google Scholar] [CrossRef]
- Nandi, A.; Hazarika, P.J.; Biswas, A.; Hamedani, G.G. A new three-parameter discrete distribution to model over-dispersed count data. Pak. J. Stat. Oper. Res. 2024, 20, 197–215. [Google Scholar] [CrossRef]
| Distribution | Dispersion a | Expected Value E(Y) b | Variance b | Interpretation of Coefficients c | ||
|---|---|---|---|---|---|---|
| Under- | Equi- | Over- | ||||
| Poisson | − | + | − | IRR | ||
| Negative Binomial | − | + | + | IRR | ||
| Restricted Generalized Poisson | (+) | + | + | IRR | ||
| Conway– Maxwell–Poisson | + | + | + | (IRR) after mean- parameterization | ||
| Double Poisson | + | + | + | IRR | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Appelbaum, S.; Stronski, J.; Konerding, U.; Ostermann, T. The Use of Double Poisson Regression for Count Data in Health and Life Science—A Narrative Review. Stats 2025, 8, 90. https://doi.org/10.3390/stats8040090
Appelbaum S, Stronski J, Konerding U, Ostermann T. The Use of Double Poisson Regression for Count Data in Health and Life Science—A Narrative Review. Stats. 2025; 8(4):90. https://doi.org/10.3390/stats8040090
Chicago/Turabian StyleAppelbaum, Sebastian, Julia Stronski, Uwe Konerding, and Thomas Ostermann. 2025. "The Use of Double Poisson Regression for Count Data in Health and Life Science—A Narrative Review" Stats 8, no. 4: 90. https://doi.org/10.3390/stats8040090
APA StyleAppelbaum, S., Stronski, J., Konerding, U., & Ostermann, T. (2025). The Use of Double Poisson Regression for Count Data in Health and Life Science—A Narrative Review. Stats, 8(4), 90. https://doi.org/10.3390/stats8040090






