1. Introduction
Research on reliability studies cannot be complete without mentioning exponential distributions. This has led many researchers to overlook other more flexible distributions in the analysis of lifetime data such as Gamma, Weibull, Lindley, and Log-normal distributions. The Lindley distribution was proposed by Lindley [
1,
2] as part of the larger exponential family and as a more superior competitor distribution for models based on the exponential distribution. In fact, Ghitany et al. [
3] found that the Lindley distribution is a better alternative distribution for exponential distributions and provided a wide range of properties of the Lindley distribution such as moments, failure rate function, mean residual life function, and maximum likelihood estimation, among many others. The Lindley distribution is an example of an exponential family and has been expressed as a mixture of two well-known distributions, Exponential and Gamma distributions such that its probability distribution function (pdf),
in Equation (
1) can be written as
where
,
,
and
is the scale parameter.
In recent years, studies involving Lindley distribution have gained momentum and have shown great success in areas such as modeling and analyzing survival, reliability, and failure lifetime-related data. One advantage of the Lindley distribution over the exponential distribution is the fact that it possesses an increasing hazard rate function and a decreasing mean residual life function whereas in the latter both functions are constant; see more details in Ghitany et al. [
3]. These studies are very important and common in applied sciences such as construction, engineering, medicine, insurance, banking, and many others. Several authors have studied possible applications of the Lindley distribution. Such studies stem from distribution properties (Ghitany et al. [
3], Lindley [
1]), bayesian estimation (Ali et al. [
4], Ali et al. [
4]), estimation of the stress–strength reliability parameter (Al-Mutairi et al. [
5]) and load-sharing parallel system model and its application (Singh and Gupta [
6]). Currently, there are several generalizations and extensions of the Lindley distribution such as the double Lindley distribution, the Kumaraswamy quasi Lindley distribution, the Log-Lindley distribution, the exponentiated power Lindley distribution, and the generalized weighted Lindley distribution, among others; see, for example, Satheesh Kumar and Jose [
7], Ibrahim et al. [
8], Nedjar and Zeghdoudi [
9], Ramos and Louzada [
10], Gómez-Déniz et al. [
11], and Elbatal and Elgarhy [
12].
Definition 1. Let . The pdf and cdf of X are given by andrespectively, and θ is the scale parameter. Its mean and variance are given as
and
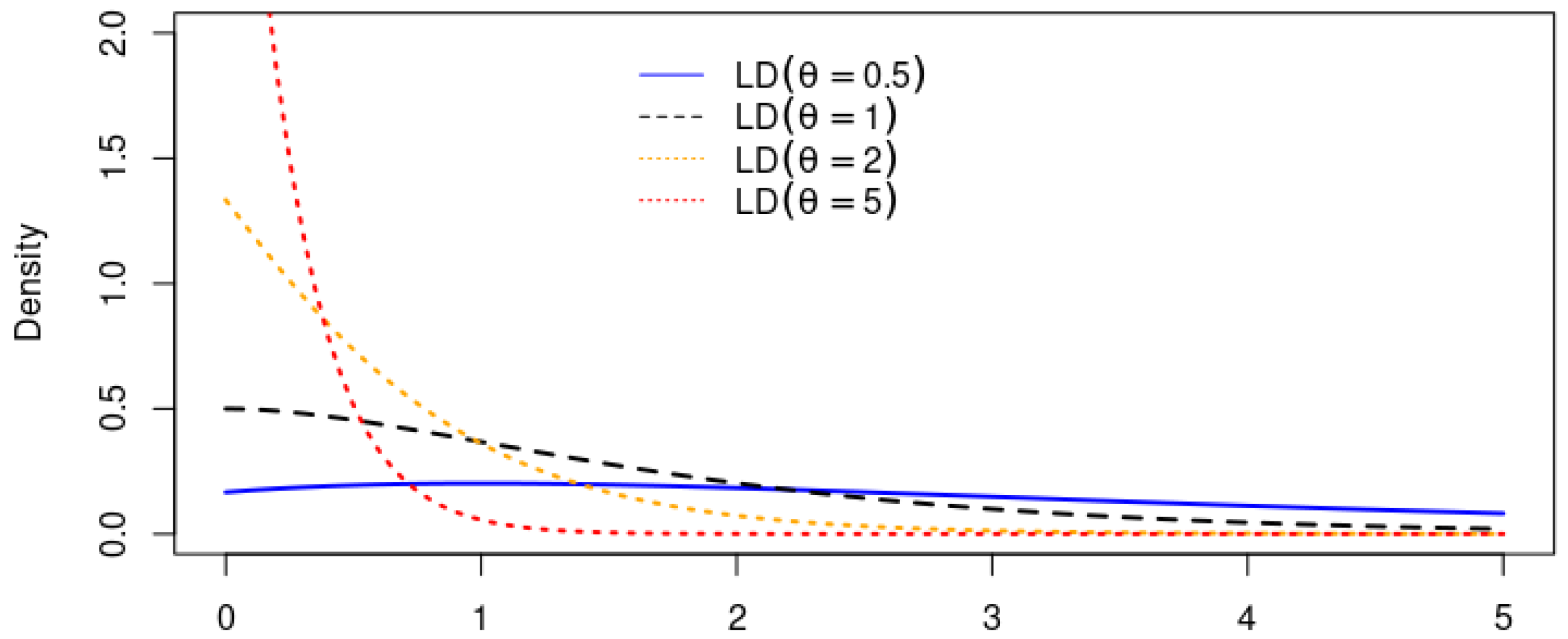
Figure 1 provides some examples of the forms that the density function in Equation (
1) can take for selected values of the scale parameter
We note that both method of moments (MoM) and maximum likelihood (ML) estimates of the scale parameter
are the same and defined as follows.
Definition 2. Let be a random sample from the Lindley distribution, the maximum likelihood (ML) or method of moments (MoM) estimate of the scale parameter θ is given aswhere is the sample mean. Ghitany et al. [
3] proved that in this estimate,
is positively biased, that is,
. In addition, the estimate is consistent and asymptotically normal with mean zero and standard deviation
, where
is given in Equation (
4); for further details, see, for example, Ghitany et al. [
3]. We will use this estimate of the scale parameter
in the development of the energy goodness-of-fit statistic for the Lindley distribution. These well-established properties of the Lindley distribution to provide a desirable environment for the construction of goodness-of-fit tests. Although we have seen a significant amount of research on the Lindley distribution and its applications, there is limited research in the literature on the goodness-of-fit test for the distribution. Authors such as Noughabi and Noughabi [
13], Noughabi and Noughabi [
14], and Noughabi [
15] have proposed a goodness-of-fit test for the Lindley distribution based on estimates of the Gini index, Empirical likelihood ratio (ELR) and Kullback–Leibler (KL) discrimination, respectively. In the literature, different goodness-of-fit tests for different statistical distributions have been proposed, see, for example, Best and Rayner [
16], Shan et al. [
17], Vexler et al. [
18], and Rizzo [
19], Noughabi and Noughabi [
20], among many others. For example, Vexler et al. [
18] and Vexler and Gurevich [
21] applied the empirical likelihood ratio to test goodness-of-fit for inverse gaussian distribution and on sample entropy, respectively. Best and Rayner [
16] proposed smooth tests of fit for the Lindley and Poisson–Lindley distributions. Ning and Ngunkeng [
22] and Gupta and Chen [
23] proposed goodness-of-fit tests for the Skew-normal distribution based on the empirical likelihood ratio and Pearson’s
tests, respectively. Other tests available in the literature are the well-known and common EDF tests, which are based on empirical distribution functions, see, for example, Stephens [
24] and Stephens [
25]. We thus introduce a more competitive testing procedure based on energy statistics proposed by Sźekely [
26] and Rizzo [
27]. Sźekely and Rizzo [
28] have demonstrated extensively the superiority of energy-based tests over many other tests, such as EDF-based, Gini index and Kullback–Leibler discrimination tests.
In this article, we propose a one-sample (univariate) goodness-of-fit test based on energy statistics ( Sźekely [
26] and Rizzo [
27]). In a more recent work, Logan and Ning [
29] proposed a goodness-of-fit test using energy statistics for the Skew-normal distribution and Ofosuhene [
30] developed a goodness-of-fit test based on energy statistics and distance correlation for inverse-gaussian distribution. There are a few other research works in the literature involving the energy goodness-of-fit test for some known distributions, see, for example, Sźekely and Rizzo [
28] and Rizzo [
19]. For a given sequence of independent random variables of size
n and with a cdf
, the test statistic based on energy statistics will reject the null that
for large values of test statistics. If the null distribution
and the given data come from the same underlying distribution, then values of the test statistic are expected to be small. In addition, there are several other studies involving energy distance statistics such as testing for multivariate normality (Sźekely and Rizzo [
31]), testing for equality of distributions (Sźekely and Rizzo [
32], Rizzo [
33]), and change point analysis (Njuki and Ning [
34], Njuki [
35], Matterson and James [
36], Kim et al. [
37]), among many others.
The energy distance is defined as a statistical distance between the distributions of random vectors which characterizes equality of distributions, see, for example, Sźekely and Rizzo [
28,
38,
39] and Sźekely [
26]. The concept of energy statistics initially described by Sźekely [
40] is based on the notion of Newton’s gravitational potential energy, which is a function of the distance between two bodies; for further details, see Sźekely and Rizzo [
38]. The idea of energy statistics therefore is to consider statistical observations as heavenly bodies governed by a statistical potential energy, which is zero if and only if an underlying statistical null hypothesis is true, see, for example, Sźekely and Rizzo [
28,
38]. In this work, we propose a procedure that is more superior for the goodness-of-fit test for the Lindley distribution (Lindley [
1])-based energy statistics. Unlike the proposed method based on energy statistics, most of the existing methods depend on the (empirical) distribution function of random variables. Energy-type tests have been shown to be typically more powerful against general alternatives than corresponding tests, especially those based on classical statistics (non-energy type) such as Kolmogorov–Smirnov, Anderson Darling (Anderson and Darling [
41]), Watson statistic (Watson [
42]), and Kuiper statistic (Kuiper [
43]). Furthermore, energy statistic-based tests have an additional advantage such that these tests have an invariance property with respect to any distance-preserving transformation of the dataset, see, for example, Sźekely and Rizzo [
28,
38] and Matterson and James [
36]. Tests based on energy statistics can be easily extended to multivariate and high dimension settings, see, for example, Sźekely and Rizzo [
31], Rizzo [
33] and Sźekely and Rizzo [
32].
We organize this article as follows. In
Section 2, we propose a testing procedure based on energy statistics for the goodness-of-fit test and establish its theoretical results on the Lindley distribution. We perform different simulations in
Section 3 to compare the results of our energy goodness-of-fit test with other existing ones. In
Section 4, we demonstrate the application of our method using three real-life datasets. The conclusion is provided in
Section 5. The proofs to new results and other supplemental materials are given in the
Appendix A.
2. The Energy Goodness-of-Fit Statistic for the Lindley Distribution
We propose a test procedure for the goodness-of-fit test based on the energy statistics for the Lindley distribution. Next, we define the energy goodness-of-fit test based on the characterization of equal distributions.
Definition 3. (Energy distance). If X and Y are independent random vectors with and , then the energy distance between X and Y is defined as follows: , , and equality holds if and only if X and Y are identically distributed.
The energy distance between two independent distributions is thus given by Equation (
6) and hence, under the null hypothesis, it is assumed that the data follow a null (Lindley) distribution against a general alternative hypothesis. Let
be a sample of random observations from the distribution
F and
null distribution, then the empirical one-sample goodness-of-fit test based on energy statistics for testing
versus
is defined as
where
X and
are independently and identically distributed random variables from the null distribution,
The null hypothesis,
is rejected for large values of the test statistic
, where
in our case. Under the null hypothesis, the limiting distribution of
is a quadratic quantity of the form
such that
are i.i.d. standard normal random variables and
are nonnegative constants that depend on the null distribution. Thus, the goodness-of-fit test can be implemented by finding the constants
In practice, this could be difficult, and we therefore resort to the use of the Monte Carlo simulation approach to obtain empirical critical values of
so that
This fact is guaranteed since the test based on
is a consistent goodness-of-fit test against all general alternatives, see, for example Sźekely and Rizzo [
31] and Móri et al. [
44].
The establishment of the energy statistic-based goodness-of-fit test for the Lindley distribution in Equation (
7) depends on the expected distances
and
, where
X and
are i.i.d. copies from the Lindley distribution.
Proposition 1. Let , then for any fixed A full proof of Proposition 1 is provided in
Appendix A.
Proposition 2. Let X and be independent and identically distributed random variables from a Lindley distribution with the shape parameter Then, The detailed proof of Proposition 2 involving integration by parts and expansion of the joint expectation is deferred to
Appendix A.
Proposition 3. Let be a sequence of independent random variables from the null distribution and let be the ordered sample. Then, the last term of the test statistic in Equation (7) can be linearized as follows; Proof. The proof of Proposition 3 is given by Proposition 3.3 of Ofosuhene [
30] and Rizzo [
27]. □
This linearization will reduce the computational complexity of the test from
to
, which is useful during extensive operations and simulations. Thus, the one-sample (univariate case) energy goodness-of-fit test for the Lindley distribution based on Equation (
7) together with Propositions 1, 2, and 3 is defined as
where
is the observed sample values and
4. Application to the Real-Life Datasets
In this section, the performance of the proposed test is investigated using three real datasets. We will apply the test to determine whether or not the underlying distribution is the Lindley one. We use the bootstrap algorithm process through simulations to find the approximate p-value associated with the proposed test as described below.
Fit the original data
with a Lindley distribution,
, and use the formula in Equation (
5) to obtain the maximum likelihood estimate (MLE) of
.
Use the formula in Equation (
11) to calculate the energy goodness-of-fit statistic of the original data and denote it
.
Simulate , a random sample of size from a distribution, where is obtained in step 1.
Compute the energy goodness-of-fit statistic using the formula in Equation (
11) for the simulated data and denote it
.
Repeat this simulation procedure for B times and obtain B energy goodness-of-fit statistics and denote them as .
The
p-value will then be approximated as
where
is an indicator function that takes the value of one when
and zero otherwise.
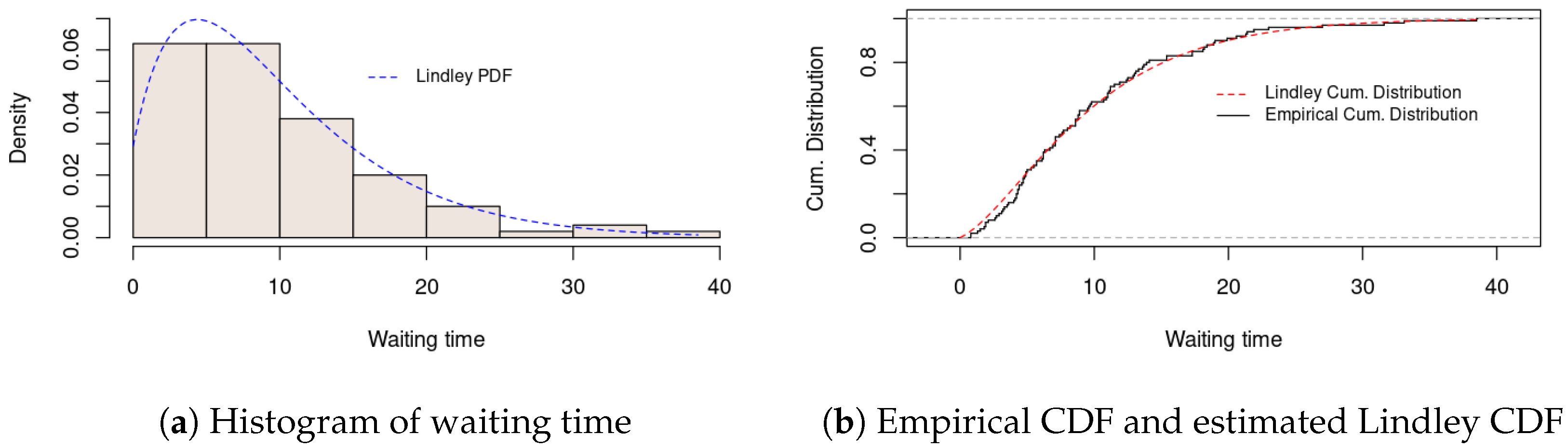
In our applications, the first dataset is listed in
Table A1, which contains waiting times (in minutes) before service for 100 bank customers analyzed in [
3]. The maximum likelihood estimate (MLE) of the scale parameter is
, and its corresponding value of our test statistic is
. Since the simulated
p-value is approximately
, we do not reject the null that the data follow the Lindley distribution. Other tests except the Cramer-von-Mises statistic suggested that the data follow the Lindley distribution. Their estimated
p-values and test statistics are reported in
Table A4.
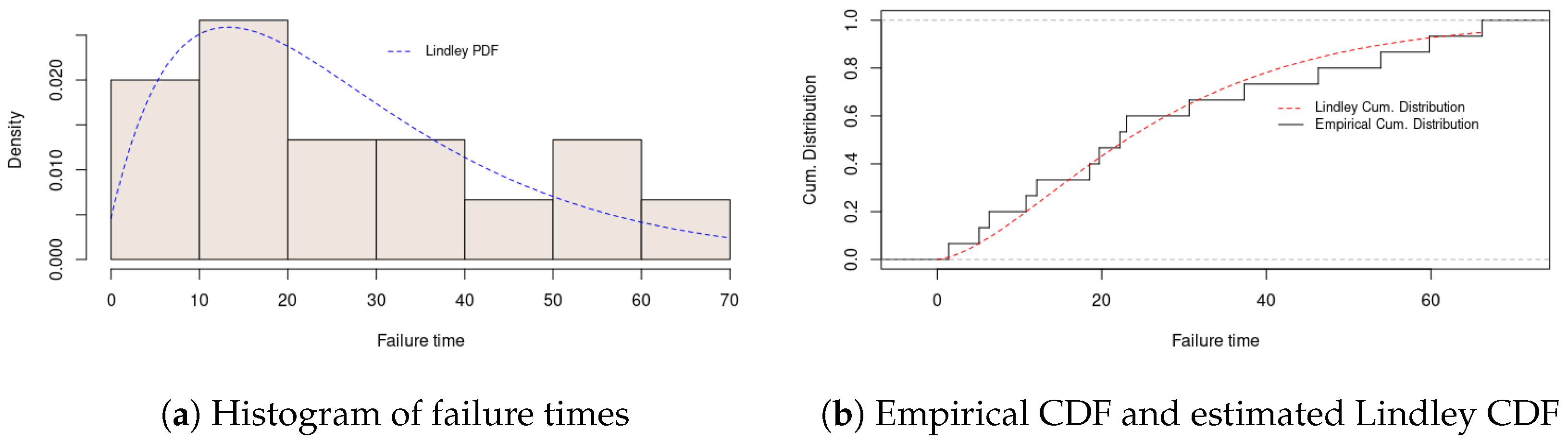
The second dataset provided in
Table A2 contains failure times of the electronic components in an accelerated life test. The data are reported and analyzed by Lawless [
45]. The MLE of our test statistic is
, and its corresponding value of test statistic is
. Since the simulated
p-value is approximately
, we do not reject the null that the data follow the Lindley distribution. We observe in
Table A5 a similar conclusion for other tests except for the Cramer-von-Mises test statistic, which fails to support the underlying distribution assumption as the Lindley one.
Table A3 provides our last dataset, which contains the quality of the yarn by recording the number of stress cycles needed before the yarn breaks. This dataset was originally analyzed by [
46], and Shanker and Fesshaye [
47] used the same dataset as an illustrative example in their analysis. The MLE of our test statistic is
, and the test statistic value is
. The empirical
p-value is approximately
, and therefore we do not reject the null hypothesis that the data follow the Lindley distribution. In addition, the Kolmogorov–Smirnov test statistic, the Anderson–Darling test statistic, the Kuiper test statistic, and the Watson test statistic provide little to no evidence to reject the null hypothesis that the data do follow the Lindley distribution. The Cramer-von-Mises test statistic again fails to support the fact that the data can be modeled with the Lindley distribution. The approximate
p-values and their corresponding test statistics are reported in
Table A6.
Finally,
Figure 2a,
Figure 3a, and
Figure 4a provide density estimates for each of our three datasets considered in this study. In addition,
Figure 2b,
Figure 3b, and
Figure 4b compare empirical and theoretical distribution functions for these real datasets. In both situations, the Lindley distribution seems to fit the datasets adequately. Surprisingly, it is worthy to note that the Cramer-von-Mises test rejected the null hypothesis for all of our empirical applications.