A Simulation-Based Comparative Analysis of Two-Parameter Robust Ridge M-Estimators for Linear Regression Models
Abstract
1. Introduction
2. Materials and Method
2.1. Existing Estimators
- The groundbreaking ridge estimator introduced by Hoerl & Kennard (1970a) is as follows [5]:where
- The second ridge estimator introduced by Hoerl & Kennard (1970b) is as follows [24]:
- 3.
- Ref. [14] generalized the idea of Hoerl & Kennard (1970a) and suggested a new estimator, denoted as HKB:
- 4.
- 5.
2.2. Two-Parameter Ridge Regression Estimator
- 3.
- The latest advancements in the field of TPRRE were introduced by Khan et al. (2024) [11], who proposed six new estimators with the goal of enhancing the accuracy of ridge estimation.
2.3. Proposed Estimator
3. Simulation Study
3.1. Simulation Design
3.2. Performance Evaluation Criteria
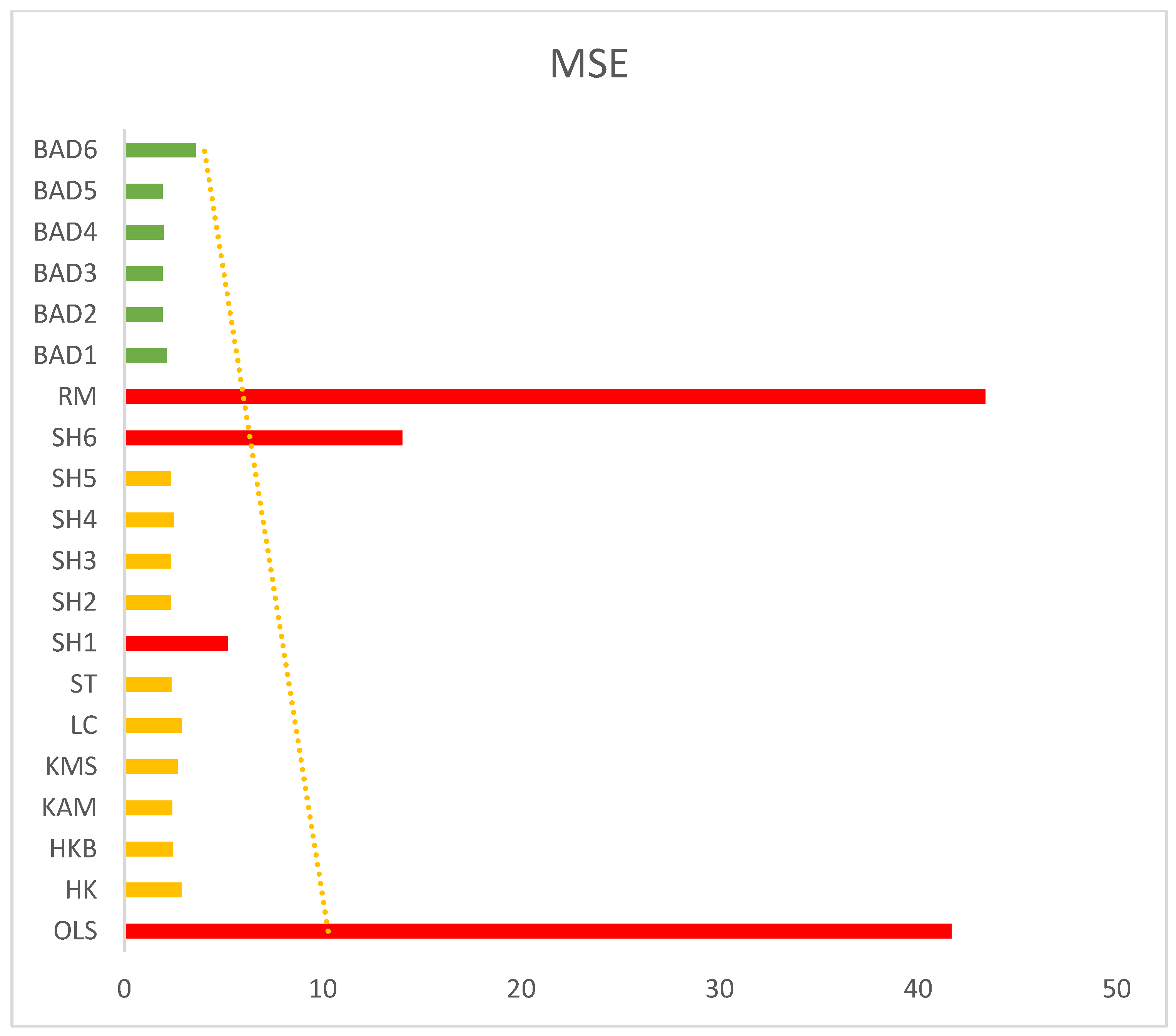
3.3. Simulation Results Discussion
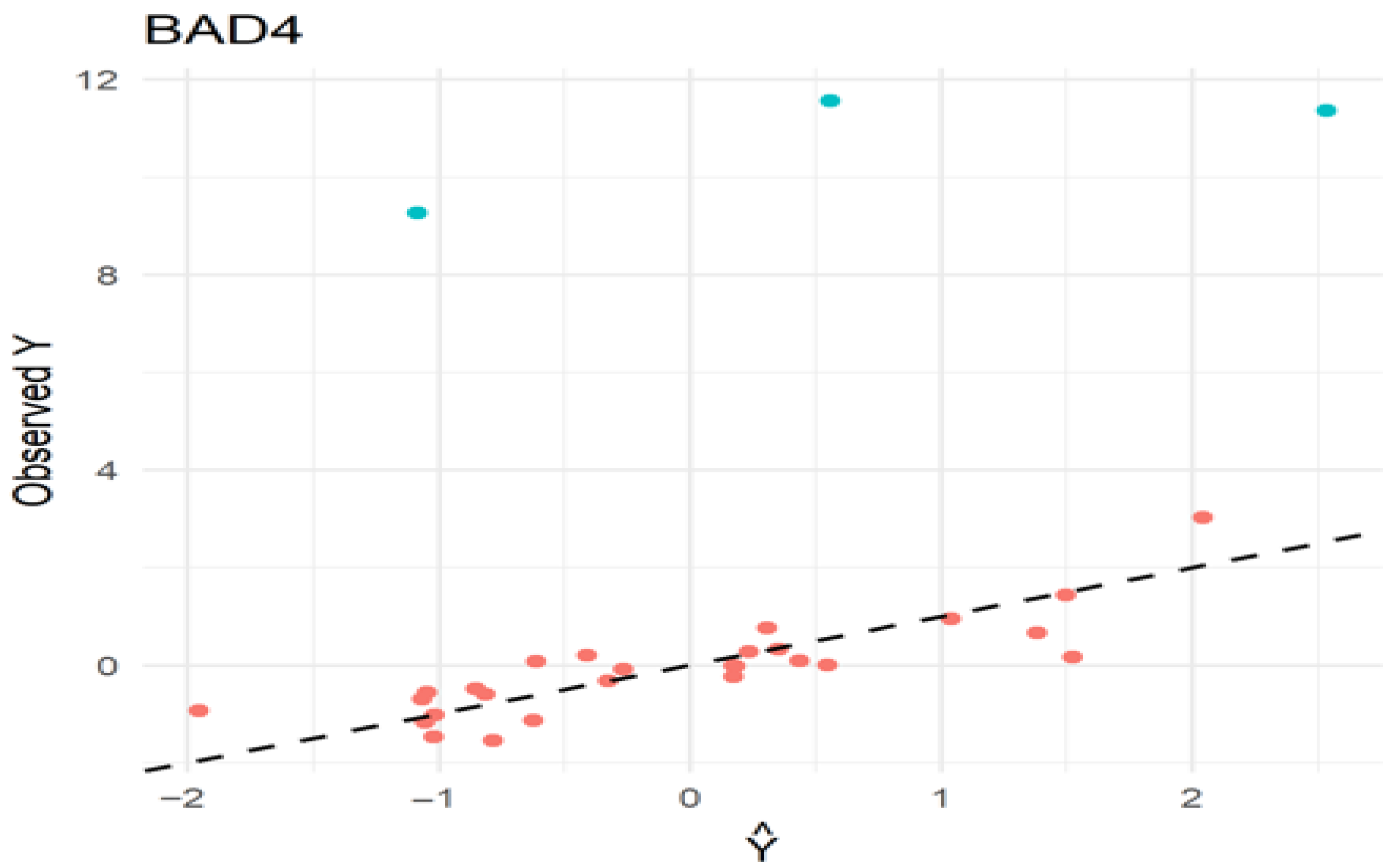
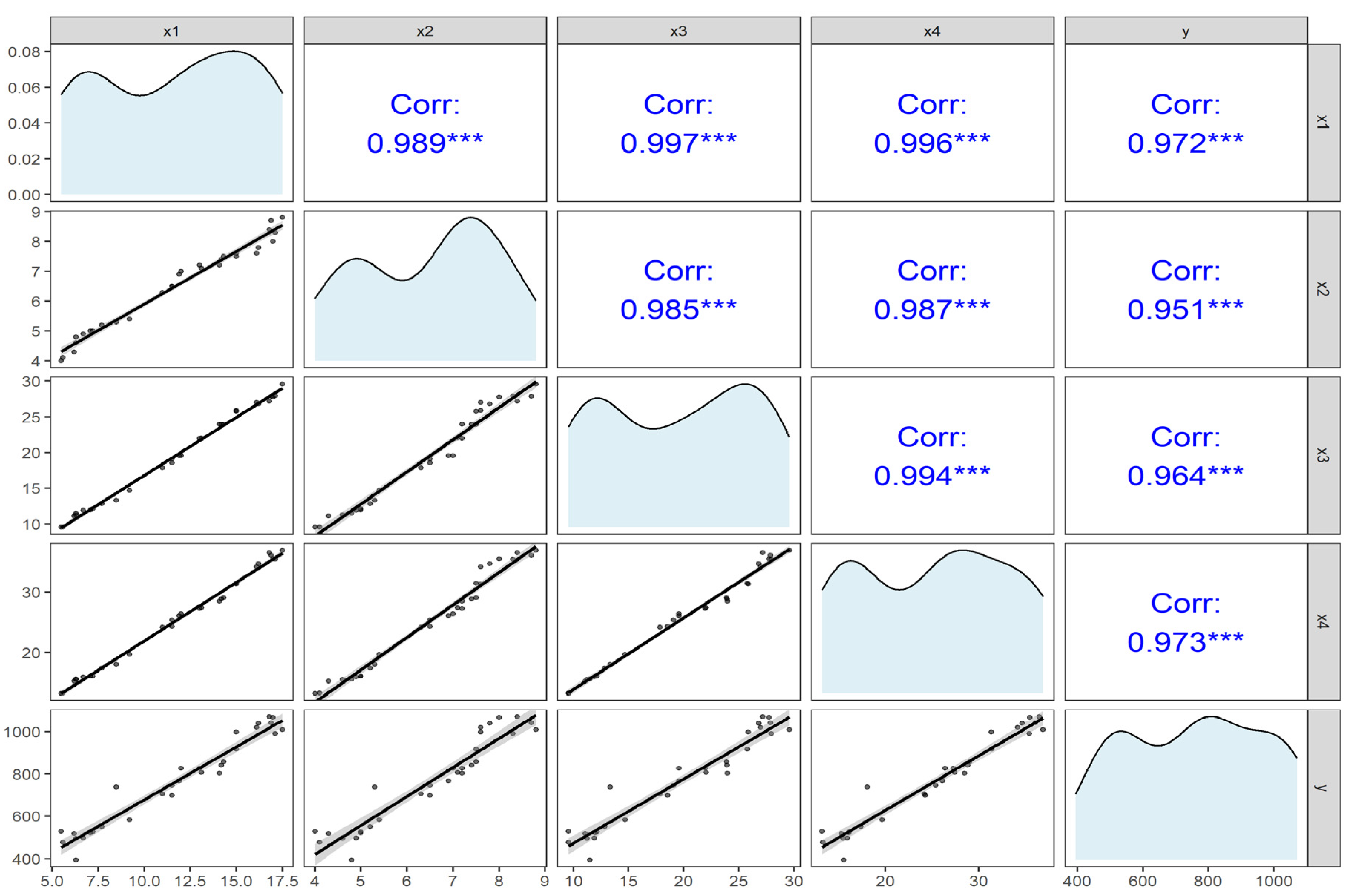
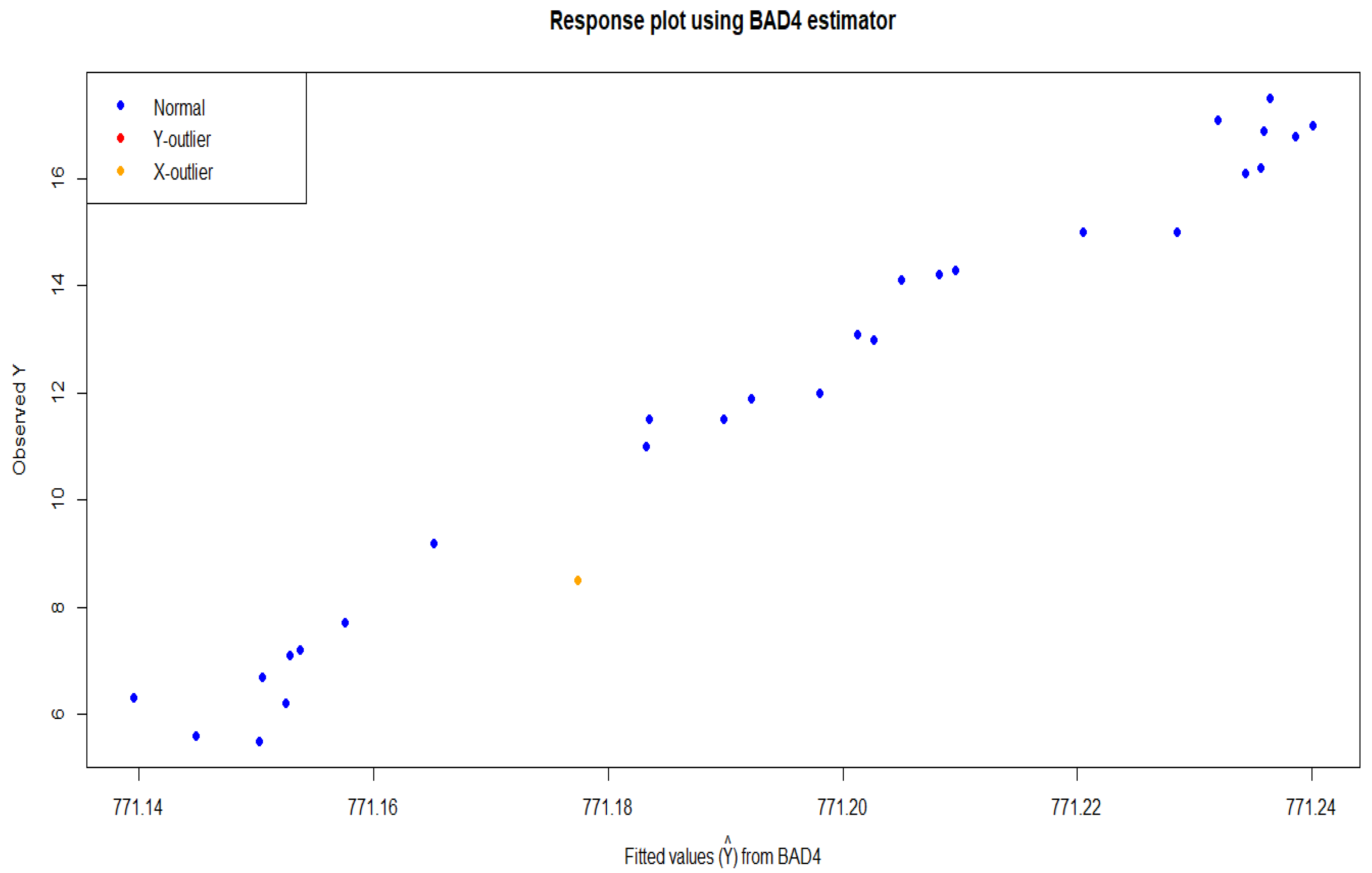
4. Real Life Application
4.1. Tobacco Data
4.2. Gasoline Consumption Data
5. Some Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mao, S. Statistical Derivation of Linear Regression. In International Conference on Statistics, Applied Mathematics, and Computing Science (CSAMCS 2021); SPIE: Bellingham, WA, USA, 2022; Volume 12163, pp. 893–901. [Google Scholar]
- Maulud, D.; Abdulazeez, A.M. A Review on Linear Regression Comprehensive in Machine Learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Lukman, A.F.; Mohammed, S.; Olaluwoye, O.; Farghali, R.A. Handling Multicollinearity and Outliers in Logistic Regression Using the Robust Kibria–Lukman Estimator. Axioms 2024, 14, 19. [Google Scholar] [CrossRef]
- Lukman, A.F.; Jegede, S.L.; Bellob, A.B.; Binuomote, S.; Haadi, A. Modified Ridge-Type Estimator with Prior Information. Int. J. Eng. Res. Technol. 2019, 12, 1668–1676. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Mermi, S.; Göktaş, A.; Akkuş, Ö. How Well Do Ridge Parameter Estimators Proposed so Far Perform in Terms of Normality, Outlier Detection, and MSE Criteria? Commun. Stat. Comput. 2024. [Google Scholar] [CrossRef]
- Lipovetsky, S.; Conklin, W.M. Ridge Regression in Two-Parameter Solution. Appl. Stoch. Model. Bus. Ind. 2005, 21, 525–540. [Google Scholar] [CrossRef]
- Toker, S.; Kaçiranlar, S. On the Performance of Two Parameter Ridge Estimator under the Mean Square Error Criterion. Appl. Math. Comput. 2013, 219, 4718–4728. [Google Scholar] [CrossRef]
- Abdelwahab, M.M.; Abonazel, M.R.; Hammad, A.T.; El-Masry, A.M. Modified Two-Parameter Liu Estimator for Addressing Multicollinearity in the Poisson Regression Model. Axioms 2024, 13, 46. [Google Scholar] [CrossRef]
- Alharthi, M.F.; Akhtar, N. Modified Two-Parameter Ridge Estimators for Enhanced Regression Performance in the Presence of Multicollinearity: Simulations and Medical Data Applications. Axioms 2025, 14, 527. [Google Scholar] [CrossRef]
- Shakir, M.; Ali, A.; Suhail, M.; Sadun, E. On the Estimation of Ridge Penalty in Linear Regression: Simulation and Application. Kuwait J. Sci. 2024, 51, 100273. [Google Scholar] [CrossRef]
- Khan, M.S. Adaptive Penalized Regression for High-Efficiency Estimation in Correlated Predictor Settings: A Data-Driven Shrinkage Approach. Mathematics 2025, 13, 2884. [Google Scholar] [CrossRef]
- Silvapulle, M.J. Robust Ridge Regression Based On An M-Estimator. Austral. J. Stat. 1991, 33, 319–333. [Google Scholar]
- Hoerl, A.E.; Kannard, R.W.; Baldwin, K.F. Ridge Regression: Some Simulations. Commun. Stat. Methods 1975, 4, 105–123. [Google Scholar] [CrossRef]
- Lawless, J.F.; Wang, P. A Simulation Study Of Ridge And Other Regression Estimators. Commun. Stat.—Theory Methods 1976, 5, 307–323. [Google Scholar] [CrossRef]
- Begashaw, G.B.; Yohannes, Y.B. Review of Outlier Detection and Identifying Using Robust Regression Model. Int. J. Syst. Sci. Appl. Math. 2020, 5, 4–11. [Google Scholar] [CrossRef]
- Majid, A.; Ahmad, S.; Aslam, M.; Kashif, M. A Robust Kibria–Lukman Estimator for Linear Regression Model to Combat Multicollinearity and Outliers. Concurr. Comput. Pract. Exp. 2023, 35, e7533. [Google Scholar] [CrossRef]
- Suhail, M.; Chand, S.; Aslam, M. New Quantile Based Ridge M-Estimator for Linear Regression Models with Multicollinearity and Outliers. Commun. Stat. Simul. Comput. 2023, 52, 1418–1435. [Google Scholar] [CrossRef]
- Wasim, D.; Suhail, M.; Albalawi, O.; Shabbir, M. Weighted Penalized M-Estimators in Robust Ridge Regression: An Application to Gasoline Consumption Data. J. Stat. Comput. Simul. 2024, 94, 3427–3456. [Google Scholar] [CrossRef]
- Ertaş, H.; Toker, S.; Kaçıranlar, S. Robust Two Parameter Ridge M-Estimator for Linear Regression. J. Appl. Stat. 2015, 42, 1490–1502. [Google Scholar] [CrossRef]
- Yasin, S.; Salem, S.; Ayed, H.; Kamal, S.; Suhail, M.; Khan, Y.A. Modified Robust Ridge M-Estimators in Two-Parameter Ridge Regression Model. Math. Probl. Eng. 2021, 2021, 1845914. [Google Scholar] [CrossRef]
- Wasim, D.; Khan, S.A.; Suhail, M. Modified Robust Ridge M-Estimators for Linear Regression Models: An Application to Tobacco Data. J. Stat. Comput. Simul. 2023, 93, 2703–2724. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistical Procedures; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Applications to Nonorthogonal Problems. Technometrics 1970, 12, 69–82. [Google Scholar] [CrossRef]
- Kibria, B.M.G. Performance of Some New Ridge Regression Estimators. Commun. Stat. Part B Simul. Comput. 2003, 32, 419–435. [Google Scholar] [CrossRef]
- Khalaf, G.; Mansson, K.; Shukur, G. Modified Ridge Regression Estimators. Commun. Stat.—Theory Methods 2013, 42, 1476–1487. [Google Scholar] [CrossRef]
- Dar, I.S.; Chand, S.; Shabbir, M.; Kibria, B.M.G. Condition-Index Based New Ridge Regression Estimator for Linear Regression Model with Multicollinearity. Kuwait J. Sci. 2023, 50, 91–96. [Google Scholar] [CrossRef]
- Ali, A.; Suhail, M.; Awwad, F.A. On the Performance of Two-Parameter Ridge Estimators for Handling Multicollinearity Problem in Linear Regression: Simulation and Application. AIP Adv. 2023, 13, 115208. [Google Scholar] [CrossRef]
- Ertaş, H. A Modified Ridge M-Estimator for Linear Regression Model with Multicollinearity and Outliers. Commun. Stat. Simul. Comput. 2018, 47, 1240–1250. [Google Scholar] [CrossRef]
- Suhail, M.; Chand, S.; Kibria, B.M.G. Quantile-Based Robust Ridge m-Estimator for Linear Regression Model in Presence of Multicollinearity and Outliers. Commun. Stat. Simul. Comput. 2021, 50, 3194–3206. [Google Scholar] [CrossRef]
- Wasim, D.; Khan, S.A.; Suhail, M.; Shabbir, M. New Penalized M-Estimators in Robust Ridge Regression: Real Life Applications Using Sports and Tobacco Data. Commun. Stat. Simul. Comput. 2025, 54, 1746–1765. [Google Scholar] [CrossRef]
- Myers, R.H.; Sliema, B. Classical and Modern Regression with Applications; Duxbury Thomson Learning: Pacific Grove, CA, USA, 1990. [Google Scholar]
- Babar, I.; Ayed, H.; Chand, S.; Suhail, M.; Khan, Y.A.; Marzouki, R. Modified Liu Estimators in the Linear Regression Model: An Application to Tobacco Data. PLoS ONE 2021, 16, e0259991. [Google Scholar] [CrossRef]

| 0.85 | 0.95 | 0.99 | 0.999 | 0.85 | 0.95 | 0.99 | 0.999 | |
|---|---|---|---|---|---|---|---|---|
| OLS | 6.54715199 | 20.95106882 | 105.5304231 | 1066.107042 | 8.78480056 | 27.33002393 | 139.1731178 | 1345.611102 |
| HK | 3.33311058 | 10.47577522 | 52.14910175 | 525.7322212 | 4.51098404 | 13.83365763 | 70.61252185 | 669.4597999 |
| HKB | 1.94987753 | 5.57549348 | 26.39481325 | 263.6889613 | 2.59025794 | 7.31764713 | 36.07807873 | 334.5928801 |
| KAM | 0.51929794 | 0.39756238 | 0.24831816 | 0.21161024 | 0.7286564 | 0.77529207 | 0.86278377 | 0.44779355 |
| KMS | 1.42824372 | 7.761373 | 69.62319025 | 972.668171 | 2.19101398 | 11.39166435 | 97.70809437 | 1239.587147 |
| LC | 4.00838268 | 12.25215963 | 60.2990279 | 605.6202206 | 5.51814168 | 16.45496312 | 82.64997568 | 783.1625333 |
| ST | 36,880.4599 | 11,807.55971 | 319.6213161 | 38.78512917 | 19,398.96541 | 17,193.6689 | 336.9727693 | 190.8436776 |
| SH1 | 14.81471775 | 14.05215153 | 8.92650916 | 1.3568562 | 18.52235209 | 18.64904267 | 12.75262638 | 1.85909349 |
| SH2 | 0.08559237 | 0.19857319 | 0.07770096 | 0.07376037 | 0.11696336 | 0.29742759 | 0.11235643 | 0.09623571 |
| SH3 | 0.19472094 | 0.09973364 | 0.07699223 | 0.07375463 | 0.28193051 | 0.14878645 | 0.11081441 | 0.09622856 |
| SH4 | 0.3077928 | 0.09033178 | 0.07391053 | 0.0734318 | 0.45020753 | 0.13388056 | 0.10210345 | 0.09582625 |
| SH5 | 0.19211242 | 0.09953795 | 0.07698625 | 0.07375458 | 0.27800616 | 0.14848181 | 0.110801 | 0.09622849 |
| SH6 | 3.2720966 | 9.75407515 | 47.52873911 | 475.6987902 | 4.50813068 | 13.10802796 | 64.55541601 | 616.1533227 |
| RM | 0.01250155 | 0.03866251 | 0.1923938 | 1.9469604 | 1.18578052 | 3.72506188 | 18.26307215 | 181.1788334 |
| BAD1 | 0.00019202 | 0.00019042 | 0.0001415 | 0.00014299 | 0.02006897 | 0.04835483 | 0.02844459 | 0.09703252 |
| BAD2 | 0.00020615 | 0.00016157 | 0.00013975 | 0.00014243 | 0.02035481 | 0.01533975 | 0.01407996 | 0.01421816 |
| BAD3 | 0.00020656 | 0.00016143 | 0.00013975 | 0.00014243 | 0.02048838 | 0.01527999 | 0.01407695 | 0.01421774 |
| BAD4 | 0.0002068 | 0.0001614 | 0.00013974 | 0.00014242 | 0.02056896 | 0.01527077 | 0.01406013 | 0.01419418 |
| BAD5 | 0.00020655 | 0.00016143 | 0.00013975 | 0.00014243 | 0.02048631 | 0.01527981 | 0.01407692 | 0.01421774 |
| BAD6 | 0.00021634 | 0.00017176 | 0.00016521 | 0.00157747 | 0.02462344 | 0.02483693 | 0.33748625 | 37.31415504 |
| 0.85 | 0.95 | 0.99 | 0.999 | 0.85 | 0.95 | 0.99 | 0.999 | |
|---|---|---|---|---|---|---|---|---|
| OLS | 10.34256 | 31.88066 | 157.9254 | 1569.838901 | 13.22569722 | 40.38766039 | 202.9435159 | 1936.173262 |
| HK | 3.96519 | 11.97882 | 58.46895 | 580.7742392 | 5.19255344 | 15.82247589 | 79.48724404 | 734.9093383 |
| HKB | 2.04085 | 5.709157 | 26.36743 | 262.5894907 | 2.63296273 | 7.47857277 | 36.36066518 | 330.6130589 |
| KAM | 0.763378 | 0.793959 | 0.600503 | 0.22312187 | 0.826874 | 0.86341291 | 0.65346602 | 0.23961787 |
| KMS | 1.601057 | 9.110767 | 92.12482 | 1404.612699 | 2.46446791 | 13.9291572 | 130.8824147 | 1760.583628 |
| LC | 5.39856 | 15.54303 | 74.13663 | 729.3512174 | 7.22677512 | 20.89479407 | 102.1910372 | 949.0051419 |
| ST | 4102.904 | 693.9592 | 1887.41 | 170.7013897 | 19,454.36377 | 2825.472693 | 8103.52933 | 161,495.9898 |
| SH1 | 19.50584 | 23.27372 | 17.81338 | 3.75526815 | 23.94366267 | 29.74590963 | 24.49427889 | 3.6694769 |
| SH2 | 0.098567 | 0.335446 | 0.090245 | 0.08256641 | 0.13126183 | 0.4963387 | 0.27441331 | 0.10774046 |
| SH3 | 0.321303 | 0.132414 | 0.088944 | 0.08255631 | 0.48453326 | 0.20317726 | 0.2687795 | 0.10771952 |
| SH4 | 0.552865 | 0.113572 | 0.083324 | 0.081998 | 0.81256928 | 0.17380233 | 0.22732701 | 0.10669985 |
| SH5 | 0.315981 | 0.13202 | 0.088933 | 0.08255621 | 0.47675686 | 0.20257605 | 0.26872923 | 0.10771931 |
| SH6 | 5.903449 | 17.31502 | 83.06208 | 818.0131153 | 7.6608864 | 22.26423997 | 108.6451659 | 1031.511647 |
| RM | 0.016182 | 0.04885 | 0.243162 | 2.44535836 | 1.44260978 | 4.48611961 | 21.97417925 | 217.3198248 |
| BAD1 | 0.000217 | 0.00022 | 0.000158 | 0.00015759 | 0.0254554 | 0.07285979 | 0.04312353 | 0.18796203 |
| BAD2 | 0.000239 | 0.000177 | 0.000155 | 0.0001565 | 0.02512139 | 0.016518 | 0.01507368 | 0.01527896 |
| BAD3 | 0.000239 | 0.000177 | 0.000155 | 0.0001565 | 0.02543111 | 0.01642001 | 0.01506854 | 0.01527816 |
| BAD4 | 0.00024 | 0.000177 | 0.000155 | 0.0001565 | 0.02561886 | 0.01640499 | 0.0150402 | 0.01523528 |
| BAD5 | 0.000239 | 0.000177 | 0.000155 | 0.0001565 | 0.02542629 | 0.01641973 | 0.0150685 | 0.01527815 |
| BAD6 | 0.000255 | 0.000192 | 0.000196 | 0.00309636 | 0.0359694 | 0.03309437 | 0.59384201 | 53.76964961 |
| 0.85 | 0.95 | 0.99 | 0.999 | 0.85 | 0.95 | 0.99 | 0.999 | |
|---|---|---|---|---|---|---|---|---|
| OLS | 78.30101157 | 246.2671071 | 1282.484366 | 12,681.89645 | 97.90390012 | 297.3277576 | 1581.400823 | 15,639.95389 |
| HK | 59.70684765 | 185.1787591 | 960.3022424 | 9447.402076 | 73.30407106 | 219.851777 | 1165.903069 | 11,516.97663 |
| HKB | 24.36907358 | 74.99720452 | 390.3026983 | 3860.345127 | 29.66030948 | 88.31886929 | 471.0762527 | 4702.277742 |
| KAM | 0.6135111 | 1.02795064 | 3.21425694 | 3.12285301 | 0.89011157 | 1.43331643 | 3.38579123 | 2.47170042 |
| KMS | 53.1599361 | 198.6214028 | 1198.017093 | 12,561.75534 | 67.73458451 | 241.8175466 | 1482.81145 | 15,497.30392 |
| LC | 63.55698725 | 196.4577794 | 1018.226315 | 10,015.06346 | 78.69633868 | 234.945313 | 1246.347394 | 12,308.08624 |
| ST | 40,876.59522 | 2597.150442 | 5612.97101 | 67,589.01596 | 8917.600689 | 3248.416821 | 212.4032474 | 161.2248544 |
| SH1 | 14.98125309 | 10.00843044 | 3.30767597 | 0.3538509 | 19.83737185 | 13.32517305 | 4.52547536 | 0.45598036 |
| SH2 | 0.109851 | 0.04961304 | 0.03755306 | 0.03380807 | 0.14702082 | 0.10129581 | 0.0481887 | 0.04236365 |
| SH3 | 0.09775184 | 0.04909948 | 0.03753775 | 0.03380792 | 0.12925867 | 0.10005417 | 0.04816896 | 0.04236346 |
| SH4 | 0.0813807 | 0.04414316 | 0.03660443 | 0.03371711 | 0.10497725 | 0.08061929 | 0.04696956 | 0.04224744 |
| SH5 | 0.0976654 | 0.0490947 | 0.0375376 | 0.03380792 | 0.12913108 | 0.10004234 | 0.04816877 | 0.04236346 |
| SH6 | 34.98795682 | 110.9290664 | 584.0681269 | 5812.991517 | 45.09842247 | 137.4538888 | 740.8571305 | 7377.198788 |
| RM | 0.18697271 | 0.584734 | 3.01649314 | 30.73515333 | 15.64477956 | 48.39233284 | 251.8368436 | 2529.300274 |
| BAD1 | 0.00014484 | 0.00010145 | 0.00008836 | 0.00008188 | 0.03349657 | 0.01868657 | 0.03515327 | 0.28948076 |
| BAD2 | 0.00014087 | 0.00010058 | 0.00008793 | 0.00008108 | 0.0125961 | 0.00903863 | 0.00782488 | 0.00732175 |
| BAD3 | 0.00014086 | 0.00010058 | 0.00008793 | 0.00008108 | 0.01257577 | 0.00903695 | 0.00782459 | 0.00732166 |
| BAD4 | 0.00014084 | 0.00010058 | 0.00008793 | 0.00008108 | 0.01254239 | 0.00901624 | 0.00780328 | 0.00727014 |
| BAD5 | 0.00014086 | 0.00010058 | 0.00008793 | 0.00008108 | 0.01257562 | 0.00903694 | 0.00782459 | 0.00732166 |
| BAD6 | 0.00015539 | 0.00012606 | 0.00060024 | 0.18068773 | 0.16795153 | 0.69643475 | 22.6771572 | 1184.093386 |
| 0.85 | 0.95 | 0.99 | 0.999 | 0.85 | 0.95 | 0.99 | 0.999 | |
|---|---|---|---|---|---|---|---|---|
| OLS | 114.5824414 | 361.587 | 1888.761 | 18,724.23 | 139.0351 | 434.956 | 2291.063 | 23,059.4307 |
| HK | 70.53059487 | 218.4392 | 1143.448 | 11,128.21 | 84.73393 | 261.6553 | 1369.973 | 13,805.1276 |
| HKB | 21.88435176 | 67.16994 | 357.5224 | 3487.577 | 26.2948 | 80.86005 | 426.6157 | 4368.603253 |
| KAM | 0.92014958 | 1.029153 | 1.728026 | 0.927162 | 1.033155 | 1.202124 | 1.769106 | 0.84455065 |
| KMS | 65.56693152 | 263.3651 | 1706.408 | 18,451.98 | 82.85135 | 327.1805 | 2097.182 | 22,783.94644 |
| LC | 79.90803527 | 244.9398 | 1278.349 | 12,459.42 | 97.12311 | 296.866 | 1553.46 | 15,649.26391 |
| ST | 7643.924984 | 936.1121 | 263.4593 | 51.03767 | 285,876.3 | 6944.461 | 20,035.39 | 72.26809438 |
| SH1 | 27.71243324 | 20.42312 | 7.044821 | 0.768801 | 35.10892 | 26.86367 | 11.23122 | 0.87839776 |
| SH2 | 0.21860749 | 0.091586 | 0.067434 | 0.065076 | 0.323573 | 0.235869 | 0.132894 | 0.07912513 |
| SH3 | 0.18605972 | 0.090179 | 0.067406 | 0.065076 | 0.279072 | 0.231278 | 0.132104 | 0.07912482 |
| SH4 | 0.14091301 | 0.077381 | 0.065756 | 0.064917 | 0.216052 | 0.17176 | 0.088677 | 0.07893107 |
| SH5 | 0.18582474 | 0.090166 | 0.067406 | 0.065076 | 0.278749 | 0.231235 | 0.132096 | 0.07912482 |
| SH6 | 57.31405626 | 178.9567 | 936.075 | 9340.357 | 71.19536 | 220.7642 | 1161.877 | 11,802.61724 |
| RM | 9.07072174 | 28.48965 | 163.0869 | 1509.564 | 34.80965 | 109.5238 | 553.2336 | 5853.776643 |
| BAD1 | 0.11094867 | 0.307179 | 0.356093 | 5.742583 | 0.424227 | 2.610388 | 0.750185 | 24.01817765 |
| BAD2 | 0.00909016 | 0.006582 | 0.005895 | 0.00536 | 0.07027 | 0.031189 | 0.018725 | 0.02142807 |
| BAD3 | 0.00904067 | 0.006568 | 0.005894 | 0.005358 | 0.060203 | 0.030799 | 0.018722 | 0.02141773 |
| BAD4 | 0.00896176 | 0.006418 | 0.005844 | 0.004721 | 0.049771 | 0.026617 | 0.018587 | 0.0175246 |
| BAD5 | 0.00904029 | 0.006567 | 0.005894 | 0.005358 | 0.06014 | 0.030795 | 0.018722 | 0.02141763 |
| BAD6 | 0.40524965 | 4.699362 | 37.93707 | 1104.892 | 1.430925 | 12.33273 | 115.2717 | 3981.876529 |
| 0.85 | 0.95 | 0.99 | 0.999 | 0.85 | 0.95 | 0.99 | 0.999 | |
|---|---|---|---|---|---|---|---|---|
| OLS | 327.773 | 1063.451 | 6,268,975.814 | 100,402.3703 | 4,617,964.808 | 352.2587 | 19,921.32 | 211,053.8726 |
| HK | 189.935 | 378.6552 | 5,010,510.541 | 46,279.68842 | 2,201,062.274 | 197.93 | 11,162.19 | 22,670.4271 |
| HKB | 121.5978 | 164.8643 | 3,341,404.932 | 20,747.83637 | 680,283.2972 | 100.5954 | 4761.444 | 9209.271088 |
| KAM | 6.147392 | 3.682777 | 2190.607255 | 17.20230342 | 42.94847546 | 7.328559 | 9.723722 | 6.26712893 |
| KGM | 46.82245 | 26.95606 | 427,858.6245 | 892.3312934 | 5001.186514 | 26.48541 | 315.3168 | 542.2703827 |
| LC | 265.8935 | 616.8498 | 5,957,957.417 | 60,018.41381 | 4,164,713.177 | 272.4177 | 15,175.53 | 35,094.67056 |
| ST | 2568.241 | 1696.132 | 20,761.03864 | 31.57042703 | 36,294.57483 | 1761.211 | 28.6355 | 59.91351106 |
| SH1 | 442.1007 | 880.3275 | 2,989,821.812 | 417.1621511 | 4,909,038.35 | 295.8112 | 2211.58 | 1029.955269 |
| SH2 | 6.300368 | 53.94683 | 3029.511305 | 18.56646637 | 9123.135724 | 16.02873 | 18.3849 | 44.84214598 |
| SH3 | 69.94817 | 24.27765 | 2896.131609 | 18.56580021 | 84,911.70162 | 7.391764 | 16.9755 | 44.83676737 |
| SH4 | 105.4299 | 21.30047 | 2295.865319 | 18.5238428 | 544,190.952 | 8.236192 | 12.42405 | 44.51518299 |
| SH5 | 68.87312 | 24.21705 | 2895.003736 | 18.56579358 | 82,802.94645 | 7.37234 | 16.96386 | 44.8367139 |
| SH6 | 266.9576 | 740.8614 | 5,538,159.019 | 52,561.7822 | 3,672,641.926 | 242.0055 | 10,702.79 | 167,915.1946 |
| RM | 0.052478 | 0.157602 | 0.82912929 | 8.45217319 | 0.02025559 | 0.056358 | 0.282383 | 2.73867735 |
| BAD1 | 0.000961 | 0.001 | 0.00078341 | 0.00082409 | 0.00040181 | 0.000364 | 0.000235 | 0.00023702 |
| BAD2 | 0.001039 | 0.000757 | 0.00066915 | 0.00062743 | 0.00042194 | 0.0003 | 0.000234 | 0.00023601 |
| BAD3 | 0.001041 | 0.000756 | 0.0006691 | 0.00062743 | 0.00042247 | 0.000299 | 0.000234 | 0.00023601 |
| BAD4 | 0.001042 | 0.000756 | 0.00066877 | 0.00062731 | 0.0004234 | 0.000299 | 0.000234 | 0.00023601 |
| BAD5 | 0.001041 | 0.000756 | 0.00066909 | 0.00062743 | 0.00042246 | 0.000299 | 0.000234 | 0.00023601 |
| BAD6 | 0.0011 | 0.000834 | 0.00214831 | 0.26228891 | 0.00043533 | 0.000323 | 0.000255 | 0.00261408 |
| 0.85 | 0.95 | 0.99 | 0.999 | 0.85 | 0.95 | 0.99 | 0.999 | |
| OLS | 1962.465031 | 30,316.14864 | 1,143,828.418 | 140,897.3123 | 146,739.8517 | 3,645,514.819 | 13,285,691 | 3,169,694,630 |
| HK | 1221.364651 | 19,700.14084 | 763,572.5955 | 69,907.96299 | 98,328.61683 | 1,310,513.345 | 4,946,739 | 2,020,877,309 |
| HKB | 575.9853444 | 9406.327958 | 396,470.2673 | 25,064.08437 | 38,577.65478 | 480,423.8818 | 1,478,068 | 883,580,608 |
| KAM | 4.94997946 | 8.10652667 | 12.3067322 | 3.36912377 | 406.4612545 | 1589.516305 | 3198.181 | 42,966.64378 |
| KGM | 50.20853656 | 1337.44452 | 34,208.67529 | 2717.510672 | 6972.491737 | 79,112.74147 | 122,181 | 61,197,547.54 |
| LC | 1551.863026 | 24,223.87956 | 922,548.394 | 91,379.3289 | 120,271.6096 | 2,305,440.218 | 6,811,175 | 2,395,866,595 |
| ST | 13,689.51613 | 1,379,972.324 | 7959.799135 | 14.5727323 | 316,128.3279 | 1,217,601.802 | 3932.842 | 47,924.76525 |
| SH1 | 1360.21416 | 12,070.8463 | 241,504.0424 | 800.6949586 | 75,359.33336 | 1,401,920.536 | 371,453.3 | 30,246,242.64 |
| SH2 | 222.7789415 | 95.96141799 | 55.95572777 | 1.77309945 | 10,441.58518 | 3340.472875 | 3684.657 | 39,857.14819 |
| SH3 | 159.9684552 | 85.72753855 | 55.37968966 | 1.77289538 | 8763.684835 | 3205.675921 | 3682.009 | 39,856.55337 |
| SH4 | 130.7920201 | 36.30574976 | 32.31876464 | 1.70545238 | 9832.474763 | 2364.856794 | 3552.198 | 39,530.93114 |
| SH5 | 159.5755176 | 85.6386311 | 55.37400947 | 1.77289332 | 8751.614784 | 3204.448434 | 3681.983 | 39,856.54738 |
| SH6 | 1480.758112 | 22,928.06242 | 854,495.7785 | 97,626.04957 | 94,579.9674 | 2,811,101.673 | 8,812,898 | 2,122,229,381 |
| RM | 0.3606254 | 1.32566275 | 5.59342398 | 51.79212546 | 9.83669772 | 32.58118421 | 166.1978 | 1679.712846 |
| BAD1 | 0.00122618 | 0.05193378 | 0.00069859 | 4.37533073 | 0.18818027 | 0.0575509 | 0.073741 | 8.31706426 |
| BAD2 | 0.00097651 | 0.00178907 | 0.00049695 | 0.00054845 | 0.11393138 | 0.01474653 | 0.011736 | 0.01139534 |
| BAD3 | 0.00097576 | 0.00170428 | 0.00049694 | 0.00054837 | 0.11386395 | 0.01474037 | 0.011734 | 0.01139511 |
| BAD4 | 0.00097543 | 0.00134147 | 0.00049661 | 0.00052335 | 0.11390606 | 0.01469784 | 0.011626 | 0.01127013 |
| BAD5 | 0.00097575 | 0.00170356 | 0.00049694 | 0.00054837 | 0.1138635 | 0.01474031 | 0.011734 | 0.0113951 |
| BAD6 | 0.00139616 | 0.10623231 | 0.06870748 | 5.99888172 | 73.79663749 | 1.30656839 | 16.80283 | 2179.907373 |
| Outliers | 4 | 10 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.85 | 0.95 | 0.99 | 0.999 | 0.85 | 0.95 | 0.99 | 0.999 | |||
| 10% | 25 | 0.1 | BAD1 | BAD4 | BAD4 | BAD 4 | BAD4 | BAD2345 | BAD2345 | BAD2345 |
| 1 | BAD1 | BAD4 | BAD4 | BAD4 | BAD4 | BAD4 | BAD4 | BAD4 | ||
| 50 | 0.1 | BAD1 | BAD2345 | BAD2345 | BAD2345 | BAD2345 | BAD2345 | BAD2345 | BAD2345 | |
| 1 | BAD1 | BAD4 | BAD4 | BAD4 | BAD5 | BAD4 | BAD4 | BAD4 | ||
| 100 | 0.1 | BAD1 | BAD35 | BAD2345 | BAD2345 | BAD2345 | BAD2345 | BAD2345 | BAD2345 | |
| 1 | BAD1 | BAD35 | BAD4 | BAD4 | BAD35 | BAD4 | BAD4 | BAD4 | ||
| 20% | 25 | 0.1 | BAD1 | BAD4 | BAD4 | BAD2345 | BAD4 | BAD4 | BAD4 | BAD4 |
| 1 | BAD2 | BAD4 | BAD4 | BAD4 | BAD4 | BAD4 | BAD4 | BAD4 | ||
| 50 | 0.1 | BAD1 | BAD4 | BAD2345 | BAD2345 | BAD345 | BAD4 | BAD4 | BAD4 | |
| 1 | BAD1 | BAD4 | BAD4 | BAD4 | BAD5 | BAD4 | BAD4 | BAD4 | ||
| 100 | 0.1 | BAD1 | BAD35 | BAD2345 | BAD2345 | BAD35 | BAD2345 | BAD2345 | BAD2345 | |
| 1 | BAD1 | BAD5 | BAD4 | BAD4 | BAD35 | BAD4 | BAD4 | BAD4 | ||
| Estimators | MSE | |||||
|---|---|---|---|---|---|---|
| OLS | 32.4972 | 0.0229 | 0.4857 | −0.6728 | 1.0744 | 1.4438 |
| HK | 3.6366 | 0.048619 | 0.4856 | −0.6438 | 0.9561 | 1.0548 |
| HKB | 3.4022 | 0.093024 | 0.4856 | −0.6438 | 0.9561 | 1.0548 |
| KAM | 3.4452 | 0.067052 | 0.4856 | −0.6438 | 0.9561 | 1.0548 |
| KMS | 3.6284 | 0.0229 | 0.4856 | −0.6435 | 0.9549 | 1.0515 |
| LC | 3.6391 | 0.0229 | 0.4867 | −0.6453 | 0.9582 | 1.0572 |
| ST | 3.4095 | 0.037977 | 0.2959 | 0.2242 | −0.0961 | −0.0394 |
| SH1 | 3.4286 | 3.759727 | 0.487 | −0.628 | 0.8942 | 0.8987 |
| SH2 | 3.7361 | 3.971751 | 0.4863 | −0.0831 | 0.0521 | 0.0243 |
| SH3 | 3.7394 | 1855.526 | 0.4863 | −0.0793 | 0.0496 | 0.023 |
| SH4 | 3.9102 | 3.973893 | 0.4857 | −0.0032 | 0.0018 | 0.0008 |
| SH5 | 3.7394 | 0.002142 | 0.4863 | −0.0792 | 0.0495 | 0.023 |
| SH6 | 12.5412 | 0.203844 | 0.4858 | −0.6701 | 1.0624 | 1.3961 |
| RM | 6.9082 | 20.18056 | 0.4888 | −0.65 | 1.232 | 0.8844 |
| BAD1 | 2.5162 | 21.31861 | 0.491 | −0.4672 | 0.5899 | 0.2078 |
| BAD2 | 2.8615 | 9959.644 | 0.489 | −0.0188 | 0.0132 | 0.0032 |
| BAD3 | 2.8647 | 21.3301 | 0.489 | −0.018 | 0.0126 | 0.003 |
| BAD4 | 2.9447 | 0.011495 | 0.4888 | −0.0029 | 0.002 | 0.0005 |
| BAD5 | 2.8647 | 0.0229 | 0.489 | −0.018 | 0.0126 | 0.003 |
| BAD6 | 1.7834 | 0.048619 | 0.4893 | −0.6364 | 1.1613 | 0.7471 |
| Estimator | ||||||||
|---|---|---|---|---|---|---|---|---|
| OLS | 0.005905409 | 3.00888230 | −1.081589605 | 0.03945686 | −1.939348004 | 0.25614058 | −0.158615271 | 1.80203453 |
| HK | 0.086753653 | 2.2905041 | −0.992556171 | 0.0693747 | −1.472925571 | 0.2829355 | 0.002113015 | 1.6676833 |
| HKB | 0.13701839 | 1.83847598 | −0.91527338 | 0.09201028 | −1.15820596 | 0.30739028 | 0.09383117 | 1.53919381 |
| KAM | 0.1830328 | 1.4101702 | −0.8106986 | 0.1178389 | −0.8334673 | 0.3345412 | 0.1710530 | 1.3623161 |
| KMS | 0.087449377 | 2.28429487 | −0.991640189 | 0.06966175 | −1.468742092 | 0.28323228 | 0.003428956 | 1.66620587 |
| LC | 0.086753653 | 2.2905041 | −0.992556171 | 0.0693747 | −1.472925571 | 0.2829355 | 0.002113015 | 1.6676833 |
| ST | 0.086753653 | 2.2905041 | −0.992556171 | 0.0693747 | −1.472925571 | 0.2829355 | 0.002113015 | 1.6676833 |
| SH1 | 0.11945717 | 1.9974122 | −0.94523488 | 0.0836136 | −1.27146581 | 0.2981569 | 0.06258856 | 1.5897296 |
| SH2 | 0.23338782 | 0.3065626 | 0.09152924 | 0.2272470 | 0.17599167 | 0.2728077 | 0.23910454 | 0.3340377 |
| SH3 | 0.23255299 | 0.3031387 | 0.09761709 | 0.2274706 | 0.17824594 | 0.2710924 | 0.23811747 | 0.3291206 |
| SH4 | 0.01307684 | 0.01553164 | 0.01275406 | 0.01521052 | 0.01296331 | 0.01541858 | 0.01309625 | 0.01555145 |
| SH5 | 0.23254468 | 0.3031058 | 0.09767539 | 0.2274726 | 0.17826721 | 0.2710757 | 0.23810770 | 0.3290733 |
| SH6 | 0.01593272 | 2.91995177 | −1.07199693 | 0.04285575 | −1.88313513 | 0.25867334 | −0.13789222 | 1.78860732 |
| RM | 0.00590541 | 3.00888230 | −1.08158961 | 0.03945686 | −1.93934800 | 0.25614058 | −0.15861527 | 1.80203453 |
| BAD1 | 0.2258518 | 0.9607248 | −0.6281803 | 0.1526566 | −0.4481616 | 0.3590181 | 0.2352873 | 1.0772170 |
| BAD2 | 0.1950698 | 0.2326699 | 0.1683647 | 0.2127897 | 0.1852614 | 0.2249406 | 0.1973076 | 0.2366952 |
| BAD3 | 0.1932249 | 0.2303480 | 0.1679842 | 0.2113445 | 0.1839646 | 0.2229785 | 0.1953685 | 0.2341155 |
| BAD4 | 0.00255732 | 0.00303745 | 0.00249660 | 0.00297679 | 0.00253601 | 0.00301615 | 0.00256080 | 0.00304094 |
| BAD5 | 0.1932065 | 0.2303250 | 0.1679798 | 0.2113299 | 0.1839515 | 0.2229589 | 0.1953492 | 0.2340901 |
| BAD6 | 0.05284466 | 2.59234445 | −1.03357815 | 0.05606784 | −1.67271552 | 0.26987847 | −0.06347370 | 1.73209874 |
| Estimators | MSE | |||||
|---|---|---|---|---|---|---|
| OLS | 41.6654 | --- | −1.3852 | −0.0776 | 0.7395 | −0.1818 |
| HK | 2.8849 | 0.125136 | −1.0441 | 0.0062 | 0.3216 | −0.1841 |
| HKB | 2.4426 | 0.391949 | −0.7742 | 0.0343 | 0.0345 | −0.192 |
| KAM | 2.4143 | 11.0074 | −0.265 | −0.1474 | −0.2048 | −0.206 |
| KMS | 2.6778 | 0.180161 | −0.9613 | 0.0201 | 0.2275 | −0.1857 |
| LC | 2.8957 | 0.125136 | −1.0513 | 0.0062 | 0.3238 | −0.1854 |
| ST | 2.3682 | 0.125136 | 0.4766 | −0.6728 | 0.093 | −0.2518 |
| SH1 | 5.2235 | 0.029569 | −1.2763 | −0.0468 | 0.5998 | −0.1825 |
| SH2 | 2.3456 | 2.927352 | −0.4054 | −0.0778 | −0.2043 | −0.2255 |
| SH3 | 2.3522 | 3.59956 | −0.3809 | −0.0942 | −0.2108 | −0.2275 |
| SH4 | 2.4876 | 531.1282 | −0.243 | −0.2195 | −0.2354 | −0.2124 |
| SH5 | 2.3523 | 3.60635 | −0.3807 | −0.0943 | −0.2108 | −0.2275 |
| SH6 | 14.0126 | 0.00679 | −1.3577 | −0.0695 | 0.7039 | −0.1819 |
| RM | 43.3854 | --- | −1.2593 | −0.0761 | 0.6094 | −0.1586 |
| BAD1 | 2.1431 | 0.230061 | −0.8418 | 0.013 | 0.108 | −0.1658 |
| BAD2 | 1.9266 | 22.77608 | −0.2618 | −0.1912 | −0.2292 | −0.2112 |
| BAD3 | 1.9338 | 28.00615 | −0.2573 | −0.1958 | −0.2296 | −0.2106 |
| BAD4 | 1.9738 | 4132.409 | −0.2373 | −0.2178 | −0.2317 | −0.2054 |
| BAD5 | 1.9339 | 28.05898 | −0.2572 | −0.1958 | −0.2297 | −0.2106 |
| BAD6 | 3.6023 | 0.052829 | −1.1027 | −0.0342 | 0.4113 | −0.16 |
| Estimator | ||||||||
|---|---|---|---|---|---|---|---|---|
| OLS | −2.8055562 | 0.03505633 | −0.8672192 | 0.71210810 | −1.0835724 | 2.56266260 | −0.5072373 | 0.14366063 |
| HK | −1.9825876 | −0.1055709 | −0.6418893 | 0.6542284 | −0.8043292 | 1.4475464 | −0.5008870 | 0.1327180 |
| HKB | −1.3771884 | −0.1712334 | −0.4905127 | 0.5591917 | −0.5980824 | 0.6671426 | −0.4939614 | 0.1099976 |
| KAM | −0.3487039 | −0.18136093 | −0.2543979 | −0.04044512 | −0.2747117 | −0.13486242 | −0.3469731 | −0.06510444 |
| KMS | −0.8061589 | −0.18855485 | −0.3582714 | 0.31477895 | −0.4132073 | 0.08948395 | −0.4736704 | 0.05204371 |
| LC | −0.9645881 | −0.18691899 | −0.3937764 | 0.40638817 | −0.4623507 | 0.22131849 | −0.4830179 | 0.07408722 |
| ST | −1.7915100 | −0.1311066 | −0.5928314 | 0.6331199 | −0.7391093 | 1.1940173 | −0.4991013 | 0.1277443 |
| SH1 | −1.9825876 | −0.1055709 | −0.6418893 | 0.6542284 | −0.8043292 | 1.4475464 | −0.5008870 | 0.1327180 |
| SH2 | −1.9825876 | −0.1055709 | −0.6418893 | 0.6542284 | −0.8043292 | 1.4475464 | −0.5008870 | 0.1327180 |
| SH3 | −0.5420450 | −0.18992433 | −0.3014015 | 0.12048930 | −0.3352603 | −0.06977346 | −0.4357091 | −0.00148512 |
| SH4 | −0.04862990 | −0.03127241 | −0.04484962 | −0.02730786 | −0.04736591 | −0.03003570 | −0.04395334 | −0.02587430 |
| SH5 | −0.5415998 | −0.18992344 | −0.3013062 | 0.12012548 | −0.3351310 | −0.06997787 | −0.4355971 | −0.00160123 |
| SH6 | −2.7351129 | 0.02166785 | −0.8470784 | 0.70808765 | −1.0597851 | 2.46656350 | −0.5067362 | 0.14312908 |
| RM | −2.8055562 | 0.03505633 | −0.8672192 | 0.71210810 | −1.0835724 | 2.56266260 | −0.5072373 | 0.14366063 |
| BAD1 | −1.6971556 | −0.14224850 | −0.5690558 | 0.62040530 | −0.7068929 | 1.07056110 | −0.4981252 | 0.12469070 |
| BAD2 | −0.2815145 | −0.16555419 | −0.2274766 | −0.08380654 | −0.2441799 | −0.13846204 | −0.2835324 | −0.08844829 |
| BAD3 | −0.2636527 | −0.15873567 | −0.2179411 | −0.09060437 | −0.2336887 | −0.13602504 | −0.2636417 | −0.09219561 |
| BAD4 | −0.00777730 | −0.00500441 | −0.00721815 | −0.00444137 | −0.00760737 | −0.00483503 | −0.00698284 | −0.00419447 |
| BAD5 | −0.2634937 | −0.15866962 | −0.2178510 | −0.09065279 | −0.2335898 | −0.13599593 | −0.2634617 | −0.09222115 |
| BAD6 | −2.3824579 | −0.04213433 | −0.7485814 | 0.68629135 | −0.9403875 | 1.98667893 | −0.5041413 | 0.13955386 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haider, B.; Asim, S.M.; Wasim, D.; Kibria, B.M.G. A Simulation-Based Comparative Analysis of Two-Parameter Robust Ridge M-Estimators for Linear Regression Models. Stats 2025, 8, 84. https://doi.org/10.3390/stats8040084
Haider B, Asim SM, Wasim D, Kibria BMG. A Simulation-Based Comparative Analysis of Two-Parameter Robust Ridge M-Estimators for Linear Regression Models. Stats. 2025; 8(4):84. https://doi.org/10.3390/stats8040084
Chicago/Turabian StyleHaider, Bushra, Syed Muhammad Asim, Danish Wasim, and B. M. Golam Kibria. 2025. "A Simulation-Based Comparative Analysis of Two-Parameter Robust Ridge M-Estimators for Linear Regression Models" Stats 8, no. 4: 84. https://doi.org/10.3390/stats8040084
APA StyleHaider, B., Asim, S. M., Wasim, D., & Kibria, B. M. G. (2025). A Simulation-Based Comparative Analysis of Two-Parameter Robust Ridge M-Estimators for Linear Regression Models. Stats, 8(4), 84. https://doi.org/10.3390/stats8040084







