Factor Analysis Biplots for Continuous, Binary and Ordinal Data

Abstract

This article presents biplots derived from factor analysis of correlation matrices for both continuous and ordinal data. It introduces biplots specifically designed for factor analysis, detailing the geometric interpretation for each data type and providing an algorithm to compute biplot coordinates from the factorization of correlation matrices. The theoretical developments are illustrated using a real dataset that explores the relationship between volunteering, political ideology, and civic engagement in Spain.

1. Introduction

Let ${\mathbf{X}}_{I\times J}=\left(x_{ij}\right)$ be a multivariate data matrix containing measurements of J variables across I units. We suppose that all variables are of the same type—either continuous, binary, or ordinal—although, as we will see later, binary and ordinal variables can be dealt with in the same way.

To analyze each matrix separately, principal component analysis (PCA) or factor analysis (FA) is commonly used. These techniques allow for detecting the underlying structure of the data. PCA first obtains a dimensionality reduction by identifying directions that explain most of the variance—or the correlation—if each column is standardized. Then, for continuous data, the complete set of observations (individuals) is projected onto the principal directions. Results can be visually represented by means of a biplot (a joint representation of rows and columns of the data matrix) [1]. We focus here on standardized data matrices, which result in analyses based on correlations. Principal components are traditionally used as a factorization method, but other forms of factor analysis could also be employed, as described in the article.

Factor analysis (FA) is a technique used to discover hidden dimensions, or factors, that explain why certain variables are correlated. Instead of treating each variable separately, it groups them based on shared patterns, reducing complexity and revealing the underlying structure that drives the data. Whereas PCA primarily aims to reduce dimensionality by identifying directions that explain the largest share of variance, FA is oriented toward uncovering latent factors that account for the observed correlations among variables. Unlike PCA, which provides a unique solution apart from the arbitrary orientation of its components, FA admits multiple equivalent solutions, which can be further rotated to achieve a representation that is often more interpretable.

When data are ordinal (for example, Likert scales) or binary, the previous methods are not optimal, although many authors still use them for analysis. Dimensionality reduction for analyzing ordinal matrices can be performed using polychoric correlations—or tetrachoric correlations in the binary case.

In this paper, we study biplot representations for factor analysis and their properties, especially for ordinal and binary data, although we begin with continuous data. Biplots provide a simple and intuitive way to visualize complex multivariate data, helping to elucidate both the structure of the observations and the interrelationships among variables.

Section 2.1 and Section 2.2 describe methods for the dimensionality reduction of individual matrices with continuous data, whereas Section 2.3 addresses analogous methods for ordinal data. The main contributions of this paper are as follows: a biplot for factor analysis applied to continuous data (Section 2.2.3) and biplots designed for ordinal and binary data (Section 2.3.2 and Section 2.3.3). Section 2.4 introduces two datasets used to illustrate the proposed methods, and Section 3 presents the corresponding results. Finally, Section 4 provides concluding remarks.

2. Material and Methods

2.1. Principal Components and Associated Biplots for Continuous Data

2.1.1. Principal Components

Given a data matrix ${\mathbf{X}}_{I\times J}=\left(x_{ij}\right)$, the I individuals can be represented as a cloud of points

$$\mathrm{In}=trace\left(\mathbf{X}{\mathbf{X}}^T\right)$$

(1)

The total inertia (variance) provides a global measure of the variability within the data. It is also equal to the sum of the squared distances of each point from the origin. From another perspective, the total inertia—or total variance—can be expressed as the sum of the variances of each variable. Since the variables are centered and standardized, the matrix in Equation (1) is closely related to the correlation matrix of the $\mathbf{X}$-variables, $\mathbf{R}$, as follows:

$$\mathbf{R}={\displaystyle \frac{1}{I}}{\mathbf{X}}^T\mathbf{X}$$

(2)

Principal component analysis (PCA) is a statistical technique that transforms a set of possibly correlated variables into a smaller set of uncorrelated variables, known as principal components. These components are linear combinations of the original variables and are ordered to capture the maximum possible variance in the data.

It is well known that the principal components are obtained through the eigen-decomposition of the correlation matrix:

$$\mathbf{R}=\mathbf{V}\mathbf{\Lambda }{\mathbf{V}}^T$$

(3)

where $\mathbf{V}=({\mathbf{v}}_1,\dots ,{\mathbf{v}}_J)$ contains the eigenvectors, and $\mathbf{\Lambda }=diag({\lambda }_1,\dots ,{\lambda }_J)$ is the diagonal matrix of eigenvalues arranged in decreasing order.

Each column ${\mathbf{v}}_j$ ($j=1,\dots ,J$) of $\mathbf{V}$ defines a principal component. The individuals represented in $\mathbf{X}$ can be projected onto the principal components (PCs) to obtain their corresponding scores:

$$\mathbf{Z}=\mathbf{X}\mathbf{V}=\sum _{j=1}^J\mathbf{X}{\mathbf{v}}_j$$

(4)

The total inertia (variance) is thus decomposed into J components of decreasing importance:

$$\mathrm{In}=\sum _{j=1}^J{\mathbf{v}}_j^T{\mathbf{X}}^T\mathbf{X}{\mathbf{v}}_j=\sum _{j=1}^J{\lambda }_j$$

(5)

By selecting the first S components, we obtain the best approximation in an S-dimensional subspace. The proportion of the total variance explained by the first S components is given by the following:

$${\rho }_S={\displaystyle \frac{{\sum }_{s=1}^S{\lambda }_s}{{\sum }_{j=1}^J{\lambda }_j}}$$

(6)

2.1.2. Classical Biplots for PCA

From the previous decomposition, the original data matrix can be reconstructed as

$$\mathbf{X}=\mathbf{Z}{\mathbf{V}}^T$$

(7)

Equation (7) defines an exact biplot for the matrix $\mathbf{X}$ in the full-dimensional space, as described by [1]. When only the first components are used, an approximate biplot in a reduced dimension is obtained. This is referred to in the literature as the JK-Biplot or RMP-Biplot. The row markers, $\mathbf{Z}$, represent the coordinates of individuals on the principal components, while the column markers, $\mathbf{V}$, correspond to the eigenvectors of $\mathbf{R}$. The eigenvectors define the directions of the principal components in the multidimensional space.

Reorganizing terms, the expression

$$\mathbf{X}=\mathbf{Z}{\mathbf{\Lambda }}^{-1/2}{\mathbf{\Lambda }}^{1/2}{\mathbf{V}}^T=\left(\mathbf{X}\mathbf{V}{\mathbf{\Lambda }}^{-1/2}\right){\mathbf{B}}^T=\mathbf{A}{\mathbf{B}}^T$$

(8)

with

$$\mathbf{A}=\mathbf{X}\mathbf{V}{\mathbf{\Lambda }}^{-1/2}$$

(9)

and

$$\mathbf{B}=\mathbf{V}{\mathbf{\Lambda }}^{1/2}$$

(10)

also defines a biplot, known in the literature as the GH-Biplot or CMP-Biplot. This representation is more closely related to factor analysis because the column markers correspond to the factor loadings.

The advantage of biplots lies in their ability to provide a graphical representation of the data matrix $\mathbf{X}$, using markers for both its rows, $\mathbf{A}={({\mathbf{a}}_1,\dots ,{\mathbf{a}}_I)}^T$ (or $\mathbf{Z}={({\mathbf{z}}_1,\dots ,{\mathbf{z}}_I)}^T$), and its columns, $\mathbf{B}={({\mathbf{b}}_1,\dots ,{\mathbf{b}}_J)}^T$ (or $\mathbf{V}={({\mathbf{v}}_1,\dots ,{\mathbf{v}}_J)}^T$), such that the inner product between a row and a column marker approximates the corresponding element of the data matrix, i.e.,

$$x_{ij}\approx {\mathbf{a}}_i^T{\mathbf{b}}_j(\mathrm{or}{x}_{ij}\approx {\mathbf{z}}_i^T{\mathbf{v}}_j)$$

(11)

We will use the appropriate expression for each case; here, we focus on the factor-analytic version.

The same biplot can also be obtained from the singular value decomposition (SVD) of $\mathbf{X}$:

$$\mathbf{X}=\mathbf{U}{\left(I\mathbf{\Lambda }\right)}^{1/2}{\mathbf{V}}^T$$

(12)

where $\mathbf{U}$ contains the left singular vectors, $\mathbf{V}$ contains the right singular vectors (which are also the eigenvectors in Equation (3)), and ${\left(I\mathbf{\Lambda }\right)}^{1/2}=diag(\sqrt{I{\lambda }_1},\dots ,\sqrt{I{\lambda }_J})$ contains the singular values, which are closely related to the eigenvalues of the correlation matrix.

Thus,

$$\mathbf{Z}=\mathbf{U}{\left(I\mathbf{\Lambda }\right)}^{1/2}=\mathbf{X}\mathbf{V},$$

(13)

$$\mathbf{A}=I^{1/2}\mathbf{U}$$

(14)

and $\mathbf{B}$ is given in Equation (10).

Based on the singular value decomposition, several alternative biplot formulations can be derived. In general, a biplot for $\mathbf{X}$ is a factorization of the data matrix into the product of two lower-rank matrices.

Using the SVD ensures that the best possible low-rank approximation is obtained, in the sense of [2]. Other factorizations of the correlation matrix may also yield valid biplots, which, although not optimal in this sense, can still provide valuable insights for data interpretation, as will be discussed later.

2.2. Factor Analysis and Associated Biplots for Continuous Data

Factor analysis (FA) is a statistical method used to explain the correlations among observed variables in terms of a smaller set of unobserved variables, referred to as factors. It assumes that each observed variable is a linear combination of common factors and a unique factor, thereby allowing researchers to identify the underlying latent structures that account for the patterns in the data. FA is closely related to principal component analysis (PCA); the latter can be viewed as a particular solution to the factor-analytic problem.

2.2.1. The Linear Factor Model

The linear factor model for I observations can be expressed as follows:

$${\mathbf{X}}_{I\times J}={\mathbf{1}}_I{\mu }_J^T+{\mathbf{F}}_{I\times S}{\mathbf{\Delta }}_{J\times S}^T+{\mathbf{E}}_{I\times J},$$

(15)

where

• ${\mathbf{X}}_{I\times J}$: data matrix with I observations and J observed variables;
• ${\mathbf{1}}_I$: $I\times 1$ vector of ones used to replicate the mean vector;
• $\mu$: $J\times 1$ vector of variable means (intercepts);
• ${\mathbf{F}}_{I\times S}$: matrix of factor scores for I observations;
• ${\mathbf{\Delta }}_{J\times S}$: factor loading matrix;
• ${\mathbf{E}}_{I\times J}$: matrix of unique errors for all observations.

Since the data matrix is centered, the means are zero and can be omitted, leading to the simplified form:

$$\mathbf{X}=\mathbf{F}{\mathbf{\Delta }}^T+\mathbf{E}.$$

(16)

If both the observed variables and the factors are standardized, the matrix $\mathbf{\Delta }$ contains the correlations between observed and latent variables. The squared loadings, ${\mathbf{\Delta }}^2$, are referred to as contributions and represent the amount of variance in each variable explained by each factor. The sum of the contributions of a given variable across all common factors,

$$h_j=\sum _{s=1}^S{\delta }_{js}^2,$$

is called the communality, representing the variance of the variable explained by all common factors. Conversely, the quantity

$$u_j=1-h_j,$$

is known as the unicity, denoting the proportion of unique variance not explained by the common factors. The total variance explained by all factors is obtained by summing the communalities across variables, while the variance explained by a subset of factors is determined by the sum of their respective contributions.

In general, the factor model can be expressed as a decomposition of the correlation matrix:

$$\mathbf{R}=\mathbf{\Delta }{\mathbf{\Delta }}^T+\mathbf{U},$$

(17)

where the main diagonal of ${\mathbf{R}}^{*}=\mathbf{\Delta }{\mathbf{\Delta }}^T$ contains the communalities, and $\mathbf{U}$ is a diagonal matrix containing the unicities.

The factor loading matrix $\mathbf{\Delta }$, which contains the correlations between observed and latent variables, can be obtained as

$$\mathbf{\Delta }=\mathbf{B}=\mathbf{V}{\mathbf{\Lambda }}^{1/2},$$

(18)

based on the SVD in Equation (12). This corresponds to the principal component solution to the factor problem, obtained by selecting the first S eigenvectors of $\mathbf{R}$ to compute the loadings.

Apart from PCA, several alternative methods exist for extracting factors:

• Principal Factor Method (Principal Axis Factoring): Replace the diagonal elements of $\mathbf{R}$ with estimated communalities to obtain ${\mathbf{R}}^{*}$; then perform eigen-decomposition as before.
• Maximum Likelihood Method: Estimate $\mathbf{\Delta }$ to maximize the likelihood under the assumption of multivariate normality.
• Other Methods: Image factoring, alpha factoring, and related approaches.

Once the factor loading matrix is obtained, factor scores can be estimated using several methods (e.g., regression, Bartlett, or Anderson–Rubin). For instance, the regression method is given by the following equation:

$$\widehat{\mathbf{F}}=\mathbf{X}\mathbf{\Delta }{\left({\mathbf{\Delta }}^T\mathbf{\Delta }\right)}^{-1}.$$

(19)

For the PCA solution, this expression coincides with the scores defined in Equation (14).

2.2.2. Rotations

In factor analysis, rotation is applied to the factor loading matrix $\mathbf{\Delta }$ to enhance the interpretability of the factors. The initial extracted solution often contains complex loadings, where variables exhibit moderate associations with multiple factors. Rotation serves to simplify and clarify these relationships without altering the underlying factor model.

The main purposes of rotation are as follows:

• To simplify the factor structure for improved interpretability;
• To maximize high and minimize low loadings within each factor;
• To help identify which variables are most strongly associated with each factor.

Let $\mathbf{\Delta }$ denote the initial factor loading matrix. A rotation matrix $\mathbf{T}$ is then applied as follows:

$${\mathbf{\Delta }}_{\mathrm{rotated}}=\mathbf{\Delta }\mathbf{T}.$$

(20)

Rotation matrices satisfy the orthogonality condition $\mathbf{T}{\mathbf{T}}^T=\mathbf{I}$. Accordingly, the factor scores are rotated as well:

$${\mathbf{F}}_{\mathrm{rotated}}=\mathbf{F}\mathbf{T}.$$

Rotations can be classified as either orthogonal or oblique, depending on whether the resulting factors are constrained to remain uncorrelated or are allowed to be correlated, respectively.

Importantly, rotation does not alter the fundamental form of the factor model:

$$\mathbf{X}=\mathbf{1}{\mathit{\mu }}^T+\mathbf{F}\mathbf{T}{\mathbf{T}}^T{\mathbf{\Delta }}^T+\mathbf{E}.$$

(21)

For more detailed discussions of rotation methods and their applications in factor analysis, see [3,4].

2.2.3. Biplot for Factor Analysis

In this section, we present the biplot methodology for factor analysis. While biplots have traditionally been developed for principal component analysis (PCA), their extension to factor analysis is conceptually straightforward.

Equation (16) defines a biplot representation of the data matrix:

$$\mathbf{X}=\mathbf{A}{\mathbf{B}}^T,$$

where $\mathbf{A}=\mathbf{F}$ and $\mathbf{B}=\mathbf{\Delta }$ are the row and column markers, respectively. Typically, row markers are represented as points and column markers as vectors or directions in the reduced-dimensional space. This construction corresponds to a GH- or CMP-Biplot associated with factor analysis, extending the classical PCA biplot framework.

Biplots are commonly displayed in two dimensions, using two of the retained factors to provide a partial yet interpretable representation of the data. As in any biplot, the inner product

$${\widehat{x}}_{ij}={\mathbf{a}}_i^T{\mathbf{b}}_j$$

approximates the element $x_{ij}$ of $\mathbf{X}$, analogous to the interpretation in classical PCA biplots.

This inner product relationship is illustrated in Figure 1a. The interpretation is based on the projections of the row markers onto the column marker vectors: all individuals projecting to the same value of a variable lie on a line perpendicular to that variable’s vector (Figure 1b). Points predicting different values lie on parallel lines (Figure 1c), and scales can be added along each variable direction to facilitate visual reading of predicted values (Figure 1d).

The construction of scales does not depend on the particular biplot representation and proceeds as follows. To find the point on the variable axis that predicts a fixed value $\mu$ of the observed variable when projecting an individual point, we seek a point $(x,y)$ lying on the biplot axis that satisfies the following:

$$y={\displaystyle \frac{b_{j2}}{b_{j1}}}x,\mu =b_{j0}+b_{j1}x+b_{j2}y.$$

Solving for x and y yields the following:

$$x=(\mu -b_{j0}){\displaystyle \frac{b_{j1}}{b_{j1}^2+b_{j2}^2}},y=(\mu -b_{j0}){\displaystyle \frac{b_{j2}}{b_{j1}^2+b_{j2}^2}},$$

or equivalently,

$$(x,y)=(\mu -b_{j0}){\displaystyle \frac{{\mathbf{b}}_j}{{\mathbf{b}}_j^T{\mathbf{b}}_j}}.$$

Thus, the unit marker for the jth variable is computed by dividing the coordinates of its corresponding vector by its squared length. Several points corresponding to specific values of $\mu$ can then be labeled to obtain a reference scale.

If the data are standardized, these marks are multiplied by the variable’s standard deviation, and the mean is added so that the labeled values correspond to actual variable scales, i.e., $\mu s_j+{\overline{x}}_j$. The resulting representation is shown in Figure 2.

The variable markers correspond to the factor loadings, which represent the correlations between observed variables and latent factors. In the full multidimensional space, these vectors have unit length; however, when projected onto a lower-dimensional space, their lengths decrease, reflecting the degree to which the variable’s information is preserved in the reduced representation.

To aid interpretation, a unit circle (radius 1) or several concentric circles with radii between 0 and 1 can be added to the plot. This approach is analogous to the correlation circle commonly used in PCA (see, for example, [5]). In a two-dimensional factor biplot, the coordinates of each vector represent its correlations with the retained factors, while the vector length indicates the multiple correlation with both factors. The concentric circles serve as a reference scale, helping to identify which variables carry meaningful interpretative information within the biplot.

The contributions described earlier are also useful for assessing which variables are interpretable within a particular biplot. These contributions are equivalent to the squared cosines used in PCA biplot interpretations (e.g., [5,6]). They can also be regarded as measures of predictiveness [7] or as discrimination measures in the context of Multiple Correspondence Analysis and HOMALS (see [8,9]).

In the following section, we propose a modified correlation plot that displays the magnitude of contributions rather than simple correlations, using an adjusted axis scale.

2.3. Factor Analysis and Biplots for Ordinal Data

2.3.1. Factor Analysis on Polychoric Correlation Matrices

When the data are ordinal, we use polychoric correlations rather than Pearson correlations.

The data matrix $\mathbf{X}$ contains J ordinal variables $X_j$ ($j=1,\dots ,J$). We assume that the observed categorical responses are discretized manifestations of an underlying continuous process.

Consider an ordinal variable $X_j$ with $C_j$ ordered categories. This variable is assumed to arise from an underlying continuous latent variable $X_j^{*}$ that follows a standard normal distribution. There exist $C_j-1$ thresholds, ${\tau }_{j\left(1\right)},{\tau }_{j\left(2\right)},\dots ,{\tau }_{j(C_j-1)}$, that divide the continuous variable $X_j^{*}$ into $C_j$ ordinal categories.

The relationship between $X_j$ and its underlying latent variable $X_j^{*}$ can be expressed as follows:

$$X_j=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{X}_j^{*}\le {\tau }_{j\left(1\right)},\hfill \\ 2\hfill & \mathrm{if}{\tau }_{j\left(1\right)}<X_j^{*}\le {\tau }_{j\left(2\right)},\hfill \\ 3\hfill & \mathrm{if}{\tau }_{j\left(2\right)}<X_j^{*}\le {\tau }_{j\left(3\right)},\hfill \\ ⋮\hfill & ⋮\hfill \\ C_j\hfill & \mathrm{if}{X}_j^{*}>{\tau }_{j(C_j-1)}.\hfill \end{array}\right.$$

Note that the numerical labels $(1,2,3,\dots )$ assigned to categories do not have intrinsic meaning; only their ordinal ordering is interpretable.

The polychoric correlations are the estimated correlations among the latent continuous variables $X_j^{*}$, $j=1,\dots ,J$. Let $\mathbf{R}$ denote the $J\times J$ matrix of polychoric correlations among the J ordinal variables, and let ${\tau }_{j\left(c\right)}$, for $j=1,\dots ,J$ and $c=1,\dots ,C_j$, denote the estimated thresholds.

We can express the correlation structure of the latent variables through a factor model as follows:

$$\mathbf{R}\cong \mathbf{\Gamma }{\mathbf{\Gamma }}^T,$$

(22)

where $\mathbf{\Gamma }$ contains the factor loadings of the linear factor model for the latent continuous variables.

The loading matrix can be obtained from the eigen-decomposition of the polychoric correlation matrix, analogous to Equation (3), as follows:

$${\mathbf{\Gamma }}_X=\mathbf{U}{\mathbf{\Lambda }}^{1/2},$$

(23)

where $\mathbf{U}$ contains the eigenvectors and $\mathbf{\Lambda }$ is the diagonal matrix of eigenvalues.

As before, several alternative methods may be used to factorize the correlation matrix, depending on the estimation framework and the intended interpretation of the factors.

2.3.2. Biplot for Ordinal Data

Constructing a biplot from the factorization is more challenging because the relationships between latent factors and manifest variables are nonlinear. A biplot with a logistic is possible as described in [10]. More recently [11] have developed estimation procedures based on cumulative probabilities.

Let ${\mathbf{P}}_{I\times L}$ be the indicator matrix with $L={\sum }_j\left(C_j\right)$ columns. The indicator ${\mathbf{P}}_j$ matrix of size $I\times C_j$ for each categorical variable $X_j$ contains binary indicators for each category, and $\mathbf{P}=\left({\mathbf{P}}_1,\dots ,{\mathbf{P}}_J\right)$. Each row of ${\mathbf{P}}_j$ sums to 1, and each row of $\mathbf{P}$ sums to J. Then, $\mathbf{P}$ is the matrix of observed probabilities for each category of each variable. We can also define the cumulative observed probabilities as $p_{ij\left(c\right)}^{*}=1$ if $x_{ij}\le c$ and $p_{ij\left(c\right)}^{*}=0$ otherwise $(c=1,\dots ,C_j-1)$, that is, the indicators of the cumulative categories. Observe that $p_{ij\left(C_j\right)}^{*}=1$, so we can eliminate the last category for each variable. We organize the observed cumulative probabilities for each variable into an $I\times (C_j-1)$ matrix ${\mathbf{P}}_{\mathbf{j}}^{*}=\left(p_{ij\left(c\right)}^{*}\right)$. Then, ${\mathbf{P}}^{*}=(P_1^{*},\dots ,P_J^{*})$ is the $I\times (L-J)$ matrix of observed cumulative probabilities.

Let ${\pi }_{ij\left(c\right)}^{*}=P(x_{ij}\le c)$ be the (expected) cumulative probability that individual i has a value lower than or equal to c on the j-th ordinal variable, and let ${\pi }_{ij\left(c\right)}=P(x_{ij}=c)$ be the (expected) probability that individual i takes the c-th value on the j-th ordinal variable. Then, ${\pi }_{ij\left(C_j\right)}^{*}=P(x_{ij}\le C_j)=1$, and ${\pi }_{ij\left(c\right)}={\pi }_{ij\left(c\right)}^{*}-{\pi }_{ij(c-1)}^{*}$ (with ${\pi }_{ij\left(0\right)}^{*}=0$). A multidimensional (S-dimensional) logistic latent trait model for the cumulative probabilities can be written, for ($1\le c\le C_j-1$), as

$${\pi }_{ij\left(c\right)}^{*}={\displaystyle \frac{1}{1+e^{-\left(d_{j\left(c\right)}+{\sum }_{s=1}^S{a}_{is}{b}_{js}\right)}}}={\displaystyle \frac{1}{1+e^{-(d_{j\left(c\right)}+{\mathbf{a}}_i^T{\mathbf{b}}_j)}}},$$

(24)

In logit scale, the model is

$$logit\left({\pi }_{ij\left(c\right)}^{*}\right)=d_{j\left(c\right)}+\sum _{s=1}^S{a}_{is}{b}_{js}=d_{j\left(c\right)}+{\mathbf{a}}_i^T{\mathbf{b}}_j,c=1,\dots ,C_j-1$$

(25)

which defines a binary logistic biplot for the cumulative categories.

In matrix form,

$$logit\left({\mathbf{\Pi }}^{*}\right)=\mathbf{1}{\mathbf{d}}^{\prime }+{\mathbf{AB}}^{\prime },$$

(26)

where ${\mathbf{\Pi }}^{*}=({\mathsf{\Pi }}_1^{*},\dots ,{\mathsf{\Pi }}_J^{*})$ is the $I\times (L-J)$ matrix of expected cumulative probabilities, ${\mathbf{1}}_I$ is a vector of ones, and $\mathbf{d}={({\mathbf{d}}_1^T,\dots ,{\mathbf{d}}_J^T)}^T$, with ${\mathbf{d}}_j^T=(d_{j\left(1\right)},\dots ,d_{j(C_j-1)})$, is the vector containing thresholds. $\mathbf{A}={({\mathbf{a}}_1^T,\dots ,{\mathbf{a}}_I^T)}^{\prime }$ with ${\mathbf{a}}_i^T=(a_{i1},\dots ,a_{iS})$ is the $I\times S$ matrix containing the individual scores, and $\mathbf{B}={({\mathbf{B}}_1^T,\dots ,{\mathbf{B}}_J^T)}^{\prime }$ with ${\mathbf{B}}_j={\mathbf{1}}_{C_j-1}\otimes {\mathbf{b}}_j^T$ and ${\mathbf{b}}_j^T=(b_{j1},\dots ,b_{jS})$ is the $(L-J)\times S$ matrix containing the slopes for all variables. This expression defines a biplot for the odds that will be called the ordinal logistic biplot. Each equation of the cumulative biplot shares the geometry described for the binary case [12]; moreover, all curves share the same direction when projected on the biplot.

The set of parameters $\left\{d_{j\left(c\right)}\right\}$ provides a different threshold for each cumulative category, while the second part of (25) does not depend on the particular category, meaning that all the $C_j-1$ curves share the same slopes.

It can be shown that there is a close relationship between the factor model in (22) and the model in (24). You can find the details in [13]. The relation between both models depends on the equal slopes model, also known as the proportional odds model in the context of ordinal logistic regression [14], or the equal discrimination assumption in Multidimensional Item Response Models (MIRT) as in [15].

If the proportional odds assumption is violated, the model may not be appropriate for the data matrix. Although there are tests available to assess this assumption when working with observed variables, these tests are not applicable in the current context, where we deal with latent rather than observed variables. A more exploratory approach could involve fitting a model with varying slopes—for example, by converting the ordinal variables into binary indicators and refitting the model, or by using a nominal model as in [16]. In both cases, we can examine whether the slopes are approximately consistent, providing an exploratory check of the assumption.

The current proposal relies on the proportional odds assumption. In future work, we plan to investigate alternative modeling frameworks that relax this restriction, such as the Partial Proportional Odds Model (PPOM), the Generalized Ordered Logit Model, or other ordinal formulations including the Adjacent-Category and Continuation-Ratio models. These approaches could lead to new variants of the biplot better suited to different data-generating mechanisms. However, in all these cases, the link with the factor analysis of the polychoric model would be lost, and alternative estimation algorithms would be required.

If the factor model loadings $\mathbf{\Gamma }=({\gamma }_{js},j=1,\dots ,J;s=1,\dots ,S)$ and the thresholds ${\tau }_{j\left(c\right)}^X,j=1,\dots ,J;c=1,\dots ,C_j$ are known, the parameters for the variables in our model (24) can be calculated as follows:

$$d_{j\left(c\right)}={\tau }_{j\left(c\right)}{\left(1-\sum _{s=1}^S{\gamma }_{js}^2\right)}^{-1/2},$$

(27)

$$b_{js}={\gamma }_{js}{\left(1-\sum _{s=1}^S{\gamma }_{js}^2\right)}^{-1/2}.$$

(28)

This means that the parameters $d_{j\left(c\right)}$ and $b_{js}$ are obtained from the factorization of the polychoric correlation matrix. The relation between the two models can be found explicitly in [13].

The remaining parameters for the individuals $a_{is}$ can then be estimated using the gradient descent method to minimize the cost function:

$$L=-\sum _{i=1}^I\sum _{j=1}^J\sum _{c=1}^{C_j}{p}_{ij\left(c\right)}^{*}log\left({\pi }_{ij\left(c\right)}^{*}\right),$$

(29)

where the expected cumulative probabilities are

$${\pi }_{ij\left(c\right)}^{*}={\displaystyle \frac{1}{1+e^{-\left(d_{j\left(c\right)}+{\sum }_{s=1}^S{a}_{is}{b}_{js}\right)}}}={\displaystyle \frac{1}{1+e^{-(d_{j\left(c\right)}+{\mathbf{a}}_i^T{\mathbf{b}}_j)}}},$$

(30)

Observe that the cost is the negative of the likelihood as it is normally used in a machine learning context, so it is essentially equivalent to maximizing the likelihood.

The updates are then

$$\begin{array}{c}\hfill a_{is}\Leftarrow a_{is}-\alpha {\displaystyle \frac{\partial L}{\partial a_{is}}}=a_{is}-\alpha \sum _{j=1}^J{b}_{js}\sum _{k=1}^{K_j}({\pi }_{ij\left(k\right)}^{*}-p_{ij\left(k\right)}^{*}),\end{array}$$

(31)

where $\alpha$ is a constant (the learning rate) chosen by the user.

Let ${\mathbf{a}}_s={(a_{1s},\dots ,a_{Is})}^T$ and ${\mathbf{b}}_s={(b_{1s},\dots ,b_{Js})}^T$ be the vectors containing the row and column parameters for dimension s. Let $\mathbf{Z}$ be an $(L-J)\times J$ indicator matrix in which the j-th column takes the value 1 for the rows corresponding to categories of the j-th variable, and 0 elsewhere.

The updates are written in matrix form:

$${\mathbf{a}}_s\Leftarrow {\mathbf{a}}_s-\alpha ({\mathbf{\Pi }}^{*}-{\mathbf{P}}^{*})\mathbf{Z}{\mathbf{b}}_s,$$

(32)

We can organize the calculations in the Algorithm 1 as follows:

Algorithm 1 Algorithm to calculate the scores for ordinal data.

1: procedure P-Ordinal-Scores($\mathbf{P},\mathbf{d},\mathbf{B},S$) 2:     Choose learning rate $\alpha$ (optional if using an optimization routine) 3:     Set tolerance and maximum number of iterations (e.g., $Tol={10}^{-5}$ and $MaxIter=500$) 4:     for $s=1\to S$ do 5:         Init: ${\mathbf{a}}_{\left(s\right)}\leftarrow \mathrm{random}$ (or any other choice, for instance, the PCA scores) 6:         $Iterations=0$ 7:         repeat 8:            $Iterations=Iterations+1$ 9:            Calculate: $L_{old}$ with Equation (29) 10:          Update: ${\mathbf{a}}_{\left(s\right)}$ with Equation (32) 11:          Update: ${\mathbf{\Pi }}^{*}=\left({\pi }_{ij}^{*}\right)$ with Equation (30) 12:          Update: $L_{new}$ with Equation (29) 13:          Update: $ϵ=L_{old}-L_{new}$ 14:       until $(ϵ\le tolerance)$ or $(Iterations=MaxIter)$       return $\mathbf{A}=\left[{\mathbf{a}}_{\left(1\right)},\dots ,{\mathbf{a}}_{\left(S\right)}\right]$

This Algorithm 1 produces decreasing values of the cost function and will eventually converge, at least to a local minimum. A useful strategy is to initialize the algorithm from multiple starting points and select the solution corresponding to the lowest achieved cost. In practice, the choice of $\alpha$ can be avoided by using a pre-programmed optimization routine. In R, we have used the conjugate-gradient method in the optimr routine, although other alternatives could be used.

This algorithm will be implemented in Version 25.11 of the package MultBiplotR ([17]) developed in the R language ([18]). It is also available from the corresponding authors.

Finally, we have a biplot for the ordinal data closely related to the factorization of the polychoric correlation matrix:

$$logit\left({\mathbf{\Pi }}^{*}\right)=\mathbf{1}{\mathbf{d}}^T+\mathbf{A}{\mathbf{B}}^T,$$

(33)

The geometry of both biplots is detailed in [10].

From a practical point of view, we are mainly interested in the regions that predict each category, that is, the set of points whose expected probabilities are highest for each category. These regions are separated by parallel straight lines, all perpendicular to the direction of ${\mathbf{b}}_j$ (see Figure 3).

If we denote $(x,y)$ as one of those intersection points between the direction of the variable and the line separating the predictions of two categories, it must lie on the biplot direction, that is,

$$y={\displaystyle \frac{b_{j2}}{b_{j1}}}x.$$

(34)

We can develop a simple numerical procedure to calculate these intersection points:

• Calculate the predicted category for a set of values for z along the direction of the variable (for example, a sequence from $-6$ to 6 with small steps such as 0.01). The precision of the procedure can be adjusted by the step size.
• Search for the z values at which the prediction changes from one category to another.
• Then calculate the $(x,y)$ values as $x=z{\displaystyle \frac{b_{j1}}{b_{j1}^2+b_{j2}^2}}$ and $y=z{\displaystyle \frac{b_{j2}}{b_{j1}^2+b_{j2}^2}}$.

Hidden categories are those with zero frequencies in the predictions obtained by the algorithm.

2.3.3. Biplot for Binary Data

We have not described biplots for binary data because they are simply a particular case of ordinal data with only two categories ($C_j=2$). Rather than polychoric correlations, we use tetrachoric correlations, but conceptually they are similar. Biplots for binary data were proposed by [12]. Details and algorithms for their computation can be found in [19]. All the calculations presented above are valid for binary data.

2.4. Data for Illustration of the Proposed Procedures

In this section, we present two datasets. The first illustrates the biplot for continuous data, while the second demonstrates its application to ordinal and binary data. For the first example, we employ the proposed biplot for factor analysis based on the Pearson correlation matrix, and for the second, we apply the proposed biplot based on polychoric correlations.

2.4.1. Illustration of an FA Biplot for Continuous Data

For illustration, we use the protein dataset that is a multivariate collection of real-valued measurements representing the average protein consumption across 25 European countries. Each country is characterized by nine columns indicating different types of protein sources. It is an old dataset (which contains old European countries) but is good for our illustration purposes. The dataset appears in [20].

Table 1. Protein consumption of 25 European countries.

	Red_Meat	White_Meat	Eggs	Milk	Fish	Cereal	Starch	Nuts	Fruits_Veg.
Albania	10.10	1.40	0.50	8.90	0.20	42.30	0.60	5.50	1.70
Austria	8.90	14.00	4.30	19.90	2.10	28.00	3.60	1.30	4.30
Belgium	13.50	9.30	4.10	17.50	4.50	26.60	5.70	2.10	4.00
Bulgaria	7.80	6.00	1.60	8.30	1.20	56.70	1.10	3.70	4.20
Czechoslovakia	9.70	11.40	2.80	12.50	2.00	34.30	5.00	1.10	4.00
Denmark	10.60	10.80	3.70	25.00	9.90	21.90	4.80	0.70	2.40
E_Germany	8.40	11.60	3.70	11.10	5.40	24.60	6.50	0.80	3.60
Finland	9.50	4.90	2.70	33.70	5.80	26.30	5.10	1.00	1.40
France	18.00	9.90	3.30	19.50	5.70	28.10	4.80	2.40	6.50
Greece	10.20	3.00	2.80	17.60	5.90	41.70	2.20	7.80	6.50
Hungary	5.30	12.40	2.90	9.70	0.30	40.10	4.00	5.40	4.20
Ireland	13.90	10.00	4.70	25.80	2.20	24.00	6.20	1.60	2.90
Italy	9.00	5.10	2.90	13.70	3.40	36.80	2.10	4.30	6.70
Holand	9.50	13.60	3.60	23.40	2.50	22.40	4.20	1.80	3.70
Norway	9.40	4.70	2.70	23.30	9.70	23.00	4.60	1.60	2.70
Poland	6.90	10.20	2.70	19.30	3.00	36.10	5.90	2.00	6.60
Portugal	6.20	3.70	1.10	4.90	14.20	27.00	5.90	4.70	7.90
Romania	6.20	6.30	1.50	11.10	1.00	49.60	3.10	5.30	2.80
Spain	7.10	3.40	3.10	8.60	7.00	29.20	5.70	5.90	7.20
Sweden	9.90	7.80	3.50	24.70	7.50	19.50	3.70	1.40	2.00
Switzerland	13.10	10.10	3.10	23.80	2.30	25.60	2.80	2.40	4.90
UK	17.40	5.70	4.70	20.60	4.30	24.30	4.70	3.40	3.30
USSR	9.30	4.60	2.10	16.60	3.00	43.60	6.40	3.40	2.90
W_Germany	11.40	12.50	4.10	18.80	3.40	18.60	5.20	1.50	3.80
Yugoslavia	4.40	5.00	1.20	9.50	0.60	55.90	3.00	5.70	3.20

contains the complete dataset.

2.4.2. Illustration of an FA Biplot for Ordinal Data

The present study examines volunteering within formal organizations. Distinctions in types of volunteering arise according to the domains in which voluntary activities are undertaken. The following types of volunteering have been analyzed:

• Social volunteering (SOCIAL);
• Community volunteering/international development cooperation (COMMUN);
• Sports/leisure and free time volunteering (LEISURE);
• Social and health volunteering (HEALTH);
• Educational/cultural volunteering (CULTURAL);
• Environmental volunteering (ENVIRONM).

Beyond the typologies of volunteering, this study also examines its nature, distinguishing between transformative and welfare-oriented forms, and explores whether these two approaches differ in their perspectives on the state’s role within the third sector. Transformative volunteering aims to address social, environmental, or other causes by fostering sustainable, long-term change through altering the structural conditions that generate problems. In contrast, welfare-oriented volunteering focuses on mitigating the immediate consequences of social issues without necessarily challenging their root causes or advocating for policy reforms. While transformative volunteering is closely connected to political demands and the expectation of state involvement in problem-solving, the state itself adopts varying approaches to social assistance, which are shaped by different welfare state models. Thus, four models of the welfare state can be identified:

• Conservative welfare state: Responsibility for social assistance does not primarily rest with the state but with traditional institutions such as the family, friends, community, and religious organizations. As a result, the provision of social support largely depends on volunteers.
• Social democratic welfare state: The state assumes full responsibility for welfare provision, which leaves volunteering with only a marginal role, as social assistance is conceived as an exclusively public service.
• Liberal welfare state: State involvement in welfare provision is minimal, and private social protection schemes are encouraged. Within this framework, neoliberalism increasingly relies on volunteers and civil society organizations as service providers, subjecting them to market principles and managerial criteria. Volunteering becomes instrumental to the liberalization of welfare, transforming the third sector into a quasi-market of social enterprises.
• Welfare state and the new left: Welfare provision is based on collaboration between the state and third-sector organizations. Since the state cannot fully meet social needs on its own, it relies on coordination with volunteers and social organizations to maximize outreach and effectiveness.

Considering the variations among welfare state models and their differing interpretations of responsibility for social assistance, we examine whether volunteers’ perceptions of the state’s role in welfare provision vary according to the nature of their volunteering. Specifically, it explores whether engagement in transformative, as opposed to welfare-oriented, volunteering aligns with particular conceptions of the welfare state and social assistance. The relationship between the state, the market, and the third sector is inherently political, shaping, enabling, or constraining the expansion and development of third-sector organizations. One of the central aims of this study is to investigate the ideology of volunteering, offering both a descriptive account of its ideological dimensions and a multivariate analysis to illuminate the links between forms of volunteering and political orientations.

We conducted an anonymous online survey with volunteers from different organizations. Data are available from the authors on request. There is no way to identify any of the original respondents, as no personal data has been stored. A total of 201 respondents have answered the survey.

Finally, we have 9 variables (inside the parenthesis is the name on tables and plots):

• Type of volunteering (Type): The 6 categories are described before. This is a nominal variable with 6 categories that will be only used for interpretation and not included in the factor analysis.
• Interest in politics (IntPolit): None, Some, A lot (Ordinal).
• Political ideology (Ideology): Left, Center, Right (Ordinal).
• Should the state finance the organizations? (FinancState): No, Neutral, Yes (Ordinal).
• Should the organization be autonomous? (Autonomy): Financed and Autonomous, Indifferent, Autonomous and not Financed (Ordinal).
• Ideological orientation of the organization (Orientation): No, Some, Yes (Ordinal).
• Nature of the organization (Orientation): Welfare, Transformation (Binary).
• The organization has clear political demands (Demands): No, Yes (Binary).
• The organization has volunteers with different profiles (Orientation): No, Yes (Binary).

So we have 9 variables that are either binary, nominal, or ordinal and can be combined into the analysis described in the previous sections.

3. Results

3.1. Protein Consumption in European Countries

First, we normalize the data matrix by subtracting the mean and dividing by the standard deviation for each column. This implies that our analysis is based on correlations. We then apply a factor analysis method; in this case, we used the maximum likelihood solution with a varimax rotation and obtained the individual scores by regression. We have chosen this method because it provides a simple solution, but any other method could have been chosen. The objective is simply to illustrate the construction of a biplot from any factor structure. The variance explained by each factor is shown in

Table 2. Variance explained by 4 factors.

	Eigenvalue	Exp. Var	Cumulative
Factor_1	3.34	37.07	37.07
Factor_2	1.63	18.12	55.19
Factor_3	1.05	11.67	66.85
Factor_4	0.73	8.10	74.95

.

The factor matrix (

Table 3. Factor matrix. Correlations among factors and observed variables. In bold numbers, we have highlighted the highest correlations.

	Factor_1	Factor_2	Factor_3	Factor_4
Red_Meat	0.00	0.03	0.68	−0.20
White_Meat	0.97	−0.13	0.15	−0.01
Eggs	0.46	0.07	0.85	0.02
Milk	0.16	0.16	0.53	−0.53
Fish	−0.11	0.99	0.04	0.05
Cereal	−0.36	−0.55	−0.57	0.21
Starch	0.32	0.43	0.26	−0.08
Nuts	−0.60	−0.24	−0.21	0.67
Fruits_Vegetables	0.02	0.24	−0.04	0.69

) contains correlations among observed variables and factors. We have highlighted the highest loadings for each variable in order to know what variables are most related to each factor.

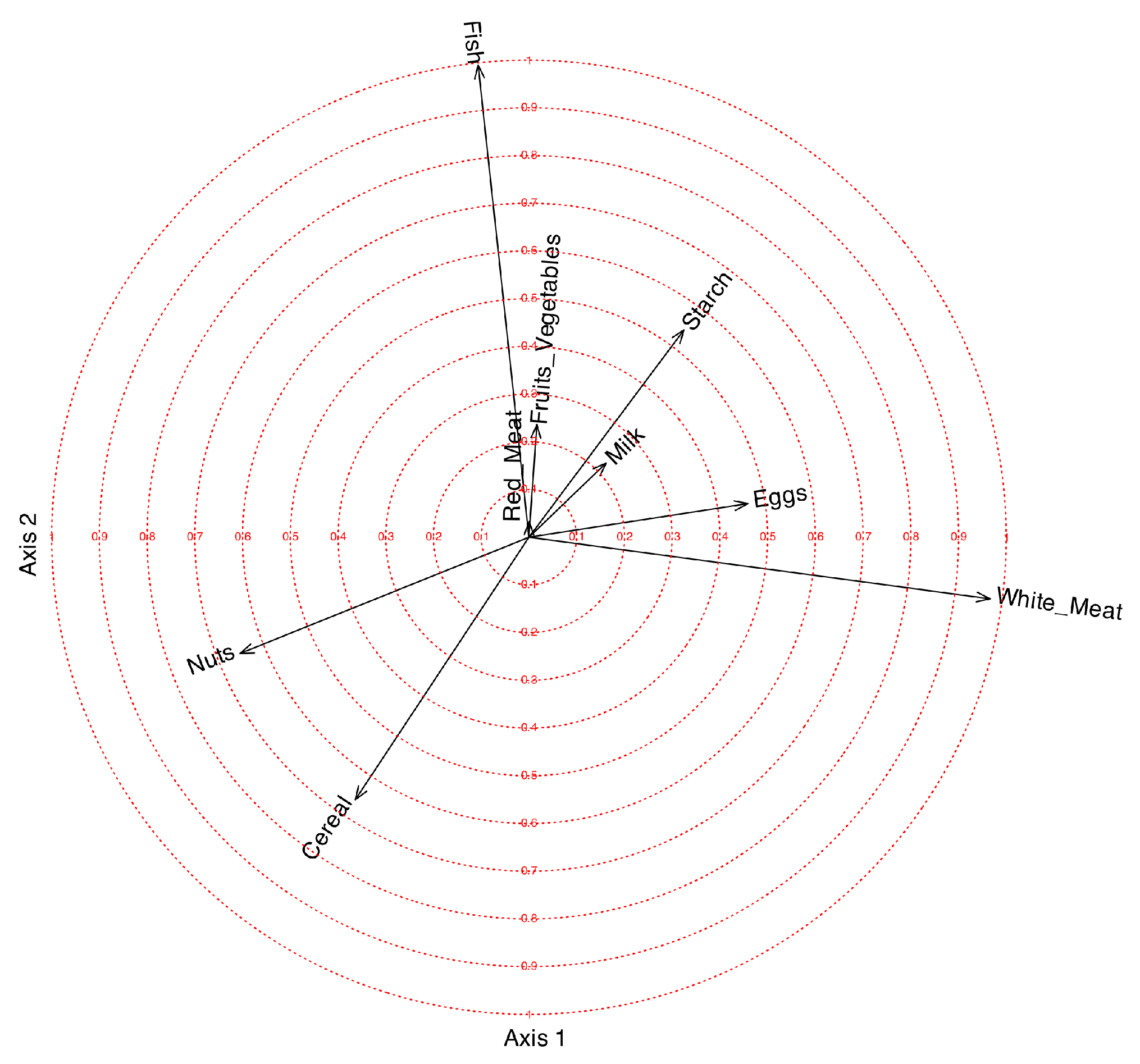
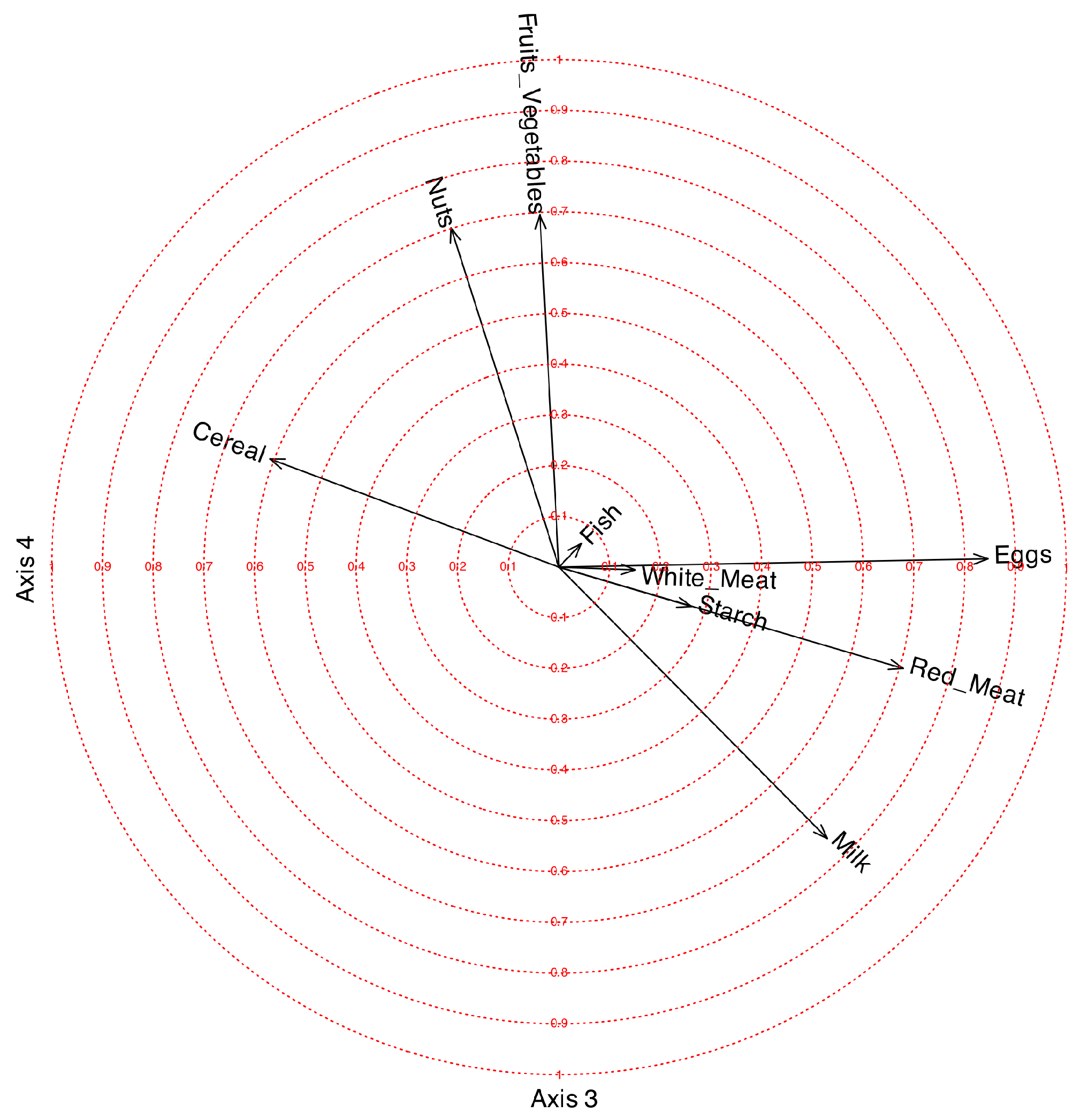
When dealing with PCA, many software packages construct what is known as a correlation plot, which represents the coordinates for variables, in $\mathbf{B}$, inside a circle of radius 1. Instead of ticks on the axes, concentric circles are drawn for different values between 0 and 1. The correlation plot can also be applied to any factorization of the data matrix. A circle of correlations for Factors 1 and 2 is shown in Figure 4, for Factors 3 and 4 in Figure 5.

The first factor is mainly related to White_Meat with a positive correlation and to Nuts with a smaller negative correlation. The objective of rotations in factor analysis is to provide a structure as simple as possible, with some of the loadings close to 1 and others close to 0. We observe that the loading for White_Meat is 0.97; therefore, the first factor differentiates very well between countries that consume white meat and those that do not. White_Meat is negatively related to Nuts.

The second factor is positively related to Fish and negatively to Cereal. The loading for Fish is also very high (0.99), so it differentiates quite well among countries consuming fish. The third factor is positively related to Eggs, Red_Meat, and Milk, and negatively to Cereal. The fourth factor is positively related to Nuts and Fruits_Vegetables. The variable Starch is not clearly related to any of the factors.

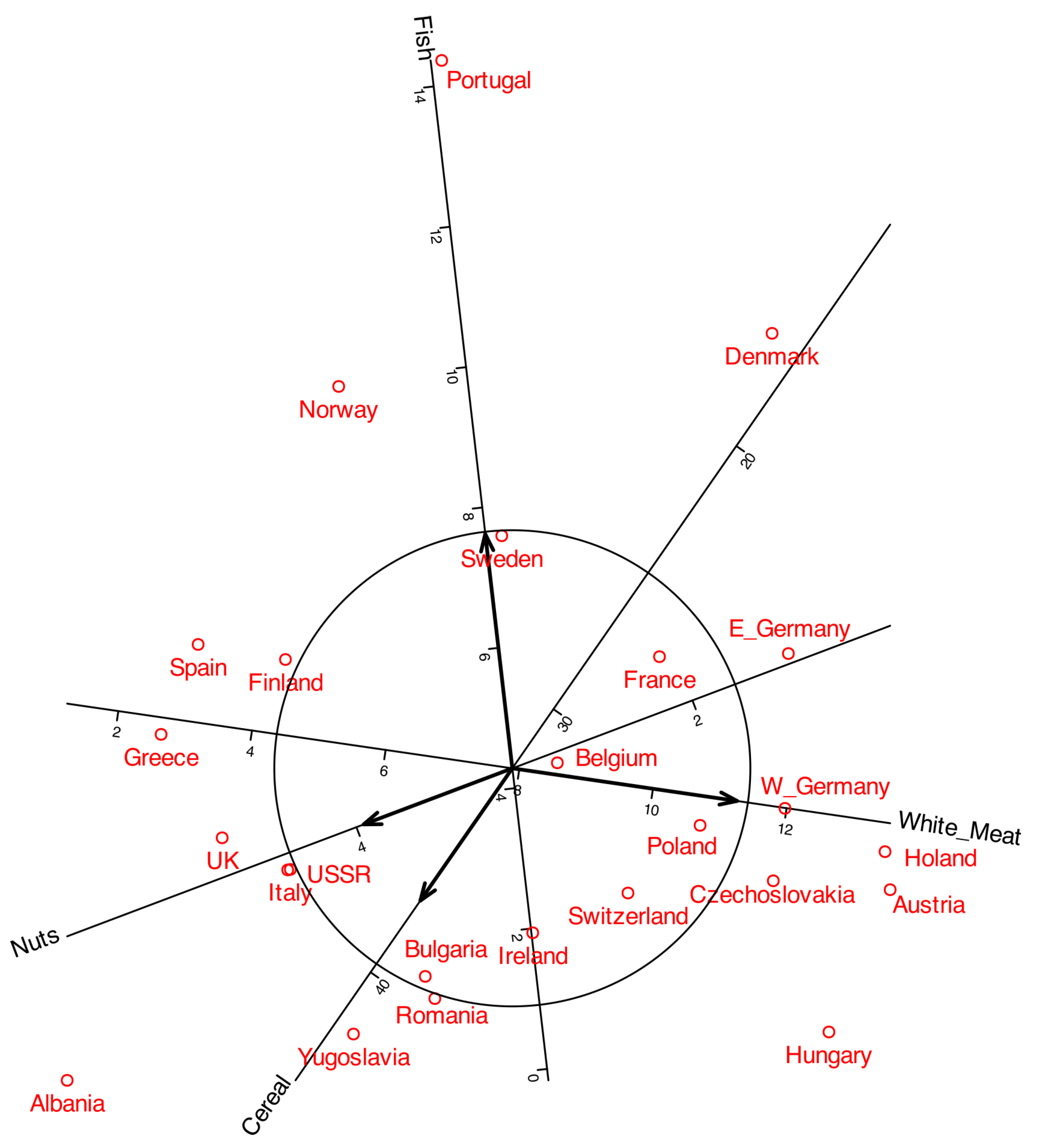
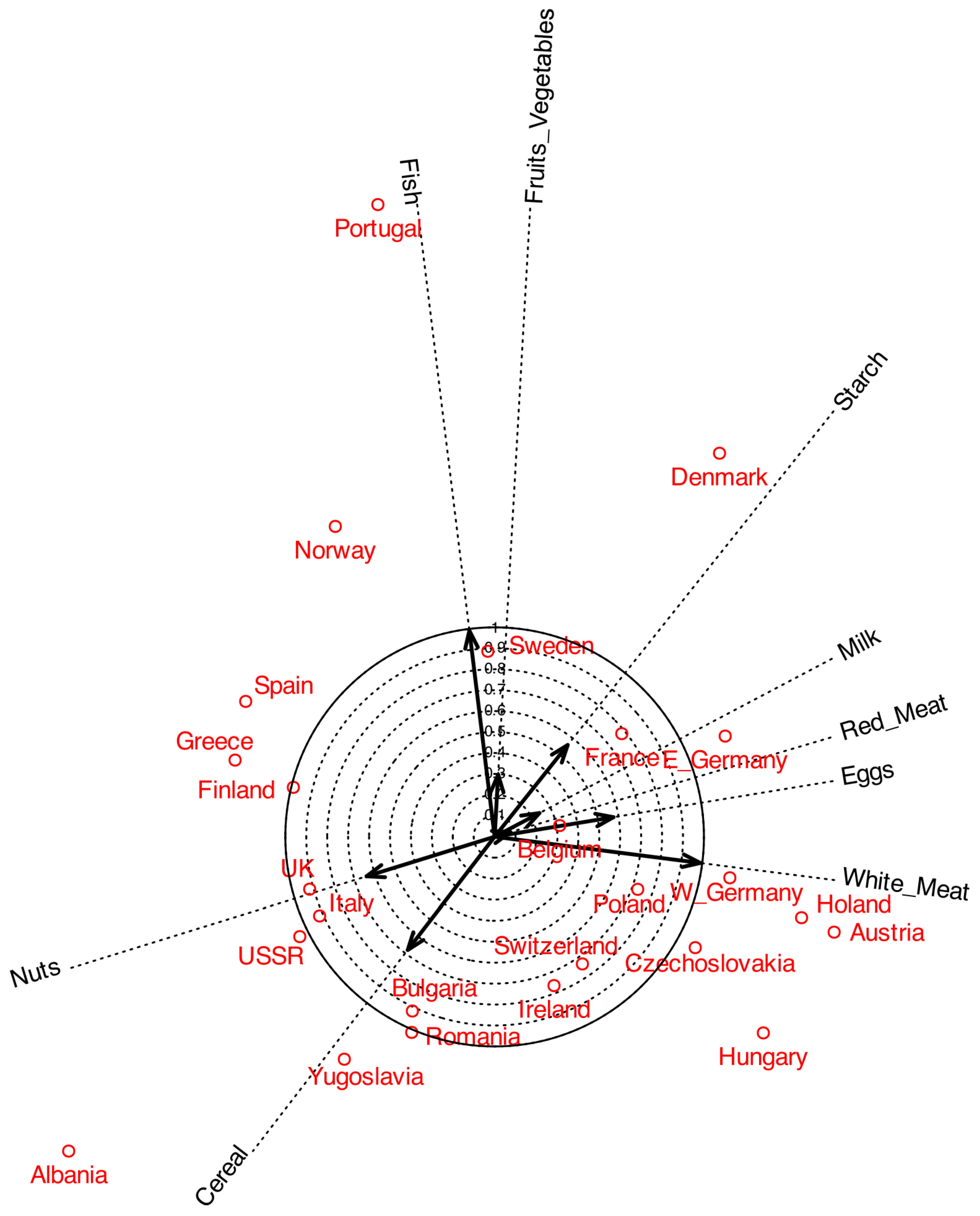
The coordinates for rows, in $\mathbf{A}$, can be added to the plot to obtain a biplot. Figure 6 shows a typical biplot together with the correlation circles. To make the plot easier to read, some labels were moved outside the main area. The arrows represent the variables, and by projecting them onto the principal component axes, we can observe how strongly each variable is correlated with the components. For instance, White_Meat shows a strong correlation with the first component, whereas Fish is more closely associated with the second. The length of each arrow represents the multiple correlation with both components. The circles shown in the plot serve as a reference for interpreting both the arrow length and its projection onto the axes.

As in standard PCA, only variables represented by longer arrows can be reliably interpreted in the plot, whereas shorter arrows should be treated with caution. For example, White_Meat and Fish can be meaningfully interpreted, while variables such as Milk and Fruits_Vegetables provide little reliable information in this representation. The latter may instead be better explained by other components. A useful strategy is to remove from the plot those variables with low correlations. For instance, variables with correlations smaller than 0.6 can be excluded to obtain the representation shown in Figure 2.

3.2. Volunteering and Ideology

All variables, with the exception of Type, were included in the analysis. The variable Type was subsequently projected onto the plot to explore potential associations with the other variables. Factor extraction was conducted using the principal components method, and the resulting factors were subjected to Varimax rotation. The first two factors have been selected.

Table 4. Variance explained by the two first factors.

	Dim 1	Dim 2
Variance	2.77	2.30
Cumulative	2.77	5.07
Percentage	34.61	28.72
Cum. Percentage	34.61	63.33

contains the variance explained by each factor.

Both factors together explain 63.33% of the variability, which is adequate in this context. In psychology and other social sciences, a solution explaining around 50–60% of the total variance is generally regarded as acceptable (see [21] or [22], for example). The factor matrix is shown in

Table 5. Factor structure (loadings and communalities). In bold numbers, we have highlighted the highest correlations.

	Dim 1	Dim 2	Communalities
IntPolit	0.69	0.08	0.48
Ideology	−0.33	0.67	0.56
FinancState	0.04	−0.93	0.88
Autonomy	0.14	0.91	0.85
Orientation	0.90	0.07	0.81
Nature	0.77	−0.28	0.66
Demands	0.88	−0.20	0.81
DifProf	0.01	−0.11	0.01

.

The first factor loaded positively on Interest in Politics, Organizational Orientation, Organizational Nature, and Political Demands, indicating that these variables are strongly interrelated. The second factor showed positive loadings for Ideology and Autonomy, and a negative loading for State Support of the Organization. This pattern suggests that Ideology and Autonomy are positively associated with each other, while both are negatively associated with State Support.

All communalities were relatively high, except for Different Profiles, which exhibited little association with the first two factors.

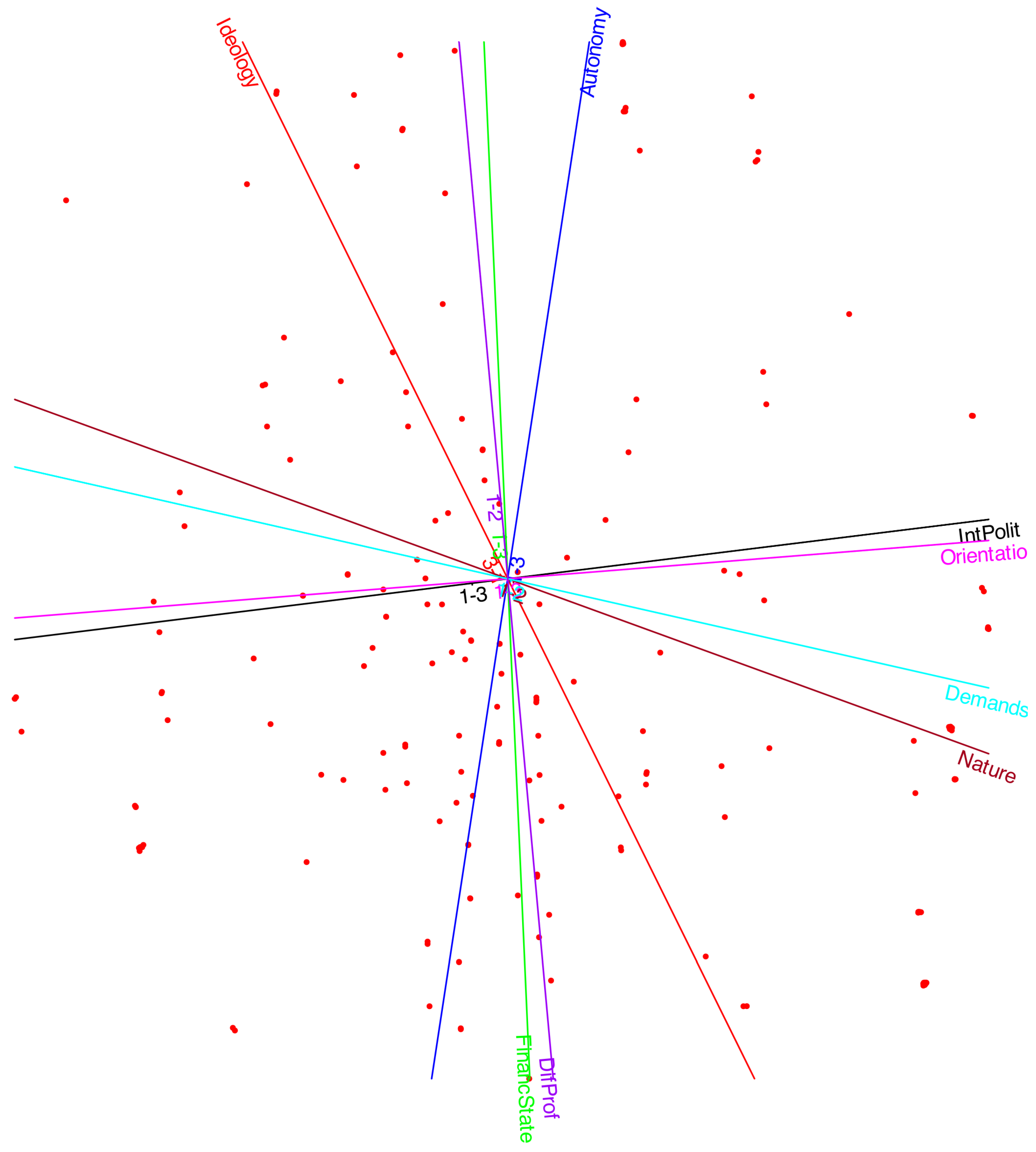
The factor biplot with correlation circles is presented in Figure 7. As noted earlier, Interest in Politics, Organizational Orientation, Organizational Nature, and Political Demands are strongly and positively correlated. This cluster of variables shows little association with Ideology, Autonomy, or State Support of the Organization. Thus, the choice of an organization with political demands or a transformative nature appears to be more closely linked to political interest than to ideological orientation.

Conversely, Ideology and Autonomy are positively associated, while both are negatively related to State Support. This indicates that individuals on the left of the political spectrum tend to believe that organizations should be both autonomous and supported by the state, whereas those on the right favor autonomy but oppose state financing.

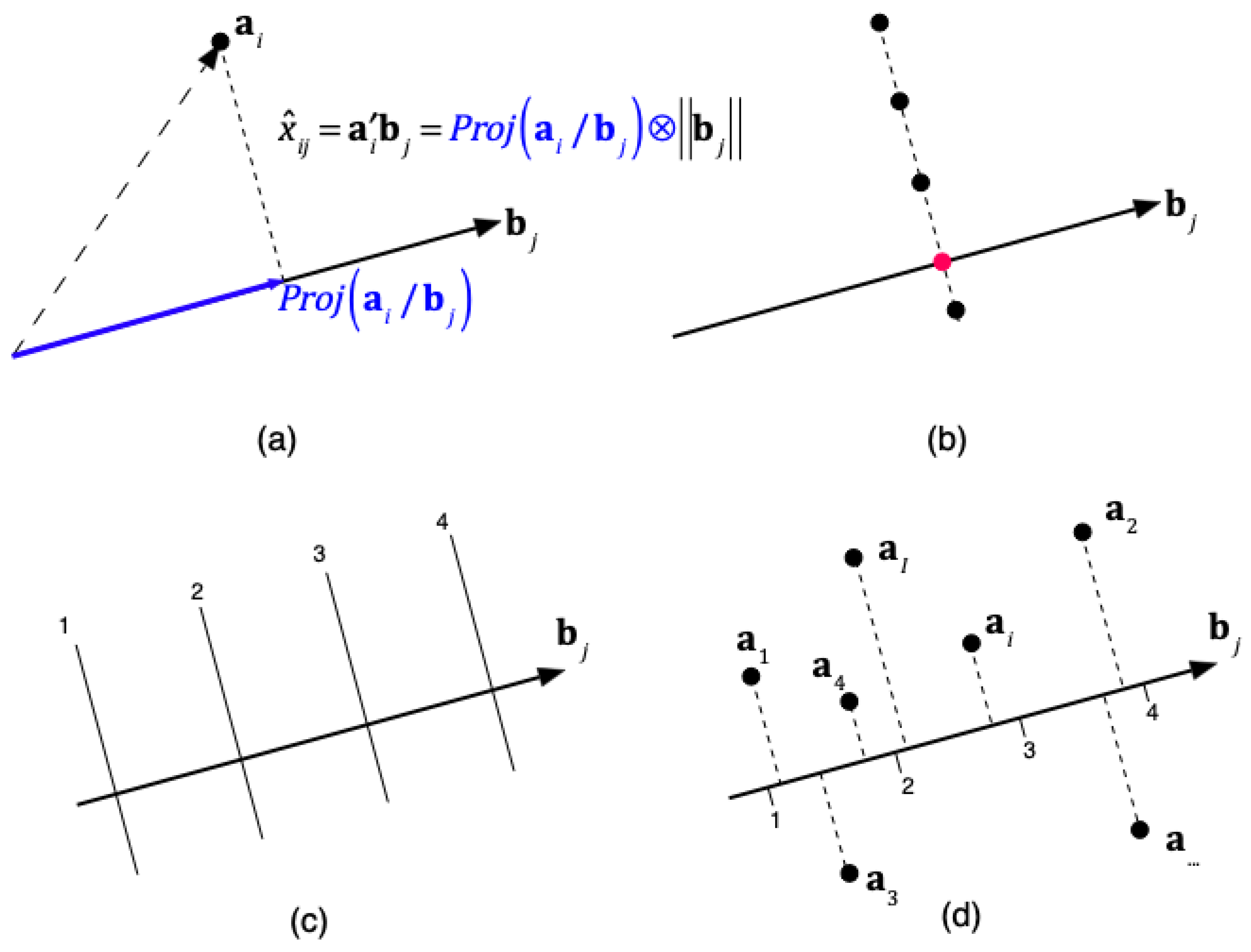
In the biplot, each point represents an individual. By projecting an individual onto the direction of a variable, one could, in principle, estimate the probabilities for each category. However, this is complex, as it would require separate probability scales along the same direction for each category. Our goal is not to predict exact probabilities but rather to predict ordinal categories. For this purpose, it is sufficient to identify the points that separate the different category values.

Together with the correlation biplot, we can define a prediction biplot showing the points that separate each prediction region, as illustrated in Figure 3. The prediction biplot is shown in Figure 8. We used different colors to distinguish the variables; however, some overlap remains, making the plot difficult to read. The software allows partial displays of selected variables to facilitate interpretation.

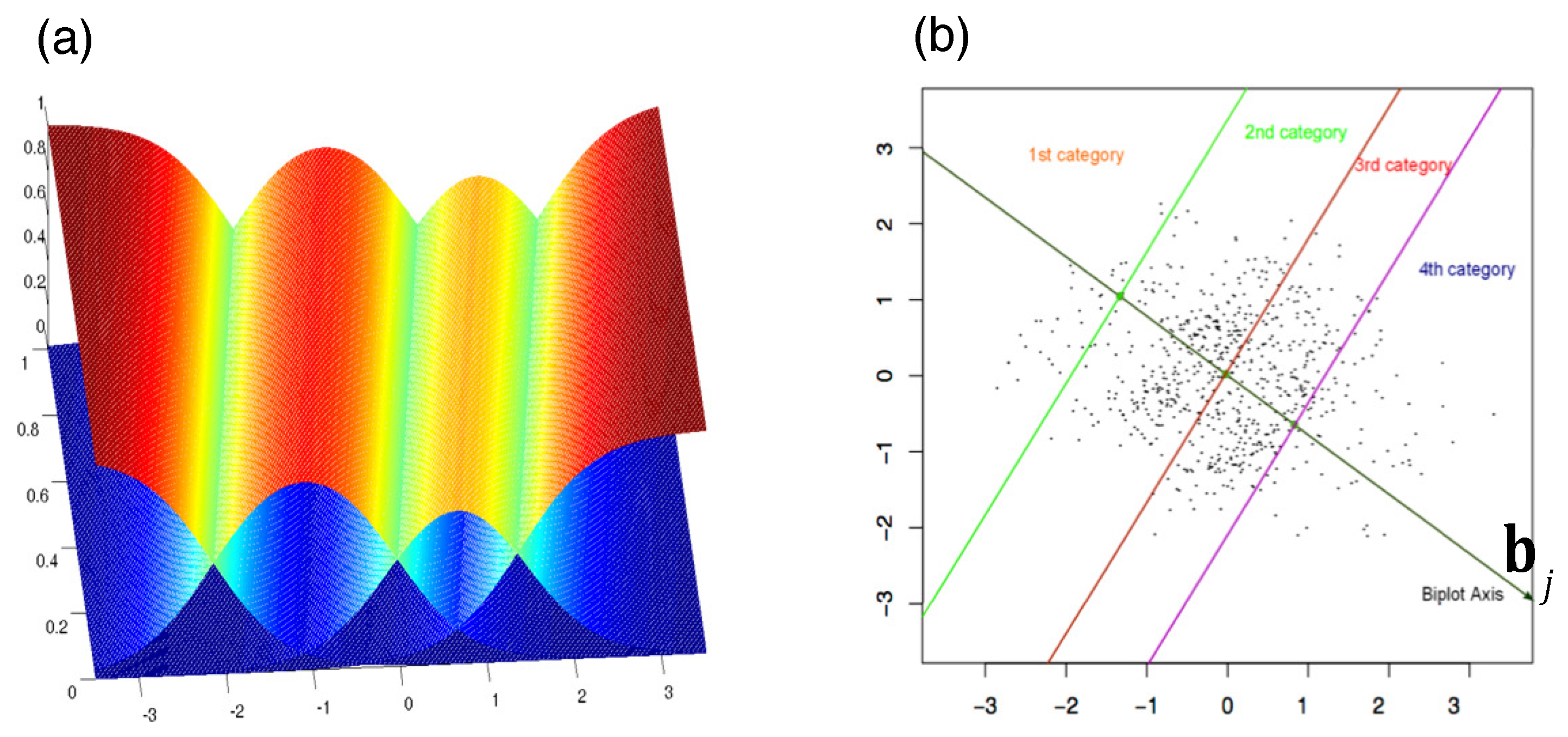
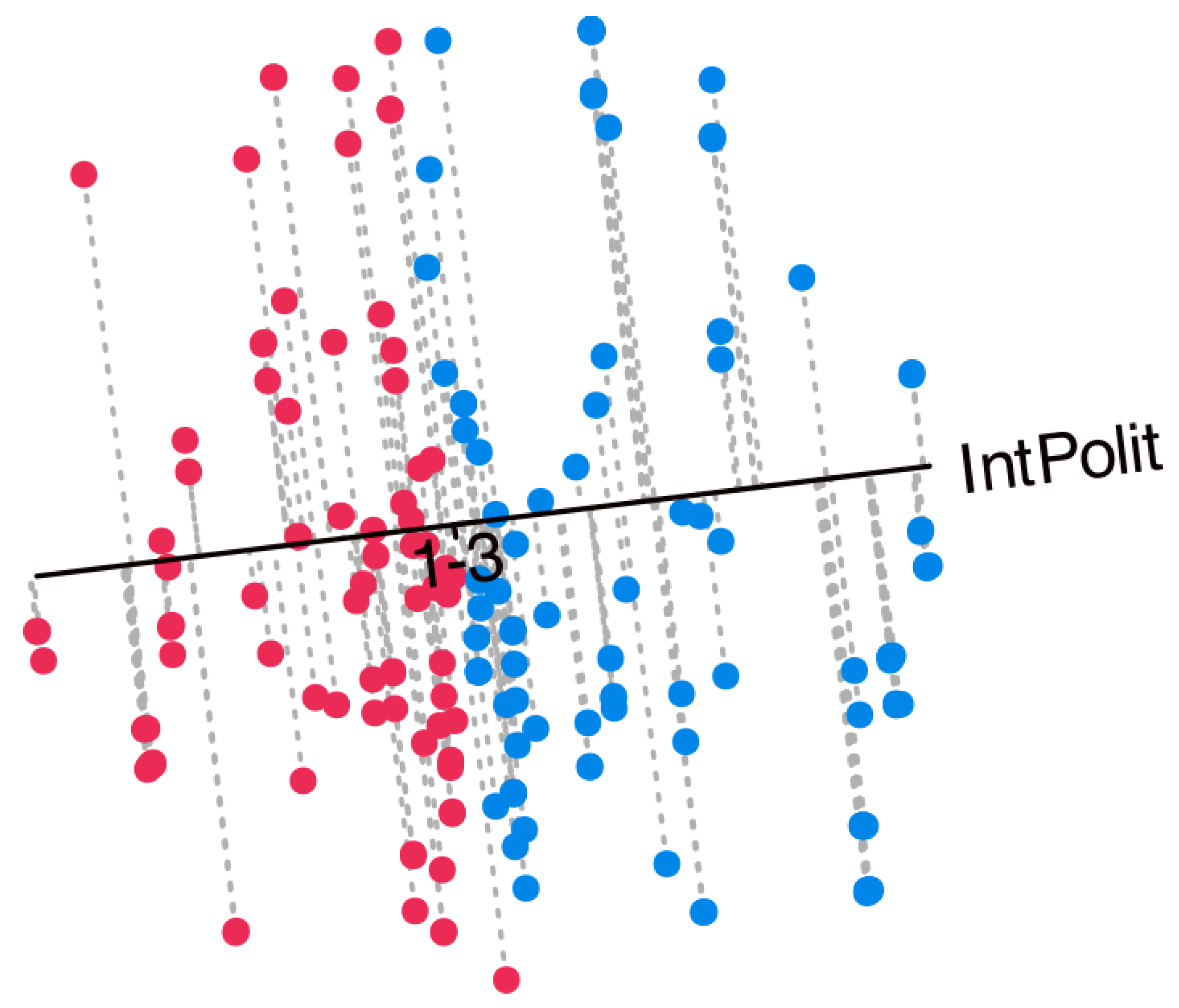
As previously discussed, the projection of individual points onto the variable axes allows for the prediction of the original categories by identifying the prediction region in which the projection falls. Figure 9 presents the projections onto the variable Interest in Politics, serving as an example of how to interpret the biplot. Along the axis, cut-off points separating the prediction regions are indicated. For this variable, which comprises three categories (1 = None, 2 = Some, 3 = A lot), two separation points would be expected: one between categories 1 and 2 (“1–2”) and another between categories 2 and 3 (“2–3”). However, only a single point labeled “1–3” is observed. This indicates that the separation occurs exclusively between categories 1 and 3, with the intermediate category (2) remaining unrepresented and, therefore, never predicted. A similar pattern emerges for all variables with three categories, whereby the intermediate level is consistently absent from the predictions. Furthermore, the separation points across variables are located near the center of the plot and tend to overlap, leading to a mixed configuration. This is probably due to the fact that intermediate categories were not clearly understood by the respondents.

Figure 9 also displays the individuals together with their projections onto the selected variable. This is merely an illustration of how to interpret the biplot. To assess the quality of the predictions, you should refer to the goodness-of-fit indices presented in the article. Points in red correspond to predictions of category 1 (None), whereas points in blue correspond to predictions of category 3 (A lot). The intermediate category 2 (Some) is not represented and is therefore never predicted. When considering all variables jointly, the resulting biplot provides a comprehensive view that facilitates the interpretation of the main structural features of the data.

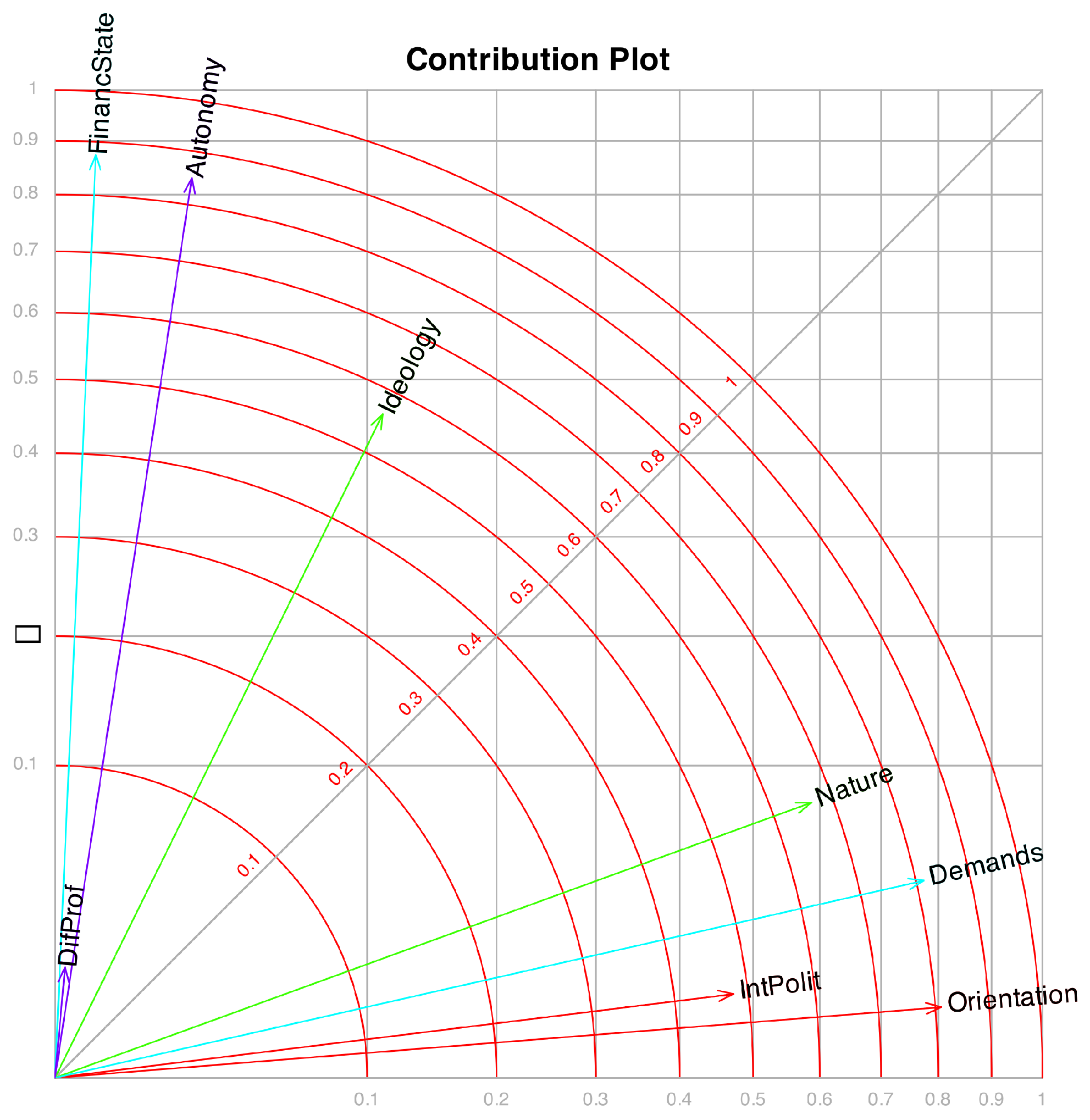
Along with the correlations, we can also display the contributions or qualities of representation, which indicate how much of the variance of each observed variable is explained by the factors. These contributions are usually computed as squared correlations, and they can also be understood geometrically as the squared cosines of the angles between the original variables and the latent factors. In addition, they may be interpreted as measures of the discriminant power of each variable. The sum of the contributions across two factors corresponds to the contribution of the plane defined by those factors.

Although the information may be somewhat redundant given the previous representations, we include it for comparison with other techniques, such as Multiple Correspondence Analysis. The user can choose the way the results are presented: correlation circle plots, tables, or contribution plots.

Figure 10 displays the contributions associated with the first two factors, where each variable is represented by a vector. The plot is scaled so that the projection of a vector onto an axis corresponds to its contribution to the respective factor, while the concentric circles indicate the contribution of the plane formed by the two factors.

Beyond correlations and contributions, additional measures associated with the prediction biplot may be employed. Given that Equations (24) and (25) define an ordinal logistic regression model, any conventional measure of model fit within this framework can be used as an indicator of goodness of fit for each variable. In particular, pseudo-$R^2$ indices (such as those proposed by Cox–Snell, McFadden, or Nagelkerke), the proportion of correct classifications, and the Kappa coefficient assessing the agreement between observed and predicted values may be considered.

Table 6. Measures of fit (global and for each separate variable).

	CoxSnell	Macfaden	Nagelkerke	PCC	Kappa
IntPolit	0.64	0.60	0.69	66.67
Ideology	0.71	0.53	0.77	67.66
FinancState	0.70	0.52	0.76	80.60
Autonomy	0.73	0.51	0.79	78.11
Orientation	0.72	0.54	0.77	77.11
Nature	0.40	0.63	0.53	77.11	0.55
Demands	0.44	0.58	0.59	78.61	0.57
DifProf	−0.01	1.00	−0.01	54.23	0.02
Global				72.51

presents these measures.

We observe that the pseudo-$R^2$ measures are reasonably high, except for the variable DifProf. A review of the interpretation of these coefficients can be found in [23].

Although pseudo-$R^2$ statistics are conceptually similar to the coefficient of determination in ordinary least squares regression, they do not represent the proportion of variance explained. Instead, they quantify the relative improvement in model fit achieved by the fitted model compared to a null (intercept-only) model. Higher values of pseudo-$R^2$ imply better model fit relative to the null model.

For instance, typical rough guidelines for interpreting McFadden’s $R^2$ state that a value higher than 0.26 indicates a strong fit.

These thresholds should be viewed as heuristic rather than absolute, and pseudo-$R^2$ values are best interpreted comparatively across models fitted to the same data.

The percentages of correct classification are reasonably high. We have to consider that we are dealing with measurements in the behavioral sciences, which are often less precise. The percentages are also lower because the intermediate category is never predicted.

Ordinarily, the points representing individual subjects are not directly examined, except perhaps when the focus is on specific characteristics of a given subject and their corresponding behavior. More commonly, the analysis is directed toward understanding how groups of individuals perform in relation to the variables.

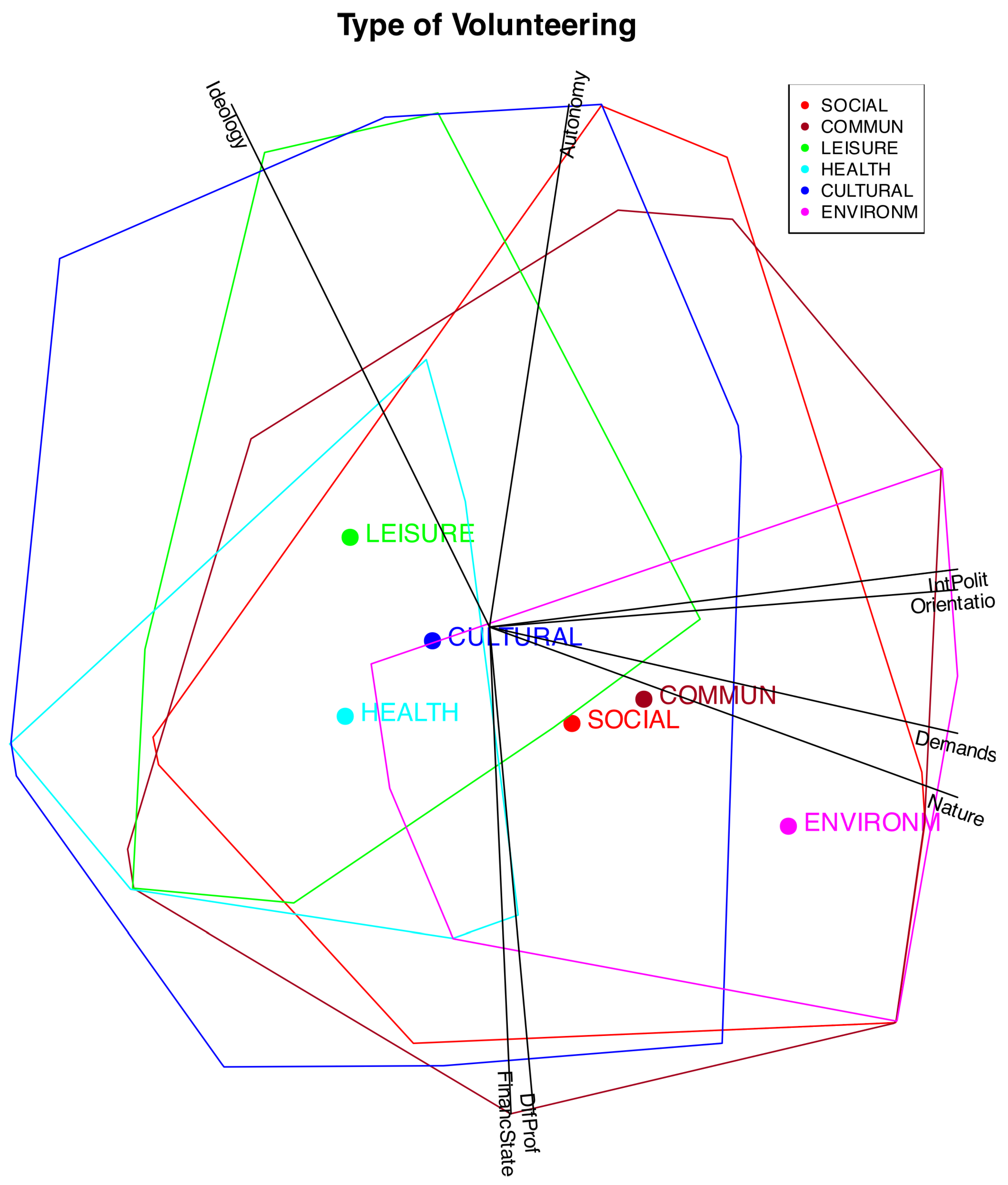
An effective strategy is to distinguish individuals from different groups or clusters by using color coding, enclosing them within convex hulls, or representing them through their group centroids. For instance, Figure 11 illustrates convex hulls and centroids corresponding to various types of volunteering.

It can be observed that the different types are distributed along a gradient associated, on the one hand, with Ideology, and on the other, with Interest in Politics, Political Demands, Orientation of the Volunteering, and Nature of the Organization. In particular, the types Leisure, Health, and Cultural are linked to lower levels of political interest among volunteers, weaker political demands and orientations within organizations, and a stronger emphasis on welfare-oriented activities. They are also somewhat associated with a Right Ideology.

The other types—Social, Community, and Environmental—are associated with individuals who have a stronger interest in volunteer-related politics and with organizations that exhibit higher political demands, greater political orientation, and a transformative nature. Volunteers in these organizations, particularly in the environmental category, tend to align with left-leaning ideologies.

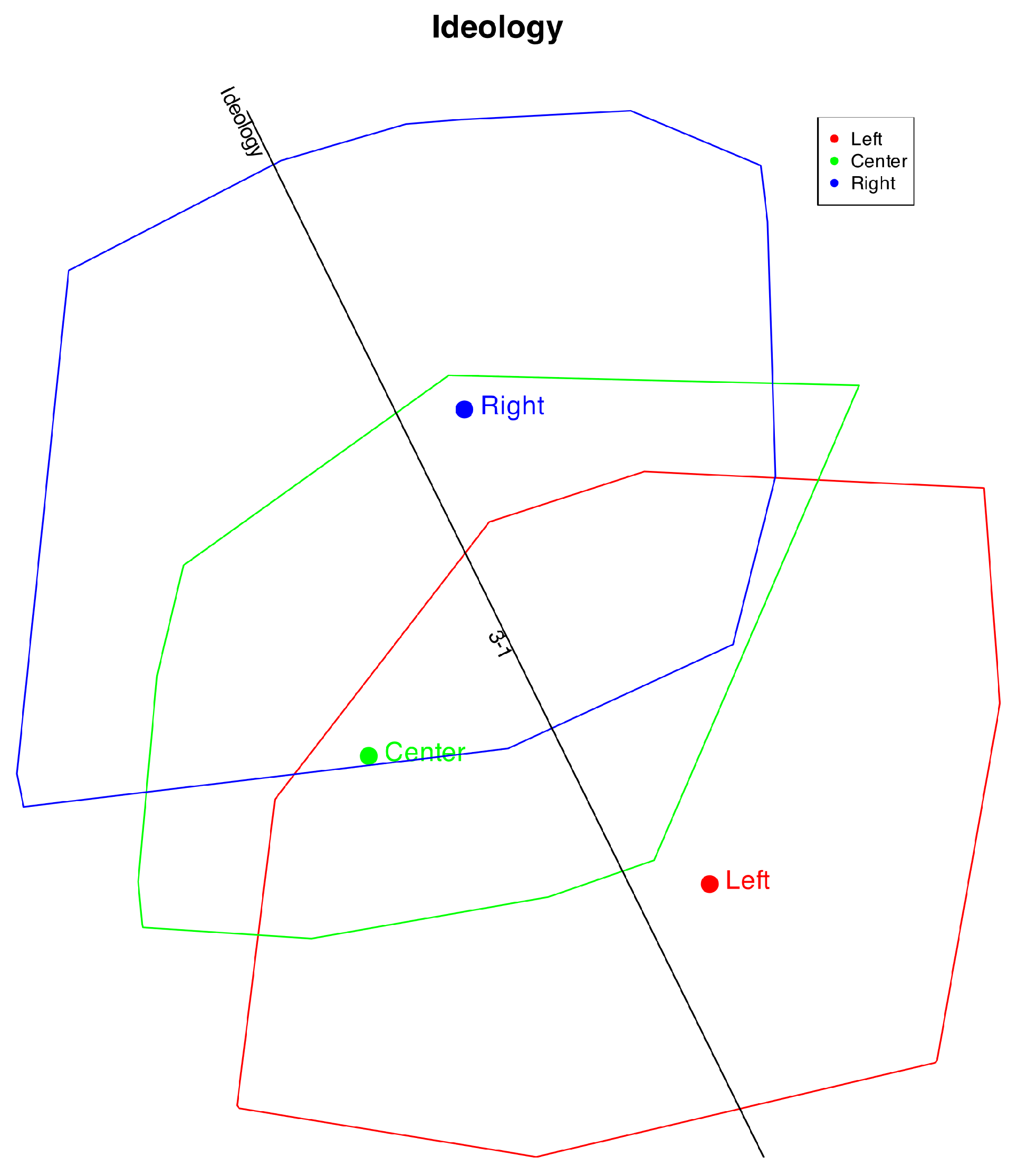
To check the performance of the method, we can also include clusters based on the observed variables. For instance, Figure 12 shows the clusters formed by ideology.

We observe that the ideological direction closely reflects the original data. The Left and Right positions are well distinguished, whereas the Center is not—likely because individuals identifying as Center sometimes hold opinions aligned with the Left and at other times with the Right. A similar pattern is observed for the middle categories in the other items.

In the prediction, category 2 is never identified; only categories 1 and 3 are predicted, as indicated by the “1–3” mark. Individuals with Right or Left ideologies are mostly classified correctly, while those in the Center are split between the two extremes. Consequently, the overall classification accuracy is slightly lower. Overall, the respondents’ ideologies are well represented in the plot.

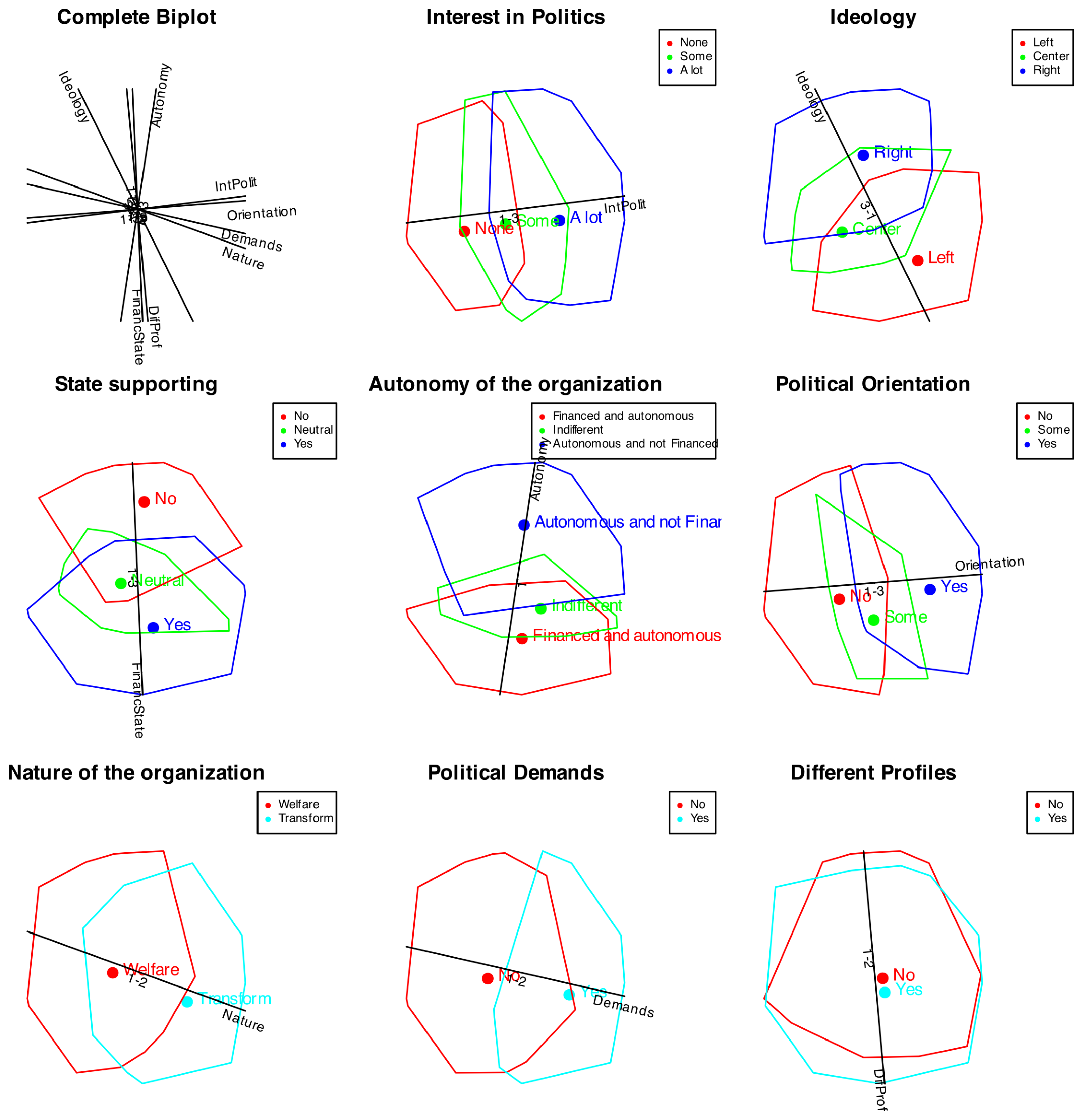
Figure 13 shows the clusters including all variables.

We can see that all variables, except Profiles, are well represented in the plot. For all cases with three categories, the middle value is not well represented. For the variable Profiles, both groups appear mixed together, indicating that the factors do not discriminate between profiles.

4. Concluding Remarks

This work presents an extension of the biplot methodology to factor analysis, enabling the joint graphical representation of individuals and variables for both continuous and ordinal data. For continuous data, the approach begins with standardization of the data matrix and factor extraction—here illustrated through maximum likelihood estimation with varimax rotation. The resulting biplot provides a clear visual interpretation of factor structures, where variables are represented as vectors and individuals as points. Correlation circles, arrow lengths, and projection geometry allow for an intuitive understanding of variable relationships, contributions, and communalities. Using the classical Protein Consumption Dataset ([20]), the analysis demonstrates how factors differentiate patterns in dietary habits across European countries.

For ordinal and binary data, the study employs polychoric (and tetrachoric) correlations to capture relationships between latent continuous variables underlying categorical responses. The corresponding ordinal logistic biplot extends the traditional framework by modeling cumulative probabilities via a multidimensional logistic latent trait model. Parameters are estimated through a gradient-based optimization algorithm, ensuring convergence to a local minimum. This model relates closely to the factor analysis of the polychoric correlation matrix, preserving the interpretability of loadings while adapting the geometry for ordinal outcomes.

Illustrative examples show how prediction regions can be visualized for each variable, with category boundaries represented by parallel lines perpendicular to the variable direction. Empirical applications reveal that intermediate ordinal categories are often poorly represented, suggesting interpretive limitations in respondent perception.

Model performance is assessed using pseudo-$R^2$ indices (Cox–Snell, McFadden, Nagelkerke), classification accuracy, and Kappa coefficients. These measures indicate satisfactory model fit, though intermediate categories are rarely predicted. Additional visualizations—such as correlation and contribution plots—assist in assessing variable relevance, while grouping individuals through convex hulls or centroids enhances interpretability in applied contexts (e.g., ideological or volunteering-type clusters).

Finally, the paper highlights that biplots are powerful exploratory tools capable of revealing structure, similarity, and differentiation within complex multivariate data. By integrating factor analysis for continuous data and ordinal logistic models for categorical variables, this extended methodology broadens the scope of biplot applications. The resulting graphical representations remain interpretable, informative, and computationally accessible through implementation in the MultBiplotR package.

5. Software Note

The procedures of this paper will be added to Version 25.11 of the package MultBiplotR ([17]) developed in the R language ([18]). The package is also available from the corresponding authors.