Pattern Classification for Mixed Feature-Type Symbolic Data Using Supervised Hierarchical Conceptual Clustering
Abstract
1. Introduction
2. Cartesian System Model (CSM) and Feature Selection Using Hierarchical Conceptual Clustering
2.1. The Cartesian System Model (CSM)
- (1)
- Continuous quantitative feature (e.g., height and weight);
- (2)
- Discrete quantitative feature (e.g., the number of family members);
- (3)
- Ordinal qualitative feature (e.g., academic career, etc., where there is some kind of ordered relationships between values)
- (4)
- Nominal qualitative feature (e.g., gender and blood type).
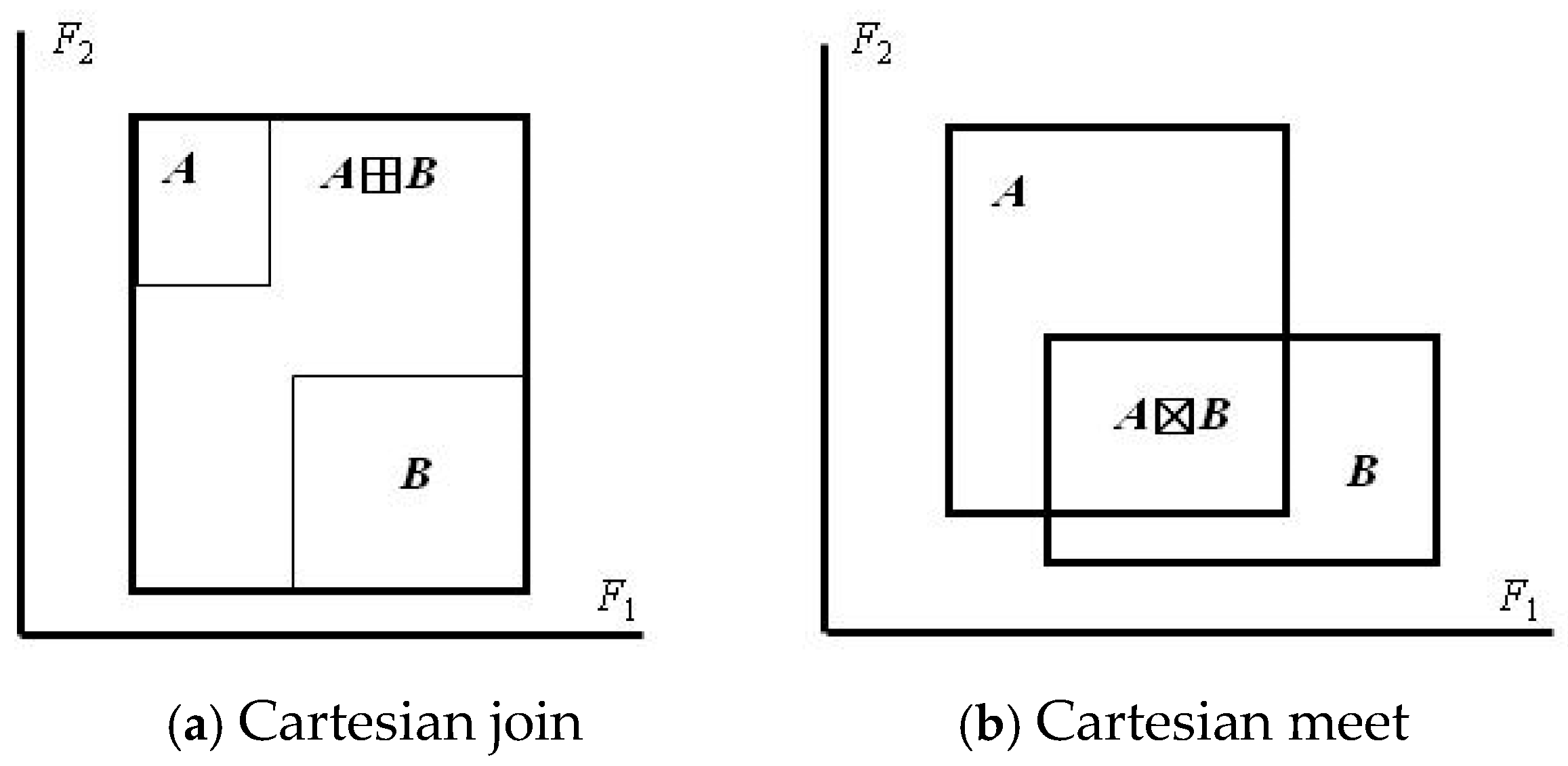
2.1.1. The Cartesian Join Operator
2.1.2. The Cartesian Meet Operator
2.1.3. Concept Size
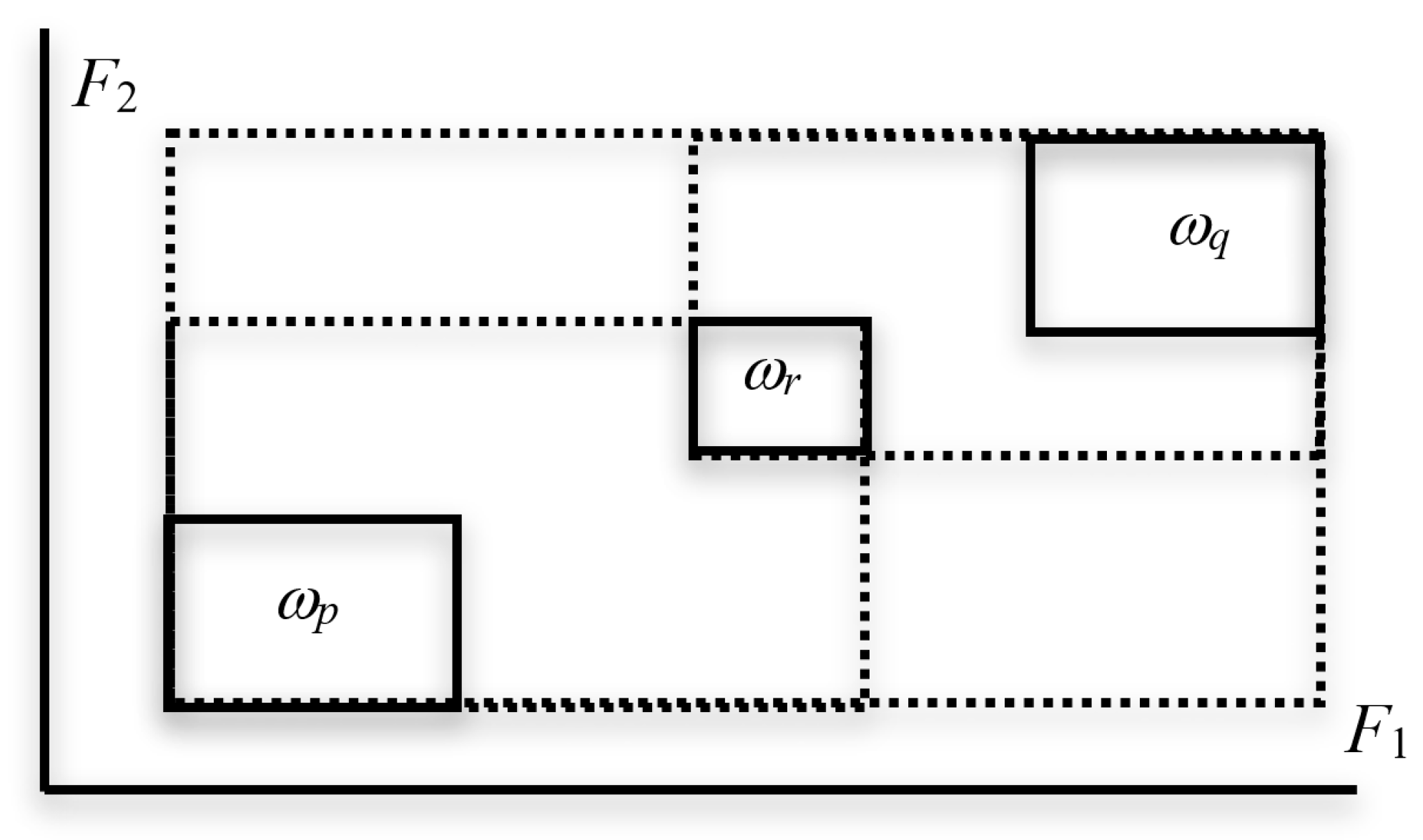
2.2. Measure of Compactness and Unsupervised Hierarchical Conceptual Clustering
2.2.1. Measure of Compactness
- (1)
- 0 ≤ C(ωp, ωq) ≤ 1;
- (2)
- C(ωp, ωp) = P(Ep) ≥ 0;
- (3)
- C(ωp, ωq) = C(ωq, ωp);
- (4)
- C(ωp, ωq) = 0 iff Ei ≡El and has null size (P(Ei) = 0);
- (5)
- C(ωp, ωp), C(ωq, ωq) ≤ C(ωp, ωq);
- (6)
2.2.2. Unsupervised Hierarchical Conceptual Clustering
- Step (1)
- For each pair of sample objects ω and ω’ in U, calculate the compactness C(ω, ω’) in (13) and find the pair ωp and ωq that has the minimum compactness.
- Step (2)
- Generate the merged concept ωpq of ωp and ωq in U, and replace ωp and ωq in U by the new concept ωpq, where ωpq is described by the Cartesian join Epq = Ep⊞Eq in the feature space D(d).
- Step (3)
- Repeat Step 2 until U includes only one concept (i.e., the whole concept generated by the given N sample objects). (End of Algorithm)
- (1)
- Specific gravity,
- (2)
- Freezing point (°C),
- (3)
- Iodine value,
- (4)
- Saponification value,
- (5)
- Major acids.
| Sample | Specific G. | Freezing P. | Iodine V. | Saponification V. | Major Acids |
|---|---|---|---|---|---|
| Linseed | [0.930, 0.935] | [−27, −18] | [170, 204] | [118, 196] | [1.75, 4.81] |
| Perilla | [0.930, 0.937] | [−5, −4] | [192, 208] | [188, 197] | [0.77, 4.85] |
| Cotton | [0.916, 0.918] | [−6, −1] | [99, 113] | [189, 198] | [0.42, 3.84] |
| Sesame | [0.920, 0.926] | [−6,−4] | [104, 116] | [187, 193] | [0.91, 3.77] |
| Camellia | [0.916, 0.917] | [−21, −15] | [80, 82] | [189, 193] | [2.00, 2.98] |
| Olive | [0.914, 0.919] | [0, 6] | [79, 90] | [187, 196] | [0.83, 4.02] |
| Beef | [0.860, 0.870] | [30, 38] | [40, 48] | [190, 199] | [0.31, 2.89] |
| Hog | [0.858, 0.864] | [22, 32] | [53, 77] | [190, 202] | [0.37, 3.65] |
2.3. Classification Model Based on the Supervised Conceptual Clustering
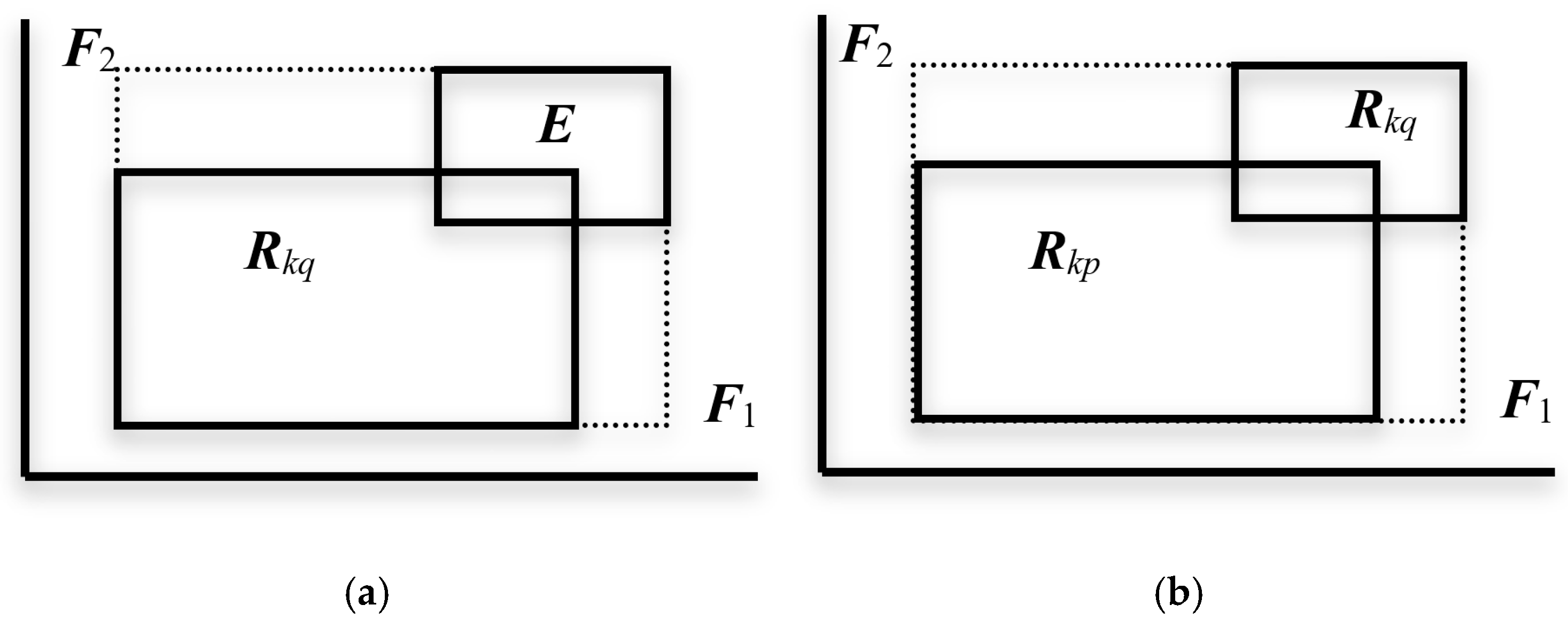
2.3.1. Classification Model
- (1)
- 0 ≤ S(ω→Ωkq) ≤ 1;
- (2)
- S(ω→Ωkq) = S(Ωkq→ω) iff ω = Ωkq;
- (3)
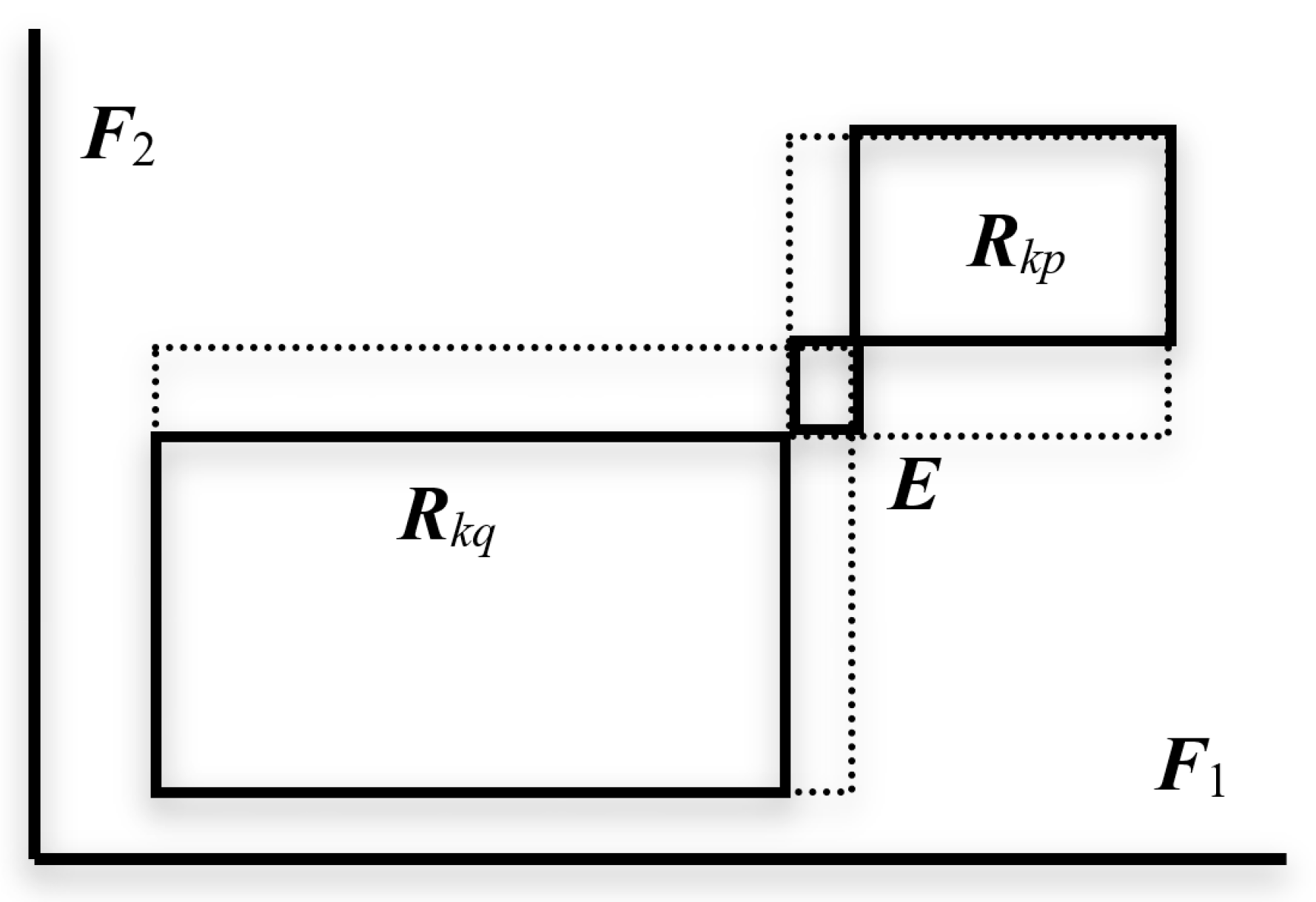
- E ⊆ Rkq implies S(ω→Ωkq) = 1; and
- (4)
- S(Ωkp→Ωkq) ≤ S(Ωkq→Ωkp) iff P(Rkq) ≤ P(Rkp).
2.3.2. Classification Rule
2.3.3. Generation of Subclasses by the Supervised Hierarchical Conceptual Clustering
- Step (1)
- For each pair of subclasses ω and ω’ in Uk, calculate the compactness C(ω, ω’) = P(E⊞E’) and find the pair ωp and ωq in Uk that minimizes C(ωp, ωq) = P(Ep⊞Eq) and satisfies also the mutual neighborhood condition in (20) against Uck.
- Step (2)
- Define the new subclass ωpq by the set {ωp, ωq}. Then, delete ωp and ωq from Uk and put the new subclass ωpq into Uk, where the subclass ωpq is described by the Cartesian join Epq = Ep⊞Eq in the feature space D(d).
- Step (3)
- Repeat Step (1) and Step (2) until the set Uk is unchanged.
- Step (4)
- Define the subclasses Ωk1, Ωk2, …, Ωkm and their descriptions Rk1, Rk2, …, Rkm in the feature space from the generated subclasses in Uk according to the cardinality of the subclasses from the largest to the smallest. (End of algorithm)
3. Experimental Results
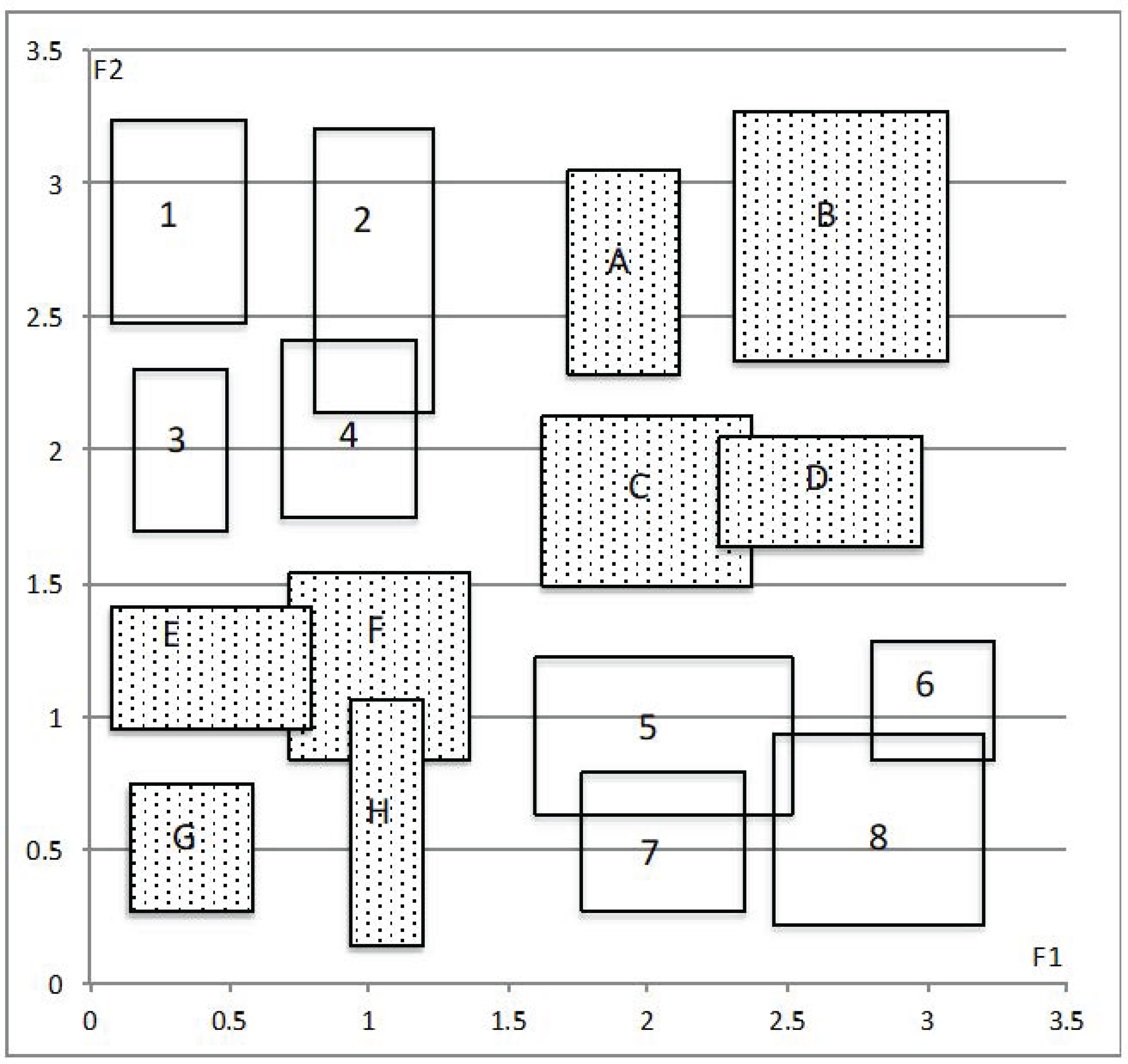
3.1. Artificial Data
| Steps | Subclass | C(p, q) | F1 | F2 | F3 | F4 | F5 |
|---|---|---|---|---|---|---|---|
| 1 | (7, 8) | 0.420 | E, F, G, H | A, B, C, D | F | C, E | C, E, F |
| 2 | (1, 3) | 0.446 | A, B, C, D | E, F, G, H | C, D, G | B, E, F | |
| 3 | (2, 4) | 0.547 | A, B, C, D | E, F, G, H | E | F | |
| 4 | ((7, 8), 6) | 0.580 | E, F, G, H | A, B, C, D | E | F | |
| 5 | ((1, 3), (2, 4)) | 0.668 | A, B, C, D | E, F, G, H | |||
| 6 | (((7, 8), 6), 5) | 0.694 | E, F, G, H | A, B, C, D | F | ||
| C11 | (1, 2, 3, 4) | 0.429 | [0.000, 0.379] | [0.507, 0.985] | |||
| C12 | (5, 6, 7, 8) | 0.429 | [0.485, 1.000] | [0.030, 0.373] |
| Steps | Subclass | C(p, q) | F1 | F2 | F3 | F4 | F5 |
|---|---|---|---|---|---|---|---|
| 1 | (A, C) | 0.387 | 1, 2, 3, 4 | 5, 6, 7, 8 | 6 | 1 | 8 |
| 2 | (G, H) | 0.414 | 5, 6, 7, 8 | 1, 2, 3, 4 | 4, 6 | 1, 6 | |
| 3 | ((A, C), D) | 0.538 | 1, 2, 3, 4 | 5, 6, 7, 8 | 4, 6 | 1 | |
| 4 | ((G, H), F) | 0.566 | 5, 6, 7, 8 | 1, 2, 3, 4 | 6 | 1 | |
| 5 | (((G, H), F), E) | 0.628 | 5, 6, 7, 8 | 1, 2, 3, 4 | 6 | ||
| 6 | (((A, C), D), B) | 0.661 | 1, 2, 3, 4 | 5, 6, 7, 8 | 6 | 1 | |
| C21 | (E, F, G, H) | 0.628 | [0.000, 0.394] | [0.000, 0.448] | |||
| C22 | (A, B, C, D) | 0.661 | [0.485, 0.955] | [0.433, 1.000] |
3.2. The Hardwood Data
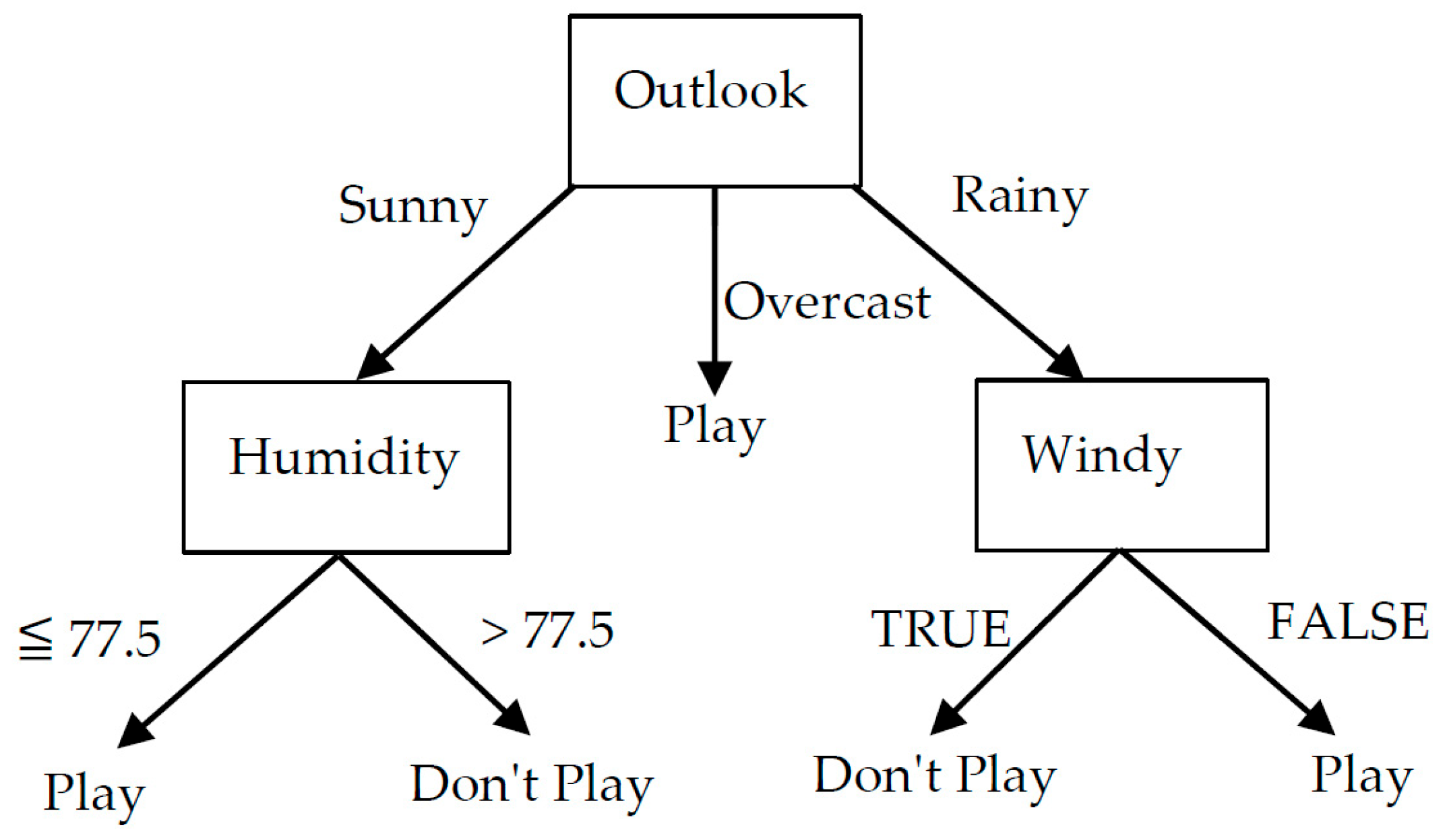
3.3. Golf Data [9]
| Class | Sample | F1: Outlook | F2: Temp. (℉) | F3: Humidity (%) | F4: Windy |
|---|---|---|---|---|---|
| 1 | Overcast | 72 | 90 | TRUE | |
| 2 | Overcast | 83 | 78 | FALSE | |
| 3 | Rainy | 75 | 80 | FALSE | |
| 4 | Overcast | 64 | 65 | TRUE | |
| C1 | 5 | Sunny | 75 | 70 | TRUE |
| (Play) | 6 | Overcast | 81 | 75 | FALSE |
| 7 | Rainy | 68 | 80 | FALSE | |
| 8 | Rainy | 70 | 96 | FALSE | |
| 9 | Sunny | 69 | 70 | FALSE | |
| A | Rainy | 71 | 80 | TRUE | |
| B | Rainy | 65 | 70 | TRUE | |
| C2 | C | Sunny | 80 | 90 | TRUE |
| (Don’t play) | D | Sunny | 85 | 85 | FALSE |
| E | Sunny | 72 | 95 | FALSE |
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, H.; Motoda, H. Computational Methods of Feature Selection; CRC Press: London, UK, 2007. [Google Scholar]
- Miao, J.; Niu, L. A survey on feature selection. Procedia Comput. Sci. 2016, 91, 919–926. [Google Scholar] [CrossRef]
- Solorio-Fernández, S.; Martínez-Trinidad, J.F.; Carrasco-Ochoa, J.A. A review of unsupervised feature selection methods. Artif. Intell. Rev. 2020, 53, 907–948. [Google Scholar] [CrossRef]
- Billard, L.; Diday, E. Symbolic Data Analysis: Conceptual Statistics and Data Mining; Wiley: Chichester, UK, 2007. [Google Scholar]
- Huang, H.S. Supervised feature selection: A tutorial. Artif. Intell. Res. 2015, 4, 22–37. [Google Scholar] [CrossRef]
- Ichino, M.; Umbleja, K.; Yaguchi, H. Unsupervised feature selection for histogram-valued symbolic data using hierarchical conceptual clustering. Stats 2021, 4, 359–384. [Google Scholar] [CrossRef]
- Ichino, M.; Yaguchi, H. Symbolic pattern classifiers based on the Cartesian system model. In Data Science, Classification, and Related Methods; Hayashi, C., Yajima, K., Bock, H.-H., Ohsumi, N., Tanaka, Y., Baba, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Histogram Data by the U.S. Geological Survey, Climate-Vegetation Atlas of North America. Available online: http://pubs.usgs.gov/pp/p1650-b/ (accessed on 20 November 2010).
- Wu, X.; Kumar, V. (Eds.) The Top Ten Algorithms in Data Mining; Chapman and Hall/CRC: New York, NY, USA, 2009. [Google Scholar]



| Class | F1 | F2 | F3 | F4 | F5 |
|---|---|---|---|---|---|
| Plant oils | [0.914, 0.937] | [−27, 6] | [79, 208] | [118, 198] | [0.42, 4.85] |
| Fats | [0.858, 0.870] | [22, 38] | [40, 77] | [190, 202] | [0.31, 3.65] |
| Sample | F1 Min | F1 Max | F2 Min | F2 Max | F3 Min | F3 Max | F4 Min | F4 Max | F5 Min | F5 Max |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.000 | 0.182 | 0.746 | 0.985 | 0.386 | 0.590 | 0.000 | 0.150 | 0.367 | 0.992 |
| 2 | 0.212 | 0.379 | 0.657 | 0.970 | 0.299 | 0.330 | 0.262 | 1.000 | 0.507 | 0.524 |
| 3 | 0.045 | 0.121 | 0.507 | 0.687 | 0.468 | 0.906 | 0.112 | 0.426 | 0.585 | 0.776 |
| 4 | 0.197 | 0.364 | 0.522 | 0.731 | 0.778 | 0.949 | 0.409 | 0.856 | 0.157 | 0.877 |
| 5 | 0.485 | 0.773 | 0.149 | 0.358 | 0.000 | 1.000 | 0.020 | 0.800 | 0.714 | 0.781 |
| 6 | 0.848 | 1.000 | 0.224 | 0.373 | 0.925 | 0.941 | 0.722 | 0.893 | 0.044 | 0.778 |
| 7 | 0.530 | 0.697 | 0.045 | 0.209 | 0.221 | 0.410 | 0.342 | 0.666 | 0.363 | 0.600 |
| 8 | 0.727 | 0.985 | 0.030 | 0.254 | 0.459 | 0.564 | 0.259 | 0.609 | 0.319 | 0.338 |
| A | 0.515 | 0.652 | 0.672 | 0.940 | 0.301 | 0.485 | 0.335 | 0.480 | 0.522 | 0.984 |
| B | 0.697 | 0.955 | 0.701 | 1.000 | 0.108 | 0.862 | 0.297 | 0.767 | 0.235 | 0.339 |
| C | 0.485 | 0.712 | 0.433 | 0.642 | 0.227 | 0.511 | 0.673 | 0.858 | 0.685 | 0.944 |
| D | 0.682 | 0.909 | 0.478 | 0.612 | 0.399 | 0.448 | 0.466 | 0.489 | 0.030 | 0.725 |
| E | 0.000 | 0.227 | 0.239 | 0.418 | 0.310 | 0.877 | 0.112 | 0.151 | 0.000 | 0.179 |
| F | 0.212 | 0.394 | 0.224 | 0.448 | 0.668 | 0.799 | 0.303 | 0.752 | 0.971 | 1.000 |
| G | 0.030 | 0.167 | 0.060 | 0.155 | 0.283 | 0.406 | 0.516 | 0.537 | 0.479 | 0.848 |
| H | 0.258 | 0.364 | 0.000 | 0.299 | 0.211 | 0.629 | 0.352 | 0.386 | 0.013 | 0.735 |
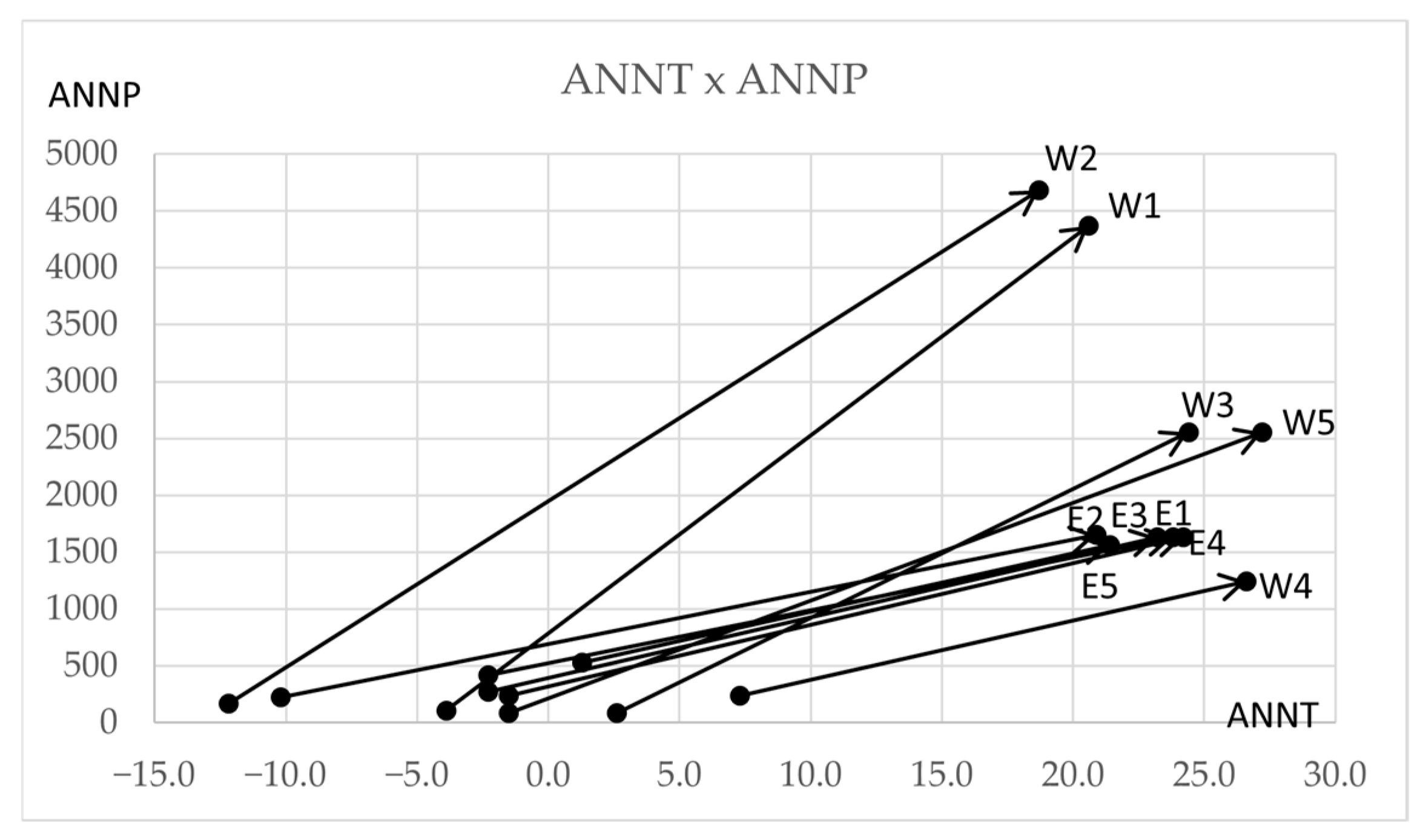
| Taxon Name | ANNT: F1 | JANT: F2 | JULT: F3 | ANNP: F4 | JANP: F5 | JULP: F6 | GDC5: F7 | MITM: F8 |
|---|---|---|---|---|---|---|---|---|
| ACER EAST: E1 min | −2.3 | −24.6 | 11.5 | 415 | 10 | 56 | 0.5 | 0.62 |
| max | 23.8 | 18.9 | 28.8 | 1630 | 166 | 222 | 6.8 | 1.00 |
| ACER WEST: W1 min | −3.9 | −23.8 | 7.1 | 105 | 5 | 0 | 0.1 | 0.14 |
| max | 20.6 | 11.0 | 29.2 | 4370 | 616 | 160 | 5.6 | 1.00 |
| ALNUS EAST: E2 min | −10.2 | −30.9 | 7.1 | 220 | 9 | 28 | 0.1 | 0.22 |
| max | 20.9 | 14.1 | 29.1 | 1650 | 166 | 212 | 5.9 | 1.00 |
| ALNUS WEST: W2 min | −12.2 | −30.5 | 7.1 | 170 | 4 | 0 | 0.1 | 0.22 |
| max | 18.7 | 10.8 | 28.3 | 4685 | 667 | 452 | 4.8 | 1.00 |
| FRAXINUS EAST: E3 min | −2.3 | −23.8 | 13.5 | 270 | 6 | 18 | 0.8 | 0.39 |
| max | 23.2 | 18.1 | 29.5 | 1630 | 166 | 218 | 6.7 | 1.00 |
| FRAXINUS EAST: W3 min | 2.6 | −7.4 | 12.5 | 85 | 5 | 0 | 0.9 | 0.09 |
| max | 24.4 | 16.9 | 33.1 | 2555 | 414 | 206 | 6.9 | 0.97 |
| JUGLANS EAST: E4 min | 1.3 | −14.6 | 15.2 | 525 | 9 | 41 | 1.0 | 0.63 |
| max | 21.4 | 12.4 | 29.4 | 1560 | 150 | 204 | 6.0 | 1.00 |
| JUGLANS WEST: W4 min | 7.3 | −1.3 | 17.1 | 235 | 1 | 0 | 1.6 | 0.20 |
| max | 26.6 | 26.2 | 31.3 | 1245 | 166 | 328 | 8.5 | 0.94 |
| QUERCUS EAST: E5 min | −1.5 | −22.7 | 13.5 | 240 | 7 | 32 | 0.8 | 0.21 |
| max | 24.2 | 19.6 | 31.8 | 1630 | 161 | 222 | 7.0 | 1.00 |
| QUERCUS EAST: W5 min | −1.5 | −12.0 | 9.7 | 85 | 1 | 0 | 0.3 | 0.08 |
| max | 27.2 | 26.2 | 33.8 | 2555 | 400 | 350 | 8.5 | 0.99 |
| Steps | 1 | 2 | 3 | 4 | ||||
|---|---|---|---|---|---|---|---|---|
| Subclass | (E1, E4) | ((E1, E4), E3) | (((E1, E4), E3), E5) | ((((E1, E4), E3), E5), E2) | ||||
| C(p, q) = 0.520 | Separability | C(p, q) = 0.562 | Separability | C(p, q) = 0.604 | Separability | C(p, q) = 0.671 | Separability | |
| F1min | [−2.3, 1.3] | W1–W4 | [−2.3, 1.3] | W1–W4 | [−2.3, 1.3] | W1–W4 | [−10.2, 1.3] | W2, W3, W4 |
| F1max | [21.4, 23.8] | W1–W5 | [21.4, 23.8] | W1–W5 | [21.4, 24.2] | W1–W5 | [20.9, 24.2] | W1–W5 |
| F2min | [−24.6, −14.6] | W2, W3, W4, W5 | [−24.6, −14.6] | W2, W3, W4, W5 | [−24.6, −14.6] | W2, W3, W4, W5 | [−30.9, −14.6] | W3, W4, W5 |
| F2max | [12.4, 18.9] | W1, W2, W4, W5 | [12.4, 18.9] | W1, W2, W4, W5 | [12.4, 19.6] | W1, W2, W4, W5 | [12.4, 19.6] | W1, W2, W4, W5 |
| F3min | [11.5, 15.2] | W1, W2, W4, W5 | [11.5, 15.2] | W1, W2, W4, W5 | [11.5, 15.2] | W1, W2, W4, W5 | [7.1, 15.2] | W4 |
| F3max | [28.8, 29.4] | W2–W5 | [28.8, 29.5] | W2–W5 | [28.8, 31.8] | W2, W3, W5 | [28.8, 31.8] | W2, W3, W5 |
| F4min | [415, 525] | W1–W5 | [270, 525] | W1–W5 | [240, 525] | W1–W5 | [220, 525] | W1, W2, W3, W5 |
| F4max | [1560, 1630] | W1–W5 | [1560, 1630] | W1–W5 | [1560, 1630] | W1–W5 | [1560, 1650] | W1–W5 |
| F5min | [9, 10] | W1–W5 | [6, 10] | W1–W5 | [6, 10] | W1–W5 | [6, 10] | W1–W5 |
| F5max | [150, 166] | W1, W2, W3, W5 | [150, 166] | W1, W2, W3, W5 | [150, 166] | W1, W2, W3, W5 | [150, 166] | W1, W2, W3, W5 |
| F6min | [41, 56] | W1–W5 | [18, 56] | W1–W5 | [18, 56] | W1–W5 | [18, 56] | W1–W5 |
| F6max | [204, 222] | W1, W2, W4, W5 | [204, 222] | W1, W2, W4, W5 | [204, 222] | W1, W2, W4, W5 | [204, 222] | W1, W2, W4, W5 |
| F7min | [0.5, 1.0] | W1, W2, W4, W5 | [0.5, 1.0] | W1, W2, W4, W5 | [0.5, 1.0] | W1, W2, W4, W5 | [0.1, 1.0] | W4 |
| F7max | [6.0, 6.8] | W1–W5 | [6.0, 6.8] | W1–W5 | [6.0, 7.0] | W1, W2, W4, W5 | [5.9, 7.0] | W1, W2, W4, W5 |
| F8min | [0.62, 0.63] | W1–W5 | [0.39, 0.63] | W1–W5 | [0.21, 0.63] | W1, W3, W4, W5 | [0.21, 0.63] | W1, W3, W4, W5 |
| F8max | [1.0, 1.0] | W3, W4, W5 | [1.0, 1.0] | W3, W4, W5 | [1.0, 1.0] | W3, W4, W5 | [1.0, 1.0] | W3, W4, W5 |
| Steps | 1 | 2 | 3 | |||
|---|---|---|---|---|---|---|
| Subclass | (W3, W4) | ((W3, W4), W5) | (W1, W2) | |||
| C(p, q) = 0.714 | Separability | C(p, q) = 0.775 | Separability | C(p, q) = 0.872 | Separability | |
| F1min | [2.6, 7.3] | E1–E5 | [−1.5, 7.3] | E1, E2, E3 | [−12.2, −3.9] | E1, E3, E4 |
| F1max | [24.4, 26.6] | E1–E5 | [24.4, 27.2] | E1–E5 | [18.7, 20.6] | E1–E5 |
| F2min | [−7.4, −1.3] | E1–E5 | [−12.0, −1.3] | E1–E5 | [−30.5, −23.8] | E2, E4, E5 |
| F2max | [16.9, 26.2] | E2, E4 | [16.9, 26.2] | E2, E4 | [10.8, 11.0] | E1–E5 |
| F3min | [12.5, 17.1] | E1, E2 | [9.7, 17.1] | E2 | [7.1, 7.1] | E1, E3, E4, E5 |
| F3max | [31.3, 33.1] | E1, E2, E3, E4 | [31.3, 33.8] | E1, E2, E3, E4 | [28.3, 29.2] | E3, E4, E5 |
| F4min | [85, 235] | E1, E3, E4, E5 | [85, 235] | E1, E3, E4, E5 | [105, 170] | E1–E5 |
| F4max | [1245, 2555] | None | [1245, 2555] | None | [4370, 4685] | E1–E5 |
| F5min | [1, 5] | E1–E5 | [1, 5] | E1–E5 | [4, 5] | E1–E5 |
| F5max | [166, 414] | E4, E5 | [166, 414] | E4, E5 | [616, 667] | E1–E5 |
| F6min | [0, 0] | E1–E5 | [0, 0] | E1–E5 | [0, 0] | E1–E5 |
| F6max | [206, 328] | E4 | [206, 350] | E4 | [160, 452] | None |
| F7min | [0.9, 1.6] | E1, E2, E3, E5 | [0.3, 1.6] | E2 | [0.1, 0.1] | E1, E3, E4, E5 |
| F7max | [6.9, 8.5] | E1, E2, E3, E4 | [6.9, 8.5] | E1, E2, E3, E4 | [4.8, 5.6] | E1–E5 |
| F8min | [0.09, 0.20] | E1–E5 | [0.08, 0.20] | E1–E5 | [0.14, 0,22] | E1, E3, E4 |
| F8max | [0.94, 0.97] | E1–E5 | [0.94, 0.99] | E1–E5 | [1.0, 1.0] | None |
| Class | ANNT Max | ANNP Max | JANP Min |
|---|---|---|---|
| C1: E1–E5 | [20.9, 24.2] | [1560, 1650] | [6, 10] |
| C21: W3, W4, W5 | [24.2, 27.2] | [1245, 2555] | [1, 5] |
| C22: W1, W2 | [18.7, 20.6] | [4370, 4685] | [4, 5] |
| Taxon Name | ANNT | ANNP | JANP |
|---|---|---|---|
| BETURA | [−13.4, 20.3] | [90, 4370] | [4, 612] |
| CARYA | [3.6, 23.5] | [410, 1755] | [2, 150] |
| CASTANEA | [4.4, 21.5] | [765, 1630] | [32, 150] |
| TILIA | [1.1, 19.9] | [415, 1560] | [9, 150] |
| ULMUS | [−2.3, 23.8] | [325, 1145] | [6, 166] |
| Class | Features | BETURA | CARYA | CASTANEA | TILIA | ULMUS |
|---|---|---|---|---|---|---|
| C1 | F1max | 0.846 | 1 | 1 | 0.767 | 1 |
| F4max | 0.032 | 0.462 | 1 | 1 | 0.178 | |
| F5min | 0.667 | 0.5 | 0.154 | 1 | 1 | |
| Avg. | 0.504 | 0.654 | 0.718 | 0.922 | 0.726 | |
| C21 | F1max | 0.074 | 0.811 | 0.526 | 0.411 | 0.235 |
| F4max | 0.419 | 1 | 1 | 1 | 0.929 | |
| F5min | 1 | 1 | 0.129 | 0.5 | 0.8 | |
| Avg. | 0.498 | 0.937 | 0.552 | 0.637 | 0.655 | |
| C22 | F1max | 1 | 0.396 | 0.679 | 1 | 0.373 |
| F4max | 1 | 0.108 | 0.103 | 0.101 | 0.089 | |
| F5min | 1 | 1 | 0.036 | 0.2 | 0.8 | |
| Avg. | 1 | 0.501 | 0.272 | 0.403 | 0.421 |
| Steps | Subclass | C(p, q) | Outlook | Temp. | Humidity | Windy |
|---|---|---|---|---|---|---|
| 1 | (2, 6) | 0.256 | A, B, C, D, E | A, B, C, D, E | A, B, C, D, E | A, B, C |
| 2 | (3, 7) | 0.291 | C, D, E | B, C, D | B, C, D, E | A, B, C |
| 3 | (5, 9) | 0.405 | A, B | B, C, E | A, C, D, E | A, B, C |
| 4 | ((3, 7), 8) | 0.421 | C, D, E | C, D | B, D | A, B, C |
| 5 | (1, 4) | 0.505 | A, B, C, D, E | C, D | E | D, E |
| 6 | ((2, 6), (1, 4)) | 0.761 | A, B, C, D, E | D | E | |
| C11 | (1, 2, 4, 6) | 0.333 | Overcast | |||
| C12 | (3, 7, 8) | 0.417 | Rainy | FALSE | ||
| C13 | (5, 9) | 0.167 | Sunny | [70, 70] |
| Steps | Subclass | C(p, q) | Outlook | Temp. | Humidity | Windy? |
|---|---|---|---|---|---|---|
| 1 | (C, D) | 0.244 | 1, 2, 3, 4, 6, 7, 8 | 1, 3, 4, 5, 7, 8, 9 | 2, 3, 4, 5, 6, 7, 8, 9 | |
| 2 | (A, B) | 0.360 | 1, 2, 4, 5, 6, 9 | 7, 8, 9 | 2, 3, 5, 6, 7, 9 | 2, 3, 6, 7, 8, 9 |
| 3 | ((C, D), E) | 0.569 | 1, 2, 3, 4, 6, 7, 8 | 1, 2, 3, 5, 6 | 2, 3, 4, 5, 6, 7, 8, 9 | |
| C21 | (C, D, E) | 0.328 | Sunny | [85, 95] | ||
| C22 | (A, B) | 0.417 | Rainy | TRUE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ichino, M.; Yaguchi, H. Pattern Classification for Mixed Feature-Type Symbolic Data Using Supervised Hierarchical Conceptual Clustering. Stats 2025, 8, 76. https://doi.org/10.3390/stats8030076
Ichino M, Yaguchi H. Pattern Classification for Mixed Feature-Type Symbolic Data Using Supervised Hierarchical Conceptual Clustering. Stats. 2025; 8(3):76. https://doi.org/10.3390/stats8030076
Chicago/Turabian StyleIchino, Manabu, and Hiroyuki Yaguchi. 2025. "Pattern Classification for Mixed Feature-Type Symbolic Data Using Supervised Hierarchical Conceptual Clustering" Stats 8, no. 3: 76. https://doi.org/10.3390/stats8030076
APA StyleIchino, M., & Yaguchi, H. (2025). Pattern Classification for Mixed Feature-Type Symbolic Data Using Supervised Hierarchical Conceptual Clustering. Stats, 8(3), 76. https://doi.org/10.3390/stats8030076





