Reliability Assessment via Combining Data from Similar Systems
Abstract
1. Introduction
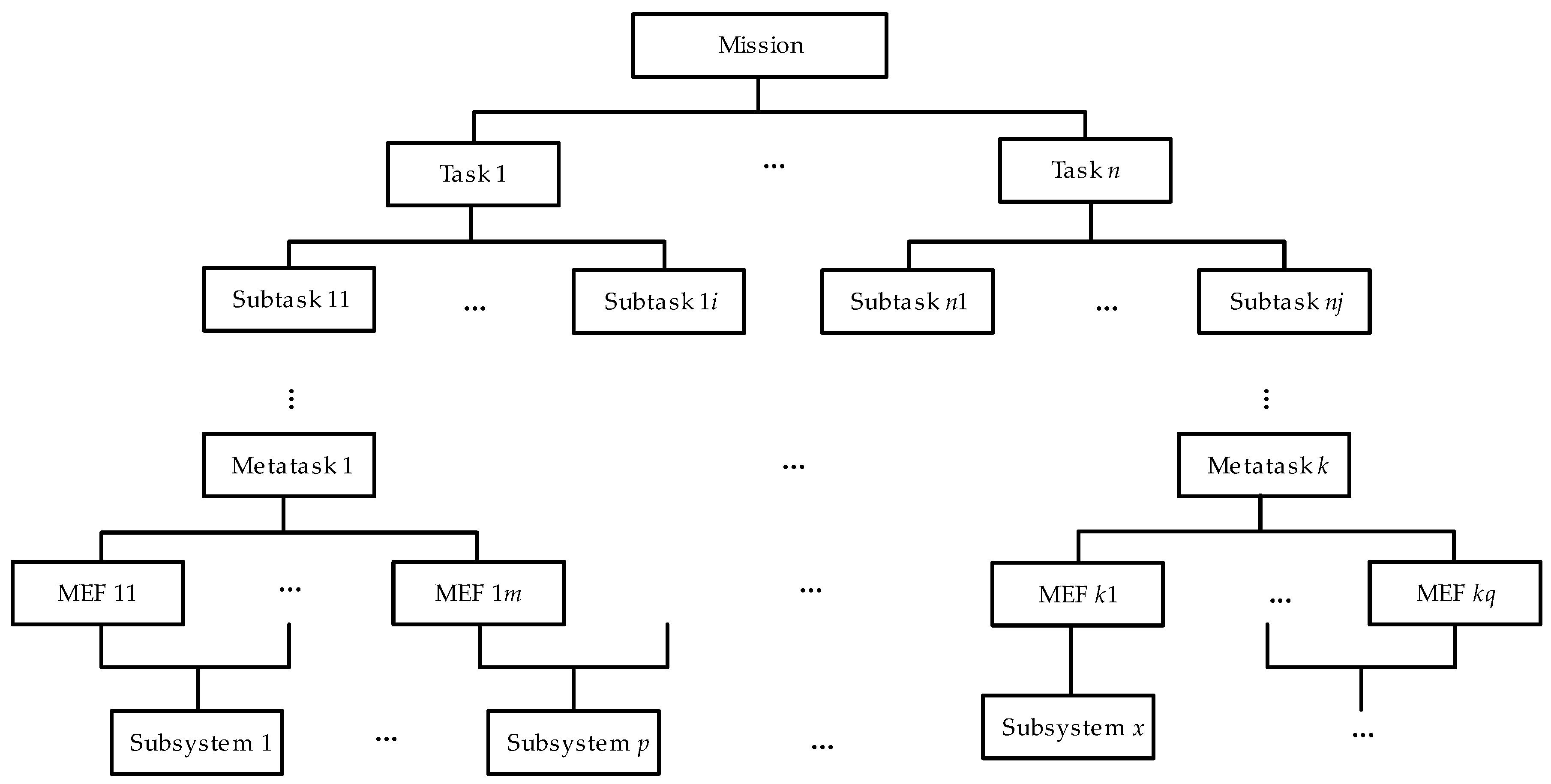
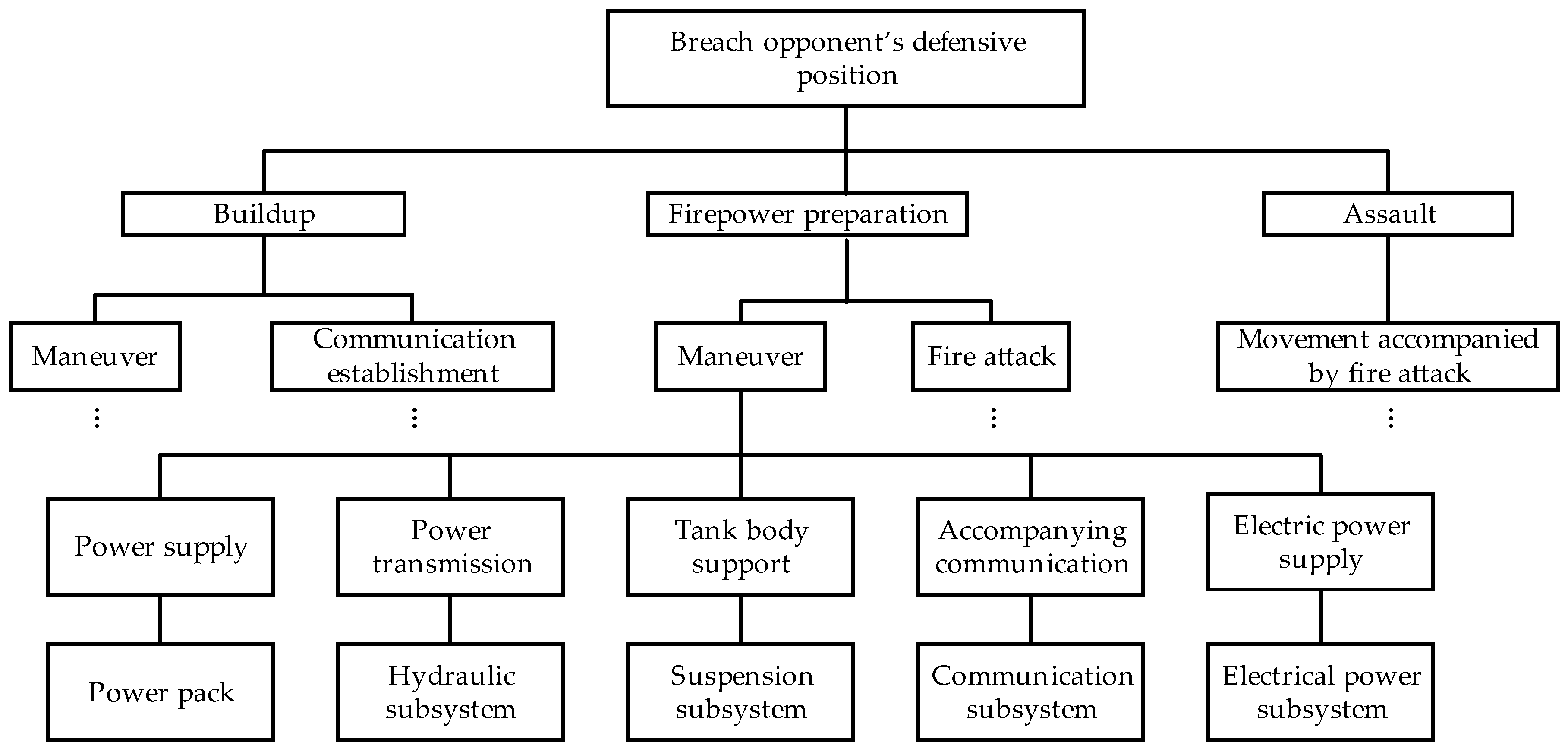
2. Hierarchical Decomposition of the SUT’s Mission
3. Similarity Factor Calculation
3.1. Establishment of PT Representation
3.2. Distance Calculation Principle
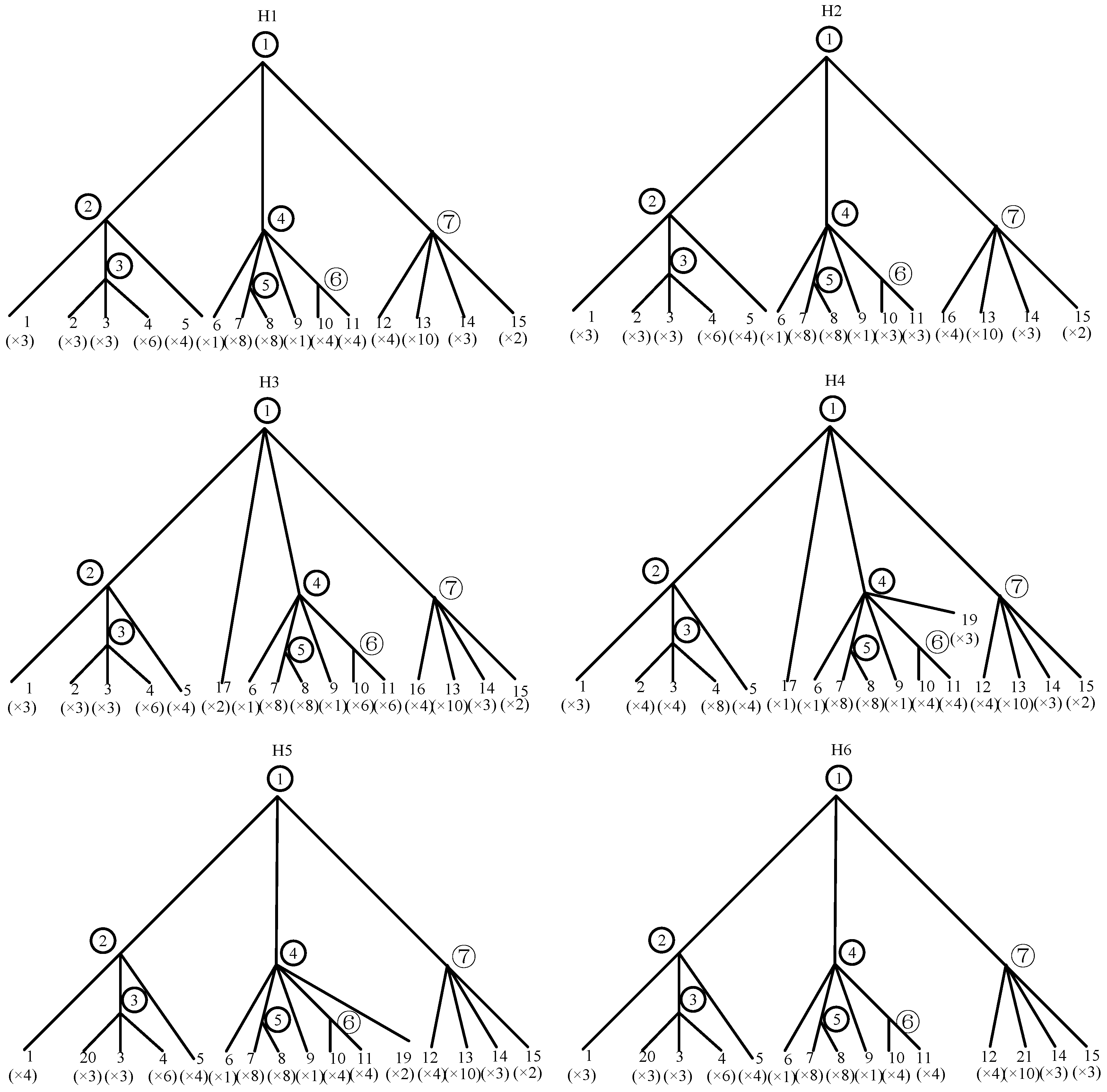
3.3. MIP Solution of Distance and Determination of Similarity Factor
3.3.1. Matrix Encoding Corresponding to PT
3.3.2. MIP Construction and Similarity Factor Calculation
4. Reliability Assessment Model
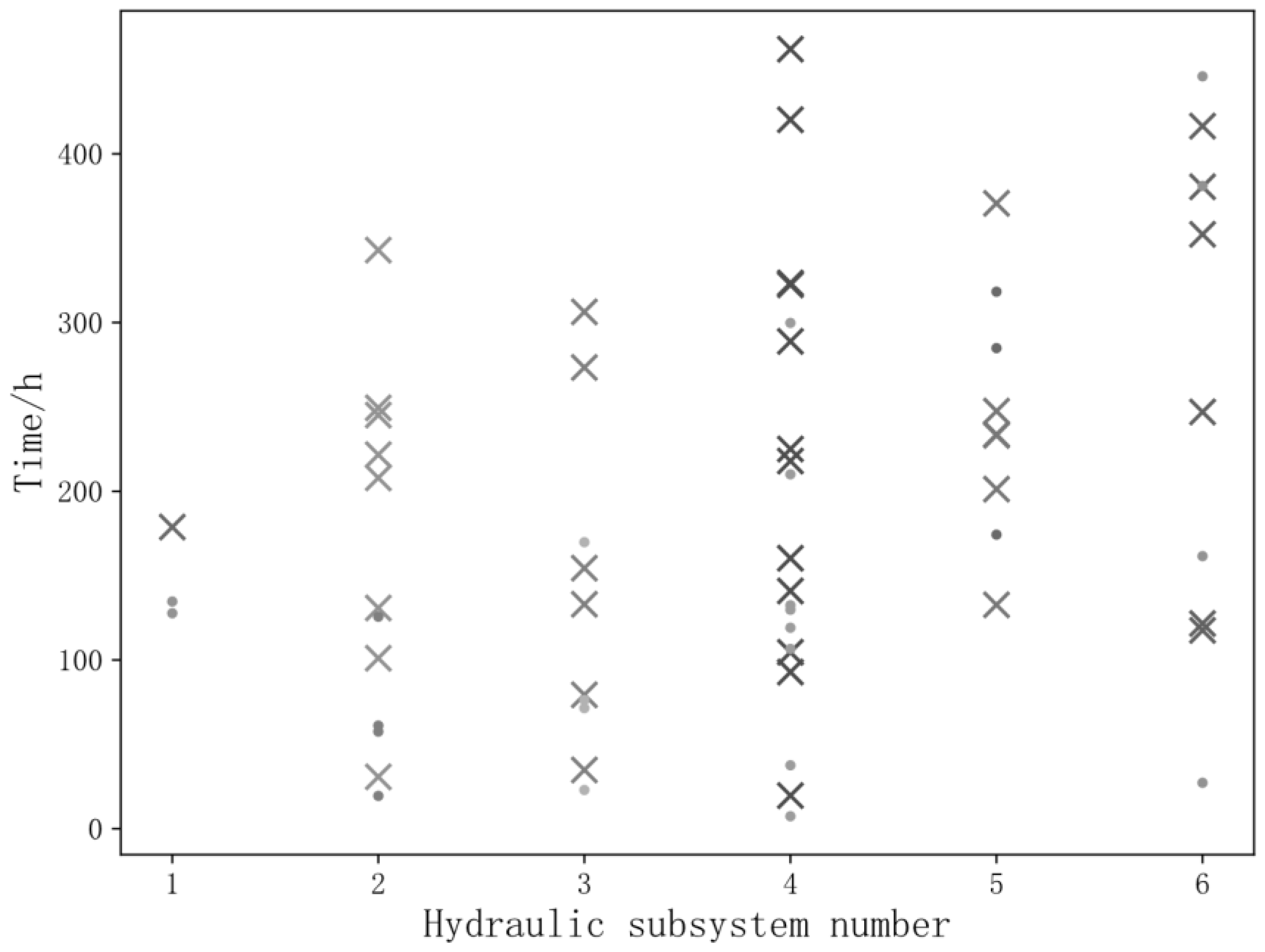
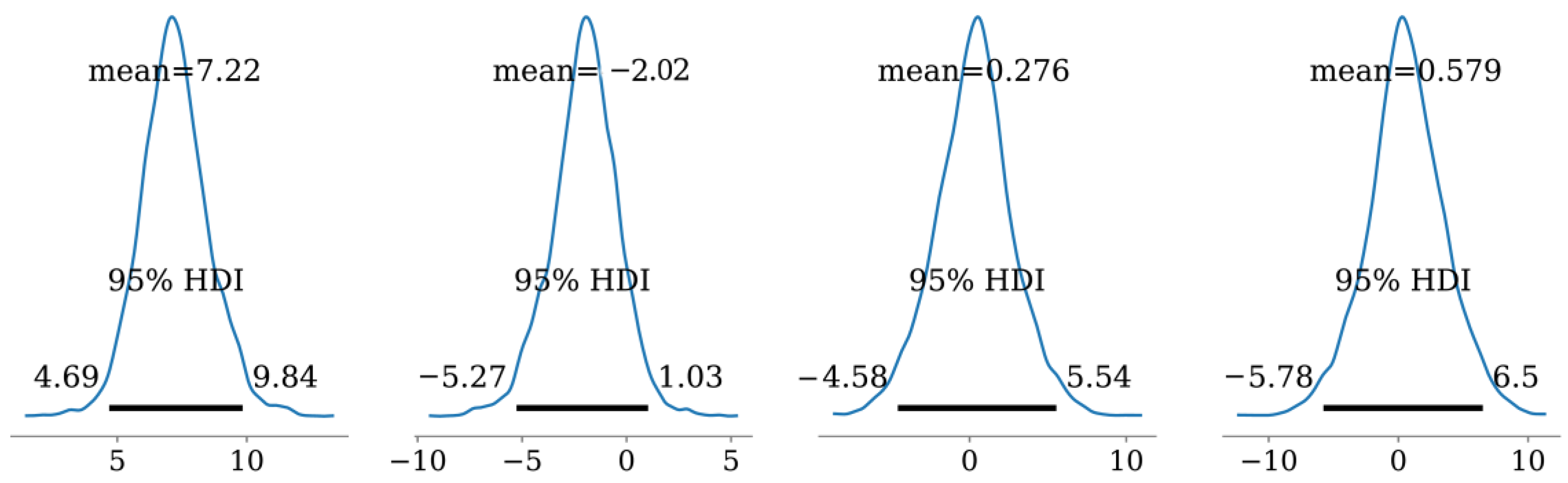
5. Numerical Experiments
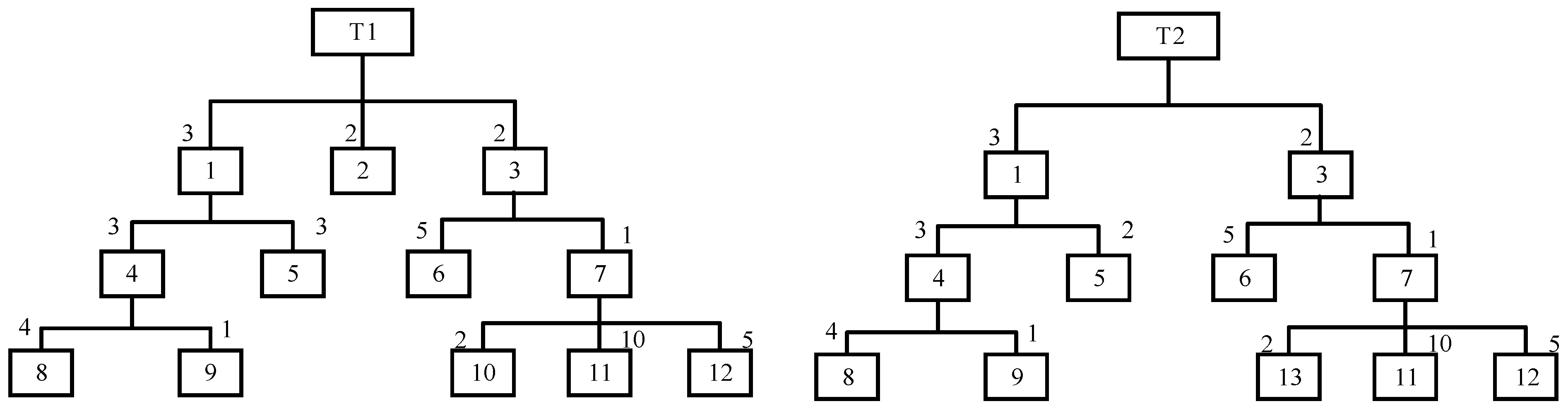
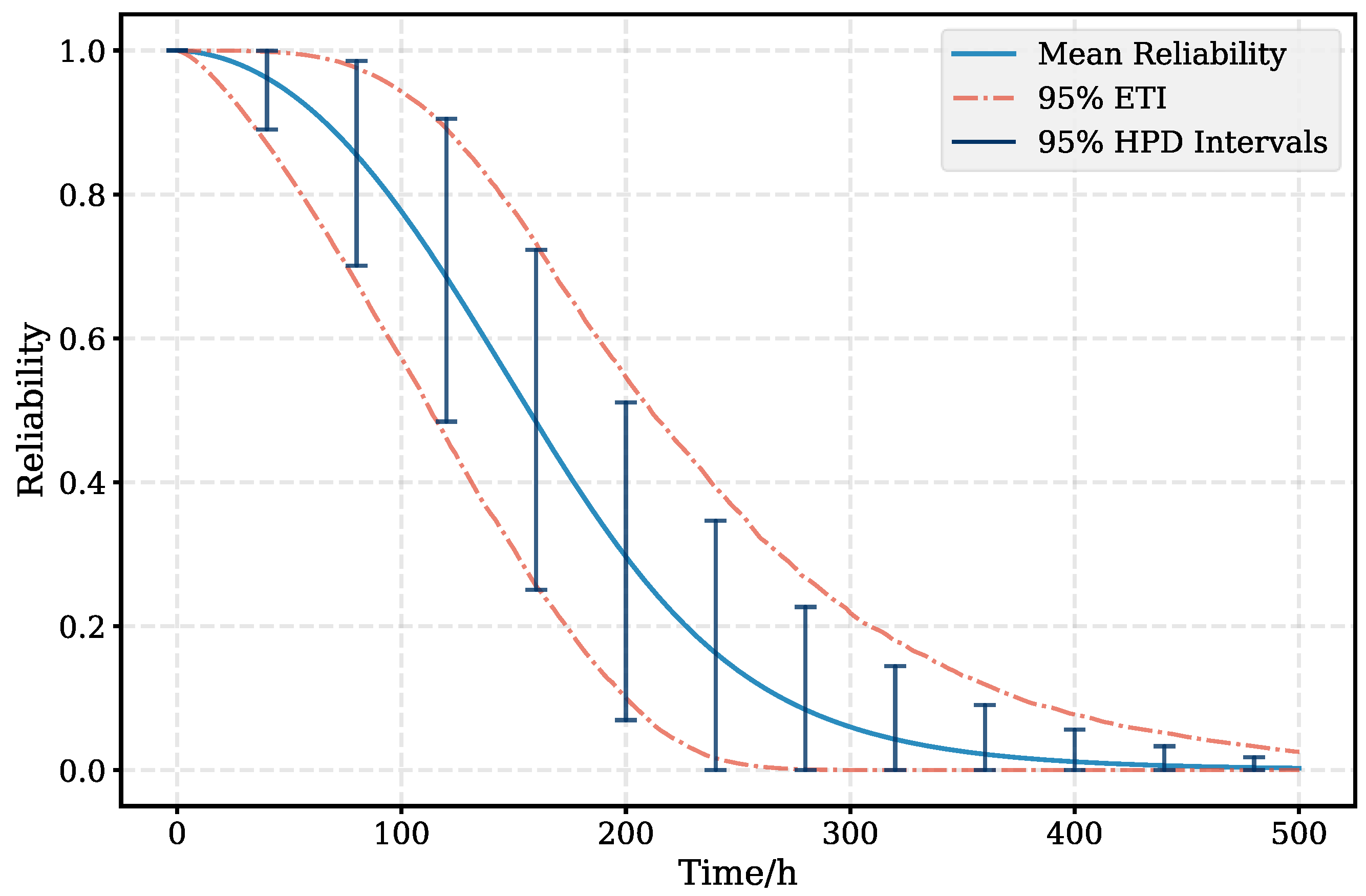
5.1. Application of the Proposed Method
5.2. Comparison of Methods
5.3. Application Extensions
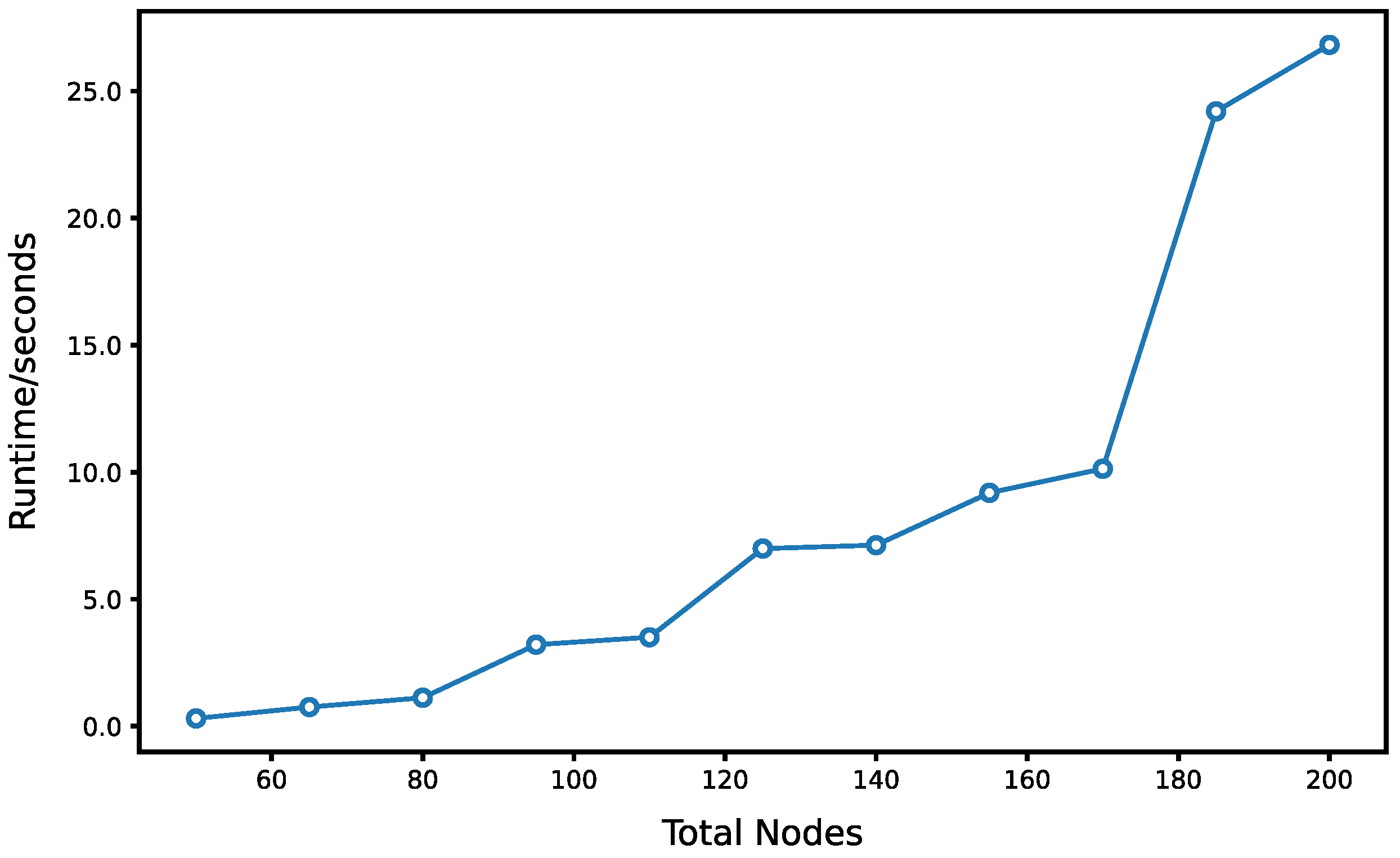
5.3.1. Computational Scalability in Complex Subsystems
5.3.2. Processing of Missing and Noisy Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dement, A.; Hartman, R. Operational suitability evaluation of a tactical fighter system. In Proceedings of the 3rd Flight Testing Conference and Technical Display, Las Vegas, NV, USA, 2–4 April 1986; p. 9753. [Google Scholar]
- Li, J.; Nie, C.; Wang, L. Overview of weapon operational suitability test. In Proceedings of the 2016 International Conference on Artificial Intelligence and Engineering Applications, Hong Kong, China, 16–18 March 2016; Atlantis Press: Dordrecht, The Netherlands, 2016; pp. 423–428. [Google Scholar]
- National Research Council; Division of Behavioral; Committee on National Statistics; Panel on Operational Test Design and Evaluation of the Interim Armored Vehicle. Improved Operational Testing and Evaluation and Methods of Combining Test Information for the Stryker Family of Vehicles and Related Army Systems: Phase II Report; National Academies Press: Washington, DC, USA, 2003. [Google Scholar]
- Lee, B.; Seo, Y. A design of operational test & evaluation system for weapon systems thru process-based modeling. J. Korea Soc. Simul. 2014, 23, 211–218. [Google Scholar]
- Ke, X.C. Reliability predictions of a canister cover based on similar product method. Environ. Adapt. Reliab. 2022, 40, 35–37. [Google Scholar]
- Li, L.; Liu, Z.; Du, X. Improvement of analytic hierarchy process based on grey correlation model and its engineering application. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 04021007. [Google Scholar] [CrossRef]
- Ahlgren, P.; Jarneving, B.; Rousseau, R. Requirements for a cocitation similarity measure, with special reference to Pearson’s correlation coefficient. J. Am. Soc. Inf. Sci. Technol. 2003, 54, 550–560. [Google Scholar] [CrossRef]
- Xiang, S.; Nie, F.; Zhang, C. Learning a Mahalanobis distance metric for data clustering and classification. Pattern Recognit. 2008, 41, 3600–3612. [Google Scholar] [CrossRef]
- Elmore, K.L.; Richman, M.B. Euclidean distance as a similarity metric for principal component analysis. Mon. Weather Rev. 2001, 129, 540–549. [Google Scholar] [CrossRef]
- Li, J.; Dai, W. Multi-objective evolutionary algorithm based on included angle cosine and its application. In Proceedings of the 2008 International Conference on Information and Automation, Changsha, China, 20–23 June 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1045–1049. [Google Scholar]
- Rui, H.D. Research on Reliability Growth AMSAA Model of Complex Equipment Based on Grey Information. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2016. [Google Scholar]
- Meeker, W.Q.; Escoba, L.A. Reliability: The other dimension of quality. Qual. Technol. Quant. Manag. 2004, 1, 1–25. [Google Scholar] [CrossRef]
- Jin, S.; Chen, J.; Gu, R. Study on similarity criterion of equivalent life model of wind turbine main shaft bearing. Manuf. Technol. Mach. 2021, 7, 146–152. [Google Scholar]
- Liu, Y.; Huang, H.Z.; Ling, D. Reliability prediction for evolutionary product in the conceptual design phase using neural network-based fuzzy synthetic assessment. Int. J. Syst. Sci. 2013, 44, 545–555. [Google Scholar] [CrossRef]
- Fang, S.; Li, L.; Hu, B.; Chen, X. Evidential link prediction by exploiting the applicability of similarity indexes to nodes. Expert Syst. Appl. 2022, 210, 118397. [Google Scholar] [CrossRef]
- Yang, J.; Shen, L.J.; Huang, J.; Zhao, Y. Bayes comprehensive assessment of reliability for eectronic products by using test information of similar products. Acta Aeronaut. Astronaut. Sin. 2008, 29, 1550–1553. [Google Scholar]
- Wen, Y. Study on the Reliability Analysis and Assessment Method of the Aerospace Pyrotechnic Devices. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2015. [Google Scholar]
- Jeong, Y. A study on the development of the OMS/MP based on the Fundamentals of Systems Engineering. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 468–476. [Google Scholar] [CrossRef]
- Mokhtarpour, B.; Stracener, J.T. Mission reliability analysis of phased-mission systems-of-systems with data sharing capability. In Proceedings of the 2015 Annual Reliability and Maintainability Symposium (RAMS), Palm Harbor, FL, USA, 26–29 January 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- King, J.R.; Nakornchai, V. Machine-component group formation in group technology: Review and extension. Int. J. Prod. Res. 1982, 20, 117–133. [Google Scholar] [CrossRef]
- Chen, Y.J.; Chen, Y.M.; Chu, H.C.; Wang, C.B.; Tsaih, D.C.; Yang, H.M. Integrated clustering approach to developing technology for functional feature and engineering specification-based reference design retrieval. Concurr. Eng. 2005, 13, 257–276. [Google Scholar] [CrossRef]
- Karaulova, T.; Kostina, M.; Shevtshenko, E. Reliability assessment of manufacturing processes. Int. J. Ind. Eng. Manag. 2012, 3, 143. [Google Scholar] [CrossRef]
- Shih, H.M. Product structure (BOM)-based product similarity measures using orthogonal procrustes approach. Comput. Ind. Eng. 2011, 61, 608–628. [Google Scholar] [CrossRef]
- Orlicky, J.A.; Plossl, G.W.; Wight, O.W. Structuring the Bill of Material for MRP. In Operations Management: Critical Perspectives on Business and Management; Taylor & Francis: Oxfordshire, UK, 2003; pp. 58–81. [Google Scholar]
- Romanowski, C.J.; Nagi, R. On comparing bills of materials: A similarity/distance measure for unordered trees. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2005, 35, 249–260. [Google Scholar] [CrossRef]
- Kashkoush, M.; ElMaraghy, H. Product family formation by matching Bill-of-Materials trees. CIRP J. Manuf. Sci. Technol. 2016, 12, 1–13. [Google Scholar] [CrossRef]
- Xu, X.S.; Wang, C.; Xiao, Y. Similarity Judgment of Product Structure Based on Non-negative Matrix Factorization and Its Applications. China Mech. Eng. 2016, 27, 1072–1077. [Google Scholar]
- Kapli, P.; Yang, Z.; Telford, M.J. Phylogenetic tree building in the genomic age. Nat. Rev. Genet. 2020, 21, 428–444. [Google Scholar] [CrossRef]
- Pattengale, N.D.; Gottlieb, E.J.; Moret, B.M.E. Efficiently computing the Robinson-Foulds metric. J. Comput. Biol. 2007, 14, 724–735. [Google Scholar] [CrossRef] [PubMed]
- Wolsey, L.A. Mixed Integer Programming; Wiley Encyclopedia of Computer Science and Engineering: Hoboken, NJ, USA, 2007; pp. 1–10. [Google Scholar]
- Desrosiers, J.; Lübbecke, M.E. Branch-price-and-cut algorithms. In Encyclopedia of Operations Research and Management Science; John Wiley & Sons: Chichester, UK, 2011; pp. 109–131. [Google Scholar]
- Parganiha, K. Linear Programming with Python and Pulp. Int. J. Ind. Eng. 2018, 9, 1–8. [Google Scholar] [CrossRef]
- Jia, X.; Guo, B. Reliability evaluation for products by fusing expert knowledge and lifetime data. Control Decis. 2022, 37, 2600–2608. [Google Scholar]
- Emura, T.; Wang, H. Approximate tolerance limits under log-location-scale regression models in the presence of censoring. Technometrics 2010, 52, 313–323. [Google Scholar] [CrossRef]
- Panza, C.A.; Vargas, J.A. Monitoring the shape parameter of a Weibull regression model in phase II processes. Qual. Reliab. Eng. Int. 2016, 32, 195–207. [Google Scholar] [CrossRef]
- Lv, S.; Niu, Z.; Wang, G.; Qu, L.; He, Z. Lower percentile estimation of accelerated life tests with nonconstant scale parameter. Qual. Reliab. Eng. Int. 2017, 33, 1437–1446. [Google Scholar] [CrossRef]
- Lv, S.; Niu, Z.; He, Z.; Qu, L. Estimation of lower percentiles under a Weibull distribution. In Proceedings of the 2015 First International Conference on Reliability Systems Engineering (ICRSE), Beijing, China, 21–23 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Puig, P.; Stephens, M.A. Tests of fit for the Laplace distribution, with applications. Technometrics 2000, 42, 417–424. [Google Scholar] [CrossRef]
- Hoffman, M.D.; Gelman, A. The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Turkkan, N.; Pham-Gia, T. Computation of the highest posterior density interval in Bayesian analysis. J. Stat. Comput. Simul. 1993, 44, 243–250. [Google Scholar] [CrossRef]
- Patil, A.; Huard, D.; Fonnesbeck, C.J. PyMC: Bayesian stochastic modelling in Python. J. Stat. Softw. 2010, 35, 1–81. [Google Scholar] [CrossRef]
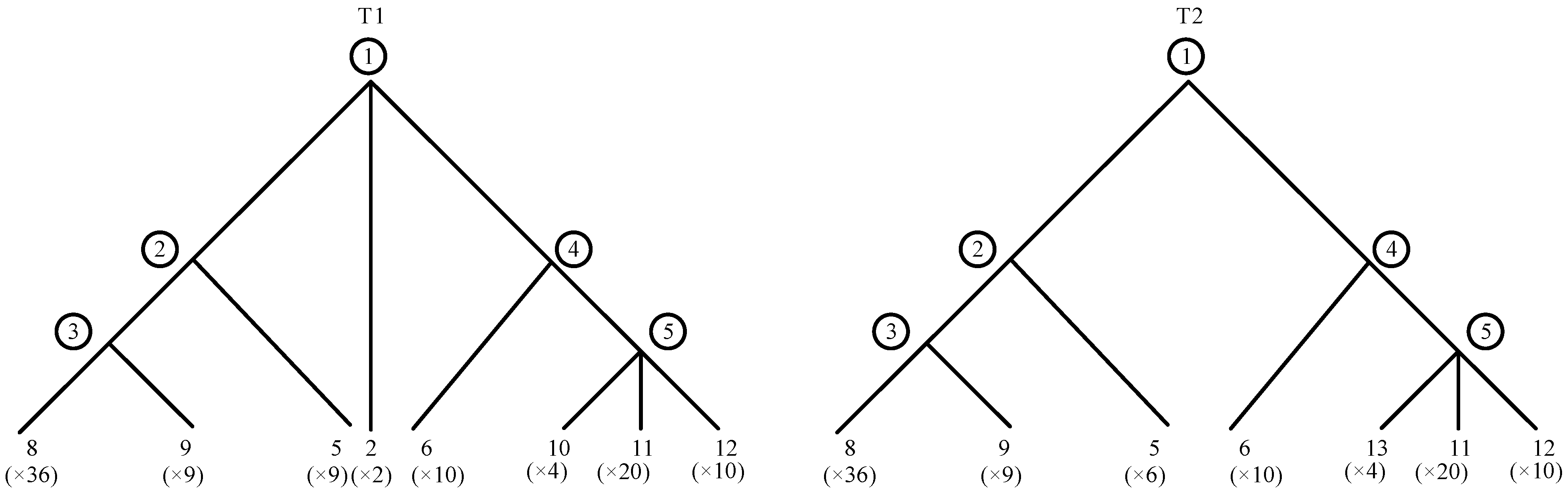
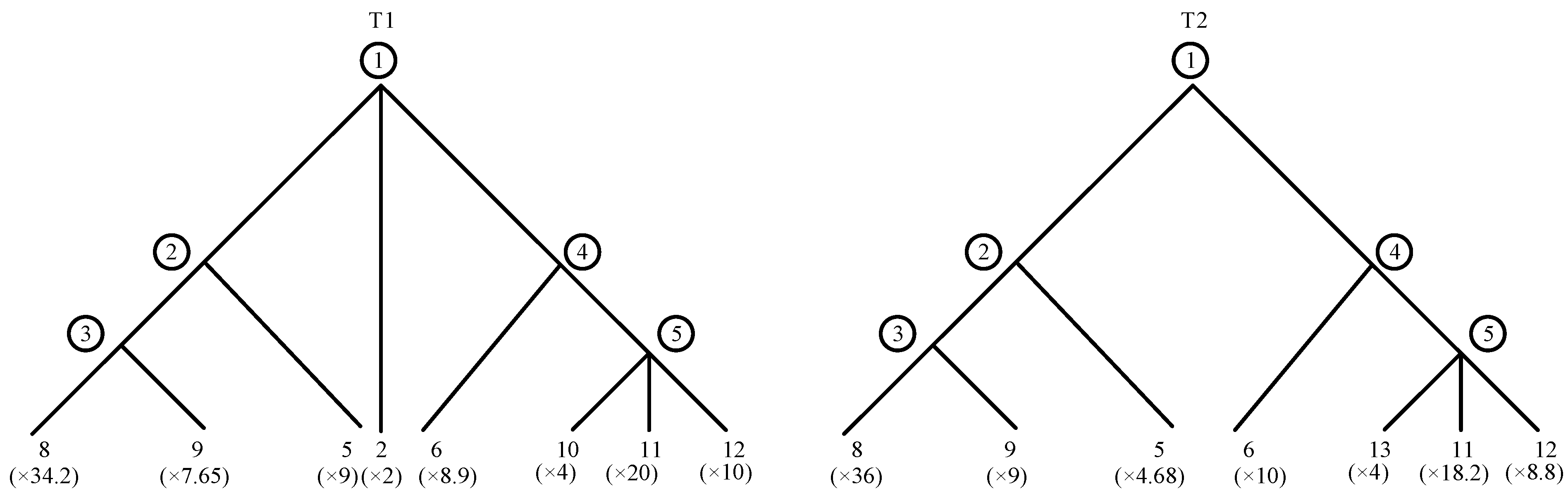




| Node in T1 | Most Similar Node in T2 | Component in T1 but Not in T2 | Shared Component with Higher Quantity in T1 | Level Difference | Quantity Difference | Distance |
|---|---|---|---|---|---|---|
| 1 | 1 | 2, 10 | 5 | 1, 3, 2 | 2, 4, 3 | 4.83 |
| 2 | 2 | - | 5 | 1 | 3 | 3 |
| 3 | 3 | - | - | - | - | 0 |
| 4 | 4 | 10 | - | 2 | 4 | 2 |
| 5 | 5 | 10 | - | 1 | 4 | 4 |
| Total | 13.83 | |||||
| Node in T2 | Most Similar Node in T1 | Component in T2 but Not in T1 | Shared Component with Higher Quantity in T2 | Level Difference | Quantity Difference | Distance |
|---|---|---|---|---|---|---|
| 1 | 1 | 13 | - | 3 | 4 | 1.33 |
| 2 | 2 | - | - | - | - | 0 |
| 3 | 3 | - | - | - | - | 0 |
| 4 | 4 | 13 | - | 2 | 4 | 2 |
| 5 | 5 | 13 | - | 1 | 4 | 4 |
| Total | 7.33 | |||||
| Name | Assigned Number | Name | Assigned Number |
|---|---|---|---|
| Pressure control valve | 1 | Copper pipe | 12 |
| Ceramic cartridge | 2 | Steel chrome-plated connector | 13 |
| Valve body | 3 | Housing partition manifold | 14 |
| Spring | 4 | Turret partition manifold | 15 |
| Direction control valve | 5 | Steel pipe | 16 |
| Cylinder block | 6 | Cooler | 17 |
| Guide sleeve | 7 | Copper pipe | 18 |
| Mandrel | 8 | Reinforced armor | 19 |
| Port plate | 9 | Copper alloy cartridge | 20 |
| Suction valve | 10 | Brass connector | 21 |
| Discharge valve | 11 |
| Subsystem | Parameter | Relative Deviation | |
|---|---|---|---|
| Existing Method | Proposed Method | ||
| SSUT | h | 0.158 | 0.053 |
| λ | 0.218 | 0.068 | |
| Subsystem 1 | h | 0.413 | 0.214 |
| λ | 0.216 | 0.169 | |
| Subsystem 2 | h | 0.324 | 0.231 |
| λ | 0.317 | 0.112 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, J.; Pei, M. Reliability Assessment via Combining Data from Similar Systems. Stats 2025, 8, 35. https://doi.org/10.3390/stats8020035
Hao J, Pei M. Reliability Assessment via Combining Data from Similar Systems. Stats. 2025; 8(2):35. https://doi.org/10.3390/stats8020035
Chicago/Turabian StyleHao, Jianping, and Mochao Pei. 2025. "Reliability Assessment via Combining Data from Similar Systems" Stats 8, no. 2: 35. https://doi.org/10.3390/stats8020035
APA StyleHao, J., & Pei, M. (2025). Reliability Assessment via Combining Data from Similar Systems. Stats, 8(2), 35. https://doi.org/10.3390/stats8020035




