Longitudinal Survival Analysis Using First Hitting Time Threshold Regression: With Applications to Wiener Processes

Abstract

First-hitting time threshold regression (TR) is well-known for analyzing event time data without the proportional hazards assumption. To date, most applications and software are developed for cross-sectional data. In this paper, using the Markov property of processes with stationary independent increments, we present methods and procedures for conducting longitudinal threshold regression (LTR) for event time data with or without covariates. We demonstrate the usage of LTR in two case scenarios, namely, analyzing laser reliability data without covariates, and cardiovascular health data with time-dependent covariates. Moreover, we provide a simple-to-use R function for LTR estimation for applications using Wiener processes.

1. Introduction

Degradation of the health of a patient, or an engineering system, can be described mathematically as a stochastic process. The patient (or system) experiences a failure event when the degradation of patient health (or the wear-and-tear of a system) first reaches a critical threshold level. This happening defines a failure event and a first hitting time (FHT).

For many years, boundary crossing probabilities for diffusion processes have been an important research topic in applied probability. First hitting time (also known as first passage time) models have been investigated and used in various fields, including tracer dilution curves in cardiology [1], lengths of strikes [2], hospital stays [3], equipment lives [4], psychology [5], cognitive and neural mechanisms [6], credit risks [7], cure rate estimation [8], system reliability [9,10,11], machine learning [12,13], etc. Many equations and computational methods have been developed for some random processes under different conditions. The novelty of this article is to extend the first hitting time regression models to longitudinal data.

First hitting time threshold regression (TR) models [14,15] are based on an underlying stochastic process with a clear conceptual mechanism. They do not require the proportional hazards (PH) assumption and represent a realistic alternative to the Cox PH model. Using examples, ref. [16] compared the first hitting time TR model with a Cox PH model in an interesting review article. A comprehensive overview of the theory and applications in earlier development of the first hitting time regression models can be found in a book by [17]. The concept of a TR model was adapted by [18,19,20] for analyzing their health data in different ways.

Recently, the TR model has been used in examining the effects of dose-response in a genome based therapeutic drug study [21]. TR methods also provide a more flexible model for group sequential clinical trial design [22]. A boosting first-hitting-time model for survival analysis in high-dimensional settings was introduced in [23]. Application of the TR model in causal inference with neural network extension was investigated in [13]. Also, an economic model of transitions in and out of employment was developed [24], where heterogeneous workers switch employment status when the net benefit from working, a Brownian motion with drift, hits optimally chosen barriers. A more general semiparametric TR model for the family of Lévy processes was introduced in [25].

In a review article [26] comparing different regression models for time-to-event data, including the TR model, the author mentioned in the conclusion that “many of the methods that have been proposed have seen little or no practical use. Lack of user-friendly software is certainly a factor in this”. On the other hand, a computational R package in [27] for cross-sectional TR models has been widely used by many investigators. The longitudinal extension of the TR model with covariates, however, has never been clearly defined and presented. How to extend the TR method for analyzing longitudinal event data with time-dependent covariates is not a simple matter. The purpose of this paper is to give a clear definition of longitudinal threshold regression and develop methods for analyzing longitudinal event data with time-dependent covariates. We create an R function for LTR using Wiener processes and demonstrate the procedures and results in analyzing real applications.

Note that health and disease states are mirror images in a medical context, as same as device strength and degradation in an engineering context. For convenience of exposition, we consider the health state in a medical context and refer to the stochastic process as a health process. We define the event of interest as the first entry of the process into a critical region defined usually by a threshold level. Our observation process generally provides longitudinal data for the process and the first-entry event, if it occurs, or a censored outcome. Therefore, the analysis of cross-sectional data can be considered as a special case of longitudinal analysis with observations limited to one period.

The rest of the paper is organised as follows. We define inter-visit intervals in Section 2. A reliability example is presented in Section 3. We introduce LTR for a longitudinal latent Wiener health process in Section 4 with a real example. Discussion, assumption checking, and scope of future projects are included in Section 5.

2. Decompose Longitudinal Data into Inter-Visit Intervals

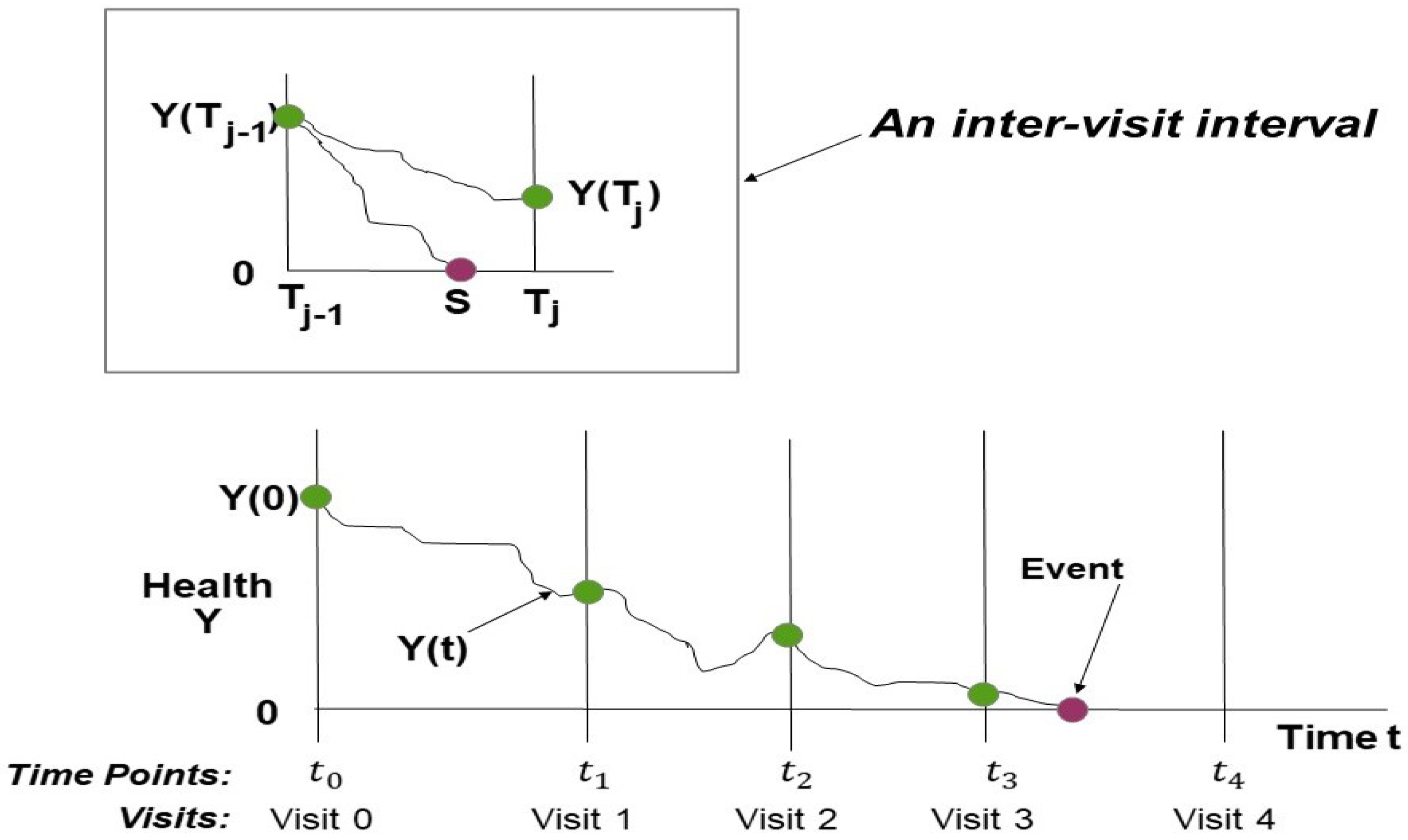
In Figure 1, assume that the subject’s health process $Y\left(t\right)$ progresses from baseline level $y_0$ at the initial visit through a chain of consecutive inter-visit intervals. The assumed Markov property for the health process assures that health increments for non-overlapping time intervals are independent. In each inter-visit interval j, the subject either survives to the end of the interval at time $t_j$ with health level $Y\left(t_j\right)=y_j$ or fails as the health path first hits or crosses level 0 (the critical threshold) at survival time $S=s$. Each inter-visit interval j has a covariate vector ${\mathit{z}}_{\mathit{j}-\mathbf{1}}$ at the opening of the interval, which can differ across visits. As shown by the figure, each interval including covariates contributes a data element.

We denote the sequence of observation times by $t_0=0<t_1<\cdots <t_m$ and associated covariate vectors by at times $j=0,\dots ,m$. The advantages of this model is that the length of the inter-visit intervals $(t_{j-1},t_j]$ may be different from visit to visit and that the model can include time-dependent covariates measured at different visits. Index m marks the last observation time, which is either the end of follow-up or the first time the system is found to have failed. Indicator variable ${\eta }_j$ records whether the system failed within inter-visit interval j or not. Thus, the failure event indicator ${\eta }_j=1$ if $S\in (t_{j-1},t_j]$ and ${\eta }_j=0$ if $S>t_j$. Note that $t_m$ is the censoring time if failure does not occur at the end of the study period.

We describe the data elements by ${\mathit{E}}_j$ = ($y_j$, $t_j$, ${\mathbf{z}}_j$, ${\eta }_j$) for $j=1,\dots ,m$. For each subject, the probability of the observation sequence can be expanded as a product of conditional probabilities and, with the Markov property, the joint probability of the sequence of observations can be simplified.

$$\begin{array}{cc}\hfill P({\mathit{E}}_0,\dots ,{\mathit{E}}_{m-1},{\mathit{E}}_m)& =\prod _{j=1}^{m}P\left({\mathit{E}}_0\right)P\left({\mathit{E}}_j\right|{\mathit{E}}_{j-1},\dots ,{\mathit{E}}_0)=\prod _{j=1}^{m}P\left({\mathit{E}}_0\right)P\left({\mathit{E}}_j\right|{\mathit{E}}_{j-1})\hfill \\ \hfill P\left({\mathit{E}}_j\right|{\mathit{E}}_{j-1})& =P(S>t_j,y_j,{\mathit{z}}_j|S>t_{j-1},y_{j-1},{\mathit{z}}_{j-1})\mathrm{if} {\eta }_j=0,j=1,\dots ,m-1\hfill \\ \hfill P\left({\mathit{E}}_m\right|{\mathit{E}}_{m-1})& =P(S\in (t_{m-1},t_m],y_m,{\mathit{z}}_m|S>t_{m-1},y_{m-1},{\mathit{z}}_{m-1})\mathrm{if} {\eta }_m=1.\hfill \end{array}$$

(1)

These data elements for the inter-visit interval have the Markov property whereby the probability for one element depends only on its predecessor element and not any earlier elements. The level $y_{j-1}$ and covariate vector ${\mathit{z}}_{j-1}$ are the baseline values for the interval $(t_{j-1},t_j]$ from which the overall product of likelihood values can be computed from longitudinal sample data for each individual. Our notation here differs slightly from that in [14,15]. We have also slightly generalized the mathematical form of terminal data element ${\mathit{E}}_m$ for a failure case.

Many variations of the formulation in (1) are theoretically coherent and may arise in practical applications. Model variations depend on many factors, such as whether failures are soft or hard events, whether the health process is observable, which covariates are known (if any), whether survival time S is known or is interval censored, and many other data features.

3. LTR for Measurable Longitudinal Data Without Covariates

In this section, we show that, for measurable longitudinal data without covariates, the LTR method can be easily applied to estimate the process mean and variance using simple estimating equations without assuming a parametric process. This method is very useful especially when a parametric Wiener assumption may be in doubt for reliability data as Wiener process drifts up and down but reliability degradation is usually in an increasing trend.

Using cumulant generation functions, it was proved in [25] that two estimating equations for a random pair ($\Delta T$, $\Delta D$) of time and the wear-and-tear increments for any subject are given by

$$\left(\mathrm{a}\right)\mathrm{E}(\Delta D-\delta \Delta T)=0, \mathrm{and} \left(\mathrm{b}\right)\mathrm{E}{(\Delta D-\delta \Delta T)}^2={\sigma }^2\mathrm{E}\left(\Delta T\right),$$

(2)

where $\delta$ is the mean drift and ${\sigma }^2$ is the variance of the degradation process $D\left(t\right)$ for a unit time increment.

Let $\Delta d_{i,j}=d_{i,j}-d_{i,j-1}$ and $\Delta t_{i,j}=t_{i,j}-t_{i,j-1}$ denote the degradation increment and time increment for subject i at time $t_{i,j}$ for $i=1,\dots ,n,j=1,\dots ,m_i$ and $t_{i,0}=0$. The empirical analogs of the estimating equations in (2) are

$$\left(\mathrm{a}\right)\sum _{i=1}^n\sum _{j=1}^{m_i}(\Delta d_{i,j}-\delta \Delta t_{i,j})=0,\left(\mathrm{b}\right)\sum _{i=1}^n\sum _{j=1}^{m_i}{(\Delta d_{i,j}-\delta \Delta t_{i,j})}^2={\sigma }^2\sum _{i=1}^n\sum _{j=1}^{m_i}\Delta t_{i,j}.$$

(3)

Sequential solution of Equation (3)a,b gives the following explicit estimates for the process parameters:

$$\left(\mathrm{a}\right)\widehat{\delta }={\displaystyle \frac{{\sum }_{i=1}^n{\sum }_{j=1}^{m_i}\Delta d_{i,j}}{{\sum }_{i=1}^n{\sum }_{j=1}^{m_i}\Delta t_{i,j}}},\left(\mathrm{b}\right){\widehat{\sigma }}^2={\displaystyle \frac{{\sum }_{i=1}^n{\sum }_{j=1}^{m_i}{(\Delta d_{i,j}-\widehat{\delta }\Delta t_{i,j})}^2}{{\sum }_{i=1}^n{\sum }_{j=1}^{m_i}\Delta t_{i,j}}}.$$

(4)

Using a simple case study, we demonstrate first-hitting-time LTR analysis for reliability applications.

Example 1: Measurable Reliability of the Longitudinal Laser Data

We consider the laser data published in [28] where a Weibull model was originally used to analyze the reliability of the laser devices. The case study involves 15 new laser devices subjected to a degradation test, where the operating current, a quality characteristic, is measured every 250 h for each device. The original data set does not contain any covariates. The experiment is terminated at 4000 h and each unit has 16 measurements in total. A device is considered to have failed when its operating current increases by more than 10%. Three units (ID = 1, 6, and 10) overshoot the 10% threshold before the experiment ends.

The percentage increase in operating current for the laser devices can be interpreted as the wear-and-tear or degradation characteristic. Thus, the degradation process $D\left(t\right)$ of each test unit starts at an initial baseline $D\left(0\right)=0$ and fails when it first crosses the 10% threshold at time $S=s$, with $D\left(s\right)\ge 10$. For simplicity of presentation, we suppress the notation % for percentage changes in operating current when the context makes the measurement unit clear. Each sample path covers the observation period from the initial baseline until the end of the experiment at 4000 h.

For each laser i, the observed data set contains a column of times $t_{i,j}$ and a column of degradation levels $d_{i,j}$, with $i=1,\dots ,15,j=1,\dots ,16$. For illustration,

Table 1. Fragment of laser data for unit with ID i = 1.

ID	Visit	Time In Hours	Degradation Level in %	Failure Indicator	Time Increment	Degradation Increment
$\mathit{i}$	$\mathit{j}$	${\mathit{t}}_{\mathit{i},\mathit{j}}$	${\mathit{d}}_{\mathit{i},\mathit{j}}$	${\mathit{\eta }}_{\mathit{i},\mathit{j}}=\mathit{I}({\mathit{d}}_{\mathit{i},\mathit{j}}>=\mathbf{10})$	${\mathbf{diff}}_{{\mathit{t}}_{\mathit{j}}}={\mathit{t}}_{\mathit{i},\mathit{j}}-{\mathit{t}}_{\mathit{i},\mathit{j}-\mathbf{1}}$	${\mathbf{diff}}_{{\mathit{d}}_{\mathit{j}}}={\mathit{d}}_{\mathit{i},\mathit{j}}-{\mathit{d}}_{\mathit{i},\mathit{j}-\mathbf{1}}$
1	1	250	0.47	0	250	0.47
1	2	500	0.93	0	250	0.46
1	3	750	2.11	0	250	1.18
1	4	1000	2.72	0	250	0.61
1	5	1250	3.51	0	250	0.79
1	6	1500	4.34	0	250	0.83
1	7	1750	4.91	0	250	0.57
1	8	2000	5.48	0	250	0.57
1	9	2250	5.99	0	250	0.51
1	10	2500	6.72	0	250	0.73
1	11	2750	7.13	0	250	0.41
1	12	3000	8.00	0	250	0.87
1	13	3250	8.92	0	250	0.92
1	14	3500	9.49	0	250	0.57
1	15	3750	9.87	0	250	0.38
1	16	4000	10.94	1	250	1.07

shows longitudinal observations from the test unit with ID i = 1. For the jth inter-visit interval $(t_{i,j-1},t_{i,j}]$, we define the failure indicator ${\eta }_{i,j}=I(d_{i,j}\ge 10)$, the time-increment variable ${\mathrm{diff}}_{t_j}=t_{i,j}-t_{i,j-1}$, and the degradation-increment variable ${\mathrm{diff}}_{d_j}=d_{i,j}-d_{i,j-1}$, with each test unit’s degradation level at initial time $t_{i,0}=0$ being $D\left(0\right)=0$.

In this case example, the data for each laser device has the format shown in Table 1 for ID i = 1. The data records for the remaining test units are appended vertically to form a sequence of inter-visit data records that runs through all the units and all the measurements within units.

We fit the LTR model to the laser data and estimate process mean parameter $\delta$ and variance ${\sigma }^2$. This analysis takes no account of any covariates. We also construct jackknife confidence intervals to assess the precision of estimated parameters, as mentioned in [25].

We provide simple R code for conducting semiparametric LTR analysis as below:

• R> laser <- get(load(“laser.Rdata”))
• R> delta <- sum(laser$diff_dj)/sum(laser$diff_tj)
• R> s2 <- sum((laser$diff_dj-delta*laser$diff_tj)^2)/sum(laser$diff_tj)
• R> print(c(delta,s2))
• R code for constructing jackknife confidence intervals are included in the Appendix A.

Table 2. LTR estimation for the laser data using Equation (4) without a Wiener assumption.

Process Parameter	Estimate	95% Jackknife Confidence Interval
Mean ($\delta$)	$2.04\times {10}^{-3}$	[$1.78\times {10}^{-3}$, $2.30\times {10}^{-3}$]
Variance (${\sigma }^2$)	$1.60\times {10}^{-4}$	[$1.01\times {10}^{-4}$, $2.20\times {10}^{-4}$]

displays LTR results using Equation (4) without a Wiener assumption.

The same laser data set was analyzed in [29]. Using a parametric Wiener degradation model, they estimated the Wiener process mean as $2.04\times {10}^{-3}$ with a 95% likelihood ratio confidence interval [$1.94\times {10}^{-3}$, $2.14\times {10}^{-3}$], and the variance $1.60\times {10}^{-4}$ with a 95% likelihood ratio confidence interval [$1.36\times {10}^{-4},1.91\times {10}^{-4}$].

The degradation level in the laser data listed in Table 1 shows an increasing trend with an overshoot level of 10.94 at visit 16. The benefit of the LTR method is that in this example, using simple estimation equalities listed in Equation (4), one can estimate process mean and variance without a Wiener assumption like the other investigator did. Table 2 shows that our simple point estimation results are the same as those obtained from the parametric Wiener model in [29]. As can be expected, likelihood ratio confidence intervals produced from the parametric Wiener model are narrower than those obtained using jackknife for models without a parametric assumption.

This example also show that the LTR model is well adapted to engineering reliability applications as the method can effectively handle overshoots that occur with physical failures.

4. LTR for Latent Longitudinal Wiener Health Processes

Most of the theoretical results of TR methods were developed in [14,15,25] with the only requirements for the health process being stationary independent increments and a cumulant generating function. Adopting the assumption of stationary independent increments implies that we limit our attention in TR applications to the family of Lévy processes. The most well-known examples of Lévy process families are Brownian motion, Wiener processes, Poisson processes, and Gamma processes.

Asymptotics for the distribution of the first passsage times of Lévy Processes can be found in [30].

Assume that the latent health for each subject follows a Wiener process $\left\{Y\right(t),t\ge 0\}$ with the mean rate of degradation $\mu$, the initial health value $Y\left(0\right)=y_0>0$, and the variance ${\sigma }^2$. When the process mean parameter $\mu$ is negative, the process tends to drift down to the failure threshold zero.

First, we review existing TR methods for cross-sectional data. Then, to extend TR methods to longitudinal data, in Section 4.2 we derive the probability for a Wiener process of a survivor who avoids a threshold barrier in an inter-visit interval. The likelihood function and the matrix of simultaneous regressions for LTR analysis for the class of Wiener processes are presented in Section 4.3 and Section 4.4. Application to a real example using the R function we created is demonstrated in Section 4.5, Section 4.6, Section 4.7.

4.1. Review of Existing TR Model for Cross-Sectional Data with Wiener Process

The probabilities of the first hitting times for Brownian motion and Wiener processes have been investigated by many, see [4,31,32,33,34,35,36], among others. Specifically, for cross-sectional data, the distribution of the first event time S, modeled as the first hitting time (FHT) of the Wiener health process, follows an inverse Gaussian distribution with probability density function (p.d.f.) given by

$$f\left(s\right|\mu ,{\sigma }^2,y_0)={\displaystyle \frac{y_0}{\sqrt{2\pi {\sigma }^2{s}^3}}}exp\left[-{\displaystyle \frac{{(y_0+\mu s)}^2}{2{\sigma }^{2}s}}\right],\mathrm{for}-\infty <\mu <\infty ,{\sigma }^2>0,y_0>0.$$

(5)

The cumulative distribution function (c.d.f.) of the FHT time S corresponding to (5) is

$$F\left(t\right|\mu ,{\sigma }^2,y_0)=\Phi \left[-{\displaystyle \frac{(\mu t+y_0)}{\sqrt{{\sigma }^{2}t}}}\right]+exp(-2y_0\mu /{\sigma }^2)\Phi \left[{\displaystyle \frac{(\mu t-y_0)}{\sqrt{{\sigma }^{2}t}}}\right],$$

(6)

where $\Phi (·)$ denotes the c.d.f. of the standard normal distribution. The survival function (s.f.) corresponding to (5) is

$$\overline{F}\left(t\right|\mu ,{\sigma }^2,y_0)=1-F\left(t\right|\mu ,{\sigma }^2,y_0)=\Phi \left[{\displaystyle \frac{(\mu t+y_0)}{\sqrt{{\sigma }^{2}t}}}\right]-exp(-2y_0\mu /{\sigma }^2)\Phi \left[{\displaystyle \frac{(\mu t-y_0)}{\sqrt{{\sigma }^{2}t}}}\right].$$

(7)

The mean and variance of the inverse Gaussian distributed S are given by

$$E\left(S\right|\mu ,{\sigma }^2,y_0)={\displaystyle \frac{y_0}{\left|\mu \right|}},\mathrm{Var}\left(S\right|\mu ,{\sigma }^2,y_0)={\displaystyle \frac{{\sigma }^2{y}_0}{{\left|\mu \right|}^3}},$$

(8)

The mathematical forms of the p.d.f and c.d.f. of an inverse Gaussian distribution in (5) and (6), as well as the mean and variance of S in (8), depend only on two of the three parameters $y_0$, $\mu$ and ${\sigma }^2$. To be estimable, one of these three parameters can be fixed arbitrarily. In applications, we often set ${\sigma }^2=1$ and model both the mean rate $\mu$ and baseline $y_0$ in simultaneous regressions using each subject’s relevant covariates.

For a reveiw of TR model, see [17]. Also, for cross-sectional data, Bayesian random-effects TR model was introduced in [37] and semiparametric Dirichlet process mixture for TR was proposed in [38].

4.2. Derivation of the Probability of a Survivor Who Avoids a Threshold in a Wiener Process

It is important to note that, by decoupling a longitudinal dataset into a sequence of inter-visit intervals, the subject may survive one or more intervals before the event is observed or the sequence is censored at the mth interval. Therefore, one needs to derive the probability that the latent health of a subject does not hit the threshold in any given interval. Using differential equations, ref. [39] discussed a Wiener process with absorbing barriers. Extending the method of [40], we derive the probability density function (p.d.f.) for the level of a Wiener process that avoids hitting a fixed threshold during its passage to a specified future time horizon. Here, we show the derivation for the first inter-visit interval and the formulas can be generalized to any inter-visit interval in a longitudinal sequence.

Consider a Wiener diffusion process $\left\{Y\right(t\left)\right\}$, starting at level $Y\left(0\right)=y_0$ at time 0, with mean drift $\mu$, variance ${\sigma }^2>0$ and a fixed threshold at 0. The process will operate until termination at time horizon $T>0$. Let $g\left(y_1\right)$ denote the p.d.f. for the terminal process level $y_1$ at time T given that the process does not exit the threshold prior to T. Furthermore, let $p\left(y\right)$ denote the normal density function of the Wiener process level y at time T if it operates without interference between onset and time T. This function has the following form:

$$p\left(y\right)={\left(2\pi {\sigma }^{2}T\right)}^{-1/2}exp\left[-{(y_0-y+\mu T)}^2/2{\sigma }^{2}T\right].$$

(9)

We also let function $R\left(y\right)$ denote a likelihood ratio of two density functions. The denominator is the density for the sample path of the process if it first exits the threshold at time $S>0$ before reaching level y at time T. The numerator is the density for the mirror image of the denominator sample path, reflected in the threshold at level 0, between time points S and T. Equation (2) of [40] shows that this ratio has the following form in our notation and setup:

$$R\left(y\right)=exp\left[-2\mu y/{\sigma }^2\right].$$

(10)

Equation (10) shows that the ratio is mathematically independent of the first exit time S.

We now focus on sample paths that end at position $y_1=-y$ at time T, where $y<0$. Observe that y and $y_1$ are mirror-image levels with respect to the threshold at 0. The density $p\left(y_1\right)$ is determined by sample paths that proceed to time T without exiting the threshold plus sample paths that exit the threshold at some time before T but return above the threshold before T to land at level $y_1$. The latter paths have density $p\left(y\right)R\left(y\right)$. Thus, the density function $g\left(y_1\right)$ for paths that terminate at level $y_1$ at T without exiting the threshold has form:

$$g\left(y_1\right)=p\left(y_1\right)-p\left(y\right)R\left(y\right)\mathrm{for} y_1>0.$$

(11)

Using Equations (9) and (10) for $p\left(y\right)$ and $R\left(y\right)$, slightly modifying $R\left(y\right)$, and then expanding and collapsing terms gives the following expression for their product:

$$\begin{array}{ccc}\hfill p\left(y\right)R\left(y\right)& =& {\left(2\pi {\sigma }^{2}T\right)}^{-1/2}exp\left[-{\displaystyle \frac{{(y_0-y+\mu T)}^2}{2{\sigma }^{2}T}}\right]exp\left(-{\displaystyle \frac{4\mu yT}{2{\sigma }^{2}T}}\right)\hfill \\ & =& {\left(2\pi {\sigma }^{2}T\right)}^{-1/2}exp\left[-{\displaystyle \frac{{(y_0+y+\mu T)}^2}{2{\sigma }^{2}T}}\right]exp\left({\displaystyle \frac{2y{y}_0}{{\sigma }^{2}T}}\right)\hfill \end{array}$$

(12)

We also have

$$p\left(y_1\right)={\left(2\pi {\sigma }^{2}T\right)}^{-1/2}exp\left[-{(y_0-y_1+\mu T)}^2/2{\sigma }^{2}T\right].\mathrm{for} y_1>0.$$

(13)

Thus,

$$p\left(y\right)R\left(y\right)=p\left(y_1\right)exp\left({\displaystyle \frac{2y{y}_0}{{\sigma }^{2}T}}\right)=p\left(y_1\right)exp\left({\displaystyle \frac{-2y_1{y}_0}{{\sigma }^{2}T}}\right)\mathrm{for} y_1>0.$$

(14)

Substituting these expressions into (11) gives the desired result:

$$g\left(y_1\right)=p\left(y_1\right)-p\left(y\right)R\left(y\right)=p\left(y_1\right)\left[1-exp\left({\displaystyle \frac{-2y_1{y}_0}{{\sigma }^{2}T}}\right)\right]\mathrm{for} y_1>0.$$

(15)

Note that the p.d.f $g\left(y_1\right)$ derived here is for the first inter-visit interval of a longitudinal sequence. Replacing $y_0$ by $y_{j-1}$ and $y_1$ by $y_j$ in the above equations, we can generalize the derivations to subsequent interval j in which the subject survives. We explain this longitudinal application of the p.d.f. in the next section.

4.3. Derivation of the Likelihood Function for LTR Model with Wiener Process

As shown in Figure 1 and Equation (1), longitudinal data can be decomposed into a sequence of Markov dependent inter-visit data elements. By this construction, the closing health state of the subject in any inter-visit interval becomes the opening health state of the subject in the next inter-visit interval. For longitudinal data, if a subject has a failure event within inter-visit interval m, then the likelihood contribution is the p.d.f. of the inverse Gaussian as in Equation (5). Consider a subject who has latent health level $y_{j-1}$ at visit $j-1$. If that subject survives until visit j with health level $y_j>0$, then the likelihood contribution for the jth inter-visit interval is the following conditional p.d.f.

$$g\left(y_j\right|\Delta t_j,{\mu }_j,{\sigma }^2,y_{j-1})={\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2\Delta t_j}}}exp\left\{-{\displaystyle \frac{{(y_j-y_{j-1}-{\mu }_j\Delta t_j)}^2}{2{\sigma }^2\Delta t_j}}\right\}\left\{1-exp\left(-{\displaystyle \frac{2y_j{y}_{j-1}}{{\sigma }^2\Delta t_j}}\right)\right\}$$

(16)

Here $\Delta t_j=t_j-t_{j-1}$ denotes the duration of the jth inter-visit interval.

Observe that the formula in (16) is a normal density function, tilted by an exponential adjustment $1-exp(-2y_j{y}_{j-1}/{\sigma }^2\Delta t_j)$. Note that the function in Equation (16) integrates to the survival probability $P(S>t)$ as given by the inverse Gaussian survival function in (7).

4.4. The Matrix of Simultaneous Regression Equations in the LTR Model

For subject i at visit $j-1$, i.e., at the opening of the jth inter-visit interval, let ${\mathit{z}}_{i,j-1}={(z_{i,1,j-1},z_{i,2,j-1},\dots ,z_{i,K,j-1})}^{\prime }$ denote the K-component covariate vector observed at time $t_{i,j-1}$ for covariates $k=1,\cdots ,K$. To include an intercept term in the regressions, the leading covariate may be set to 1, i.e., $z_{i,1,j-1}=1$. Suppressing the subject index i, let ${\mathit{z}}_{j-1}={(z_{1,j-1},z_{2,j-1},\dots ,z_{K,j-1})}^{\prime }$ denotes the covariate vector observed at time $t_{j-1}$.

Using equations derived in Section 3, one can conduct simultaneous regressions for (a) the subject’s latent health status $y_{j-1}$ at the opening of interval j, and (b) the mean degradation rate ${\mu }_j$ for the jth inter-visit interval.

$$\begin{array}{c}\hfill (y_0,y_1,\dots ,y_{m-1})={\mathit{Z}}^{\prime }\alpha ,\end{array}$$

(17)

$$\begin{array}{c}\hfill ({\mu }_1,{\mu }_2,\dots ,{\mu }_m)={\mathit{Z}}^{\prime }\beta .\end{array}$$

(18)

Here $\mathit{Z}=({\mathit{z}}_0,{\mathit{z}}_1,\dots ,{\mathit{z}}_{m-1})$ denotes the $K\times m$ matrix of observed covariate column vectors for inter-visit intervals $j=1,\dots ,m$ and $\mathit{\alpha }$ and $\mathit{\beta }$ are K-component column vectors of regression coefficients.

The estimated regression coefficient vector $\mathit{\alpha }$ for health $y_{j-1}$ can be used to understand the health of subjects when they entered the interval. The estimated regression coefficient vector $\mathit{\beta }$ can be used to compute the degradation rate ${\mu }_j$ for interval j. The probability of not having an event at the closing of an interval can be estimated by plugging into Equation (7).

The existing R function “threg” was written for analyzing cross-sectional TR model using Equations (5) and (7) in computing the likelihood. To conduct LTR, after decomposing the data into a sequence of independent inter-visit intervals, a product of conditional likelihood needs to be computed for simultaneous regressions in (17) and (18). Specifically, for subjects who survive from visit $j-1$ to visit j, we use Equation (16) to compute the likelihood contribution for that interval. And Equation (5) is used for failures. The health status $y_m$ at the close of the final inter-visit interval can be included in the sample log-likelihood for surviving subjects if covariate vector ${\mathit{z}}_m$ is observed for the survivor.

We extend the “threg” code and create the “LTR_Wiener” function for LTR analysis and demonstrate the application in an example below.

The complete source code of the “LTR_Wiener” function with user-friendly instructions is available on GitHub at https://github.com/yscheng33/LTR-Wiener (accessed on 24 April 2025). Note that the R function we created is very efficient in computations as can be seen in the example sections below.

4.5. Example 2: Longitudinal Degradation of the Latent Cardiovascular Health

The Framingham Heart Study (FHS) [41,42] is a long-term prospective study launched in 1948 to explore the causes of cardiovascular disease (CVD) in the community of Framingham, Massachusetts. It was the first such study to identify cardiovascular risk factors and their combined effects. Initially, 5209 participants were enrolled, and they have been examined every two years since. Data collected includes risk factors like blood pressure, cholesterol, smoking history, and ECGs, as well as disease markers such as lung function and echocardiograms. The study also tracks cardiovascular outcomes like angina, heart attack, heart failure, and stroke through regular hospital surveillance, participant contact, and death certificates. Participants were followed for 24 years to track events such as angina, heart attack, stroke, or death.

The FHS teaching data set we used in this example for demonstrating LTR analysis was downloaded from the NHLBI/BioLINCC repository website which contains FHS data as collected, with methods applied to ensure anonymity and protect patient confidentiality. The data set includes laboratory, clinic, questionnaire, and adjudicated event data for 4434 participants, with a total of 11,627 longitudinal records. Clinic data were collected over three examination periods approximately 6 years apart, from 1956 to 1968. Among the participants, 1157 have experienced CVD, while 3277 have not.

The covariates considered in our example include age at exam in years (AGE), participant sex (Male: yes = 1, no = 0), serum total cholesterol in mg/dL (TOTCHOL), mean arterial pressure ($\mathrm{MAP}=\mathrm{SYSBP}/3+2\mathrm{DIABP}/3$, where SYSBP and DIABP are the systolic and diastolic blood pressures, respectively, calculated as the average of the last two measurements in mmHg), pulse pressure (PP, the difference between SYSBP and DIABP), number of cigarettes smoked daily (CIGPDAY), and diabetic status (DIABETES: yes = 1, no = 0). Diabetes is defined according to the first exam criteria, either by treatment or a casual glucose level of 200 mg/dL or higher. Except for Male and DIABETES, we consider time-dependent covariates in the model and exclude records with any missing covariates. Patients with CVD event at baseline are excluded. Moreover, if a patient experiences the first CVD event before the end of follow-up, subsequent records after the CVD event are excluded. After these exclusions, the cleaned dataset consists of 3906 patients, with a total of 10,127 visits and 993 CVD event time points. Each patient starts with visit 1 and has at most 3 visits.

We model the latent cardiovascular health by a Wiener process $\left\{Y\right(t),t\ge 0\}$ with mean parameter ${\mu }_j$ and variance parameter ${\sigma }^2=1$ as described in Equations (5) and (16). Time on study t is recorded in days in the data set. We use $Y\left(t_j\right)=y_j$ to denote the latent cardiovascular health process $Y\left(t\right)$ at visit j as shown in Figure 1. If a subject encountered a CVD event, the event time $S=s$ was recorded in the FHS data, i.e., $Y\left(s\right)=0$, and we define ${\eta }_{i,j}=I\left(\mathrm{CVD}\right)$ as the outcome indicator of a CVD event.

For the convenience of the reader, in

Table 3. Fragment of FHS data for ID 5755785 and 9982118 at baseline with $t_{i,0}=0$ and $z_{i,1,j-1}=1$.

ID	Interval	Visit Time In Days	Time Increment	Outcome Indicator	${\mathbf{Z}}_{\mathbf{2}}$= AGE		${\mathbf{Z}}_{\mathbf{3}}$= Male		${\mathbf{Z}}_{\mathbf{4}}$= TOTCHOL
i	j	$t_{i,j}$	${\mathrm{diff}}_{t_j}=t_{i,j}-t_{i,j-1}$	${\eta }_{i,j}=I\left(\mathrm{CVD}\right)$	$z_{i,2,j-1}$	$z_{i,2,j}$	$z_{i,3,j-1}$	$z_{i,3,j}$	$z_{i,4,j-1}$	$z_{i,4,j}$
5755785	1	2182	2182	0	46	52	1	1	216	216
5755785	2	7643	5461	1	52	.	1	.	216	.
9982118	1	2253	2253	0	58	64	1	1	187	256
9982118	2	4429	2176	0	64	70	1	1	256	219
9982118	3	8346	3917	1	70	.	1	.	219	.
ID	Interval	$Z_5$ = MAP		$Z_6$ = PP		$Z_7$ = CIGPDAY		$Z_8$ = DIABETES
i	j	$z_{i,5,j-1}$	$z_{i,5,j}$	$z_{i,6,j-1}$	$z_{i,6,j}$	$z_{i,7,j-1}$	$z_{i,7,j}$	$z_{i,8,j-1}$	$z_{i,8,j}$
5755785	1	98.7	88.7	41	53	9	20	0	0
5755785	2	88.7	.	53	.	20	.	0	.
9982118	1	101	107.2	60	74	0	0	0	0
9982118	2	107.2	104.5	74	88.5	0	20	0	0
9982118	3	104.5	.	88.5	.	20	.	0	.

we demonstrate notations of the data element listing fragment of the longitudinal FHS data for subjects with case ID 5755785 and 9982118. For patient with ID i, data element in interval j contains the visit time $t_{i,j}$ at the closing of the interval j, with time increment ${\mathrm{diff}}_{t_j}$, event indicator ${\eta }_{i,j}$ at $t_{i,j}$, and each of the kth covariates $z_{i,k,j-1}$ and $z_{i,k,j}$ at the opening and closing of the jth interval, with $k=1,\dots ,8$ covariates for the FHS data. Note that if subject i has CVD event at a visit j, i.e., ${\eta }_{i,j}=1$. When an event occurred, it often happends that some measurements $z_{i,k,j}$ may not be available at the event, then these covariates are listed as missing and denoted as “.” in Table 3.

4.6. Steps for Conducting LTR Analysis with Covariates Using the “LTR_Wiener” Function

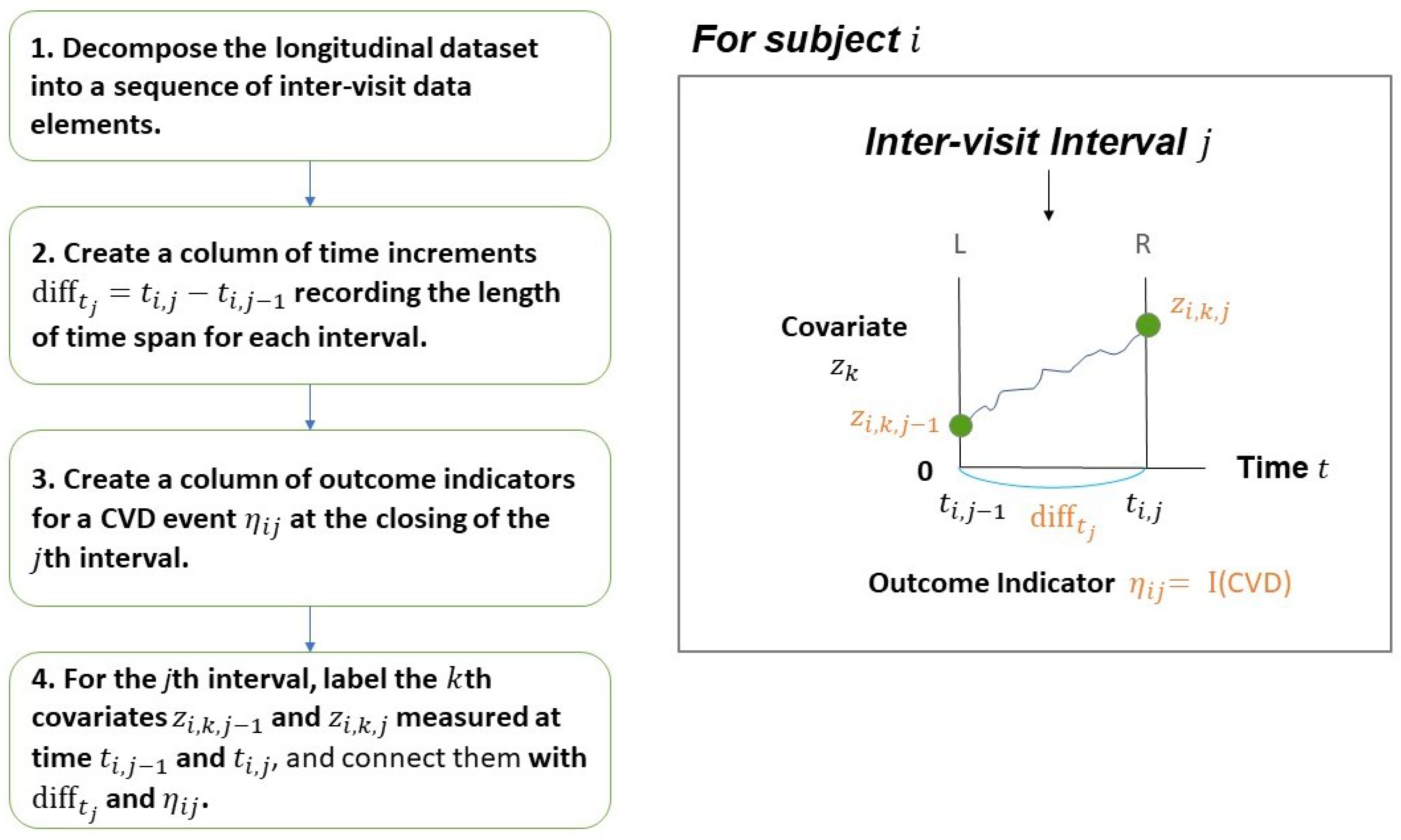
First, we decouple the longitudinal data into a sequence of inter-visit intervals as defined in Section 2. Note that the small box in Figure 1 shows the jth inter-visit interval. For subject i, Figure 2 provides the details of data element corresponding to the jth interval and labels the kth covariate at the opening and closing of the jth interval. The flowchart describes how to reformat the longitudinal data into columns of data elements to be used as the input file for the “LTR_Wiener” function.

Next, after the reformated file is created according to the flowchart above, label it as “FHS.Rdata” to be used as the input file for the R function. Then, we can fit the LTR model for the FHS data by using the “LTR_Wiener” R function as below.

• R> library(“threg”)
• R> FHS <- get(load(“FHS.Rdata”))
• R> fit <- LTR_Wiener(formula=Surv(diff_tj,eta_ij)~AGE+Male+TOTCHOL+MAP+PP
• +        |AGE+Male+TOTCHOL+MAP+PP+CIGPDAY+DIABETES
• +        data=FHS, option=“nlm”)
• R> fit

We describe the flowchart in more detail in Appendix B. Note that, for large longitudinal data set, to improve efficiency and stability of numerical computations, we standardized continuous covariates so they have mean 0 and standard deviation 1.

The “LTR_Wiener” function we created is very efficient in computations. The computation time for the FHS data example using “LTR_Wiener” took only 5.56 s. These computations were done using a 12th Gen Intel (R) Core (TM) i5-12500H system with 24 GB of memory and R version 4.5.0 (R Core Team, 2025).

4.7. LTR Analysis Results for the Framingham Heart Study Data

The results of LTR_Wiener can be summarized in the following table.

At the significance level 0.05, the simultaneous regression results in

Table 4. LTR for FHS Data: Simultaneous Regressions Defined in Equations (17) and (18).

Parameter	Regression Coefficient $\mathit{\alpha }$ for Health			Regression Coefficient $\mathit{\beta }$ for Mean Drift
Variable	Coef	Se (Coef)	$\mathit{p}$	Coef	Se (Coef)	$\mathit{p}$
Intercept	$64.70$	$0.86$	<0.001	$-5.21\times {10}^{-3}$	$3.75\times {10}^{-4}$	<0.001
AGE*	$-7.90$	$0.53$	<0.001	$-1.52\times {10}^{-3}$	$3.10\times {10}^{-4}$	<0.001
Male*	$-12.52$	$0.94$	<0.001	$-8.55\times {10}^{-4}$	$5.41\times {10}^{-3}$	$0.110$
TOTCHOL*	$-1.78$	$0.40$	<0.001	$3.19\times {10}^{-4}$	$2.74\times {10}^{-4}$	$0.240$
MAP*	$-4.01$	$0.48$	<0.001	$2.95\times {10}^{-4}$	$3.47\times {10}^{-4}$	$0.400$
PP*	$0.03$	$0.50$	$0.950$	$-8.87\times {10}^{-4}$	$3.91\times {10}^{-4}$	$\mathbf{0}.\mathbf{023}$
CIGPDAY*	−	−	−	$-6.43\times {10}^{-4}$	$2.67\times {10}^{-4}$	$\mathbf{0}.\mathbf{016}$
DIABETES*	−	−	−	$-4.84\times {10}^{-3}$	$1.37\times {10}^{-3}$	<0.001
Log-likelihood $=-39,564.15$, AIC $=79,152.31$, continuous covariates are standardized

show that variables AGE, Male, TOTCHOL and MAP are significant for modeling the latent health level $y_{j-1}$ at the opening of each inter-visit interval. Variables AGE, PP, CIGPDAY and DIABETES are significant for modeling the health process mean degradation rate ${\mu }_j$.

From the regression for health $y_{j-1}$ at the opening of each inter-visit interval, negative coefficient estimates for AGE ($-7.90$), Male ($-12.52$), TOTCHOL ($-1.78$) and MAP ($-4.01$) suggest that subjects who are older, male, or have higher serum total cholesterol or mean arterial pressure are associated with a lower latent health level at the start of the visit interval.

From the regression for ${\mu }_j$, negative coefficient estimates for AGE ($-1.52\times {10}^{-3}$), PP ($-8.87\times {10}^{-4}$), CIGPDAY ($-6.43\times {10}^{-4}$) and DIABETES ($-4.84\times {10}^{-3}$) indicate that increases in age, pulse pressure or number of cigarettes smoked daily, or patients having diabetes accelerate the degradation of the latent cardiovascular health process, bringing the patient closer to a cardiovascular event.

5. Discussion

Many physiological and physical processes, such as readings of lung function considered in [18,19], can be transformed to have the property of stationary independent increments. Thus, the assumption of stationary independent increments is often considered reasonable by physicians, engineers, scientists and others when the process is evaluated on an appropriate time scale, observed within a reasonable time interval, and measured without significant measurement error.

The LTR model is flexible, capable of handling a broad range of applications that involve different random processes and a variety of data set configurations. As demonstrated in example 1, the overshoot scenario which often occurs in reliability data, is easily tackled using semiparametric LTR. Example 2 demonstrates the usefulness of the Wiener LTR model for analyzing latent health processes in epidemiological longitudinal data. The LTR model offers clinically meaningful interpretations for the estimated results.

Importantly, in contrast to the Cox survival model which assumes a proportional hazard rate, LTR can estimate hazards as functions of time and covariates that are implied by any of the many underlying random processes which govern event histories and event times. This wide scope for modelling makes LTR suitable for the wide variety of complex situations encountered in real-world applications.

As noted in [43], while there are many models proposed in the literature for longitudinal survival analysis, they all have specific assumptions and limitations. None of these has been dominant in applications and few have the support of easily available software. We seek to have LTR fill this gap and are eager to compare the performance of other models with LTR.

This is the first paper presenting the Longitudinal TR methodology and hence leaves many research topics open for further investigation. Future research projects of interest for LTR models include testing the Markov assumption, model checking, sensitivity analysis, goodness-of-fit tests, model diagnostics, operational time-scale transformation for stationarity, competing risks, causal inference, and measurement errors are open for discussions. We plan to extend the LTR method to other parametric processes including gamma processes and other Lévy processes.

Moreover, in the era of artificial intelligence (AI), computing is an indispensable component of all data science and big data applications.

Fast and accurate calculations of first exit times for one-dimensional diffusion processes have been investigated by many, including [6,12,36], among others. Artificial neural networks are powerful machine learning tools in AI that make decisions in a manner similar to the human brain. Using the methods of LTR, we are currently extending TRNN developed in [13] for cross-sectional data to longitudinal neural networks with deep learning for use in AI applications.