Inferences About Two-Parameter Multicollinear Gaussian Linear Regression Models: An Empirical Type I Error and Power Comparison
Abstract
1. Introduction
2. Statistical Framework
2.1. Framework of Model and Several Established Estimators
2.2. Two Parameter Estimators
2.2.1. Liu Type of Two-Parameter Estimator
2.2.2. Ozkale and Kaciranlar Two-Parameter Estimator
2.2.3. New Biased Estimator Based on Ridge
2.2.4. Yang and Chang Two-Parameter Estimator
2.2.5. Almost Unbiased Two-Parameter Estimator
2.2.6. Unbiased Two-Parameter Estimator
2.2.7. Dorugade Modified Two-Parameter Estimator
2.2.8. Modified Almost Unbiased Liu Estimator
2.2.9. Modified Almost Unbiased Two-Parameter Estimator
2.2.10. Modified New Two-Parameter Estimator
2.2.11. Modified Ridge Type
2.2.12. A New Biased Estimator by Dawoud and Kibria
2.2.13. Generalized Two-Parameter Estimator
2.2.14. Siray Two-Parameter Estimator
2.2.15. Unbiased Modified Two-Parameter Estimator
2.2.16. Ahamd and Aslam’s Modified New Two-Parameter Estimator
2.2.17. Modified Liu Ridge Type
2.2.18. New Biased Regression Two-Parameter Estimator
2.2.19. Biased Two-Parameter Estimator
2.2.20. New Two-Parameter Estimator
2.2.21. New Ridge-Type Estimator
2.2.22. Modified Two-Parameter Estimator
2.2.23. Modified Two-Parameter Liu Estimator by Abonazel
2.2.24. Liu–Kibria–Lukman Two-Parameter Estimator
2.2.25. Two-Parameter Ridge Estimator
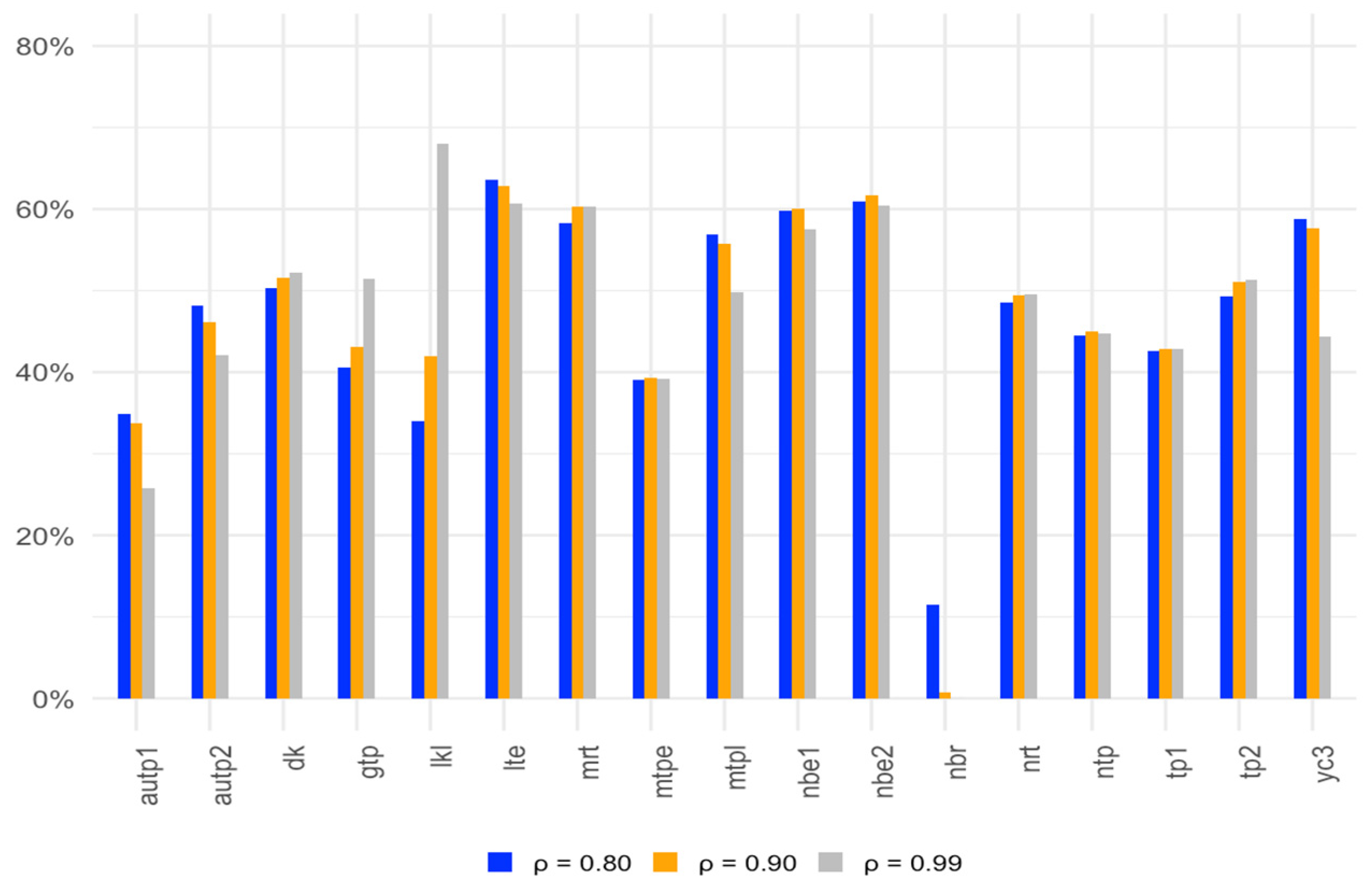
3. A Monte Carlo Simulation Study
3.1. Type I Error-Rated Simulation Procedure
3.1.1. Simulation Methodology
3.1.2. Interpretation of Simulation Results for Type I Error
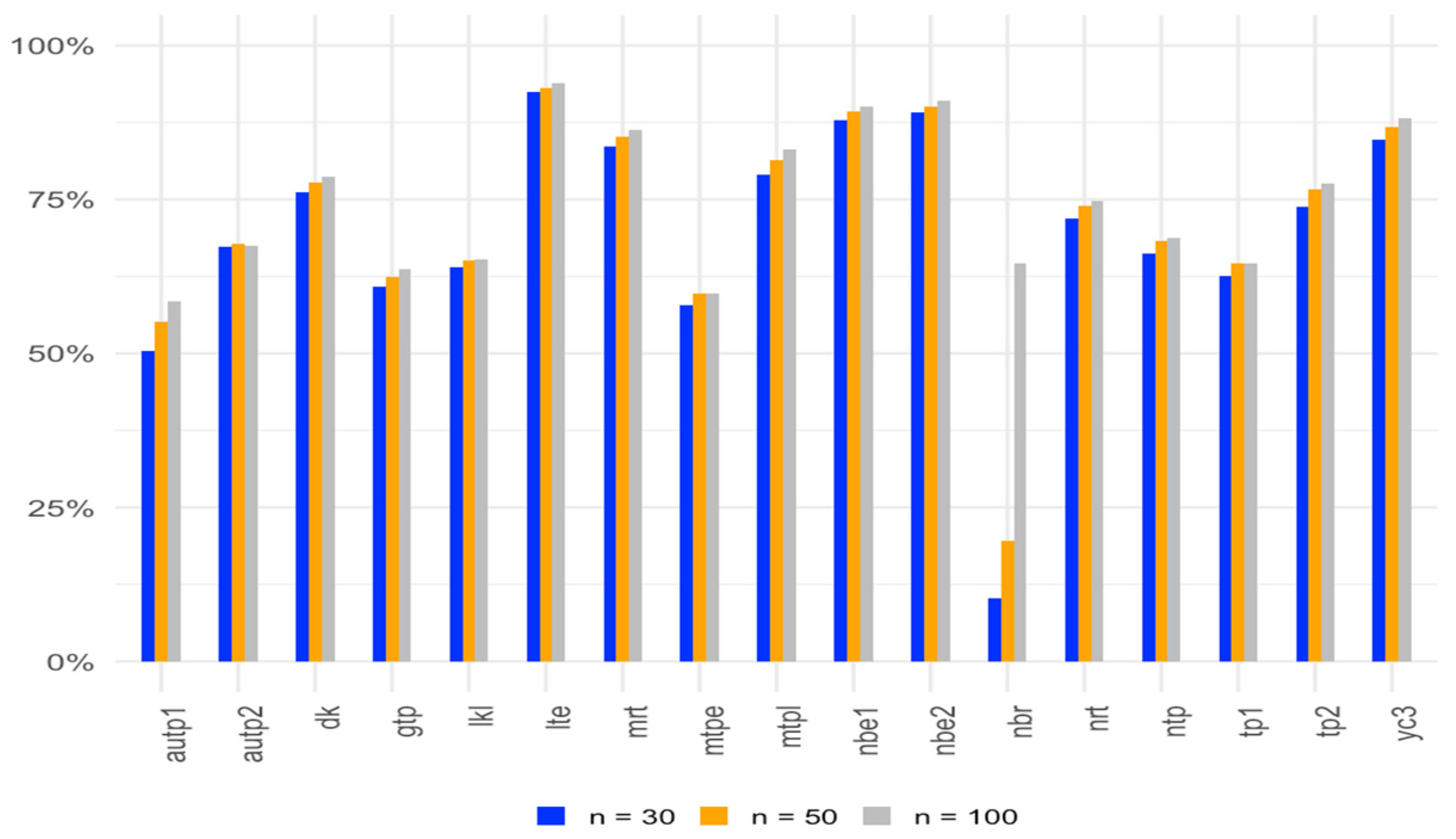
3.2. Statistical Power Simulation Procedure
3.2.1. Monte Carlo Approach for Statistical Power
3.2.2. Interpretation of Simulation Results for Power
4. Application to Real-Life Data
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kibria, B.M.G. Performance of some new ridge regression estimators. Commun. Stat. Simul. Comput. 2003, 32, 419–435. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Ehsanes Saleh, A.M.; Kibria, B.M.G. Performance of some new preliminary test ridge regression estimators and their properties. Commun. Stat. Theory Methods 1993, 22, 2747–2764. [Google Scholar] [CrossRef]
- Alheety, M.I.; Nayem, H.M.; Kibria, B.M.G. An Unbiased Convex Estimator Depending on Prior Information for the Classical Linear Regression Model. Stats 2025, 8, 16. [Google Scholar] [CrossRef]
- Dawoud, I.; Kibria, B.M.G. A new biased estimator to combat the multicollinearity of the Gaussian linear regression model. Stats 2020, 3, 526–541. [Google Scholar] [CrossRef]
- Hoque, M.A.; Kibria, B.M.G. Some one and two parameter estimators for the multicollinear gaussian linear regression model: Simulations and applications. Surv. Math. Its Appl. 2023, 18, 183–221. [Google Scholar]
- Hoque, M.A.; Kibria, B.M.G. Performance of some estimators for the multicollinear logistic regression model: Theory, simulation, and applications. Res. Stat. 2024, 2, 2364747. [Google Scholar] [CrossRef]
- Nayem, H.M.; Aziz, S.; Kibria, B.M.G. Comparison among Ordinary Least Squares, Ridge, Lasso, and Elastic Net Estimators in the Presence of Outliers: Simulation and Application. Int. J. Stat. Sci. 2024, 24, 25–48. [Google Scholar] [CrossRef]
- Yasmin, N.; Kibria, B.M.G. Performance of Some Improved Estimators and their Robust Versions in Presence of Multicollinearity and Outliers. Sankhya B 2025, 2025, 1–47. [Google Scholar] [CrossRef]
- Halawa, A.M.; El Bassiouni, M.Y. Tests of regression coefficients under ridge regression models. J. Stat. Comput. Simul. 2000, 65, 341–356. [Google Scholar] [CrossRef]
- Cule, E.; Vineis, P.; De Iorio, M. Significance testing in ridge regression for genetic data. BMC Bioinform. 2011, 12, 372. [Google Scholar] [CrossRef]
- Gökpınar, E.; Ebegil, M. A study on tests of hypothesis based on ridge estimator. Gazi Univ. J. Sci. 2016, 29, 769–781. [Google Scholar]
- Kibria, B.M.G.; Banik, S. A simulation study on the size and power Properties of some ridge regression Tests. Appl. Appl. Math. Int. J. (AAM) 2019, 14, 7. [Google Scholar]
- Perez-Melo, S.; Kibria, B.M.G. On some test statistics for testing the regression coefficients in presence of multicollinearity: A simulation study. Stats 2020, 3, 40–55. [Google Scholar] [CrossRef]
- Ullah, M.I.; Aslam, M.; Altaf, S. lmridge: A Comprehensive R Package for Ridge Regression. R J. 2018, 10, 326. [Google Scholar] [CrossRef]
- Perez-Melo, S.; Bursac, Z.; Kibria, B.M.G. Comparison of Test Statistics for Testing the Regression Coefficients in the OLS, Ridge, Liu and Kibria-Lukman Linear Regression Model: A Simulation Study. In JSM Proceedings, Biometrics Section; American Statistical Association: Alexandria, VA, USA, 2022; pp. 59–80. [Google Scholar]
- Yang, H.; Chang, X. A new two-parameter estimator in linear regression. Commun. Stat. Theory Methods 2010, 39, 923–934. [Google Scholar] [CrossRef]
- Liu, K. Using Liu-type estimator to combat collinearity. Commun. Stat. Theory Methods 2003, 32, 1009–1020. [Google Scholar] [CrossRef]
- Özkale, M.R.; Kaciranlar, S. The restricted and unrestricted two-parameter estimators. Commun. Stat. Theory Methods 2007, 36, 2707–2725. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W.; Baldwin, K.F. Ridge regression: Some simulations. Commun. Stat. Theory Methods 1975, 4, 105–123. [Google Scholar] [CrossRef]
- Sakallıoğlu, S.; Kaçıranlar, S. A new biased estimator based on ridge estimation. Stat. Pap. 2008, 49, 669–689. [Google Scholar] [CrossRef]
- Wu, J.; Yang, H. Efficiency of an almost unbiased two-parameter estimator in linear regression model. Statistics 2013, 47, 535–545. [Google Scholar] [CrossRef]
- Wu, J. An Unbiased Two-Parameter Estimation with Prior Information in Linear Regression Model. Sci. World J. 2014, 1, 206943. [Google Scholar] [CrossRef] [PubMed]
- Dorugade, A.V. A modified two-parameter estimator in linear regression. Stat. Transit. New Ser. 2014, 15, 23–36. [Google Scholar] [CrossRef]
- Arumairajan, S.; Wijekoon, P. Modified almost unbiased Liu estimator in linear regression model. Commun. Math. Stat. 2017, 5, 261–276. [Google Scholar] [CrossRef]
- Lukman, A.F.; Adewuyi, E.; Oladejo, N.; Olukayode, A. Modified almost unbiased two-parameter estimator in linear regression model. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 640, p. 012119. [Google Scholar]
- Lukman, A.F.; Ayinde, K.; Siok Kun, S.; Adewuyi, E.T. A modified new two-parameter estimator in a linear regression model. Model. Simul. Eng. 2019, 2019, 6342702. [Google Scholar] [CrossRef]
- Lukman, A.F.; Ayinde, K.; Binuomote, S.; Clement, O.A. Modified ridge-type estimator to combat multicollinearity: Application to chemical data. J. Chemom. 2019, 33, e3125. [Google Scholar] [CrossRef]
- Zeinal, A. Generalized two-parameter estimator in linear regression model. J. Math. Model. 2020, 8, 157–176. [Google Scholar] [CrossRef]
- Üstündağ Şiray, G.; Toker, S.; Özbay, N. Defining a two-parameter estimator: A mathematical programming evidence. J. Stat. Comput. Simul. 2021, 91, 2133–2152. [Google Scholar] [CrossRef]
- Abidoye, A.O.; Ajayi, I.M.; Adewale, F.L.; Ogunjobi, J.O. Unbiased Modified Two-Parameter Estimator for the Linear Regression Model. J. Sci. Res. 2022, 14, 785–795. [Google Scholar] [CrossRef]
- Ahmad, S.; Aslam, M. Another proposal about the new two-parameter estimator for linear regression model with correlated regressors. Commun. Stat. Simul. Comput. 2022, 51, 3054–3072. [Google Scholar] [CrossRef]
- Aslam, M.; Ahmad, S. The modified Liu-ridge-type estimator: A new class of biased estimators to address multicollinearity. Commun. Stat. Simul. Comput. 2022, 51, 6591–6609. [Google Scholar] [CrossRef]
- Dawoud, I.; Lukman, A.F.; Haadi, A.R. A new biased regression estimator: Theory, simulation and application. Sci. Afr. 2022, 15, e01100. [Google Scholar] [CrossRef]
- Idowu, J.I.; Oladapo, O.J.; Owolabi, A.T.; Ayinde, K. On the biased Two-Parameter Estimator to Combat Multicollinearity in Linear Regression Model. Afr. Sci. Rep. 2022, 1, 188–204. [Google Scholar] [CrossRef]
- Owolabi, A.T.; Ayinde, K.; Idowu, J.I.; Oladapo, O.J.; Lukman, A.F. A new two-parameter estimator in the linear regression model with correlated regressors. J. Stat. Appl. Probab. 2022, 11, 185–201. [Google Scholar]
- Owolabi, A.T.; Ayinde, K.; Alabi, O.O. A new ridge-type estimator for the linear regression model with correlated regressors. Concurr. Comput. Pract. Exp. 2022, 34, e6933. [Google Scholar] [CrossRef]
- Owolabi, A.T.; Ayinde, K.; Alabi, O.O. A Modified Two Parameter Estimator with Different Forms of Biasing Parameters in the Linear Regression Model. Afr. Sci. Rep. 2022, 1, 212–228. [Google Scholar] [CrossRef]
- Abonazel, M.R. New modified two-parameter Liu estimator for the Conway–Maxwell Poisson regression model. J. Stat. Comput. Simul. 2023, 93, 1976–1996. [Google Scholar] [CrossRef]
- Abdelwahab, M.M.; Abonazel, M.R.; Hammad, A.T.; El-Masry, A.M. Modified Two-Parameter Liu Estimator for Addressing Multicollinearity in the Poisson Regression Model. Axioms 2024, 13, 46. [Google Scholar] [CrossRef]
- Idowu, J.I.; Oladapo, O.J.; Owolabi, A.T.; Ayinde, K.; Akinmoju, O. Combating multicollinearity: A new two-parameter approach. Nicel Bilim. Derg. 2023, 5, 90–116. [Google Scholar] [CrossRef]
- Kibria, B.M.G.; Lukman, A.F. A new ridge-type estimator for the linear regression model: Simulations and applications. Scientifica 2020, 2020, 9758378. [Google Scholar] [CrossRef]
- Khan, M.S.; Ali, A.; Suhail, M.; Kibria, B.M.G. On some two parameter estimators for the linear regression models with correlated predictors: Simulation and application. Commun. Stat. Simul. Comput. 2024, 2024, 1–15. [Google Scholar] [CrossRef]
- R Core Team. _R: A Language and Environment for Statistical Computing_; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: https://www.R-project.org/ (accessed on 11 August 2024).
- McDonald, G.C.; Schwing, R.C. Instabilities of regression estimates relating air pollution to mortality. Technometrics 1973, 15, 463–481. [Google Scholar] [CrossRef]
- Duffy, E.A.; Carroll, R.E. United States Metropolitan Mortality, 1959–1961; PHS Publication No. 1967, 999-AP-39; U.S. Public Health Service, National Center for Air Pollution Control: Philadelphia, PA, USA, 1967.
- Triola, M.M.; Triola, M.F.; Roy, J.A. Biostatistics for the Biological and Health Sciences; Pearson Addison-Wesley: Boston, MA, USA, 2006. [Google Scholar]

| Name | Author | Parameters |
|---|---|---|
| 1. Liu Type of Two-Parameter Estimator (LTE) | Liu (2003) [18] | , . |
| 2. Ozkale and Kaciranlar Two-Parameter Estimator (TP) | Ozkale and Kaciranlar (2007) [19] | , Used both arithmetic and harmonic means. |
| 3. New Biased Estimator Based on Ridge (NBE) | Sakallıoglu˘ and Kiciranlar (2008) [21] | , and . |
| 4. Yang and Chang Two-Parameter Estimator (YC) | Yang and Chang (2010) [17] | . . |
| 5. Almost Unbiased Two-Parameter Estimator (AUTP) | Wu and Yang (2011) [22] | , . |
| 6. Unbiased Two-Parameter Estimator (UTP) | Wu (2014) [23] | , where . . |
| 7. Dorugade Modified Two-Parameter Estimator (MTP) | Dorugade (2014) [24] | and . . |
| 8. Modified Almost Unbiased Liu Estimator (MAULE) | Arumairajan and Wijekoon (2017) [25] | , . |
| 9. Modified Almost Unbiased Two-Parameter Estimator (MAUTP) | Lukman et al. (2019) [26] | , and , . |
| 10. Modified New Two-Parameter Estimator (MNTP) | Lukman et al. (2019) [27] | , Use the harmonic mean of values. . |
| 11. Modified Ridge Type (MRT) | Lukman et al. (2019) [28] | . Use harmonic mean of the . Use the harmonic means of . |
| 12. A New Biased Estimator by Dawoud and Kibria (DK) | Dawoud and Kibria (2020) [5] | , Use . where . Use . |
| 13. Generalized Two-Parameter Estimator (GTP) | Zeinal (2020) [29] | . Take the arithmetic mean. |
| 14. Siray Two-Parameter Estimator (DTP) | Siray et al. (2021) [30] | , . Take the harmonic mean and median. |
| 15. Unbiased Modified Two-Parameter Estimator (UMTP) | Abidoye et al. (2022) [31] | . |
| 16. Ahmad and Aslam’s Modified New Two-Parameter Estimator (MNTPE) | Ahmad and Aslam (2022) [32] | , Take the harmonic mean of values. . |
| 17. Modified Liu Ridge Type (MLRT) | Aslam and Ahmad (2022) [33] | , Take the max values of . . |
| 18. New Biased Regression Two-Parameter Estimator (NBR) | Dawoud et al. (2022) [34] | ; take the minimum values of . . Take the minimum values of . |
| 19. Biased Two-Parameter Estimator (BTP) | Idowu et al. (2022) [35] | , . |
| 20. New Two-Parameter Estimator (NTP) | Owolabi et al. (2022) [36] | , Take the harmonic mean. . |
| 21. New Ridge-Type Estimator (NRT) | Owolabi et al. (2022) [37] | , . |
| 22. Modified Two-Parameter Estimator (MTPE) | Owolabi et al. (2022) [38] | , Take the arithmetic mean of , . |
| 23. Modified Two-Parameter Liu Estiamtor by Abonazel (MTPL) | Abonazel (2023) [39] | , . |
| 24. Liu–Kibria–Lukman Two Parameter Estiamtor (LKL) | Idowu et al. (2023) [41] | , . |
| 25. Two-Parameter Ridge-Type Estimator (TPR) | Shakir Khan et al. (2024) [43] | , . |
| p | 3 | 5 | 10 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | Avg |
| OLS | 0.0457 | 0.0491 | 0.0497 | 0.0461 | 0.0498 | 0.0466 | 0.0441 | 0.0469 | 0.0488 | 0.0474 |
| LTE | 0.0779 | 0.0859 | 0.0905 | 0.0558 | 0.0631 | 0.0634 | 0.0369 | 0.0444 | 0.0488 | 0.063 |
| TP1 | 0.0466 | 0.0501 | 0.0509 | 0.0462 | 0.0493 | 0.047 | 0.0442 | 0.047 | 0.0489 | 0.0478 |
| TP2 | 0.0471 | 0.0509 | 0.0523 | 0.0462 | 0.0493 | 0.0478 | 0.0428 | 0.0463 | 0.0484 | 0.0479 |
| NBE1 | 0.0603 | 0.0666 | 0.0699 | 0.0499 | 0.0559 | 0.0554 | 0.0364 | 0.0435 | 0.0478 | 0.054 |
| NBE2 | 0.0564 | 0.0633 | 0.0676 | 0.049 | 0.0551 | 0.0542 | 0.0368 | 0.0441 | 0.0485 | 0.0528 |
| YC1 | 0.0481 | 0.0587 | 0.0655 | 0.0999 | 0.1243 | 0.1405 | 0.2071 | 0.2871 | 0.3328 | 0.1516 |
| YC2 | 0.0447 | 0.0521 | 0.0647 | 0.0575 | 0.0704 | 0.0816 | 0.0561 | 0.0818 | 0.1005 | 0.0677 |
| YC3 | 0.0528 | 0.0594 | 0.061 | 0.0521 | 0.0579 | 0.0597 | 0.0393 | 0.0487 | 0.0547 | 0.054 |
| AUTP1 | 0.0391 | 0.0411 | 0.0457 | 0.0372 | 0.0412 | 0.0413 | 0.027 | 0.0329 | 0.039 | 0.0383 |
| AUTP2 | 0.0409 | 0.0447 | 0.0484 | 0.0479 | 0.0527 | 0.0485 | 0.0503 | 0.0593 | 0.0575 | 0.05 |
| UTP | 0.1178 | 0.2792 | 0.4844 | 0.0167 | 0.0477 | 0.1739 | 0.002 | 0.004 | 0.0134 | 0.1266 |
| MTP1 | 0.1064 | 0.1375 | 0.1575 | 0.2042 | 0.2811 | 0.3254 | 0.3739 | 0.5744 | 0.6658 | 0.314 |
| MTP2 | 0.1053 | 0.1359 | 0.1569 | 0.2011 | 0.2779 | 0.3217 | 0.3719 | 0.572 | 0.6638 | 0.3118 |
| MAULE | 0.0015 | 0.0057 | 0.0105 | 0.0011 | 0.0015 | 0.0034 | 0.0001 | 0.0012 | 0.0031 | 0.0023 |
| MAUTP | 0.078 | 0.0876 | 0.0957 | 0.0734 | 0.0869 | 0.0928 | 0.0412 | 0.0535 | 0.063 | 0.0747 |
| MNTP | 0.191 | 0.202 | 0.2061 | 0.1016 | 0.1134 | 0.1105 | 0.0653 | 0.0725 | 0.076 | 0.1265 |
| DK | 0.0604 | 0.0667 | 0.0704 | 0.047 | 0.0506 | 0.0491 | 0.0426 | 0.0462 | 0.0483 | 0.0535 |
| MRT | 0.0509 | 0.0591 | 0.0629 | 0.0465 | 0.0537 | 0.0528 | 0.0355 | 0.0437 | 0.0484 | 0.0504 |
| GTP | 0.0257 | 0.0325 | 0.0331 | 0.0244 | 0.0276 | 0.0306 | 0.0158 | 0.0203 | 0.0248 | 0.0261 |
| DTP1 | 0.1431 | 0.1611 | 0.1815 | 0.2469 | 0.299 | 0.3289 | 0.3932 | 0.5141 | 0.5798 | 0.3164 |
| DTP2 | 0.1683 | 0.1818 | 0.2066 | 0.2467 | 0.2916 | 0.3153 | 0.4927 | 0.6189 | 0.6817 | 0.356 |
| UMTP | 0.992 | 0.9959 | 0.9983 | 0.9956 | 0.9983 | 0.9993 | 0.9978 | 0.9995 | 0.9999 | 0.9974 |
| MNTPE | 0.1333 | 0.1451 | 0.1621 | 0.1559 | 0.185 | 0.1976 | 0.1043 | 0.1453 | 0.1779 | 0.1563 |
| MLRT | 0.1175 | 0.1353 | 0.1445 | 0.2178 | 0.2583 | 0.2795 | 0.4121 | 0.5391 | 0.605 | 0.301 |
| NBR | 0.0261 | 0.0535 | 0.0891 | 0.0104 | 0.0233 | 0.0638 | 0.0026 | 0.0046 | 0.0066 | 0.0311 |
| BTP | 0.0712 | 0.0836 | 0.0931 | 0.1571 | 0.1959 | 0.2182 | 0.3919 | 0.5261 | 0.5829 | 0.2578 |
| LKL | 0.0494 | 0.0651 | 0.0774 | 0.0375 | 0.0612 | 0.0728 | 0.0115 | 0.0242 | 0.0438 | 0.0492 |
| NTP | 0.0466 | 0.0502 | 0.0513 | 0.0458 | 0.0492 | 0.047 | 0.0443 | 0.047 | 0.0486 | 0.0478 |
| NRT | 0.048 | 0.0528 | 0.0537 | 0.0456 | 0.0491 | 0.0478 | 0.0426 | 0.0462 | 0.0483 | 0.0482 |
| MTPE | 0.0394 | 0.0407 | 0.0427 | 0.0372 | 0.0408 | 0.0386 | 0.0358 | 0.0381 | 0.0395 | 0.0392 |
| MTPL | 0.0305 | 0.0369 | 0.0417 | 0.0349 | 0.0423 | 0.0462 | 0.0272 | 0.0399 | 0.0481 | 0.0386 |
| TPR1 | 0.1169 | 0.1271 | 0.1515 | 0.0826 | 0.1164 | 0.1368 | 0.0174 | 0.0499 | 0.0807 | 0.0977 |
| TPR2 | 0.0016 | 0.0021 | 0.003 | 0.0001 | 0.0001 | 0.0007 | 0.0001 | 0.0002 | 0.0003 | 0.0008 |
| p | 3 | 5 | 10 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | Avg |
| OLS | 0.0485 | 0.0455 | 0.0454 | 0.0466 | 0.0471 | 0.0506 | 0.0449 | 0.047 | 0.0484 | 0.0471 |
| LTE | 0.0679 | 0.0691 | 0.0701 | 0.049 | 0.0519 | 0.0574 | 0.0364 | 0.0425 | 0.0474 | 0.0546 |
| TP1 | 0.0487 | 0.0468 | 0.0457 | 0.0465 | 0.047 | 0.0506 | 0.0449 | 0.047 | 0.0484 | 0.0473 |
| TP2 | 0.0493 | 0.0475 | 0.0463 | 0.0457 | 0.0472 | 0.0507 | 0.0427 | 0.0458 | 0.0481 | 0.047 |
| NBE1 | 0.0586 | 0.0571 | 0.0579 | 0.0464 | 0.0495 | 0.0546 | 0.0363 | 0.0425 | 0.0469 | 0.05 |
| NBE2 | 0.0575 | 0.0561 | 0.0559 | 0.0468 | 0.0496 | 0.0542 | 0.0364 | 0.0425 | 0.0473 | 0.0496 |
| YC1 | 0.0618 | 0.0674 | 0.0732 | 0.0955 | 0.1181 | 0.1303 | 0.211 | 0.2789 | 0.3133 | 0.1499 |
| YC2 | 0.0468 | 0.0586 | 0.0676 | 0.0594 | 0.0721 | 0.0893 | 0.0633 | 0.0883 | 0.1059 | 0.0724 |
| YC3 | 0.0523 | 0.0519 | 0.0538 | 0.0481 | 0.0522 | 0.0578 | 0.0374 | 0.0444 | 0.0497 | 0.0497 |
| AUTP1 | 0.0394 | 0.0385 | 0.0399 | 0.0342 | 0.0373 | 0.0428 | 0.0269 | 0.032 | 0.0372 | 0.0365 |
| AUTP2 | 0.0451 | 0.0443 | 0.0449 | 0.0469 | 0.0493 | 0.0506 | 0.0468 | 0.0541 | 0.0538 | 0.0484 |
| UTP | 0.0475 | 0.1139 | 0.336 | 0.0092 | 0.0212 | 0.0624 | 0.0015 | 0.0033 | 0.0075 | 0.0669 |
| MTP1 | 0.1167 | 0.1506 | 0.1772 | 0.2387 | 0.315 | 0.3619 | 0.4244 | 0.6272 | 0.7175 | 0.3477 |
| MTP2 | 0.1157 | 0.1495 | 0.177 | 0.2371 | 0.3136 | 0.3606 | 0.4229 | 0.6263 | 0.7167 | 0.3466 |
| MAULE | 0.0002 | 0.0009 | 0.0011 | 0.0001 | 0.0001 | 0.0002 | 0.0001 | 0.0001 | 0.0002 | 0.0003 |
| MAUTP | 0.0777 | 0.0815 | 0.0853 | 0.0676 | 0.0776 | 0.086 | 0.0366 | 0.0469 | 0.0535 | 0.0681 |
| MNTP | 0.1403 | 0.1476 | 0.1435 | 0.0717 | 0.0753 | 0.0785 | 0.0531 | 0.0566 | 0.0596 | 0.0918 |
| DK | 0.0589 | 0.0592 | 0.0587 | 0.0463 | 0.048 | 0.052 | 0.043 | 0.0457 | 0.0482 | 0.0511 |
| MRT | 0.0545 | 0.0547 | 0.0561 | 0.0459 | 0.0497 | 0.0542 | 0.0353 | 0.042 | 0.0474 | 0.0489 |
| GTP | 0.0281 | 0.0327 | 0.0351 | 0.0171 | 0.0192 | 0.0252 | 0.0126 | 0.0161 | 0.0193 | 0.0228 |
| DTP1 | 0.165 | 0.1809 | 0.2054 | 0.2961 | 0.3404 | 0.37 | 0.4924 | 0.6027 | 0.6595 | 0.368 |
| DTP2 | 0.1739 | 0.1941 | 0.2113 | 0.299 | 0.3398 | 0.3669 | 0.5564 | 0.6721 | 0.7318 | 0.3939 |
| UMTP | 0.9901 | 0.9935 | 0.9968 | 0.9964 | 0.9982 | 0.9993 | 0.9986 | 0.9996 | 0.9998 | 0.9969 |
| MNTPE | 0.1568 | 0.1731 | 0.1917 | 0.2694 | 0.3031 | 0.3247 | 0.3376 | 0.4188 | 0.469 | 0.2938 |
| MLRT | 0.1401 | 0.1629 | 0.1761 | 0.2668 | 0.3071 | 0.3322 | 0.4937 | 0.6215 | 0.6904 | 0.3545 |
| NBR | 0.0199 | 0.0439 | 0.0898 | 0.0057 | 0.0111 | 0.0188 | 0.0017 | 0.0019 | 0.0013 | 0.0216 |
| BTP | 0.0703 | 0.0781 | 0.0865 | 0.1655 | 0.207 | 0.2324 | 0.4234 | 0.5115 | 0.5522 | 0.2585 |
| LKL | 0.0522 | 0.0699 | 0.0775 | 0.0418 | 0.0621 | 0.076 | 0.0141 | 0.0262 | 0.0455 | 0.0517 |
| NTP | 0.0485 | 0.0464 | 0.0451 | 0.0461 | 0.0472 | 0.0508 | 0.0447 | 0.0469 | 0.0484 | 0.0471 |
| NRT | 0.049 | 0.0469 | 0.0465 | 0.0455 | 0.0469 | 0.0506 | 0.043 | 0.0457 | 0.0482 | 0.0469 |
| MTPE | 0.0406 | 0.0367 | 0.0381 | 0.0382 | 0.0383 | 0.0402 | 0.0366 | 0.038 | 0.039 | 0.0384 |
| MTPL | 0.033 | 0.0354 | 0.0403 | 0.0334 | 0.0409 | 0.0479 | 0.0258 | 0.0374 | 0.0458 | 0.0378 |
| TPR1 | 0.1365 | 0.1516 | 0.1721 | 0.1387 | 0.1758 | 0.1992 | 0.0426 | 0.0918 | 0.1299 | 0.1376 |
| TPR2 | 0.0003 | 0.0009 | 0.0013 | 0.0001 | 0.0001 | 0.0002 | 0.0001 | 0.0001 | 0.0002 | 0.0003 |
| p | 3 | 5 | 10 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | Avg |
| OLS | 0.0443 | 0.0485 | 0.0467 | 0.0455 | 0.045 | 0.0474 | 0.0451 | 0.047 | 0.0482 | 0.0464 |
| LTE | 0.0482 | 0.0544 | 0.0533 | 0.0416 | 0.0439 | 0.0471 | 0.0352 | 0.0417 | 0.0456 | 0.0457 |
| TP1 | 0.0442 | 0.0483 | 0.0469 | 0.0454 | 0.045 | 0.0473 | 0.0451 | 0.047 | 0.0482 | 0.0464 |
| TP2 | 0.0457 | 0.0507 | 0.0495 | 0.0445 | 0.0448 | 0.0472 | 0.0426 | 0.0456 | 0.0476 | 0.0465 |
| NBE1 | 0.0462 | 0.0521 | 0.0512 | 0.0416 | 0.0436 | 0.0469 | 0.0352 | 0.0417 | 0.0455 | 0.0449 |
| NBE2 | 0.0477 | 0.0537 | 0.0533 | 0.0416 | 0.0438 | 0.047 | 0.0352 | 0.0416 | 0.0456 | 0.0455 |
| YC1 | 0.1587 | 0.1844 | 0.2015 | 0.2666 | 0.2887 | 0.3094 | 0.3701 | 0.4869 | 0.5574 | 0.3137 |
| YC2 | 0.075 | 0.092 | 0.1002 | 0.075 | 0.0937 | 0.108 | 0.0596 | 0.0853 | 0.1035 | 0.088 |
| YC3 | 0.0444 | 0.0504 | 0.0483 | 0.0415 | 0.0436 | 0.0478 | 0.035 | 0.0415 | 0.0456 | 0.0442 |
| AUTP1 | 0.0339 | 0.0377 | 0.0383 | 0.0323 | 0.0355 | 0.0399 | 0.0254 | 0.0317 | 0.0361 | 0.0345 |
| AUTP2 | 0.0429 | 0.0476 | 0.0467 | 0.0435 | 0.0445 | 0.0468 | 0.0406 | 0.0459 | 0.049 | 0.0453 |
| UTP | 0.0104 | 0.015 | 0.0315 | 0.0039 | 0.0062 | 0.0137 | 0.0009 | 0.0018 | 0.003 | 0.0096 |
| MTP1 | 0.131 | 0.1655 | 0.1894 | 0.2591 | 0.3366 | 0.3912 | 0.4684 | 0.6709 | 0.755 | 0.3741 |
| MTP2 | 0.1307 | 0.1651 | 0.1891 | 0.2588 | 0.3365 | 0.391 | 0.4683 | 0.6709 | 0.755 | 0.3739 |
| MAULE | 0.0001 | 0.0001 | 0.0002 | 0.0001 | 0.0001 | 0.0002 | 0.0001 | 0.0001 | 0.0002 | 0.0001 |
| MAUTP | 0.0524 | 0.0596 | 0.0612 | 0.0439 | 0.048 | 0.0523 | 0.0321 | 0.0395 | 0.0452 | 0.0482 |
| MNTP | 0.0843 | 0.0914 | 0.0902 | 0.0493 | 0.049 | 0.0508 | 0.0459 | 0.0476 | 0.0491 | 0.062 |
| DK | 0.0466 | 0.0522 | 0.051 | 0.0444 | 0.0446 | 0.047 | 0.0429 | 0.0458 | 0.0477 | 0.0469 |
| MRT | 0.0473 | 0.0526 | 0.0538 | 0.0407 | 0.0434 | 0.0467 | 0.0336 | 0.0407 | 0.0454 | 0.0449 |
| GTP | 0.0102 | 0.0108 | 0.0113 | 0.0073 | 0.0097 | 0.0104 | 0.0046 | 0.0087 | 0.0124 | 0.0095 |
| DTP1 | 0.1673 | 0.1903 | 0.2055 | 0.3222 | 0.3716 | 0.4059 | 0.5874 | 0.7021 | 0.7554 | 0.412 |
| DTP2 | 0.1661 | 0.1889 | 0.2045 | 0.3278 | 0.3714 | 0.4074 | 0.5982 | 0.7142 | 0.7701 | 0.4165 |
| UMTP | 0.9853 | 0.9893 | 0.9941 | 0.9957 | 0.9975 | 0.9987 | 0.9992 | 0.9997 | 1 | 0.9955 |
| MNTPE | 0.1659 | 0.1873 | 0.2009 | 0.3278 | 0.371 | 0.4054 | 0.5914 | 0.707 | 0.7626 | 0.4133 |
| MLRT | 0.1672 | 0.1869 | 0.2005 | 0.3252 | 0.3653 | 0.4028 | 0.5719 | 0.7044 | 0.766 | 0.41 |
| NBR | 0.0059 | 0.008 | 0.015 | 0.0026 | 0.0028 | 0.0021 | 0.001 | 0.0005 | 0.0003 | 0.0042 |
| BTP | 0.0459 | 0.0516 | 0.0567 | 0.1339 | 0.1839 | 0.2149 | 0.3678 | 0.4688 | 0.5179 | 0.2268 |
| LKL | 0.0455 | 0.0645 | 0.0743 | 0.0612 | 0.0947 | 0.1174 | 0.0654 | 0.1004 | 0.1277 | 0.0835 |
| NTP | 0.0441 | 0.0481 | 0.047 | 0.0451 | 0.045 | 0.0474 | 0.0448 | 0.0468 | 0.0482 | 0.0463 |
| NRT | 0.0457 | 0.0515 | 0.0505 | 0.0443 | 0.0446 | 0.047 | 0.0429 | 0.0458 | 0.0477 | 0.0467 |
| MTPE | 0.0359 | 0.0381 | 0.0373 | 0.0355 | 0.0353 | 0.0382 | 0.0355 | 0.0369 | 0.0376 | 0.0367 |
| MTPL | 0.0288 | 0.0376 | 0.0421 | 0.0279 | 0.0354 | 0.0429 | 0.0238 | 0.0338 | 0.0428 | 0.035 |
| TPR1 | 0.1536 | 0.1785 | 0.1948 | 0.2782 | 0.3332 | 0.3674 | 0.3122 | 0.4509 | 0.5216 | 0.31 |
| TPR2 | 0.0001 | 0.0001 | 0.0002 | 0.0001 | 0.0001 | 0.0002 | 0.0001 | 0.0001 | 0.0002 | 0.0002 |
| p | 3 | 5 | 10 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | Ave |
| OLS | 0.5927 | 0.6121 | 0.6145 | 0.3902 | 0.4089 | 0.4188 | 0.208 | 0.2298 | 0.2344 | 0.4122 |
| LTE | 0.9237 | 0.9313 | 0.9386 | 0.6641 | 0.6872 | 0.7063 | 0.2469 | 0.2995 | 0.3197 | 0.6353 |
| TP1 | 0.6249 | 0.6456 | 0.646 | 0.396 | 0.4151 | 0.4261 | 0.2088 | 0.2305 | 0.235 | 0.4253 |
| TP2 | 0.7383 | 0.7661 | 0.7753 | 0.4529 | 0.4816 | 0.4956 | 0.2204 | 0.2506 | 0.2588 | 0.4933 |
| NBE1 | 0.879 | 0.8925 | 0.9011 | 0.5974 | 0.6287 | 0.6535 | 0.2343 | 0.2853 | 0.3059 | 0.5975 |
| NBE2 | 0.8914 | 0.9003 | 0.9097 | 0.6183 | 0.6484 | 0.6703 | 0.2418 | 0.2934 | 0.313 | 0.6096 |
| YC3 | 0.8467 | 0.8679 | 0.8816 | 0.5838 | 0.6176 | 0.6433 | 0.2418 | 0.2941 | 0.3152 | 0.588 |
| AUTP1 | 0.5033 | 0.5507 | 0.5845 | 0.301 | 0.3292 | 0.3664 | 0.1487 | 0.1721 | 0.1817 | 0.3486 |
| AUTP2 | 0.6726 | 0.6781 | 0.6753 | 0.4872 | 0.4962 | 0.4842 | 0.2482 | 0.2924 | 0.3014 | 0.4817 |
| DK | 0.7616 | 0.7771 | 0.7872 | 0.4706 | 0.4971 | 0.5133 | 0.2195 | 0.2481 | 0.2556 | 0.5033 |
| MRT | 0.8359 | 0.8521 | 0.8626 | 0.583 | 0.6185 | 0.6376 | 0.243 | 0.2975 | 0.318 | 0.5831 |
| GTP | 0.6085 | 0.6247 | 0.6361 | 0.3833 | 0.4066 | 0.4181 | 0.1583 | 0.196 | 0.2141 | 0.4051 |
| NBR | 0.1022 | 0.1953 | 0.6455 | 0.018 | 0.0214 | 0.047 | 0.0032 | 0.0007 | 0.0003 | 0.1148 |
| LKL | 0.6405 | 0.6506 | 0.653 | 0.2987 | 0.312 | 0.329 | 0.0392 | 0.0536 | 0.0793 | 0.3395 |
| NTP | 0.6618 | 0.6823 | 0.6881 | 0.4135 | 0.4344 | 0.4427 | 0.212 | 0.2346 | 0.2391 | 0.4454 |
| NRT | 0.7196 | 0.7398 | 0.7471 | 0.4596 | 0.4852 | 0.4989 | 0.2193 | 0.248 | 0.2555 | 0.4859 |
| MTPE | 0.5781 | 0.5971 | 0.5973 | 0.3652 | 0.3847 | 0.3941 | 0.1842 | 0.2061 | 0.2092 | 0.3907 |
| MTPL | 0.7908 | 0.8143 | 0.8313 | 0.5596 | 0.5976 | 0.6198 | 0.246 | 0.3128 | 0.3425 | 0.5683 |
| p | 3 | 5 | 10 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | Ave |
| OLS | 0.5977 | 0.608 | 0.6285 | 0.3939 | 0.4035 | 0.422 | 0.2116 | 0.2265 | 0.2368 | 0.4143 |
| LTE | 0.9319 | 0.9399 | 0.9423 | 0.648 | 0.6741 | 0.6973 | 0.2375 | 0.2786 | 0.3062 | 0.6284 |
| TP1 | 0.6325 | 0.6444 | 0.6635 | 0.4003 | 0.4108 | 0.4299 | 0.2121 | 0.2272 | 0.2375 | 0.4287 |
| TP2 | 0.7933 | 0.8143 | 0.8266 | 0.4568 | 0.4763 | 0.503 | 0.2211 | 0.2436 | 0.2578 | 0.5103 |
| NBE1 | 0.8999 | 0.9145 | 0.9174 | 0.5932 | 0.6258 | 0.6549 | 0.2289 | 0.2694 | 0.2968 | 0.6001 |
| NBE2 | 0.9159 | 0.9272 | 0.931 | 0.6266 | 0.6544 | 0.6806 | 0.2361 | 0.2771 | 0.3047 | 0.6171 |
| YC3 | 0.8529 | 0.8793 | 0.8891 | 0.5565 | 0.5972 | 0.6298 | 0.2234 | 0.2655 | 0.2932 | 0.5763 |
| AUTP1 | 0.49 | 0.5329 | 0.5869 | 0.2837 | 0.3072 | 0.3576 | 0.1411 | 0.1591 | 0.1728 | 0.3368 |
| AUTP2 | 0.6475 | 0.6504 | 0.6649 | 0.4646 | 0.4664 | 0.4664 | 0.2358 | 0.2715 | 0.2858 | 0.4615 |
| DK | 0.8008 | 0.8161 | 0.8251 | 0.4733 | 0.4922 | 0.5176 | 0.2202 | 0.2414 | 0.2545 | 0.5157 |
| MRT | 0.8847 | 0.895 | 0.9011 | 0.6063 | 0.6367 | 0.6645 | 0.2389 | 0.2831 | 0.3124 | 0.6025 |
| GTP | 0.6527 | 0.6585 | 0.6731 | 0.4102 | 0.423 | 0.4485 | 0.1741 | 0.2091 | 0.2326 | 0.4313 |
| NBR | 0.0098 | 0.0107 | 0.0471 | 0.0016 | 0.0003 | 0.0006 | 0.0003 | 0 | 0 | 0.0078 |
| LKL | 0.7251 | 0.7349 | 0.7429 | 0.4056 | 0.4204 | 0.4437 | 0.0788 | 0.0959 | 0.1295 | 0.4196 |
| NTP | 0.6728 | 0.6901 | 0.7075 | 0.4149 | 0.4268 | 0.4481 | 0.2146 | 0.2307 | 0.241 | 0.4496 |
| NRT | 0.7486 | 0.7666 | 0.7783 | 0.4608 | 0.477 | 0.5008 | 0.2202 | 0.2413 | 0.2543 | 0.4942 |
| MTPE | 0.5813 | 0.5945 | 0.6147 | 0.3697 | 0.3789 | 0.3967 | 0.1878 | 0.2024 | 0.2123 | 0.3931 |
| MTPL | 0.7929 | 0.8197 | 0.8387 | 0.5393 | 0.5706 | 0.605 | 0.2346 | 0.2899 | 0.3245 | 0.5572 |
| p | 3 | 5 | 10 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | 30 | 50 | 100 | 30 | 50 | 100 | 30 | 50 | 100 | Ave |
| OLS | 0.5896 | 0.6055 | 0.6279 | 0.3901 | 0.405 | 0.4206 | 0.2117 | 0.2275 | 0.2345 | 0.4125 |
| LTE | 0.9333 | 0.9365 | 0.9438 | 0.6022 | 0.6354 | 0.6603 | 0.2167 | 0.2529 | 0.275 | 0.6062 |
| TP1 | 0.6289 | 0.6468 | 0.6685 | 0.3965 | 0.412 | 0.4272 | 0.2122 | 0.2279 | 0.2351 | 0.4283 |
| TP2 | 0.8171 | 0.8359 | 0.8498 | 0.4463 | 0.4696 | 0.4936 | 0.2162 | 0.2371 | 0.2478 | 0.5126 |
| NBE1 | 0.8913 | 0.9076 | 0.9225 | 0.5268 | 0.5819 | 0.6178 | 0.2094 | 0.2471 | 0.2696 | 0.5749 |
| NBE2 | 0.9268 | 0.9309 | 0.9393 | 0.5997 | 0.6345 | 0.6586 | 0.2172 | 0.2537 | 0.2758 | 0.6041 |
| YC3 | 0.4129 | 0.7207 | 0.8393 | 0.343 | 0.4591 | 0.5424 | 0.1831 | 0.2307 | 0.2584 | 0.4433 |
| AUTP1 | 0.3562 | 0.4221 | 0.5112 | 0.1898 | 0.217 | 0.2706 | 0.1073 | 0.1201 | 0.1307 | 0.2583 |
| AUTP2 | 0.6009 | 0.6118 | 0.6335 | 0.4063 | 0.4208 | 0.4307 | 0.2068 | 0.2331 | 0.2497 | 0.4215 |
| DK | 0.8409 | 0.85 | 0.8627 | 0.459 | 0.4825 | 0.5077 | 0.216 | 0.2353 | 0.2452 | 0.5221 |
| MRT | 0.9113 | 0.9166 | 0.9273 | 0.6084 | 0.6423 | 0.6642 | 0.2185 | 0.2584 | 0.2834 | 0.6034 |
| GTP | 0.7617 | 0.7689 | 0.7788 | 0.5124 | 0.5363 | 0.5613 | 0.1932 | 0.2419 | 0.2727 | 0.5141 |
| NBR | 0.0004 | 0.0001 | 0.0001 | 0.0002 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 0.0002 | 0.0001 |
| LKL | 0.9003 | 0.9063 | 0.908 | 0.7239 | 0.7483 | 0.7596 | 0.3416 | 0.3958 | 0.4354 | 0.6799 |
| NTP | 0.6689 | 0.6902 | 0.7115 | 0.4097 | 0.4263 | 0.4432 | 0.214 | 0.2301 | 0.2375 | 0.4479 |
| NRT | 0.7687 | 0.7865 | 0.8005 | 0.4471 | 0.4687 | 0.493 | 0.216 | 0.2353 | 0.2452 | 0.4957 |
| MTPE | 0.5737 | 0.5912 | 0.6128 | 0.3666 | 0.3812 | 0.3961 | 0.1881 | 0.2036 | 0.2085 | 0.3913 |
| MTPL | 0.6837 | 0.7466 | 0.8001 | 0.4593 | 0.508 | 0.5464 | 0.2041 | 0.2529 | 0.2825 | 0.4982 |
| p | 3 | 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 30 | 30 | 50 | 50 | 100 | 100 | 30 | 30 | 50 | 50 | 100 | 100 |
| 5 | 10 | 5 | 10 | 5 | 10 | 5 | 10 | 5 | 10 | 5 | 10 | |
| OLS | 0.1615 | 0.0997 | 0.1692 | 0.1067 | 0.1693 | 0.1132 | 0.0758 | 0.0604 | 0.0813 | 0.0616 | 0.086 | 0.0659 |
| LTE | 0.3626 | 0.1973 | 0.3907 | 0.2195 | 0.4015 | 0.2309 | 0.0716 | 0.054 | 0.0859 | 0.0613 | 0.0967 | 0.0701 |
| NBE2 | 0.287 | 0.1553 | 0.3157 | 0.1725 | 0.3297 | 0.1839 | 0.0714 | 0.0538 | 0.0853 | 0.0611 | 0.0959 | 0.0697 |
| YC3 | 0.2547 | 0.1343 | 0.2861 | 0.151 | 0.2993 | 0.1653 | 0.0732 | 0.0544 | 0.0902 | 0.0633 | 0.1031 | 0.0738 |
| DK | 0.257 | 0.1457 | 0.2791 | 0.1607 | 0.29 | 0.1724 | 0.0758 | 0.0594 | 0.083 | 0.0622 | 0.0891 | 0.0674 |
| MRT | 0.2636 | 0.1442 | 0.2906 | 0.1641 | 0.3039 | 0.1753 | 0.0701 | 0.0525 | 0.0859 | 0.0609 | 0.0979 | 0.0704 |
| LKL | 0.2539 | 0.1379 | 0.2738 | 0.1577 | 0.286 | 0.1735 | 0.0095 | 0.0051 | 0.0198 | 0.0129 | 0.0396 | 0.0309 |
| p | 3 | 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 30 | 30 | 50 | 50 | 100 | 100 | 30 | 30 | 50 | 50 | 100 | 100 |
| 5 | 10 | 5 | 10 | 5 | 10 | 5 | 10 | 5 | 10 | 5 | 10 | |
| OLS | 0.1624 | 0.1031 | 0.1653 | 0.1027 | 0.1679 | 0.1085 | 0.0757 | 0.0582 | 0.0801 | 0.0651 | 0.0857 | 0.0667 |
| LTE | 0.4057 | 0.2237 | 0.4322 | 0.2307 | 0.4441 | 0.2467 | 0.0697 | 0.0513 | 0.0826 | 0.0636 | 0.0942 | 0.0696 |
| NBE2 | 0.3556 | 0.1856 | 0.3813 | 0.1934 | 0.3979 | 0.2078 | 0.0697 | 0.0513 | 0.0825 | 0.0635 | 0.0941 | 0.0696 |
| YC3 | 0.2851 | 0.1521 | 0.3111 | 0.1617 | 0.3276 | 0.1765 | 0.0713 | 0.0515 | 0.0845 | 0.0649 | 0.0964 | 0.0715 |
| DK | 0.3059 | 0.1717 | 0.3239 | 0.177 | 0.3346 | 0.1853 | 0.0753 | 0.0573 | 0.0813 | 0.0652 | 0.0884 | 0.0675 |
| MRT | 0.3401 | 0.18 | 0.3728 | 0.1923 | 0.3912 | 0.207 | 0.0685 | 0.0502 | 0.0828 | 0.0631 | 0.0954 | 0.0701 |
| LKL | 0.3881 | 0.2199 | 0.4074 | 0.2403 | 0.4179 | 0.2623 | 0.0239 | 0.0123 | 0.0359 | 0.0221 | 0.0593 | 0.0423 |
| p | 3 | 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 30 | 30 | 50 | 50 | 100 | 100 | 30 | 30 | 50 | 50 | 100 | 100 |
| 5 | 10 | 5 | 10 | 5 | 10 | 5 | 10 | 5 | 10 | 5 | 10 | |
| OLS | 0.1641 | 0.1033 | 0.1641 | 0.1073 | 0.1694 | 0.111 | 0.0768 | 0.0591 | 0.0786 | 0.0648 | 0.0874 | 0.0678 |
| LTE | 0.4299 | 0.26 | 0.4615 | 0.2711 | 0.4855 | 0.2815 | 0.0677 | 0.0508 | 0.078 | 0.062 | 0.0914 | 0.0687 |
| NBE2 | 0.4401 | 0.2632 | 0.4727 | 0.2777 | 0.4977 | 0.2908 | 0.0679 | 0.0509 | 0.0781 | 0.062 | 0.0915 | 0.0688 |
| YC3 | 0.2395 | 0.1759 | 0.2747 | 0.1895 | 0.3101 | 0.2069 | 0.0638 | 0.0492 | 0.0748 | 0.0605 | 0.0893 | 0.0675 |
| DK | 0.3227 | 0.1993 | 0.3306 | 0.2066 | 0.3448 | 0.2119 | 0.0758 | 0.0574 | 0.0793 | 0.0645 | 0.089 | 0.0685 |
| MRT | 0.4959 | 0.2993 | 0.5279 | 0.3241 | 0.5508 | 0.3473 | 0.0663 | 0.0492 | 0.078 | 0.0614 | 0.0923 | 0.0689 |
| LKL | 0.6239 | 0.4448 | 0.6508 | 0.4957 | 0.6647 | 0.5095 | 0.0881 | 0.0786 | 0.1304 | 0.1218 | 0.1666 | 0.1476 |
| p | 3 | 3 | 5 | 5 | 10 | 10 |
|---|---|---|---|---|---|---|
| n | 200 | 300 | 200 | 300 | 200 | 300 |
| OLS | 0.8159 | 0.8216 | 0.6038 | 0.6017 | 0.3497 | 0.3483 |
| LTE | 0.9834 | 0.9858 | 0.8561 | 0.8598 | 0.4714 | 0.4721 |
| NBE2 | 0.9747 | 0.9777 | 0.8342 | 0.8381 | 0.4634 | 0.4635 |
| YC3 | 0.9613 | 0.9639 | 0.8112 | 0.815 | 0.4593 | 0.4593 |
| DK | 0.9098 | 0.9128 | 0.7014 | 0.7033 | 0.3804 | 0.3785 |
| MRT | 0.953 | 0.9571 | 0.8074 | 0.8088 | 0.4677 | 0.4672 |
| LKL | 0.7362 | 0.7398 | 0.4124 | 0.4176 | 0.1365 | 0.1474 |
| p | 3 | 3 | 5 | 5 | 10 | 10 |
|---|---|---|---|---|---|---|
| n | 200 | 300 | 200 | 300 | 200 | 300 |
| OLS | 0.8149 | 0.8198 | 0.6 | 0.6047 | 0.3473 | 0.3536 |
| LTE | 0.9846 | 0.9849 | 0.8512 | 0.853 | 0.4487 | 0.4555 |
| NBE2 | 0.9793 | 0.9811 | 0.841 | 0.8418 | 0.4464 | 0.4534 |
| YC3 | 0.9595 | 0.9643 | 0.8024 | 0.8056 | 0.4314 | 0.4394 |
| DK | 0.9187 | 0.9211 | 0.7067 | 0.7104 | 0.3735 | 0.3804 |
| MRT | 0.9637 | 0.9665 | 0.823 | 0.8224 | 0.4553 | 0.4632 |
| LKL | 0.8003 | 0.8035 | 0.5242 | 0.5306 | 0.2021 | 0.217 |
| p | 3 | 3 | 5 | 5 | 10 | 10 |
|---|---|---|---|---|---|---|
| n | 200 | 300 | 200 | 300 | 200 | 300 |
| OLS | 0.8171 | 0.8206 | 0.5988 | 0.6115 | 0.3492 | 0.3481 |
| LTE | 0.985 | 0.9841 | 0.8301 | 0.8389 | 0.4155 | 0.4171 |
| NBE2 | 0.9831 | 0.9826 | 0.8292 | 0.8374 | 0.4165 | 0.4184 |
| YC3 | 0.9459 | 0.9523 | 0.7561 | 0.7717 | 0.3968 | 0.399 |
| DK | 0.9303 | 0.9342 | 0.7003 | 0.7109 | 0.3671 | 0.3658 |
| MRT | 0.9737 | 0.9732 | 0.8259 | 0.8311 | 0.4272 | 0.4296 |
| LKL | 0.9309 | 0.9335 | 0.8142 | 0.8225 | 0.543 | 0.5516 |
| p | 3 | 5 | ||||||
|---|---|---|---|---|---|---|---|---|
| n | 10 | 20 | 30 | 10 | 20 | 30 | 20 | 30 |
| OLS | 0.3622 | 0.5199 | 0.5609 | 0.1728 | 0.3304 | 0.3604 | 0.162 | 0.1996 |
| LTE | 0.6885 | 0.8826 | 0.9102 | 0.2004 | 0.5611 | 0.6191 | 0.1533 | 0.234 |
| NBE2 | 0.5577 | 0.8272 | 0.8675 | 0.1701 | 0.51 | 0.5755 | 0.1505 | 0.2294 |
| YC3 | 0.4016 | 0.7678 | 0.8267 | 0.1243 | 0.474 | 0.5439 | 0.1512 | 0.23 |
| DK | 0.4393 | 0.6917 | 0.7372 | 0.1765 | 0.3878 | 0.4366 | 0.163 | 0.2099 |
| MRT | 0.4929 | 0.7641 | 0.8121 | 0.1643 | 0.4761 | 0.5446 | 0.1481 | 0.231 |
| LKL | 0.4569 | 0.5987 | 0.6219 | 0.0684 | 0.2597 | 0.2816 | 0.0264 | 0.0381 |
| p | 3 | 5 | ||||||
|---|---|---|---|---|---|---|---|---|
| n | 10 | 20 | 30 | 10 | 20 | 30 | 20 | 30 |
| OLS | 0.2728 | 0.3514 | 0.3606 | 0.1376 | 0.2226 | 0.2334 | 0.1162 | 0.1313 |
| LTE | 0.5647 | 0.7293 | 0.7594 | 0.1525 | 0.3513 | 0.3904 | 0.0972 | 0.1363 |
| NBE2 | 0.4835 | 0.6897 | 0.7243 | 0.1362 | 0.3328 | 0.3706 | 0.0969 | 0.1358 |
| YC3 | 0.2512 | 0.5703 | 0.6239 | 0.0836 | 0.2834 | 0.3272 | 0.0928 | 0.1322 |
| DK | 0.3893 | 0.5654 | 0.6026 | 0.1408 | 0.2581 | 0.2771 | 0.1144 | 0.1345 |
| MRT | 0.4157 | 0.6503 | 0.6871 | 0.1273 | 0.322 | 0.3659 | 0.0938 | 0.1363 |
| LKL | 0.4692 | 0.5931 | 0.6047 | 0.0615 | 0.2816 | 0.3039 | 0.0293 | 0.0504 |
| Variable | VIF |
|---|---|
| PREC | 4.113888 |
| JANT | 6.143551 |
| JULT | 3.967774 |
| OVR65 | 7.470045 |
| POPN | 4.307618 |
| EDUC | 4.860538 |
| HOUS | 3.994781 |
| DENS | 1.658281 |
| NONW | 6.779599 |
| WWDRK | 2.841582 |
| POOR | 8.717068 |
| HC | 98.639935 |
| NOX | 104.982405 |
| SOx | 4.228929 |
| HUMID | 1.907092 |
| OLS | LTE | NBE2 | |||||||
| Coef | SE | p-value | Coef | SE | p-value | Coef | SE | p-value | |
| PREC | 1.175 | 1.06 | 0.274 | 1.036 | 1.373 | 0.455 | 1.209 | 1.078 | 0.268 |
| JANT | −1.516 | 1.291 | 0.247 | −1.328 | 1.672 | 0.431 | −1.789 | 1.251 | 0.16 |
| JULT | 1.319 | 1.819 | 0.472 | 1.164 | 2.356 | 0.624 | 1.6 | 1.79 | 0.376 |
| OVR65 | 11.184 | 8.008 | 0.17 | 9.822 | 10.369 | 0.349 | 10.381 | 8.225 | 0.214 |
| POPN | 128.036 | 45.007 | 0.007 | 112.444 | 58.28 | 0.06 | 113.282 | 39.854 | 0.007 |
| EDUC | −1.463 | 13.112 | 0.912 | −1.284 | 16.979 | 0.94 | −2.157 | 14.285 | 0.881 |
| HOUS | 1.221 | 1.996 | 0.544 | 1.078 | 2.585 | 0.679 | 1.591 | 1.985 | 0.427 |
| DENS | 0.007 | 0.005 | 0.108 | 0.032 | 0.006 | 0.001 | 0.007 | 0.005 | 0.122 |
| NONW | 4.13 | 1.55 | 0.011 | 3.628 | 2.008 | 0.078 | 4.089 | 1.593 | 0.014 |
| WWDRK | 0.447 | 1.936 | 0.818 | 0.397 | 2.507 | 0.875 | 0.463 | 2.03 | 0.821 |
| POOR | 1.886 | 3.73 | 0.616 | 1.658 | 4.83 | 0.733 | 2.445 | 3.711 | 0.513 |
| HC | −0.373 | 0.568 | 0.514 | −0.328 | 0.736 | 0.658 | −0.382 | 0.573 | 0.509 |
| NOX | 0.874 | 1.169 | 0.458 | 0.768 | 1.514 | 0.614 | 0.907 | 1.182 | 0.447 |
| SOx | 0.16 | 0.171 | 0.357 | 0.14 | 0.222 | 0.532 | 0.154 | 0.174 | 0.381 |
| HUMID | 1.915 | 1.264 | 0.137 | 1.687 | 1.637 | 0.308 | 2.127 | 1.242 | 0.094 |
| YC3 | DK | MRT | |||||||
| Coef | SE | p-value | Coef | SE | p-value | Coef | SE | p-value | |
| PREC | 2.05 | 0.799 | 0.014 | 1.222 | 1.058 | 0.254 | 1.461 | 1.065 | 0.177 |
| JANT | −3.199 | 0.788 | 0.001 | −1.769 | 1.237 | 0.16 | −2.996 | 1.06 | 0.007 |
| JULT | 4.357 | 1.098 | 0.001 | 1.589 | 1.777 | 0.376 | 2.908 | 1.671 | 0.089 |
| OVR65 | 1.449 | 1.191 | 0.23 | 10.353 | 7.898 | 0.197 | 6.262 | 7.474 | 0.407 |
| POPN | 0.65 | 0.151 | 0.001 | 113.923 | 40.077 | 0.007 | 45.208 | 16.413 | 0.009 |
| EDUC | 0.155 | 0.727 | 0.832 | −1.714 | 12.99 | 0.896 | −2.595 | 11.723 | 0.826 |
| HOUS | 3.165 | 1.082 | 0.005 | 1.538 | 1.938 | 0.432 | 3.054 | 1.747 | 0.087 |
| DENS | 0.007 | 0.005 | 0.128 | 0.007 | 0.005 | 0.114 | 0.007 | 0.005 | 0.153 |
| NONW | 3.193 | 0.883 | 0.001 | 4.076 | 1.546 | 0.012 | 3.807 | 1.543 | 0.018 |
| WWDRK | 0.166 | 1.195 | 0.89 | 0.427 | 1.928 | 0.826 | 0.298 | 1.871 | 0.874 |
| POOR | 4.294 | 1.563 | 0.009 | 2.401 | 3.652 | 0.514 | 4.899 | 3.443 | 0.162 |
| HC | −0.452 | 0.517 | 0.386 | −0.379 | 0.568 | 0.509 | −0.401 | 0.583 | 0.495 |
| NOX | 1.173 | 1.036 | 0.264 | 0.899 | 1.169 | 0.446 | 1.016 | 1.194 | 0.399 |
| SOx | 0.161 | 0.157 | 0.311 | 0.157 | 0.171 | 0.365 | 0.145 | 0.173 | 0.409 |
| HUMID | 3.835 | 0.928 | 0.001 | 2.115 | 1.23 | 0.093 | 3.084 | 1.138 | 0.01 |
| LKL | |||||||||
| Coef | SE | p-value | |||||||
| PREC | 1.639 | 1.117 | 0.149 | ||||||
| JANT | −3.947 | 1.07 | 0.001 | ||||||
| JULT | 3.924 | 1.731 | 0.028 | ||||||
| OVR65 | 3.134 | 7.676 | 0.685 | ||||||
| POPN | −7.781 | 3.22 | 0.02 | ||||||
| EDUC | −3.455 | 11.6 | 0.767 | ||||||
| HOUS | 4.24 | 1.779 | 0.022 | ||||||
| DENS | 0.006 | 0.005 | 0.206 | ||||||
| NONW | 3.606 | 1.609 | 0.03 | ||||||
| WWDRK | 0.215 | 1.924 | 0.912 | ||||||
| POOR | 6.833 | 3.559 | 0.061 | ||||||
| HC | −0.42 | 0.615 | 0.499 | ||||||
| NOX | 1.108 | 1.257 | 0.383 | ||||||
| SOx | 0.134 | 0.182 | 0.464 | ||||||
| HUMID | 3.832 | 1.173 | 0.002 |
| Variable | VIF |
|---|---|
| x1—weight (kg) | 89.942300 |
| x2—height (cm) | 19.724450 |
| x3—waist circumference (cm) | 8.249625 |
| x4—arm circumference (cm) | 5.793885 |
| x5—BMI | 77.377840 |
| OLS | LTE | NBE2 | |||||||
| Coef | SE | p-value | Coef | SE | p-value | Coef | SE | p-value | |
| x1 | −0.6869 | 0.1024 | 0.001 | −0.6595 | 0.0984 | 0.001 | −0.6839 | 0.1018 | 0.001 |
| x2 | 0.5866 | 0.0552 | 0.001 | 0.5741 | 0.0531 | 0.001 | 0.5771 | 0.0535 | 0.001 |
| x3 | −0.4446 | 0.1443 | 0.0023 | −0.4231 | 0.1384 | 0.0024 | −0.4233 | 0.1416 | 0.003 |
| x4 | −0.7695 | 0.4189 | 0.0672 | −0.7353 | 0.4012 | 0.0678 | −0.7069 | 0.4041 | 0.0813 |
| x5 | 2.791 | 0.4491 | 0.001 | 2.6719 | 0.4301 | 0.001 | 2.693 | 0.4317 | 0.001 |
| YC3 | DK | MRT | |||||||
| Coef | SE | p-value | Coef | SE | p-value | Coef | SE | p-value | |
| x1 | −0.6218 | 0.0937 | 0.001 | −0.6844 | 0.1019 | 0.001 | −0.6773 | 0.1008 | 0.001 |
| x2 | 0.4717 | 0.0366 | 0.001 | 0.5777 | 0.0536 | 0.001 | 0.556 | 0.0498 | 0.001 |
| x3 | −0.1627 | 0.1109 | 0.1436 | −0.4248 | 0.1418 | 0.003 | −0.3758 | 0.1357 | 0.006 |
| x4 | −0.0778 | 0.2349 | 0.7408 | −0.7096 | 0.4051 | 0.0809 | −0.5674 | 0.3716 | 0.1278 |
| x5 | 1.5139 | 0.2348 | 0.001 | 2.6998 | 0.4328 | 0.001 | 2.4746 | 0.3931 | 0.001 |
| LKL | |||||||||
| Coef | SE | p-value | |||||||
| x1 | −0.6866 | 0.1023 | 0.001 | ||||||
| x2 | 0.5854 | 0.055 | 0.001 | ||||||
| x3 | −0.4418 | 0.1439 | 0.0023 | ||||||
| x4 | −0.7608 | 0.417 | 0.0691 | ||||||
| x5 | 2.778 | 0.4468 | 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoque, M.A.; Bursac, Z.; Kibria, B.M.G. Inferences About Two-Parameter Multicollinear Gaussian Linear Regression Models: An Empirical Type I Error and Power Comparison. Stats 2025, 8, 28. https://doi.org/10.3390/stats8020028
Hoque MA, Bursac Z, Kibria BMG. Inferences About Two-Parameter Multicollinear Gaussian Linear Regression Models: An Empirical Type I Error and Power Comparison. Stats. 2025; 8(2):28. https://doi.org/10.3390/stats8020028
Chicago/Turabian StyleHoque, Md Ariful, Zoran Bursac, and B. M. Golam Kibria. 2025. "Inferences About Two-Parameter Multicollinear Gaussian Linear Regression Models: An Empirical Type I Error and Power Comparison" Stats 8, no. 2: 28. https://doi.org/10.3390/stats8020028
APA StyleHoque, M. A., Bursac, Z., & Kibria, B. M. G. (2025). Inferences About Two-Parameter Multicollinear Gaussian Linear Regression Models: An Empirical Type I Error and Power Comparison. Stats, 8(2), 28. https://doi.org/10.3390/stats8020028








