The Gamma-G Family: Brief Survey and COVID-19 Application

Abstract

In recent years, the gamma-G family has gained significant popularity for generating new distributions by incorporating an additional shape parameter into the baseline model. This article compiles and documents the existing gamma-G distributions and demonstrates their application to real COVID-19 data.

1. Introduction

Classical distributions are widely used across various fields, but their extended forms are often necessary for more flexible modeling of real-world data. The literature has witnessed a surge in generalized distributions by incorporating additional parameters in baseline ones. Notable generators include Marshall–Olkin-G  [1], Beta-G [2], and gamma odd Burr X-G  [3]. This has resulted in numerous new distributions, some of which, like the exponentiated Weibull [4], beta flexible Weibull [5], and Kumaraswamy generalized Lomax [6], are now well-established.

The gamma-G family [7,8] has been extensively studied by investigating its mathematical properties for any baseline distribution [9,10]. This work compiles existing distributions in this family, citing their names and authors (see references for details), aiming to inspire further research into unexplored gamma-G distributions.

The gamma-G family of distributions occupies a significant place in the statistical literature due to its flexibility in modeling diverse datasets. The emergence of more than forty distributions highlights its importance. In addition, their densities can be expressed as linear combinations of exponentiated-G densities, making their main properties easy to obtain [9,10,11,12]. Thus, this combination of flexibility and analytical ease makes the gamma-G family an important tool for theoretical and applied statistical research.

The article proceeds as follows. Section 2 gives an overview of the gamma-G family. Section 3 examines its dual family and addresses related works. Section 4 presents simulations based on the two families. Section 5 applies both families to the COVID-19 data. Finally, Section 6 concludes the paper.

2. The Gamma-G Family

Ref. [7] defined the gamma-G (“ZB-G”) generator, whose probability density function (PDF) and cumulative distribution function (CDF) are

$$f\left(x\right)={\displaystyle \frac{g\left(x\right)}{\mathrm{\Gamma }\left(a\right)}}{\{-log[1-G\left(x\right)]\}}^{a-1},$$

(1)

and

$$F\left(x\right)={\displaystyle \frac{\gamma (a,-log[1-G\left(x\right)\left]\right)}{\mathrm{\Gamma }\left(a\right)}},$$

(2)

respectively, where $G\left(x\right)$ is any baseline CDF, $g\left(x\right)=\mathrm{d}G\left(x\right)/\mathrm{d}x$, $x\in \mathrm{I}\mathrm{R}$, $\gamma (a,z)={\int }_0^z{t}^{a-1}{\mathrm{e}}^{-t}\mathrm{d}t$ is the lower incomplete gamma function, $\mathrm{\Gamma }(·)$ is the gamma function, and $a>0$ is a shape parameter. For $a=1$, Equation (1) reduces to the baseline density. The hazard rate function (HRF) is derived from Equations (1) and (2) as $h\left(x\right)=f\left(x\right)/[1-F(x\left)\right]$.

The ZB-modified Weibull (ZB-MW) [13], an example of the ZB-G family, uses the CDF $G\left(x\right)=1-exp\{-\alpha x^{\beta }exp\left(\lambda x\right)\}$, where $\alpha >0$ is a scale parameter and $\lambda$ and $\beta$ are shape parameters. Consequently, its PDF and HRF (for $x>0$) are

$$f\left(x\right)={\displaystyle \frac{1}{\mathrm{\Gamma }\left(a\right)}}\alpha x^{\beta -1}(\beta +\lambda x){\{\alpha x^{\beta }exp\left(\lambda x\right)\}}^{a-1}exp\{\lambda x-\alpha x^{\beta }exp\left(\lambda x\right)\},$$

and

$$h\left(x\right)={\displaystyle \frac{\alpha x^{\beta -1}(\beta +\lambda x){\{\alpha x^{\beta }exp\left(\lambda x\right)\}}^{a-1}exp\{\lambda x-\alpha x^{\beta }exp\left(\lambda x\right)\}}{\mathrm{\Gamma }\left(a\right)-\gamma [a,\alpha x^{\beta }exp\left(\lambda x\right)]}}.$$

The four-parameter ZB-MW model includes, as special cases, the gamma Weibull, gamma exponential, gamma modified exponential, gamma modified Rayleigh, exponential, Rayleigh, and Weibull distributions. Figure 1a displays potential density shapes, suitable for right-skewed data. Figure 1b reports the HRF with four shapes: increasing, decreasing, bathtub, and unimodal.

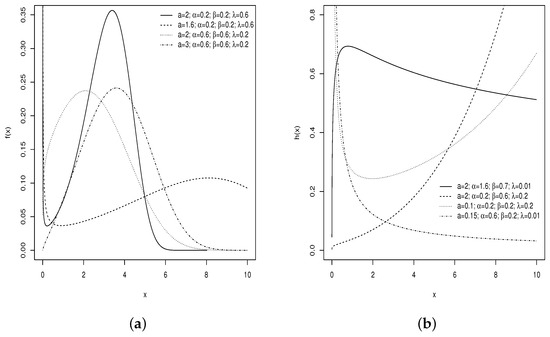
Figure 1. Plots of the PDF (a) and HRF (b) of the ZB-MW distribution.

3. The Dual Gamma Generalized Family

Similarly, ref. [8] introduced the Ristić–Balakrishnan-G (“RB-G”) family, with PDF defined as (for $x\in \mathrm{I}\mathrm{R}$)

$$f\left(x\right)={\displaystyle \frac{g\left(x\right)}{\mathrm{\Gamma }\left(a\right)}}{\{-log\left[G\left(x\right)\right]\}}^{a-1}.$$

The RB-Burr XII (RB-BXII) distribution [14] comes from the BXII CDF $G\left(x\right)=1-{[1+{(x/s)}^c]}^{-d}$, where $s>0$ is a scale and $d,c>0$ are shape parameters, whose PDF and HRF (for $x>0$) are

$$f\left(x\right)={\displaystyle \frac{cd{x}^{c-1}}{s^c\mathrm{\Gamma }\left(a\right)}}{\left[1+{\left({\displaystyle \frac{x}{s}}\right)}^c\right]}^{-(d+1)}{\left\{-log\left(1-{\left[1+{\left({\displaystyle \frac{x}{s}}\right)}^c\right]}^{-d}\right)\right\}}^{a-1},$$

and

$$h\left(x\right)={\displaystyle \frac{cd{x}^{c-1}{\left[1+{\left(\frac{x}{s}\right)}^c\right]}^{-(d+1)}}{s^c\gamma \left(a,-log\left\{1-{\left[1+{\left(\frac{x}{s}\right)}^c\right]}^{-d}\right\}\right)}}{\left\{-log\left(1-{\left[1+{\left({\displaystyle \frac{x}{s}}\right)}^c\right]}^{-d}\right)\right\}}^{a-1}.$$

Figure 2a,b depict the PDF and HRF of the RB-BXII model for some parameters, which show various forms. The ZB-G and RB-G families include the baseline parameters plus an extra shape parameter. Table 1 lists thirty-six members of these classes.

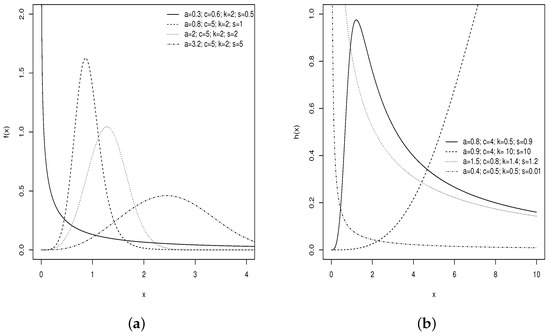
Figure 2. Plots of the PDF (a) and HRF (b) of the RB-BXII distribution.

Table 1. Distributions in the gamma-G family.

No.	Distribution	Author(s)
1.	Gamma exponentiated exponential	[8]
2.	Gamma exponentiated Weibull	[15]
3.	Gamma Pareto	[16]
4.	Gamma uniform	[17]
5.	Gamma extended Fréchet	[18]
6.	Gamma half normal	[19]
7.	ZB-LL	[20]
8.	Gamma linear failure rate	[21]
9.	Gamma Dagum	[22,23]
10.	Gamma normal	[24]
11.	Gamma generalized Weibull	[11]
12.	Gamma log-normal	[9]
13.	Gamma Weibull	[9,10]
14.	Gamma Gumbel	[9,10]
15.	ZB-MW	[13]
16.	Gamma half-Cauchy	[25]
17.	Gamma logistic	[10]
18.	Gamma exponentiated exponential Weibull	[26]
19.	Gamma Burr type X	[27]
20.	Gamma Maxwell	[28]
21.	Gamma log-logistic Weibull	[29]
22.	RB-BXII	[14]
23.	Gamma Burr III	[30]
24.	Gamma Slash	[31]
25.	Gamma extended exponential	[32]
26.	Gamma Lindley–Poisson	[33]
27.	Gamma Kumaraswamy	[34]
28.	Gamma Rayleigh	[35]
29.	Gamma power half-logistic	[36]
30.	Gamma log-logistic Erlang truncated exponential	[37]
31.	Gamma generalized Maxwell	[38]
32.	Gamma generalized Lindley log-logistic	[39]
33.	Gamma power Lindley	[40]
34.	Gamma Chen	[41]
35.	Gamma Lindley	[42]
36.	Gamma Gompertz	[43]

The properties of both families are derived from the exponentiated-G class, as detailed by [11] for ZB-G and [12] for RB-G. Thus, the main properties, such as moments and generating function, are derived from the exponentiated baseline distribution. The random number generation method is detailed in [9] in the form (for $0<u<1$)

$$\begin{array}{c}\hfill F^{-1}\left(u\right)=G^{-1}\left\{1-exp\left[-Q^{-1}\left(a,1-u\right)\right]\right\}\end{array}$$

(3)

where $Q^{-1}(a,u)$ is the inverse function of $Q(a,x)=1-\gamma (a,x)/\mathrm{\Gamma }\left(a\right)$ and $G^{-1}(·)$ is the inverse CDF of any baseline distribution. The results in Section 4 are obtained in this way.

4. Simulation

A simulation study is conducted to assess the consistency of the estimates in the models exemplified for each family (ZB-MW and RB-BXII). Random samples of sizes $n=50$, 100, 200, and 500 are generated in three different scenarios. One thousand Monte Carlo replicates are performed, and the average estimates (AEs), biases, and mean squared errors (MSEs) are calculated. The log-likelihood functions for $\mathit{\theta }={(a,\alpha ,\beta ,\lambda )}^{\top }$ and $\mathbf{\zeta }={(a,c,d,s)}^{\top }$ are optimized using the Nelder–Mead numerical method within the Optim function of the R statistical software 4.4.1, with the actual values of the parameters as initial inputs.

In order to detail the process of the results obtained in Table 2 and Table 3, the case of the ZB-MW distribution follows, and the RB-BXII case is similar. So, the quantile function (qf) of the ZB-MW follows from (3) as (for $0<u<1$)

$$\begin{array}{c}\hfill Q_{\left(u\right)}={\displaystyle \frac{\beta }{\lambda }}W\left({\displaystyle \frac{\lambda {\left\{{\alpha }^{-1}{Q}^{-1}(a,1-u)\right\}}^{1/\beta }}{\beta }}\right),\end{array}$$

where the function $W(·)$ is the log product function. The R script below generates random variates from the ZB-MW model.

Table 2. Simulations from the ZB-MW distribution.

		(0.9, 0.6, 1.2, 1.5)			(1.9, 0.4, 0.8, 2.5)			(2.0, 0.2, 0.2, 0.6)
$\mathit{n}$	$\mathit{\theta }$	AE	Bias	MSE	AE	Bias	MSE	AE	Bias	MSE
50	a	0.9728	0.0728	1.0307	2.0957	0.4197	3.8420	2.1033	0.1033	0.6619
	$\alpha$	1.0450	0.4450	2.0660	1.2353	0.8353	4.2478	0.2480	0.0480	0.0501
	$\beta$	2.3106	1.1106	12.8133	2.3474	1.5474	14.7544	0.4817	0.2817	0.3140
	$\lambda$	1.4252	−0.0747	1.5578	2.2546	−0.2453	2.1023	0.5540	−0.0459	0.0449
100	a	0.9304	0.0304	0.5110	1.9530	0.0530	2.1756	2.0475	0.0475	0.5442
	$\alpha$	0.8391	0.2391	0.6581	0.8094	0.4094	1.1510	0.2387	0.0387	0.0427
	$\beta$	1.9481	0.7481	4.5213	1.7120	0.9120	4.4432	0.3222	0.1222	0.0972
	$\lambda$	1.4085	−0.0914	0.8180	2.3235	−0.1764	1.2409	0.5987	−0.0012	0.0230
200	a	0.8961	−0.0038	0.2995	1.8995	−0.0004	1.1542	1.9906	−0.0093	0.4053
	$\alpha$	0.6618	0.0618	0.1359	0.5345	0.1345	0.1900	0.2201	0.0201	0.0318
	$\beta$	1.6463	0.4463	1.3229	1.3082	0.5082	1.7515	0.2511	0.0511	0.0205
	$\lambda$	1.4269	−0.0730	0.2520	2.3528	−0.1471	0.4407	0.6161	0.0161	0.0106
500	a	0.8995	−0.0004	0.2667	1.9002	0.0002	1.0055	2.0173	0.0173	0.3730
	$\alpha$	0.6509	0.0509	0.0947	0.4973	0.0973	0.1134	0.2243	0.0243	0.0275
	$\beta$	1.5854	0.3854	1.0946	1.2290	0.4290	1.3054	0.2384	0.0384	0.0164
	$\lambda$	1.4175	−0.0824	0.1764	2.3720	−0.1279	0.2932	0.6113	0.0113	0.0083

Table 3. Simulations from the RB-BXII distribution.

		(0.9, 2.5, 0.1, 0.2)			(0.5, 7.0, 0.3, 0.4)			(1.5, 3.2, 0.8, 0.1)
$\mathit{n}$	$\mathbf{\zeta }$	AE	Bias	MSE	AE	Bias	MSE	AE	Bias	MSE
50	a	1.1745	0.2745	0.8229	0.5867	0.0867	0.3093	3.4171	1.9171	20.8649
	c	3.5301	1.0301	10.8446	9.0703	2.0703	36.0733	4.0026	0.8026	2.2241
	d	0.1284	0.0284	0.0147	0.3496	0.0496	0.0481	2.1072	1.3072	24.2399
	s	0.3119	0.1119	0.0991	0.4308	0.0308	0.1342	0.2113	0.1113	0.0939
100	a	1.0775	0.1775	0.4930	0.5820	0.0820	0.1547	2.5576	1.0576	8.4377
	c	3.1230	0.6230	4.5324	8.1806	1.1806	17.0091	3.6160	0.4160	0.9437
	d	0.1162	0.0162	0.0085	0.3147	0.0147	0.0240	1.1418	0.3418	3.5938
	s	0.2546	0.0546	0.0299	0.4122	0.0122	0.0025	0.1461	0.0461	0.0250
200	a	0.9556	0.0556	0.2081	0.5650	0.0650	0.0788	1.8870	0.3870	0.9241
	c	2.7397	0.2397	1.2328	7.3936	0.3936	2.4543	3.3788	0.1788	0.2119
	d	0.1127	0.0127	0.0040	0.3008	0.0008	0.0142	0.7529	−0.0470	0.1796
	s	0.2143	0.0143	0.0046	0.4055	0.0055	0.0007	0.1069	0.0069	0.0008
500	a	0.9265	0.0265	0.1413	0.5518	0.0518	0.0596	1.8267	0.3267	0.5674
	c	2.6120	0.1120	0.2713	7.2273	0.2273	1.2589	3.3451	0.1451	0.1435
	d	0.1133	0.0133	0.0034	0.3021	0.0021	0.0106	0.7453	-0.0546	0.1428
	s	0.2084	0.0084	0.0025	0.4045	0.0045	0.0005	0.1047	0.0047	0.0001

require(gsl)  # Load the gsl package

RZBMW <- function(n, \alpha, \beta, \lambda, a) {

u <- runif(n, 0, 1)  # Generate n random uniform values between 0 and 1

A1 <- qgamma(1 - u, a, 1)  # Compute the quantile of the gamma distribution

A2 <- (lambda / beta) ∗ ((A1 / alpha)^(1 / beta)) qf from MW distribution

Q1 <- (beta / lambda) ∗ lambert_W0(A2)  qf from ZB-MW distribution

return(Q1)  # Return the result Q1

Next, an R function is developed that performs Monte Carlo simulations, optimizing the log-likelihood function (by taking the log of the corresponding PDF) using the Nelder–Mead method and calculating the AEs, biases, and MSEs for the parameters. The full script for this section can be found at this link: https://github.com/alexaaf31/gamma_G-family-/blob/main/Gamma-G_simulations.R (accessed on 1 January 2025).

Table 2 shows that the ZB-MW estimators are consistent. As the sample size grows, the AEs converge to true values, and biases and MSEs decrease. Variations in biases and MSEs suggest that parameter choice influences accuracy.

As expected for the RB-G family, the RB-BXII distribution also provides consistent estimators. As the sample size increases, the AEs get closer to the true parameter values, and the biases and MSEs tend towards zero, as shown in Table 3.

5. Application

The dataset reflects the lifetime (in days) of 103 patients diagnosed with COVID-19. It was compiled by a collaborative team of researchers and doctors from Qatar University in Doha, Qatar, and Dhaka Medical College Hospital in Bangladesh. Data collection took place between 12 April and 31 August 2020, at Dhaka Medical College Hospital, with the approval of the hospital’s Ethics Committee. Lifetimes were measured from the date of admission to the hospital until the time of discharge or death of the patient.

The dataset, available at https://www.kaggle.com/tawsifurrahman/covid19-complete-blood-count-clinical-database (accessed on 1 September 2021), is as follows: 61, 77, 17, 72, 71, 9, 190, 69, 98, 7, 36, 128, 128, 157, 128, 36, 127, 5, 126, 34, 122, 121, 213, 152, 152, 39, 39, 1, 243, 91, 91, 60, 30, 60, 23, 1, 151, 31, 115, 61, 183, 122, 26, 30, 46, 108, 136, 136, 8, 23, 23, 112, 6, 6, 13, 83, 13, 7, 53, 23, 12, 6, 36, 65, 95, 42, 16, 13, 14, 131, 41, 48, 137, 75, 9, 14, 14, 8, 14, 14, 7, 7, 7, 21, 14, 9, 14, 14, 18, 67, 14, 14, 14, 14, 14, 19, 13, 20, 13, 45, 14, 14, 14.

Table 4 provides statistical measures for the data, which have positive skewness and kurtosis. The mean is higher than the median and close to the standard deviation (SD), while the amplitude and variance are comparatively high.

Table 4. Descriptive statistics.

Mean	Median	SD	Variance	Skewness	Kurtosis	Min.	Max.
55.660	31.000	54.838	3007.3	1.180	3.612	1	243

The BXII, MW, and log-logistic (LL) distributions serve as baselines in the ZB-G and RB-G families for comparative analysis. The best models are selected from the Cramér–von Mises ($W^{*}$), Anderson–Darling $\left(A^{*}\right)$, Akaike information criterion (AIC), consistent AIC (CAIC), Bayesian IC (BIC), and Hannan–Quinn IC (HQIC). Lower values indicate a better fit. Maximum likelihood estimates (MLEs) and goodness-of-fit statistics are calculated using the AdequacyModel script in R.

Table 5 shows the MLEs and their standard errors (SEs) in parentheses. Notably, the ZB-MW, RB-MW, MW, RB-LL, and BXII distributions exhibit higher SE values. In contrast, the ZB-BXII, RB-BXII, RB-LL, and LL distributions provide accurate estimates.

Table 5. MLEs and their SEs for some fitted models to COVID-19 data.

Model	MLEs (SEs)
ZB-BXII $(a,c,k,s)$	$16.232$	$0.279$	$30.869$	$131.794$
	($0.819$)	($0.022$)	($1.028$)	($1.195$)
RB-BXII $(a,c,k,s)$	$0.106$	$0.985$	$63.364$	$315.082$
	($0.010$)	($0.002$)	($0.014$)	($0.014$)
ZB-MW $(a,\alpha ,\beta ,\lambda )$	$1.043$	$0.019$	$0.001$	$0.963$
	($0.796$)	($0.030$)	($0.002$)	($0.176$)
RB-MW $(a,\alpha ,\beta ,\lambda )$	$1.286$	$0.052$	$0.001$	$0.794$
	($0.527$)	($0.069$)	($0.001$)	($0.231$)
ZB-LL $(a,c,s)$	$1.082$	$28.404$	$1.432$
	($0.499$)	($20.651$)	($0.172$)
RB-LL $(a,c,s)$	$9.169$	$1115.857$	$2.573$
	($1.228$)	($16.287$)	($0.354$)
BXII $(c,k,s)$	$1.074$	$6.037$	$262.562$
	($0.107$)	($5.965$)	($300.345$)
MW $(\alpha ,\beta ,\lambda )$	$0.021$	$0.001$	$0.955$
	($0.008$)	($0.002$)	($0.117$)
LL $(c,s)$	$1.456$	$32.076$
	($0.116$)	($3.868$)

Table 6 shows the RB-LL distribution with the lowest AIC, CAIC, BIC, and HQIC values, whereas the ZB-BXII distribution has the lowest $W^{*}$ and $A^{*}$ statistics. As these models are not nested, the generalized likelihood ratio (LR) test [44] can be applied from

$$T_{LR,NN}={\displaystyle \frac{\left\{\frac{1}{\sqrt{n}}{\sum }_{i=1}^{n}log\frac{f\left(y_i\right|{\mathit{x}}_i,\widehat{\mathit{\theta }})}{g\left(y_i\right|{\mathit{x}}_i,\widehat{\mathit{\gamma }})}\right\}}{\left\{\frac{1}{n}{\sum }_{i=1}^n{\left(log\frac{f\left(y_i\right|{\mathit{x}}_i,\widehat{\mathit{\theta }})}{g\left(y_i\right|{\mathit{x}}_i,\widehat{\mathit{\gamma }})}\right)}^2-{\left(\frac{1}{n}{\sum }_{i=1}^{n}log\frac{f\left(y_i\right|{\mathit{x}}_i,\widehat{\mathit{\theta }})}{g\left(y_i\right|{\mathit{x}}_i,\widehat{\mathit{\gamma }})}\right)}^2\right\}}}.$$

(4)

Table 6. Goodness-of-fit statistics for the fitted models to COVID-19 data.

Model	${\mathit{W}}^{*}$	${\mathit{A}}^{*}$	AIC	CAIC	BIC	HQIC
ZB-BXII	0.260	1.663	$1041.918$	$1042.326$	$1052.457$	$1046.187$
RB-BXII	$0.326$	$1.945$	$1039.501$	$1039.909$	$1050.040$	$1043.770$
ZB-MW	$0.373$	$2.168$	$1040.769$	$1041.177$	$1051.308$	$1045.038$
RB-MW	$0.387$	$2.247$	$1041.798$	$1042.206$	$1052.337$	$1046.067$
ZB-LL	$0.327$	$2.029$	$1045.631$	$1045.874$	$1053.536$	$1048.833$
RB-LL	$0.313$	$1.858$	1036.393	1036.635	1044.297	1039.594
BXII	$0.368$	$2.177$	$1040.784$	$1041.026$	$1048.688$	$1043.985$
MW	$0.386$	$2.245$	$1039.813$	$1040.055$	$1047.717$	$1043.014$
LL	$0.334$	$2.065$	$1043.644$	$1043.764$	$1048.913$	$1045.778$

Equation (4) converges to a standard normal distribution under the null hypothesis of model equivalence, which is not rejected if $|T_{LR,NN}|\le z_{\alpha /2}$. At significance level $\alpha$, the null hypothesis is rejected in favor of $F_{\theta }$ over $G_{\gamma }$ if $T_{LR,NN}>z_{\alpha }$ (or $T_{LR,NN}<-z_{\alpha }$). For the ZB-GBXII ($f\left(y_i\right|{\mathit{x}}_i,\mathit{\theta })$) and RB-GLL ($g\left(y_i\right|{\mathit{x}}_i,\mathit{\gamma })$) models, the test statistic is $T_{LR,NN}=-6.3725$. Since $T_{LR,NN}<-1.96$, the null hypothesis is rejected at the level of 0.05 in favor of the RB-GLL distribution.

Figure 3a displays estimated densities, and Figure 3b shows estimated and empirical cumulative functions for the top models. The ZB-BXII, RB-BXII, RB-LL, and LL distributions fit well, but the RB-LL distribution fits the data best. Thus, $\widehat{f}\left(x\right)$ from the RB-LL distribution, obtained by substituting the MLEs of the parameters into its PDF, can accurately estimate various quantities of interest. For example, consider X as a random variable representing the lifetime of individuals with COVID-19. The probability of X falling within an arbitrary interval $[a,b]$ can be estimated by ${\int }_a^b\widehat{f}\left(x\right)\mathrm{d}x$, while the probability of X being less than a certain value c is given by ${\int }_0^c\widehat{f}\left(x\right)\mathrm{d}x$. Furthermore, the mean can be estimated by ${\int }_0^{\infty }x\widehat{f}\left(x\right)\mathrm{d}x$, and so on.

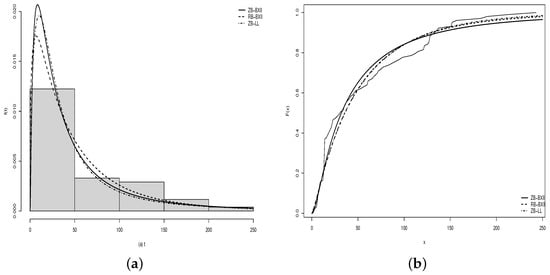
Figure 3. (a) Estimated densities of the ZB-BXII, RB-BXII, and RB-LL; (b) estimated and empirical cumulative functions of these models.

All previous results are obtained using the AdequacyModel package in R with the Broyden–Fletcher–Goldfarb–Shanno (BFGS) numerical method. The R script is available at https://github.com/alexaaf31/gamma_G-family-/blob/main/Gamma-G%20Application.R (accessed on 1 January 2025).

6. Conclusions

This article briefly surveyed the gamma-G families pioneered by [7,8]. It provided some of their main functions, a few special cases, and an application for COVID-19 data. A list of published articles on the gamma-G family was also presented. It was noted that many distributions remain to be generated compared to other families, such as Beta-G [2] and Marshall–Olkin-G [1].