STATom@ic: R Package for Automated Statistical Analysis of Omic Datasets
Abstract
1. Introduction
2. Materials and Methods
2.1. STATom@ic R Package Development
2.2. Confusion Matrix Precision–Recall Analysis Between DeSeq2 (Wald Test) and STATom@ic
3. Results
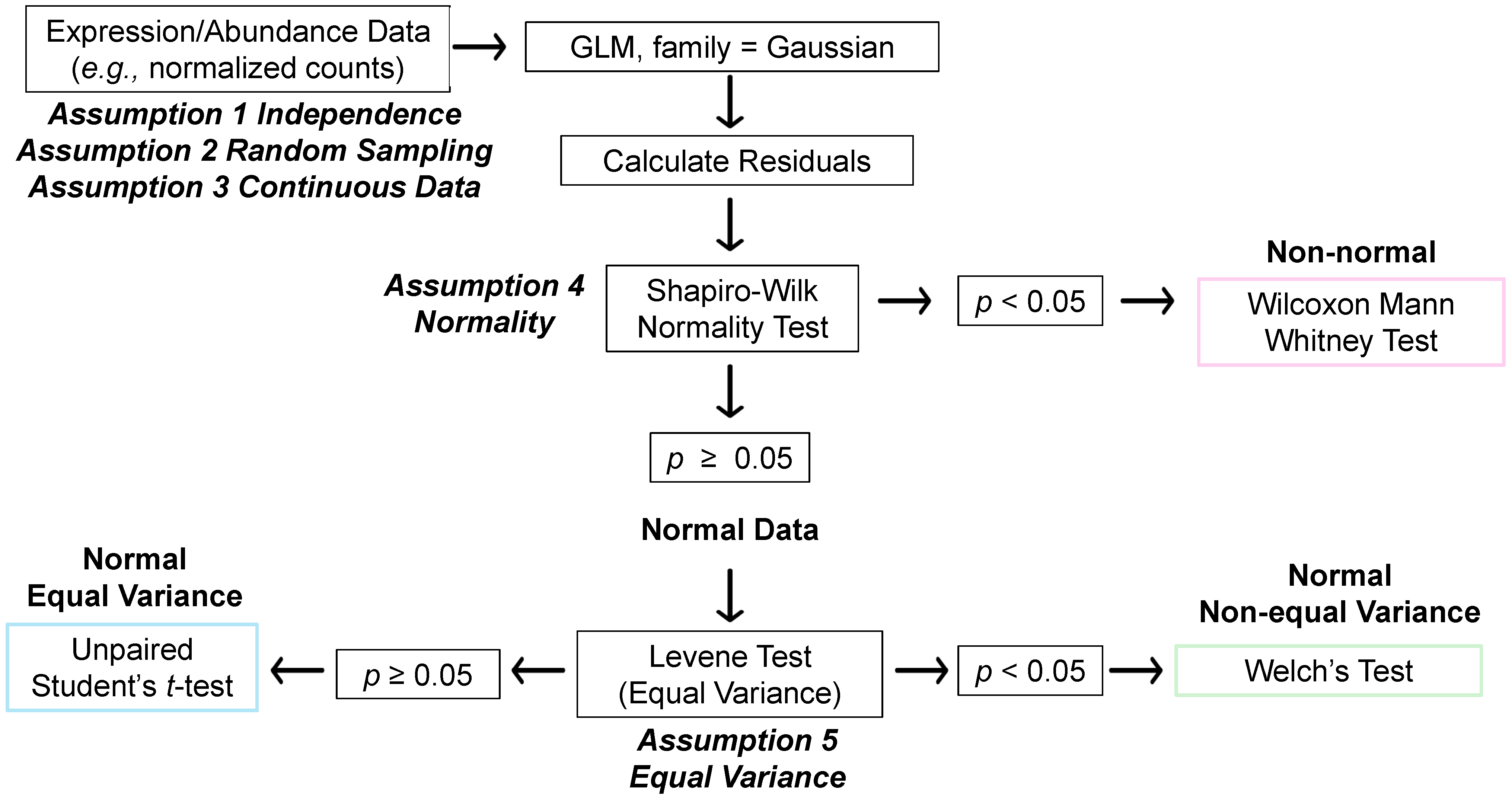
3.1. STATom@ic: Two-Group Statistical Comparisons
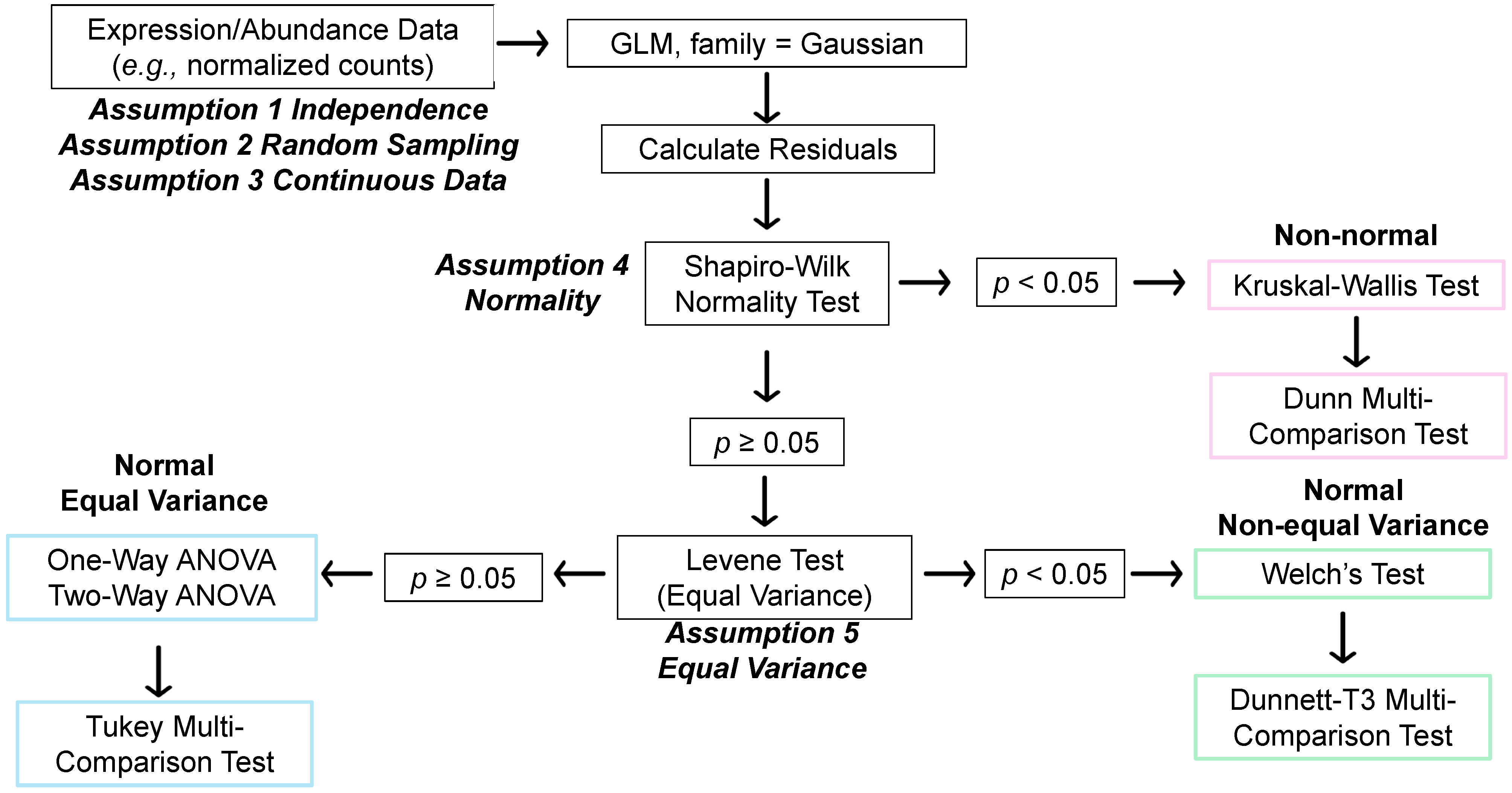
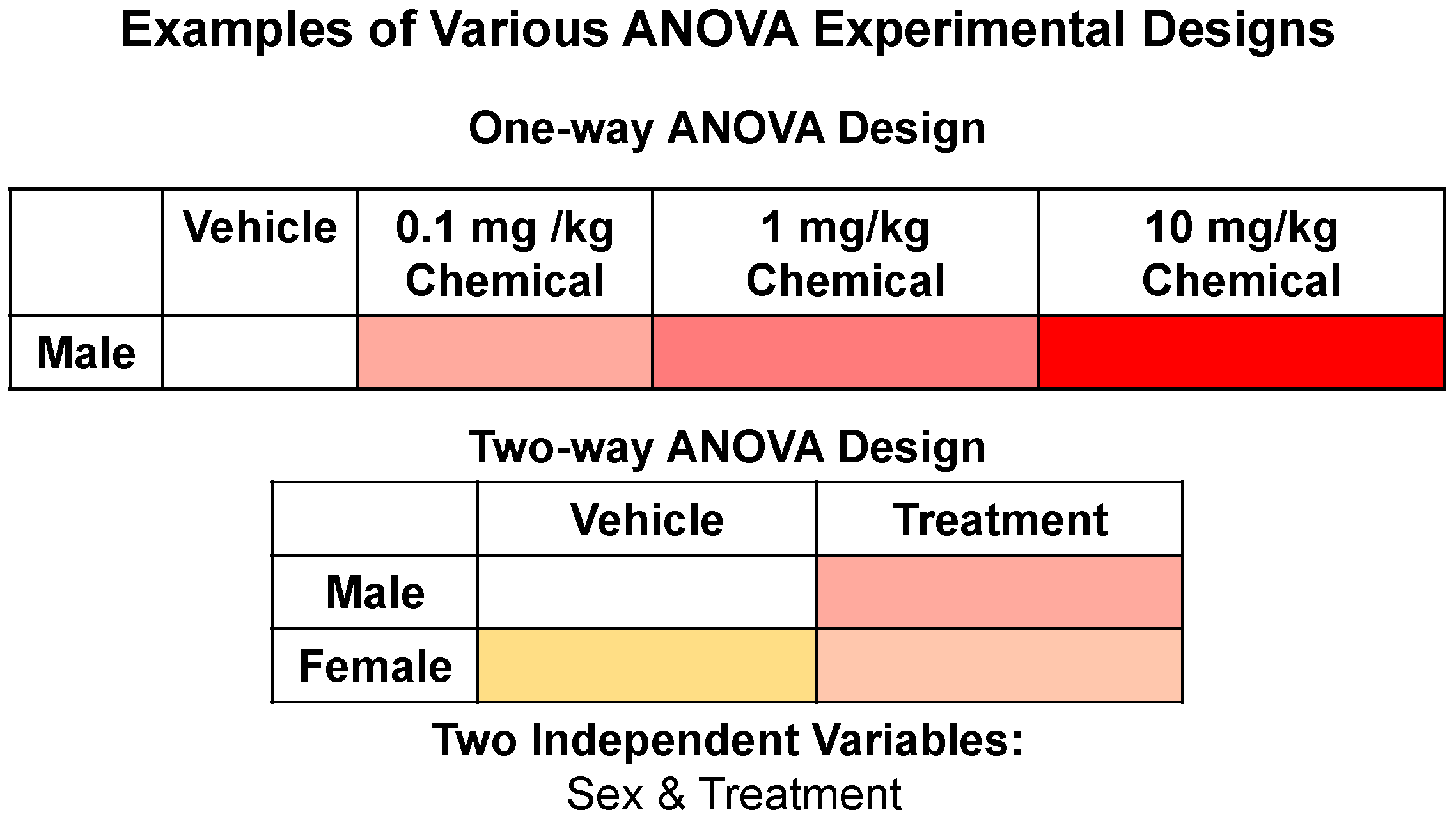
3.2. STATom@ic Multi-Group Statistical Comparisons
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, C.; Wang, J.; Pan, D.; Wang, X.; Xu, Y.; Yan, J.; Wang, L.; Yang, X.; Yang, M.; Liu, G.P. Applications of multi-omics analysis in human diseases. MedComm 2023, 4, e315. [Google Scholar] [CrossRef]
- Ott, A.W.; Sol-Church, K.; Deshpande, G.M.; Knudtson, K.L.; Meyn, S.M.; Mische, S.M.; Taatjes, D.J.; Sturges, M.R.; Gregory, C.W. Rigor, Reproducibility, and Transparency in Shared Research Resources: Follow-Up Survey and Recommendations for Improvements. J. Biomol. Tech. 2022, 33, 3fc1f5fe.fa789303. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.J.; Drew, J.C.; Galindo-Gonzalez, S.; Robic, S.; Dinsdale, E.; Morgan, W.R.; Triplett, E.W.; Burnette, J.M., 3rd; Donovan, S.S.; Fowlks, E.R.; et al. Barriers to integration of bioinformatics into undergraduate life sciences education: A national study of US life sciences faculty uncover significant barriers to integrating bioinformatics into undergraduate instruction. PLoS ONE 2019, 14, e0224288. [Google Scholar] [CrossRef]
- Aron, S.; Jongeneel, C.V.; Chauke, P.A.; Chaouch, M.; Kumuthini, J.; Zass, L.; Radouani, F.; Kassim, S.K.; Fadlelmola, F.M.; Mulder, N. Ten simple rules for developing bioinformatics capacity at an academic institution. PLoS Comput. Biol. 2021, 17, e1009592. [Google Scholar] [CrossRef]
- R Core Team. A Language and Environment for Statistical Computing; Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- John Fox, S.W. An {R} Companion to Applied Regression; Sage Publications: New York, NY, USA, 2019. [Google Scholar]
- Dag, O.; Dolgun, A.; Konar, N.M. Onewaytests: An R Package for One-Way Tests in Independent Groups Designs. R J. 2018, 10, 175–199. [Google Scholar] [CrossRef]
- Dinno, A. Dunn.test: Dunn’s Test of Multiple Comparisons Using Rank Sums. CRAN, 2024. Available online: https://cran.r-project.org/web/packages/dunn.test/dunn.test.pdf (accessed on 1 January 2025).
- Pohlert, T. PMCMRplus: Calculate Pairwise Multiple Comparisons of Mean Rank Sums Extended_. R Package version 1.9.12. CRAN, 2024. Available online: https://cran.r-project.org/web/packages/PMCMRplus/PMCMRplus.pdf (accessed on 1 January 2025).
- Nelder, J.A.; Wedderburn, R.W.M. Generalized Linear Models. J. R. Stat. Soc. Ser. A Stat. Soc. 1972, 135, 370–384. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Mishra, P.; Pandey, C.M.; Singh, U.; Gupta, A.; Sahu, C.; Keshri, A. Descriptive statistics and normality tests for statistical data. Ann. Card. Anaesth. 2019, 22, 67–72. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Kühnast, C.; Neuhäuser, M. A note on the use of the non-parametric Wilcoxon-Mann-Whitney test in the analysis of medical studies. Ger. Med. Sci. 2008, 6, Doc02. [Google Scholar] [PubMed]
- Levene, H. Robust Tests for Equality of Variances. Contrib. Probab. Stat. 1960, 69, 278–292. [Google Scholar]
- Wang, Y.; Rodríguez de Gil, P.; Chen, Y.H.; Kromrey, J.D.; Kim, E.S.; Pham, T.; Nguyen, D.; Romano, J.L. Comparing the Performance of Approaches for Testing the Homogeneity of Variance Assumption in One-Factor ANOVA Models. Educ. Psychol. Meas. 2017, 77, 305–329. [Google Scholar] [CrossRef] [PubMed]
- Student. The Probable Error of a Mean. Biometrika 1908, 6, 1–25. [Google Scholar] [CrossRef]
- Welch, B.L. The Generalization of ‘Student’s’ Problem When Several Different Population Varlances Are Involved. Biometrika 1947, 34, 28–35. [Google Scholar] [CrossRef]
- Derrick, B.; White, P. Why Welch’s test is Type I error robust. TQMP 2016, 12, 30–38. [Google Scholar] [CrossRef]
- Fisher, R.A. Studies in crop variation. I. An examination of the yield of dressed grain from Broadbalk. J. Agric. Sci. 1921, 11, 107–135. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods for Research Workers. In Breakthroughs in Statistics: Methodology and Distribution; Kotz, S., Johnson, N.L., Eds.; Springer: New York, NY, USA, 1992; pp. 66–70. [Google Scholar]
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Dunn, O.J. Multiple Comparisons Among Means. J. Am. Stat. Assoc. 1961, 56, 52–64. [Google Scholar] [CrossRef]
- Ostertagová, E.; Ostertag, O.; Kováč, J. Methodology and Application of the Kruskal-Wallis Test. Appl. Mech. Mater. 2014, 611, 115–120. [Google Scholar] [CrossRef]
- Dunnett, C.W. Pairwise Multiple Comparisons in the Unequal Variance Case. J. Am. Stat. Assoc. 1980, 75, 796–800. [Google Scholar] [CrossRef]
- Games, P.A.; Keselman, H.J.; Rogan, J.C. Simultaneous pairwise multiple comparison procedures for means when sample sizes are unequal. Psychol. Bull. 1981, 90, 594–598. [Google Scholar] [CrossRef]
- Tukey, J.W. Comparing Individual Means in the Analysis of Variance. Biometrics 1949, 5, 99–114. [Google Scholar] [CrossRef] [PubMed]
- Larson, M.G. Analysis of Variance. Circulation 2008, 117, 115–121. [Google Scholar] [CrossRef] [PubMed]
- Bourne, P.E.; Bonazzi, V.; Dunn, M.; Green, E.D.; Guyer, M.; Komatsoulis, G.; Larkin, J.; Russell, B. The NIH Big Data to Knowledge (BD2K) initiative. J. Am. Med. Inf. Assoc. 2015, 22, 1114. [Google Scholar] [CrossRef] [PubMed]
- Love, M.I.; Huber, W.; Anders, S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014, 15, 550. [Google Scholar] [CrossRef]
- Austin, P.C.; White, I.R.; Lee, D.S.; van Buuren, S. Missing Data in Clinical Research: A Tutorial on Multiple Imputation. Can. J. Cardiol. 2021, 37, 1322–1331. [Google Scholar] [CrossRef] [PubMed]
| Confusion Matrix (STATom@ic vs. DeSeq2) | |
|---|---|
| p < 0.05 | |
| True Positive | 852 |
| False Negative | 2575 |
| False Positive | 49 |
| True Negative | 10,256 |
| Recall | 0.2486 |
| Precision | 0.9456 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Treves, R.S.; Gripshover, T.C.; Hardesty, J.E. STATom@ic: R Package for Automated Statistical Analysis of Omic Datasets. Stats 2025, 8, 18. https://doi.org/10.3390/stats8010018
Treves RS, Gripshover TC, Hardesty JE. STATom@ic: R Package for Automated Statistical Analysis of Omic Datasets. Stats. 2025; 8(1):18. https://doi.org/10.3390/stats8010018
Chicago/Turabian StyleTreves, Rui S., Tyler C. Gripshover, and Josiah E. Hardesty. 2025. "STATom@ic: R Package for Automated Statistical Analysis of Omic Datasets" Stats 8, no. 1: 18. https://doi.org/10.3390/stats8010018
APA StyleTreves, R. S., Gripshover, T. C., & Hardesty, J. E. (2025). STATom@ic: R Package for Automated Statistical Analysis of Omic Datasets. Stats, 8(1), 18. https://doi.org/10.3390/stats8010018






