Predicting Random Walks and a Data-Splitting Prediction Region
Abstract
1. Introduction
2. Materials and Methods
2.1. A Data-Splitting Prediction Region
2.2. Prediction Intervals and Regions for the Random Walk
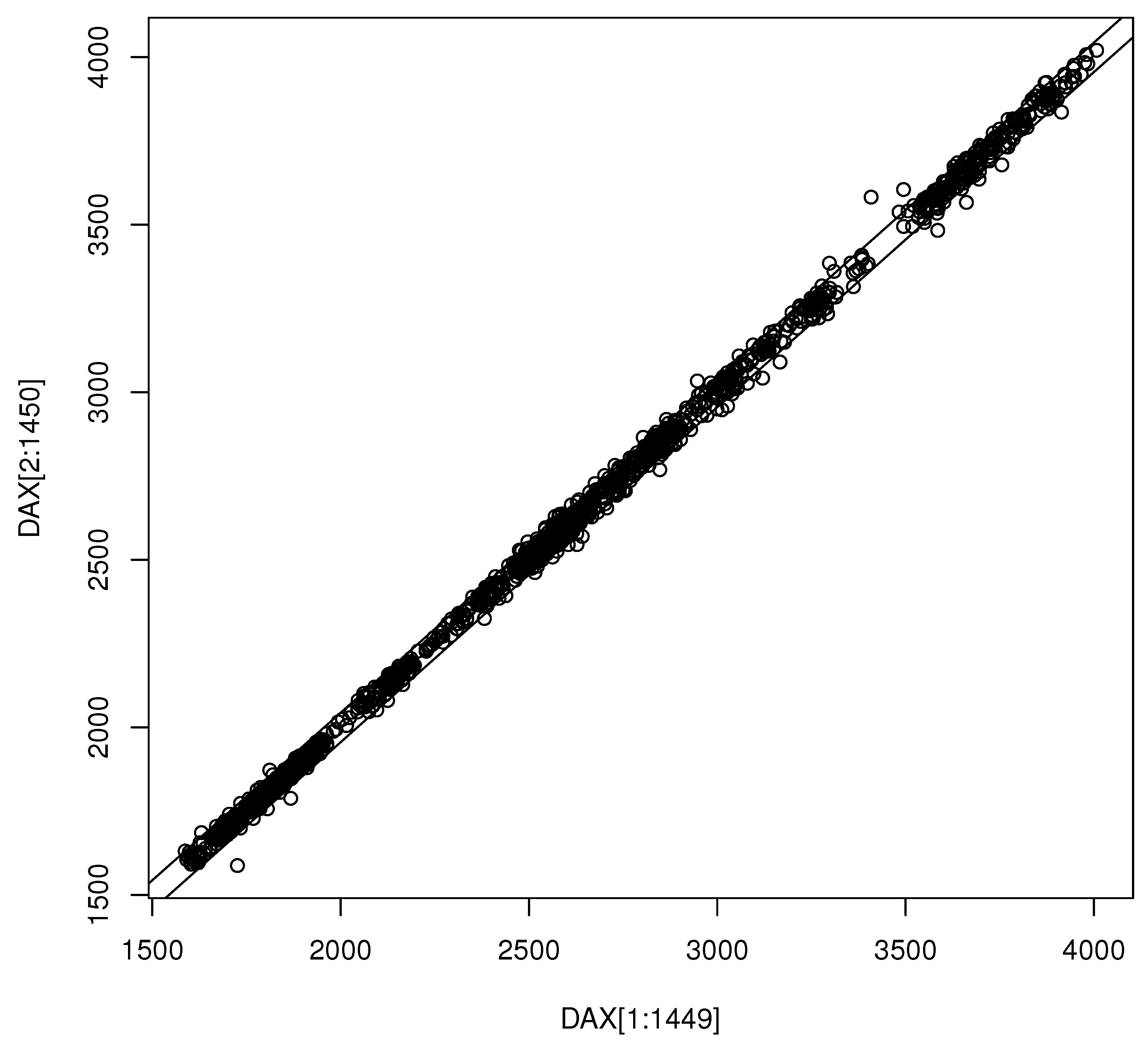
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ross, S.M. Introduction to Probability Models, 11th ed.; Academic Press: San Diego, CA, USA, 2014. [Google Scholar]
- Frey, J. Data-driven nonparametric prediction intervals. J. Stat. Plan. Inference 2013, 143, 1039–1048. [Google Scholar] [CrossRef]
- Grübel, R. The length of the shorth. Ann. Stat. 1988, 16, 619–628. [Google Scholar] [CrossRef]
- Einmahl, J.H.J.; Mason, D.M. Generalized quantile processes. Ann. Stat. 1992, 20, 1062–1078. [Google Scholar] [CrossRef]
- Chen, M.H.; Shao, Q.M. Monte carlo estimation of Bayesian credible and HPD intervals. J. Comput. Graph. Stat. 1993, 8, 69–92. [Google Scholar]
- Olive, D.J. Asymptotically optimal regression prediction intervals and prediction regions for multivariate data. Intern. J. Stat. Probab. 2013, 2, 90–100. [Google Scholar] [CrossRef]
- Olive, D.J. Applications of hyperellipsoidal prediction regions. Stat. Pap. 2018, 59, 913–931. [Google Scholar] [CrossRef]
- Beran, R. Calibrating prediction regions. J. Am. Stat. Assoc. 1990, 85, 715–723. [Google Scholar] [CrossRef]
- Beran, R. Probability-centered prediction regions. Ann. Stat. 1993, 21, 1967–1981. [Google Scholar] [CrossRef]
- Fontana, M.; Zeni, G.; Vantini, S. Conformal prediction: A unified review of theory and new challenges. Bernoulli 2023, 29, 1–23. [Google Scholar] [CrossRef]
- Guan, L. Localized conformal prediction: A generalized inference framework for conformal prediction. Biometrika 2023, 110, 33–50. [Google Scholar] [CrossRef]
- Steinberger, L.; Leeb, H. Conditional predictive inference for stable algorithms. Ann. Stat. 2023, 51, 290–311. [Google Scholar] [CrossRef]
- Tian, Q.; Nordman, D.J.; Meeker, W.Q. Methods to compute prediction intervals: A review and new results. Stat. Sci. 2022, 37, 580–597. [Google Scholar] [CrossRef]
- Pelawa Watagoda, L.C.R.; Olive, D.J. Comparing six shrinkage estimators with large sample theory and asymptotically optimal prediction intervals. Stat. Pap. 2021, 62, 2407–2431. [Google Scholar] [CrossRef]
- Lei, J.; G’Sell, M.; Rinaldo, A.; Tibshirani, R.J.; Wasserman, L. Distribution-free predictive inference for regression. J. Am. Stat. Assoc. 2018, 113, 1094–1111. [Google Scholar] [CrossRef]
- Pelawa Watagoda, L.C.R.; Olive, D.J. Bootstrapping multiple linear regression after variable selection. Stat. Pap. 2021, 62, 681–700. [Google Scholar] [CrossRef]
- Rajapaksha, K.W.G.D.H.; Olive, D.J. Wald type tests with the wrong dispersion matrix. Commun. Stat. Theory Methods 2022. [Google Scholar] [CrossRef]
- Rathnayake, R.C.; Olive, D.J. Bootstrapping some GLMs and survival regression models after variable selection. Commun. Stat. Theory Methods 2023, 52, 2625–2645. [Google Scholar] [CrossRef]
- Mykland, P.A. Financial options and statistical prediction intervals. Ann. Stat. 2003, 31, 1413–1438. [Google Scholar] [CrossRef]
- Niwitpong, S.; Panichkitkosolkul, W. Prediction interval for an unknown mean Gaussian AR(1) process following unit root test. Manag. Sci. Stat Decis. 2009, 6, 43–51. [Google Scholar]
- Panichkitkosolkul, W.; Niwitpong, S. On multistep-ahead prediction intervals following unit root tests for a Gaussian AR(1) process with additive outliers. Appl. Math. Sci. 2011, 5, 2297–2316. [Google Scholar]
- Wolf, M.; Wunderli, D. Bootstrap joint prediction regions. J. Time Ser. Anal. 2015, 36, 352–376. [Google Scholar] [CrossRef]
- Kim, J.H. Asymptotic and bootstrap prediction regions for vector autoregression. Intern. J. Forecast. 1999, 15, 393–403. [Google Scholar] [CrossRef]
- Kim, J.H. Bias-corrected bootstrap prediction regions for vector autoregression. J. Forecast. 2004, 23, 141–154. [Google Scholar] [CrossRef]
- Hyndman, R.J. Highest density forecast regions for non-linear and non-normal time series models. J. Forecast. 1995, 14, 431–441. [Google Scholar] [CrossRef]
- Haile, M.G. Inference for Time Series after Variable Selection. Ph.D. Thesis, Southern Illinois University, Carbondale, IL, USA, 2022. Available online: http://parker.ad.siu.edu/Olive/shaile.pdf (accessed on 15 December 2023).
- Wisseman, S.U.; Hopke, P.K.; Schindler-Kaudelka, E. Multielemental and multivariate analysis of Italian terra sigillata in the world heritage museum, university of Illinois at Urbana-Champaign. Archeomaterials 1987, 1, 101–107. [Google Scholar]
- Gray, H.L.; Odell, P.L. On sums and products of rectangular variates. Biometrika 1966, 53, 615–617. [Google Scholar] [CrossRef]
- Marengo, J.E.; Farnsworth, D.L.; Stefanic, L. A geometric derivation of the Irwin-Hall distribution. Intern. J. Math. Math. Sci. 2017, 2017, 3571419. [Google Scholar] [CrossRef]
- Roach, S.A. The frequency distribution of the sample mean where each member of the sample is drawn from a different rectangular distribution. Biometrika 1963, 50, 508–513. [Google Scholar] [CrossRef]
- Zhang, L. Data Splitting Inference. Ph.D. Thesis, Southern Illinois University, Carbondale, IL, USA, 2022. Available online: http://parker.ad.siu.edu/Olive/slinglingphd.pdf (accessed on 15 December 2023).
- Pan, L.; Politis, D.N. Bootstrap prediction intervals for Markov processes. Comput. Stat. Data Anal. 2016, 100, 467–494. [Google Scholar] [CrossRef]
- Vidoni, P. Improved prediction intervals for stochastic process models. J. Time Ser. Anal. 2004, 25, 137–154. [Google Scholar] [CrossRef]
- Vit, P. Interval prediction for a Poisson process. Biometrika 1973, 60, 667–668. [Google Scholar] [CrossRef]
- Makridakis, S.; Hibon, M.; Lusk, E.; Belhadjali, M. Confidence intervals: An empirical investigation of the series in the M-competition. Intern. J. Forecast. 1987, 3, 489–508. [Google Scholar] [CrossRef]
- Pankratz, A. Forecasting with Univariate Box-Jenkins Models; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Garg, A.; Aggarwal, P.; Aggarwal, Y.; Belarbi, M.O.; Chalak, H.D.; Tounsi, A.; Gulia, R. Machine learning models for predicting the compressive strength of concrete containing nano silica. Comput. Concr. 2022, 30, 33–42. [Google Scholar]
- Garg, A.; Belarbi, M.-O.; Chalak, H.D.; Tounsi, A.; Li, L.; Singh, A.; Mukhopadhyay, T. Predicting elemental stiffness matrix of fg nanoplates using Gaussian process regression based surrogate model in framework of layerwise model. Eng. Anal. Bound. Elem. 2022, 143, 779–795. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
| n | dist | h = 1 | h = 2 | h = 3 | h = 4 |
|---|---|---|---|---|---|
| 100 | N | 0.9528 | 0.9578 | 0.9456 | 0.9220 |
| 100 | 4.1683 (0.3923) | 6.3504 (0.9390) | 7.2516 (1.2066) | 7.8247 (1.4372) | |
| 100 | C | 0.9606 | 0.9656 | 0.9472 | 0.9262 |
| 100 | 47.33 (39.38) | 1075.43 (41,234.9) | 1079.36 (41,233.0) | 1065.19 (41,233.7) | |
| 100 | EXP | 0.9552 | 0.9562 | 0.9408 | 0.9242 |
| 100 | 3.6615 (0.6325) | 6.3141 (1.4891) | 7.1391 (1.6336) | 7.6647 (1.8121) | |
| 100 | U | 0.9486 | 0.9584 | 0.9408 | 0.9212 |
| 100 | 1.9023 (0.0408) | 3.2878 (0.2577) | 3.9791 (0.5093) | 4.4074 (0.6977) | |
| 400 | N | 0.9526 | 0.9506 | 0.9556 | 0.9508 |
| 400 | 4.0646 (0.1868) | 5.7753 (0.3813) | 7.2431 (0.6028) | 8.3282 (0.7921) | |
| 400 | C | 0.9600 | 0.9622 | 0.9654 | 0.9632 |
| 400 | 32.7277 (8.3139) | 71.7138 (28.29) | 133.9884 (79.20) | 188.3578 (146.52) | |
| 400 | EXP | 0.9582 | 0.9598 | 0.9602 | 0.9578 |
| 400 | 3.3131 (0.2598) | 5.1497 (0.4369) | 6.7619 (0.6877) | 7.9367 (0.8970) | |
| 400 | U | 0.9542 | 0.9534 | 0.9568 | 0.9558 |
| 400 | 1.9028 (0.0193) | 3.1602 (0.1268) | 4.0569 (0.2564) | 4.7092 (0.3808) | |
| 800 | N | 0.9514 | 0.9520 | 0.9536 | 0.9514 |
| 800 | 4.0205 (0.1334) | 5.7498 (0.2720) | 7.0086(0.4012) | 8.1579 (0.5338) | |
| 800 | C | 0.9520 | 0.9550 | 0.9516 | 0.9522 |
| 800 | 29.7122 (4.9301) | 65.2292 (16.21) | 98.9266 (31.08) | 144.3277 (57.72) | |
| 800 | EXP | 0.9564 | 0.9550 | 0.9518 | 0.9596 |
| 800 | 3.2000 (0.1727) | 5.0514 (0.3100) | 6.4202 (0.4333) | 7.6747 (0.5787) | |
| 800 | U | 0.9506 | 0.9522 | 0.9522 | 0.9518 |
| 800 | 1.9014 (0.0132) | 3.1666 (0.0908) | 3.9651 (0.1835) | 4.6357 (0.2693) |
| n | Type | h = 1 | h = 2 | h = 3 | h = 4 | |
|---|---|---|---|---|---|---|
| 400 | 0 | 1 | 0.9426 | 0.9438 | 0.9370 | 0.9214 |
| 400 | 0 | 2 | 0.9490 | 0.9502 | 0.9444 | 0.9270 |
| 400 | 0 | 3 | 0.9466 | 0.9530 | 0.9476 | 0.9392 |
| 400 | 0 | 4 | 0.9416 | 0.9446 | 0.9388 | 0.9216 |
| 400 | 0.354 | 1 | 0.9514 | 0.9446 | 0.9456 | 0.9186 |
| 400 | 0.354 | 2 | 0.9450 | 0.9572 | 0.9460 | 0.9290 |
| 400 | 0.354 | 3 | 0.9556 | 0.9546 | 0.9496 | 0.9314 |
| 400 | 0.354 | 4 | 0.9416 | 0.9412 | 0.9340 | 0.9182 |
| 400 | 0.9 | 1 | 0.9484 | 0.9462 | 0.9424 | 0.9198 |
| 400 | 0.9 | 2 | 0.9524 | 0.9502 | 0.9480 | 0.9310 |
| 400 | 0.9 | 3 | 0.9482 | 0.9576 | 0.9546 | 0.9392 |
| 400 | 0.9 | 4 | 0.9458 | 0.9376 | 0.9346 | 0.9228 |
| 800 | 0 | 1 | 0.9458 | 0.9450 | 0.9460 | 0.9484 |
| 800 | 0 | 2 | 0.9516 | 0.9554 | 0.9514 | 0.9506 |
| 800 | 0 | 3 | 0.9494 | 0.9508 | 0.9480 | 0.9544 |
| 800 | 0 | 4 | 0.9432 | 0.9408 | 0.9438 | 0.9418 |
| 800 | 0.354 | 1 | 0.9456 | 0.9464 | 0.9478 | 0.9450 |
| 800 | 0.354 | 2 | 0.9474 | 0.9550 | 0.9540 | 0.9488 |
| 800 | 0.354 | 3 | 0.9534 | 0.9516 | 0.9532 | 0.9536 |
| 800 | 0.354 | 4 | 0.9494 | 0.9466 | 0.9480 | 0.9518 |
| 800 | 0.9 | 1 | 0.9436 | 0.9482 | 0.9478 | 0.9450 |
| 800 | 0.9 | 2 | 0.9500 | 0.9494 | 0.9512 | 0.9514 |
| 800 | 0.9 | 3 | 0.9552 | 0.9520 | 0.9514 | 0.9484 |
| 800 | 0.9 | 4 | 0.9474 | 0.9450 | 0.9494 | 0.9464 |
| 1600 | 0 | 1 | 0.9506 | 0.9516 | 0.9476 | 0.9464 |
| 1600 | 0 | 2 | 0.9522 | 0.9534 | 0.9532 | 0.9514 |
| 1600 | 0 | 3 | 0.9496 | 0.9530 | 0.9524 | 0.9522 |
| 1600 | 0 | 4 | 0.9418 | 0.9428 | 0.9414 | 0.9430 |
| 1600 | 0.354 | 1 | 0.9506 | 0.9472 | 0.9504 | 0.9502 |
| 1600 | 0.354 | 2 | 0.9440 | 0.9520 | 0.9488 | 0.9502 |
| 1600 | 0.354 | 3 | 0.9506 | 0.9572 | 0.9574 | 0.9570 |
| 1600 | 0.354 | 4 | 0.9488 | 0.9418 | 0.9444 | 0.9462 |
| 1600 | 0.9 | 1 | 0.9510 | 0.9496 | 0.9476 | 0.9458 |
| 1600 | 0.9 | 2 | 0.9492 | 0.9500 | 0.9532 | 0.9474 |
| 1600 | 0.9 | 3 | 0.9524 | 0.9558 | 0.9548 | 0.9540 |
| 1600 | 0.9 | 4 | 0.9450 | 0.9508 | 0.9452 | 0.9500 |
| n | p | nv | xtype | dtype | cov |
|---|---|---|---|---|---|
| 50 | 100 | 20 | 1 | 1 | 0.9560 |
| 50 | 100 | 20 | 2 | 1 | 0.9466 |
| 50 | 100 | 20 | 3 | 1 | 0.9504 |
| 50 | 100 | 20 | 1 | 2 | 0.9558 |
| 50 | 100 | 20 | 2 | 2 | 0.9508 |
| 50 | 100 | 20 | 3 | 2 | 0.9522 |
| 100 | 100 | 50 | 1 | 1 | 0.9620 |
| 100 | 100 | 50 | 2 | 1 | 0.9622 |
| 100 | 100 | 50 | 3 | 1 | 0.9596 |
| 100 | 100 | 50 | 1 | 2 | 0.9638 |
| 100 | 100 | 50 | 2 | 2 | 0.9578 |
| 100 | 100 | 50 | 3 | 2 | 0.9638 |
| 100 | 100 | 25 | 1 | 1 | 0.9588 |
| 100 | 100 | 25 | 2 | 1 | 0.9658 |
| 100 | 100 | 25 | 3 | 1 | 0.9568 |
| 100 | 100 | 25 | 1 | 2 | 0.9622 |
| 100 | 100 | 25 | 2 | 2 | 0.9672 |
| 100 | 100 | 25 | 3 | 2 | 0.9662 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haile, M.G.; Zhang, L.; Olive, D.J. Predicting Random Walks and a Data-Splitting Prediction Region. Stats 2024, 7, 23-33. https://doi.org/10.3390/stats7010002
Haile MG, Zhang L, Olive DJ. Predicting Random Walks and a Data-Splitting Prediction Region. Stats. 2024; 7(1):23-33. https://doi.org/10.3390/stats7010002
Chicago/Turabian StyleHaile, Mulubrhan G., Lingling Zhang, and David J. Olive. 2024. "Predicting Random Walks and a Data-Splitting Prediction Region" Stats 7, no. 1: 23-33. https://doi.org/10.3390/stats7010002
APA StyleHaile, M. G., Zhang, L., & Olive, D. J. (2024). Predicting Random Walks and a Data-Splitting Prediction Region. Stats, 7(1), 23-33. https://doi.org/10.3390/stats7010002





