New Vessel Extraction Method by Using Skew Normal Distribution for MRA Images

Abstract

Vascular-related diseases pose significant public health challenges and are a leading cause of mortality and disability. Understanding the complex structure of the vascular system and its processes is crucial for addressing these issues. Recent advancements in medical imaging technology have enabled the generation of high-resolution 3D images of vascular structures, leading to a diverse array of methods for vascular extraction. While previous research has often assumed a normal distribution of image data, this paper introduces a novel vessel extraction method that utilizes the skew normal distribution for more accurate probability distribution modeling. The proposed method begins with a preprocessing step to enhance vessel structures and reduce noise in Magnetic Resonance Angiography (MRA) images. The skew normal distribution, known for its ability to model skewed data, is then employed to characterize the intensity distribution of vessels. By estimating the parameters of the skew normal distribution using the Expectation-Maximization (EM) algorithm, the method effectively separates vessel pixels from the background and non-vessel regions. To extract vessels, a thresholding technique is applied based on the estimated skew normal distribution parameters. This segmentation process enables accurate vessel extraction, particularly in detecting thin vessels and enhancing the delineation of vascular edges with low contrast. Experimental evaluations on a diverse set of MRA images demonstrate the superior performance of the proposed method compared to previous approaches in terms of accuracy and computational efficiency. The presented vessel extraction method holds promise for improving the diagnosis and treatment of vascular-related diseases. By leveraging the skew normal distribution, it provides accurate and efficient vessel segmentation, contributing to the advancement of vascular imaging in the field of medical image analysis.

1. Introduction

Numerous individuals experience major cerebrovascular diseases. These illnesses, specifically acute strokes, contribute significantly to mortality rates. Severe vascular conditions such as carotid stenosis, aneurysms, and arterio-venous malformations (AVM) have the potential to lead to strokes if not detected early on. This is where the visualization of vessels in brain Magnetic Resonance Angiography (MRA) images becomes crucial. Surgeons heavily rely on these images to identify irregularities and plan surgeries. The vessels act as important landmarks and roadmaps during surgical procedures, playing a vital role in making critical decisions in the operating room. Nevertheless, analyzing these vessels can pose a great challenge due to their intricate nature, various shapes, branching patterns, varying densities, narrow diameters, and wide range of intensity.

There are three primary techniques used for MRA: time-of-flight (TOF) angiography, phase contrast angiography (PCA), and contrast-enhanced MRA (CE-MRA) [1]. Both TOF and PCA are non-invasive techniques, while CE-MRA requires the injection of a contrast agent, typically gadolinium. PCA offers excellent background suppression and can measure flow velocity vectors for each voxel. On the other hand, although the TOF technique lacks quantitative accuracy, it is widely adopted in clinical settings due to its speed and ability to generate high-contrast images [2].

Unfortunately, MRA images frequently fail to meet expectations as they are plagued by issues such as excessive noise, noticeable artifacts, low intensity, and the intricate nature of the vascular structure. As a result, there is a growing need to create precise algorithms for extracting vessels that can overcome these limitations [3]. The primary objective of vessel extraction is to efficiently partition the image into separate components that delineate the vessel and the background.

Vessel extraction techniques have been continuously evolving since 1985 [4]. Over the years, researchers have explored various innovative approaches to address this challenging problem. In-depth surveys and analyses on vessel extraction techniques and algorithms have been conducted by esteemed experts like Kirbas and Quek [5]. Drawing inspiration from mathematical morphology, Cline [6] proposed a unique technique that leverages non-linear mathematical operators. In order to incorporate the concept of fuzziness, several researchers [7,8,9] successfully implemented fuzzy connectivity-based techniques utilizing fuzzy methods. Alternatively, Prinet et al. [10] adopted a geometric differential approach for vessel segmentation, treating the MRA image as a hypersurface. Their approach involved connecting crest points which represent the extreme points of curvature on the hypersurface in order to obtain vessel centerlines.

To tackle the segmentation of curvilinear structures in medical images, researchers have proposed a variety of methods to enhance precision and minimize similarities. One such approach involves the utilization of multiscale filtering, wherein the image is convolved with Gaussian filters and the eigenvalues of the Hessian matrix are examined [11,12,13]. Krissian et al. [14] introduced a technique known as directional anisotropic diffusion, which effectively reduces noise through the implementation of anisotropic diffusion. In a similar vein, Caselles et al. [15] and Malladi et al. [16] employed propagating interfaces with a curvature-dependent speed function to represent anatomical shapes, utilizing the level set method (LSM). Lastly, a notable alternative formulated by Osher and Sethian [17] is based on Hamilton–Jacobi principles. These diverse approaches collectively contribute to the advancement of curvilinear structure segmentation in medical images.

In the exciting realm of vessel extraction, a breakthrough algorithm called the TFA algorithm was proposed by Cai et al. [18]. This innovative approach, rooted in the concept of tight frame, has been developed with the specific goal of achieving highly efficient and effective vessel extraction. With its unique methodology and techniques, the TFA algorithm has pushed the boundaries of vessel extraction, opening new possibilities and empowering researchers and practitioners alike to delve deeper into this fascinating field.

Wilson presented distributions for the data, inspired by a physical model of blood flow, utilized in a modified version of the expectation-maximization (EM) algorithm [19]. The EM algorithm is a versatile iterative algorithm for maximum likelihood (ML) estimation in incomplete-data problems. In numerous significant instances, the EM algorithm is straightforward and computationally efficient. The EM algorithm has been suggested in various specialized contexts for many years. The earliest citation for this algorithm can be traced back to McKendrick’s 1927 paper [20]. Baum employed the algorithm in a Markov model and established mathematical results in this scenario [21]. Orchard and Woodbury were the first to observe the “missing information principle” [22]. The term EM was coined by Dempster, Laird, and Rubin in 1977 [23]. Wang et al. conducted a comprehensive thematic survey on medical image segmentation using deep learning techniques [24]. Hesamian et al. presented deep learning techniques for medical image segmentation [25]. Ghosh et al. explored and explained the intricacies of deep learning techniques for image segmentation [26]. Na et al. [27] utilized the statistical modeling and knowledge-based segmentation of a cerebral artery based on TOF-MRA and MR-T1. Yuan et al. [28] proposed an effective CNN and Transformer complementary network for medical image segmentation. Trombini et al. [29] introduced a goal-driven unsupervised image segmentation method combining graph-based processing and Markov random fields. Qureshi et al. [30] provided a review of deep semantic-based methods for medical image segmentation, highlighting the techniques, applications, and emerging trends in the field. Dash et al. [31] presented a guidance image-based enhanced matched filter with a modified thresholding approach for blood vessel extraction. Their method showed promising results in extracting blood vessels from medical images, particularly in the context of symmetry. Abdulsahib et al. [32] proposed an automated image segmentation and feature extraction algorithm specifically designed for retinal blood vessels in fundus images. Their algorithm demonstrated effective segmentation and extraction capabilities, contributing to the analysis of retinal health. Bhatia et al. [33] introduced a retinal vessel extraction method that utilized an assisted multi-channel feature map and U-net. This technique showed potential in accurately extracting retinal vessels, aiding in the diagnosis and monitoring of various retinal diseases. Qin et al. [34] focused on super-resolution vessel extraction in X-ray coronary angiography. They proposed a robust PCA unrolling network, which achieved accurate vessel extraction and enhanced visualization of coronary arteries. Sun et al. [35] developed a scale-adaptive hybrid parametric tracker for 3D vessel extraction. Their approach showed promising results in extracting vessels from medical images, providing valuable information for clinical diagnoses and treatment planning. Additionally, other relevant research works could be considered, such as the study by Sun et al. [36], who proposed the LIVE-Net framework for comprehensive 3D vessel extraction in CT angiography. Their approach demonstrated effectiveness in extracting vessels from CT scans, enabling detailed analysis of vascular structures. Yang et al. [37] introduced a contour attention network for accurately segmenting cerebrovascular structures in medical images. This novel approach uses attention mechanisms to highlight important features, improving segmentation precision. The paper offers valuable insights into the potential of attention-based methods for medical image segmentation. Chen et al. [38] introduced a novel approach for segmenting cerebrovascular structures in medical images using a topology regularization adversarial model. Klepaczko [39] introduced a method for segmenting cerebral blood vessels in contrast-enhanced MR images using deep learning and synthetic training data.

In this paper, our proposed model presents a unique and innovative approach to representing the distributions of vessels in MRA images. Instead of using conventional normal distributions, we employ skew normal distributions. The parameters of these distributions can be accurately estimated through the EM algorithm [23]. The skew normal (SN) distribution, introduced by Azzalini [40], is specifically designed to handle skewed data. Unlike the traditional normal distribution, the skew normal distribution family includes a shape parameter that enables regulation of skewness. This added flexibility is particularly valuable when dealing with real data that exhibit skewness. Pewsey [41] addresses the issue of inference for Azzalini’s skew normal distribution. The author discusses the challenges associated with parameter estimation and hypothesis testing for this distribution, and proposes a solution based on the use of a modified likelihood function. Considering the inherent asymmetry of vessel pixel intensities in MRA images, it is evident that the skew normal distribution outperforms the normal distribution in accurately modeling vessels.

This method is highly proficient at segmenting twisted, convoluted, and occluded structures, providing an exceptional ability to trace the intricate branching of various layers, spanning from delicate to substantial formations. Moreover, it excels at extracting vessels that closely resemble the background in terms of intensity. When compared to the approaches in [18,19] based on real-life 2D MRA images, our method demonstrates superior performance in achieving precise vessel segmentation.

This paper is structured as follows:

• In Section 2, we introduce the preliminary concepts of the skew normal distribution and the EM algorithm.
• The presented segmentation algorithm is presented in Section 3.
• Section 4 includes the testing of the presented method on different real 2D MRA images. We provide a comparison with two representative algorithms from different segmentation approaches: the K-means clustering method, EMS algorithm, TFA algorithm, and Wilson methods.
• Discussion and conclusion are given in Section 5.

2. EM Algorithm

In this section, the EM algorithm is briefly discussed. The EM algorithm is a very general iterative algorithm for ML estimation in incomplete-data problems. Suppose that we have a model for the complete random variables data $Y=\left(Y_{obs},Y_{mis}\right)$ with associated probability distribution $f(Y|\theta )$ indexed by unknown parameters $\theta$, where $Y_{obs}$ and $Y_{mis}$ denote the observed part of $Y$ and the missing values, respectively. Consider the likelihood function

$$L(\theta |Y)=\int f(Y_{obs},Y_{mis}|\theta )d{Y}_{mis}.$$

(1)

The goal is to maximize likelihood function with respect to $\theta$ for estimating unknown parameters $\theta$. If the likelihood function is differentiable and unimodal, maximum of (1) can be found by solving the following equation

$$S(\theta |Y_{obs})=\frac{\partial l(\theta |Y_{obs})}{\partial \theta },$$

(2)

where $l(\theta |Y_{obs})=logL(\theta |Y_{obs})$ is the log likelihood function. When the exact solution of (2) cannot be found, iterative methods can be applied. One of the iterative methods is the Newlon–Raphson algorithm. The Newlon–Raphson algorithm requires second derivatives to be calculated or approximated. The EM algorithm is a simple iterative algorithm for maximum likelihood estimation in incomplete-data problems. The EM algorithm does not require second derivatives; thus, this algorithm is simple, both conceptually and computationally. Each iteration of EM consists of an E step (expectation step) and an $M$ step (maximization step). The E-step of EM finds the expected log likelihood if $\theta$ were ${\theta }^{\left(t\right)}$:

$$Q\left(\theta |{\theta }^{\left(t\right)}\right)=\int l(\theta |Y)f\left(Y_{mis}|Y_{obs}, \theta ={\theta }^{\left(t\right)}\right)d{Y}_{obs}.$$

(3)

The M step of EM determines ${\theta }^{\left(t+1\right)}$ by maximizing expected log likelihood (3):

$$Q\left({\theta }^{\left(t+1\right)}|{\theta }^{\left(t\right)}\right)=Q\left(\theta |{\theta }^{\left(t\right)}\right) for all \theta .$$

For more discussion, consider the complete random variables data $Y=\left(Y_{obs},Y_{mis}\right)$. The associated probability distribution $f(Y|\theta )$ can be written as follows:

$$f(Y|\theta )=f\left(Y_{obs},Y_{mis}|\theta \right)=f\left(Y_{obs}|\theta \right)f\left(Y_{mis}|Y_{obs},\theta \right),$$

(4)

where $f\left(Y_{obs}|\theta \right)$ and $f\left(Y_{mis}|Y_{obs},\theta \right)$ are the densities of the observed data and the missing data given the observed data. The log likelihood that corresponds to (4) is

$$l(\theta |Y)=l\left(\theta |Y_{obs},Y_{mis}\right)=l\left(\theta |Y_{obs}\right)+\ln f\left(Y_{mis}|Y_{obs},\theta \right).$$

To estimate unknown parameter $\theta$, we maximize $l(\theta |Y)$ with respect to $\theta$ for fixed $Y_{obs}$; this task can be difficult to carry out directly. Hence, write

$$l(\theta |Y_{obs})=l(\theta |Y)-\ln f(Y_{mis}|Y_{obs},\theta ),$$

(5)

where $l(\theta |Y_{obs})$ is to be maximized, $l(\theta |Y)$ is relatively easy to maximize. The expectation of both sides of (5) over the data $Y_{mis}$ is

$$l\left(\theta |Y_{obs}\right)=Q\left(\theta |{\theta }^{\left(t\right)}\right)-H\left(\theta |{\theta }^{\left(t\right)}\right),$$

where ${\theta }^{\left(t\right)}$ is a current estimate of $\theta$ and

$$H\left(\theta |{\theta }^{\left(t\right)}\right)=\int \mathrm{l}\mathrm{n}f\left(Y_{mis}|Y_{obs},\theta \right)f\left(Y_{mis}|Y_{obs}, \theta ={\theta }^{\left(t\right)}\right)\mathrm{d}{Y}_{mis}.$$

Using Jensen’s inequality gives $H\left(\theta |{\theta }^{\left(t\right)}\right)\le H\left({\theta }^{\left(t\right)}|{\theta }^{\left(t\right)}\right).$ Therefore, we have

$$H\left({\theta }^{\left(t+1\right)}|{\theta }^{\left(t\right)}\right)-H\left({\theta }^{\left(t\right)}|{\theta }^{\left(t\right)}\right)\le 0.$$

(6)

By the $M$-step EM algorithm, it shows that

$$Q\left({\theta }^{\left(t+1\right)}|{\theta }^{\left(t\right)}\right)-Q\left({\theta }^{\left(t\right)}|{\theta }^{\left(t\right)}\right)>0.$$

(7)

According to inequalities (6) and (7), the difference

$$\begin{gathered} l\left({\theta }^{\left(t+1\right)}|Y_{obs}\right)-l\left({\theta }^{\left(t\right)}|Y_{obs}\right)= \\ \left[Q\left({\theta }^{\left(t+1\right)}|{\theta }^{\left(t\right)}\right)-Q\left({\theta }^{\left(t\right)}|{\theta }^{\left(t\right)}\right)\right]-\left[H\left({\theta }^{\left(t+1\right)}|{\theta }^{\left(t\right)}\right)-H\left({\theta }^{\left(t\right)}|{\theta }^{\left(t\right)}\right)\right] \end{gathered}$$

is positive. This proves the following theorem.

Theorem 1. 

Every EM algorithm increases $l(\theta |Y_{obs})$ at each iteration, that is,

$$l\left({\theta }^{\left(t+1\right)}|Y_{obs}\right)\ge l\left({\theta }^t|Y_{obs}\right),$$

with equality if and only if

$$Q\left({\theta }^{\left(t+1\right)}|{\theta }^{\left(t\right)}\right)=Q\left({\theta }^{\left(t\right)}|{\theta }^{\left(t\right)}\right).$$

3. Skew Normal Distribution

The skew normal distribution is a probability distribution that is commonly used in statistics and probabilistic modeling. It is an extension of the normal distribution, which is often referred to as the bell curve. However, unlike the normal distribution, the skew normal distribution allows for asymmetric and skewed data.

The skew normal distribution is characterized by three parameters: location, scale, and shape. The location parameter determines the center or location of the distribution, similar to the mean in the normal distribution. The scale parameter controls the spread or standard deviation of the distribution. Lastly, the shape parameter governs the skewness, determining whether the distribution is positively or negatively skewed.

One of the key advantages of the skew normal distribution is its flexibility in modeling a wide range of data with different skewness properties. It can handle data that exhibit departure from symmetry or have a long tail on one side. This makes it particularly useful in various fields such as finance, economics, and epidemiology, where skewed data are frequently observed.

The skew normal distribution has been widely studied and has several properties that make it appealing for statistical analysis. It has well-defined moments, allows for easy estimation of parameters, and can be used in various inferential procedures, including hypothesis testing and estimation of confidence intervals.

Overall, the skew normal distribution provides a valuable tool for modeling and analyzing data with skewed characteristics. Its ability to capture asymmetric behavior helps to better understand and interpret real-world phenomena.

A random variable $Z$ is said to be skew normal with parameter $\lambda$, denoted by $Z\sim SN\left(\lambda \right)$, if its density is given by

$$p\left(z,\lambda \right)=2\varphi \left(z\right)\Phi \left(\lambda z\right),$$

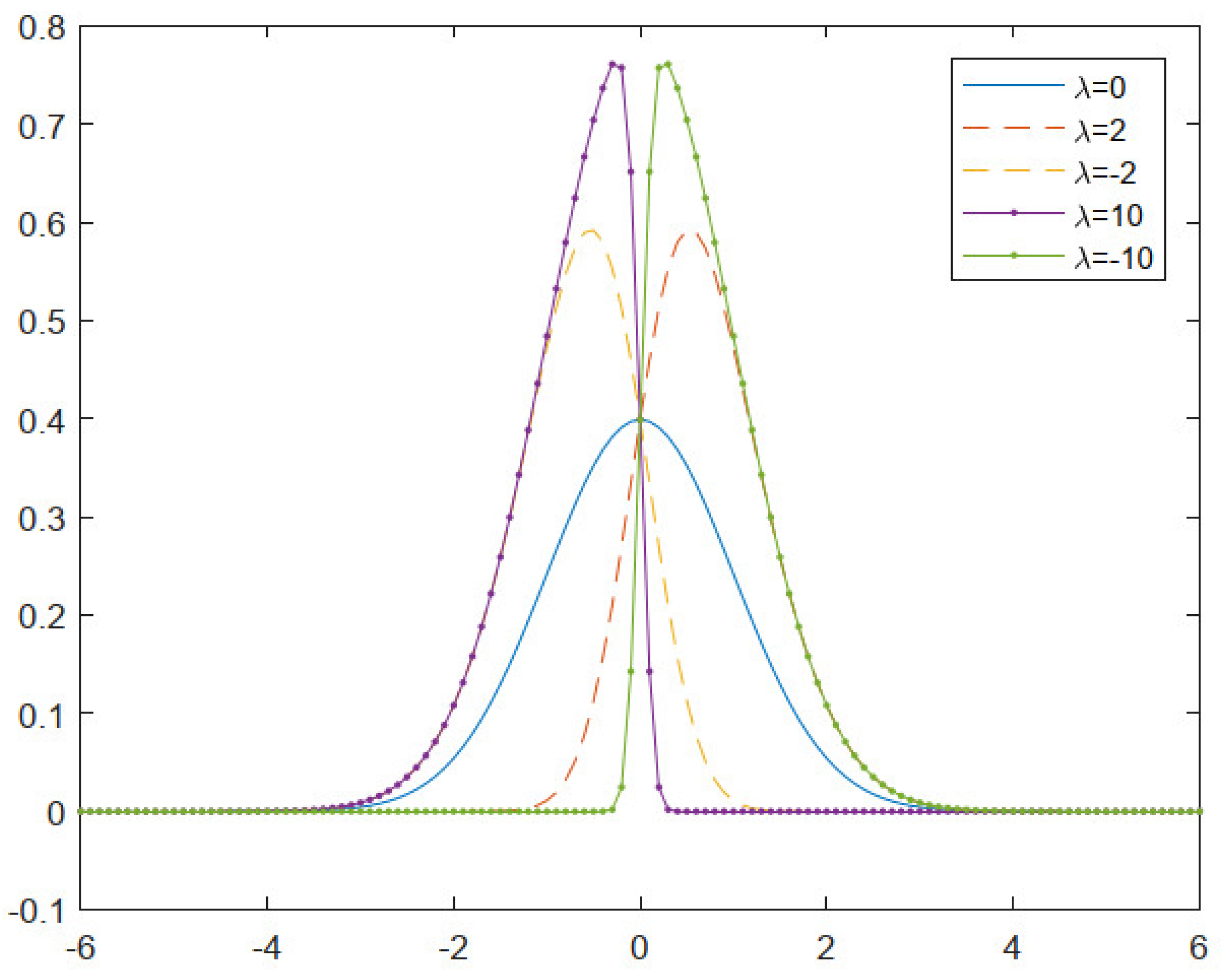
where $\varphi$ and $\Phi$ are the standard normal density and distribution, respectively, and $z$ and $\lambda$ are real numbers. The parameter $\lambda$ controls skewness, where positive (negative) values denote positive (negative) skewness. Figure 1 shows the skew normal distribution for several values of $\lambda .$ The SN class has some basic properties:

• The $SN\left(0\right)$ density is the $N\left(0, 1\right)$ density;
• If $Z\sim SN\left(\lambda \right)$ then $-Z\sim SN\left(-\lambda \right)$;
• As $\to \pm \infty$, $SN\left(\lambda \right)$ tends to the half-normal density;
• log $\log p\left(z;\lambda \right)$ is a concave function of $z.$

The corresponding distribution function of skew normal is

$$\Phi (z;\lambda )=2{\int }_{-\infty }^z{\int }_{-\infty }^{\lambda t}\varphi (t)\varphi (u)dudt.$$

(8)

We recall the function $T\left(h,a\right)$ introduced by Owen [42], where

$$T(h,a)=\frac{1}{\sqrt{2\pi }}{\int }_0^a\frac{\mathrm{e}\mathrm{x}\mathrm{p}[-\frac{1}{2}{h}^2(1+x^2)]}{1+x^2}\mathrm{d}x.$$

Therefore, Equation (8) can be written by

$$\Phi \left(z;\lambda \right)=\Phi \left(z\right)-2T\left(z;\lambda \right).$$

By using the properties of Owens function, we obtain the following important results:

• $1-\Phi \left(z;\lambda \right)=\Phi \left(z;-\lambda \right);$
• $\Phi \left(z;1\right)=\Phi {(z)}^2;$
• $\Phi \left(z;\lambda \right)+\Phi \left(z;-\lambda \right)=2\Phi \left(z\right).$

The moment generating function of the $Z$ is given by

$$M\left(t\right)=2exp\left(\frac{t^2}{2}\right)\Phi \left(\delta t\right),$$

where $\delta =\frac{\lambda }{\sqrt{1+{\lambda }^2}}.$ Hence, the first two moments are obtained as follows:

$$E\left(Z\right)=b\delta , V\left(Z\right)=1-{(b\delta )}^2,$$

where $b=\sqrt{\frac{2}{\pi }}.$

For more on skew normal distribution and its application, interested readers are referred to Azzalini and Valle [43], Uyen et al. [44], and Shakil et al. [45], among others.

4. New Vessel Extraction Method

MRA is a medical imaging technique that allows for visualization and evaluation of blood vessels in the body using magnetic resonance imaging (MRI) technology. It provides detailed information about the structure, function, and blood flow patterns within the vascular system.

In MRA images, it is essential to accurately extract and analyze the vascular information to aid in the diagnosis and treatment of various diseases. However, traditional image analysis methods often assume a symmetric and Gaussian distribution of intensity values, which might not be suitable for MRA images due to the presence of subtle or prominent signal variations.

That is where skew normal distribution comes into play. The skew normal distribution is a statistical model that allows for the representation of asymmetric data and can capture the skewness or asymmetry in the intensity values of MRA images. It extends the traditional normal distribution by introducing an additional shape parameter, which controls the degree of skewness in the distribution.

By utilizing the skew normal distribution, researchers and medical professionals can better model and understand the intensity variations in MRA images, enabling more accurate segmentation, enhancement, and detection of blood vessels. This can contribute to improved diagnosis, treatment planning, and monitoring of vascular diseases.

In summary, the application of skew normal in MRA images offers a valuable tool to address the asymmetry and intensity variations present in vascular structures, ultimately enhancing the analysis and interpretation of these crucial medical images.

Initially, we can assume that the distribution of each of our three selected classes is Gaussian, based on the physical properties of the brain tissues. However, in MRA data- sets with large fields of view, accurately fitting a parametric distribution to the artery class is challenging due to insufficient support. To address this, Wilson introduced a modification to the three Gaussian class assumption. According to Wilson’s modification, the entire dataset now consists of two Gaussian classes and a third class with a uniform distribution that spans across all data intensities. It is important to note that real data may not exhibit symmetry, and to account for this, we modify the Gaussian distribution to a skew normal distribution.

Letting class zero be the vessel class, its distribution as a uniform density is given by

$$f_0\left(x\right)=\frac{1}{I_{max}},$$

where $I_{max}=\max \left\{x_{ij}\right|x_{ij} \mathrm{are} \mathrm{intensities} \mathrm{of} \mathrm{the} \mathrm{gray} \mathrm{MRA} \mathrm{image}\}.$ The other two classes $k=1,2,$ are defined by skew normal distributions with location parameter ${\mu }_k,$ scale parameter ${\sigma }_k$, and skewness parameter ${\lambda }_k$ such that

$$f_k\left(x\right)=2\varphi \left(x|{\mu }_k,{\sigma }_k^2\right)\Phi \left({\lambda }_k\frac{x-{\mu }_k}{{\sigma }_k}\right),$$

where $\varphi (x|\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi }}exp\left(\frac{-{(x-\mu )}^2}{2{\sigma }^2}\right),\Phi \left(\lambda \frac{x-\mu }{\sigma }\right)={\int }_{-\infty }^{\lambda \frac{x-\mu }{\sigma }}\varphi (t|\mu ,{\sigma }^2)dt$. Hence,

$$f_k(x)=\sqrt{\frac{2}{\pi }}exp\left(\frac{-(x-{\mu }_k{)}^2}{2{\sigma }_k^2}\right){\int }_{-\infty }^{{\lambda }_k\frac{x-{\mu }_k}{{\sigma }_k}}\frac{1}{\sqrt{2\pi }}exp\left(-\frac{1}{2}{t}^2\right)dt, k=\mathrm{1,2}.$$

Thus, the mixture distribution is defined by

$$f(x)=\frac{{\omega }_0}{I_{max}}+{\sum }_{k=1}^2{\omega }_k{f}_k(x),$$

(9)

where ${\omega }_k,\left(k=0,1,2\right)$ are the weight of each class $i$ in the mixture model such that ${\omega }_0+{\omega }_1+{\omega }_2=1$.

4.1. Vessel Extraction Mask

To estimate the unknown parameters ${\mu }_k, {\sigma }_k, {\lambda }_k, {\omega }_k \left(k=1,2\right)$, the EM algorithm is used. The EM algorithm aims to maximize the likelihood of the distribution in order to provide estimates. To use the final parameter estimates to segment, the pixel $ij$ belongs to the vessel class if

$$\frac{{\omega }_0}{I_{max}}\ge 2{\omega }_k\varphi \left(x|{\mu }_k,{\sigma }_k^2\right)\Phi \left({\lambda }_k\frac{x-{\mu }_k}{{\sigma }_k}\right), k=1,2.$$

(10)

We construct the mask $M$ as follows:

$$M_{ij}=\left\{\begin{array}{cc}1,\hfill & if the pixel ij is a vessel pixel,\hfill \\ 0,\hfill & otherwise,\hfill \end{array}\right.$$

(11)

where $M_{ij}$ denotes the $ij$-th value of mask $M$.

4.2. Estimating of Parameters by EM Algorithm

In this section, we want to estimate unknown parameters of

$$\theta =\left({\theta }_1,{\theta }_2,\dots ,{\theta }_9\right)=\left({\omega }_0,{\omega }_1,{\omega }_2,{\mu }_1,{\mu }_2,{\sigma }_1,{\sigma }_2,{\lambda }_1,{\lambda }_2\right)$$

by EM algorithm. Consider the set of independent image pixel data $Y_{obs}=\left(X_1,X_2,\dots ,X_n\right),$ with mixture density function (9), where $n$ is the number of pixels of given image. We define for each data $X_i$ a set of missing components $Z_i=\left(Z_{0i},Z_{1i},Z_{2i}\right), i=1,2,\dots ,n,$ whose values are

$$Z_{ki}=\left\{\begin{array}{cc}1,\hfill & if the pixel X_i belong to class k,\hfill \\ 0,\hfill & otherwise,\hfill \end{array}\right.$$

And $Z_{0i}+Z_{1i}+Z_{2i}=1.$ Thus, $Y_{mis}=\left(Z_1,Z_2,\dots ,Z_n\right)$ and we can rewrite mixture distribution as

$$f_X\left(x_i\right)={\left({\omega }_0{f}_0\left(x_i\right)\right)}^{z_{0i}}{\left({\omega }_1{f}_1\left(x_i\right)\right)}^{z_{1i}}{\left({\omega }_2{f}_2\left(x_i\right)\right)}^{z_{2i}}.$$

Now, we have completed data $Y=\left(Y_{obs},Y_{mis}\right).$ If $L\left(Y,\theta \right)$ is a likelihood function, then we compute the log likelihood function as follows:

$$\begin{array}{ll}l(Y,\theta )& =\sum _{i=1}^n{z}_{0i}\left\{\mathrm{l}\mathrm{o}\mathrm{g}{\omega }_0+\mathrm{l}\mathrm{o}\mathrm{g}{f}_0\left(x_i\right)\right\}\\ & +\sum _{i=1}^n{z}_{1i}\left\{\mathrm{l}\mathrm{o}\mathrm{g}{\omega }_1+\mathrm{l}\mathrm{o}\mathrm{g}{f}_1\left(x_i\right)\right\}\\ & +\sum _{i=1}^n{z}_{2i}\left\{\mathrm{l}\mathrm{o}\mathrm{g}{\omega }_2+\mathrm{l}\mathrm{o}\mathrm{g}{f}_2\left(x_i\right)\right\}.\end{array}$$

So, we have

$$\begin{array}{ll}Q(Y_{obs};\theta )& =E\left(l\right(Y,\theta \left)\right|Y_{obs})\\ & =\sum _{i=1}^{n}E\left(z_{0i}\right|Y_{obs})\left\{\mathrm{l}\mathrm{o}\mathrm{g}{\omega }_0+\mathrm{l}\mathrm{o}\mathrm{g}{f}_0\left(x_i\right)\right\}\\ & +\sum _{i=1}^{n}E\left(z_{1i}\right|Y_{obs})\left\{\mathrm{l}\mathrm{o}\mathrm{g}{\omega }_1+\mathrm{l}\mathrm{o}\mathrm{g}{f}_1\left(x_i\right)\right\}\\ & +\sum _{i=1}^{n}E\left(z_{2i}\right|Y_{obs})\left\{\mathrm{l}\mathrm{o}\mathrm{g}{\omega }_2+\mathrm{l}\mathrm{o}\mathrm{g}{f}_2\left(x_i\right)\right\},\end{array}$$

where

$$\begin{array}{ll}E(z_{ki}|Y_{obs})\hfill & ={\widehat{Z}}_k\hfill \\ \hfill & =\frac{{\omega }_k{f}_k\left(x_i\right)}{f\left(x_i\right)}.\hfill \end{array}$$

Therefore, we can write $Q\left(Y_{obs};\theta \right)$ as

$$\begin{array}{ll} Q(Y_{obs};\theta )& =\sum _{i=1}^n\left\{{\widehat{z}}_{0i}\mathrm{l}\mathrm{o}\mathrm{g}{\omega }_0+{\widehat{z}}_{1i}\mathrm{l}\mathrm{o}\mathrm{g}{\omega }_1+{\widehat{z}}_{2i}\mathrm{l}\mathrm{o}\mathrm{g}{\omega }_2\right\}\\ & +\sum _{i=1}^n\left\{{\widehat{z}}_{0i}\mathrm{l}\mathrm{o}\mathrm{g}{f}_0\left(x_i\right)+{\widehat{z}}_{1i}\mathrm{l}\mathrm{o}\mathrm{g}{f}_1\left(x_i\right)+{\widehat{z}}_{2i}\mathrm{l}\mathrm{o}\mathrm{g}{f}_2\left(x_i\right)\right\}.\end{array}$$

Now, we can maximize $Q\left(Y_{obs};\theta \right)$ with respect to $\theta .$ For the parameters of ${\omega }_k$, we must take constraint ${\omega }_0+{\omega }_1+{\omega }_2=1.$ This is performed by using Lagrange multiplier $\alpha$ and maximizing the

$$Q\left(Y_{obs};\theta \right)-\alpha \left({\omega }_0+{\omega }_1+{\omega }_2-1\right).$$

(12)

Setting the derivatives of (12) with respect to ${\omega }_k$ equal to zero, we obtain

$$\begin{gathered} \frac{\partial \left[Q\left(Y_{obs};\theta \right)-\alpha \left({\omega }_0+{\omega }_1+{\omega }_2-1\right)\right]}{\partial {\omega }_0}{|}_{{\widehat{\omega }}_0}={{\displaystyle \sum }}_{i=1}^n\frac{{\widehat{z}}_{0i}}{{\widehat{\omega }}_0}-\alpha =0 \Rightarrow {\widehat{\omega }}_0=\frac{{{\displaystyle \sum }}_{i=1}^n{\widehat{z}}_{0i}}{\alpha } \\ \frac{\partial \left[Q\left(Y_{obs};\theta \right)-\alpha \left({\omega }_0+{\omega }_1+{\omega }_2-1\right)\right]}{\partial {\omega }_1}{|}_{{\widehat{\omega }}_1}={{\displaystyle \sum }}_{i=1}^n\frac{{\widehat{z}}_{1i}}{{\widehat{\omega }}_1}-\alpha =0 \Rightarrow {\widehat{\omega }}_1=\frac{{{\displaystyle \sum }}_{i=1}^n{\widehat{z}}_{1i}}{\alpha } \\ \frac{\partial \left[Q\left(Y_{obs};\theta \right)-\alpha \left({\omega }_0+{\omega }_1+{\omega }_2-1\right)\right]}{\partial {\omega }_2}{|}_{{\widehat{\omega }}_2}={{\displaystyle \sum }}_{i=1}^n\frac{{\widehat{z}}_{2i}}{{\widehat{\omega }}_2}-\alpha =0 \Rightarrow {\widehat{\omega }}_2=\frac{{{\displaystyle \sum }}_{i=1}^n{\widehat{z}}_{2i}}{\alpha }. \end{gathered}$$

Since ${\omega }_0+{\omega }_1+{\omega }_2=1$, we have

$$\begin{array}{c}{\widehat{\omega }}_0+{\widehat{\omega }}_1+{\widehat{\omega }}_2=\frac{1}{\alpha }\left[{{\displaystyle \sum }}_{i=1}^n{\widehat{z}}_{0i}+{{\displaystyle \sum }}_{i=1}^n{\widehat{z}}_{1i}+{{\displaystyle \sum }}_{i=1}^n{\widehat{z}}_{2i}\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\frac{1}{\alpha }\left[{{\displaystyle \sum }}_{i=1}^n{\widehat{(z}}_{0i}+{\widehat{z}}_{1i}+{\widehat{z}}_{2i})\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =\frac{1}{\alpha }\left({{\displaystyle \sum }}_{i=1}^{n}1\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =\frac{n}{\alpha }\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =1\hfill \end{array}$$

Therefore, we can write $\alpha =n$ and

$${\widehat{\omega }}_k=\frac{1}{n}{\sum }_{i=1}^n{\widehat{Z}}_{ki}.$$

(13)

Now, for estimating of ${\widehat{\mu }}_k, {\widehat{\sigma }}_k$ and ${\widehat{\lambda }}_k$, we assume that

$$\begin{array}{c} {\mathcal{l}}_k={\displaystyle \sum }_{i=1}^n{\widehat{z}}_{ki}log{f}_k\left(x_i\right)\hfill \\ ={\displaystyle {\displaystyle \sum }_{i=1}^n}{\widehat{z}}_{ki}\left\{log\frac{2}{\sqrt{2\pi }}-\frac{1}{2}log{\sigma }_k^2-\frac{1}{2{\sigma }_k^2}{(x_i-{\mu }_k)}^2+log\Phi \left({\lambda }_k\frac{x_i-{\mu }_k}{{\sigma }_k}\right)\right\},\hfill \end{array}$$

and solve these equations with Newton–Raphson method:

$$\begin{gathered} S_{{\mu }_k}\left(\widehat{\theta }\right)=\frac{\partial {\mathcal{l}}_k}{\partial {\mu }_k}{|}_{\widehat{\theta }}=0, \\ {S}_{{\sigma }_k^2}\left(\widehat{\theta }\right)=\frac{\partial {\mathcal{l}}_k}{\partial {\sigma }_k^2}{|}_{\widehat{\theta }}=0, \\ {S}_{{\lambda }_k}\left(\widehat{\theta }\right)=\frac{\partial {\mathcal{l}}_k}{\partial {\lambda }_k}{|}_{\widehat{\theta }}=0. \end{gathered}$$

Finally, in $t+1$-th step of this method, the updated equations for the distribution parameters become

$${{\widehat{\mu }}_k}^{(t+1)}=\frac{\sum _{i=1}^n{x}_i{{\widehat{z}}_{ki}}^{\left(t\right)}-{{\widehat{\lambda }}_k}^{\left(t\right)}{{\widehat{\sigma }}_k}^{\left(t\right)}\sum _{i=1}^n{{\widehat{z}}_{ki}}^{\left(t\right)}\frac{\varphi \left({{\widehat{\lambda }}_k}^{\left(t\right)}\frac{x_i-{{\widehat{\mu }}_k}^{\left(t\right)}}{{{\widehat{\sigma }}_k}^{\left(t\right)}}\right)}{\mathsf{\Phi }\left({{\widehat{\lambda }}_k}^{\left(t\right)}\frac{x_i-{{\widehat{\mu }}_k}^{\left(t\right)}}{{{\widehat{\sigma }}_k}^{\left(t\right)}}\right)}}{\sum _{i=1}^n{{\widehat{z}}_{ki}}^{\left(t\right)}}$$

(14)

$${\left({\sigma }_k^{(t+1)}\right)}^2=\frac{\sum _{i=1}^n{{\widehat{z}}_{ki}}^{\left(t\right)}{\left(x_i-{{\widehat{\mu }}_k}^{\left(t\right)}\right)}^2}{\sum _{i=1}^n{{\widehat{z}}_{ki}}^{\left(t\right)}+{{\widehat{\lambda }}_k}^{\left(t\right)}\sum _{i=1}^n{{\widehat{z}}_{ki}}^{\left(t\right)}\left(\frac{x_i-{{\widehat{\mu }}_k}^{\left(t\right)}}{{{\widehat{\sigma }}_k}^{\left(t\right)}}\right)\left(\frac{\varphi \left({\widehat{\lambda }}_k\frac{x_i-{{\widehat{\mu }}_k}^{\left(t\right)}}{{{\widehat{\sigma }}_k}^{\left(t\right)}}\right)}{\mathsf{\Phi }\left({{\widehat{\lambda }}_k}^{\left(t\right)}\frac{x_i-{{\widehat{\mu }}_k}^{\left(t\right)}}{{{\widehat{\sigma }}_k}^{\left(t\right)}}\right)}\right)}$$

(15)

Remark 1. 

We can use Newton–Raphson method to find the root of the function $S_{{\lambda }_k}\left(\theta \right)$. We will have

$${{\widehat{\lambda }}_k}^{\left(t+1\right)}={{\widehat{\lambda }}_k}^{\left(t\right)}-\frac{S_{{{\widehat{\lambda }}_k}^{\left(t\right)}}\left(\theta \right)}{S_{{{\widehat{\lambda }}_k}^{\left(t\right)}}^{\prime }\left(\theta \right)}$$

(16)

where

$$S_{{\widehat{\lambda }}_k}^{\prime }\left(\theta \right)=-{\sum }_{i=1}^n{\widehat{z}}_{ki}\left(\frac{x_i-{\widehat{\mu }}_k}{{\widehat{\sigma }}_k}\right)\left(\frac{\lambda {\left(\frac{x_i-{\widehat{\mu }}_k}{{\widehat{\sigma }}_k}\right)}^2\mathsf{\Phi }\left({\widehat{\lambda }}_k\frac{x_i-{\widehat{\mu }}_k}{{\widehat{\sigma }}_k}\right)\varphi \left({\widehat{\lambda }}_k\frac{x_i-{\widehat{\mu }}_k}{{\widehat{\sigma }}_k}\right)+\left(\frac{x_i-{\widehat{\mu }}_k}{{\widehat{\sigma }}_k}\right){\varphi }^2\left({\widehat{\lambda }}_k\frac{x_i-{\widehat{\mu }}_k}{{\widehat{\sigma }}_k}\right)}{{\left[\mathsf{\Phi }\left({\widehat{\lambda }}_k\frac{x_i-{\widehat{\mu }}_k}{{\widehat{\sigma }}_k}\right)\right]}^2}\right).$$

4.3. Initialization of the Parameters

Also, in order to initialize two location parameters ${\mu }_1,{\mu }_2$, two scale parameters ${\sigma }_1,{\sigma }_2$, and two skewness parameters ${\lambda }_1,{\lambda }_2$ in the iteration process, we initialize ${\mu }_1,{\mu }_2$ as the intensity values at each of the peaks of the data histogram, ${\sigma }_k^2={\left(\frac{{\mu }_k-I_{min}}{2}\right)}^2$, ${\lambda }_1={\lambda }_2=0$, and ${\omega }_0=0.04, {\omega }_1=0.5, {\omega }_2=0.46$, where $I_{min}$ is the intensity corresponding to the minimum histogram frequency between the two peaks (Algorithm 1).

Algorithm 1. The presented algorithm

Input given image. Initialize the parameters of ${\omega }_0,{\omega }_1,{\omega }_2,{\mu }_1,{\mu }_2,{\sigma }_1,{\sigma }_2,{\lambda }_1,{\lambda }_2.$ While $\left|Q\left(Y_{obs};{\widehat{\theta }}^{\left(t+1\right)}\right)-Q\left(Y_{obs};{\widehat{\theta }}^{\left(t\right)}\right)\right|<ϵ$, (a) Compute ${\widehat{z}}_{ki}=\frac{{\omega }_k{f}_k\left(x_i\right)}{f\left(x_i\right)}$. (b) Compute ${{\widehat{\omega }}_0}^{\left(t+1\right)}, {{\widehat{\omega }}_1}^{\left(t+1\right)}$ and ${{\widehat{\omega }}_2}^{\left(t+1\right)}$ by Equation (13). (c) Update ${\mu }_1^{\left(t+1\right)},{\mu }_2^{\left(t+1\right)},{\sigma }_1^{\left(t+1\right)},{\sigma }_2^{\left(t+1\right)},{\lambda }_1^{\left(t+1\right)},{\lambda }_2^{\left(t+1\right)} \mathrm{by} \mathrm{Equations} \left(14\right)–\left(16\right).$ Construct vessel extraction mask by Equations (10) and (11).

5. Numerical Examples

In this section, we test the presented method on three different TOF-MRA Circle of Willis Inverted MIP images. The tests have been performed on a laptop with core i7, 2 GHz processor, and 4 GB RAM. We compare our results with the K-means clustering method [46], expectation maximization segmentation [47] (EMS), the dual-tree complex wavelet tight frame algorithm [18] (TFA), and the Wilson method [19]; also, we take $ϵ={10}^{-6}$.

The blood vessels contain regions with high and low intensities, containing some thin vessels with intensities as low as the intensity of the background. Intersections of partial structures even increase the difficulty of the segmentation [18]. Validation and evaluation are essential for medical image analysis. But the automation of these processes is still not sufficient. There is still no satisfying way to assess whether one algorithm produces more accurate segmentations than another. The most common way to compare segmentation results is visual comparison. Of course, there is no single method that is best everywhere. There is no ground truth for MRA images, so we can only compare the results qualitatively. A qualitative comparison among different approaches can only be conducted by direct observation of figures.

Table 1. Estimation parameters of Wilson model and proposed model.

Example	Method	${\mathit{\omega }}_0$	${\mathit{\omega }}_1$	${\mathit{\omega }}_2$	${\mathit{\mu }}_1$	${\mathit{\mu }}_2$	${\mathit{\sigma }}_1^2$	${\mathit{\sigma }}_2^2$
1	Wilson Proposed method	$0.4189$ $0.2818$	$0.2592$ $0.4388$	$0.3288$ $0.2795$	$15.8541$ $17.06848$	$42.3461$ $46.8288$	$102.8609$ $100.07$	$237.2980$ $173.7886$
2	Wilson Proposed method	$0.3869$ $0.312$	$0.4731$ $0.2428$	$0.1400$ $0.4451$	$23.1723$ $23$	$33.9808$ $30$	$0.1426$ $0.16$	$28.1638$ $106.96$
3	Wilson Proposed method	$0.3137$ $0.2169$	$0.0931$ $0.2011$	$0.5923$ $0.5820$	$19.3591$ $19.14$	$43.8482$ $49.99$	$188.6965$ $89$	$397.5523$ $283$

shows the parameters estimation of the Wilson and presented models. The speed of applying programs is less than five seconds.

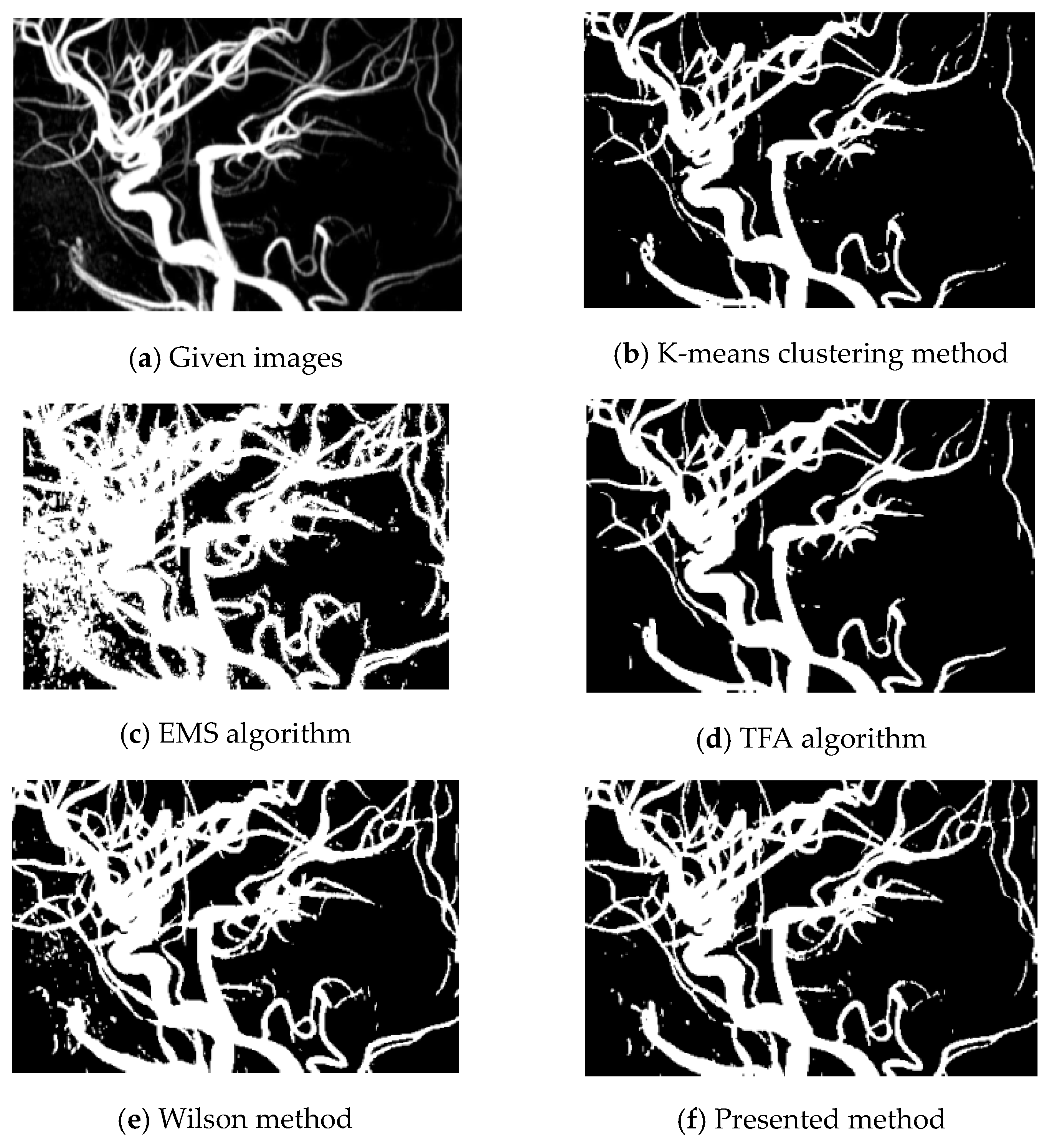
Example 1. 

Based on this example, several algorithms were applied to extract vessels from a 512 × 512 TOF-MRA Circle of Willis image of the carotid vascular system. The results were compared and analyzed.

The K-means clustering method (Figure 2b) did not perform well in vessel detection, as it failed to detect most of the vessels.

The TFA algorithm (Figure 2d) also had some limitations as it failed to extract certain vessels from the image.

On the other hand, the EMS algorithm (Figure 2c), Wilson method (Figure 2e), and the presented method (Figure 2f) showed comparable results.

However, the presented method had an advantage over the other algorithms as it managed to avoid some artifacts, improving the quality of the extracted vessels.

In summary, the K-means clustering method and TFA algorithm had unsatisfactory results in vessel extraction, while the EMS algorithm, Wilson method, and the presented method showed better performance overall, with the presented method demonstrating the ability to avoid artifacts. We see that fine vessels could be detected when the presented method is employed. Our method approach is indeed helpful in finding the edges of the vascular system with low contrast.

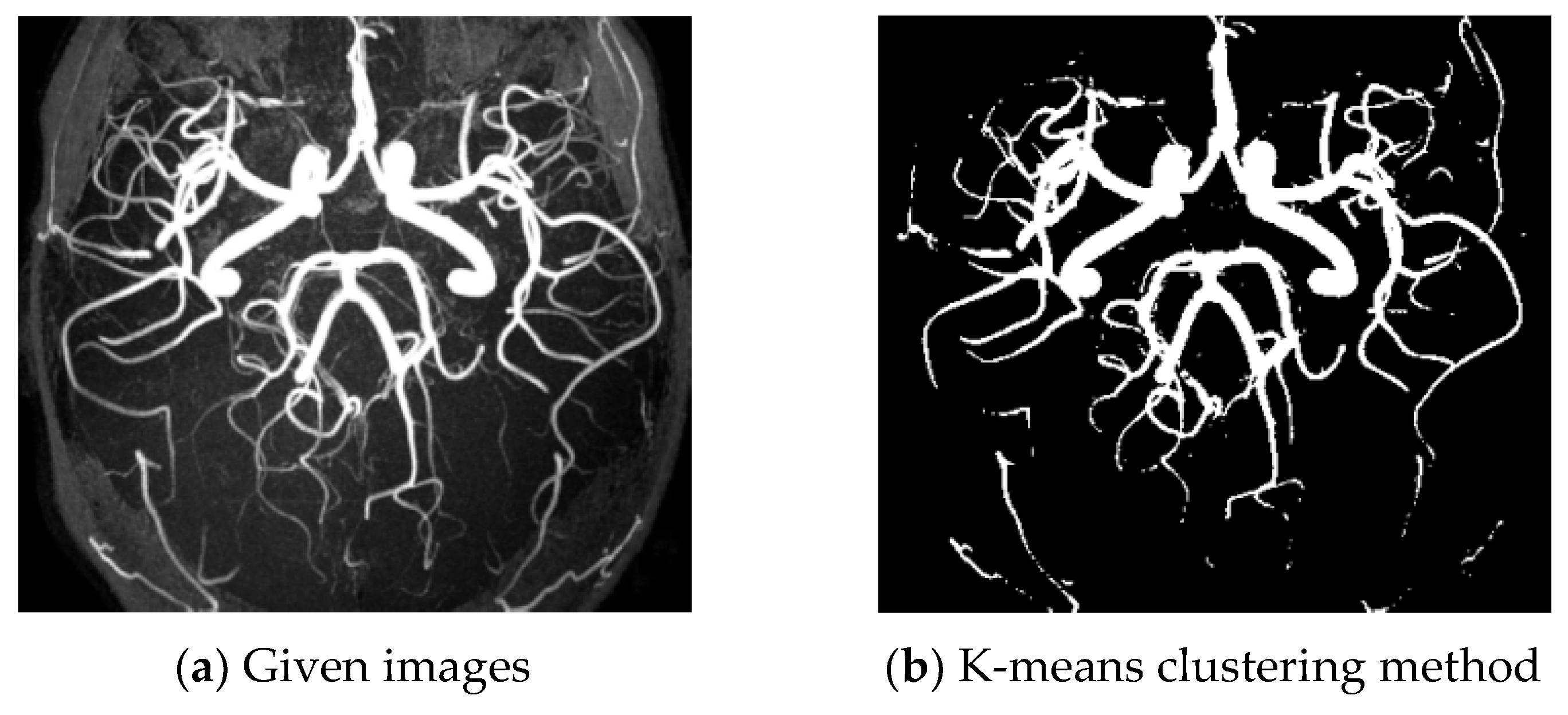
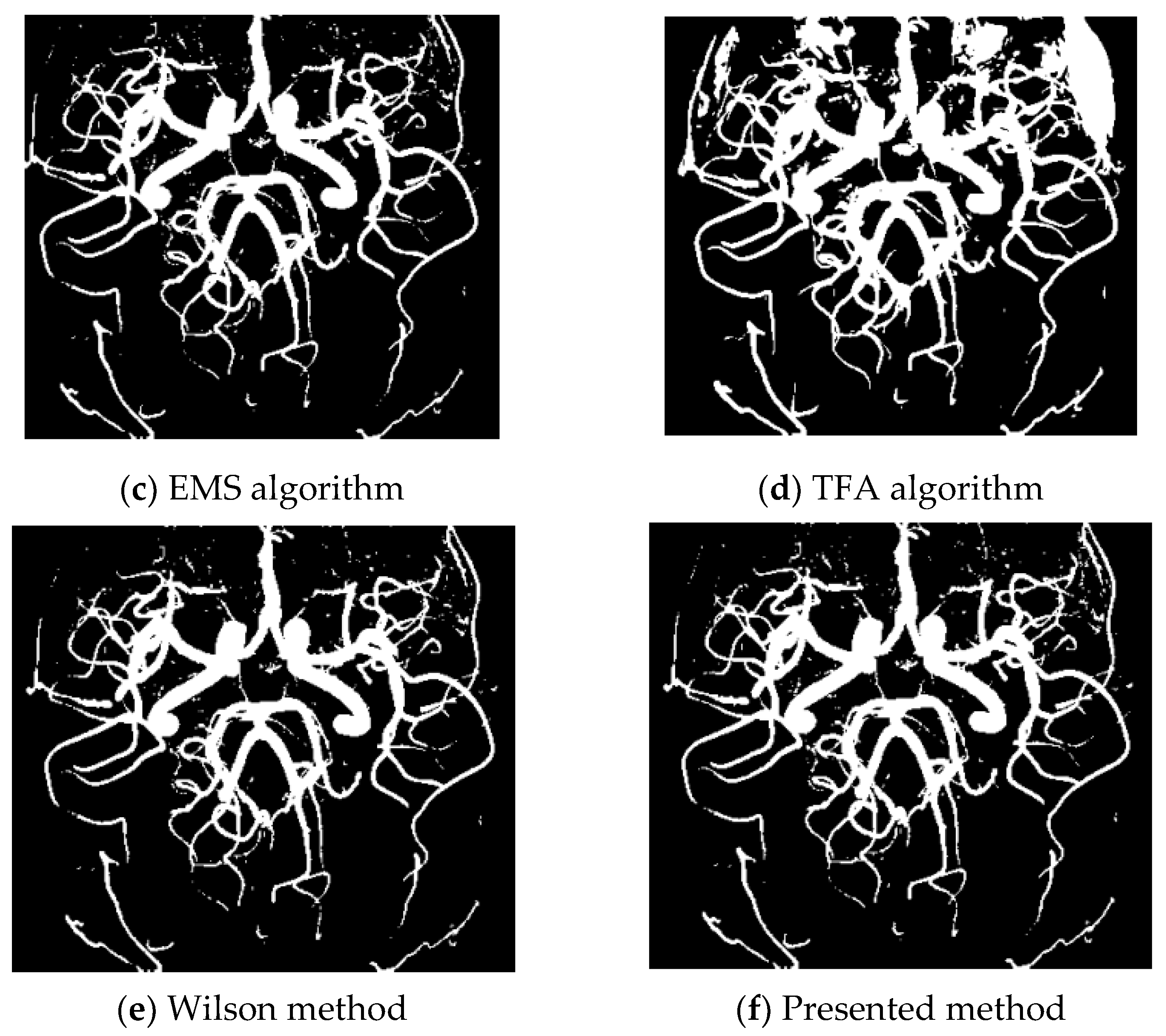
Example 2. 

In this example, a 512 × 512 TOF-MRA Circle of Willis coronal image of the carotid vascular system is taken into consideration. Various methods, including K-means, EMS, TFA, Wilson, and the presented method, are used for vessel extraction.

The K-means clustering method (Figure 3b) fails to detect most of the vessels in the image. The EMS algorithm (Figure 3c) also produces unsatisfactory results. Both K-means and EMS methods do not provide acceptable vessel extraction.

The TFA algorithm (Figure 3d) is unable to detect some vessels, particularly the long ones, as evident when comparing the right parts of the given image (Figure 3a) with Figure 3d.

The Wilson method (Figure 3e) is also found to have poor results, creating artifacts in the left part of the image.

On the other hand, the presented method (Figure 3f) demonstrates acceptable results. It successfully extracts vessels while avoiding artifacts near the boundaries and maintaining the smoothness of the vessel boundary. Our method proves particularly effective in detecting thin vessels, essential for identifying pathological lesions and enhancing the delineation of vascular edges with low contrast.

Furthermore, Figure 4b shows the histogram plots of the given data, vessel, and non-vessel distributions for the second example, illustrating the outcomes of applying the presented algorithm.

Overall, the K-means, EMS, TFA, and Wilson methods exhibit limitations and unsatisfactory results in vessel extraction, whereas the presented method proves to be effective and successful in this regard.

Example 3. 

In this example, a 512 × 512 TOF-MRA Circle of Willis coronal image of the carotid vascular system was analyzed using different algorithms for vessel extraction. The image, obtained from http://www.mr-tip.com, is shown in Figure 5a.

Figure 4b displays the result of vessel extraction using the K-means clustering method, which fails to capture most of the vessels.

The TFA algorithm, shown in Figure 4d, incorrectly identifies regions of the background as vessels due to their intensity similarity, leading to inaccurate segmentation. We see that the K-means clustering and TFA algorithm methods cannot detect many pixels that should be on the boundary of the vessels, especially those on the tips of the thin vessels. Therefore, both the K-means clustering method and TFA algorithm produce unsatisfactory results.

On the other hand, the EMS algorithm, Wilson method, and the presented method produce similar results, as depicted in Figure 5c,e,f, respectively. However, the presented method manages to avoid some artifacts, improving the quality of the extracted vessels. Our method is able to extract smoother boundaries than the Wilson method and, in particular, it avoids some artifacts near the boundary.

In conclusion, among the algorithms tested, the presented method appears to be the most effective in extracting vessels accurately while minimizing artifacts.

6. Discussion and Conclusions

This paper evaluates different methods for vessel extraction in brain images, focusing specifically on TOF-MRA Circle of Willis images. The performance of various algorithms, including K-means clustering, expectation maximization segmentation (EMS), dual-tree complex wavelet tight frame algorithm (TFA), and the Wilson method, is compared against a newly proposed method. The evaluation criteria include accurate vessel extraction, artifact avoidance, and smooth boundary production.

The tests were conducted on a laptop with a core i7, 2GHz processor, and 4GB RAM. The comparison reveals that the K-means clustering method and TFA algorithm yield unsatisfactory results in vessel extraction, while the EMS algorithm, Wilson method, and the proposed method demonstrate better performance. In particular, the proposed method shows an advantage in avoiding artifacts and improving the quality of the extracted vessels.

This work emphasizes the challenges in validating and evaluating medical image analysis algorithms, highlighting the lack of a satisfying way to assess algorithm accuracy. Visual comparison remains the most common method for evaluating segmentation results due to the absence of a ground truth for MRA images.

Furthermore, this study provides detailed insights into specific examples, demonstrating how the proposed method outperforms other algorithms in vessel extraction, particularly in detecting fine vessels with low contrast. The results of each example are visually presented, showcasing the effectiveness of the presented method compared to other algorithms.

This article introduces a new approach for vessel extraction using the skew normal distribution and EM algorithm, highlighting the precision of the method in extracting vessels with smooth boundaries while eliminating artifacts. It includes a comprehensive analysis of the EM algorithm and the skew normal distribution, acknowledging the importance of starting values in the EM algorithm and the potential of the generalized skew normal distribution for future research.

Additionally, the estimation parameters of the proposed model are compared with those of the Wilson model, demonstrating the superior performance of the proposed method in accurately capturing the characteristics of vessel data.

In conclusion, this paper introduces a new and innovative approach for extracting vessels in brain images using the skew normal distribution and EM algorithm. The method demonstrates remarkable precision in extracting vessels with smooth boundaries and eliminating artifacts. Extensive testing on real MRA images confirms the effectiveness of the approach.

Histogram plots are included to visually represent the data distributions, providing a clear representation of the data distributions for brain MRA images. The comprehensive analysis of the EM algorithm and the skew normal distribution highlights the importance of starting values and suggests the potential of the generalized skew normal distribution for future research.

Furthermore, a comparison of the estimation parameters between the proposed model and the Wilson model illustrates the improved performance of the presented method in accurately capturing the characteristics of the vessel data.

In summary, the proposed method offers both efficiency and accuracy in vessel extraction from brain images. The combination of the skew normal distribution and the EM algorithm allows for precise parameter estimation, resulting in superior vessel segmentation results. Future research can explore the potential of the generalized skew normal distribution and further improve the Proposed method’s performance.