Abstract
This study considers the statistical estimation of relations presented by implicit functions. Such structures define mutual interconnections of variables rather than outcome variable dependence by predictor variables considered in regular regression analysis. For a simple case of two variables, pairwise regression modeling produces two different lines of each variable dependence using another variable, but building an implicit relation yields one invertible model composed of two simple regressions. Modeling an implicit linear relation for multiple variables can be expressed as a generalized eigenproblem of the covariance matrix of the variables in the metric of the covariance matrix of their errors. For unknown errors, this work describes their estimation by the residual errors of each variable in its regression by the other predictors. Then, the generalized eigenproblem can be reduced to the diagonalization of a special matrix built from the variables’ covariance matrix and its inversion. Numerical examples demonstrate the eigenvector solution’s good properties for building a unique equation of the relations between all variables. The proposed approach can be useful in practical regression modeling with all variables containing unobserved errors, which is a common situation for the applied problems.
Keywords:
implicit function; OLS regression; orthogonal regression; diagonal regression; geometric mean regression; residual variance; generalized eigenproblem MSC:
62J02; 15A18
1. Introduction
This paper describes several approaches to the statistical estimation of relations expressed via implicit functions. In regular regression analysis, an outcome variable is observed or measured with errors, and it is presented as an explicit function of the other variables, which are free from errors. The minimization of squared errors by the outcome variable produces an estimation of the parameters in ordinary least-squares (OLS) regression [1]. Depending on which variable is taken as the outcome variable, it is possible to build its own model based on the other variables. These models are different and cannot be reduced from one to another. Even in the simple case of two variables, y and x, in their linear dependence, there are two solutions corresponding to minimizations of deviations in the y-axis or x-axis directions, respectively. These models can be presented graphically as two different lines of each variable dependence by another variable, intersecting at the point of the variables’ mean values. These two relations are not inversible, and only in the case of correlation |r| = 1 do the models coincide. The same two OLS solutions correspond to another scheme of statistical modeling when two random variables satisfy the binormal distribution, and each regression can be obtained as the conditional expectation of one variable by the fixed values of the other variable.
In a general case of n variables, there are n different linear regressions of each variable formed by all the others. These models are not inversible, and thus cannot be reduced from one to another. Such a situation raises a question—is it possible to build a unique model of all the variables connected in one relationship and to make it inversible to express any needed variable as a function of all other variables? A reasonable approach for simultaneous fitting by all directions consists of the minimization of the shortest distances or the length of perpendiculars from the observations to the line, plane, or surface of the variables’ connection in their theoretical model. The first results on such modeling were probably obtained by the American statistician Robert Adcock [2,3,4], and their development led to orthogonal regression by any number of variables, proposed by Karl Pearson [5] as the eigenvector with the minimum eigenvalue of the correlation matrix. In contrast to OLS regression, orthogonal regression is not invariant to the scaling transformation; therefore, it can be applied only to the variables of the same units or to the standardized variables, and its properties have been studied further in many works [6,7,8].
If a functional relation, for example, a physics law or an economics supply–demand link, or any other kind of mutual interconnection, can be assumed for variables measured with errors, then a more general approach of the maximum likelihood objective can be applied to building the models. Such models are called deterministic functional relations (notably, this does not concern functional data analyses, which deal with curves, surfaces, or other structures varying over time). For linear or linearized functional relations, such an approach produces a generalized eigenproblem with two covariance matrices—one of the observed variables and one of the errors of observations by the variables [9]. For uncorrelated errors with equal variances, the generalized eigenproblem reduces to the regular eigenproblem for orthogonal regression.
In the simple case of two variables, if the errors’ variances are proportional to the variances of the variables themselves, the result corresponds to the so-called diagonal regression, which can be presented graphically as a diagonal line of the first and third, or otherwise the second and fourth, quadrants in the plane of the standardized variables [10]. Diagonal regression was proposed by Ragnar Frisch, a Nobel laureate in economics, in his work on confluence analysis, in which functional structure relations were built for random or non-random variables observed with additional random noise [11]. In contrast to OLS regression, for which the slope depends on the pair correlation r, the diagonal regression of the standardized variables depends only on the sign of r, and similar constructs have been described for models using two predictors [12,13].
Diagonal regression is also known as geometric mean regression, standard (reduced) major axis regression, and other names, as described in an extensive review [14]. More references on orthogonal and diagonal regressions and related problems can be found in [15,16,17,18,19,20,21,22,23,24]. The so-called total least squares of the errors-in-variables regression and various other techniques have been developed as well [25,26,27,28,29,30,31].
The current paper considers regression modeling for the functional relations defined in an implicit form. For two variables, the explicit dependence of one variable on another can be written as y = f(x) or x = g(y), while the implicit function can be presented as F(x, y) = 0. In many cases, it is more convenient to use the implicit form in statistical modeling. For example, if the theoretical relation is assumed to be a circle x2 + y2 = ρ2 in the center of coordinates with the radius ρ, it is easier to use two new variables, u1 = x2 and u2 = y2, and to build one simple linear model, u1 + u2 =k, where the estimated constant will then be used to find the radius as ρ = k0.5. Otherwise, initially transforming the model to an explicit form, we would have a more complicated problem of splitting the data to fit each portion to one of the two branches of the functions y1 = +(ρ2 − x2)0.5 and y2 = −(ρ2 − x2)0.5 and then to combine the estimations into one value for the radius. A similar problem of restoring a Pythagorean linear relation between the squares of three variables can be considered by the measurement of three sides of right triangles. The well-known ideal gas law PV/T = constant can be restored from data on the pressure, volume, and temperature, which is modeled in the general linear equation after the logarithmic transformation of this relation.
The implicit function helps to evaluate data corresponding to non-unique but possible multi-value dependencies. The implicit function of the second-order curve of conical sections given by two variables in the linear, quadratic, and mixed items was applied for statistical modeling in [32]. It helps to build a model of two possible values of y at one given value of x, as observed, for instance, in a parabola function extending at some angle to the x-axis. An implicit relations approach was applied for modeling the unitary response data useful for the estimation of shares in the total, and for Thurstone scaling data [33]. Building an implicit logistic regression for description of the so-called supercritical pitchfork bifurcation known in chaotic systems was used in [34]. Bifurcation is a function behavior where a number of solutions and their structure can change abruptly, and such modeling can be helpful in dealing with messy data characterized by a wide range of response variables at each point of the predictors’ values, for instance, those known in advertising and marketing research. Various other applications of the implicit multi-value functions are also known [35,36,37,38,39]. Data fitting for implicit functions can be performed by various techniques of nonlinear statistical estimation available in modern software packages. It is also often possible to use new variables in which the original implicit function can be transformed to a linear function, similar to reducing a circle to the line in the coordinates squared from the original variables.
The regression model of an implicit linear relation for multiple variables can be expressed as the generalized eigenproblem containing two covariance matrices—of the variables and of the errors of their observations. As shown in this study, in the common case of unknown errors, these can be estimated by the residual errors in each variable linear regression by the other predictors. Then, the generalized eigenproblem is reduced to diagonalization of the special matrix constructed from the covariance matrix of the variables and its inversion. The proposed approach enables building a unique equation of relations between all variables when they contain unobserved errors.
2. Modeling for Two Variables
Let us briefly consider OLS regressions. As it is assumed in applied regression modeling, the outcome variable is observed or measured with errors and depends on predictors which are free from errors. For a simple case of two variables, y and x, when a theoretical unobserved value of the dependent variable z2 is linearly connected to x, the model can be written as
where i denotes observations (i = 1, 2, …, N, where N—their total number), a and b are unknown parameters, and is the error by y. The OLS minimizing the sum of squared deviations in Equation (1) yields the solution for the regression of y by x:
where the sample mean values are denoted as mx and my, the standard deviations are and , and r is the correlation between the variables.
Similarly, assuming errors in the x variable, when a theoretical unobserved dependent variable z1 is linearly related to y, we obtain another model:
where c and d are unknown parameters, and is the error by x. The OLS criterion for the total of squared deviations in (3) leads to the regression of x by y:
The two solutions, (2) and (4), correspond to minimizations of deviations in the y-axis or x-axis directions, respectively, and they can be presented graphically as two different lines of each variable dependence by another one. The lines intersect at the point (mx, my) of mean values, and (4) inclines more steeply than (2) to the x-axis, because the slope of the line (2) is proportional to the correlation |r| < 1, and the slope of the line (4) is proportional to the inverse value |1/r| > 1. Only in the case of correlation reaching one by the absolute value, |r| = 1, do both these equations coincide. If y-my is expressed by x-mx from (4), it would not coincide with (2) because there will be the term 1/r instead of r, as in (2), but taking the geometric mean of the slopes of these equations yields the expression
which does not depend on the value of the correlation, but only on its sign sgn(r). Building this model explains its name of “geometric mean regression”, and it presents a compromise between two OLS solutions, is symmetric by both variables, and can be inverted. The coordinates of the standardized variables (centered and normalized by the standard deviations) graphically present a diagonal line with the slope sgn(r), which explains the name of “diagonal regression”.
In addition to classical regression modeling, the relationship models between both variables observed with errors have been considered, with their theoretical values z1 and z2 satisfying the general linear equation of their connection:
where the alphas are unknown parameters. Using this general equation for both variables observed with errors (1) and (3), and taking into account the identical relation (6), yields the relation:
and the errors by each variable are assumed to be of zero mean value. To simplify the derivation, let the variables be centered, then the intercept on the left-hand side of (7) can be omitted, and this side in matrix form can be written as where and are the column-vectors of N observations by the variables. Then, the scalar product of this total vector by itself yields the quadratic form:
where prime denotes transposition, cxx and cyy are the second moments, or sample variances for the variables x and y, respectively, and cxy (equal cyx) is their sample covariance. The second-order matrix C on the right-hand side of (8) is the variance–covariance matrix of the variables, and the vector contains both alpha parameters of the model. Similarly, the right-hand side of (7) in the matrix form can be written as , where the column-vectors contain N errors by the observed variables. The scalar product of this total vector of errors by itself yields another quadratic form:
where sxx and syy are the second moments, or sample variances for the errors by the variables x and y, respectively, and sxy (or syx) is the sample covariance of the errors. Thus, the second-order matrix S on the right-hand side of (9) is the variance–covariance matrix of the variables’ errors.
Finding the minimum sum of squares of the observations’ deviations from the model on the left-hand side of (7) subject to the fixed value at its right-hand side (needed for the parameters identifiability) can be presented as the Rayleigh quotient of two quadratic forms . Minimization of this ratio can be reduced to the conditional least squares problem:
where is the Lagrange term. The derivative of (10) with vector set to zero for finding the extrema yields the relation:
which is the generalized eigenproblem.
In practical modeling, it is commonly assumed that the errors by different variables are independent, so their covariance equals zero, sxy = 0, and S is the diagonal matrix. Then, problem (11) reduces to the regular eigenproblem:
The characteristic equation for problem (12) is defined by the zero value of the determinant:
Solving this quadratic equation and taking the minimum root corresponding to the minimization of the objective (10) produces the expression:
With the minimum eigenvalue (14), the eigenvector can be found. Substituting (14) into one of the equations of the homogeneous system (12), for example, the first one, yields:
The elements and of the eigenvector (11) are defined up to a constant; thus, for their identifiability, we can fix one of them, for instance, . Then, the expression (15) reduces to
with the solution for the unknown element of the eigenvector as follows:
Then, the general linear relation (6) for the centered variables, expressed as the dependence of y by x (for the sake of comparison with the models (2), (4), and (5)), becomes:
This is the generalized eigenproblem solution for a reversable relation between two measured variables with different errors.
In the special case of the equal variances of the errors, sxx = syy, Equation (18) reduces to the following expression:
Equation (19) defines the orthogonal regression which is obtained from the general solution (18) in assumption of the equal precision (measured by the variances) in observations by both variables.
Another special case is defined by the proportion:
This means that the quotient of a variable’s variance by its error’s variance is equal for both variables. The same proportion holds if the ratio of the variances of two variables equals the ratio of the variances of their errors. In assumption (20), Equation (18) simplifies to:
The covariance and correlation are of the same sign, and the standard deviation equals the square root of the variance, (similarly to the other variable); therefore, the result (21) coincides with Equation (5) for diagonal regression. The same results (19)–(21) can be obtained by the maximum likelihood method based on the normal distribution of errors [9,10], but the considered approach dealing with quadratic forms (6)–(11) does not depend on a specific distribution of the errors.
Another reason for choosing the diagonal regression when the errors of observation are unknown could be as follows: let us estimate the error’s variance for each variable using the residual variance of this variable by the other available predictor. In the case of two variables, the residual variance of the model (1)–(2) equals the variance of the dependent variable, multiplied by the term 1 − r2, where r is the coefficient of pair correlation, and a similar construct holds for the second model (3)–(4):
From (22), the first proportion (20) can be derived; thus, in assumption of the residual variances serving as estimates of the unobserved error variances, the diagonal regression (21) can be obtained.
3. Modeling for Many Variables
In a general case of many variables, an implicit function of their connection can be presented in the series by variables in the linear, quadratic, and other order of power and the mix effects. All these items can be considered as new additional variables, and the function can be written as a general linear form:
where denotes each jth theoretical unobserved variable without the errors (j = 1, 2, …, n—the total number of variables) in the ith observation, which is an extension of the equation (6) from two to many variables. The observed variables in each ith point (i = 1, 2, …, N—the total number of observations in the sample) can be defined as:
in which is an error in the ith observation by jth variable, and the errors by each variable are assumed to have zero mean value. Substituting (24) into (23), and taking into account the identical relation (23), yields:
Suppose only one variable is observed with errors, for example, the first variable: , but all other errors equal zero. Dividing by the first alpha coefficient reduces (25) to the explicit model for x1 by new parameters a:
Then, we can build the multiple linear OLS regression of outcome x1 by the other variables. The solution for this model (26) with the centered variables can be presented as the inverted covariance matrix of n − 1 predictors multiplied by the vector of their covariances with the outcome variable x1; the intercept can be found by this equation in the point of mean values of the variables. Instead of the first variable, assumption on the error in another variable leads to its own regression by the remaining n-1 variables.
All possible n regressions of each variable by the other predictors can be obtained in one matrix inversion of all n variables. Consider the matrix X of the order N-by-n with elements xij of ith observations by all jth variables. Suppose the variables are centered, so there are no intercepts in the models. Then, the matrix C = X′X is the sample variance–covariance matrix of the nth order (a generalization of the matrix in (8)). Let C−1 be the inverted matrix, with its elements denoted by the upper indices, (C−1)jk = cjk (these are the cofactors of the elements of the covariance matrix), and the diagonal elements presented in the diagonal matrix D:
As is known, matrix C−1 contains parameters of all n regressions of each variable by all the others. More specifically, any of the models of one variable by the rest of them can be written in the so-called Yule’s notations as follows:
where ajk. denotes the coefficient of the jth regression by the kth variable, and the dot denotes the rest of the variables [9,40]. The non-diagonal elements in any jth row of matrix C−1 divided by the diagonal element in the same row and taken with opposite signs coincide with coefficients of regression xj by all other xs (28) that can be presented as the following matrix of all parameters of all the models:
Additionally, the product Am of matrix A (29) by the vector of mean values m of all predictors coincides with the vector of intercepts a0 for all regressions (28):
The product of the data matrix X by the transposed matrix (29) yields the total matrix E of N-by-n order consisting of the residual errors in all ith observations of all jth regression models (28):
Then, the matrix of the errors’ variance–covariances can be found by the expression:
because is the identity matrix. In assumption of errors’ independence by different outcome variables, matrix (32) can be reduced to its diagonal:
Notably, the values (27) are the so-called variance inflation factors (VIFs), and their reciprocal values (33) are the residual sums of squares in the regressions of each variable xj by the rest of them:
where is the coefficient of multiple determination in the models of each xj by all the other variables. In the case n = 2, Equation (34) reduces to the expression (22), because for two variables, the coefficients of determination coincide with the squared pair correlation, .
Similar to obtaining the geometric mean pair regression (5) from the slopes of the two regressions (2) and (4), if expressing one variable, xj, from the regressions for all other predictors (28) using the coefficients (29), it is easy to see that all these models would coincide if the following relations for the coefficient (29) hold by all the variables:
where the transposed elements of the symmetric inverted matrix are equal, , and the coefficient with a tilde denotes the built parameter of the geometric mean regression model. These parameters can be defined from (35) as . Using them in Equation (28) for the centered variables yields:
This expression presents a heuristic generalization of the geometric mean (5) or diagonal regression (21) for a case of many variables. Recalling the Cramer’s rule that a diagonal element cjj of the inverted matrix equals the quotient of the first minor (which is a determinant of the matrix C(-j) without the jth row and column, equal to the cofactor for the diagonal elements) and the determinant of the whole matrix, we can write the relation:
Substituting this equation into (36) and canceling the total determinant, we can rewrite this equation in a more symmetric form:
This expression has an interesting interpretation in terms of the generalized variance, defined as the determinant of the covariance matrix [41]: a value of each jth coefficient of the diagonal regression (38) equals the square root of the generalized variance of all additional variables to the xj variable.
Let us return to the general relation (25) and rewrite it for the centered variables in the matrix form as , where E is the matrix of the unknown errors by all observations in the model (25). The scalar products of these vectors by themselves yield the expression:
where the matrices C = X′X and S = E′E are the nth order extensions of the second-order matrices in (8) and (9). For solving this problem for vector of n parameters, we can find the minimum of the quadratic form on the left-hand side of (39) subject to the normalizing condition on its right-hand side (needed for the identifiability of the parameters defined up to an arbitrary constant). It corresponds to presenting (39) as the Rayleigh quotient of two quadratic forms, , reduced to the conditional least squares problem (10), and then to the generalized eigenproblem (11) for the nth order covariance matrices C and S of the variables and their errors, respectively.
For unknown errors of observations, let us estimate the error’s variance for each variable as the residual variance of this variable by all the rest of predictors, as it is considered in the case of two variables in the relation (22). For the case of independent errors, we substitute the diagonal matrix of variances (33) into the generalized eigenproblem (11), which produces the following relation:
For the more general case of the possibly correlated errors, we substitute the variance–covariance matrix (32) into the generalized eigenproblem (11) which yields the expression:
where the eigenvalue is renamed to to distinguish it from eigenvalue in the problem (40). The matrix D is defined by the inverted matrix C−1 (27); therefore, both last generalized eigenproblems can be expressed via the variance–covariance matrix of the variables. Transforming (40) to the regular eigenproblem yields the equation:
and a similar transformation of (41) leads to the equation:
If the matrix DC is multiplied by the problem (42), we derive the relation:
Therefore, the eigenvalues in (43) equal the squared eigenvalues in (42), . However, the sets of eigenvectors of both problems (42) and (43) coincide; thus, the eigenvector solution related to the minimum eigenvalue in any of these two problems is the same. It is an unexpected result that this solution does not depend on the assumption of the correlated or non-correlated errors used in (40) and (41), respectively. Therefore, it is sufficient to solve the simpler problem (42) which, utilizing the definition (27), can be presented as follows:
The solution (45) for the eigenvector related to the minimum eigenvalue defines the functional implicit multiple linear regression (23).
Suppose all diagonal elements of the matrix C−1, or the errors’ variances are the same; thus, diag(C−1) is a scalar matrix, and the problem (45) is essentially the eigenproblem of a covariance matrix. Then, its maximum and several next big eigenvalues define the main eigenvectors used in the well-known principal component analysis (PCA), and in the regression modeling of the PCA scores employed in place of the original predictors for a multicollinearity reduction. On the other hand, of the covariance, or correlation matrix, defines the eigenvector which presents the coefficients of the orthogonal regression [5]. Although they are based on the same eigenproblem, the PCA and regression on PCA differ from the orthogonal regression, as well as from the functional implicit regression in the case of different variances of errors.
Problem (45) presents a generalization of the solution (16)–(18) to the multiple models with n > 2 variables. Such a model is symmetrical by all variables, and any one of them can be expressed via the others from this unique equation. Eigenproblem (45) with n variables reduces to the explicit eigenproblem (12) if n = 2. The errors’ variances sxx and syy in (12) are extended to many variables with the errors’ variances defined by (34) in a general case of n variables.
The eigenproblem (45) of the non-symmetric matrix can be transformed to the eigenproblem of a symmetric matrix which is more convenient in numerical calculations because it produces a higher precision of estimations. For this aim, let us rewrite problem (42) as the following expression:
where D1/2 is the square root of the diagonal matrix D (27). The problem (46) can be represented as the following eigenproblem:
where the symmetric matrix, B, and its eigenvectors are defined by the relations:
The regular eigenproblem of the symmetric matrix (47) can be solved by most modern statistical and mathematical software packages. When the eigenvector for the minimum eigenvalue in (47) is found, the original eigenvector can be obtained from (48) by the inversed transformation:
Taking into account the relations (27) and (37), we can find each jth element of the diagonal matrix in (49):
Then, the original estimated model (25) with parameter alpha (49) can be presented for the centered variables as follows:
where the common constant of determinant det(C) (50) is cancelled. In the case of an ill-conditioned or even singular sample covariance matrix C, the inverted matrix could not exist, but it is still possible to present the solution (51) via the determinants without each individual variable.
The functional implicit linear regression (51) obtained with the errors assumed by all variables can be solved with respect to any one variable xj, similar to the heuristically constructed diagonal regression (38). Both models (38) and (51) have parameters proportional to the square root of the generalized variances; however, in place of the sign functions in (38) there are coefficients (51) of the eigenproblem (47). Finding one of two possible signs for each variable presents an additional problem in building the model (38), while the coefficients are uniquely defined in solving the eigenproblem (47) for the minimum eigenvalue .
For the characteristics of quality, the minimum eigenvalue of the standardized matrix B (48) can serve as a measure of the residual sum of squares , taken by the shortest distances from the observations to the hyperplane of the orthogonal regression in the metric of the matrix D1/2. An analogue of the coefficient of determination R2 in multiple regression can also be constructed as one minus the quotient of the minimum eigenvalue to the mean of all eigenvalues:
4. Numerical Examples
For the first example, consider the simulated data for the conic section curve defined by the implicit equation of the second order:
This corresponds to the parabola with its axis of symmetry extending at the angle −45° to the x-axis. Solving this quadratic equation with respect to the y variable yields two branches of this parabola,
which are shown in Figure 1.
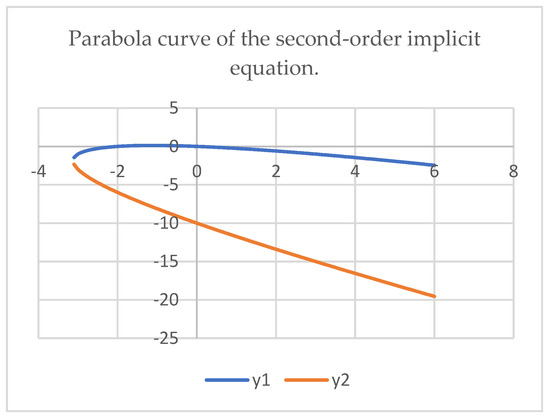
Figure 1.
Parabola defined by Equation (53), with its branches defined in relations (54).
Having a set of numeric data on x and y variables, it is still a problem to restore such a parabola equation because it has not the unique, but dual values of y at each x, so a regression of y by x could produce a line of the axis of symmetry between the branches. By the same reason, building a quadratic regression of x by y also has a problem of dual x values for the same y in the upper branch, which would distort the model. Separate modeling for the branches (54) requires splitting the data related to each branch and application of the nonlinear estimation.
If the numeric values on the x variable and on y variable defined in (54) were obtained with an additional noise of errors, it increases the difficulty of the adequate restoration of the original implicit Equation (53). The higher variability in the errors, the more fuzzified the scatter plot of the original function hidden behind the empirical data.
An example for the implicit function (53) with data by x taken from −3.1 to 6.0 with the step 0.1, for the sample size N = 92, was used to build the values of the functions (54). The random noise of normal distribution N(0, 1) with zero mean value and the standard deviation std = 1 was added to x and y variables. These values are presented in the scatter plot shown in Figure 2.
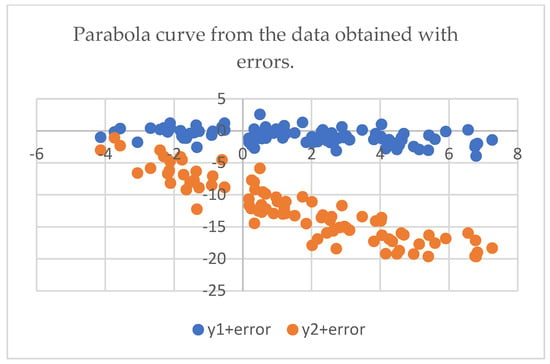
Figure 2.
Parabola data with the added normal random errors N(0, 1).
To restore the original function from the data obtained with errors, we can rewrite Equation (53) as a generalized linear implicit function:
where the notations for the new variables, uj, are:
The coefficients in (55) for the original implicit function (53) are as follows:
Applying the considered above approach for evaluating these parameters by the data distorted with errors, we can build each variable uj regression by the other u-variables, find their residual variances, and use them for the errors’ estimates in the generalized eigenproblem. The obtained results are shown in Table 1, the columns in which present the intercept and parameters of the original function (53), five OLS regressions (29), and the general eigenvector solution (51).

Table 1.
Original function, OLS regressions, and eigenvector (parabola example).
The last two rows in Table 1 show the residual variance S2resid and the coefficient of multiple determination R2 for each OLS regression, as well as their analogues for the eigenvector solution (52). For the original exact function (53), S2resid = 0, and R2 = 1; therefore, by comparison, it can be determined which models are of a better quality than the others.
Table 2 presents parameters in each model divided by the coefficient for the first variable, which is more convenient for comparison across the models. It is easy to see that some models reconstruct the original model more accurately than the other models.

Table 2.
The models normalized by the first coefficients (parabola example).
To find a measure of this closeness, we calculate pair correlations between the solutions. The correlations of the vectors in the columns of Table 2 (except for the intercepts, which depend on the slope parameters) are presented in Table 3.

Table 3.
Correlations between the normalized solutions (parabola example).
Table 3 shows that many models are highly correlated with the original function and among themselves. The last row of the mean correlations also indicates that the OLS models for u2, u3, and u5 (56), as well as the eigenvector solution, are the best performers, with high correlations with the original function.
Using any obtained solution for regression parameters from Table 1, we can calculate the values of the parabola (55) and (56) branches by the formula:
For illustration, using parameters of the solution by the eigenvector in the last column of Table 1, we can restore the parabola from the data with random noise—Figure 3 presents the original parabola and the restored curve.
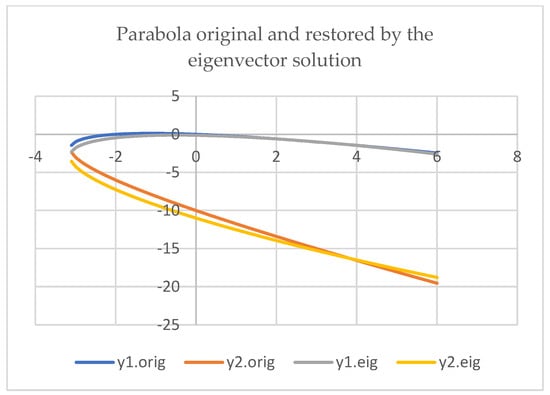
Figure 3.
The exact original parabola and the curve restored by the eigenvector.
The results of the eigenvector solution with the data distorted by the random noise yield a good approximation for the original exact data. The difference in the restored from the original values of the function can be estimated by the mean absolute error (MAE) or by the standard deviation (STD). For the results presented in Figure 3, these estimates are MAE = 0.442 and STD = 0.505, that are acceptable values in comparison with the standard deviation used in the random normal noise N(0, 1) added to x and y variables.
For the second numerical example, the dataset on physicochemical properties of the red wine [42] was taken (freely available at the site Wine Quality—UCI Machine Learning Repository; also available through the link Red Wine Quality | Kaggle). From that total dataset of 1599 observations and 12 variables, the following 10 variables describing chemical features were used: x1—fixed acidity; x2—volatile acidity; x3—citric acid; x4—residual sugar; x5—chlorides; x6—free sulfur dioxide; x7—total sulfur dioxide; x8—pH; x9—sulphates; and x10—alcohol.
To predict each of these characteristics using the others, we considered the outcome variable in the regression model, so ten such models could be built. These models differ and do not reduce from one to another one. However, it was possible to assume that all these characteristics were connected among themselves, and to construct one implicit relation of their interdependence by which any variable can be expressed via the rest of them. The next three tables are organized similarly to the first three tables (with an exception of the original function which is not known in these data).
Table 4 presents all ten OLS regression parameters (29) (the columns in this table correspond to the rows in the matrix on the right-hand side of (29)), as well as the general eigenvector solution (51).

Table 4.
OLS regressions and eigenvector (wine example).
Each column in Table 4 shows the intercept and the coefficients of regression which are given as in the implicit form (23); thus, to obtain the actual OLS model (28) in explicit form, we changed the signs of all coefficients. For instance, the model for the outcome x1 is:
The eigenvector model given in Table 4, is as following:
Each of the OLS regressions presents a model of the dependence of one particular variable by all the others of them; for example, the model for x1 in Equation (59) can find the values of the dependent variable by the given values of its predictors. In contrast to the OLS models, the generalized linear relation (60) shows how, and in which proportions, all chemical components in this example can be combined in the relation of their interconnection. This can facilitate examination and interpretation of the components in their compound of a better property product.
The two bottom rows in Table 4 present the residual variance and the coefficient of multiple determination R2 for each OLS regression model, as well as their analogues for the eigenvector solution (52). Most of the models were of good quality.
For the sake of comparison, we divided the parameters in each model by its coefficient for the first variable, which yielded the results presented in Table 5.

Table 5.
The models normalized by the first coefficients (wine example).
There is a wide variability in the parameters across the models in Table 5; therefore, to estimate the closeness between these solutions, we identified pair correlations. Table 6 shows the pair correlations of the vectors from the columns in Table 5.

Table 6.
Correlations between the normalized solutions (wine example).
Correlations were determined by the regressions’ coefficients only, without the intercepts. Many of the models are closely related. The bottom row of the mean correlations in the matrix columns in Table 6 indicates that the last model had the highest mean value; thus, the eigenvector solution presents a good compromise between the partial regression models of each one variable by the others of them.
5. Summary
This paper describes a statistical estimation of interconnections among the variables presented by the implicit functions. In the regular regression analysis for a given dataset, there could be many regressions with different variables taken as the dependent; however, building an implicit relation yields one unique invertible model of connection between all the variables. This kind of statistical modeling rather corresponds to restoring existing physical laws between the variables than to an approximation of the dependence of one outcome variable by the other predictors.
Modeling of the implicit linear relation is expressed as the generalized eigenproblem of the covariance matrix of the variables in the metric of the covariance matrix of their errors. Derivation was performed using relations between the quadratic forms in (6)–(11), (23)–(25), and (39)–(40), which are free from assumptions on a specific distribution of the errors, which could find wider practical applications.
For unknown errors, this study suggests performing their estimation via the residual errors of the ordinary least square regression of each variable by the other ones. In the simple case of two variables, the analytical close-form solutions are presented, including the orthogonal and diagonal, or geometric mean regressions. In the case of many variables, the generalized eigenproblem can be reduced to diagonalization of the matrix built from the covariance matrix of the variables and its inversed matrix. As shown in the derivations (40)–(45), the interesting feature of this generalized eigenvector problem is that the results are the same for both cases of the correlated and non-correlated estimated errors. The generalized eigenproblem solution holds the scale invariant property as well.
Numerical examples show that the eigenproblem solution presents a good compromise between all particularly regular regressions. The considered method of modeling with variables containing errors enables a unique equation of relations between all variables to be built that can be useful in practical regression modeling.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data sources are given in the references.
Acknowledgments
I am thankful to the three reviewers for their comments and suggestions which improved the paper.
Conflicts of Interest
The author declares no conflict of interest.
References
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Adcock, R.J. Note on the method of least squares. Analyst 1877, 4, 183–184. [Google Scholar] [CrossRef]
- Adcock, R.J. A problem in least squares. Analyst 1878, 5, 53–54. [Google Scholar] [CrossRef]
- Adcock, R.J. Extension of the method of least squares to any number of variables. Analyst 1880, 7, 22–23. [Google Scholar] [CrossRef]
- Pearson, K. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Koopmans, T.C. Linear Regression Analysis of Economic Time Series; DeErven F. Bohn: Haarlem, The Netherlands, 1937. [Google Scholar]
- Deming, W.E. Statistical Adjustment of Data; Wiley: New York, NY, USA, 1943. [Google Scholar]
- Jackson, J.D.; Dunlevy, J.A. Orthogonal least squares and the interchangeability of alternative proxy variables in the social sciences. Statistician 1988, 37, 7–14. [Google Scholar] [CrossRef]
- Kendall, M.G.; Stuart, A. The Advanced Theory of Statistics: Inference and Relationship, 2nd ed.; Griffin: London, UK, 1983; Chapter 29. [Google Scholar]
- Leser, C.E.V. Econometric Techniques and Problems; Griffin: London, UK, 1974; Chapter 2. [Google Scholar]
- Frisch, R.A.K. Statistical Confluence Analysis by Means of Complete Regression Systems; Economics Institute, University of Oslo: Oslo, Norway, 1934. [Google Scholar]
- Cobb, C.W. Note on Frisch’s diagonal regression. Econometrica 1939, 7, 77–80. [Google Scholar] [CrossRef]
- Cobb, C.W. A regression. Econometrica 1943, 11, 265–267. [Google Scholar] [CrossRef]
- Xe, S. A property of geometric mean regression. Am. Stat. 2014, 68, 277–281. [Google Scholar]
- Durbin, J. Errors in variables. Rev. Int. Stat. Inst. 1954, 22, 23–32. [Google Scholar] [CrossRef]
- Creasy, M.A. Condense limits for the gradient in the linear functional relationship. J. R. Stat. Soc. Ser. B 1956, 18, 65–69. [Google Scholar]
- Sprent, P.; Dolby, G.R. Query: The geometric mean functional relationship. Biometrics 1980, 36, 547–550. [Google Scholar] [CrossRef]
- Barker, F.; Soh, Y.C.; Evans, R.J. Properties of the geometric mean functional relationship. Biometrics 1988, 44, 279–281. [Google Scholar] [CrossRef]
- Draper, N.R.; Yang, Y.F. Generalization of the geometric mean functional relationship. Comput. Stat. Data Anal. 1997, 23, 355–372. [Google Scholar] [CrossRef]
- Leng, L.; Zhang, T.; Kleinman, L.; Zhu, W. Ordinary least square regression, orthogonal regression, geometric mean regression and their applications in aerosol science. J. Phys. Conf. Ser. 2007, 78, 012084. [Google Scholar] [CrossRef]
- Tofallis, C. Fitting Equations to Data with the Perfect Correlation Relationship; Working Paper Series; University of Hertfordshire Business School: Hertfordshire, UK, 2015. [Google Scholar] [CrossRef]
- Bottai, M.; Kim, T.; Lieberman, B.; Luta, G.; Pena, E. On Optimal Correlation-Based Prediction. Am. Stat. 2022, 76, 313–321. [Google Scholar] [CrossRef]
- Christensen, R. Comment on “On Optimal Correlation-Based Prediction,” by Bottai et al. (2022). Am. Stat. 2022, 76, 322. [Google Scholar] [CrossRef]
- Lipovetsky, S. Comment on “On Optimal Correlation-Based Prediction,” by Bottai et al. (2022). Am. Stat. 2023, 77, 113. [Google Scholar] [CrossRef]
- Tan, C.Y.; Iglewicz, B. Measurement-methods comparisons and linear statistical relationship. Technometrics 1999, 41, 192–201. [Google Scholar] [CrossRef]
- Kukush, A.; Mandel, I. Does regression approximate the influence of the covariates or just measurement errors? A model validity test. arXiv 2019, arXiv:1911.07556. [Google Scholar]
- Francq, B.G.; Govaerts, B.B. Measurement methods comparison with errors-in-variables regressions. From horizontal to vertical OLS regression, review and new perspectives. Chemom. Intell. Lab. Syst. 2014, 134, 123–139. [Google Scholar] [CrossRef]
- Yi, G.Y.; Delaigle, A.; Gustafson, P. Handbook of Measurement Error Models; Chapman and Hall/CRC: Boca Raton, FL, USA, 2021. [Google Scholar]
- Lipovetsky, S. The review on the book: “Handbook of Measurement Error Models, by Yi, G.Y. et al., Eds.”. Technometrics 2023, 65, 302–304. [Google Scholar] [CrossRef]
- Fuller, W.A. Measurement Error Models; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Van Huffel, S.; Lemmerling, P. (Eds.) Total Least Squares and Errors-in-Variables Modeling: Analysis, Algorithms and Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Lipovetsky, S. Regression models of implicit functions. Ind. Lab. 1979, 45, 1136–1141. [Google Scholar]
- Lipovetsky, S. Unitary response regression models. Int. J. Math. Educ. Sci. Technol. 2007, 38, 1113–1120. [Google Scholar] [CrossRef]
- Lipovetsky, S. Supercritical pitchfork bifurcation in implicit regression modeling. Int. J. Artif. Life Res. 2010, 1, 1–9. [Google Scholar] [CrossRef][Green Version]
- Schmidt, M.; Lipson, H. Symbolic regression of implicit equations. In Genetic Programming Theory and Practice VII; Riolo, R., O’Reilly, U.M., McConaghy, T., Eds.; Springer: Boston, MA, USA, 2010; pp. 73–85. [Google Scholar]
- Wooten, R.D.; Baah, K.; D’Andrea, J. Implicit Regression: Detecting Constants and Inverse Relationships with Bivariate Random Error. Cornell University Library, 2015. Available online: https://arxiv.org/abs/1512.05307v1 (accessed on 24 August 2023).
- Wooten, R.D. Introduction to Implicit Regression: Extending Standard Regression to Rotational Analysis and Non-Response Analysis. Cornell University Library, 2016. Available online: https://arxiv.org/abs/1602.00158v1 (accessed on 24 August 2023).
- Miao, Z.; Zhong, J.; Yang, P.; Wang, S.; Liu, D. Implicit neural network for implicit data regression problems. In Neural Information Processing; Mantoro, T., Lee, M., Ayu, M.A., Wong, K.W., Hidayanto, A.N., Eds.; Springer: Cham, Switzerland, 2021; pp. 187–195. [Google Scholar]
- Zhong, J.; Yang, J.; Chen, Y.; Liu, W.-L.; Feng, L. Mining implicit equations from data using gene expression programming. IEEE Trans. Emerg. Top. Comput. 2022, 10, 1058–1074. [Google Scholar] [CrossRef]
- Yule, G.U.; Kendall, M.G. An Introduction to the Theory of Statistics; Griffin: London, UK, 1950. [Google Scholar]
- Kocherlakota, S.; Kocherlakota, K. Generalized Variance. In Encyclopedia of Statistical Sciences; Johnson, N.L., Kotz, S., Eds.; Wiley: New York, NY, USA, 1983; Volume 3, pp. 354–357. [Google Scholar]
- Cortez, P.; Cerdeira, A.; Almeida, F.; Matos, T.; Reis, J. Modeling wine preferences by data mining from physicochemical properties. Decis. Support Syst. 2009, 47, 547–553. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).