Abstract
P-values have played a central role in the advancement of research in virtually all scientific fields; however, there has been significant controversy over their use. “The ASA president’s task force statement on statistical significance and replicability” has provided a solid basis for resolving the quarrel, but although the significance part is clearly dealt with, the replicability part raises further discussions. Given the clear statement regarding significance, in this article, we consider the validity of p-value use for statistical inference as de facto. We briefly review the bibliography regarding the relevant controversy in recent years and illustrate how already proposed approaches, or slight adaptations thereof, can be readily implemented to address both significance and reproducibility, adding credibility to empirical study findings. The definitions used for the notions of replicability and reproducibility are also clearly described. We argue that any p-value must be reported along with its corresponding s-value followed by confidence intervals and the rejection replication index.
1. Introduction
P-value reporting has been an issue of controversy for the different schools of thought in statistics [1]. A consensus exists pertinent to their misinterpretation though. The latter has been an issue of concern within the whole statistics community [2]. The abuse of p-value use, such as characterizing as a “trend” or “near significant” any result greater than but close to the nominal level (typically 0.05), has been extensively documented in the literature (see [3]). There is ample evidence that applied researchers misuse and misinterpret p-values in practice, and even expert statisticians are sometimes prone to misusing and misinterpreting them. The large majority are generally aware that statistical significance at the 0.05 level is a mere convention, but this convention strongly affects the interpretation of evidence [4]. General guidance regarding misinterpretations has appeared in the literature [5].
Reflection articles or short communications have appeared, trying to elaborate or constructively comment, without aphorisms, on the proper use of p-values [6,7,8,9,10,11,12,13]. Harsher criticism via reflection articles, essays, and whole books has also widely appeared [14,15,16,17,18,19], while complete rejection of its use has been proposed in essays published in highly prestigious journals [20,21]. Some authors even find it hard to decide after all [22]. Solutions proposed by prominent researchers, such as using confidence intervals instead of hypothesis tests for parameters of interest [23,24] have been criticized by others [25,26]. Adapting the alpha level in an ad hoc fashion has also been proposed [27].
The Board of Directors of the American Statistical Association (ASA) issued a Statement on Statistical Significance and p-values [28]. The ASA Statement, aimed at “researchers, practitioners, and science writers who are not primarily statisticians”, and consists of six principles:
- p-values can indicate how incompatible the data are with a specified statistical model.
- p-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone.
- Scientific conclusions and business or policy decisions should not be based only on whether a p-value passes a specific threshold.
- Proper inference requires full reporting and transparency.
- A p-value, or statistical significance, does not measure the size of an effect or the importance of a result.
- By itself, a p-value does not provide a good measure of evidence regarding a model or hypothesis.
The ASA Statement notes the following: “Nothing in the ASA statement is new. Statisticians and others have been sounding the alarm about these matters for decades, to little avail” [29].
Statistical significance often does not equate to clinical significance. Stating an example from the literature, a large trial estimates a risk ratio of 0.97 and a 95% confidence interval of 0.95 to 0.99, then the treatment effect is potentially small, even though the p-value is much lower than 0.05. Conversely, the absence of evidence does not mean evidence of absence; if a small trial estimates a risk ratio of 0.70 and a 95% confidence interval of 0.40 to 1.10, then the magnitude of effect is still potentially large, even though the p-value is greater than 0.05. As a result, statements such as “significant finding” must be less definitive overall. A Bayesian approach may be helpful to express probabilistic statements (e.g., there is a probability of 0.85 that the risk ratio is <0.9) [30]. Indeed, nicely described Bayesian formulations and analogues have appeared [31,32]. A number of researchers have proposed moving to Bayesian principles (e.g., [33]). The theoretical framework of these principles has been studied in the literature [34,35]. The advantages of using Bayesian alternatives have been discussed within a rather limited generalizability framework though [36], while standard Bayesian data-analytic measures have been shown to have the same fundamental limitations as p-values [37]. It has been documented that subjective Bayesian approaches have some hope [38] but still exhibit severe limitations [15].
Bayesian criticism has been formally described as an overreaction [39,40]. In fact, recently [41], it has been shown that under noninformative prior distributions, there is equivalence between the p-value and Bayesian posterior probability of the null hypothesis for one-sided tests and, more importantly, there is equivalence between the p-value and a transformation of posterior probabilities of the hypotheses for two-sided tests. In contrast to the common belief, such an equivalence relationship renders the p-value an explicit interpretation of how strongly the data support the null. Contrary to broad criticisms on the use of p-value in evidence-based studies, its utility is thus justified, and its importance from the Bayesian perspective is reclaimed, establishing a common ground for both frequentist and Bayesian views of statistical hypothesis testing [41].
Good decision making depends on the magnitude of effects, the plausibility of scientific explanations of the mechanisms involved, and the reproducibility of the findings by others [42]. Even in well-designed, carefully executed studies, inherent uncertainty remains, and the statistical analysis should account properly for this uncertainty [28]. Overinterpretation of very significant but highly variable p-values is an important factor contributing to the unexpectedly high incidence of non-replication [43].
In part, limitations of p-values stem from the fact that they are all too often used to summarize a complex situation with false simplicity [44]. Overall, however, there is a broad consensus that p-values are useful tools if properly used [45,46]. One needs to keep in mind the general principles of the role of statistical significance tests in the analysis of empirical data. Decision making in contexts such as medical screening and industrial inspection must be followed with an assessment of the security of conclusions [1].
A concise critical evaluation on the p-value controversy [47] offered the opportunity to expand on the subject in a special issue in the Biometrical Journal, Volume 59, Issue 5 (2017), with contributions from several renowned researchers [48]. Several articles from therein are cited in this work. Other prestigious journals have also dedicated special issues in this discussion and a complete set of guidelines on the appropriate use of p-values [49,50]. A wealth of proposals can be found in these. A large part of the overall criticism on the use of p-values appears in the relevant special issue of the American Statistician, Volume 73, Issue sup1 (2019). Overall, topics tackled therein involve the evolution of statistical significance/decision making in the hypothesis testing, interpretation and use of p-values, supplementing and replacing p-values, and other holistic approaches. A total of more than 40 articles is a useful collection; however, one may claim that a Babel tower of scientific research has thus been constructed. The lack of consensus and further solid actions appear to have hampered forward progress. Furthermore, standard textbooks still employ and support the use of the traditional p-value approach (e.g., [51]), though reference to possible extensions and adaptations can be found (e.g., [52], pp. 8–11).
Overall, from our experience, we gather that, apart from the reassuring ASA statement regarding p-values, reasons for the stagnation in terms of the better reporting results of statistical inference include that a big proportion of researchers in the subject matter literature might not even be aware of the relevant controversy and its importance. This might be the result of paywalls for the journals that took part in this dialog so far. Most importantly, possible changes also need to be implemented in widely used statistical software and introductory statistics textbooks alike; otherwise, not much can be expected to change.
The p-value seems to be here to stay. We may complement this in the need to reach firmer conclusions regarding statistical inference and to provide a reference point regarding the replicability of statistical analysis results. Subtle differences exist between the notions of reproducibility and replicability as defined in the literature. Specifically, reproducibility refers to the ability of a researcher to duplicate the results of a prior study using the same materials as those used by the original investigator. This requires, at minimum, the sharing of data sets, relevant metadata, analytical code, and related software. Replicability refers to the ability of a researcher to duplicate the results of a prior study if the same procedures are followed but new data are collected [53,54]. We adopted this definition in this work, although the notions of replicability and reproducibility are often used interchangeably in published research. Specifically, to quantitatively account for reproducibility, in this work, we revisit the proposed approach in Boos and Stefanski (2011) [55], illustrate its use and argue that it provides a path which allows to move forward in statistical inference in a world of availability of the respective stipulated, rather minimal nowadays, computational power.
In most cases, by simply using a p-value, we ignore the scientific tenet of both replicability and reproducibility, which are important characteristics of the practical relevance of test outcomes [56]. Poor replicability from studies demonstrating significant p-values at the 5% level has been documented [57,58]. Several researchers have tried to build on the concept [59], while the need for a replicability accompanying index has also been documented [60]. The use of B-values in a two-stage testing approach has been proposed as a procedure that can improve reproducibility [61]. The adaptations studied in this article make use of bootstrapped data. Since no actual new data are sampled, we adopt “reproducibility” as the appropriate term for the described methods.
The accurate interpretation of the p-value is probably the most important advice in the relevant literature reviewed above. A number of authors have proposed complementing this for good reason, pertinent to the replication of the study findings. We argue here that complementing all p-values in any statistical analysis report in the direction of reproducibility may actively help in decision making. In fact, the use of three quantities—(i) p-value, (ii) s-value along with corresponding CIs, and (iii) the rejection replication index (rri)—as an output of any statistical testing procedure may be a prudent way to move forward, complementing the current practice.
A review of the proposed approaches and their implementation is illustrated in the Materials and Methods section that follows. Methods are illustrated in the Application section. We end with a discussion.
2. Materials and Methods
Statistical inference relies on p-value reporting, thus focusing on the validity of the null hypothesis. Supplementing the p-value with its Shannon information transform (s-value or surprisal), offers some advantages. Specifically, it actually measures as an effect size the amount of information supplied by the test against the tested hypothesis (or model). The s-value is a useful measure of the evidence against the null hypothesis, in which the larger the s-value, the more evidence against . Rounded off, the s-value shows the number of heads in a row one would need to see when tossing a coin to obtain the same amount of information against the tosses being “fair” (independent with “heads” probability of 1/2) instead of being loaded for heads. For example, if p = 0.03125, this represents − bits of information against the hypothesis (such as getting 5 heads in a trial of “fairness” with 5 coin tosses); and if p = 0.25, this represents only − bits of information against the hypothesis (such as getting 2 heads in a trial of “fairness” with only 2 coin tosses). Notice that −, entailing the quantification of a single bit of information against the null [14].
As a second step, it is suggested that a bootstrap distribution of p-values must be produced (a process referring to the bootstrap prediction intervals in [55]), offering a reference for the variability of the p-value (and as a result of this of the s-value) and an estimate of the probability of the independent replication of a statistically significant result. This is simply derived by bootstrapping the dataset at hand and calculating the corresponding p-value. Transforming the bootstrapped p-values using the Shannon information transform results in a distribution for the corresponding s-values. The s-value follows an asymptotically normal distribution as formally shown in Boos and Stefanski (2011) [55]. The distribution of the s-value, being more symmetric than its p-value counterpart, offers a better reference for effect sizes against the null hypothesis. Confidence intervals for the s-value can then be readily constructed using any bootstrap variant of choice. The replication rejection index (rri) is simply defined as the number of times is rejected based on the bootstrap distribution of the p-value at a given significance level.
Given the computational burden involved, the proposed practice might have been difficult to follow in the early days of applied statistics; however, it is not an issue of even remote concern nowadays.
3. Revisiting a Real-World Published Application
We illustrate the described adjustment/procedure on p-value use analyzing publicly available data (http://dx.doi.org/10.13140/RG.2.2.22805.96482 (accessed on 10 March 2023)) from a study evaluating the utility of biomarkers sTREM-1 and IL-6 (the latter is an established marker) for the detection of late-onset sepsis (LoS) in neonates [62]. We revisit the analysis therein, supplementing p-values with corresponding s-values and their confidence intervals, and the rri.
In general, neonates that develop LoS have elevated values for the two biomarkers (Figure 1). ROC curve analysis has been used to assess the accuracy of the two biomarkers and to formally compare them using the AUC [63].
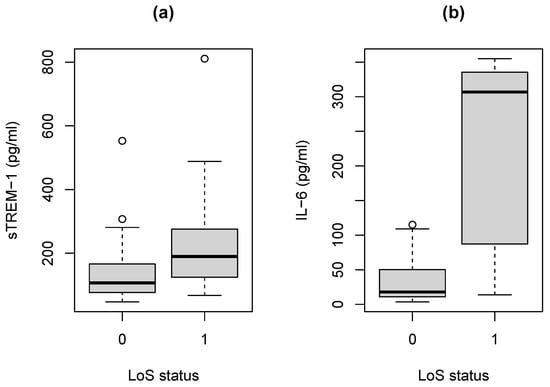
Figure 1.
Boxplots of biomarker measurements for neonates developing LoS (denoted by ‘1’) vs. controls (‘0’). (a) Biomarker sTREM-1. (b) Biomarker IL-6.
For sTREM-1, , and , while for IL-6 , , . One thousand bootstrap replications were used for the construction of 95% CIs via the corresponding 2.5% and 97.5% quantiles of the derived bootstrap distribution. The AUC comparison of the two biomarkers leads to , . The nonparametric approach of DeLong et al. (1988) was used for ROC curve analysis [64] via the pROC package [65] in R version 4.1.2 (The R Foundation for Statistical Computing, Vienna, Austria). R code for the reproduction of results is given in Appendix A. Results are summarized in Table 1. The analogy of the s-value size relative to coin tossing described in the previous section gives the big picture. The relevant bootstrap s-value distributions are illustrated in Figure 2. Specifically, we estimate that for sTERM-1, there are seven bits against the null hypothesis, while for IL-6, there are 21. Each bit represents the number of “heads” in a row that one would need to see when tossing a coin to obtain the same amount of information against the tosses being “heads” with probability equal to 50%.

Table 1.
Inference results for biomarkers sTREM-1 and IL-6.
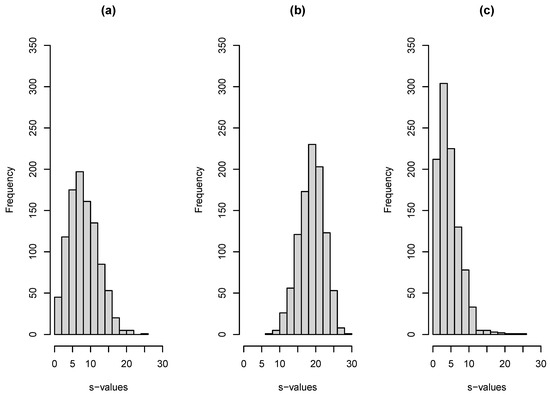
Figure 2.
Bootstrap s-value distributions for the LoS biomarker study illustration. (a) For biomarker sTREM-1. (b) For biomarker IL-6. (c) For the comparison of the two biomarkers (two-sided alternative).
We conclude that IL-6 consistently discriminates between noninfected (controls) and infected (cases) neonates (illustrated in Figure 2b). The estimated rri can be regarded as evidence that one can always replicate the significance of IL-6 as a diagnostic marker for LoS, while this is true most of the time (about 80%) for sTREM-1. The latter can thus be considered a useful biomarker (illustrated in Figure 2a). The formal comparison of AUCs shows that IL-6 is, in general, a better biomarker, but this evidence is not overwhelming given the rri = 0.441, suggesting that the reproducibility of a significant difference between IL6 and sTREM-1 can be expected in about 45% of replications of the experiment. The corresponding bootstrap distribution of the s-values is illustrated in Figure 2c. A more complete assessment is thus provided relative to a reference to a “marginally significant” result of p = 0.0534.
4. Discussion
Statistics quantify uncertainty. We should be skeptical of peddling impossible guarantees, rather than demanding them, and celebrate those who tell us about risk and imprecision [66]. One could claim that most statisticians would agree that the answer to both questions below is a clear ‘No’ [67]:
- Is hypotheses testing (or some other approach to binary decision making) unsuitable as a methodological backbone of the empirical, inductive sciences?
- Should p-values (or Bayesian analogs of them) be banned as a basic tool of statistical inference?
Citing Wellek (2017) [47], the logic behind statistical hypotheses testing is not free of elements deemed artificial and, in line with this, it becomes difficult to grasp for many applied researchers. Perhaps the most conspicuous of these features is the intrinsic asymmetry of the roles played by the two hypotheses making up a testing problem: the possibility of being rejected subject to a known bound to the risk of taking a wrong decision and hence of confirming its logical counterpart (typically its complement) exists only for . In fact, there is no need to even state an alternative hypothesis in the framework of classical hypothesis testing (see [68], p. 9 and [39]), and important textbooks avoid even simple reference to alternative hypotheses [68,69]. Rather than having formal rules for when to reject the null model, it has been suggested that one can just report the evidence against the null model [69]. However, the notion of an alternative hypothesis is fundamental in the study design and sample size calculation as a first step in an experimental study and can be useful in deciphering the null from the alternative hypothesis distributions given the data. Specifically, the distribution function of a test statistic under the alternative hypothesis is equivalent to the ROC curve of the distribution of the corresponding p-value under the null hypothesis vs. the distribution of p under the alternative [70,71]. Theoretical and specific technical properties have been detailed [55,72,73,74]. This equivalence is also spotted in ROC-related research [75,76,77]. As a result, the use of ROC-based criteria for general statistical inference can also offer a wide area of future research on the topic.
Other concepts trying to replace or complement the traditional p-value have appeared in the literature [12,49,70,71,78,79,80,81,82,83,84,85,86,87,88,89,90,91]. The wealth of possible options has probably left a puzzled community. Although the problem has been rather “easy to spot”, conflicting solutions have appeared. Among the proposed solutions, one could specifically mention second-generation p-values [92], which have also been supported with implementation options [93]; the calibration of p-values which has, however, been developed in a rather limited framework [94]; the fragility index, i.e., the minimum required number of patients, whose status would have to change from a nonevent to an event, to turn a statistically nonsignificant result to a significant result, with smaller numbers indicating a more fragile result [95]. The simultaneous testing of superiority, equivalence and inferiority has also been studied and proposed [96,97]. Another idea that has been developed in a limited framework is the replication probability approach [98,99].
Leaving the controversy aside, the p-value is gaining even further use in methodological development and decision-making approaches [100,101,102,103,104,105,106,107] as it had done so already in the past [108,109]. However, does it suffice to settle with, all is well? Obviously the lack of consensus does not help much with moving forward [110,111]. Much of the controversy surrounding statistical significance can be dispelled through a better appreciation of uncertainty and replicability [28]. In this regard, the NEJM adapted their guidelines. The journal’s revised policies on p-values rest on three premises: it is important to adhere to a prespecified analysis plan if one exists; the use of statistical thresholds for claiming an effect or association should be limited to analyses for which the analysis plan outlines a method for controlling type I errors; and the evidence about the benefits and harms of a treatment or exposure should include both point estimates and their margins of error [112]. All in all, there is nothing wrong with p-values as long as they are used as intended [39,113]. Thoughts on the difficulties envisioned in a possible effort to abandon the use of p-values have been concisely described [114].
We illustrated in this work both the implementation of the s-value approach that can help provide more complete inference in terms of significance and rri that can help address the reproducibility issue in empirical study findings. rri can also be considered a frequentist analogue to the predictive probability of success as given in [115]. The use of a jackknife approach for the calculation of confidence intervals for the p-value itself has been proposed [116], but the corresponding distribution is typically skewed [55], giving an advantage to the accompanying s-value interpretation. Implementation for s-values has also appeared elsewhere [117,118]. The addition of confidence intervals to the corresponding s-value will also most probably affect the notorious practice of p-value hacking [119,120], making published results more reliable. The proposed inferential procedure can be readily used when a study involves multiplicity adjustments, statistical model building, etc., one limitation being the extra burden asked of researchers to accurately calculate indices and CIs, and further interpret results.
The proposed bootstrap approach may present limitations pertinent to the dependence on the observed data, sample size limitations, and sensitivity to model assumptions. Specifically, we assume that the observed data are a representative sample of the population, a sufficiently large sample size is used to generate stable bootstrap estimates, and the observed data provide unbiased bootstrap estimates. These are inherent limitations of the bootstrap per se, and the study of alternative approaches is a topic of further research.
Thresholds are helpful when actions are required. The discussion of p-values is so extensive because it has been expanded to cover the very broad and challenging issues of quantifying the strength of the evidence from a study and of deciding whether the evidence is adequate for a decision. Comparing p-values to a significance level can be useful, though p-values themselves provide valuable information. p-values and statistical significance should be understood as assessments of the observations or effects relative to sampling variation, and not necessarily as measures of practical significance. If thresholds are deemed necessary as a part of decision making, they should be explicitly defined based on study goals, considering the consequences of incorrect decisions. Conventions vary by discipline and purpose of analyses [28]. Indeed, following the instructions of the voices of harsh criticism or complete rejection implies changing things radically regarding how research is conducted. As a result we will be intensely interfering with other people’s jobs, affecting a huge industry of asset allocation and scientific process. The routine of conducting statistical analysis cannot change radically since alternatives have not been widely convincing [121].
Complementing p-values in order to make better decisions seems reasonable, and there are various approaches for doing so [122]. Reproducibility and replicability are probably reasonable complements as a central scientific goal [54,123]. A small revolution might be a consensus between scientific societies and major statistical software developers on specific solutions, such as the one illustrated in this work, that will be widely implemented and will—by default—-be introduced in everyday practice. Textbook authors will follow along. An unavoidable evolution will be reached.
Author Contributions
Conceptualization, C.T.N.; methodology, C.T.N.; software, C.N and E.V.; validation, E.V.; formal analysis, C.T.N. and E.V.; investigation, C.T.N. and E.V.; resources, C.T.N. and E.V.; data curation, C.T.N. and E.V.; writing—original draft preparation, C.T.N.; writing—review and editing, C.T.N. and E.V.; visualization, C.T.N. and E.V.; supervision, C.T.N.; project administration, C.T.N. and E.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are publicly available at http://dx.doi.org/10.13140/RG.2.2.22805.96482 (accessed on 10 March 2023).
Acknowledgments
The authors are grateful to Constantine Gatsonis for all the fruitful discussions on the topic and would like to thank the reviewers for the insightful comments.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. R-Code for the Application
#tremdata<-read.csv(file.choose())
tremdatabasic<-tremdata[-47,]
library(pROC)
#trem
xtrem<-tremdatabasic[,3][tremdatabasic[,2]==0]
ytrem<-tremdatabasic[,3][tremdatabasic[,2]==1]
#il6
xil6<-tremdatabasic[,4][tremdatabasic[,2]==0]
yil6<-tremdatabasic[,4][tremdatabasic[,2]==1]
ptremdstbtn<-matrix(0,1,1000)
pil6dstbtn<-matrix(0,1,1000)
pcomp<-matrix(0,1,1000)
#bootstrap~procedure
set.seed(2022)
for (i in 1:1000){
xbt<-sample(xtrem,replace=T)
ybt<-sample(ytrem,replace=T)
atestbt<-wilcox.test(xbt,ybt)
pvaltbt<-atestbt[[3]]
ptremdstbtn[1,i]<-pvaltbt
xbi<-sample(xil6,replace=T)
ybi<-sample(yil6,replace=T)
atestbi<-wilcox.test(xbi,ybi)
pvaltbi<-atestbi[[3]]
pil6dstbtn[1,i]<-pvaltbi
roctremb<-roc(controls=xbt,cases=ybt)
rocil6b<-roc(controls=xbi,cases=ybi)
pvalcompb<-roc.test(rocil6b,roctremb)[[8]]
pcomp[1,i]<-pvalcompb
}
#Reporting
#ref
-log2(0.05)
#hist(pdstbtn)
stremdstbtn<--log2(sort(ptremdstbtn))
stremdstbtn[25]
stremdstbtn[975]
sum(ptremdstbtn<0.05)/1000
#hist(stremdstbtn)
roctrem<-roc(controls=xtrem,cases=ytrem)
roctrem
ci(roctrem)
plot(roctrem)
#hist(pdstbtn)
sil6dstbtn<--log2(sort(pil6dstbtn))
sil6dstbtn[25]
sil6dstbtn[975]
sum(pil6dstbtn<0.05)/1000
#hist(sil6dstbtn)
rocil6<-roc(controls=xil6,cases=yil6)
rocil6
ci(rocil6)
plot(rocil6)
scomp<--log2(sort(pcomp))
scomp[25]
scomp[975]
sum(pcomp<0.05)/1000
roc.test(rocil6,roctrem)
References
- Cox, D.R. Statistical Significance. Annu. Rev. Stat. Its Appl. 2020, 7, 1–10. [Google Scholar] [CrossRef]
- Hubbard, R.; Bayarri, M.J.; Berk, K.N.; Carlton, M.A. Confusion over Measures of Evidence (p’s) versus Errors (α’s) in Classical Statistical Testing. Am. Stat. 2003, 57, 171–182. [Google Scholar] [CrossRef]
- Wood, J.; Freemantle, N.; King, M.; Nazareth, I. Trap of trends to statistical significance: Likelihood of near significant p value becoming more significant with extra data. BMJ 2014, 348, g2215. [Google Scholar] [CrossRef]
- McShane, B.B.; Gal, D. Statistical Significance and the Dichotomization of Evidence. J. Am. Stat. Assoc. 2017, 112, 885–895. [Google Scholar] [CrossRef]
- Greenland, S.; Senn, S.J.; Rothman, K.J.; Carlin, J.B.; Poole, C.; Goodman, S.N.; Altman, D.G. Statistical tests, p values, confidence intervals, and power: A guide to misinterpretations. Eur. J. Epidemiol. 2016, 31, 337–350. [Google Scholar] [CrossRef] [PubMed]
- Bauer, P. Comment on ‘A critical evaluation of the current “p-value controversy”’. Biom. J. 2017, 59, 873–874. [Google Scholar] [CrossRef] [PubMed]
- Brannath, W. Contribution to the discussion of “A critical evaluation of the current ‘p-value controversy’”. Biom. J. 2017, 59, 875–876. [Google Scholar] [CrossRef]
- Di Leo, G.; Sardanelli, F. Statistical significance: p value, 0.05 threshold, and applications to radiomics—Reasons for a conservative approach. Eur. Radiol. Exp. 2020, 4, 18. [Google Scholar] [CrossRef]
- Farcomeni, A. Contribution to the discussion of the paper by Stefan Wellek: “A critical evaluation of the current p-value controversy”. Biom. J. 2017, 59, 880–881. [Google Scholar] [CrossRef]
- Gasparini, M. Contribution to the discussion of “A critical evaluation of the current ‘p-value controversy’”. Biom. J. 2017, 59, 882–883. [Google Scholar] [CrossRef]
- Goeman, J.J. Contribution to the discussion of “A critical evaluation of the current ‘p-value controversy’”. Biom. J. 2017, 59, 884–885. [Google Scholar] [CrossRef]
- Held, L. An objective Bayes perspective on p-values. Biom. J. 2017, 59, 886–888. [Google Scholar] [CrossRef]
- Laber, E.B.; Shedden, K. Statistical Significance and the Dichotomization of Evidence: The Relevance of the ASA Statement on Statistical Significance and p-Values for Statisticians. J. Am. Stat. Assoc. 2017, 112, 902–904. [Google Scholar] [CrossRef]
- Greenland, S. Valid p-Values Behave Exactly as They Should: Some Misleading Criticisms of p-Values and Their Resolution with S-Values. Am. Stat. 2019, 73 (Suppl. 1), 106–114. [Google Scholar] [CrossRef]
- Berry, D. A p-Value to Die For. J. Am. Stat. Assoc. 2017, 112, 895–897. [Google Scholar] [CrossRef]
- Ioannidis, J.P.A. Why Most Published Research Findings Are False. PLoS Med. 2005, 2, e124. [Google Scholar] [CrossRef]
- Mayo, D.G. Statistical Inference as Severe Testing: How to Get beyond the Statistics Wars; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Nuzzo, R. Scientific method: Statistical errors. Nature 2014, 506, 150–152. [Google Scholar] [CrossRef] [PubMed]
- Perezgonzalez, J.D.; Frias-Navarro, M.D. Retract p < 0.005 and propose using JASP, instead. F1000Research 2017, 6, 2122. [Google Scholar]
- Amrhein, V.; Greenland, S.; McShane, B. Retire statistical significance. Nature 2019, 567, 305–307. [Google Scholar] [CrossRef]
- Halsey, L.G. The reign of the p-value is over: What alternative analyses could we employ to fill the power vacuum? Biol. Lett. 2019, 15, 20190174. [Google Scholar] [CrossRef]
- Amrhein, V.; Trafimow, D.; Greenland, S. Inferential Statistics as Descriptive Statistics: There Is No Replication Crisis if We Don’t Expect Replication. Am. Stat. 2019, 73 (Suppl. 1), 262–270. [Google Scholar] [CrossRef]
- Gardner, M.J.; Altman, D.G. Confidence intervals rather than p values: Estimation rather than hypothesis testing. Br. Med. J. (Clin. Res. Ed.) 1986, 292, 746–750. [Google Scholar] [CrossRef] [PubMed]
- Kuss, O.; Stang, A. The p-value—A well-understood and properly used statistical concept? Contact Dermat. 2011, 66, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Feinstein, A.R. p-Values and Confidence Intervals: Two Sides of the Same Unsatisfactory Coin. J. Clin. Epidemiol. 1998, 51, 355–360. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J. Some Natural Solutions to the p-Value Communication Problem—And Why They Won’t Work. J. Am. Stat. Assoc. 2017, 112, 899–901. [Google Scholar] [CrossRef]
- Berger, V.W. On the generation and ownership of alpha in medical studies. Control. Clin. Trials 2004, 25, 613–619. [Google Scholar] [CrossRef]
- Benjamini, Y.; De Veaux, R.D.; Efron, B.; Evans, S.; Glickman, M.; Graubard, B.I.; He, X.; Meng, X.L.; Reid, N.; Stigler, S.M.; et al. The ASA president’s task force statement on statistical significance and replicability. Ann. Appl. Stat. 2021, 15, 1084–1085. [Google Scholar] [CrossRef]
- Wasserstein, R.L.; Lazar, N.A. The ASA’s Statement on p-Values: Context, Process, and Purpose. Am. Stat. 2016, 70, 129–133. [Google Scholar] [CrossRef]
- Riley, R.D.; Cole, T.J.; Deeks, J.; Kirkham, J.J.; Morris, J.; Perera, R.; Wade, A.; Collins, G.S. On the 12th Day of Christmas, a Statistician Sent to Me. BMJ 2022, 379, e072883. [Google Scholar] [CrossRef]
- Meng, X.L. Posterior Predictive p-Values. Ann. Stat. 1994, 22, 1142–1160. [Google Scholar] [CrossRef]
- Sellke, T.; Bayarri, M.J.; Berger, J.O. Calibration of p Values for Testing Precise Null Hypotheses. Am. Stat. 2001, 55, 62–71. [Google Scholar] [CrossRef]
- Piegorsch, W.W. Are p-values under attack? Contribution to the discussion of ‘A critical evaluation of the current “p-value controversy”’. Biom. J. 2017, 59, 889–891. [Google Scholar] [CrossRef]
- Bayarri, M.J.; Berger, J.O. The Interplay of Bayesian and Frequentist Analysis. Stat. Sci. 2004, 19, 58–80. [Google Scholar] [CrossRef]
- Held, L.; Ott, M. How the Maximal Evidence of p-Values Against Point Null Hypotheses Depends on Sample Size. Am. Stat. 2016, 70, 335–341. [Google Scholar] [CrossRef]
- Novick, S.; Zhang, T. Mean comparisons and power calculations to ensure reproducibility in preclinical drug discovery. Stat. Med. 2021, 40, 1414–1428. [Google Scholar] [CrossRef]
- Gelman, A.; Robert, C.P. Revised evidence for statistical standards. Proc. Natl. Acad. Sci. USA 2014, 111, E1933. [Google Scholar] [CrossRef]
- Browner, W.S.; Newman, T.B. Are all significant p-values created equal? The analogy between diagnostic tests and clinical research. JAMA 1987, 257, 2459–2463. [Google Scholar] [CrossRef] [PubMed]
- Kuffner, T.A.; Walker, S.G. Why are p-Values Controversial? Am. Stat. 2019, 73 (Suppl. 1), 1–3. [Google Scholar] [CrossRef]
- Senn, S. A comment on “replication, p-values and evidence, S.N.Goodman, Statistics in Medicine 1992; 11:875–879”. Stat. Med. 2002, 21, 2437–2444. [Google Scholar] [CrossRef]
- Shi, H.; Yin, G. Reconnecting p-Value and Posterior Probability under One- and Two-Sided Tests. Am. Stat. 2021, 75, 265–275. [Google Scholar] [CrossRef]
- Gaudart, J.; Huiart, L.; Milligan, P.J.; Thiebaut, R.; Giorgi, R. Reproducibility issues in science, is p value really the only answer? Proc. Natl. Acad. Sci. USA 2014, 111, E1934. [Google Scholar] [CrossRef] [PubMed]
- Lazzeroni, L.C.; Lu, Y.; Belitskaya-Lévy, I. p-values in genomics: Apparent precision masks high uncertainty. Mol. Psychiatry 2014, 19, 1336–1340. [Google Scholar] [CrossRef]
- Senn, S. Contribution to the discussion of ‘A critical evaluation of the current “p-value controversy”’. Biom. J. 2017, 59, 892–894. [Google Scholar] [CrossRef] [PubMed]
- Hand, D.J. Trustworthiness of statistical inference. J. R. Stat. Soc. Ser. A Stat. Soc. 2022, 185, 329–347. [Google Scholar] [CrossRef]
- Senn, S. Two cheers for p-values? J. Epidemiol. Biostat. 2001, 6, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Wellek, S. A critical evaluation of the current ”p-value controversy”. Biom. J. 2017, 59, 854–872. [Google Scholar] [CrossRef]
- Alfo, M.; Boehning, D. Editorial for the discussion papers on the p-value controversy. Biom. J. 2017, 59, 853. [Google Scholar] [CrossRef]
- Johnson, V.E. Revised standards for statistical evidence. Proc. Natl. Acad. Sci. USA 2013, 110, 19313–19317. [Google Scholar] [CrossRef]
- Wasserstein, R.L.; Schirm, A.L.; Lazar, N.A. Moving to a World Beyond “p < 0.05”. Am. Stat. 2019, 73 (Suppl. 1), 1–19. [Google Scholar]
- Indrayan, A.; Malhotra, R.K. Medical Biostatistics, 4th ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Vexler, A.; Hutson, A.D.; Chen, X. Statistical Testing Strategies in the Health Sciences; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Goodman, S.N.; Fanelli, D.; Ioannidis, J.P.A. What does research reproducibility mean? Sci. Transl. Med. 2016, 8, 341ps12. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Reproducibility and Replicability in Science; The National Academies Press: Washington, DC, USA, 2019. [Google Scholar]
- Boos, D.D.; Stefanski, L.A. p-Value Precision and Reproducibility. Am. Stat. 2011, 65, 213–221. [Google Scholar] [CrossRef] [PubMed]
- Stodden, V. Reproducing Statistical Results. Annu. Rev. Stat. Its Appl. 2015, 2, 1–19. [Google Scholar] [CrossRef]
- Halsey, L.G.; Curran-Everett, D.; Vowler, S.L.; Drummond, G.B. The fickle p value generates irreproducible results. Nat. Methods 2015, 12, 179–185. [Google Scholar] [CrossRef] [PubMed]
- van Zwet, E.W.; Goodman, S.N. How large should the next study be? Predictive power and sample size requirements for replication studies. Stat. Med. 2022, 41, 3090–3101. [Google Scholar] [CrossRef]
- Coolen, F.P.A.; Bin Himd, S. Nonparametric Predictive Inference for Reproducibility of Basic Nonparametric Tests. J. Stat. Theory Pract. 2014, 8, 591–618. [Google Scholar] [CrossRef]
- Goodman, S.N. A comment on replication, p-values and evidence. Stat. Med. 1992, 11, 875–879. [Google Scholar] [CrossRef]
- Zhao, Y.; Caffo, B.S.; Ewen, J.B. B-value and empirical equivalence bound: A new procedure of hypothesis testing. Stat. Med. 2022, 41, 964–980. [Google Scholar] [CrossRef]
- Sarafidis, K.; Soubasi-Griva, V.; Piretzi, K.; Thomaidou, A.; Agakidou, E.; Taparkou, A.; Diamanti, E.; Drossou-Agakidou, V. Diagnostic utility of elevated serum soluble triggering receptor expressed on myeloid cells (sTREM)-1 in infected neonates. Intensive Care Med. 2010, 36, 864–868. [Google Scholar] [CrossRef]
- Nakas, C.T.; Bantis, L.E.; Gatsonis, C.A. ROC Analysis for Classification and Prediction in Practice, 1st ed.; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- DeLong, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 1998, 44, 837–845. [Google Scholar] [CrossRef]
- Robin, X.; Turck, N.; Hainard, A.; Tiberti, N.; Lisacek, F.; Sanchez, J.-C.; Mueller, M. pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinform. 2011, 12, 77. [Google Scholar] [CrossRef]
- Richardson, S. Statistics in times of increasing uncertainty. J. R. Stat. Soc. Ser. A Stat. Soc. 2022, 185, 1471–1496. [Google Scholar] [CrossRef]
- Wellek, S. Author response to the contributors to the discussion on ‘A critical evaluation of the current “p-value controversy”’. Biom. J. 2017, 59, 897–900. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T. Computer Age Statistical Inference. Algorithms, Evidence, and Data Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Christensen, R. Analysis of Variance, Design, and Regression: Linear Modeling for Unbalanced Data, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Bhattacharya, B.; Habtzghi, D. Median of the p Value Under the Alternative Hypothesis. Am. Stat. 2002, 56, 202–206. [Google Scholar] [CrossRef]
- Sackrowitz, H.; Samuel-Cahn, E. p Values as Random Variables—Expected p Values. Am. Stat. 1999, 53, 326–331. [Google Scholar] [CrossRef]
- Browne, R.H. The t-Test p Value and Its Relationship to the Effect Size and P(X > Y). Am. Stat. 2010, 64, 30–33. [Google Scholar] [CrossRef]
- De Martini, D. Reproducibility probability estimation for testing statistical hypotheses. Stat. Probab. Lett. 2008, 78, 1056–1061. [Google Scholar] [CrossRef]
- Hung, J.H.M.; O’Neill, R.T.; Bauer, P.; Koehne, K. The Behavior of the p-Value When the Alternative Hypothesis is True. Biometrics 1997, 53, 11–22. [Google Scholar] [CrossRef]
- Nakas, C.; Yiannoutsos, C.T.; Bosch, R.J.; Moyssiadis, C. Assessment of diagnostic markers by goodness-of-fit tests. Stat. Med. 2003, 22, 2503–2513. [Google Scholar] [CrossRef] [PubMed]
- Pepe, M.S.; Janes, H.; Longton, G.; Leisenring, W.; Newcomb, P. Limitations of the odds ratio in gauging the performance of a diagnostic, prognostic, or screening marker. Am. J. Epidemiol. 2004, 159, 882–890. [Google Scholar] [CrossRef] [PubMed]
- Pepe, M.S.; Cai, T. The Analysis of Placement Values for Evaluating Discriminatory Measures. Biometrics 2004, 60, 528–535. [Google Scholar] [CrossRef] [PubMed]
- Benjamin, D.J.; Berger, J.O. Three Recommendations for Improving the Use of p-Values. Am. Stat. 2019, 73 (Suppl. 1), 186–191. [Google Scholar] [CrossRef]
- Berger, V.W. The p-Value Interval as an Inferential Tool. J. R. Stat. Soc. Ser. D Stat. 2001, 50, 79–85. [Google Scholar] [CrossRef]
- Berry, G.; Armitage, P. Mid-P confidence intervals: A brief review. J. R. Stat. Soc. Ser. Stat. 1995, 44, 417–423. [Google Scholar] [CrossRef]
- Briggs, W.M. The Substitute for p-Values. J. Am. Stat. Assoc. 2017, 112, 897–898. [Google Scholar] [CrossRef]
- De Capitani, L.; De Martini, D. Reproducibility Probability Estimation and RP-Testing for Some Nonparametric Tests. Entropy 2016, 18, 142. [Google Scholar] [CrossRef]
- Demidenko, E. The p-Value You Can’t Buy. Am. Stat. 2016, 70, 33–38. [Google Scholar] [CrossRef]
- Goodman, W.M.; Spruill, S.E.; Komaroff, E. A Proposed Hybrid Effect Size Plus p-Value Criterion: Empirical Evidence Supporting its Use. Am. Stat. 2019, 73 (Suppl. 1), 168–185. [Google Scholar] [CrossRef]
- Infanger, D.; Schmidt-Trucksaess, A. p value functions: An underused method to present research results and to promote quantitative reasoning. Stat. Med. 2019, 38, 4189–4197. [Google Scholar] [CrossRef]
- Ioannidis, J.P.A. How to Make More Published Research True. PLoS Med. 2014, 11, e1001747. [Google Scholar] [CrossRef]
- Jakobsen, J.C.; Gluud, C.; Winkel, P.; Lange, T.; Wetterslev, J. The thresholds for statistical and clinical significance—A five-step procedure for evaluation of intervention effects in randomised clinical trials. BMC Med. Res. Methodol. 2014, 14, 34. [Google Scholar] [CrossRef]
- Kieser, M.; Friede, T.; Gondan, M. Assessment of statistical significance and clinical relevance. Stat. Med. 2013, 32, 1707–1719. [Google Scholar] [CrossRef]
- Matthews, R.A.J. Moving Towards the Post p < 0.05 Era via the Analysis of Credibility. Am. Stat. 2019, 73 (Suppl. 1), 202–212. [Google Scholar]
- Rice, K.; Ye, L. Expressing Regret: A Unified View of Credible Intervals. Am. Stat. 2022, 76, 248–256. [Google Scholar] [CrossRef]
- Stahel, W.A. New relevance and significance measures to replace p-values. PLoS ONE 2021, 16, e0252991. [Google Scholar] [CrossRef]
- Blume, J.D.; Greevy, R.A.; Welty, V.F.; Smith, J.R.; Dupont, W.D. An Introduction to Second-Generation p-Values. Am. Stat. 2019, 73 (Suppl. 1), 157–167. [Google Scholar] [CrossRef]
- Bormann, S.-K. A Stata implementation of second-generation p-values. Stata J. 2022, 22, 496–520. [Google Scholar] [CrossRef]
- Schuemie, M.J.; Ryan, P.B.; DuMouchel, W.; Suchard, M.A.; Madigan, D. Interpreting observational studies: Why empirical calibration is needed to correct p-values. Stat. Med. 2014, 33, 209–218. [Google Scholar] [CrossRef]
- Walsh, M.; Srinathan, S.K.; McAuley, D.F.; Mrkobrada, K.; Levine, O.; Ribic, C.; Molnar, A.O.; Dattani, N.D.; Burke, A.; Guyatt, G.; et al. The statistical significance of randomized controlled trial results is frequently fragile: A case for a Fragility Index. J. Clin. Epidemiol. 2014, 67, 622–628. [Google Scholar] [CrossRef] [PubMed]
- Goeman, J.J.; Solari, A.; Stijnen, T. Three-sided hypothesis testing: Simultaneous testing of superiority, equivalence and inferiority. Stat. Med. 2010, 29, 2117–2125. [Google Scholar] [CrossRef] [PubMed]
- Solari, A. Contribution to the discussion of ‘A critical evaluation of the current “p-value controversy”’. Biom. J. 2017, 59, 895–896. [Google Scholar] [CrossRef] [PubMed]
- Killeen, P.R. An Alternative to Null-Hypothesis Significance Tests. Psychol. Sci. 2005, 16, 345–353. [Google Scholar] [CrossRef] [PubMed]
- Lecoutre, B.; Lecoutre, M.P.; Poitevineau, J. Killeen’s probability of replication and predictive probabilities: How to compute, use, and interpret them. Psychol. Methods 2010, 15, 158–171. [Google Scholar] [CrossRef] [PubMed]
- Bickel, D.R. Testing prediction algorithms as null hypotheses: Application to assessing the performance of deep neural networks. Stat 2020, 9, e270. [Google Scholar] [CrossRef]
- Bland, M. Do Baseline p-Values Follow a Uniform Distribution in Randomised Trials? PLoS ONE 2013, 8, e76010. [Google Scholar] [CrossRef]
- Buehlmann, P.; Kalisch, M.; Meier, L. High-Dimensional Statistics with a View Toward Applications in Biology. Annu. Rev. Stat. Its Appl. 2014, 1, 255–278. [Google Scholar] [CrossRef]
- Held, L. The harmonic mean χ2-test to substantiate scientific findings. Appl. Stat. 2020, 69, 697–708. [Google Scholar] [CrossRef]
- van Reenen, M.; Reinecke, C.J.; Westerhuis, J.A.; Venter, J.H. Variable selection for binary classification using error rate p-values applied to metabolomics data. BMC Bioinform. 2016, 17, 33. [Google Scholar] [CrossRef] [PubMed]
- Zumbrunnen, N.R. p-Values for Classification—Computational Aspects and Asymptotics. Ph.D. Thesis, University of Bern, Bern, Switzerland, University of Goettingen, Goettingen, Germany, 2014. [Google Scholar]
- Zumbrunnen, N.; Duembgen, L. pvclass: An R Package for p Values for Classification. J. Stat. Softw. 2017, 78, 1–19. [Google Scholar] [CrossRef]
- Zuo, Y.; Stewart, T.G.; Blume, J.D. Variable Selection with Second-Generation p-Values. Am. Stat. 2022, 76, 91–101. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B Methodol. 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Elston, R.C. On Fisher’s method on combining p-values. Biom. J. 1991, 33, 339–345. [Google Scholar] [CrossRef]
- Johnson, V.E. Reply to Gelman, Gaudart, Pericchi: More reasons to revise standards for statistical evidence. Proc. Natl. Acad. Sci. USA 2014, 111, E1936–E1937. [Google Scholar] [CrossRef]
- Pericchi, L.; Pereira, C.A.; Pérez, M.-E. Adaptive revised standards for statistical evidence. Proc. Natl. Acad. Sci. USA 2014, 111, E1935. [Google Scholar] [CrossRef] [PubMed]
- Harrington, D.; D’Agostino, R.B.S.; Gatsonis, C.; Hogan, J.W.; Hunter, D.J.; Normand, S.-L.T.; Drazen, J.M.; Hamel, M.B. New Guidelines for Statistical Reporting in the Journal. N. Engl. J. Med. 2019, 381, 285–286. [Google Scholar] [CrossRef] [PubMed]
- Schervish, M.J. p values: What they are and what they are not. Am. Stat. 1996, 50, 203–206. [Google Scholar] [CrossRef]
- Goodman, S.N. Why is Getting Rid of p-Values So Hard? Musings on Science and Statistics. Am. Stat. 2019, 73 (Suppl. 1), 26–30. [Google Scholar] [CrossRef]
- Saville, B.R.; Connor, J.T.; Ayers, G.D.; Alvarez, J.A. The utility of Bayesian predictive probabilities for interim monitoring of clinical trials. Clin. Trials 2014, 11, 485–493. [Google Scholar] [CrossRef]
- Marinell, G.; Steckel-Berger, G.; Ulmer, H. Not Significant: What Now? J. Probab. Stat. 2012, 2012, 804691. [Google Scholar] [CrossRef]
- Linden, A. SVALUE: Stata module for computing and graphically displaying S-values against their respective p-values. In Statistical Software Components; Boston College Department of Economics: Chestnut Hill, MA, USA, 2019; p. S458650. [Google Scholar]
- Rafi, Z.; Greenland, S. Semantic and cognitive tools to aid statistical science: Replace confidence and significance by compatibility and surprise. BMC Med. Res. Methodol. 2020, 20, 244. [Google Scholar] [CrossRef]
- Guo, D.; Ma, Y. The “p-hacking-is-terrific” ocean - A cartoon for teaching statistics. Teach. Stat. 2022, 44, 68–72. [Google Scholar] [CrossRef]
- Head, M.L.; Holman, L.; Lanfear, R.; Kahn, A.T.; Jennions, M.D. The Extent and Consequences of P-Hacking in Science. PLoS Biol. 2015, 13, e1002106. [Google Scholar] [CrossRef] [PubMed]
- Senn, S. Dicing with Death: Living by Data, 2nd ed.; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- De Santis, F. Contribution to the discussion of “A critical evaluation of the current ‘p-value controversy’”. Biom. J. 2017, 59, 877–879. [Google Scholar] [CrossRef] [PubMed]
- Open Science Collaboration. Estimating the reproducibility of psychological science. Science 2015, 349, aac4716. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).