The Network Bass Model with Behavioral Compartments
Abstract
1. Introduction
2. The Network Bass Model in Heterogeneous Mean Field Approximation
2.1. Model without Behavioral Compartments
2.2. General Case with K Compartments
3. Network Bass Equations with Two Behavioral Compartments
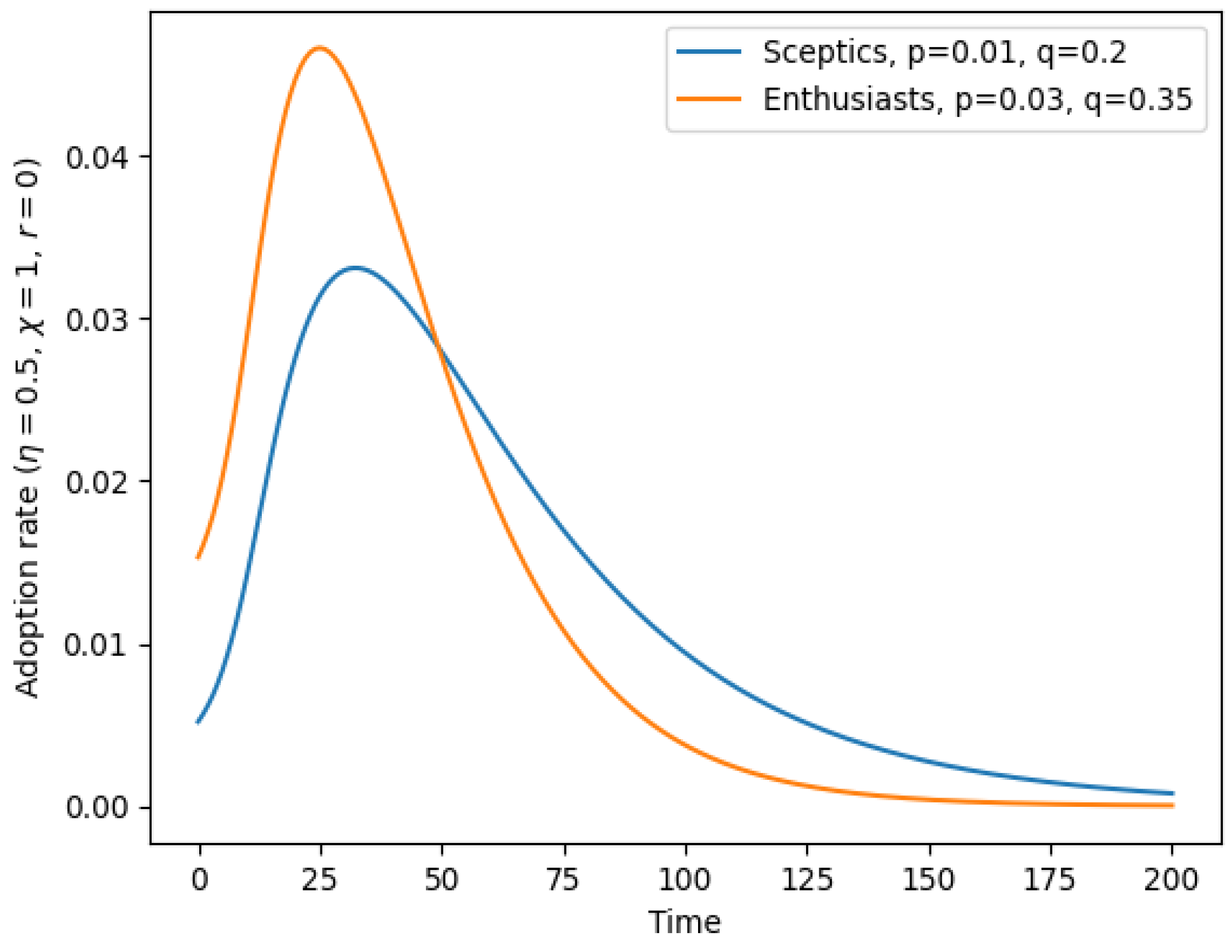
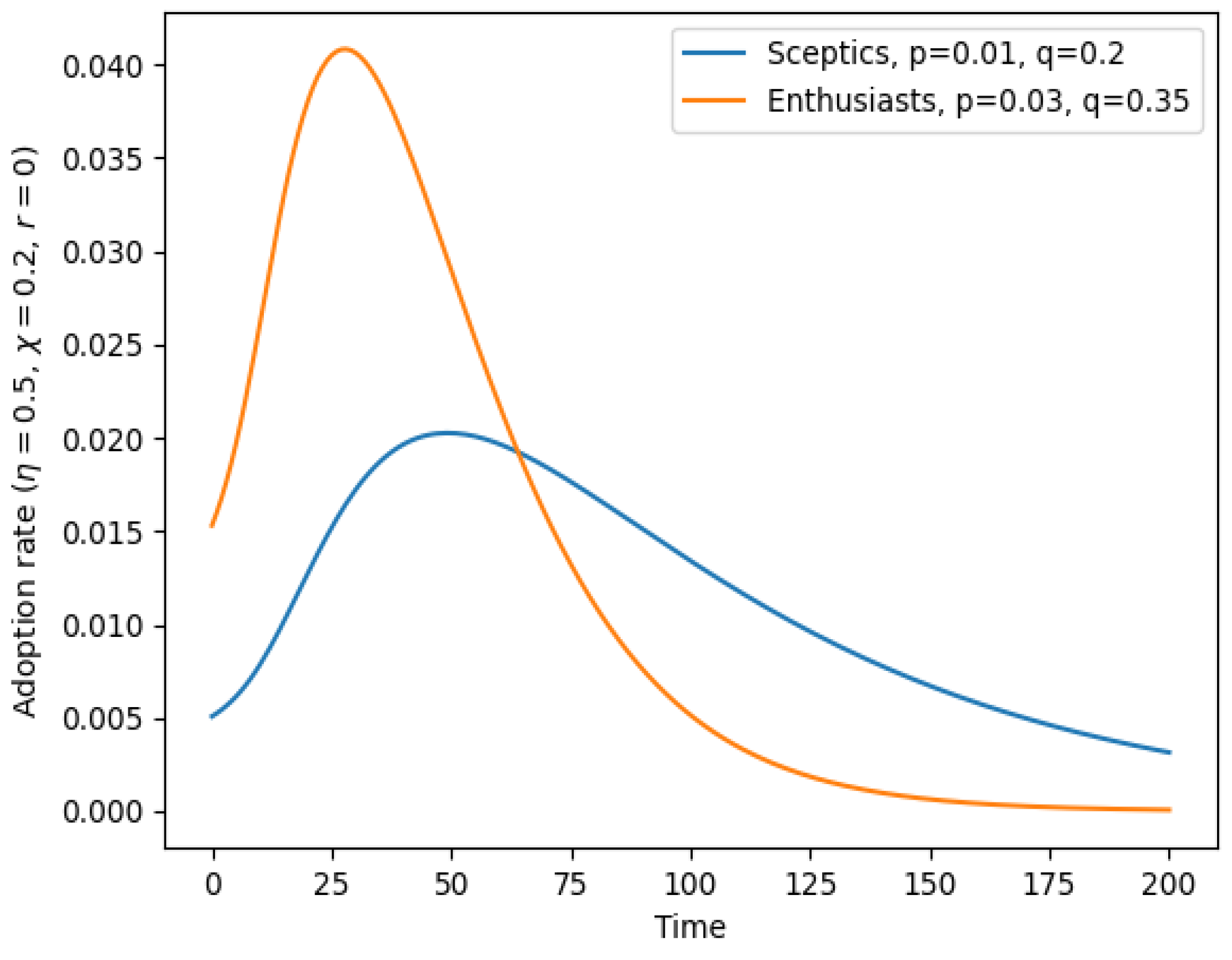
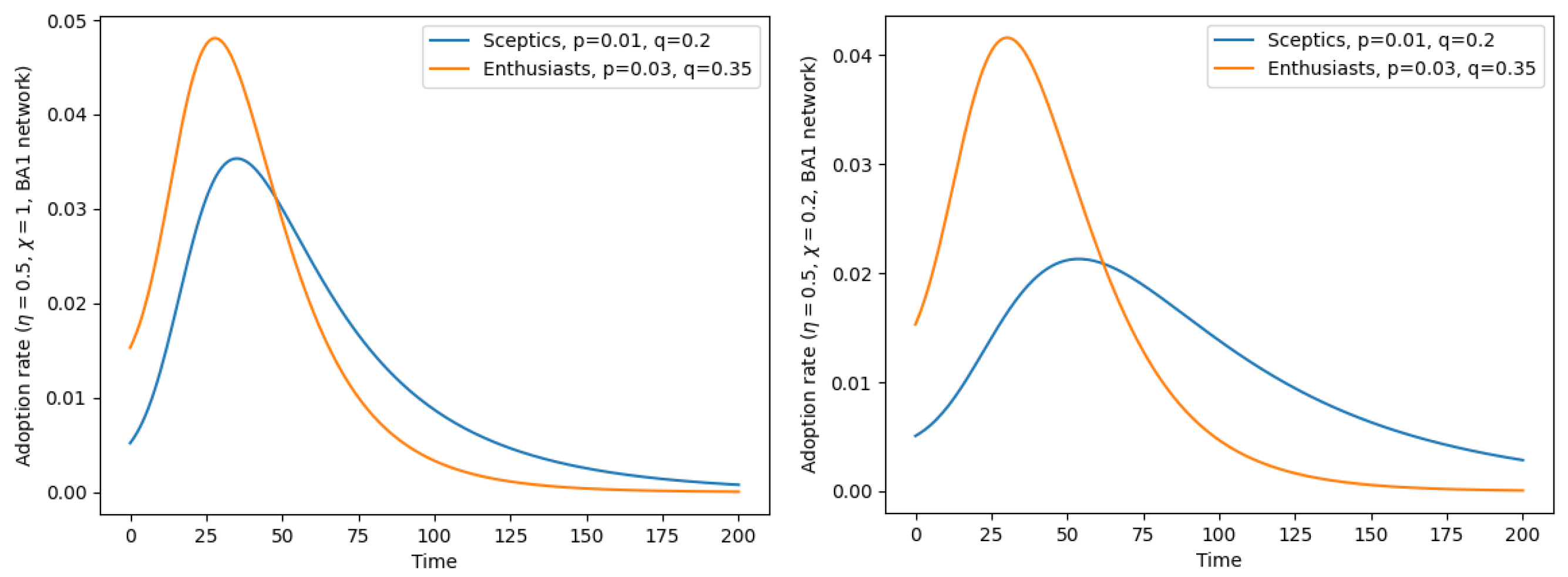
3.1. Simulating Stronger Polarization
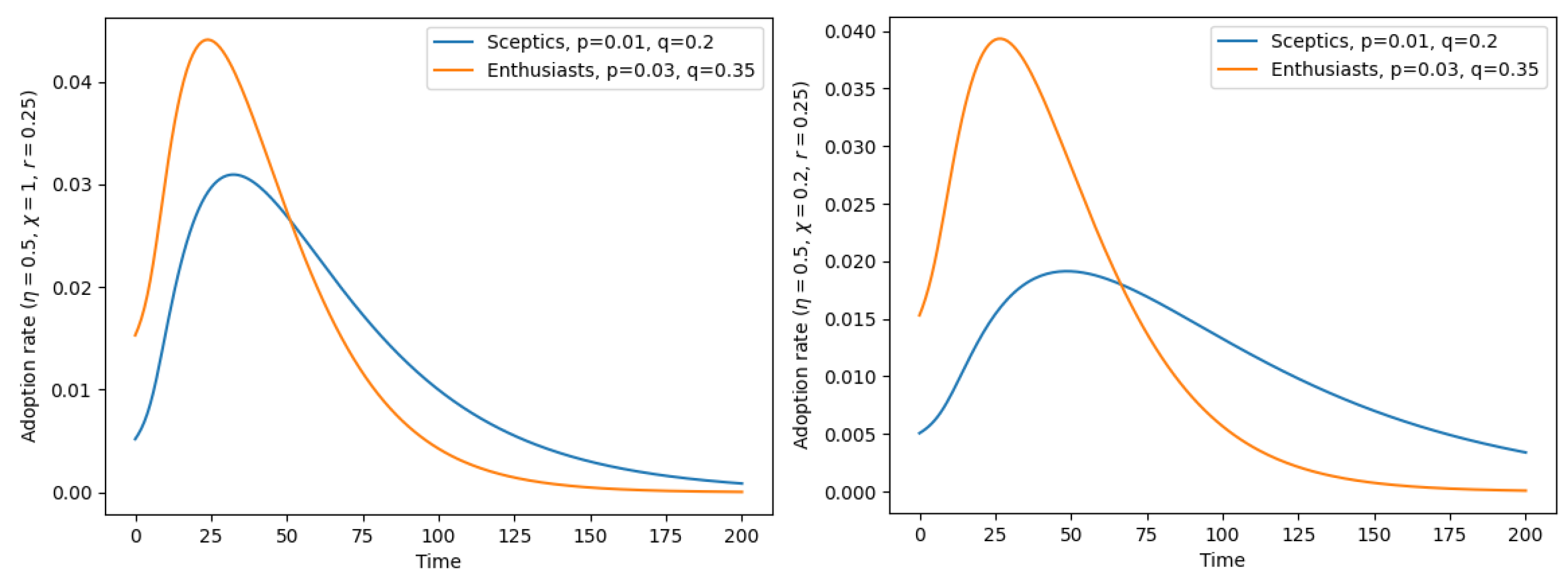
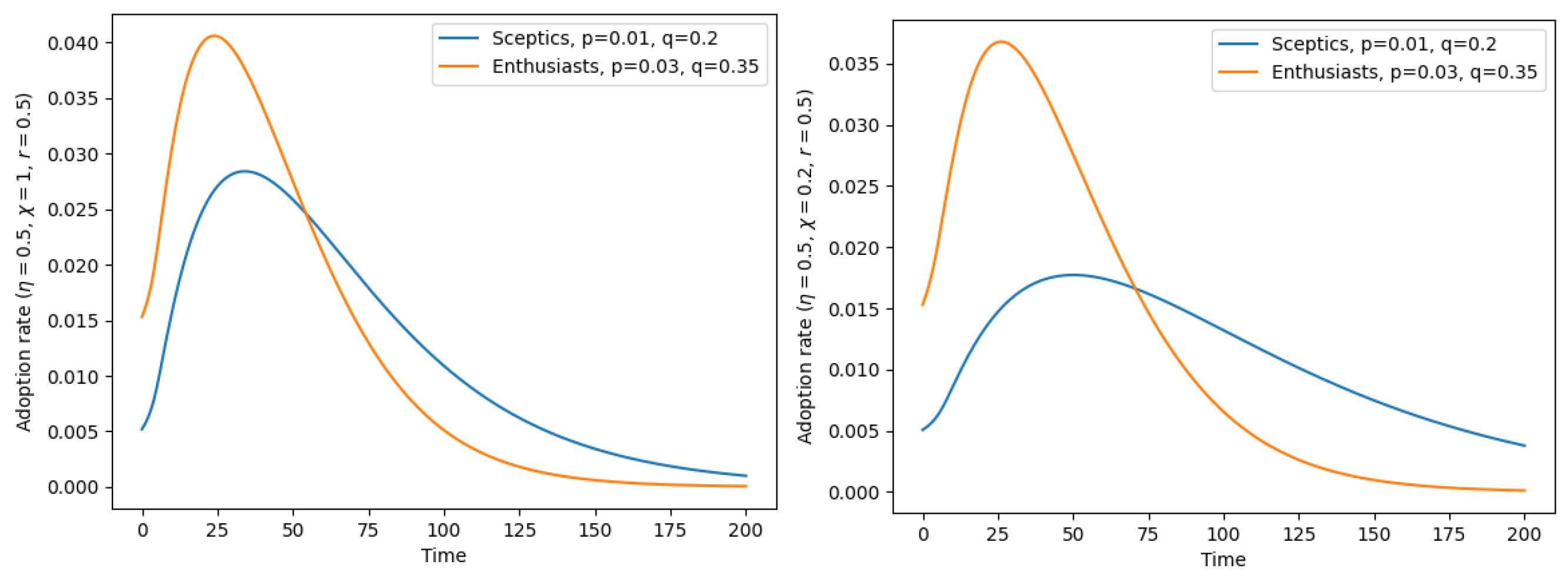
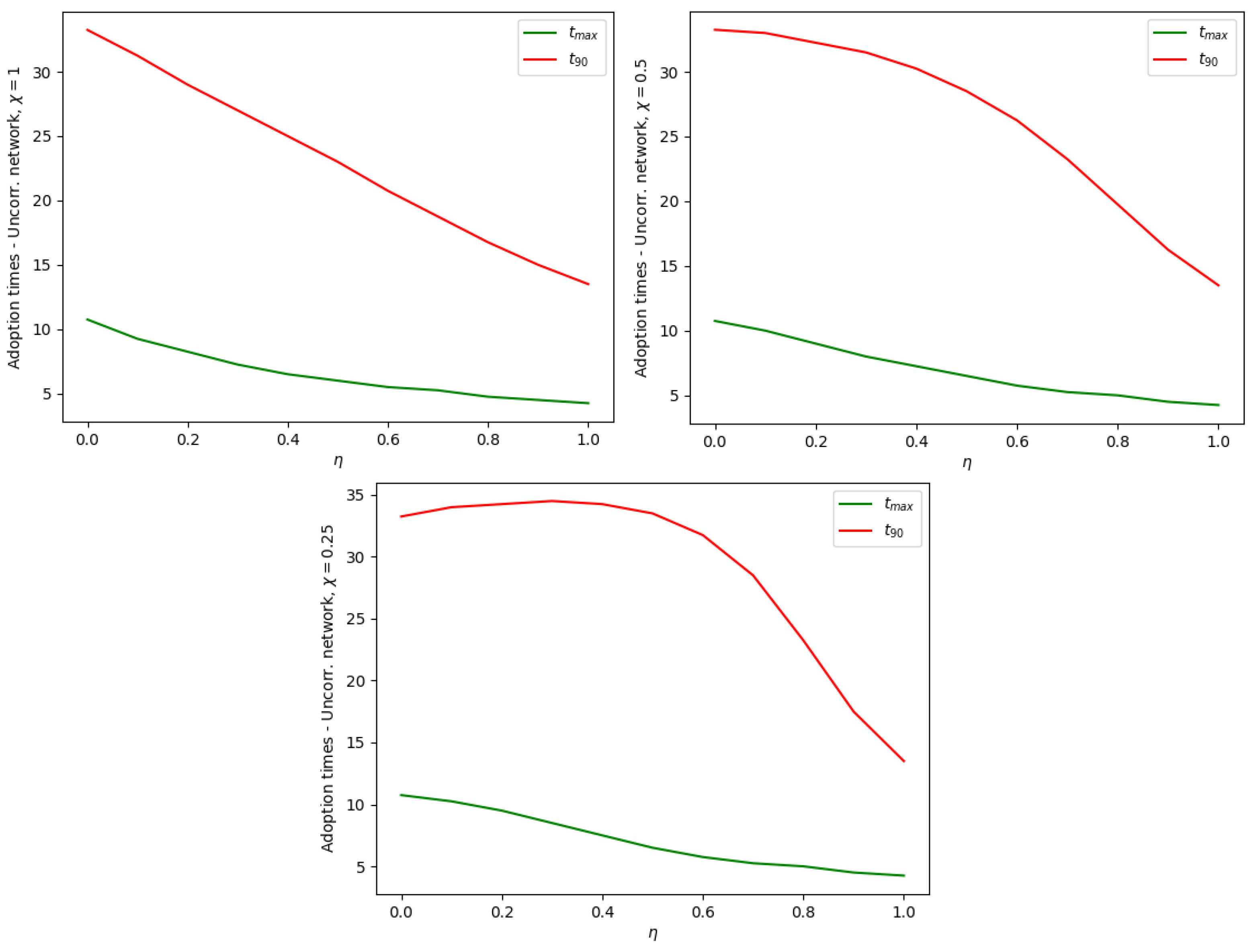
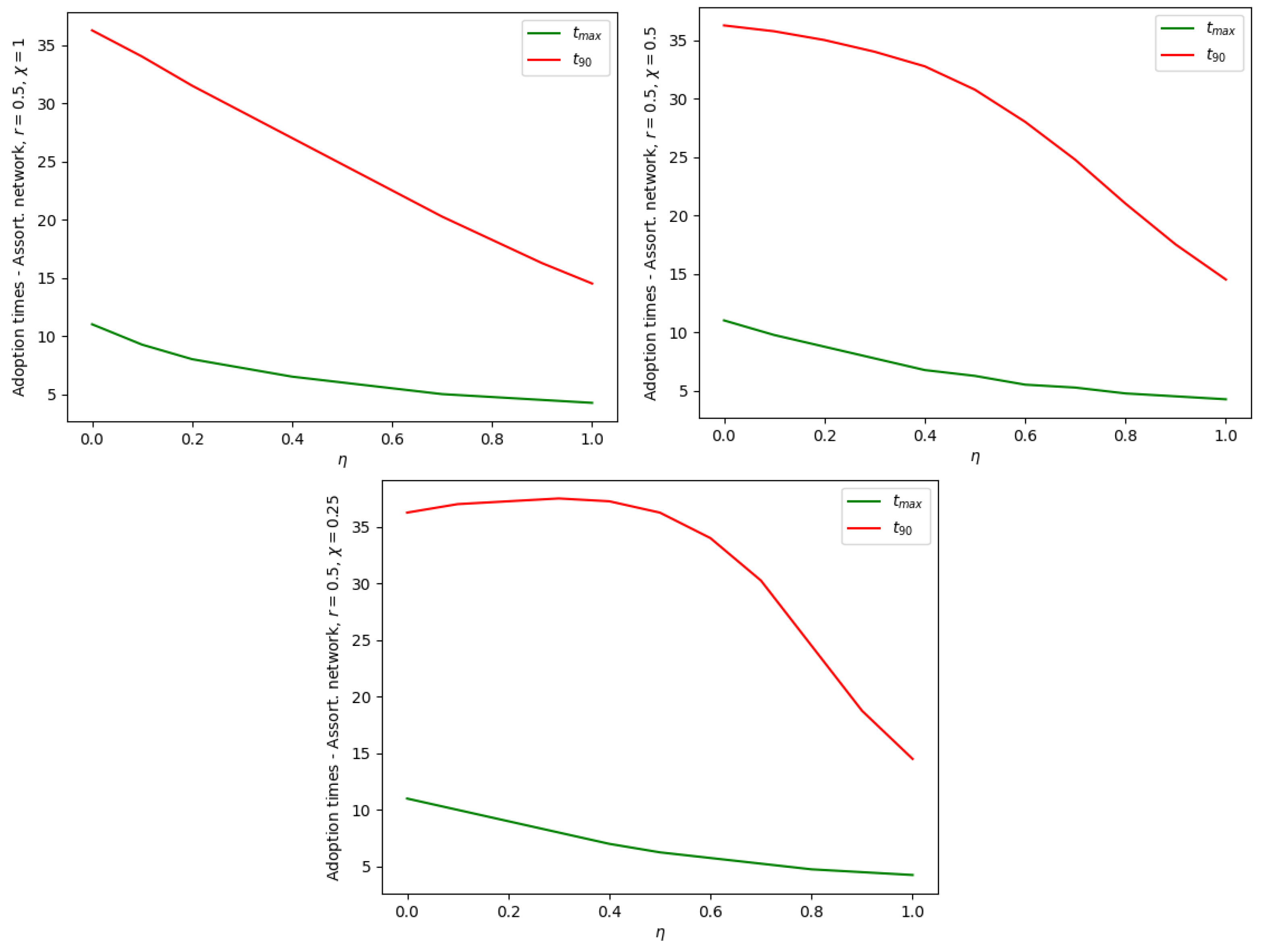
4. Dependence of the Adoption Times on Polarization
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Python Code for Integration of the Equation System
References
- Bass, F.M. A new product growth for model consumer durables. Manag. Sci. 1969, 15, 215–227. [Google Scholar] [CrossRef]
- Meade, N.; Islam, T. Modelling and forecasting the diffusion of innovation–A 25-year review. Int. J. Forecast. 2006, 22, 519–545. [Google Scholar] [CrossRef]
- Gleeson, J.P. High-accuracy approximation of binary-state dynamics on networks. Phys. Rev. Lett. 2011, 107, 068701. [Google Scholar] [CrossRef]
- Kiesling, E.; Günther, M.; Stummer, C.; Wakolbinger, L.M. Agent-based simulation of innovation diffusion: A review. Cent. Eur. J. Oper. Res. 2012, 20, 183–230. [Google Scholar] [CrossRef]
- Fok, D.; Franses, P.H. Modeling the diffusion of scientific publications. J. Econom. 2007, 139, 376–390. [Google Scholar] [CrossRef]
- Goldenberg, J.; Han, S.; Lehmann, D.R.; Hong, J.W. The role of hubs in the adoption process. J. Mark. 2009, 73, 1–13. [Google Scholar] [CrossRef]
- Schilling, M.A.; Shankar, R. Strategic Management of Technological Innovation; McGraw-Hill Education: New York, NY, USA, 2019. [Google Scholar]
- Keeling, M.J.; Eames, K.T. Networks and epidemic models. J. R. Soc. Interface 2005, 2, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Bertotti, M.L.; Brunner, J.; Modanese, G. The Bass diffusion model on networks with correlations and inhomogeneous advertising. Chaos Solitons Fractals 2016, 90, 55–63. [Google Scholar] [CrossRef]
- Bertotti, M.L.; Modanese, G. The Bass diffusion model on finite Barabasi–Albert networks. Complexity 2019, 2019, 6352657. [Google Scholar] [CrossRef]
- Bertotti, M.L.; Modanese, G. On the evaluation of the takeoff time and of the peak time for innovation diffusion on assortative networks. Math. Comput. Model. Dyn. Syst. 2019, 25, 482–498. [Google Scholar] [CrossRef]
- Vespignani, A. Modelling dynamical processes in complex socio-technical systems. Nat. Phys. 2012, 8, 32–39. [Google Scholar] [CrossRef]
- Li, S.; Jin, Z. Modeling and analysis of new products diffusion on heterogeneous networks. J. Appl. Math. 2014, 2014, 940623. [Google Scholar] [CrossRef]
- Manshadi, V.; Misra, S.; Rodilitz, S. Diffusion in random networks: Impact of degree distribution. In Proceedings of the 13th Workshop on Economics of Networks, Systems and Computation, Irvine, CA, USA, 18 June 2018; p. 1. [Google Scholar]
- Rogers, E. Diffusion of Innovations; Simon and Schuster: New York, NY, USA, 2010. [Google Scholar]
- Norton, J.A.; Bass, F.M. A diffusion theory model of adoption and substitution for successive generations of high-technology products. Manag. Sci. 1987, 33, 1069–1086. [Google Scholar] [CrossRef]
- Jiang, Z.; Jain, D.C. A generalized Norton–Bass model for multigeneration diffusion. Manag. Sci. 2012, 58, 1887–1897. [Google Scholar] [CrossRef]
- Krishnan, T.V.; Jain, D.C. Optimal dynamic advertising policy for new products. Manag. Sci. 2006, 52, 1957–1969. [Google Scholar] [CrossRef]
- Mahajan, V.; Muller, E.; Srivastava, R.K. Determination of adopter categories by using innovation diffusion models. J. Mark. Res. 1990, 27, 37–50. [Google Scholar] [CrossRef]
- Van den Bulte, C.; Joshi, Y.V. New product diffusion with influentials and imitators. Mark. Sci. 2007, 26, 400–421. [Google Scholar] [CrossRef]
- Øverby, H.; Audestad, J.A.; Szalkowski, G.A. Compartmental market models in the digital economy—Extension of the Bass model to complex economic systems. Telecommun. Policy 2023, 47, 102441. [Google Scholar] [CrossRef]
- Eryarsoy, E.; Delen, D.; Davazdahemami, B.; Topuz, K. A novel diffusion-based model for estimating cases, and fatalities in epidemics: The case of COVID-19. J. Bus. Res. 2021, 124, 163–178. [Google Scholar] [CrossRef] [PubMed]
- Fotouhi, B.; Rabbat, M.G. Degree correlation in scale-free graphs. Eur. Phys. J. B 2013, 86, 510. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Modanese, G. The Network Bass Model with Behavioral Compartments. Stats 2023, 6, 482-494. https://doi.org/10.3390/stats6020030
Modanese G. The Network Bass Model with Behavioral Compartments. Stats. 2023; 6(2):482-494. https://doi.org/10.3390/stats6020030
Chicago/Turabian StyleModanese, Giovanni. 2023. "The Network Bass Model with Behavioral Compartments" Stats 6, no. 2: 482-494. https://doi.org/10.3390/stats6020030
APA StyleModanese, G. (2023). The Network Bass Model with Behavioral Compartments. Stats, 6(2), 482-494. https://doi.org/10.3390/stats6020030





