1. Introduction
Zipf’s law is well known in linguistics [
1,
2,
3]. When words are ranked according to their frequency of use (from highest to lowest), the frequency
of a word turns out to be inversely proportional to its rank
r. In other words, the most frequent word (
) occurs roughly twice as often as the second-most frequent word (
), three times as often as the third-most frequent word (
), and so on.
This inverse relationship is a special case of a more general mathematical
power law
with the parameter
being (close to) one in the case of Zipf’s law.
Somewhat related, Gibrat’s law states that the proportional growth rate of a firm is independent of its current size [
4]. Such size-independent proportionate growth gives rise to a log-normal distribution, i.e., a random variable of which the logarithm is normally distributed. Power laws and log-normal distributions are part of a larger family of so-called “heavy tailed” distributions.
However, such rank-proportional behavior and/or proportionate growth is not restricted to languages or firm sizes. It shows up in many different situations, such as academic citations, website hits, earthquake magnitudes, intensity of solar flares, city sizes, wealth distributions [
5], molecular networks [
6], technological innovation [
7], and many more. Indeed, it seems to be a universal phenomenon [
8]. It is not surprising, then, that it also shows up in sports rankings.
For example, Deng et al. [
9] showed that power laws can be found in ranking statistics across a range of different sports, including snooker, a popular British billiards game [
10]. However, they used cumulative distributions rather than explicit rank distributions. Furthermore, they only considered statistics from one particular point in time.
Morales et al. [
11], Morales et al. [
12] confirmed power law occurrences in ranking statistics of various sports (although not including snooker), using actual rank distributions. They also studied a dynamic aspect of rankings, in terms of what they call rank diversity (a measure of the number of players occupying a given rank during a particular time period). However, they do not investigate if or how the parameter
of the power laws change over time.
Building on an earlier preliminary investigation [
13], a more detailed and comprehensive study of the occurrence of power laws in snooker statistics is presented here. First, power laws are shown to occur in two different player ranking statistics: total prize money earned, and number of centuries scored. Next, it is shown that there is a difference between the estimated power law parameter values for these two ranking types, and also between all-time statistics and shorter time frame statistics (one year or one decade). Moreover, it is investigated whether these estimated parameter values change over time, and what might cause such variations. Finally, it is shown that although individual snooker rankings can actually be somewhat more accurately described using a log-normal distribution, this does not change the overall conclusions derived from the power law analyses.
2. Methods
A power law shows up as a straight line in a log-log plot. In such a plot, both axes are on a logarithmic scale, rather than a linear scale. So, as a first indication of whether a particular data set might follow a power law, this data can be visualized in a log-log plot to see how closely the data points fall along a straight line.
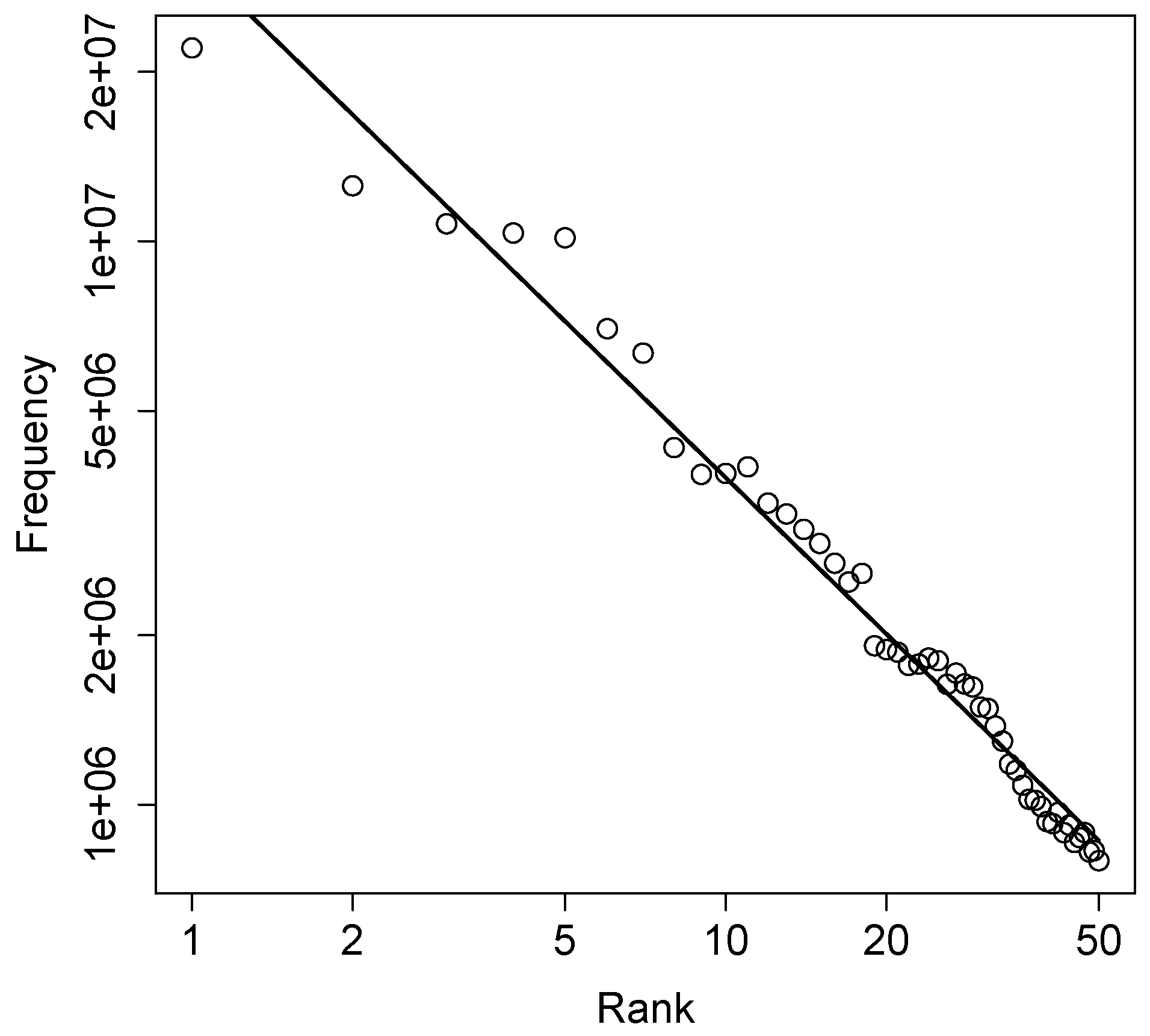
An example is given in
Figure 1, using the 50 most frequent words from the
Corpus of Contemporary American English, or COCA [
14]. The COCA contains more than one billion words from contemporary English texts, spanning many different literature categories and authors. This data appears to fall along a straight line quite accurately.
Next, a power law can be estimated to fit the data by performing a linear regression on the logarithms of the rank and frequency values. This fit is represented by the solid line in the plot, and results in an estimated parameter value . This value is indeed close to one, as originally noted by Zipf more than 80 years ago. The value of actually determines the slope of the straight line representing the power law in a log-log plot. A larger value of results in a steeper line; a smaller value in a shallower line.
A linear regression also provides a “goodness-of-fit” measure (), a value between zero and one. The closer to one, the better the fit. As expected, the fit in the example above is very good: .
Real-world data never falls exactly along a straight line though, partly because of finite size effects. An ideal power law assumes that arbitrarily large frequencies are possible, and that the sample size is large enough so that rare events are always observed. Neither of these is hardly ever the case with real data, so there will always be deviations from a perfect straight line, especially at the top of the ranking (upper left in the plot).
Since the primary goal here is not so much to account for every (small) deviation from a straight line, but to compare the estimated values of the main power law parameter
between different types of rankings and across time, a basic power law formula (as shown in the introduction above) is used here. This is then fit to the data with a linear regression on the logarithmic values. These statistical analyses were done using the
R language for statistical computing [
15].
However, although the validity of Gibrat’s law was later questioned [
16], it has been argued that heavy tailed distributions other than a power law can often improve the fit by taking the finite size effects into account [
17]. To check this for the snooker data, a comparison is made between an estimated power law and a log-normal distribution. This comparison was performed using the maximum likelihood estimation method provided in the
R package
poweRlaw [
18].
The snooker statistics used here consist of two types of professional player rankings: (1) the total prize money earned, and (2) the number of centuries scored (a century in snooker is a score of 100 or more points in a single visit to the table). Three different time frames are considered: all-time, decade, and year. The all-time rankings were current as of January 2022, and the past decade (2010–2019) and past year (2021) were considered for the shorter time frames. Furthermore, to investigate how the resulting power laws may have changed over time, data for the two previous decades (1990–1999 and 2000–2009), and for the years 1990, 1995, 2000, 2005, 2010, 2015, and 2020 were also included. All ranking data were obtained from
CueTracker [
19]. Finally, for a fair comparison across the different ranking types and time frames, the data sets were ensured to all be of the same length by taking the top 100 entries of each ranking.
3. Results
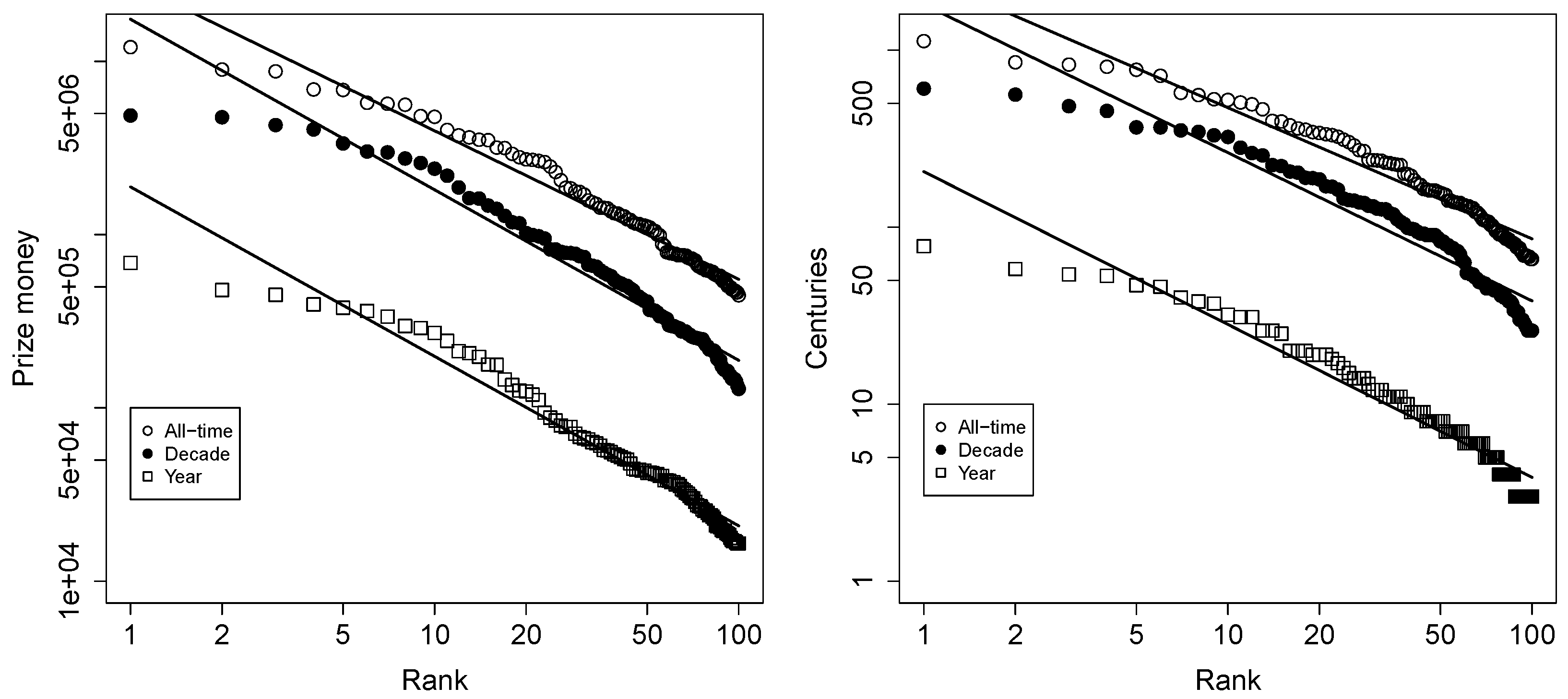
Figure 2 shows the snooker statistics in a log-log plot for the two rankings based on prize money (left) and centuries (right), and for the three time frames of all-time (open circles), past decade (closed circles), and past year (open squares). The solid lines represent estimated power laws to fit the data.
The resulting estimated parameter values
and goodness-of-fit values
are presented in
Table 1, for the two rankings and three time frames.
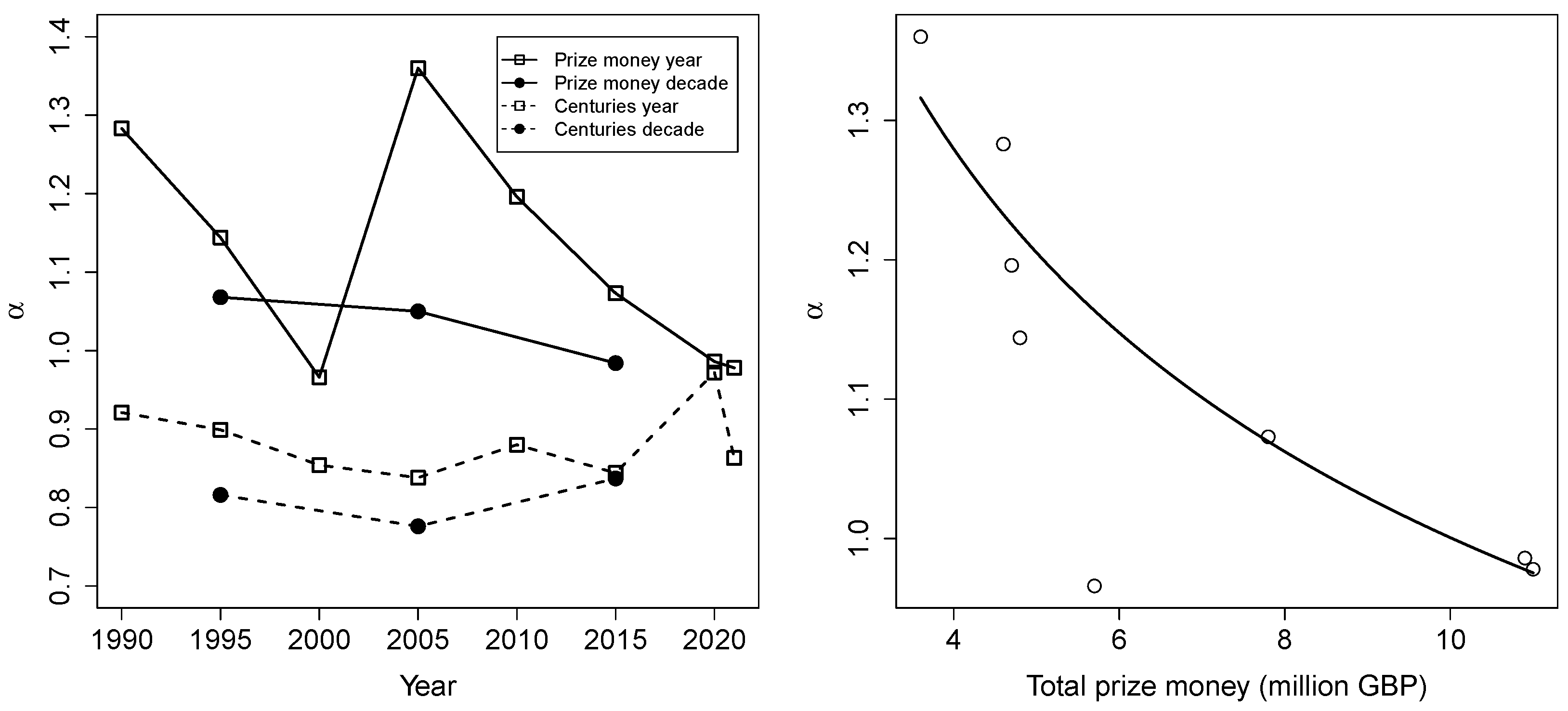
Figure 3 (left) shows how the estimated parameter values
change over time, for the two rankings based on prize money (solid lines) and centuries (dashed lines), and the two time frames of a year (open squares) and a decade (closed circles).
Figure 3 (right) shows the values of
for the prize money ranking in a given year, against the total amount of prize money available, combined over all tournaments that year, in million GBP (this plot is explained in more detail below in the Discussion section).
Figure 4 shows the results of fitting both a power law (solid line) and a log-normal distribution (dashed line) to the all-time centuries ranking, using the maximum likelihood method provided in the
poweRlaw package. Note that this package treats (and plots) the data as a cumulative probability distribution, rather than an explicit ranking.
Figure 4 is still a log-log plot, but the values (in this case the number of centuries) are now on the horizontal axis, while on the vertical axis are their cumulative probabilities. For example, the probability that the value is equal to or larger than the maximum value in the ranking is 0.01, given that there are 100 entries in the ranking and that there is a unique maximum value. This is represented by the dot at the bottom-right of the plot. Similarly, the probability that the value is equal to or larger than the second-highest value in the ranking is 0.02 (second dot up from the bottom-right), and so on, until the probability that the value is equal to or larger than the minimum value in the ranking, which of course is 1.0 (represented by the dot at the top-left of the plot).
Finally,
Table 2 shows the estimated parameters for a log-normal distribution for the two ranking types and three time frames. Note that a log-normal distribution has two parameters:
(mean) and
(standard deviation).
4. Discussion
As
Figure 2 shows, power laws do indeed show up in snooker statistics. However, the finite size effects (i.e., deviations from a straight line in a log-log plot) are more pronounced than in the word frequency example of
Figure 1. This is also reflected in the
values (
Table 1), which range from 0.92 to 0.96 for snooker statistics, compared to 0.98 for word frequencies.
This slightly lower goodness-of-fit is still quite acceptable though, and not surprising, given that the word frequencies are based on a corpus (the COCA) of more than one billion words. In contrast, the number of snooker tournaments played is around 30 per year, or 300 per decade. So, even with the all-time rankings based on several thousand tournaments, that is still only a tiny fraction of the size of the COCA.
What
Figure 2 and
Table 1 also show, is that there is a clear distinction between the estimated power law parameter values
of the all-time rankings on the one hand, and the rankings over shorter time frames such as a year or decade, on the other hand. For both ranking types (prize money and centuries), the all-time rankings result in a smaller value of
than for the shorter time frames.
Similarly, there is a clear distinction between the two ranking types themselves, with the estimated values of being consistently larger (given the time frame considered) for the prize money ranking than for the centuries ranking. Also note that for the prize money ranking, and the decade and year time frames, the estimated values are very close to one, as in the original Zipf’s law.
As
Figure 3 (left) shows, the estimated parameter values might fluctuate over time, although in most cases, they appear to be fairly robust, the estimated values of
vary quite significantly for the prize money rankings on a yearly basis.
To find a possible explanation for this behavior, the total amount of prize money available, combined over all tournaments in a given year, was also obtained from
CueTracker [
19] for the years considered here. The estimated value of
for a given year was then plotted against the total amount of prize money (in million GBP) available in that year. This plot is shown in
Figure 3 (right).
Clearly, a smaller amount of total prize money results in a larger value of , and vice versa. There is one outlier, near the bottom-left of the plot (with a total prize money of close to 6 million GBP, and a value of below 1.0). Interestingly, though, when ignoring this outlier, the remaining points seem to follow a power law as well.
To check this, a power law was estimated for this data (minus the outlier), the result of which is represented by the solid curve in
Figure 3 (right). Note that this plot is on a regular (linear) scale, so that the power law does not show up as a straight line, but is curved. The estimated power law seems to be a fairly reasonable fit (
), and thus, it provides a plausible explanation for the variation in the estimated values of
for the prize money ranking on a yearly basis.
The total amount of available prize money obviously constrains the possible distribution of this money among the players. For example, for any series of
n ranked values (such as prize money earned)
, with
the upper bound
holds, where
C would, in this case, be the total available prize money [
20]. Moreover, in each tournament, the amounts for the winner, runner-up, losing semi-finalists, and so on, are predetermined. Consequently, a player cannot win just any amount of money in a given time frame, but only combinations of those predetermined amounts.
Variations in the parameter are interesting in the sense that this parameter indicates how much a ranking is dominated by the top players. This relates to the well-known “80–20 rule”, which says that, for example, 20% of the people own 80% of the wealth in a society. However, with a power law, it depends on the value of as to what the actual percentage of the top players is that is responsible for 80% of the prize money earned, or centuries scored.
For example, when , as in Zipf’s law, it is actually the top 35% of the ranking that earns 80% of the prize money, or that has scored 80% of all centuries (assuming that there are 100 players competing). However, when (corresponding to a steeper line in the log-log plot), the ranking is mainly dominated by the top players. For a value of , just the top 15% of the players together already earn 80% of the prize money. In contrast, when (corresponding to a shallower line in the log-log plot), the distribution becomes somewhat more equal. For a value of , it takes more than half (56%) of the top players to earn 80% of the prize money.
Finally,
Figure 4 shows that the deviations from a straight line in a log-log plot can be taken into account by fitting a somewhat more elaborate two-parameter log-normal distribution (dashed line) instead of a one-parameter power law (solid line). However, although visually, the log-normal distribution indeed seems to provide a better fit, the
p-value of a test on the hypothesis that both distributions provide an equally good fit is 0.053. So, this hypothesis cannot be rejected with very high confidence.
Furthermore, as
Table 2 shows, the general conclusion that the specific shape (i.e., slope) of an estimated power law depends largely on the type of ranking used and the time frame considered, remains valid. A similar clear distinction can be seen for the estimated log-normal distribution parameters. In particular, for any given time frame, the estimated parameters for the prize money ranking are consistently and significantly higher than those for the centuries ranking. In addition, for both ranking types, there is a clear and significant difference in the estimated
parameter for the yearly time frame on the one hand, and the decade and all-time time frames on the other hand.
So, although the fit can indeed be improved somewhat by using a log-normal distribution instead of a power law, it does not change the main conclusions derived from the power law analysis. Moreover, a power law provides an intuitively easier way of understanding and interpreting the results.
5. Conclusions
In conclusion, although power laws indeed appear to be common in snooker statistics, their particular form (i.e., parameter value or slope) depends strongly on the type of ranking used, as well as the time frame considered. Furthermore, this parameter value may change over time, and a plausible explanation for such behavior was provided in terms of the total amount of resources (in this case prize money) available. In addition, the value of the parameter indicates how much a ranking is dominated by the top players. The larger the value of , the more the top players dominate the rankings and total earnings. Finally, it was shown how the data can be somewhat more accurately described by a log-normal distribution, but that this does not change the overal conclusions derived from the easier-to-interpret power law analysis.
It would be interesting to see if the results obtained here can be observed in the ranking statistics of other sports as well. Deng et al. [
9] and Morales et al. [
11], Morales et al. [
12] do provide estimated power law parameter values for a range of different sports, but did not analyze to what extent these depend on the ranking type used or time frame considered, or whether these values change over time. Axtell [
21] presents the estimated power law parameter values for the US firm size statistics measured over the span of one decade. However, those values seem very robust and do not change at all over time. Further investigation into these dependencies for general sports statistics would be useful.
Although power laws are a common phenomenon that can be generated by many different types of processes [
5], Deng et al. [
9] and Morales et al. [
11], Morales et al. [
12] suggest possible mechanisms specific to competitive sports. Using computer simulations, they then confirmed the emergence of power laws from these specific mechanisms, which might therefore, also be relevant to snooker statistics. Furthermore, O’Brien and Gleeson [
22] propose an alternative way to analyze snooker player rankings, based on complex networks. These studies all suggest useful directions for further and more detailed research in the specific context of snooker statistics.
There are several obvious connections between billiards and mathematics, such as the geometry in the way the balls move across the table, or linear algebra in calculating the maximum score still achievable, given how many reds are left on a snooker table. A less straightforward example of such a connection was studied previously, using so-called “billiard sequences” to solve a difficult problem in queueing theory [
23]. Here, another less obvious connection is investigated in more detail, by exploring mathematical patterns in snooker rankings.
As a final note, in the year 1935, when Zipf first described his findings of an inverse relationship between word frequency and rank [
1], there was only one professional snooker tournament held: the world championship. Just five players competed in the tournament, and there was no prize money (apparently, the players made some money from spectator ticket sales). Even if Zipf had been interested in snooker, he certainly would not have found his famous relationship in such scant data. However, almost 90 years later now, rank-proportional behavior and proportionate growth are clearly abundant in snooker statistics.