1. Introduction
In comparisons of the distributional values of a given psychological or physical trait between two populations (e.g., treated/untreated, male/female, exposed/nonexposed, elderly/youthful), the relative proportion of each population with values exceeding specified threshold or cutoff levels is often of more interest than comparisons of average values, standard deviations, or combinations thereof such as the Cohen d effect-size measure. The (right) tail ratio of one distribution compared to a second distribution, a measure of the relative tail proportions, is the ratio of the fraction of the first population above a given cutoff to the fraction of the second population above that same cutoff.
Tail ratios are a common measure of differences in extremes between populations in general and are of particular interest in psychological research, as emphasized by [
1] in their review of the background, history, and practical advantages of tail ratios. For example, ref. [
2] reported actual numerical ranges (between two and four) of certain male/female tail ratios and [
3] studied how certain male/female tail ratios have changed over time. More generally, the issues of over- and underrepresentation of various factions of populations consisting of two or more subpopulations has become an important subject of study (see [
4,
5,
6,
7,
8]).
The values of many biological or psychological traits (e.g., blood pressure, IQ, height) are often assumed to have normal (Gaussian) distributions (e.g., [
9,
10,
11]), and the goal of this note is to record a simple fact about normal distributions that may be useful in interpreting statistical data concerning both tail ratios and over- and underrepresentation in mixed populations. In particular, it is shown below that in every population consisting of a finite number of subpopulations with different distributions of a normally distributed trait, exactly one of the subpopulations will not only dominate every other one in the right tail but also will do this in an extreme manner, eventually overwhelming all the other subpopulations. This property, although not unique to normal distributions, is not shared by other common distributions, including ones that are also continuous, centrally symmetric, and unimodal, nor even by other bell-shaped distributions such as the common Cauchy (Lorentz) distributions.
2. Tail Ratios and Right-Tail Dominance
Recall that a probability measure P on the real line is uniquely determined by its complementary cumulative distribution function (ccdf) , defined by for all . ( is also often called the survival function of P, since represents the P-probability of the set above the cutoff threshold c, i.e., the fraction that survives when all values less than or equal to c are removed.) With this notation, the formal definition of the tail ratio of to is as follows.
Definition 1. Given probability distributions and , the tail ratio of to is the function , where and are the ccdfs for and , respectively.
(N.B. By convention, the tail ratio of to is that of the right tail; i.e., the ratio of the ccdf of to the ccdf of , not the ratio of the cdf of to the cdf of , which would yield the left tail ratio.)
A distribution may be said to dominate another distribution in the right tail if, for all sufficiently large cutoffs c, the tail ratio of to is strictly greater than 1, i.e., . A much stronger notion of domination in the right tail is when the survival probabilities of eventually become arbitrarily larger than those of as the cutoff increases; this is formalized in the next definition.
Definition 2. A probability distribution strongly dominates distribution in the right tail if the (right) tail ratio of to becomes infinitely large as the cutoff increases, i.e., if We also recall that a continuous (absolutely continuous) probability distribution P is uniquely determined by its probability density function via ; so, in particular, . The next lemma, which records a simple relationship between the quotients of probability density functions (pdfs) and the quotients of the corresponding ccdfs, is used in several examples and proofs below.
Lemma 1. Suppose and are continuous probability distributions with strictly positive continuous pdfs and and with ccdfs and , respectively. If , then .
Proof. Let
and
be strictly positive continuous pdfs with corresponding ccdfs
and
, respectively. Then, since
, and
for all
x,
where the first equality follows by the general form of L’Hôpital’s rule, the second since
, and the third by hypothesis. □
The next example illustrates the difference between domination and strong domination.
Example 1. - (i)
Let and be Cauchy distributions with medians and and scale parameters and , i.e., with density functions respectively. Then by Lemma 1,which implies that, as , the -probability of the set of numbers greater than c approaches exactly twice the -probability of numbers greater than c. Thus, although dominates in the right tail, neither nor strongly dominates the other in the right tail. - (ii)
Let and be Laplace distributions with medians and and scale parameters , i.e., with density functions , respectively. Then,again, neither nor
strongly dominates the other in the right tail.
- (iii)
Let and be Laplace distributions with medians and scale parameters and , respectively. Then, strongly dominates in the right tail since - (iv)
Let and be normal distributions with identical variances and with means 1 and 0, respectively. Then, the density functions and for and , respectively, satisfy as ; so, by Lemma 1, strongly dominates in the right tail.
3. Tail Ratios in Normal Distributions
When population research studies report only the means and standard deviations of their results, the default scientific understanding is that the data are approximately normally distributed. That is, the distributions in question are close to normal (Gaussian) distributions (see [
12] for a comprehensive treatment of this classic distribution.)
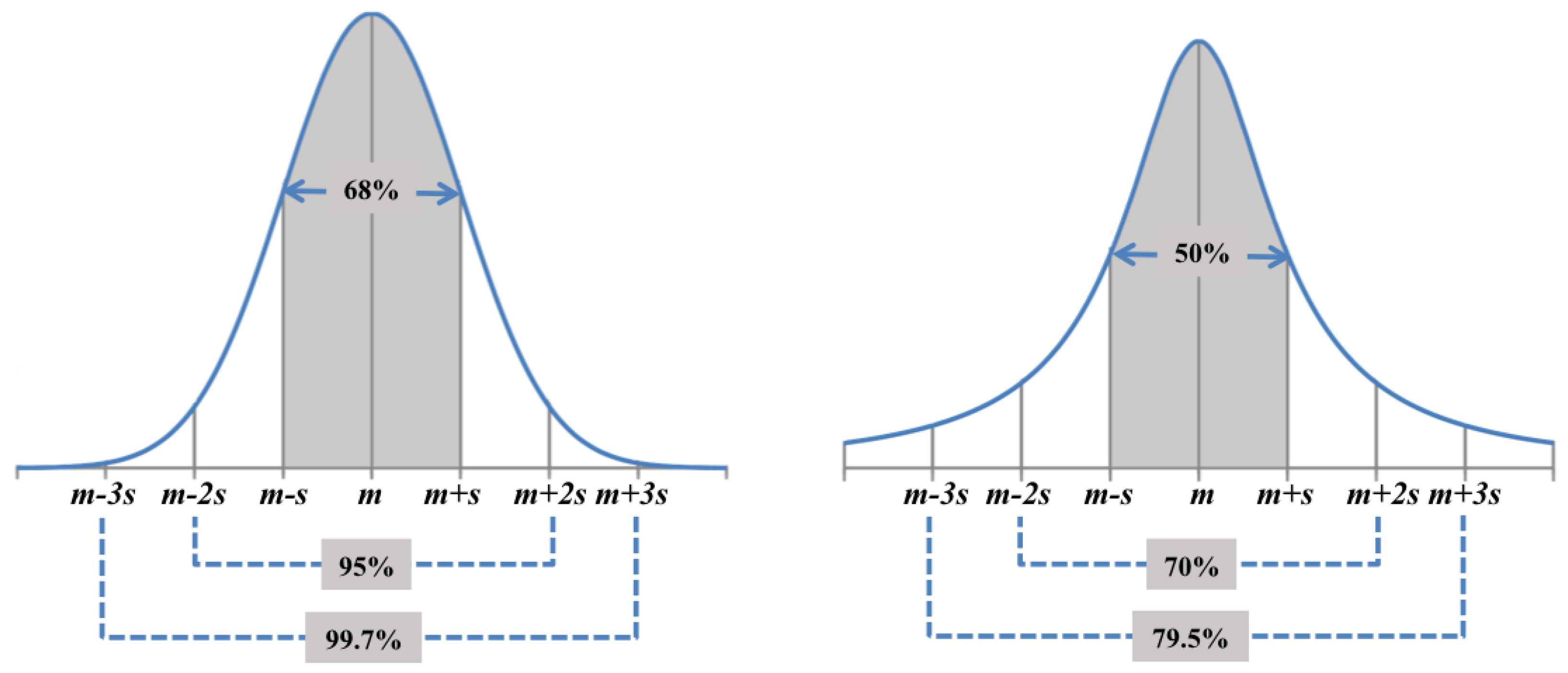
For example, if a research study reports that their data have an average value of 2 and a standard deviation of 1, then the usual understanding is that the underlying dataset looks like the diagram in
Figure 1(left) with
and
, not like the somewhat similar Cauchy distribution in
Figure 1(right). The underlying theoretical basis for the assumption of normality in most cases is the remarkable Central Limit Theorem, which says that if the numerical results of independent repetitions of
any experiment are added, the empirical distribution (and consequently the sample average) always approaches a normal distribution. For instance, in the present context of tail ratios, the survey article by Voracek, Mohr, and Hagmann states “all tail-ratio calculations discussed here assume normally distributed variables” ([
1], p. 882).
The appropriateness of assuming that given data have a normal distribution is often tested using the well-known empirical observation called the “68%–95%–99.7% rule” of normality illustrated in
Figure 1(left). The one key property of a continuous centrally symmetric unimodal distribution that makes it normal is the unique (after rescaling) rate of decrease in its density function away from its mean. The normal density function, discovered by Gauss in 1809 in connection with his studies of astronomical observation errors, decreases from its mean at a rate exactly proportional to
and not to
or
, for example, as is the case for the Laplace and Cauchy distributions, respectively.
The Cauchy distribution, for instance, which sees widespread application in physics, also has a continuous centrally symmetric unimodal bell-shaped density similar to the normal distribution, but the Cauchy distribution has an undefined mean and variance and satisfies a different empirical rule, namely the 50%–70%–79.5% rule illustrated in
Figure 1(right). Thus, it is very easy in practice to distinguish between these two similar-looking common bell-shaped distributions.
As is easy to see, the density functions of every two different normal distributions intersect in either exactly one or in exactly two distinct points. Thus, the density function of one of those two distributions is strictly larger than that of the other at all points greater than the larger of the two intersection points (or the unique one, if there is only one). This, in turn, implies that the proportion of that distribution from that point on is strictly larger than that of the other distribution from that point on; thus, this distribution will be overrepresented in the right tail. This is illustrated in the following example.
(N.B. For brevity, the standard notation will be used throughout this note to denote a normal distribution with mean m and standard deviation .)
Example 2. - (i)
Let and . It is clear that the unique crossing point of the density functions of and is at , which implies that the proportion of that is above any cutoff is greater than the proportion of above c, i.e., the tail ratio of to is greater than 1 for all cutoff values c strictly greater than 105. Conversely, the proportion of below any is greater than the proportion of below c.
- (ii)
Let and . By basic algebra, the two crossing points of the density functions of and are seen to be at and , which implies that the tail ratio of to is greater than 1 for all cutoffs . Similarly, in this case also dominates in the lower tail in that the proportion of that is below any cutoff is also greater than the proportion of below c.
As was seen in Example 1, for two given different Cauchy distributions or two different Laplace distributions, neither distribution may strongly dominate the other in the right tail. This is in sharp contrast to the main conclusion in this note, where it will be shown that in every finite collection of different normal distributions, there is always a unique one of those distributions that strongly dominates every one of the other distributions in the right tail.
Theorem 1. Let and be different normal distributions. Then,
- (i)
eitherstrongly dominates in the right tail or strongly dominates in the right tail;
- (ii)
if strongly dominates in the right tail, then either has greater mean (average value) than or has greater variance than or both;
- (iii)
if has greater variance than , then strongly dominates in both right and left tails, independent of the means.
Proof. Suppose that and are normal distributions with pdfs and , respectively. Since and are different, either or and .
Case 1.
. Without loss of generality,
. Then,
Since
,
, then (
1) implies that
, and thus by Lemma 1,
strongly dominates
in the right tail.
Case 2.
and
. Without loss of generality,
. Then,
In addition, without loss of generality,
, in which case (
2) implies, via Lemma 1 as in Case 1, that
strongly dominates
in the right tail. This concludes the proof of (i); the proofs of (ii) and (iii) follow similarly. □
The same essential argument extends easily to show that among every finite collection of different normal distributions, strong domination in the right tail by exactly one of those distributions is inevitable.
Corollary 1. Given a finite number of different normal distributions , there is a unique one of these distributions that strongly dominates all the others in the right tail.
Proof. For each , let normal distributions have mean and standard deviation , respectively. Since the distributions are all different, if and then , which implies that there exists a unique such that . By the arguments for Cases 1 and 2 in Theorem 1, strongly dominates in the right tail for all . □
As was seen in Theorem 1, if
has either greater variance than
or the same variance and higher mean, then
will strongly dominate
in the right tail. Moreover, for many practical purposes, “most important, what might appear to be trivial group differences in both variability and central tendency can cumulate to yield very appreciable differences between the groups in numbers of extreme scorers” ([
10], p. 11). The next example, a slight modification of the numerical example suggested by Feingold, illustrates this observation with the two normal distributions in Example 2(ii) that are close in mean value (100 vs. 101) and in standard deviation (10 vs. 11).
Example 3. Suppose a population X consists of two mutually exclusive subpopulations and , where the values of a given trait are normally distributed with distributions and , respectively, as in Example 2(ii). A normal distribution calculator yields that and , which yields the tail ratio Thus, even with distributions this close in average value and standard deviation, if the two subpopulations and are of the same size, then the population will comprise more than 75% of the combined population beginning only three standard deviations above the mean.
Note that the results in Theorem 1 and Corollary 1 for normal distributions only depend on first-order asymptotic terms, and the question of which more general classes of distributions with rapidly decaying tails satisfy the same conclusions is left to the interested reader.
4. Overrepresentation in the Right Tail
Whether a particular subpopulation is overrepresented or underrepresented among the other subpopulations with respect to given values for a specific trait depends on the relative size of that subpopulation with those trait values compared to the size of the whole population with those trait values. For example, if subpopulation comprises 30% of the total population, but comprises 40% of the population with trait values above a given cutoff c, then is overrepresented in the portion of the total population with values greater than c.
The goal of this section is to show that a simple consequence of Corollary 1 is that in every finite mixture of different normal distributions, exactly one of those distributions will be strongly overrepresented in the right tail. (Recall that a finite mixture of distributions is a probability distribution with cdf F satisfying , where , are cdfs, and are strictly positive weights with . )
Definition 3. Given a finite mixture of distributions , the distribution is strongly overrepresented in the right tail of F if, as , the proportion of subpopulation with values above c approaches 100% of the total population of F with values above c, that is, if Theorem 2. In every finite mixture of different normal distributions , there is a unique such that is strongly overrepresented in the right tail of F.
Proof. For all
, let
denote the ccdf of
. By Corollary 1, there exists a unique
such that
strongly dominates
for all
, i.e.,
Since
for all
, (
3) implies that
which implies that
so
is strongly overrepresented in the right tail of
F. □
Two concrete examples of normally-distributed traits among human populations are height and test scores such as those in the College Board Scholastic Aptitude Test (SAT). There are enormous amounts of data on human height, which are essentially continuous and are very close to being normally distributed ([
11], p. 24). Scores on the SAT, on the other hand, are originally discrete but the distribution “obtained from a continuized, smoothed frequency distribution of original SAT scores” is a linear transformation of a normal distribution ([
9], p. 59). Thus, since all linear transformations of normal distributions are normal, for all practical purposes, the resulting smoothed SAT scores have normal distributions.
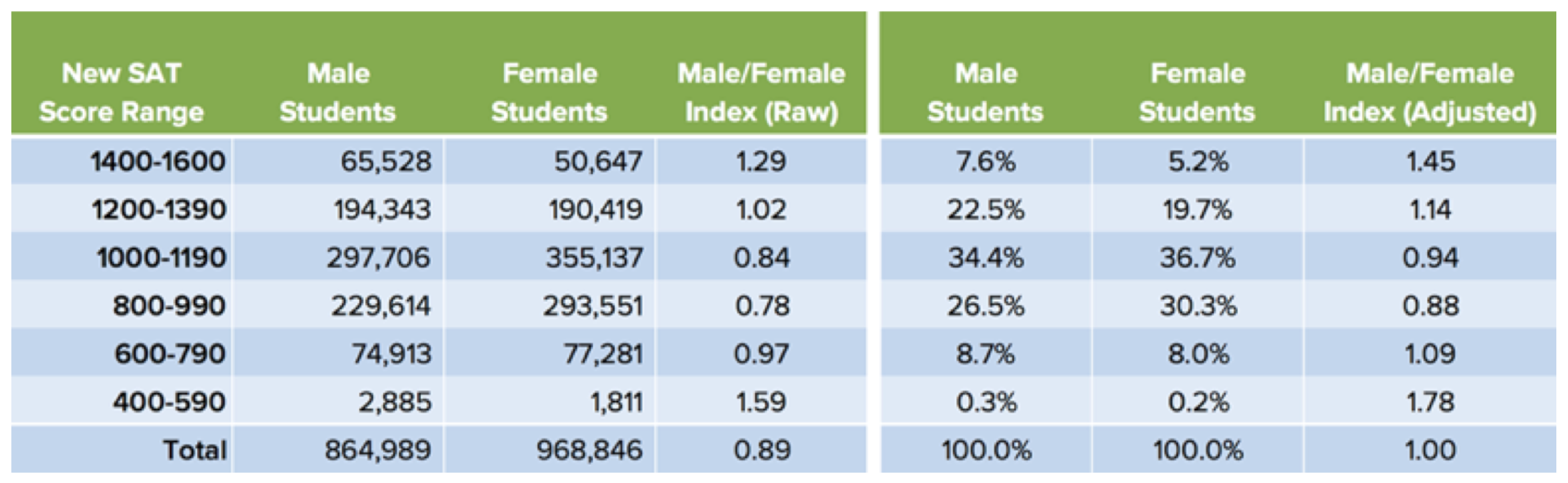
Example 4. The SAT scores of males and females are usually assumed (or designed) to be approximately normally distributed [9]. Unless the distributions are identical, Theorem 2 implies that exactly one of those two sexes must be strongly overrepresented in the right tail, and that this overrepresentation will increase as the score range increases; Figure 2 illustrates this with actual College Board statistics.
Figure 2.
Figure from [
13], p. 7, titled “The numbers College Board didn’t publish” showing statistics for nearly two million students for the 2016 Edition of the Scholastic Aptitude Test, with breakdown by gender and score ranges. Note that the proportions of males in various score ranges, i.e., the tail ratios, increase as the score range increases and the left tail ratios also increase as the score range decreases.(About 10% more females participated than males, which is reflected in the Adjusted Male/Female Ratios).
Figure 2.
Figure from [
13], p. 7, titled “The numbers College Board didn’t publish” showing statistics for nearly two million students for the 2016 Edition of the Scholastic Aptitude Test, with breakdown by gender and score ranges. Note that the proportions of males in various score ranges, i.e., the tail ratios, increase as the score range increases and the left tail ratios also increase as the score range decreases.(About 10% more females participated than males, which is reflected in the Adjusted Male/Female Ratios).