On the Bivariate Composite Gumbel–Pareto Distribution
Abstract
:1. Introduction
2. Preliminaries
2.1. Notation
2.2. Bivariate Classical Distributions
2.2.1. Gumbel’s Bivariate Exponential Distribution,
2.2.2. Bivariate Pareto Distribution of the First Kind,
3. A Bivariate Composite Model
4. Particular Case: Bivariate Composite Gumbel–Pareto Distribution
4.1. Some Properties
- (i)
- By imposing the continuity condition to the marginal we obtain
- (ii)
- By imposing the continuity condition to the marginal we obtain
- (iii)
- By simultaneously imposing continuity conditions to the marginals and we obtainIf, moreover, we also impose the continuity condition at the following restriction must be fulfilled
4.2. Simulation
- 1.
- Generate a value from the marginal distribution of by inverting its cdf given in Proposition 1;
- 2.
- Generate a value from the conditional distribution of given by inverting the conditional cdf given in Proposition 5. Thus, the resulting pair is simulated from (10).
- 1.
- Generate a value b from the Bernoulli distribution with parameter r;
- 2.
- If , then generate the pair from the Gumbel distribution truncated on D;
- 3.
- If , then generate the pair from the bivariate Pareto distribution (4).
4.3. Parameter Estimation
- I.
- Perform marginal estimation for both marginals; since the marginals are univariate composite distributions, the approach described above for the univariate case can be used. This would give starting values for the marginal parameters and the approximate location of the marginally estimated thresholds .
- II.
- Let and denote the (increasing) sorted marginal data and assume that the marginally estimated thresholds , where . Now consider the l intervals preceding and the l intervals following the interval that covers , as long as they exist; for each combination of such intervals, perform full MLE and keep the best solution. The resulting algorithm is:
- Step 1. For to , ,evaluate as solutions of the optimization problem:under the constraints and in the corresponding intervals, and continuity conditions, if imposed.
- Step 2. Among the solutions obtained from Step 1, choose the one that maximizes the log-likelihood function.
Note that in this way, for reasonable choices of and l, the computing time is significantly reduced.
- Step 1. Obtain initial values for the parameters , , and as follows:
- -
- The initially estimated thresholds are and , where , , are two given large proportions, and denotes the integer part. An initial value for each proportion can be deduced from the Hill plot or by doing MLE of the univariate Pareto for the tail.
- -
- The initially estimated value of the exponential parameter is obtained by MLE of the univariate truncated exponential distribution with density function:
- Step 2. Define a grid for , i.e., . For each , the estimated parameters , , and are obtained by maximizing the conditional log-likelihood function . The optim() function of R software with the “Nelder–Mead” method can be used; this works reasonably well for non-differentiable functions. The parameters and are estimated using the continuity conditions.
- Step 3. Let be the optimal values of the log-likelihood obtained at Step 2, and let be the corresponding parameters. The final estimated parameters are:with
5. Numerical Illustration
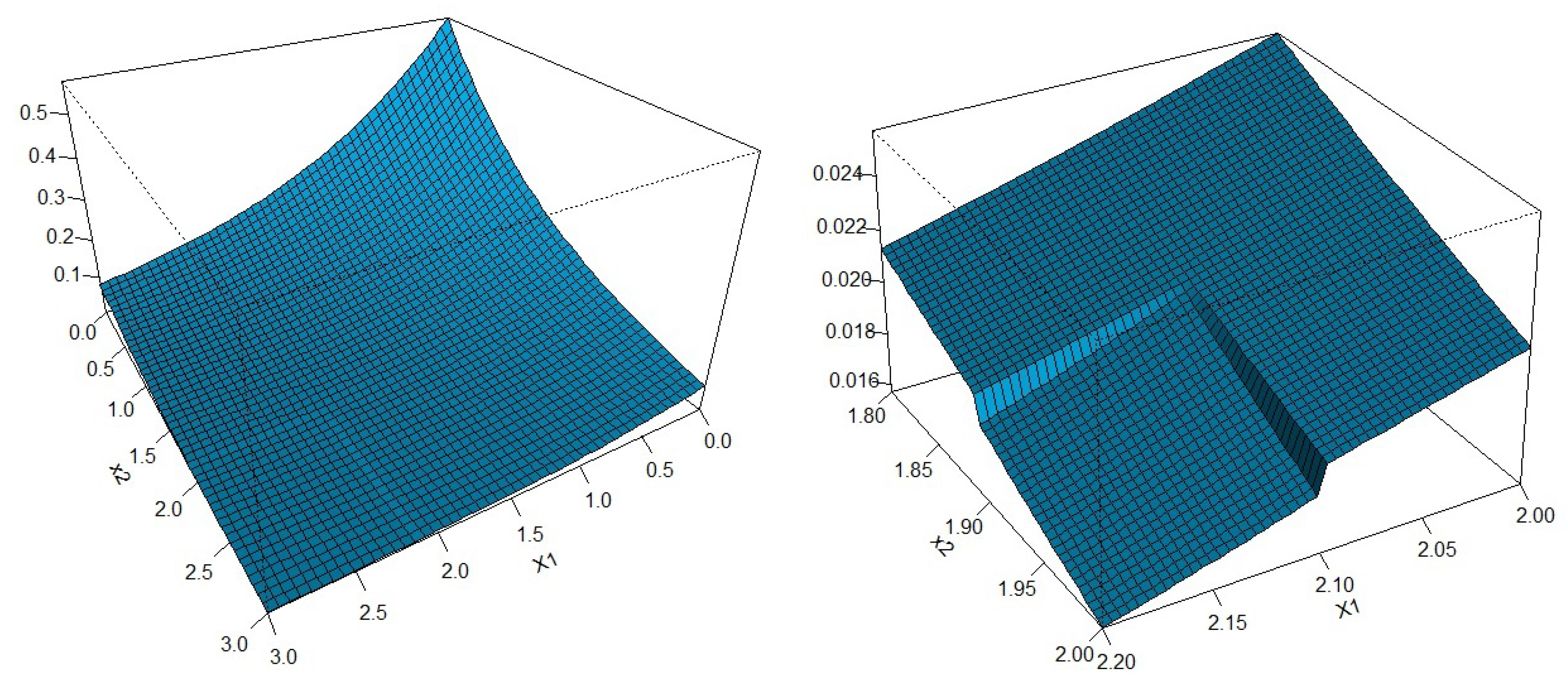
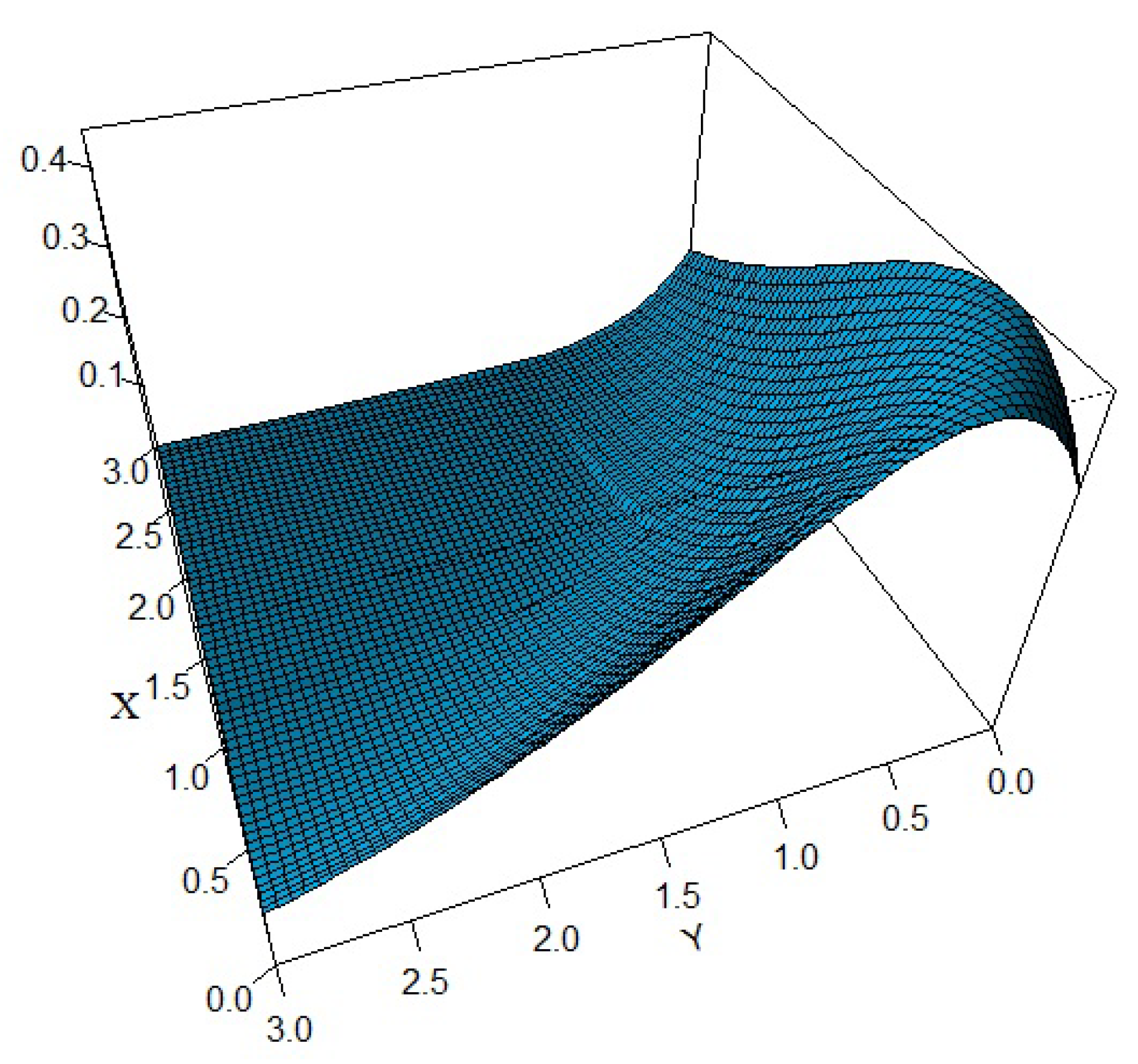
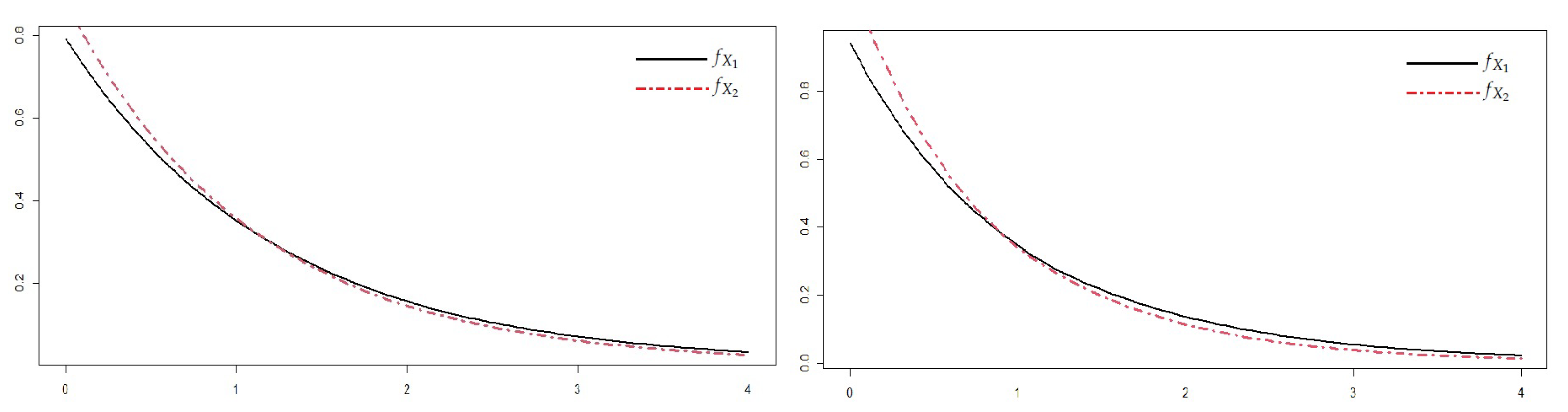
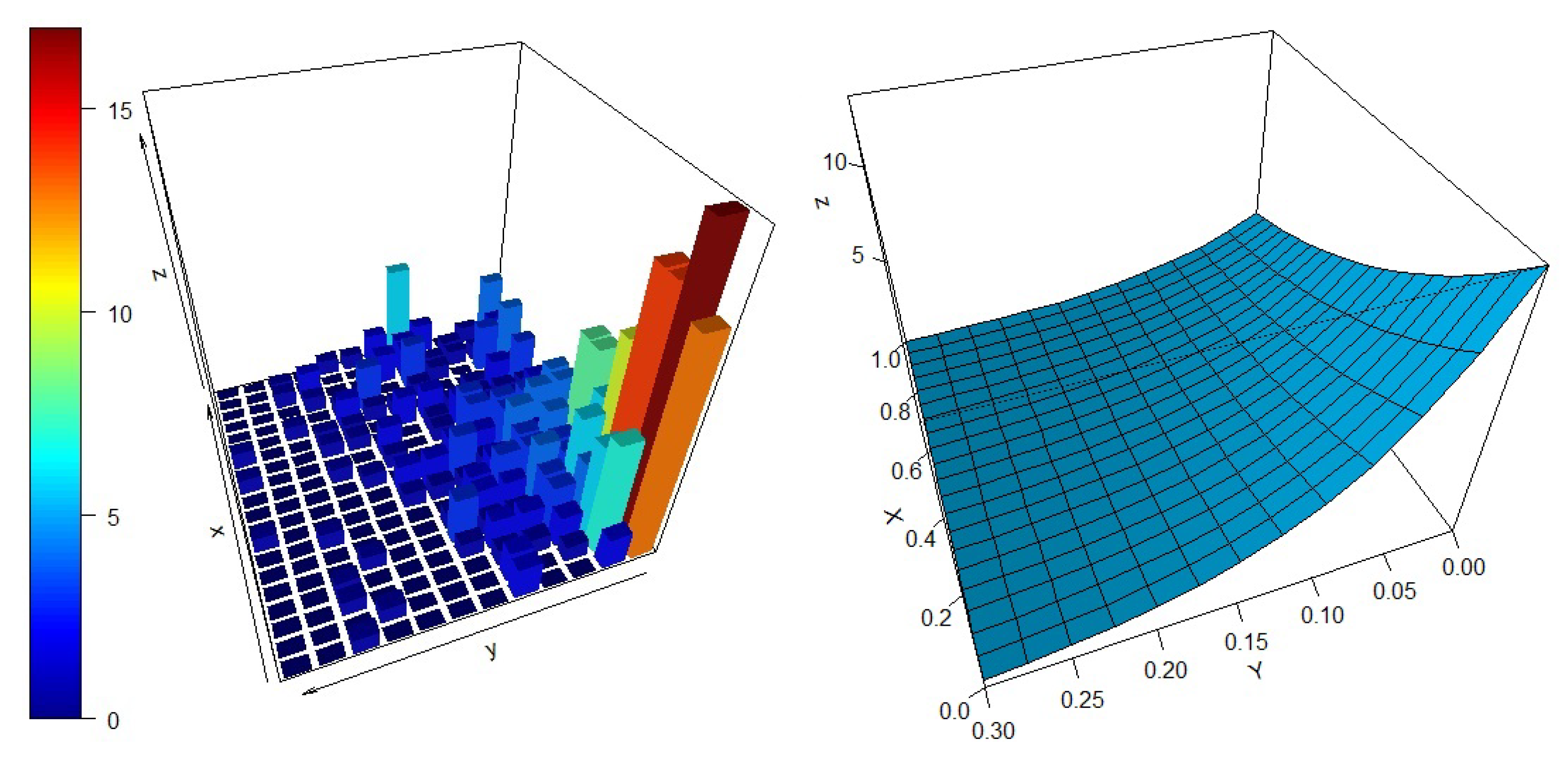
5.1. Numerical Illustration Using Simulated Data
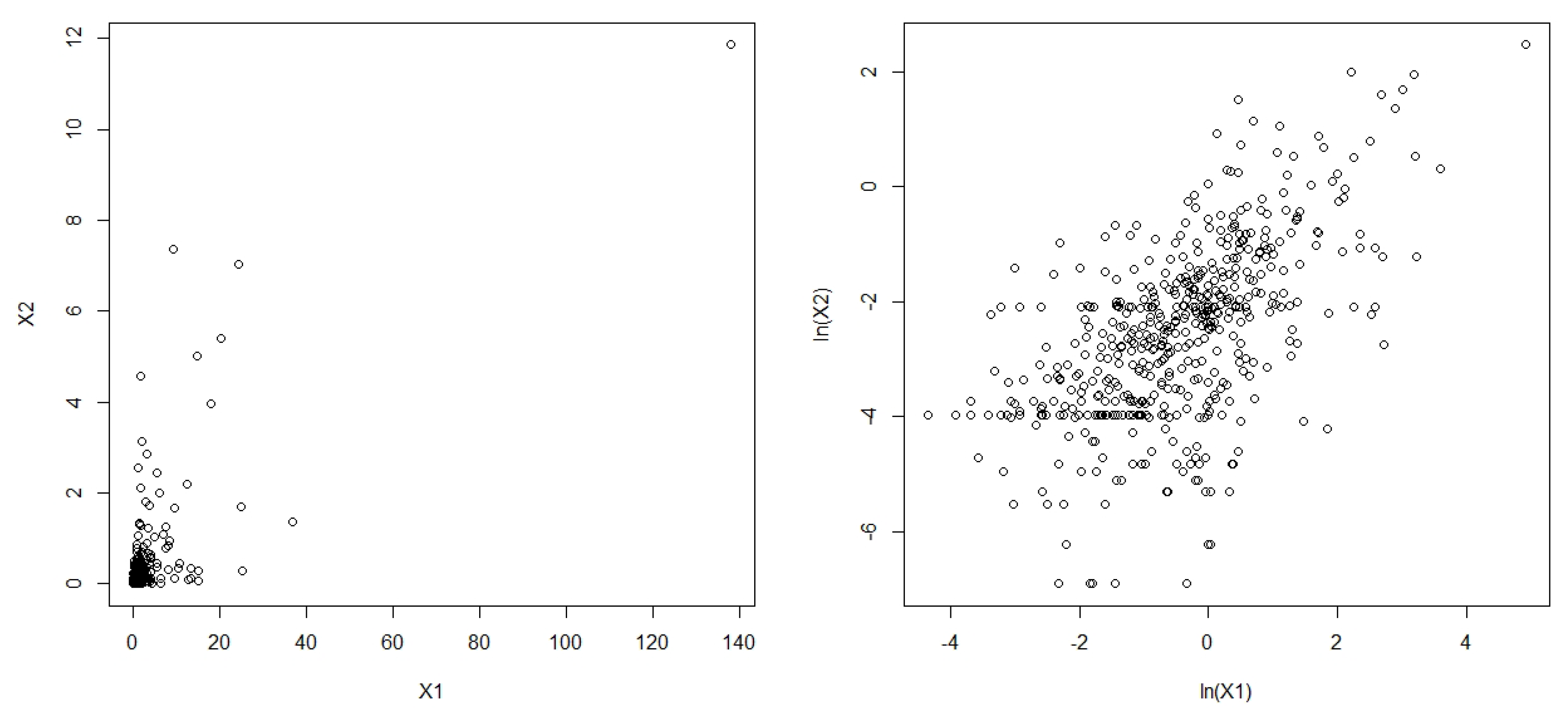
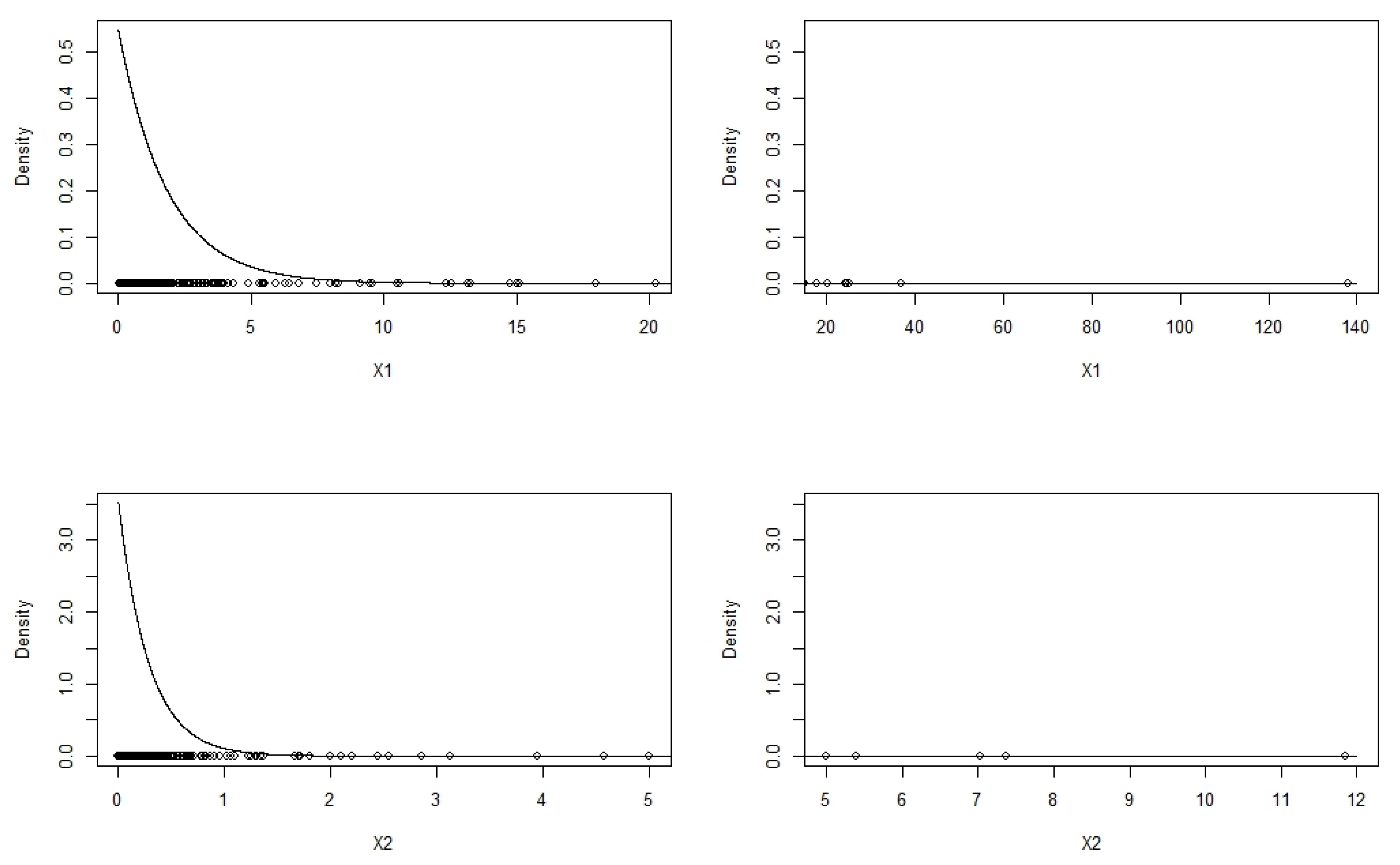
5.2. Numerical Illustration with Real Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
Appendix A. Proofs
- (i)
- Since , we have two cases:Case : it is easy to see thatCase : in this case,We insert the formula of from Lemma 3 and obtain the stated formula of .
- (ii)
- Based on the formula of , we again have two cases:Case : clearly, here we obtain the cdf of the exponential distribution of .Case : in this case,The first two integrals add to the cdf of the exponential distribution of in , while the last integral yields the cdf of the Pareto distribution of . Therefore,where for the last equality, we used formula (3) of . From here, the formula of is immediate. □
- (iii)
- We equate from (i) and (ii) and obtainMoreover, the continuity condition at means ; hence, using (11) and , we obtainfrom which results the stated formula of a. □
References
- Sarabia, J.M.; Gómez-Déniz, E. Construction of multivariate distributions: A review of some recent results. SORT 2008, 32, 3–36. [Google Scholar]
- Klugman, S.A.; Panjer, H.H.; Willmot, G.E. Loss Models: From Data to Decisions; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Scarrott, C. Univariate extreme value mixture modeling. In Extreme Value Modeling and Risk Analysis: Methods and Applications; Dipak, K.D., Jun, Y., Eds.; CRC Press: Boca Raton, FL, USA, 2016; pp. 41–67. [Google Scholar]
- Cooray, K.; Ananda, M.M. Modeling actuarial data with a composite lognormal-Pareto model. Scand. Actuar. J. 2005, 5, 321–334. [Google Scholar] [CrossRef]
- Bolancé, C.; Guillen, M.; Pelican, E.; Vernic, R. Skewed bivariate models and nonparametric estimation for the CTE risk measure. Insur. Math. Econ. 2008, 43, 386–393. [Google Scholar] [CrossRef]
- Bahraoui, Z.; Bolancé, C.; Pelican, E.; Vernic, R. On the bivariate Sarmanov distribution and copula. An application on insurance data using truncated marginal distributions. SORT 2015, 39, 209–230. [Google Scholar]
- Gumbel, E.J. Bivariate exponential distributions. J. Am. Stat. Assoc. 1960, 55, 698–707. [Google Scholar] [CrossRef]
- Kotz, S.; Balakrishnan, N.; Johnson, N.L. Continuous Multivariate Distributions, Volume 1: Models and Applications; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Castillo, E.; Sarabia, J.M.; Hadi, A.S. Fitting continuous bivariate distributions to data. Statistician 1997, 46, 355–369. [Google Scholar] [CrossRef]
- Mardia, K.V. Multivariate Pareto distributions. Ann. Math. Stat. 1962, 33, 1008–1015. [Google Scholar] [CrossRef]
- Scarrott, C.J.; MacDonald, A. A review of extreme value threshold estimation and uncertainty quantification. REVSTAT Stat. J. 2012, 10, 33–60. [Google Scholar]
- Bahraoui, Z.; Bolancé, C.; Pérez-Marín, A.M. Testing extreme value copulas to estimate the quantile. SORT 2014, 38, 89–102. [Google Scholar]
- Chen, J. Optimal rate of convergence for finite mixture models. Ann. Stat. 1995, 23, 221–233. [Google Scholar] [CrossRef]
- Kim, D.; Lindsay, B.G. Empirical identifiability in finite mixture models. Ann. Inst. Stat. Math. 2015, 67, 745–772. [Google Scholar] [CrossRef]

| Simulation Method I | ||||||||||||
| a | ||||||||||||
| n | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE |
| 200 | 0.0037 | 0.0538 | 0.0060 | 0.0717 | 0.0124 | 0.1077 | 0.3855 | 0.6152 | 0.0530 | 0.2226 | 0.0144 | 0.1069 |
| 1000 | 0.0034 | 0.0511 | 0.0048 | 0.0610 | 0.0118 | 0.1044 | 0.0275 | 0.1625 | 0.0450 | 0.2109 | 0.0049 | 0.0619 |
| Simulation Method II | ||||||||||||
| a | ||||||||||||
| n | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE |
| 200 | 0.0054 | 0.0721 | 0.0041 | 0.0447 | 0.1530 | 0.3900 | 0.0640 | 0.2493 | 0.0694 | 0.2619 | 0.0985 | 0.3010 |
| 1000 | 0.0048 | 0.0610 | 0.0002 | 0.0131 | 0.1234 | 0.3367 | 0.0174 | 0.1267 | 0.0638 | 0.2564 | 0.0567 | 0.2229 |
| Mean | STD | Min | Q25 | Median | Q75 | Max | Kurtosis | Skewness | |
|---|---|---|---|---|---|---|---|---|---|
| X1 | 1.83 | 6.87 | 0.01 | 0.26 | 0.68 | 1.39 | 137.94 | 15.70 | 301.30 |
| X2 | 0.28 | 0.86 | 0.00 | 0.02 | 0.09 | 0.20 | 11.86 | 8.06 | 85.35 |
| Pearson | Kendall | Spearman | |
|---|---|---|---|
| Correlation | 0.7288 | 0.4252 | 0.5903 |
| Gumbel | Gumbel–Pareto | |
|---|---|---|
| 0.5472 (0.0240) | 1.4184 (0.0328) | |
| 3.5221 (0.1548) | 11.1996 | |
| - | 0.9870 (0.0040) | |
| - | 0.1250 (0.0003) | |
| 0.0000 | 0.0455 (0.0465) | |
| a | - | 0.4292 |
| r | - | 0.8303 |
| −696.1630 | −272.5549 | |
| AIC | 1398.3261 | 557.1097 |
| BIC | 1411.0759 | 582.6096 |
| CAIC | 1414.0759 | 588.6096 |
| 95% | 99% | 99.50% | |
|---|---|---|---|
| Empirical | 7.926 | 25.409 | 31.216 |
| Gumbel | 6.312 | 9.700 | 11.178 |
| Gumbel–Pareto | 6.361 | 114.067 | 410.897 |
| Log-normal | 6.529 | 15.122 | 20.787 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badea, A.; Bolancé, C.; Vernic, R. On the Bivariate Composite Gumbel–Pareto Distribution. Stats 2022, 5, 948-969. https://doi.org/10.3390/stats5040055
Badea A, Bolancé C, Vernic R. On the Bivariate Composite Gumbel–Pareto Distribution. Stats. 2022; 5(4):948-969. https://doi.org/10.3390/stats5040055
Chicago/Turabian StyleBadea, Alexandra, Catalina Bolancé, and Raluca Vernic. 2022. "On the Bivariate Composite Gumbel–Pareto Distribution" Stats 5, no. 4: 948-969. https://doi.org/10.3390/stats5040055
APA StyleBadea, A., Bolancé, C., & Vernic, R. (2022). On the Bivariate Composite Gumbel–Pareto Distribution. Stats, 5(4), 948-969. https://doi.org/10.3390/stats5040055







