Abstract
Variable transformations have a long and celebrated history in statistics, one that was rather academically glamorous at least until generalized linear models theory eclipsed their nurturing normal curve theory role. Still, today it continues to be a covered topic in introductory mathematical statistics courses, offering worthwhile pedagogic insights to students about certain aspects of traditional and contemporary statistical theory and methodology. Since its inception in the 1930s, it has been plagued by a paucity of adequate back-transformation formulae for inverse/reciprocal functions. A literature search exposes that, to date, the inequality E(1/X) ≤ 1/(E(X), which often has a sizeable gap captured by the inequality part of its relationship, is the solitary contender for solving this problem. After documenting that inverse data transformations are anything but a rare occurrence, this paper proposes an innovative, elegant back-transformation solution based upon the Kummer confluent hypergeometric function of the first kind. This paper also derives formal back-transformation formulae for the Manly transformation, something apparently never done before. Much related future research remains to be undertaken; this paper furnishes numerous clues about what some of these endeavors need to be.
1. Introduction
Early comprehensive, fruitful statistical advances in normal curve (i.e., Gaussian distribution; e.g., [1]) theory, which benefits from the relative simplicity of its univariate and multivariate mathematical statistics, allowed it to dominate most sectors of statistical analysis methodology for many decades. The advent of its affiliated normal approximation power transformation technique [e.g., Box and Cox [2], who (especially p. 212) present a brief early history of data transformations, tracing these techniques back at least to 1937 (work by Bartlett), and crediting Tukey for considerable contributions about them prior to the publication of their classic Box–Cox paper; others they recognize include Ascombe, Kleczkowski, Moore, and Tidwell; Rojas-Perilla [3] provides an insightful contemporary update to their story] that extended its suitability to many of the hundreds of other univariate random variable (RV) distributions that exist (e.g., [4,5,6]) preserved its prominence until, for example, Nelder and Wedderburn’s formalization and implementation of generalized linear model (GLM; [7]) theory in the early 1970s [8]. Regardless of the data analysis specification error risks affiliated with approximations, recognition of especially normal curve theory’s pedagogic value continues to this day [9]).
Normal curve theory treats continuous interval/ratio measurement scale RVs over a (–∞, ∞) support domain, with Box–Cox [2] power and Manly ([10]; also see [11]) exponential transformations as well as other normal approximations (e.g., [12]) artificially expanding its practical applicability to more limited domains such as the truncated support [0, ∞). Griffith [13], for example, discusses RV transformations together with their accompanying back-transformations, employing fractional calculus to achieve such final results. A serious drawback of this approach is that it applies only to non-negative Box–Cox power transformation exponents. A study [14] using 2010 United States socio-economic/demographic census data, by census tracts (i.e., areal units), for both Dallas County, TX (529 tracts), and the Dallas-Fort Worth-Arlington Metropolitan Statistical Area (DFW MSA; 1324 tracts) containing it, reveals that roughly a third of the 70 (i.e., 35 × 2) selected but commonly utilized attributes measured as either percentages or densities—two time-honored standardization adjustments to geospatial and other aggregate data to minimize size effects—require a negative (i.e., inverse, reciprocal—one having a constant in its numerator and an algebraic expression in its denominator) rather than non-negative power transformation (Table 1; also see Appendix A). The sizeable proportion of reciprocal transformations reported here testifies to the importance of establishing appropriate back-transformations for this case, too, with a focus on inverse moments rather than the more general inverted distributions (e.g., [15]).

Table 1.
Attribute counts for which reciprocal Box–Cox power (i.e., inverse polynomial) and Manly exponential transformations maximize the Shapiro–Wilk [16] normality diagnostic statistic †.
2. Basic Concepts and Methodology
The central issue here concerns the inverse first moment (e.g., [18,19,20]). Although Stephan [21] derives E(l/Y) results for non-negative binomial RVs (i.e., Y = 0 does not exist) in the context of negative exponents, a broad interest in inverse moments barely predates Box and Cox, with the first published mentioning of this phraseology apparently appearing in 1962 (retrieved via a MATHSCINET search on 29 June 2022). Initial attention concentrated on continuous univariate RVs (e.g., [22]) because E(l/Y) does not exist for a discrete univariate RV Y mass function with non-zero mass at Y = 0. Nevertheless, Stephan [21] treats a modified binomial RV, and Kabe [23] devises an expression for truncated binomial and Poisson RV rth-order inverse moments, with both continuous and discrete research themes being pursued throughout the subsequent decades (e.g., [24,25,26]). Meanwhile, the more recent literature reflects somewhat of a preoccupation with individual RVs (e.g., [27]).
Cressie et al. [28] highlight that the moment generating function of a RV holds information about both its positive and negative integer moments. Unfortunately, as Griffith [13] demonstrates for positive exponent Box–Cox transformations, most empirical transformations involve fractional moments. Regardless, the first relevant proposition is as follows: given certain regularity conditions, an inverse moment can be approximated by its inverse; i.e., E(l/Y) ≈ 1/E(Y). The critical condition is that E(Y) exists and is non-zero. Furthermore, the probability density/mass function support must be positive for E(Y) always to be real. These requirements are the reasons authors devote so much writing about this topic to positive RVs. However, inclusion of a translation (i.e., shift) term δ in a two-parameter transformation allows Y to take on zero, or even negative values, as long as the minimum Y values plus δ is positive. Within the context of maximum likelihood estimation, including a translation parameter δ creates the typical non-regular estimation problem in which the likelihood function becomes unbounded as this parameter approaches −ymin, the minimum RV Y sample value [29] (p. 185). Seber and Wild note that the maximum likelihood estimate of δ is −ymin, exacerbating this situation, and comment that a “satisfactory estimation procedure is needed” [30] (p. 72). An alternative part of the associated complication is that a nonlinear trade-off frequently exists between estimates of the power exponent γ and the translation parameters δ, whereas another is that the range of values for the modified RV depends upon the resulting estimate .
Within this preceding setting, Hu et al. [31] and Yang et al. [26] propose that, for nonnegative RVs Y, the inverse moment , where is the sample mean, asymptotically approximates , if RV Y is suitably truncated and satisfies Rosenthal-type inequalities (i.e., specific relationships between moments of order higher than 2 and the variance of partial sums of RVs; [32] (p. 279))—given independent and real centered RVs Xi, i = 1, 2, …, n, for every positive integer n, if E(|Xi|p) < ∞ for p > 1, where |●| denotes the absolute value of its argument represented by ●, then . Acknowledging that many variants of the adage “a reciprocal moment approximates the reciprocal of that moment” exist, Garcia and Palacios [33] enumerate an additional sufficient condition required for it to be true. More specifically, they address a limit of the form.
This limit holds when non-negative RV Y is expressible, at least asymptotically, as a standard normal RV. However, as Groves and Rothenberg [34] emphasize, the general relationship is given by
with the gap between the left- (LHS) and right-hand side (RHS) reciprocal polynomials sometimes being very substantial, and the foregoing discussion mostly absorbed by the (near-)equality instance. In addition, this equivalence is adequate only when its transformed distribution exhibits skewness and excess kurtosis of roughly zero (see Appendix A).
2.1. The Manly Back-Transformation for the Negative Exponential Function e−βY
Conspicuously missing from the entire variable transformation literature is any debate about the inverse Manly transformation and its attendant back-transformation; perhaps surprisingly, the same can be said regarding its positive coefficient version (i.e., eβY, β > 0; of the 140 empirical attribute variables constituting the database for this paper, six transformations were of this variety). Table 1 suggests that this oversight is problematic. For the inverse case of interest here, the back-transform arithmetic mean, ignoring its seemingly trivial imaginary part involving the Erfc function—the complementary error function defined by for argument z—is given by (see Appendix B for its derivation).
where LN denotes natural logarithm, and, respectively, μ and σ, are the mean and the standard deviation of the ideal normal distribution approximated by an inverse Manly transformation. The individual conditional expectations are given by substituting each original transformed value, in turn, for μ in Equation (3). Table 2 tabulates computations for an illustrative application of Equation (3). Following guidelines advocated in Griffith [13], the nearly identical raw and back-transformed arithmetic means imply the presence of little data analysis specification error attributable to employing a normal approximation transformation. Furthermore, for the most part, the reported extremes and their corresponding conditional back-transformed means [based upon the quantiles Blom [35] promotes (see Table 2) imply that these Manly transformations also essentially preserve the ranges of the raw attribute values.

Table 2.
Selected Manly transformed 2010 percentage attribute variables experiencing improvement of their individual correspondences with a Gaussian probability density function.
As an aside, for a non-reciprocal Manly transformation, the first moment expected value given by Equation (3) simply has a sign change.
2.2. The Box–Cox Back-Transformation for the Inverse Power Function (Y + δ)−γ
The inverse case of interest here preoccupying applied statisticians and other researchers in their relevant literature writings argues for some form of E(Y*) = 1/E(Y), where variable Y* denotes a Box–Cox inverse transformation. Now this back-transform arithmetic mean, ignoring the imaginary part in the calculation reported by Mathematica 12.3—this outcome seems to be an artifact of the software’s symbolic manipulations (e.g., [36])—is given by (see Appendix B for its derivation).
where Γ[•] denotes the standard gamma function with argument •. This expression resembles Equation (3), chiefly because it includes the same type of infinite summations. Table 3 tabulates computations for an illustrative application of Equation (4). Again, following guidelines advocated in Griffith [13], the nearly identical raw and back-transformed means imply the presence of little data analysis specification error attributable to employing a normal approximation.

Table 3.
Selected Box–Cox power transformed 2010 density attribute variables experiencing improvement of their individual correspondences with a Gaussian probability density function.
Table 3 results based upon Equation (2) demonstrate the potential superiority of the proposed Box–Cox back-transformation arithmetic mean expression vis à vis contemporary conceptualizations. Evidence supporting Equation (4), beyond that summarized in Appendix B, merits more intensive future scrutiny and research, particularly with regard to the efficacy of ignoring its imaginary part.
3. Applications: More Specimen Empirical Illustrations
Preceding sections present empirical findings for seven of the 49 inverse transformations (see Appendix A) identified for 140 (= 2 × 2 × 35) attribute variables selected from the 2010 US census for either Dallas County or the DFW MSA. Table 4 compilation uncovers a strong tendency for Manly and Box–Cox inverse transformations to be competitive in situations for which the exponent γ is relatively large in absolute value (i.e., |γ| > 2); for example, the percentage of retail employment, whose respective goodness-of-fit error sums of squares (ESSs) are 5.48 and 5.94 [with an accompanying total sum of squares (TSS) of 525.8] yields an exponent of −8.44, well below the lower limit of −2 in Tukey’s [37] transformation ladder of reasonable powers (ranging from −2 to 2).

Table 4.
Selected Manly transformed 2010% and density attribute variables experiencing improvement in their individual correspondences with a Gaussian probability density function.
Table 4 furnishes numerical outcomes extremely supportive of this aforementioned contention. All back-transformed arithmetic means are nearly identical to their raw data counterparts, implying the presence of little data analysis specification error attributable to employing a normal approximation transformation. This type of conclusion almost always is the expectation when the mean percentage is roughly 50; in the suite of cases investigated here, percentages range from roughly 3% to 18%, which are substantially less than 50%. One reason these consequences may appear so good is that the worst raw data Shapiro–Wilk (S-W) statistic is 0.83, which is low but not excessively low; one raw data diagnostic statistic is 0.992, which is significantly less than one, but reflects considerable symmetry (i.e., its companion skewness measure is 0.31, which improves to 0.01 with the Manly transformation), and a distributional form approaching a bell-shaped curve.
Figure 1 portrays the two extreme specimens, with regard to their S-W normality diagnostic statistics, appearing in Table 4. The transformed plots are inversely related to their affiliated raw data plots, by construction. Although both raw data diagnostic statistics are significantly less than one, these graphics disclose noticeably better alignment for the 0.83→0.99, and questionably better alignment for the 0.992→0.997, increase in S-W cases. Regardless, in both instances, Equation (3) furnishes an excellent back-transformation as judged by a comparison of the raw and back-transformed data arithmetic means.
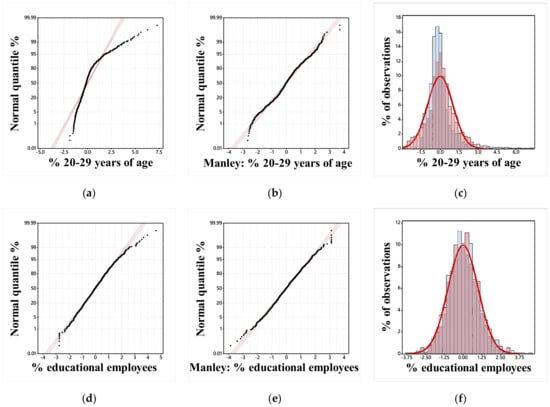
Figure 1.
Normal quantile (red lines denote 95% confidence intervals and trendlines) and histogram portrayals for two Manly transformation extreme cases appearing in Table 4. Top left (a): raw DFW% age cohort. Top middle (b): Manly transformed DFW% age cohort. Top right (c): overlaid DFW% age cohort variates with superimposed bell-shaped curve. Bottom left (d) raw DFW% employment category. Bottom middle (e): Manly transformed DFW% employment category. Bottom right (f): overlaid DFW% employment category variates with superimposed bell-shaped curve.
Table 5 also furnishes extremely supportive numerical outcomes. Although not as similar as the Manly pairings, all Box–Cox back-transformed arithmetic means are nearly identical to their raw data counterparts, again implying the presence of little data analysis specification error attributable to employing a normal approximation transformation. In addition, Table 5 compilation reveals a strong tendency for Box–Cox logarithmic and inverse transformations to be competitive in situations for which the exponent γ lies in the interval [0, −0.1]. For example, the Dallas County associate degree percentage variable has goodness-of-fit ESSs of 0.9700 for the logarithmic, and 0.9622 for the Box–Cox negative power (), transformations (TSS = 523.8); however, is not sufficiently close enough to zero to justify replacing this latter with this former transformation.

Table 5.
Selected Box–Cox power transformed 2010% and density attribute variables experiencing individual Gaussian probability density function correspondence improvement.
Figure 2 portrays the two extreme specimens, with regard to their S-W normality diagnostic statistics, appearing in Table 5. As before, the transformed plots are inversely related to their affiliated raw data plots, which is by construction. Although both raw data diagnostic statistics are significantly less than one, these graphics disclose noticeably better alignment for the 0.44→0.997, and modestly better alignment for the 0.97→0.99, increase in S-W cases. Regardless, in both instances, Equation (4) furnishes an excellent back-transformation as judged by a comparison of the raw and back-transformed data arithmetic means.
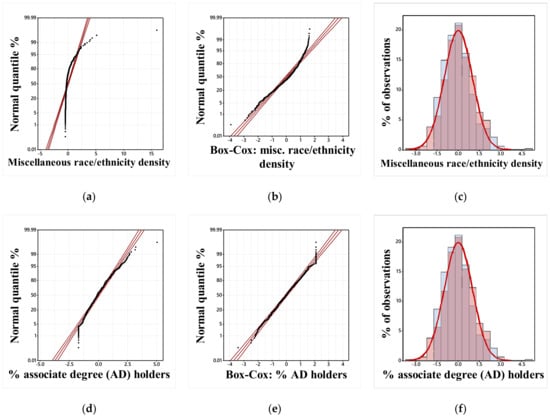
Figure 2.
Normal quantile (red lines denote 95% confidence intervals and trendlines) and histogram portrayals for two Box–Cox power transformation extreme cases appearing in Table 5. Top left (a): raw DC% associate degree holders. Top middle (b): Box–Cox transformed raw DC% associate degree holders. Top right (c): overlaid DC% associate degree holder variates with superimposed bell-shaped curve. Bottom left (d): raw DC% associate degree holders. Bottom middle (e): Box–Cox transformed raw DC% associate degree holders. Bottom right (f): overlaid DC% associate degree holder variates with superimposed bell-shaped curve.
In summary, the back-transformations proposed in this paper perform extremely well across a wide range of arbitrarily selected variates. The Manly negative exponential back-transformation seems to accomplish its goal better than the Box–Cox negative power back-transformation. Nonetheless, both appear to be superior to the Equation (2) proposition frequently endorsed, studied, and presumably applied in the literature. The average absolute error for the 49 specimen variables is roughly 1%, with a maximum of slightly less than 7%. Figure 3 portrays features of these errors, which overwhelming ratify Equations (3) and (4); see Appendix Figure A1 for a more comprehensive visualization.

Figure 3.
Specimen absolute error percentage visualizations: % error = |raw—back-transformed|/raw (gray solid denotes Table 5 DFW%, open circles denote Table 5 DC%, and solid black circles denote Table 5 DC density entries). Left (a): scatterplot portrayal of the relationship between the raw and back-transformed arithmetic means. Middle (b): boxplot of the percent absolute error. Right (c): histogram of the percent absolute error.
4. Discussion
Normal curve theory no longer enjoys the statistical methodology dominance it held prior to the advent of GLM theory and practice. Yet, a perusal of introductory mathematical statistics textbooks divulges that teaching about variable transformations is customary. This is an excellent place in a curriculum to treat normal RV back-transformations. After all, as Lesch and Jeske [9] (p. 277) point out, “Although the modern computing environment [coupled with mathematical statistics advances] has obviously alleviated the necessity of [a normal] approximation, it is still both historically relevant and quite insightful from an instructional perspective.” In keeping with this contention, the assessment presented in this paper urges future research pursuits addressing normal back-transformations for inverse RVs. Evidence provided in it contends that the Manly transformation, coupled with its accompanying back-transformation, exhibits considerable promise, especially for large negative power exponent values; the Manly transformation appears to preserve the Tukey power exponents ladder and augment its two ends, replacing these exponents when they become too extreme, a notion consistent with both parsimony and the use of an ESS criterion to help decide upon a particular transformation (i.e., Manly or Box–Cox power).
Given the preceding materials, at this time, the five ensuing themes of this section merit more thorough discussion to complete this paper.
4.1. The Inverse Back-Transformation Conceptualization
To date, reliable general inverse back-transformations continue to be a tool eluding applied statisticians, even after the emergence of a sizeable literature seeking these instruments. Conceivably, Equation (2) represents the prevailing best case scenario; unfortunately, Table 3 documents that this option can supply poor results. Furthermore, Manly [10] formulated an additional transformation that has been, and is, all but ignored in practice. One appealing advantage of his construction is that it substitutes for more extreme Box–Cox power exponents whose data calculations generate massively large or minutely small numerical values. An important contribution here is the derivation of the back-transformation for Manly’s invention.
GLM theory furnishes another crucial modern-day component to understanding data transformations and their back-transformations. Initially, the only option was to work with normal curve theory. Today, side-by-side analyses completed with it and the appropriate GLM technique allow a detailed examination of how well a transformation-based normal curve theory approach works. This type of insight can become indispensable in large or massive data settings. GLM estimation often requires an iteratively reweighted least squares routine, which essentially involves repetition of calculus-guided estimation, whereas a normal approximation might allow a linear regression substitution, dramatically reducing daunting computational demands and burdens to solve a problem. Table 6 summarizes illustrative GLM estimation output for the variates appearing in Table 2 and Table 3.

Table 6.
Comparative GLM results for certain specimen attribute variables.
Georeferenced data tend to be extraordinarily overdispersed. Accordingly, Table 6 tabulates calculations that utilized beta-binomial parametric mixture regression, and gamma-Poisson parametric (i.e., negative binomial) mixture, rather than Poisson, regression to accommodate for any excess variation. The reported GLM estimates further corroborate the validity of Equations (3) and (4).
4.2. Some Mathematics Underlying the Inverse Back-Transformations
Griffith [13] derives positive Box–Cox power exponent back-transformation formulae using fractional calculus (with a detailed appendix overview of this topic; e.g., [38]). These derivations encompass complicated, sophisticated sums having arguments written as powers of and ratios containing μ and σ combined with gamma functions.
Not surprisingly, then, Equations (3) and (4) build upon similar complex arithmetic operations. The Kummer confluent hypergeometric function, a degenerate mathematical construct introduced in the early 1800s [39], has two of its three regular singular points merge into an irregular singularity (hence, the term confluent in its description), and is the solution to the following differential equation:
where d denotes derivative, with a regular singular point at z = 0 and an irregular singular point at z = ∞. This solution is reminiscent of the fractional calculus form, containing the general summation
where the Prochhammer symbol denoting the rising factorial x(x−1) (x−2)…(x − n+1. Its integral representation is given by (after Abramowitz and Stegun [40] (p. 505)),
whereas, after taking the first partial derivative of its numerator with respect to a and then setting a to 0 for Equation (3), the numerator becomes
Its final solution has the imaginary term Erfc[μ/σ√2]πi, whose contribution to Equation (3) appears to be rather trivial (e.g., Table 7; the magnitude of the complex number essentially is its real part), and thus has been discarded here.

Table 7.
Complex solutions to Equations (3) and (4) for specimen attribute variables.
Meanwhile, Equation (4) embraces two specific Kummer confluent hypergeometric functions, the first with a = 1/(2γ) and b = 1/2, and the second with a = (1+γ)/(2γ) and b = 3/2, each pair of which substitutes into
Together, these mathematical functions are the source of the imaginary part for Equation (4), which accordingly is twofold: (−σ)1/γ and −(−σ)1/γ−1. These two terms are not totally ignorable, jointly or separately, although their final composite imaginary part seems to be. This particular conjecture warrants future scrutiny and research.
Wolfram Mathematica 12.3, for example, implements the Kummer confluent hypergeometric function for both symbolic and numerical manipulations (see https://reference.wolfram.com/language/ref/Hypergeometric1F1.html for its operationalization in Mathematica 12.3 (accessed on 6 July 2022)). Support for this latter maneuver comprises arithmetical evaluation to arbitrary numerical precision. Furthermore, this function’s executable capabilities include automatic cycling through lists of values, such as those comprising a transformed dataset in need of back-transforming. Its principal shortcoming is that it can encounter under- and over-flow calculation warnings and failures, as the next section shows.
4.3. The Specimen Empirical Example
A principal objective of the specimen data examined in this paper is to exemplify the relatively large number of times applied statisticians can encounter the necessity for adopting inverse transformations during normal curve theory exercises with their own data. The literature seems to lack any narratives about Manly back-transformations in general, let alone explanations directing their use for inverse (i.e., negative exponential) transformation cases. This paper not only fills that knowledge gap, but it also furnishes more definitive and rigorous Box–Cox inverse back-transformations. The benchmark here is a comparison of raw data and back-transformed arithmetic means (see [13]). However, Fisher’s [41] probability integral transform together with Angus’s [42] quantile function theorems, which may be stated as follows, enable one of its extensions to an entire dataset: for data values constituting any attribute variable transformable to a formal RV (e.g., the normal), this transformation is exact if the underlying distribution is the true one, and approximate in large samples if the distribution was fitted to these data. This theory is the foundation sustaining the extreme back-transformed values reported in Table 2, which build upon Blom’s [35] uniform-based systematic sample spanning a probability density function support.
Table 8 continues inspections initiated with Table 2 and Table 3; the left-hand amount in each column is the observed quantity, whereas the right-hand stack is the analytical algebraic Equations (3) and (4) quantity on the top, and the simulated parametric resampling quantity on the bottom. Numerical failures of Mathematica 12.3 in the outermost tails of normal probability density functions (see Table 8 notes) prompted verification by simulation. Of note is that Box–Cox transformations creating small means and variances may suffer from numerical distortions during their back-transformations, requiring this type of remedial intervention The protocol for this paper was to draw a systematic sample of values based upon the Blom [35] calculated CDF percentages, namely (ri − 3/8)/(n + 1 + 4). This strategy failed for occupied housing units and Dallas County 20–29 years of age densities, because they involve extreme cumulative percentages that are excessive outliers in the normal distribution tails. Its replacement strategy was to draw 10,000 random samples of size n (= 529 or 1324) from a posited ideal normal probability distribution, rejecting negative values (<0.38% of the selections for one, and none for another Dallas County attribute variable; <0.04% for the DFW MSA variate), sort them in ascending order, and then compute a back-transformation using Mathematica 12.3 for each of the n summary averages. This procedural switch causes differences between certain Table 3 and Table 8 entries. One outcome is a modest number of negative values (e.g., smallest) and non-monotonicity in the very largest (e.g., misrepresentations attributable to underflow calculations), miscalculations not certified by the simulation exercises. In addition, because they are conditional means, this complication motivating a trimming (i.e., similar to data Winsorizing) of these inadmissible values is in keeping with back-transformed values shrinking toward their mean.

Table 8.
Summary statistics calculated with complete dataset back-transformations.
Table 8 highlights possible back-transformation confusion between the mean and the median, with reference to a data analysis specification error appraisal criterion, because the ideal transformed RVs are flawlessly Gaussian, and hence these two quantities are the same. Figure 3a portrays a near-perfect matching that this table convincingly contradicts, both with analytical and with replication simulation displays. Rather, it endorses the Equation (3) Manly back-transformation, while raising serious questions about any general improvements Equation (4) might offer Box–Cox back-transformations vis à vis the RHS of Equation (2); this deficiency may be an artifact of simply ignoring the imaginary part of the complex number solutions generated by the Kummer confluent hypergeometric function. In other words, the Box–Cox inverse back-transformation comparisons here signify a potential for its use to introduce moderate-to-severe specification error into a data analysis. In general, Table 8 standard error tabulations are consistent with shrinkage conjectures, whereas, more or less, skewness and kurtosis tabulations are consistent with smoothing expectations. In a nutshell, Table 8 results imply a need for considerable comparative future research.
4.4. Alternative Transformations
The Box–Cox power and Manly exponential data transformations are not unique; Yeo–Johnson [12] transformations, for example, do not complete the set of possibilities, either. History reveals that alternatives exist for especially proportions and percentages, two of the most popular being the logit and the arcsine, this latter being the target of some derision (e.g., [43]).
The logit transform is given by the natural logarithm LN[p/(1 − p)], where 0 < p < 1 is an empirical probability, equivalent to a percentage (when multiplied by 100). It maps probability values in the interval (0, 1) {\displaystyle (0,1)} (0, 1) to real numbers in the range (−∞, +∞) {\displaystyle (−\infty, +\infty)} (–∞, ∞), paralleling the real number support for the normal probability density function. One constraining weakness of this conceptualization is that p ≠ 0, 1. Therefore, its slightly more general form may be written as LN[(p + Δ)/(1 − p + 2Δ)], Δ > 0, which allows 0 ≤ p ≤ 1; it also may be written as LN{k(p + Δ)/[k(1 − p + 2Δ)]}, where k = 100 is usual (i.e., the values become percentages), and k = 1 in the preceding empirical probabilities example. Its back-transformation is 1/(1 + e−x). Meanwhile, the inverse for this function is LN[(1 − p)/p], with a back-transformation of e−x/(1 + e−x). In other words, the notion of an inverse transformation is inconsequential in this context, because estimation is either for p or for (1 − p). Furthermore, it directly relates to binomial regression (see Table 6). Table 9 documents that this variable transformation is not uniformly better than those studied in this paper (e.g., its S-W falls between the raw and the Manly transformed outcomes). In addition, indications from evidence conveyed in Table 6 are that it may well be inferior to its comparable precedingly reflected upon beta-binomial operationalization or Equation (3) output.

Table 9.
Selected specimen attribute summary statistics for the logit back-transformation.
4.5. Alternative RV Specifications
Not only do alternative transformations exist, but alternative RV specifications also exist. Perhaps the logarithm is the one deserving the most consideration and contemplation when it competes with an inverse Box–Cox transformation with a power exponent within the interval (0, −0.10); Vélez et al. [44] establish a more precise case-specific lower bound via confidence intervals (CIs) for , accompanied by the standard criterion based upon whether or not zero falls within a CI. Its back-transformation is well-known to be ; fortunately, analytical formulae exist for all of its entries in Table 9. The other competition previously mentioned is between the Manly negative exponential and the Box–Cox power exponent of −γ < −2 transformations; the Box–Cox option in this latter case automatically should revert to its Manly competitor on the basis of numerical—for example underflow—difficulties alone.
Table 10 contents corroborate the exchangeability of the Box–Cox logarithmic and Equation (4) results when a negative power exponent is close to 0; Griffith [13] accentuates this point for its mirror positive γ interval (0, 0.10). Both back-transformations furnish competitive and reasonably accurate mean, median, and variance estimates. In contrast, because of smoothing effects induced by a transformation and its subsequent back-transformation, skewness and kurtosis frequently undergo the kinds of alterations that materialized in Table 10. One valuable insight and takeaway from this extended discussion is that parsimony is a useful concurrent criterion when selecting a data transformation, a contention alluded to by the Tukey ladder of powers. The newly stated analytical back-transformation solution provided by Equations (3) and (4) forge this as well as other new comprehensions about variable transformations.

Table 10.
Equation (4) and Box–Cox LN specimen attribute back-transformation comparisons.
5. Final Remarks
In conclusion, a cadre of statistical methodologist have been and are obsessed with trying to compel inverse/reciprocal/negative back-transformations to adhere to the functional form E(1/X) ≈ 1/E(X). However, disappointing sequels to their efforts often follow the application of this specific answer prototype, to which certain Table 3 and Table 6 entries attest. Nonetheless, determining such a solution is very important in general because many empirical attribute variables appear to require a transformation containing a negative exponent in order to improve, for example, their frequency distribution alignment with a bell-shaped curve, or stabilize their variance. One of the most important contributions of this paper is the pair of Equations (3) and (4), which furnish a solution defying the quest to exploit the relationship E(1/X) ≈ 1/E(X). Its accompanying critical implication is that the Kummer confluent hypergeometric function of the first kind supplies the necessary formula to excogitate an appropriate, accurate reciprocal function back-transformation solution.
In keeping with Freedman and Modarres [45], among others, Equation (3) needs a collection of algebraic formulae for the median, the variance, skewness, and kurtosis, replicating what presently is available for the logarithmic back-transformation, for example, to complement it. In addition, it needs a numerically sound implementation that avoids the normal tail computational adulteration issues currently encountered with Mathematica 12.3, and most likely other symbolic algebra software packages (e.g., Maplesoft; https://www.maplesoft.com/products/maple/features/symbolicnumericmath.aspx, accessed on 6 July 2022). One implication emerging here is that perseverance with the applicable algebraic manipulations should be productive; after all, this is the approach that rendered Equations (3) and (4).
Equation (4), a second novel contribution of this paper, needs considerable refinement that effectively and definitively handles its imaginary part. The real-world attribute variables explored in this paper repeatedly exhibited monotonically decreasing covarying magnitudes of their real and imaginary parts. Table 8 notes communicate that some of these amounts are not necessarily trivial in size. This pernicious Equation (4) property needs to be resolved. Nevertheless, the real number part of its output (a la Table 5, Table 6, Table 9 and Table 10) tends to match both designated observed data statistics and measures generated by competing back-transformations. The attendant chief implication here derives from the simulation experiments précised in this paper, namely both the imaginary part of the numbers, and the corrupted tail calculations by Mathematica 12.3, appear to be vestiges of symbolic manipulation rules (e.g., [36]) combined with machine and software precision and other computational inadequacies. Consequently, a refinement of Equation (4) should be void of complex numbers. This situation is reminiscent of, and encouraged by, Cardan’s formulas versus trigonometric solutions for determining the three roots of cubic equations.
Finally, the ultimate advancement spawned by this paper is completion of the back-transformation conceptualization devised by Griffith [13], extending his positive power exponents composition to embrace negative power exponents. The primary implication stemming from this particular provision is that a unified back-transformation theory is draftable now.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The empirical data were accessed and downloaded via https://www.census.gov/geographies/mapping-files/time-series/geo/carto-boundary-file.html (accessed on 6 July 2022). The simulated data were generated with the SAS 9.4 normal random number generator.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Specimen Attribute RV Pre-Assessments
As already mentioned in the narrative, the Box–Cox power and Manly exponential data transformations attempt to align an attribute RV with a normal distribution, and in in doing so stabilize the RV’s variance to a normal distribution’s constant dispersion. In their inverse forms, these transformations tend to be more applicable to RVs whose observations exhibit right-skewness, tending to concentrate relatively close to zero ([3] (p. 29) within their non-negative support. A noteworthy difference between the inverse polynomial and negative exponential functions is that the former suggests a more complex distribution, whereas the latter indicates a simple distribution. Therefore, when exponents are outside of the [−2, 2] Tukey power ladder interval, parsimony argues for swapping these descriptive equations; this is the same type of argument backing Table 9. This replacement occurs three times in Table A1: Dallas County 40–49 years of age density ( = −4.98), and DFW MSA professional ( = −2.64) and wholesale ( = −4.51) employment percentages.

Table A1.
Some relevant facets of reciprocal Manly exponential data transformation oriented attribute RVs.
Table A1.
Some relevant facets of reciprocal Manly exponential data transformation oriented attribute RVs.
| Attribute | Standardization | Geographic Landscape | Manly Transformation Coefficient | MSE | S-W p-Value | Skewness | Excess Kurtosis |
|---|---|---|---|---|---|---|---|
| owner occupied housing units | density | DC | −0.09605 | 0.02 | <0.0001 | −0.042 | −0.359 |
| 20–29 years of age | % | DC | −0.05560 | 0.03 | <0.0001 | 0.067 | 1.117 |
| DFW MSA | −0.06414 | 0.01 | <0.0001 | 0.043 | 0.403 | ||
| 30–39 years of age | % | DC | −0.03990 | 0.04 | <0.0001 | −0.009 | 1.990 |
| DFW MSA | −0.04609 | 0.02 | <0.0001 | 0.009 | 1.354 | ||
| 40–49 years of age | % | DFW MSA | −0.02020 | 0.04 | <0.0001 | −0.090 | 2.318 |
| density | DC † | −0.25250 | <0.01 | 0.0688 | −0.029 | −0.261 | |
| 50–64 years of age | % | DC | −0.04494 | 0.01 | 0.0076 | 0.026 | 0.868 |
| DFW MSA | −0.03367 | <0.01 | 0.0284 | 0.019 | 0.213 | ||
| density | DC | −0.14757 | 0.01 | 0.0115 | −0.016 | −0.114 | |
| 65+ years of age | density | DC | −0.30756 | 0.01 | <0.0001 | −0.033 | −0.370 |
| manufacturing employment | % | DC | −0.04699 | <0.01 | 0.1743 | 0.004 | 0.082 |
| DFW MSA | −0.04324 | <0.01 | 0.1044 | 0.008 | 0.136 | ||
| wholesale employment | % | DFW MSA † | −0.11909 | <0.01 | 0.0001 | −0.044 | −0.234 |
| retail employment | % | DC | −0.04737 | 0.01 | 0.0035 | 0.104 | 0.900 |
| DFW MSA | −0.03975 | 0.01 | 0.0003 | 0.063 | 0.685 | ||
| professional employment | % | DC | −0.04216 | <0.01 | 0.1129 | −0.005 | −0.057 |
| DFW MSA † | −0.04950 | <0.01 | 0.0247 | −0.009 | −0.120 | ||
| education employment | % | DFW MSA | −0.01346 | <0.01 | 0.0109 | 0.016 | 0.452 |
| miscellaneous employment | % | DC | −0.10405 | <0.01 | 0.2357 | −0.006 | −0.126 |
| DFW MSA | −0.10412 | <0.01 | 0.0203 | −0.003 | −0.022 |
† although the reciprocal polynomial is marginally superior in its description, its exponent is < −2. Note: DC denotes Dallas County; MSE denotes mean squared error for normality quantile fit; bold italic font denotes statistics significantly different from zero based upon a multiple testing Bonferroni adjusted two-tailed sig-sigma level of significance.
The literature cited in this paper, as well as other readily available publications, furnish a preponderance of evidence attesting to these two reciprocal transformations being very efficient and effective when undertaking their data modification task: empirical frequency distribution makeovers that deform them into mimicking a bell-shaped curve. In this paper, the S-W statistic provides an index of success for such metamorphoses. Hoeffding [46] posits a theorem concerning moment matching and the convergence in probability of density functions. For normal approximations, the first and second moments are of limited importance because they minimally impact density function shape; kurtosis governs the relative heaviness of tails incidental with respect to variance size. A positive support often chaperons reciprocal transformations; certainly, this support cannot contain zero, whose inverse is undefined. In addition, variance must be finite. Meanwhile, Romano and Siegel [47] (pp. 48–49), for example, note counter-examples to the claim that two distributions with the same moments are identical. The notion of a normal approximation already concedes their point. Nevertheless, if one distribution imitates another, then some of their moments should harmonize. For a bell-shaped curve, the intuitive synchronization expectation is for those moments affiliated with skewness and kurtosis: ideal normal and after-transformation histograms should reflect symmetry and peakedness similarities.
Table A1 and Table A2 tabulate these summary statistics for the attribute RVs discussed in this paper. Both theoretical values of interest are zero: the balance of symmetry begets zero, and excess kurtosis equals kurtosis minus three, the theoretical value for a normal RV. Each of these two tables presents three simultaneous statistical examinations, requiring a multiple testing correction; the Bonferroni adjustment is for a two-tailed 5% significance level, creating the following confidence intervals:
skewness for Dallas County of ± 0.254, and for the DFW MSA of ± 0.161; and,
kurtosis for Dallas County of ± 0.509, and for the DVW MSA of ± 0.322.

Table A2.
Some relevant facets of reciprocal Box–Cox data transformation oriented attribute RVs.
Table A2.
Some relevant facets of reciprocal Box–Cox data transformation oriented attribute RVs.
| Attribute | Standardization | Geographic Landscape | Data Transformation | MSE | S-W p-Value | Skewness | Excess Kurtosis | |
|---|---|---|---|---|---|---|---|---|
| δ | γ | |||||||
| persons with some college | density | DC | 5.17 | −1.58479 | 0.01 | 0.0183 | −0.017 | −0.227 |
| persons with associate degree | % | DC | 12.07 | −0.31589 | <0.01 | 0.0190 | −0.026 | −0.208 |
| no public assistance count | density | DC | 12.84 | −1.64439 | 0.01 | 0.0012 | 0.005 | −0.098 |
| owner occupied housing units | density | DC | 15.58 | −1.97132 | 0.01 | 0.0011 | 0.010 | −0.083 |
| DFW MSA | 10.09 | −1.08372 | 0.02 | <0.0001 | −0.088 | −0.373 | ||
| vacant housing units | % | DC | 5.15 | −0.45848 | <0.01 | 0.4316 | −0.002 | −0.111 |
| DFW MSA | 1.99 | −0.04822 | <0.01 | 0.4396 | −0.005 | −0.043 | ||
| density | DC | 0.05 | −0.13852 | <0.01 | 0.1897 | −0.009 | −0.137 | |
| <20 years of age | density | DC | 2.63 | −0.28963 | <0.01 | 0.2893 | −0.000 | −0.128 |
| 20–29 years of age | density | DC | 0.61 | −0.23163 | <0.01 | 0.3897 | −0.002 | −0.100 |
| 30–39 years of age | density | DC | 0.12 | −0.37042 | <0.01 | 0.1980 | −0.003 | −0.099 |
| 65+ years of age | % | DC | 2.96 | −0.03533 | <0.01 | 0.9467 | −0.001 | −0.090 |
| retail employment | density | DC | 0.27 | −0.13021 | <0.01 | 0.0312 | −0.005 | −0.103 |
| transportation employment | density | DC | 0.19 | −0.27852 | <0.01 | 0.0123 | −0.029 | −0.197 |
| financial employment | % | DC | 24.58 | −1.02556 | <0.01 | 0.2481 | −0.011 | −0.148 |
| density | 0.32 | −0.30390 | <0.01 | 0.0087 | −0.016 | −0.202 | ||
| professional employment | density | DC | 0.36 | −0.26838 | <0.01 | 0.0259 | −0.018 | −0.155 |
| education employment | density | DC | 3.45 | −1.78403 | 0.01 | 0.0088 | −0.025 | −0.171 |
| arts employment | % | DC | 5.33 | −0.03122 | <0.01 | 0.7045 | 0.000 | −0.116 |
| DFW MSA | 12.67 | −0.81549 | <0.01 | 0.0223 | −0.004 | −0.060 | ||
| density | DC | 0.06 | −0.03833 | <0.01 | 0.3089 | −0.028 | −0.115 | |
| miscellaneous employment | density | DC | 0.08 | −0.08133 | <0.01 | 0.1671 | −0.020 | −0.108 |
| public employment | % | DC | 2.89 | −0.52241 | <0.01 | 0.0001 | −0.130 | −0.494 |
| DFW MSA | 5.63 | −0.70713 | <0.01 | <0.0001 | −0.084 | −0.449 | ||
| Hispanic population count | % | DFW MSA | 1.15 | −0.09025 | 0.02 | <0.0001 | 0.037 | −0.636 |
| miscellaneous racial/ethnic count | % | DC | 0.23 | −0.08165 | <0.01 | 0.0819 | −0.011 | −0.252 |
| DFW MSA | 0.33 | −0.05555 | <0.01 | 0.0341 | −0.003 | −0.182 | ||
| density | DC | 0.03 | −0.03085 | <0.01 | 0.5073 | 0.011 | −0.102 | |
NOTE: bold italic font denotes statistically significant.
These tables reveal that the transformations virtually always adequately induce skewness, but perhaps have a slightly lower chance of also inducing kurtosis. Furthermore, even with near-perfect fits to normal quantile values, as measured by the MSE, they are even less likely to generate a non-significant S-W statistic. As an aside, the relatively large sample sizes of 529 and 1324 complicate this inferential appraisal; as Table 4 and Table 5 coupled with Figure 1 and Figure 2 demonstrate, almost all alignment gains through the use of transformations are substantial, even when transformed data S-W values remain statistically significant; this situation reflects the contemporary need to development substantive differences to replace statistical inference criteria.
Nevertheless, these larger sample sizes signify a situation in which modest departures from normality tend to be far less problematic. Accordingly, invoking the six-sigma rule here increases the confidence intervals to
skewness for Dallas County of ± 0.516, and for the DFW MSA of ± 0.326; and,
kurtosis for Dallas County of ± 1.236, and for the DVW MSA of ± 0.784.
Unfortunately, the reporting style of SAS software prevents a more precise scrutiny of the <0.0001 S-W p-values. Additionally, because the six-sigma rule classifies only 3.4 per million random samples as extreme outcomes, the natural presence of sampling error does not convincingly account for the few significant kurtosis cases appearing in Table A1; these particular few variable transformations may well be prone to serious specification error, a theme meriting future research.
On the one hand, because the assumption of normality rests upon symmetry, and a prominent characteristic of many non-normal RV probability density functions is asymmetry, skewness could be viewed as the more important of the two moments in a normality diagnosis. In keeping with this viewpoint, DeCarlo [48] suggests that skewness has a higher priority in equality of means tests. On the other hand, Khan and Rayner [49] (p. 204) state: “Both the ANOVA and Kruskal–Wallis tests are vastly more affected by the kurtosis of the error distribution rather than by its skewness.” This incongruity arises because correlation exists between skewness and kurtosis moments; their effects are not completely separable—for example, increasing skewness tends to demand increasing kurtosis in a frequency distribution. Ryu [50] highlights one consequence of this covariation: selected empirical distribution quantile plots disclose a thicker upper tail attributable to skewness as well as a longer upper tail attributable to kurtosis. With regard to data transformations, skewness usually is easier than kurtosis to manipulate: simultaneously and systematically stretching/shrinking measurement scale segments differentially to better center any clustering tendency of values—alluding to the Tukey-Mosteller bulge—can entail less effort than trying to increase/decrease this clustering propensity. Therefore, until some consensus decision-making rationale crystalizes for weighting one of these moments more than the other, data transformation evaluations should treat them equally, which essentially is the tactic taken in this paper.
Finally, especially Table A2 tabulates findings that would, for an overwhelming number of its entries, remain statistically non-significant even if the significance level criterion was more restrictive than that for six-sigma (e.g., the preceding 5% level three-test Bonfronni adjustment). In conclusion, the illustrative reciprocal transformations staged in this paper successfully align their corresponding empirical frequency distributions with a bell-shaped normal curve, when judged by a normal RV lower moments matching yardstick.
Appendix B. Deducing Equations (3) and (4)
In today’s academic world, the nature of mathematical proofs materializes in a multitude of appearances beyond their earlier formalisms, in part coinciding with the unfolding of experimental mathematics. Gone are the days of solely deductive/inductive, counter-example, and complete enumeration demonstrations. Now acceptable proofs also are by simulation [51], with some vigilance, as well as by, again with some caution, computer assisted algebraic/symbolic manipulations (e.g., [36]). The determination and justification of Equations (3) and (4) are ascribable to both of these avant-garde tools: Mathematica 12.3 aided in the postulating of these two mathematical formulae, and simulation experimentation helps validate the presumable superfluousness of the discarded imaginary parts reported in Mathematica symbolic output. Accordingly, this backdrop insinuates that these two expressions are conjectures rather than theorems, and this appendix outlines the process and rationale used to posit them. Future research needs to convert them into theorems with proofs.
The formulation of Equation (3) begins with the following back-transformation for the reciprocal Manly exponential transformation:
where e denotes Euler’s number (i.e., 2.71828…), and LN denotes the natural logarithm. The original data transformation e−βy creates X ~ (μ, σ2), presuming (μ − 6σ) >> 0—whose gap size is relative to the magnitude of the mean and standard deviation—where denotes a normal RV. The companion Mathematica problem becomes
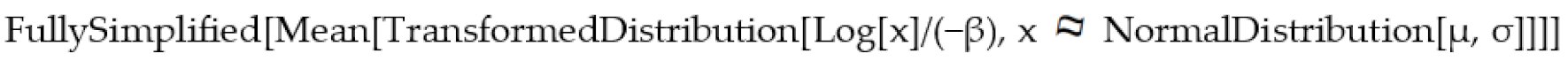
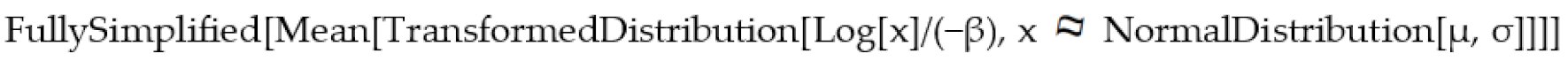
The computational outcome generated by executing this command is
where the imaginary part, appears to be trivial (e.g., see Table 7), is the Kummer confluent hypergeometric function of the first kind, the superscript (1, 0, 0) denotes the partial derivative with respect to only the first argument of hypergeometric function 1F1, say a in its 3-tuple [a, b, z] argument, and EulerGamma ≈ 0.577216. Setting to zero, and replacing the Mathematica notation Log with the natural logarithmic notation LN, yields
Simulation experiments (e.g., Table 2) verify this reduced result. Nonetheless, future research needs to document definitively that the imaginary number part source term is irrelevant in general.
This last expression may be rewritten as follows, writing latent Prochhammer symbols with summation and product terms:
Theory of equations states that the coefficients for the kth-order polynomial generated by are given by, for each of its a1 terms that disappear with the first partial differentiation and after substitution of a = 0 in the resulting derivative, (k − 1)!. Thus, the new reduced expression becomes
which is Equation (3). For this paper, specimen empirical data for Dallas County and the DFW MSA submitted to Mathematica 12.3 supplies numerical illustrations employing this expression.
Equation (4) has a similar mathematical pedigree, and hence its derivation parallels the preceding protocol sketched for Equation (3). This new proposition begins with the following back-transformation for the reciprocal Box–Cox polynomial transformation:
where, as mentioned in the text of this paper, δ is a translation/shift parameter. This data transformation also creates X ~ N(μ, σ2), presuming (μ − 6σ) >> 0. The companion Mathematica problem becomes
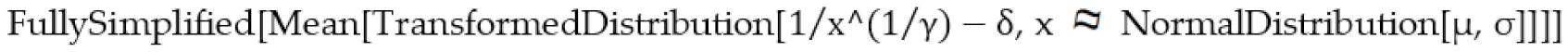
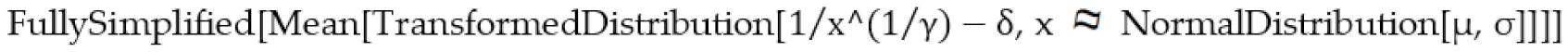
The computational outcome generated by executing this symbolic computer code is
where the imaginary part spawned by appears to be trivial, enabling its removal. Next, factoring out from the two terms and , and then combining it with renders Equation (4), once more with the appropriate notational replacements (e.g., Γ for Gamma, and the embedded Prochhammer symbol based summations and products):
Interestingly, although the twice-appearing term causes the solution to be a complex number, trial-and-error experiments reveal that it cannot be deleted from this expression without nontrivial real number part consequences. This undesirable complication warrants future research. In addition, equivalent to the Equation (3) situation for this paper, specimen empirical data for Dallas County and the DFW MSA submitted to Mathematica 12.3 supply confirmatory numerical illustrations employing this final expression, ignoring its imaginary part.
To conclude, these two sets of reasoning deliver new normal curve theory transformation conceptualizations pertaining to inverse data transformations. Table A3 summarizes utilized specimen dataset implementation details for exemplification purposes in this paper; Figure A1 visualizes part of their quality evaluation. No back-transformed mean results reflect error in excess of 10%: Figure A1a portrays a near-perfect linear alignment of these quantities with their corresponding source observed means. Mathematica 12.3 is able to compute the analytical expected value of X2 for Equation (4), allowing calculation of its analytical back-transformed standard error. This second moment quantity encompasses noticeably more error (e.g., Figure A1c) than its first moment counterpart, although Figure A1b indicates that even the most extreme case of this error still falls within its applicable linear regression prediction interval.

Table A3.
Some relevant facets of reciprocal Box–Cox data transformation oriented attribute RVs.
Table A3.
Some relevant facets of reciprocal Box–Cox data transformation oriented attribute RVs.
| Attribute | Standardization | Geographic Landscape | Sample | X ~ N(μ, σ2) | Analytical Back-Transform | |||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | μ | σ | Mean | Std | |||
| persons with some college | density | DC | 2.28868 | 1.78452 | 0.04504 | 0.01289 | 2.30168 | 1.82904 |
| persons with associate degree | % | DC | 5.30865 | 3.09253 | 0.40835 | 0.02235 | 5.30959 | 3.09170 |
| no public assistance count | density | DC | 7.67880 | 7.08938 | 0.00810 | 0.00289 | 7.63801 | 6.40739 |
| owner occupied housing units | density | DC | 7.94437 | 7.37202 | 0.00233 | 0.00087 | 7.81829 | 6.36004 |
| DFW MSA | 5.88595 | 6.01351 | 0.05479 | 0.01523 | 5.88984 | 5.84572 | ||
| vacant housing units | % | DC | 9.26427 | 5.36083 | 0.30598 | 0.04611 | 9.28522 | 5.61065 |
| DFW MSA | 8.27112 | 5.18106 | 0.89882 | 0.02030 | 8.27266 | 5.18001 | ||
| density | DC | 1.00941 | 1.58668 | 1.08762 | 0.15151 | 1.07676 | 3.01539 | |
| <20 years of age | density | DC | 6.00651 | 5.55741 | 0.56292 | 0.07947 | 6.00618 | 5.49232 |
| 20–29 years of age | density | DC | 3.75940 | 4.74007 | 0.77874 | 0.13213 | 3.86005 | 6.50218 |
| 30–39 years of age | density | DC | 3.42150 | 3.49520 | 0.61765 | 0.12209 | 3.47850 | 4.17092 |
| 65+ years of age | % | DC | 9.32520 | 5.66088 | 0.91842 | 0.01420 | 9.32757 | 5.71179 |
| retail employment | density | DC | 1.09802 | 1.12837 | 0.99245 | 0.08382 | 1.09837 | 1.13553 |
| transportation employment | density | DC | 0.51136 | 0.57754 | 1.18487 | 0.19236 | 0.51372 | 0.65285 |
| financial employment | % | DC | 9.22157 | 5.26190 | 0.02767 | 0.00412 | 9.22708 | 5.29164 |
| density | 0.93917 | 1.07139 | 1.01615 | 0.18628 | 0.95651 | 1.34996 | ||
| professional employment | density | DC | 1.46243 | 1.82636 | 0.93457 | 0.16866 | 1.49461 | 2.34179 |
| education employment | density | DC | 1.57018 | 1.52754 | 0.06380 | 0.02124 | 1.55729 | 1.32047 |
| arts employment | % | DC | 9.11213 | 5.14143 | 0.92179 | 0.00995 | 9.11566 | 5.17936 |
| DFW MSA | 8.34434 | 4.73567 | 0.08629 | 0.01434 | 8.34958 | 4.82226 | ||
| density | DC | 1.04784 | 1.40957 | 1.01643 | 0.03869 | 1.05496 | 1.60596 | |
| miscellaneous employment | density | DC | 0.57024 | 0.75712 | 1.06901 | 0.07125 | 0.56892 | 0.73592 |
| public admin. employment | % | DC | 2.74977 | 3.26125 | 0.43541 | 0.08752 | 2.73393 | 3.06032 |
| DFW MSA | 3.09183 | 2.73703 | 0.22569 | 0.03996 | 3.08215 | 2.56482 | ||
| Hispanic population count | % | DFW MSA | 27.60125 | 22.07140 | 0.75887 | 0.05130 | 28.30224 | 29.05083 |
| miscellaneous racial/ethnic count | % | DC | 6.67949 | 8.05657 | 0.88850 | 0.06711 | 6.81957 | 10.25678 |
| DFW MSA | 7.32560 | 7.53546 | 0.91177 | 0.04209 | 7.38822 | 8.46636 | ||
| density | DC | 1.37530 | 2.51787 | 1.01202 | 0.03669 | 1.40174 | 2.84845 | |
Note: std denotes standard deviation; bold italic font entries denote a failure for (μ − 6σ) >> 0 to hold; underlined bold italic font denotes a back-transformation deviation from its partner raw data statistic of at least 10%.
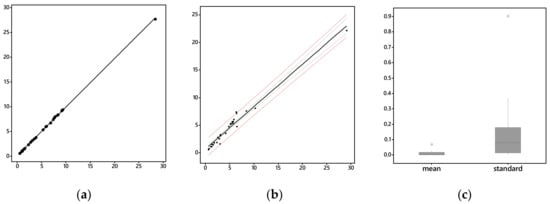
Figure A1.
Quality assessment of Table A3 specimen back-transformations. Left (a): arithmetic means scatterplot; black line denotes the linear regression trend. Middle (b): standard deviation scatterplots; black line denotes the linear regression trend, the gray lines denote 95% confidence intervals, and the red lines denote 95% prediction intervals. Right (c): |observed—back-transformed|/observed box plots.
References
- Lohnes, P.; Cooley, W. Normal curve theory. In Introduction to Statistical Procedures: With Computer Exercises; Wiley: New York, NY, USA, 1968; Chapter 7; pp. 107–125. [Google Scholar]
- Box, G.; Cox, D. An analysis of transformations. J. R. Stat. Soc. Ser. B 1964, 26, 211–252. [Google Scholar] [CrossRef]
- Rojas-Perilla, N. The Use of Data-Driven Transformations and Their Applicability in Small Area Estimation. Unpublished. Ph.D. Thesis, School of Business and Economics, Freie Universität Berlin, Berlin, Germany, 2018. Available online: https://refubium.fu-berlin.de/bitstream/handle/fub188/23214/Thesis_Rojas-Perilla.pdf?sequence=4&isAllowed=y (accessed on 27 July 2022).
- Johnson, N.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; Wiley: New York, NY, USA, 1994; Volume 1. [Google Scholar]
- Johnson, N.; Kotz, S.; Balakrishnan, N. Univariate Discrete Distributions, 3rd ed.; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Leemis, L.; McQueston, J. Univariate distribution relationships. Am. Stat. 2008, 62, 45–53. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J. Generalized Linear Models; Chapman and Hall: London, UK, 1989. [Google Scholar]
- Hilbe, J. Generalized linear models. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Lesch, S.; Jeske, D. Some suggestions for teaching about normal approximations to Poisson and binomial distribution functions. Am. Stat. 2009, 63, 274–277. [Google Scholar] [CrossRef]
- Manly, B. Exponential data transformations. J. R. Stat. Soc. Ser. D 1976, 25, 37–42. [Google Scholar] [CrossRef]
- Sakia, R. The Box-Cox transformation technique: A review. J. R. Stat. Society. Ser. D Stat. 1992, 41, 169–178. [Google Scholar] [CrossRef]
- Yeo, I.-K.; Johnson, R. A new family of power transformations to improve normality or symmetry. Biometrika 2000, 87, 954–959. [Google Scholar] [CrossRef]
- Griffith, D. Better articulating normal curve theory for introductory mathematical statistics students: Power transformations and their back-transformations. Am. Stat. 2013, 67, 157–169. [Google Scholar] [CrossRef]
- Brown, T.; Wood, J.; Griffith, D. Using spatial autocorrelation analysis to guide mixed methods survey sample design decisions. J. Mix. Methods Res. 2017, 11, 394–414. [Google Scholar] [CrossRef]
- Lehmann, E.; Shaffer, J. Inverted distributions. Am. Stat. 1988, 42, 191–194. [Google Scholar]
- Shapiro, S.; Wilk, M. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Royston, P. Approximating the Shapiro–Wilk W-test for non-normality. Stat. Comput. 1992, 2, 117–119. [Google Scholar] [CrossRef]
- Piegorsch, W.; Casella, G. The existence of the first negative moment. Am. Stat. 1985, 39, 60–62. [Google Scholar]
- Khuri, A.; Casella, G. The existence of the first negative moment revisited. Am. Stat. 2002, 56, 44–47. [Google Scholar] [CrossRef]
- Rider, P. Expected values and standard deviations of the reciprocal of a variable from a decapitated negative binomial distribution. J. Am. Stat. Assoc. 1962, 57, 439–445. [Google Scholar] [CrossRef]
- Stephan, F. The expected value and variance of the reciprocal and other negative powers of a positive Bernoullian variate. Ann. Math. Stat. 1945, 16, 50–61. [Google Scholar] [CrossRef]
- Chao, M.; Strawderman, W. Negative Moments of Positive Random Variables. J. Am. Stat. Assoc. 1972, 67, 429–431. [Google Scholar] [CrossRef]
- Kabe, D. Inverse moments of discrete distributions. Can. J. Stat. 1976, 4, 133–141. [Google Scholar] [CrossRef]
- Wu, T.-J.; Shi, X.; Miao, B. Asymptotic approximation of inverse moments of nonnegative random variables. Stat. Probab. Lett. 2009, 79, 1366–1371. [Google Scholar] [CrossRef]
- Wang, C. Recurrence relation and accurate value on inverse moment of discrete distributions. J. Probab. Stat. 2015, 2015, 972035. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Hu, S.; Wang, X. On the asymptotic approximation of inverse moment for nonnegative random variables. Commun. Stat.—Theory Methods 2017, 46, 7787–7797. [Google Scholar] [CrossRef]
- Hillier, G.; Kan, R. Properties of the inverse of a noncentral Wishart matrix. Econom. Theory 2021, 1–25, First View.. [Google Scholar] [CrossRef]
- Cressie, N.; Davis, A.; Folks, J.; Policello, G. The moment-generating function and negative integer moments. Am. Stat. 1981, 35, 148–150. [Google Scholar]
- Atkinson, A. Plots, Transformations and Regression; Clarendon: Oxford, UK, 1985. [Google Scholar]
- Seber, G.; Wild, C. Nonlinear Regression; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Hu, S.; Wang, X.; Yang, W.; Wang, X. A note on the inverse moment for the non-negative random variables. Commun. Stat. Theory Methods 2014, 43, 1750–1757. [Google Scholar] [CrossRef]
- Rosenthal, H. On the subspaces of Lp (p > 2) spanned by sequences of independent random variables. Isr. J. Math. 1970, 8, 273–303. [Google Scholar] [CrossRef]
- García, N.; Palacios, I. On inverse moments of nonnegative random variables. Stat. Probab. Lett. 2001, 53, 235–239. [Google Scholar] [CrossRef]
- Groves, T.; Rothenberg, T. A note on the expected value of an inverse matrix. Biometrika 1969, 56, 690–691. [Google Scholar] [CrossRef]
- Blom, G. Statistical Estimates and Transformed Beta Variables; Wiley: New York, NY, USA, 1958. [Google Scholar]
- Durán, A.; Pérez, M.; Varona, J. The misfortunes of a trio of mathematicians using computer algebra systems. Can we trust in them. Not. Am. Math. Soc. 2014, 61, 1249–1252. [Google Scholar] [CrossRef]
- Tukey, J. Exploratory Data Analysis; Addison-Wesley: Reading, MA, USA, 1977. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional Calculus: Integral and Differential Equations of Fractional Order. In Fractals and Fractional Calculus in Continuum Mechanics; Carpinteri, A., Mainardi, F., Eds.; Springer: New York, NY, USA, 1997; pp. 223–276. [Google Scholar]
- Kummer, E. Über die hypergeometrische reihe F(a; b; x) [translation: About the geometric series F(a; b; x)]. J. Für Die Reine Und Angew. Math. 1836, 15, 39–83. [Google Scholar]
- Abramowitz, M.; Stegun, I. (Eds.) Confluent hypergeometric function. In Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Abramowitz, M.; Stegun, I. (Eds.) Dover: New York, NY, USA, 1972; Chapter 13. [Google Scholar]
- Fisher, R. Inverse probability. Proc. Camb. Philos. Soc. 1930, 26, 528–535. [Google Scholar] [CrossRef]
- Angus, J. The probability integral transform and related results. SIAM Rev. 1994, 36, 652–654. [Google Scholar] [CrossRef]
- Warton, D.; Hui, F. The arcsine is asinine: The analysis of proportions in ecology. Ecology 2011, 92, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Vélez, J.; Correa, J.; Marmolejo-Ramos, F. A new approach to the Box–Cox transformation. Front. Appl. Math. Stat. 2015, 1, 12. [Google Scholar] [CrossRef] [Green Version]
- Freeman, J.; Modarres, R. Inverse Box–Cox: The power-normal distribution. Stat. Probab. Lett. 2006, 76, 764–772. [Google Scholar] [CrossRef]
- Hoeffding, W. The large-sample power of tests based on permutations of observations. Ann. Math. Stat. 1952, 23, 169–192. Available online: https://www.jstor.org/stable/2236445 (accessed on 27 July 2022). [CrossRef]
- Romano, J.; Siegel, A. Counterexamples in Probability and Statistics; Chapman and Hall: London, UK; CRC: Boca Raton, FL, USA, 1986. [Google Scholar]
- DeCarlo, L. On the meaning and use of kurtosis. Psychol. Methods 1997, 2, 292–307. [Google Scholar] [CrossRef]
- Khan, D.; Rayner, G. Robustness to non-normality of common tests for the many-sample location problem. J. Appl. Math. Decis. Sci. 2003, 7, 187–206. [Google Scholar] [CrossRef]
- Ryu, E. Effects of skewness and kurtosis on normal-theory based maximum likelihood test statistic in multilevel structural equation modeling. Behav. Res. Methods 2011, 43, 1066–1074. [Google Scholar] [CrossRef] [Green Version]
- Sümmermann, M.; Sommerhoff, D.; Rott, B. Mathematics in the digital age: The case of simulation-based proofs. Int. J. Res. Undergrad. Math. Educ. 2021, 7, 438–465. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).