Repeated-Measures Analysis in the Context of Heteroscedastic Error Terms with Factors Having Both Fixed and Random Levels

Abstract

The design and analysis of experiments which involve factors each consisting of both fixed and random levels fit into linear mixed models. The assumed linear mixed-model design matrix takes either a full-rank or less-than-full-rank form. The complexity of the data structures of such experiments falls in the model-selection and parameter-estimation process. The fundamental consideration in the estimation process of linear models is the special case in which elements of the error vector are assumed equal and uncorrelated. However, different assumptions on the structure of the variance–covariance matrix of error vector in the estimation of parameters of a linear mixed model may be considered. We conceptualise a repeated-measures design with multiple between-subjects factors, in which each of these factors has both fixed and random levels. We focus on the construction of linear mixed-effects models, the estimation of variance components, and hypothesis testing in which the default covariance structure of homoscedastic error terms is not appropriate. We illustrate the proposed approach using longitudinal data fitted to a three-factor linear mixed-effects model. The novelty of this approach lies in the exploration of the fixed and random levels of the same factor and in the subsequent interaction effects of the fixed levels. In addition, we assess the differences between levels of the same factor and determine the proportion of the total variation accounted for by the random levels of the same factor.

1. Introduction

Linear mixed-effects models can handle both fixed and random effects simultaneously. Not only are the models convenient for modelling the means of the data, but they are also convenient for modelling covariances [1,2]. Situations arise in fields such as psychology and medicine in which longitudinal or correlated data display notorious heterogeneity of responses to stimuli and treatment [3]. When the classical linear mixed-effects model is inappropriate, alternative approaches, which identify and consider subgroups in fixed and random effects, are necessary. The authors of [4] propose a heterogeneity model as an extension to that proposed by the authors of [5,6] by replacing the normality assumption for random effects and by assuming a non-zero mean vector and a common error vector.

Repeated-measures data are often dependent, a property that does not conform to the generality of a mixed-effects model [1,7,8]. Linear mixed-effects models are some of the most convenient statistical approaches, which account for this dependency [9]. However, setting them up for data analysis requires some care, especially in choosing the most appropriate covariance structure to keep the type I error down [10]. Selecting a suitable model for the covariance is important because the precision of the confidence intervals and the tests of hypotheses concerning model parameters depend on the correct model [11]. According to [12], selecting an appropriate mixed-effects model and construction approach, such as partitioning of fixed and random effects, allows for analysis of variance in correlated data. Numerous diagonal and non-diagonal covariance structures for correlated data, which cover a range of assumptions about the associations between responses from the same cluster data, are available [13,14]. Modern statistical software, such as SAS Studio in Linux Environment, provides options for selecting candidate covariance structures through the PROC MIXED procedure [15] (see Appendix A). The residual maximum likelihood (REML) is one of the most famous methods for estimating covariance parameters associated with linear mixed models [16,17], among other alternatives [18].

We present the construction and analysis of a three-factor linear mixed model for repeated-measures designs when the between-subjects factors consist of both fixed and random levels, and the structure of the variance–covariance matrix of the error terms is not the identity. We consider a repeated-measures design setting under a linear mixed-effects model, with factors sharing both fixed and random components of the model. For experimental designs consisting of factors with a unique composition of both fixed and random levels, we propose a partitioning approach based on factor levels in model construction, estimation, and hypothesis testing. In such a situation, the fixed levels allow for the comparison of specific levels of interest within the factor, whereas the random levels allow for the assessment of variation within the same factor. We assess the effect of introducing heterogeneity of error terms in the selection of the most appropriate covariance structure, in the assessment of the changes that occur in the estimation, and when drawing inferences. To simplify the proposed approach, we focus on the diagonal covariance structure for the repeated-measures linear mixed-effects model.

Section 2 presents the approach to model construction, for a general linear mixed-effects model in a completely randomised design (CRD) and in a repeated-measures design (RMD) under the default assumption of error terms. Section 3 presents results from a numerical example. Discussion of the results is in Section 4, followed by the conclusions in Section 5.

2. Materials and Methods

2.1. An Illustrative Data Structure

We motivate the approach using data collected from a study that investigated the impact of combining carbon tetrachloride (${CCl}_4$) with four levels (0, 1.0, 2.5, and 5.0 mM) and chloroform (${CHCl}_3$) with four levels (0, 5, 10, and 25 mM) on the toxicity of cells on in vitro toxicity of isolated hepatocyte suspensions [19]. Four flasks were assigned to each of the 16 treatments. Cell toxicity is measured by the amount of lactic dehydrogenase (LHD) enzyme percentage leakage from each of the 64 flasks after 0.01, 0.25, 0.5, 1, 2, and 3 h since the application of the treatment. For illustration purposes, we consider the between-subjects factor ${CCl}_4$ levels 2.5 and 5.0 as fixed (new technology), and levels 0 and 1.0 are considered as existing random levels (old technology). Similarly, we consider the between-subjects factor ${CHCl}_3$ levels 10 and 25 as fixed (new technology), and levels 0 and 5 are taken as random levels (old technology). Of interest in the analysis is the percentage leakage observed at times 1, 2, and 3. We demonstrate the model construction procedure under certain assumptions in a completely randomised design (CRD) and in a repeated-measures design (RMD).

2.2. Construction of a Linear Mixed-Effects Model in CRD

Consider a three-way treatment structure in a balanced, completely randomised design (CRD) with full interaction of factors A, B, and C, each consisting of $f$ fixed and $r$ random levels. Assume we have $f_A, f_B$, and $f_C$ fixed levels and $r_A, r_B$, and $r_C$ random levels of factor A, respectively. We partition the dataset based on the combinations of factor levels and construct a partitioned model in each partition. For example, the FRF partitioned model is built from the $f_A$, $r_B$, and $f_C$ levels. Similarly, other possible partitions are FFF, FFR, RFF, RRF, RFR, FRR, and RRR. We illustrate the model construction using the FRF linear mixed-effects model in CRD, having at least one replication per treatment combination and expressed as

$${\mathit{y}}_{{\mathrm{FRF}}_{ijkl}}={\mu }_{\mathrm{FRF}}+{\phi }_{A_i}+{\phi }_{B_j}+{\phi }_{C_k}+{\pi }_1+\dots +{\pi }_t+{ϵ}_{{\mathrm{FRF}}_{ijkl}},$$

(1)

where ${\mathit{y}}_{{\mathrm{FRF}}_{ijkl}}$ is the lth observation in the (ijk)th treatment cell of the FRF partition; $l=1,\dots , r_h$are the replicates (where all $r_h=r$ for balanced data); ${\mu }_{\mathrm{FRF}}$ is the overall mean; ${\phi }_{Ai}, {\phi }_{Bj}, {\phi }_{Ck}$ are the main effects of the three factors; ${\pi }_1, \dots , {\pi }_t$ are the interaction effects; and ${\phi }_{A_i}$ $\left(i=1, 2,\dots ,f_A, f_A+1,f_A+2,\dots , a \left(a=f_A+r_A\right)\right)$, ${\phi }_{B_j}$ $\left(j=r_B+1,r_B+2,\dots , b \left(b=f_B+r_B\right)\right)$, and ${\phi }_{C_k}{}_k$ $\left(k=1, 2,\dots ,f_C, f_C+1,f_C+2,\dots , c \left(c=f_C+r_C\right)\right)$ are unknown parameters corresponding to fixed factor A, random factor B, and fixed factor C, respectively. Defining the random main effect as ${\phi }_R$ and the random interaction effect as ${\pi }_R$ in (1), the random effects and the random error term ${ϵ}_{ijkl}$, are commonly assumed to have zero mean and variance, i.e., ${\phi }_R ~ N\left(0,{\sigma }_{{\phi }_R}^2\right)$, ${\pi }_R ~ N\left(0,{\sigma }_{{\pi }_R}^2\right)$, and ${ϵ}_{ijkl} ~ N\left(0,{\sigma }_{ϵ}^2\right)$.

For a balanced data scenario with $r$ replications per cell, for example, the general linear mixed model Equation (1) is normally expressed in matrix form as

$${\mathit{y}}_{\mathrm{FRF}}={\mathit{X}}_{\mathrm{FRF}}\mathit{\beta }+{\mathit{Z}}_{\mathrm{FRF}}\mathit{u}+{\mathit{ϵ}}_{\mathrm{FRF}},$$

(2)

where ${\mathit{y}}_{\mathrm{FRF}}$: $N\times 1$ is a vector of response observations in the FRF partition; matrix ${\mathit{X}}_{\mathrm{FRF}}:N\times p$ is a known incidence matrix associated with the vector of $p$ fixed-effects $\mathit{\beta }:p\times 1$ in the model; matrix ${\mathit{Z}}_{\mathrm{FRF}}:N\times q$ is a known incidence matrix associated with the vector of $q$ random-effects $\mathit{u}:q\times 1$ in the model; and ${\mathit{ϵ}}_{\mathrm{FRF}}:N\times 1$ is a vector of random errors. The usual assumption under this model is that the random effects are $\mathit{u} ~ \mathit{N}\left(0,\mathit{G}\right)$, and the random residuals are ${\mathit{ϵ}}_{\mathrm{FRF}} ~ N\left(0,\mathit{R}\right)$, where $\mathit{R}={\sigma }^2\mathit{N}$ and $\mathit{G}$ is a diagonal matrix of variance components (i.e., different variances, and all zero covariances).

$$\mathit{G}=\left[\begin{array}{ccc}{\sigma }_1^2{\mathit{I}}_r& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\sigma }_t^2{\mathit{I}}_r\end{array}\right] \mathrm{and} \mathit{R}=\left[\begin{array}{ccc}{\sigma }_{ϵ}^2& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\sigma }_{ϵ}^2\end{array}\right]$$

The total variance–covariance is the structured matrix $\mathit{V}=\mathit{Z}\mathit{G}\mathit{Z}\prime +\mathit{R}$, a structure that guarantees independence and homogeneity of residual errors. This implies that the variance of $\mathit{y}$ is modelled through $\mathit{Z}$, $\mathit{G}$, and $\mathit{R}$. The simple total variance–covariance, $\mathit{V}$, has a block-diagonal structure given by the matrix

$$\mathit{V}=\left[\begin{array}{ccc}{\sigma }_1^2{\mathit{I}}_r+{\sigma }_{ϵ}^2{\mathit{I}}_r& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\sigma }_t^2{\mathit{I}}_r+{\sigma }_{ϵ}^2{\mathit{I}}_r\end{array}\right]$$

2.3. Linear Mixed-Effects Model in RMD

Traditionally, between-subject and within-subject factors in repeated-measures experiments are designated as either fully fixed effects or random effects. Depending on the objectives of the experiment, some factors in linear mixed-effects models may exist with both fixed and random levels [12,20,21]. The same scenario is common with a repeated-measures experiment, in which either the between-subjects factor or the repeated measures consist of both fixed and random levels. For instance, for improved results, a researcher may decide to consider additional levels of a between-subjects factor, in addition to the old and existing levels. In that case, the improved analysis needs to consider the new factor levels as fixed levels, and the old and existing levels are considered random. The approach creates an opportunity to compare and evaluate the effectiveness of new factor levels (fixed) against existing ones (random) and/or to compile a combined analysis of both. In addition, random levels allow for the assessment of variation between and within the factor levels in the entire population.

We consider a three-factor repeated-measures experiment with $n$ experimental units (EU) that are randomly assigned to each of the $a$ levels of the between-subjects factor A (with $f_a$ fixed levels and $r_a$ random levels, $a=f_a+r_a$, for example), the between-subjects factor B (with $f_b$ fixed levels and $r_b$ be random levels, $b=f_b+r_b$, for example), and the within-subjects factor C with $t$ measurements (all considered to be fixed in this case) taken on each of the experimental units (EU).

$$y_{p_{ijkl}}={\mu }_p+{\alpha }_i+{\beta }_j+{\left(\alpha \beta \right)}_{ij}+{\gamma }_{k\left(ij\right)}+{\tau }_l+{\left(\alpha \tau \right)}_{il}+{\left(\beta \tau \right)}_{jl}+{\left(\alpha \beta \tau \right)}_{ijl}+{ϵ}_{p_{ijkl}},$$

(3)

where the subscript $p$ in $y_{p_{ijkl}}$ and ${ϵ}_{p_{ijkl}}$ denotes the partition $\left(p=1, 2,\dots , 4\right)$ and where $y_{p_{ijkl}}$ is the lth measurement ($l=1, 2,\dots ,t$) of the kth experimental unit ($k=1, 2,\dots n$) in the ith level ($i=1, 2,\dots a$) of factor $A$ and the jth level ($j=1, 2,\dots b$) of factor $B$ in the pth partition. Depending on whether the effects are fixed or random, the model parameters are as defined in (1).

2.4. Model Assumptions

In experimental research that involves analysis of variance (ANOVA) as a technique for comparing different treatment means, a set of assumptions that includes the usual normality and homogeneity of variance must be checked before the analysis of data [22]. These traditional normality tests, such as Q–Q plots or the Shapiro–Wilk test, and outlier detection approaches (e.g., box plots), are appropriate for diagnosing violations of assumptions.

2.4.1. Sphericity (Circularity) Assumption

Similar to the homogeneity of variances in a between-subjects analysis of variance, sphericity holds in ANOVA for repeated-measures designs when the variances of the differences among all possible pairs of the within-subject factor group means are equal [23,24]. The assumption is usually unrealistic in repeated-measures designs in which observations are correlated. Univariate tests for within-subjects effects apply when sphericity holds. If the sphericity assumption is violated, several alternatives for adjusting the numerator and denominator degrees of freedom have been suggested [25]. The most popular degrees of freedom corrections are the Greenhouse–Geisser [26] or the Huynh–Feldt [27] adjustments, which are extensions of the Box correction factor [28]. These adjustments provide a more accurate adjusted p-value [29,30]. Failure to address the problem of sphericity when conducting an analysis of variance often leads to inflated F-ratios, type I errors, biased post hoc tests for group mean differences, and inaccurate conclusions [24]. Tests for sphericity are offered in most statistical computing packages (SAS, R, SPSS, etc.).

2.4.2. Compound Symmetry Assumption

An overly restrictive assumption closely related to sphericity is the compound symmetry assumption. It states that there is a constant variance and correlation between observations from the same subject, which is not always realistic in many repeated-measures applications [31]. The Greenhouse–Geisser [26] or the Huynh–Feldt [27] adjustments are used to circumvent restrictive compound symmetry assumptions and to accommodate more general covariance structures for the repeated measures [1]. Compound symmetry implies sphericity, but not vice versa. Univariate tests for within-subject effects apply when compound symmetry holds. If compound symmetry (and hence sphericity) holds, then a split-plot analysis is used as an appropriate approximation to the repeated-measures experiment, since it provides relatively more accurate p-values for testing treatment effects [31]. Compound symmetry is simplified in the Huynh–Feldt [27] condition for sphericity. Hence, both are tested in many software packages by Mauchly’s test [32]. However, Mauchly’s test for sphericity has been criticised for its over sensitivity and tendency to reject compound symmetry [33].

2.5. Estimation Techniques

The general linear mixed-effects model (2) is used to describe data from partitioned repeated measurements, wherein the fixed-effects component, ${\mathit{X}}_{\mathit{p}}\mathit{\beta }$, consists of the design matrix ${\mathit{X}}_{\mathit{p}}$, and the fixed-effects coefficients $\mathit{\beta }$ are as defined in (3). The random-effects component, ${\mathit{Z}}_{\mathit{p}}\mathit{u}$, contains the block-diagonal random-effects design matrix ${\mathit{Z}}_{\mathit{p}}$ with design matrices for the individual subjects ($Z_i$); $\mathit{u}$ is a vector of random coefficients (the between-subject variance–covariance components), and ${ϵ}_{\mathit{p}}$ denotes the within-subject errors from the pth partition. The random effects and the residuals follow the distribution $\mathit{u} ~ N\left(0,\mathit{G}\right)$ and ${\mathit{ϵ}}_{\mathit{p}} ~ N\left(0,\mathit{R}\right)$, respectively, where $\mathit{G}$ is a block-diagonal covariance matrix of the random effects and where $\mathit{R}$ is a diagonal covariance matrix with partitions corresponding to each subject (within-subject errors) in the analysis. The covariance matrix for the repeated-measures data is composed of matrices ${\mathit{Z}}_{\mathit{p}}$, $\mathit{G}$, and $\mathit{R}$, which is a block-diagonal ${\mathbf{\Sigma }}_{\mathit{p}}=Var\left({\mathit{y}}_{\mathit{p}}\right)={\mathit{Z}}_{\mathit{p}}\mathit{G}{\mathit{Z}}_{\mathit{P}}^{\prime }+\mathit{R}$. The non-singular components $\mathit{G}$ and $\mathit{R}$ are usually estimated by two principal likelihood methods for estimating variance components [34], i.e., the maximum likelihood (ML) method and restricted maximum likelihood (REML). These procedures are available in various mixed-model statistical software, such as SAS (PROC MIXED procedure) and R, with the REML estimates generally preferred unless the data sets are quite large [34].

Assuming that both the random effects and the error terms are normally distributed, the likelihood function for the repeated-measures mixed model is given by [35]:

$$\begin{array}{c}l=\log \left[L\left({\mathit{y}}_{\mathit{p}}\right)\right]\hfill \\ =\frac{-N}{2}\log \left(2\pi \right)-\frac{1}{2}\log \left|{\mathbf{\Sigma }}_{\mathit{p}}\right|-\frac{1}{2}{\left({\mathit{y}}_{\mathit{p}}-{\mathit{X}}_{\mathit{p}}\mathit{\beta }\right)}^{\prime }{\mathbf{\Sigma }}_{\mathit{p}}{}^{-1}\left({\mathit{y}}_{\mathit{p}}-{\mathit{X}}_{\mathit{p}}\mathit{\beta }\right)\hfill \\ =C-\frac{1}{2}\log \left|{\mathbf{\Sigma }}_{\mathit{p}}\right|-\frac{1}{2}{\left({\mathit{y}}_{\mathit{p}}-{\mathit{X}}_{\mathit{p}}\mathit{\beta }\right)}^{\prime }{\mathbf{\Sigma }}_{\mathit{p}}{}^{-1}\left({\mathit{y}}_{\mathit{p}}-{\mathit{X}}_{\mathit{p}}\mathit{\beta }\right)\hfill \end{array}$$

(4)

where ${\mathit{y}}_{\mathit{p}}$ and $\mathit{V}={\mathbf{\Sigma }}_{\mathit{p}}$ are as defined in (2). Similarly, a modification of the ML procedure through factorisation of the likelihood function is proposed as an alternative method of estimating covariance parameters, which is the restricted maximum likelihood function [36]:

$$\begin{array}{c}{l}_{re}=\log \left[L\left({\mathit{y}}_{\mathit{p}}\right)\right]\hfill \\ =\frac{-N}{2}\log \left(2\pi \right)-\frac{1}{2}\log \left|{\mathbf{\Sigma }}_{\mathit{p}}\right|-\frac{1}{2}{\left({\mathit{y}}_{\mathit{p}}-{\mathit{X}}_{\mathit{p}}\mathit{\beta }\right)}^{\prime }{\mathbf{\Sigma }}_{\mathit{p}}{}^{-1}\left({\mathit{y}}_{\mathit{p}}-{\mathit{X}}_{\mathit{p}}\mathit{\beta }\right)\hfill \\ =C-\frac{1}{2}\log \left|{\mathit{X}}_{\mathit{p}}^{\prime }{\mathbf{\Sigma }}_{\mathit{p}}{}^{-1}{\mathit{X}}_{\mathit{p}}\right|-\frac{1}{2}\log \left|{\mathbf{\Sigma }}_{\mathit{p}}\right|-\frac{1}{2}{\left({\mathit{y}}_{\mathit{p}}-{\mathit{X}}_{\mathit{p}}\widehat{\mathit{\beta }}\right)}^{\prime }{\mathbf{\Sigma }}_{\mathit{p}}{}^{-1}\left({\mathit{y}}_{\mathit{p}}-{\mathit{X}}_{\mathit{p}}\widehat{\mathit{\beta }}\right) \end{array}$$

(5)

where the available covariance matrix ${\mathbf{\Sigma }}_{\mathit{p}}$ is used to estimate the fixed-effects parameters,

$$\widehat{\mathit{\beta }}={\left[{\mathit{X}}_{\mathit{p}}^{\prime }{\mathbf{\Sigma }}_{\mathit{p}}{}^{-1}{\mathit{X}}_{\mathit{p}}\right]}^{-1}{\mathit{X}}_{\mathit{p}}^{\prime }{\mathbf{\Sigma }}_{\mathit{p}}{}^{-1}{\mathit{y}}_{\mathit{p}}.$$

The main challenge in repeated-measures analysis of variance is to determine the adequate correlation structure, because the constant variance assumption for the distribution of the error terms is likely not to be reasonable for the distribution of error terms within subjects. There are various possible choices of covariance structures for repeated measures within each subject depending on the chosen parameterisation for $\mathit{G}$ and $\mathit{R}$. The choices are usually guided by limitations of the software and by insight from the researcher. The most common covariance structures include variance components, compound symmetry (common covariance plus diagonal), unstructured (general covariance), and autoregressive [37]. With the PROC MIXED statement in SAS, one can specify any repeated-measurements covariance structure for $\mathit{G}$ by using the Random statement and by specifying the form of $\mathit{R}$ with the Repeated statement, in conjunction with the Type option [38]. Excluding the Repeated statement specifies the classical $\mathit{R}$, which is assumed to be equal to ${\sigma }^2\mathit{I}$.

There are numerous ways of identifying the most appropriate covariance structure amongst set candidate structures [37]. The most recommended approach is to select the structure that gives the smallest Akaike’s Information Criterion (AIC) [39], a statistic that is defined by the model and the maximum likelihood estimates of the parameters from specifying the variance–covariance as

$$\mathrm{AIC}=\left(-2\right)\mathcal{L}\left(\widehat{\mathit{\beta }},{\widehat{\mathbf{\Sigma }}}_{\mathit{p}}\right)+2\left(g\right),$$

(6)

where $g$ is the effective number of independently adjusted parameters in the covariance matrix from the pth partition, and $\mathcal{L}\left(\widehat{\mathit{\beta }},{\widehat{\mathbf{\Sigma }}}_{\mathit{p}}\right)=log\left(ML\right)$ is the value of the likelihood function evaluated at $\left(\widehat{\mathit{\beta }},{\widehat{\mathbf{\Sigma }}}_{\mathit{p}}\right)$. A better model is the one with the smallest AIC value. Different forms of $\mathit{R}$ can be compared for adequacy using the likelihood ratio test statistic [38]. The hypotheses involved are the following: $H_0: {\mathit{R}}_1$ is as adequate as ${\mathit{R}}_2$; and $H_1: {\mathit{R}}_1$ is not as adequate as ${\mathit{R}}_2$, where ${\mathit{R}}_1$ is a special case of ${\mathit{R}}_2$. Suppose ${\mathit{R}}_1$ and ${\mathit{R}}_2$ have $g_1$and $g_2$ parameters, respectively, with ($g_1<g_2)$, and the test statistic is $Q=\left(-2\right)\left[\mathcal{L}\left({\widehat{\mathit{\beta }}}_1,{\widehat{\mathbf{\Sigma }}}_1\right)-\mathcal{L}\left({\widehat{\mathit{\beta }}}_2,{\widehat{\mathbf{\Sigma }}}_2\right)\right]$, which is distributed as ${\chi }^2\left(g_2-g_1\right)$. We reject $H_0$ when $Q\ge {\chi }_{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^2\left(g_2-g_1\right)$.

2.6. Methods of Inference

We present the algorithm for obtaining expected mean squares using the ANOVA approach for the FRF model.

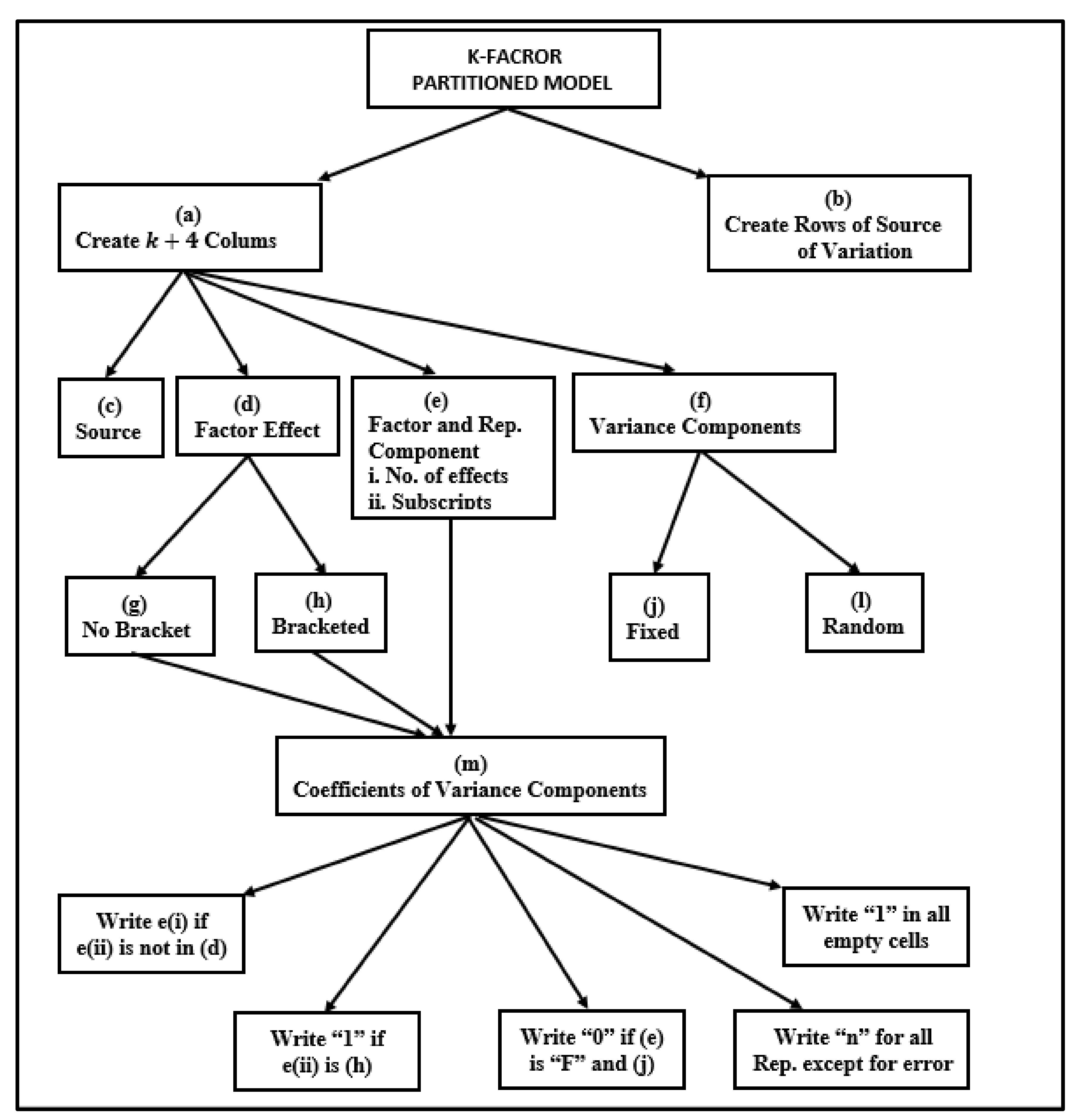
2.6.1. Process for Deriving Expected Mean Squares

(a)

Based on the model involved, construct a two-way table with column headings corresponding to the source of variation, effect labels, each of the subscripts included in the model, and row headings corresponding to each source of variation in the ANOVA table.

(b)

Above each subscript, write the associated number of factor levels and insert on top either an “F” if the factor levels are fixed or an “R” if the factor levels are random.

(c)

Create an extra column on the extreme right for the variance components corresponding to the source of variation, and insert the appropriate random variance component (${\sigma }_{.}^2$) or fixed variance component (${\theta }_{.}$) for each source of variation.

(d)

Compare the column subscript and the factor effect in each row, and write the number of levels corresponding to that subscript if the column subscript is not included in the factor effect label. Otherwise, leave it blank.

(e)

For rows that have effects that contain bracketed subscripts, write a “1” under the column if the subscript is included in the bracket.

(f)

For each row that has a fixed variance component (${\theta }_{.}$), put a zero in the cell headed by an “F” when the subscript is included in the effect label.

(g)

Enter a “1” in all remaining blank cells.

(h)

To obtain the expected mean squares for each effect, identify all the variance components associated with that effect label. Cover the column(s) headed by the effect subscript(s) in that effect, and obtain the coefficient of each of the identified components from the product of the entries in the column(s) headed by the uncovered subscript(s). Include the variance component ${\sigma }_{ϵ}^2$ with the coefficient of 1 in the list.

Figure 1 illustrates the key steps to be taken when constructing the coefficients of variance components for a partitioned linear mixed-effects model.

Once the coefficients of variance components are established in step (m) of Figure 1, the expected mean squares are found by Step (h) of the Process in Section 2.6.1.

Table 1. Variance components for a three-factor repeated-measures model.

Source of Variation	Factor Effect	F	R	F	Rep	Components of Variance
		$\mathit{a}$	$\mathit{b}$	$\mathit{t}$	$\mathit{n}$
		$\mathit{i}$	$\mathit{j}$	$\mathit{l}$	$\mathit{k}$
A	${\alpha }_i$	0	b	t	N	${\theta }_{\alpha }$
B	${\beta }_j$	a	1	t	N	${\sigma }_{\beta }^2$
AB	$\alpha {\beta }_{ij}$	1	1	t	N	${\sigma }_{\alpha \beta }^2$
EU	${\gamma }_{k\left(ij\right)}$	1	1	t	1	${\sigma }_{\gamma \left(\alpha \beta \right)}^2$
P	${\tau }_l$	a	b	0	N	${\theta }_{\tau }$
PA	$\alpha {\tau }_{il}$	0	b	0	N	${\theta }_{\alpha \tau }$
PB	$\beta {\tau }_{jl}$	a	1	1	N	${\sigma }_{\beta \tau }^2$
PAB	$\alpha \beta {\tau }_{ijl}$	1	1	1	N	${\sigma }_{\alpha \beta \tau }^2$
Error	${\epsilon }_{l\left(ijk\right)}$	1	1	1	1	${\sigma }_{ϵ}^2$

summarises the variance components obtained for a three-factor repeated-measures design, with two between-subjects factors ($A$ and $B$) on one within-subject factor ($C$) using the Process in Section 2.6.1. We use this process to build an FRF model, which assumes factors $A$ and $C$ as fixed, factor $B$ as random, and experimental units (EU) as random. The F, R, F, and Rep denote the effect; $a, b, t$, and $n$ denote levels of factors A and B, treatment number, and sample size, respectively. The subscripts $i, j, l$, and $k$ denote the indices of the corresponding levels.

For example, $E\left(MSA\right)$, with effect ${\alpha }_i$, is composed of the variance components ${\theta }_{\alpha }$, ${\sigma }_{\alpha \beta }^2$, ${\sigma }_{\gamma \left(\alpha \beta \right)}^2$, ${\theta }_{\alpha \tau }$, ${\sigma }_{\alpha \beta \tau }^2$, and ${\sigma }_{ϵ}^2$ as follows:

$$E\left(MSA\right)={\sigma }_{ϵ}^2+t{\sigma }_{\gamma \left(\alpha \beta \right)}^2+tn{\sigma }_{\alpha \beta }^2+n{\sigma }_{\alpha \beta \tau }^2+btn{\theta }_{\alpha }.$$

Table 2. Expected mean squares for a three-factor repeated-measures design.

Source of Variation	Sum of Squares	Degrees of Freedom	E(MS)
$A$	$\mathrm{SSA}$	$a-1$	${\sigma }_{ϵ}^2+t{\sigma }_{\gamma \left(\alpha \beta \right)}^2+tn{\sigma }_{\alpha \beta }^2+n{\sigma }_{\alpha \beta \tau }^2+btn{\theta }_{\alpha }$
$B$	$\mathrm{SSB}$	$b-1$	${\sigma }_{ϵ}^2+n{\sigma }_{\alpha \beta \tau }^2+an{\sigma }_{\beta \tau }^2+t{\sigma }_{\gamma \left(\alpha \beta \right)}^2+tn{\sigma }_{\alpha \beta }^2+ant{\sigma }_{\beta }^2$
$A\times B$	$\mathrm{SS}\left(A\times B\right)$	$\left(a-1\right)\left(b-1\right)$	${\sigma }_{ϵ}^2+t{\sigma }_{\gamma \left(\alpha \beta \right)}^2+n{\sigma }_{\alpha \beta \tau }^2+tn{\sigma }_{\alpha \beta }^2$
$\mathrm{Unit}\left(A\times B\right)$	$\mathrm{SSU}\left(A\times B\right)$	$ab\left(n-1\right)$	${\sigma }_{ϵ}^2+t{\sigma }_{\gamma \left(\alpha \beta \right)}^2$
$Period$	$\mathrm{SSP}$	$t-1$	${\sigma }_{ϵ}^2+n{\sigma }_{\alpha \beta \tau }^2+an{\sigma }_{\beta \tau }^2+abn{\theta }_{\tau }$
$Period\times A$	$\mathrm{SSP}\times A$	$\left(a-1\right)\left(t-1\right)$	${\sigma }_{ϵ}^2+n{\sigma }_{\alpha \beta \tau }^2+bn{\theta }_{\alpha \tau }$
$Period\times B$	$\mathrm{SSP}\times A$	$\left(b-1\right)\left(t-1\right)$	${\sigma }_{ϵ}^2+n{\sigma }_{\alpha \beta \tau }^2+an{\sigma }_{\beta \tau }^2$
$Period\times A\times B$	$\mathrm{SSP}\times A\times B$	$\left(a-1\right)\left(b-1\right)\left(t-1\right)$	${\sigma }_{ϵ}^2+n{\sigma }_{\alpha \beta \tau }^2$
$\mathrm{Residual}$	$\mathrm{SSE}$	$ab\left(t-1\right)\left(n-1\right)$	${\sigma }_{ϵ}^2$
$\mathrm{Total}$	$\mathrm{SST}$	$abtn-1$

Note that: ${\theta }_{\alpha }=\frac{1}{a-1}{\displaystyle \sum }_{i=1}^a{\alpha }_i^2$; ${\theta }_{\alpha \tau }=\frac{1}{\left(a-1\right)\left(t-1\right)}{\displaystyle \sum }_{i=1}^a{\displaystyle \sum }_{l=1}^t{\left(\alpha \tau \right)}_{il}^2$; and ${\theta }_{\tau }=\frac{1}{t-1}{\displaystyle \sum }_{l=1}^t{\tau }_l^2$.

displays the ANOVA layout and the expected mean squares for a three-factor repeated-measures design when one of the factors is a within-subject factor. The FRF model is considered for illustration, with experimental units assumed to be random.

2.6.2. Hypothesis Testing for Fixed Effects

We are interested in testing the main and interaction effects of the between-subjects factor and of the within-subjects factor in both the partitioned and combined repeated-measures linear mixed-effects model. In addition to checking model assumptions, the following hypotheses are of interest for each partitioned model:

Hypothesis 1 (H1).

Between-subjects main and interaction effects (i.e.,$H_0:{\alpha }_i=0$).

Hypothesis 2 (H2).

Within-subjects main and interaction effects (i.e.,$H_0:{\tau }_i=0$).

The test statistic for H1 is given by $F=\frac{MSA}{MSU\left(A\times B\right)} ~ F_{a-1,ab\left(n-1\right)}\left(\alpha \right)$, and the test statistic for H2 is given by $F=\frac{MSP}{MSE} ~ F_{t-1,ab\left(t-1\right)\left(n-1\right)}\left(\alpha \right)$. The interaction effects among the between-subjects and the interaction effects among within-subjects are tested by the $MSU\left(A\times B\right)$ and the $MSE$ on the denominator, respectively.

2.6.3. Hypothesis Testing for Random Effects

Variance components are estimated by equating the mean square to the expected mean squares derived in Table 2. Where there are no valid F tests, approximate F tests are constructed for the sources of variability in random effects [40]. For random factor B, the hypothesis of interest may be

Hypothesis 3 (H3).

Random effects (e.g.,$H_0:{\sigma }_{\beta }^2=0$, against$H_1:{\sigma }_{\beta }^2>0$).

2.6.4. Combined Analysis

The individual partitioned models provide pieces of information which are needed for an integrated analysis. The combined model is built by combining the degrees of freedom and sum of squares associated with each source of variation for each appropriate hypothesis test. For example, the combined effect of the within-subjects factor ($Period$) in the FC model is obtained from the partitions in which the factor $Period$ is fixed, i.e., the pieces of information are supplied by the partitioned models FFF, FRF, RFF, and RRF. Similarly, the other main and interaction effects for the combined model are obtained by summing up the associated degrees of freedom and sums of squares.

3. Results

3.1. Checking Model Assumptions

A three-factor (${CCl}_4$, ${CHCl}_3$, and $Time$) repeated-measures experiment on one of the factors ($Time$) is proposed.

Table 3. Data layout for a three-factor repeated-measures experiment.

Factors			Time Period
CCl4	CHCl3	Flask	1	2	…	t
1	1	1	$y_{1111}$	$y_{1112}$	$\dots$	$y_{111t}$
		$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
		$n$	$y_{11n1}$	$y_{11n2}$	$\dots$	$y_{11nt}$
	2	1	$y_{1211}$	$y_{1212}$	$\dots$	$y_{121t}$
		$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
		$n$	$y_{12n1}$	$y_{12n2}$	$\dots$	$y_{12nt}$
	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
	$b$	1	$y_{1b11}$	$y_{1b12}$	$\dots$	$y_{1b1t}$
		$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
		$n$	$y_{1bn1}$	$y_{1bn2}$	$\dots$	$y_{1bnt}$
2	1	1	$y_{2111}$	$y_{2112}$	$\dots$	$y_{211t}$
		$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
		$n$	$y_{21n1}$	$y_{21n2}$	$\dots$	$y_{21nt}$
	2	1	$y_{2211}$	$y_{2212}$	$\dots$	$y_{221t}$
		$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
		$n$	$y_{22n1}$	$y_{22n2}$	$\dots$	$y_{22nt}$
	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
	$b$	1	$y_{2b11}$	$y_{2b12}$	$\dots$	$y_{2b1t}$
		$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
		$n$	$y_{2bn1}$	$y_{2bn2}$	$\dots$	$y_{2bnt}$
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
$a$	1	1	$y_{a111}$	$y_{a112}$	$\dots$	$y_{a11t}$
		$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
		$n$	$y_{a1n1}$	$y_{a1n2}$	$\dots$	$y_{a1nt}$
	2	1	$y_{a211}$	$y_{a212}$	$\dots$	$y_{a21t}$
		$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
		$n$	$y_{a2n1}$	$y_{a2n2}$	$\dots$	$y_{a2nt}$
	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
	$b$	1	$y_{ab11}$	$y_{ab12}$	$\dots$	$y_{ab1t}$

shows the multivariate data (wide format) layout for a three-factor repeated-measures experiment.

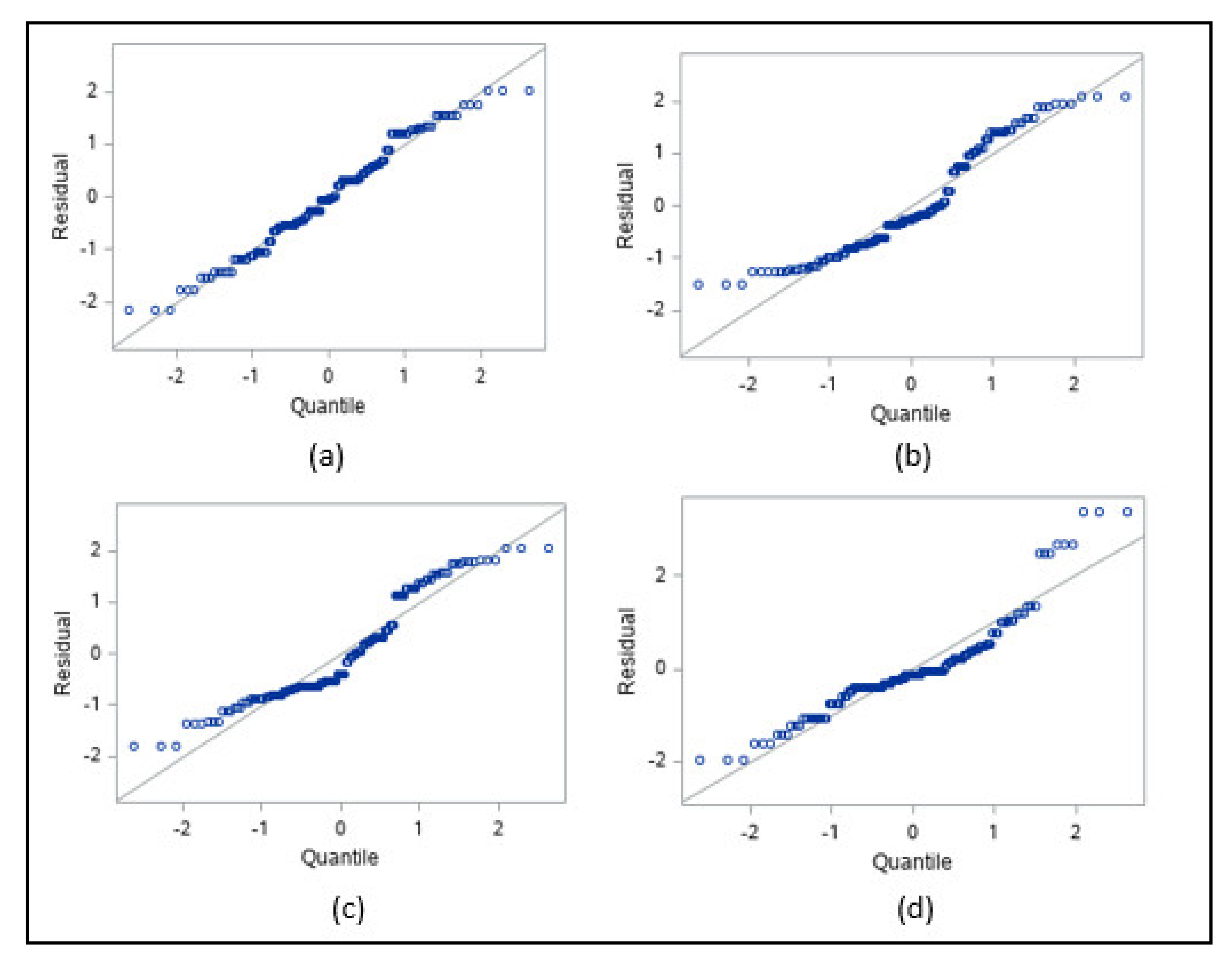
3.1.1. Normality and Outliers

Q–Q plots are used to check normality and outlier assumptions simultaneously. The FFF, FRF, RFF, and RRF data sets do not show any serious deviations from normality. Figure 2 shows the normal Q–Q plots for the four data subsets.

Furthermore, the Q–Q plots do not show any influential point (outlier) that warrants exclusion, since all plots are not very far from the diagonal.

3.1.2. Sphericity and/or Compound Symmetry

In order to test the suitability of using a repeated-measures design in the experiment, the sphericity (or compound symmetry) assumption is tested for each partitioned data subset. Sphericity test results are produced by fitting two models using the PROC MIXED procedure: one specifying the unrestricted covariance structure and the other with a less conservative Huynh–Feldt (H–F) adjustment in the Type option [41]. The null hypothesis for the test is:

Hypothesis 4 (H4).

The covariance structure fits the sphericity structure.

The difference ($D$) between the two $-2$ log-likelihoods of the two competing models follows a Chi-square distribution with degrees of freedom equal to the difference in the numbers of parameters in them.

• FFF model: ${\chi }_{35}^2\left(0.05\right)\approx 55.76$, $df=35$, $D=1722.6$, significant;
• FRF:${\chi }_{38}^2\left(0.05\right)\approx 55.76$, $df=38$, $D=184.54$, significant;
• RFF: ${\chi }_{37}^2\left(0.05\right)\approx 55.76$, $df=37$, $D=288.8$, significant;
• RRF: ${\chi }_{36}^2\left(0.05\right)\approx 55.76$, $df=35$, $D=384.1$, significant.

The sphericity assumption H4 fails in all the four (4) partitioned data sets.

3.2. Analysis of Results

We use the restricted maximum likelihood estimation (REML) approach to estimate these variance components.

Table 4. Akaike’s Information Criteria (AIC) for the covariance structures in partitioned models.

Model FFF			Model FRF
Covariance Structure	Number of Parameters	AIC	Covariance Structure	Number of Parameters	AIC
CS	2	−282.6	CS	4	−361.3
AR(1)	2	−443.1	AR(1)	3	−492.4
ARH(1)	10	−525.6	ARH(1)	13	−506.3
CSH	10	−356.7
Model RFF			Model RRF
Covariance Structure	Number of Parameters	AIC	Covariance Structure	Number of Parameters	AIC
CS	4	−450.1	CS	4	−665.8
AR(1)	4	−522.4	AR(1)	4	−782.4
ARH(1)	13	−509.3	ARH(1)	13	−785.3

AR(1): First-order autoregressive; ARH(1): Heterogeneous first-order autoregressive; CS: Compound symmetry; VC: Variance components; CSH: Heterogeneous compound symmetry.

contains the estimated AIC from each of the covariance structures as well as the number of covariance parameters estimated with a non-zero value.

The covariance structure ARH(1) has the minimum AIC values in models FFF, FRF, and RRF, and covariance structure AR(1) has the smallest AIC value in model RFF. The covariance structure ARH(1) is chosen as the most adequate covariance structure for the partitioned models based on AIC.

When the appropriate covariance structure is incorporated into the model, the relationships among the errors and variance components are specified. The PROC MIXED procedure does not require further assumptions on them [42], making it a robust and flexible procedure [15] that produces valid F-tests regardless of whether the sphericity assumption is satisfied or not.

Table 5. Type III tests of fixed effects of FFF, FRF, FFR, and FRR models.

Model	Effect	Numerator Degrees of Freedom	Denominator Degrees of Freedom	F	p-Value
FFF	CCl4	1	12	0.24	0.6363
	CHCl3	1	12	17.33	0.0013 **
	${CCl}_4\times$CHCl3	2	12	1.35	0.2678
	Time	2	24	95.99	<0.0001 **
	$Time\times$CCl4	2	24	2.66	0.0908
	$Time\times$CHCl3	2	24	20.91	<0.0001 **
	$Time\times$${CCl}_4\times$CHCl3	2	24	1.26	0.3023
FRF	CHCl3	1	1	0.5	0.6079
	Time	2	2	2.17	0.3156
	$Time\times$CCl4	2	2	2.83	0.2610
RFF	CHCl3	1	1	7.07	0.2290
	Time	2	2	5.42	0.1557
	$Time\times$CHCl3	2	2	3.26	0.2348
RRF	Time	2	2	1.01	0.4978

‘**’ significant at $\alpha =0.05$.

summarises the PROC MIXED F-tests for the main and interaction effects of the between-subjects and the within-subjects factors for the four partitioned models.

The ${CHCl}_3$ factor has a significant effect on the leakage percentage (p-value < 0.001) over time in the FFF partition. Based on the fixed-effects (FFF) repeated-measures study, it may be concluded that chloroform (${CHCl}_3$) has a significant impact on the amount of lactic dehydrogenase (LHD) enzyme percentage leakage (toxicity of cells) over time, whereas neither carbon tetrachloride (${CCl}_4$) in isolation nor the interaction thereof has significant influence. Furthermore, the $Time$ factor plays an important role in determining the amount of leakage as well. However, the interaction of old (random) and new (fixed) levels of the between-subjects factor levels has non-significant effects in FRF, RFF, and RRF models when ${CHCl}_3$ fixed levels are involved.

Table 6. Covariance parameter estimates of FRF, RFF, and RRF, models based on ARH(1) covariance structure.

Model	Covariance Parameter	Estimate	Standard Error	Proportion of Variation Accounted for
FRF	CHCl3	0	0	0
	${CCl}_4\times$CHCl3	0.04249	0.04470	22.5
	$Time\times$CHCl3	0	0	0
	$Time\times {CCl}_4\times$CHCl3	0.000621	0.000759	0.3
RFF	CCl4	0.000607	0.003056	0.05
	${CCl}_4\times$CHCl3	0	0	0
	$Time\times$CCl4	0.000149	0.000809	0.02
	$Time\times {CCl}_4\times$CHCl3	0.000806	0.000984	0.08
RRF	CCl4	0.0011	0.00401	2.6
	CHCl3	0.00306	0.00677	7.1
	${CCl}_4\times$CHCl3	0.00232	0.00396	5.4
	$Time\times$CCl4	0.000002	0.00002	0.0
	$Time\times$CHCl3	0.000065	0.000096	0.1
	$Time\times {CCl}_4\times$CHCl3	0.000013	0.000025	0.0

gives a summary of the estimated covariance parameters and the proportion (in percentage) of variation they contribute in each of the partitioned models. A zero variance for the random levels of chloroform (${CHCl}_3$) and very small estimates in other factors are obtained, which result in very low estimates of covariance parameters in the models.

The CHCl₃ and CCl₄ random levels and their interaction have a noticeable contribution to the proportion of variation in the amount of lactic dehydrogenase (LHD) enzyme percentage leakage in the RRF partition. Generally, Time has very little interaction effect with the between-subjects factors in FRF and RRF models in determining the proportion of variation of the toxicity of cells.

Since the mixed-model methodology directly computes neither sums of squares nor F-statistics from the ratio of mean squares, and since the R CRAN package $lme4$ for mixed models currently does not have options for other covariance structures to cater for correlated error variances, generating a combined analysis is not a straightforward exercise. We scrap the targeted data subset based on the effects of interest before fitting the models. Analogous to the partitioned analyses, a comparison of model fit via the AIC approach is conducted. For convenience purposes, let the factors ${CCl}_4$, ${CHCl}_3$, and $Time$ be labelled as factor $A$, $B$, and $C$, respectively. The PROC MIXED procedure is used to fit the repeated-measures linear mixed models for intended narrow inference spaces [12,43].

Table 7. Fixed-effects F-tests for the combined models in narrow inference scope.

Type III Tests of Fixed Effects in Combined Models
Model	AIC [CS]	Effect	Num DF	Den DF	F	Pr > F
FA	−127.6 [ARH(1)]	A	1	24	3.36	0.0794
		B	3	24	5.81	0.0039 **
		$\mathrm{A}\times \mathrm{B}$	3	24	9.10	0.0003 **
		C	2	48	12.33	0.0001 **
		$\mathrm{A}\times \mathrm{C}$	2	48	2.52	0.0908
		$\mathrm{B}\times \mathrm{C}$	6	48	2.33	0.0468 **
		$\mathrm{A}\times \mathrm{B}\times \mathrm{C}$	6	48	0.76	0.6027
FB	−127.6 [AR(1)]	A	3	24	0.53	0.6631
		B	1	24	16.3	0.0005 **
		$\mathrm{A}\times \mathrm{B}$	3	24	0.22	0.8801
		C	2	48	24.82	<0.0001 **
		$\mathrm{A}\times \mathrm{C}$	6	48	1.09	0.3795
		$\mathrm{B}\times \mathrm{C}$	2	48	7.82	0.0012 **
		$\mathrm{A}\times \mathrm{B}\times \mathrm{C}$	6	48	0.50	0.8064
$\mathrm{FA}\times$ FB	−69.1 [AR(1)]	A	1	12	0.14	0.7106
		B	1	12	10.63	0.0068 **
		$\mathrm{A}\times \mathrm{B}$	1	12	0.83	0.3807
		C	2	24	19.75	<0.0001 **
		$\mathrm{A}\times \mathrm{C}$	2	24	0.58	0.5667
		$\mathrm{B}\times \mathrm{C}$	2	24	4.65	0.0196 **
		$\mathrm{A}\times \mathrm{B}\times \mathrm{C}$	2	24	0.26	0.7725

‘**’ significant at $\alpha =0.05$.

shows the Type III tests for the combined models.

Of the possible candidate covariance structures (CS, CSH, AR(1), and ARH(1)), structure ARH(1) is selected as the most appropriate covariance structure for the combined fixed-effects model FA, and AR(1) is appropriate for FB and FA $\times$ FB. The factors B (CHCl₃) and C (Time) have significant effects (p-$\mathrm{value}<0.05$) in the combined models. The broad inference scope results for the combined models (assuming random factor A or B effects) are similarly analysed.

4. Discussion

Based on the illustrative example results, the approach manages to isolate the effects of new and old factor levels over time. The combined analysis confirmed the results of the partitioned analysis on the percentage leakage in cells. The proposed approach conforms to the model construction and the analysis procedures in a repeated-measures design. It can be used as a planning tool in which factor combination and time are of interest in designing experiments that involve repeated measures. In such experiments, blindly adopting the assumption of homogeneous error terms without exploring possible candidate covariance structures may compromise the ability of an experiment to detect sufficient variation in the response variable. In addition, our approach enhances the accuracy of inferences by providing partitioned analysis of heterogeneous variances and covariance structures, which sometimes are not identical in the data subsets.

Given the increased complexity of research data in various research fields, the application of a linear mixed-model methodology must be in line with data covariance structures for accurate results to be achieved. One of the approaches that has proved to be a reliable tool for managing big data complexity issues is the partitioning approach [12,20,21], in which the traditional homogeneous error variance structure is assumed. The current study extends the new approach to a three-factor treatment structure in a repeated-measures design in which linear mixed-effects models are applicable. In essence, the approach can be extended to cater for repeated-measures experiments in which any number of between-subjects and within-subjects factors are involved. In most cases, repeated-measures experiments do not assume equal and uncorrelated error vectors, since regularly timed measurements taken on the same subject over time are usually correlated [34].

For the fixed-effects partitions, the linear mixed-effects models for a repeated-measures design are fit by the PROC GLM procedure, and a combined analysis of these can be obtained by syncretising the sum of squares and degrees of freedom from the fit models. However, obtaining a combined analysis using the SAS PROC MIXED procedure is impossible using the sum of squares approach, since the PROC MIXED procedure uses a likelihood-based estimation scheme instead of the least-squares method. A comparable alternative to reduction in the sum of squares for the fit model in PROC MIXED is to consider the amount of information retained by the fit model when compared to the null model.

5. Conclusions

The proposed approach allows for construction and hypothesis testing in repeated-measures data if a heterogeneous error structure is assumed. Although the MLE method used in SAS PROC MIXED does not estimate sums of squares, data scrapping based on targeted factor levels work equally well as an alternative approach to obtain the combined analysis. The proposed approach can be adopted as an essential tool for the comparison of new inventions against existing strategies and equipment. It leads to an exploration of the fixed and random levels of the same factor and the subsequent interaction of levels of factors of interest. We can assess the differences between levels of the same factor and understand variation within the same factor. In addition, modelling allows for the assessment of various covariance structures. Although this paper focuses on a limited scope of covariance structures, we pose an open research problem on the application of the proposed approach to other designs of experiments that incorporate more complex and non-diagonal covariance structures.