Credibility of Causal Estimates from Regression Discontinuity Designs with Multiple Assignment Variables

Abstract

In this paper, we determine treatment effects when the treatment assignment is based on two or more cut-off points of covariates rather than on one cut-off point of one assignment variable. using methods that are referred to as multivariate regression discontinuity designs (MRDD). One major finding of this paper is the discovery of new evidence that both matric points and household income have a huge impact on the probability of eligibility for funding from the National Student Financial Aid Scheme (NSFAS) to study for a bachelor’s degree program at universities in South Africa. This evidence will inform policymakers and educational practitioners on the effects of matric points and household income on the eligibility for NSFAS funding. The availability of the NSFAS grant impacts greatly students’ decisions to attend university or seek other opportunities elsewhere. Using the frontier MRDD analytical results, barely scoring matric points greater than or equal to 25 points compared to scoring matric points less than 25 for students whose household income is less than R350,000 (≈US$2500) increases the probability of eligibility for NSFAS funding by a significant 3.75 ( p-value = 0.0001 < 0.05) percentage points. Therefore, we have shown that the frontier MRDD can be employed to determine the causal effects of barely meeting the requirements of one assignment variable, among the subjects that either meet or fail to meet the requirements of the other assignment variable.

1. Introduction

Multivariate regression discontinuity designs (MRDD) raise challenges that are distinct from those identified in traditional RDD [1]. Traditional RDD studies focus on units that are assigned to a treatment based on a single cut-off point and a single continuous assignment variable [2]. In reality, units are usually assigned to a treatment based on more than one continuous assignment variable [3]. Thus, treatment effects may be estimated across a multi-dimensional cut-off frontier, as opposed to a single point on the assignment variable, using methods referred to as multivariate regression discontinuity designs (MRDD) [1,3,4]. For example, using the frontier approach, [1] showed that the MRDD treatment effect estimate, ${\tau }_{MRDD}$, may be decomposed into a weighted average of two univariate RDD effects, ${\tau }_{x_1}$ at the $X_1$-cut-off and ${\tau }_{x_2}$ at the $X_2$-cut-off. The term frontier means that the average treatment effect estimates for MRDD are only for sub-populations of units located at the cut-off frontier as opposed to the average treatment effect for the overall population under study. Like in the standard RDD, the causal estimates obtained in MRDD have limited external validity as the causal estimates are only identified for observations in the immediate vicinity of the cut-off scores [4]. This paper studies the credibility of estimates of the MRDD. It is important that after estimating ${\tau }_{MRD}$, a researcher checks for the plausibility of the assumptions of the MRDD estimates. With more credible estimates, inference about causality can reduce the reliance of the causal estimates on the following modelling assumptions [5]:

• the cut-off scores determining treatment assignment are exogenously set;
• potential outcomes are continuous functions of the assignment scores at the cut-off scores and
• the functional form of the model is correctly specified.

Ref. [5] suggest extending the assumption checking for the RDD context to the MRDD. The assumptions will be assessed as they apply to the frontier regression discontinuity using supplementary analyses techniques [6]. Primary analyses in MRDD focus on estimating ${\tau }_{MRD}$. In contrast, supplementary analyses seek to shed more light on ${\tau }_{MRD}$ from the primary analyses. These supplementary analyses use the fact that assumptions behind the identification strategy often have implications for the data beyond those used in the primary analyses [6]. There are basically four approaches that can be employed for carrying out supplementary analyses, and these are: The McCrary test [7], placebo analysis, robustness and sensitivity, and checking for discontinuity of the assignment variable at the cut-off point.

This paper uses two assignment variables to study the effects of an educational funding intervention in South Africa, the National Student Financial Aid Scheme (NSFAS). The eligibility criteria for NSFAS funding is based on a student’s family annual total household income and the aggregate points they score on their matriculation certificate. In South Africa, a matriculation certificate is a school-leaving diploma or national senior certificate (NSC) that is awarded after completing Grade 12. The total number of scores achieved on seven subjects on the matriculation certificate are referred to in this paper as the matric points. The role that NSFAS funding has on access to post-school education for students from disadvantaged backgrounds in South Africa cannot be ignored. From a Government policy perspective, NSFAS was established to correct apartheid era discrimination in higher education that occurred in South Africa in the past and promote equal access to higher education. In addition, NSFAS is established a sustainable and affordable funding scheme. Therefore, one of the vital objectives of this research is to quantify the causal effect of household income and matric points on the chance of eligibility for NSFAS funding. This will help policy makers to make the right decisions that will ensure that students are adequately funded. For example, there are students who are referred to as the ‘missing middle’ [8]. These students are from households whose incomes are between R350,000 and R600,000. These students do not qualify for NSFAS funding, and yet most of them cannot afford to pay for their higher education. By quantifying the causal effect that matric points and household income has on the ‘missing middle’s eligibility for NSFAS funding, government can implement policy interventions to assist these students to get financial aid.

Related Work

MRDD is a growing approach, and yet there is not enough easily accessible information that can help researchers on how to implement MRDD, and at the same time assess the credibility of the causal estimates using supplementary analysis. MRDD presents opportunities for obtaining unbiased estimates of treatment effects using the same thinking as the single assignment variable RD designs. The MRDD is an extension of the traditional RDD, except that the treatment effects are estimated for multiple cut-offs, as opposed to a single cut-off point. Studies have been carried out with multiple assignment variables and cut-off points for treatment assignment. For example, ref. [4] gave an example of teachers who received a bonus for improving student scores in both Mathematics and English Language Arts (ELA). The authors point out that in some cases, students must pass externally defined standards in several subjects to avoid summer school or to graduate from high school. Multiple regression discontinuity designs (MRDD) have also been used in other disciplines, such as in politics [9]. Authors [2] gave a compilation of over sixty studies, showing where RDD designs have been applied in many different contexts. Ref. [10] estimates the effect of a mandatory summer school program assigned to students who fail to score higher than a preset cut-off in both math and reading exams. Ref. [11] developed a special kind of regression discontinuity design in which the assignment variable is geographic. Their approach, the geographic regression discontinuity (GRD) design, was similar to a standard RD but with two running variables.

MRDD are very appealing, and yet the statistical details regarding their implementation are not as easy as they may seem at first. This is because when the MRDD are applied in other technical journals they require a high degree of technical sophistication to read. Furthermore, the terminology that is used is not well defined and is often used inconsistently. Thus, this paper is filling a void and serving as a guide to practitioners on how to implement MRDD.

The design of this paper builds upon the work by [3,4,12]. Ref. [12]’s paper investigated how the CalGrant program impacted on the college going rates from 1998 to 1999 using a sharp regression discontinuity design. Ref. [3] conducted an extensive simulation study that was closely based on [12]’s work. This paper takes a similar approach to that of [3,12] and considers eligibility criteria for the NSFAS funding program in South Africa to estimate the impact that NSFAS funding has on subsequent enrollment for a bachelor’s degree into SA Universities. Specifically, this paper makes the following contributions:

1

This is the first time that the MRDD has been applied in the context of South Africa to quantify the causal effect that the household income and matric points have on the probability of eligibility for NSFAS funding, and eligibility to study for a bachelor’s degree. By quantifying the causal effect of household and income, policy makers in South Africa can make informed decisions on funding for for students who qualify to study for a bachelor’s degree.

2

This paper provides the first evidence on whether meeting a matric points threshold and a household income threshold increases the chance of eligibility for NSFAS funding.

3

The paper adds to the literature by combining the estimation of causal estimates using MRDD, and some of the supplementary analysis proposed by [6]. The authors noted as a concern that assessing the validity of the assumptions required for interpreting the estimates as causal effects obtained from regression discontinuity analysis is still lagging behind. Therefore, the paper extends the assumption checking of uni-variate RDD to the MRDD using supplementary analyses. These supplementary analyses are carried out to test for discontinuities in average covariate values at the threshold as well as to assess the credibility of the design, and in particular to test for evidence of manipulation of the forcing variable.This is crucial in practice because if the causal effect are not credible, then they are not useful.

4

We have successfully demonstrated that one can use simulated data that closely mimics real world or original data, and still obtain significant and credible causal effect estimates.

2. Literature Review

2.1. Multivariate Regression Discontinuity Design

The basic set-up of RDD is that we are interested in the causal effect of a binary treatment or program denoted by ${\mathit{W}}_{\mathit{i}}$, in the presence of an exogenous variable (forcing variable) denoted by ${\mathit{X}}_{\mathit{i}}$. There are different RDD methods proposed in the literature that allow us to estimate average treatment effects. Refs. [1,2,4,6,13] provide detailed overviews of these methods. The RDD is framed in the context of the potential outcomes framework, i.e., for a given unit i, there exists two potential outcomes, $Y_i\left(1\right)$ and $Y_i\left(0\right)$, and the causal effect is simply the difference, $Y_i\left(1\right)$–$Y_i\left(0\right)$. The fundamental problem of causal inference states that we cannot observe $Y_i\left(1\right)$ and $Y_i\left(0\right)$ at the same time. Because of this problem we usually focus on the average effects of the treatment, that is, averages of $Y_i\left(1\right)$–$Y_i\left(0\right)$ over all sub-populations rather than on unit level effects [2].

The Multivariate Regression discontinuity designs (MRDD) present opportunities for obtaining unbiased estimates of treatment effects using the same thinking as the single assignment variable RD designs. The MRDD is an extension of the traditional RDD, except that the treatment effects are estimated for multiple cut-offs, as opposed to a single cut-off point. Studies have been carried out with multiple assignment variables and cut-off points for treatment assignment. For example, ref. [4] gave an example of teachers who received a bonus for improving student scores in both Mathematics and English Language Arts (ELA). The authors point out that in some cases students must pass externally defined standards in several subjects to avoid summer school or to graduate from high school. Multiple regression discontinuity designs (MRDD) have also been used in other disciplines, such as in politics [9]. There are multiple strategies for estimating MRDD and these strategies present multiple possible estimands (${\tau }_{MRDD}$). Ref. [5] presents five strategies for estimating treatment effects in MRDD, namely: binding-score RD, distance based RD, frontier RD, the response surface RD, and fuzzy frontier RD. The authors mention that these four methods have their own advantages and disadvantages that depend on the structure of the data with regards to the correlation between the two assignment variables as well as the locations of the respective cut-points. Ref. [5] indicate that the fuzzy IV methods have limited practical applications as they tend to yield imprecise estimates. Additionally, the response surface RD is sensitive to the functional form mis-specification and this could be a problem when it is implemented using local linear regression, which requires full functional form specification.

In this paper, we apply the frontier RD [5] to estimate the probability of eligibility for NSFAS funding using matric points and household income as the assignment variables. The frontier approach is deemed to be straightforward to implement as the modelling assumptions mentioned earlier are easily assessed by sub-setting the data by frontier [5]. In addition, because the frontier approach reduces the MRDD to at least one single-rating RDDs, they are easily implemented using traditional RDD methods. We implement the frontier approach to obtain the primary analyses estimates. Thus, we adopt the approaches proposed by [4,5] that utilise two assignment variables to assign individuals to a range of different treatment conditions. According to [4], if there are J forcing variables such that $W_{ji}=\mathbb{1}$($X_{ji}\ge c$), ∀j = 1,…,J, then there will be $2^J$ treatment conditions. For any combination of these $2^J$ treatment effects, the parameters of interest become the left and right side limits on either side of the cut-off. MRDD with two assignment variables define four different treatment conditions.

For two assignment variables, $X_1$ and $X_2$, and respective cut-offs, $c_1$ and $c_2$, the treatment conditions $W_{1i}$ and $W_{2i}$ are defined as follows:

$$W_{1i}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{X}_{1i}\ge c_1\hfill \\ 0,\hfill & X_{1i}<c_1\hfill \end{array}\right.\mathrm{and}{W}_{2i}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{X}_{2i}\ge c_2\hfill \\ 0,\hfill & X_{2i}<c_2\hfill \end{array}\right.$$

(1)

To qualify for NSFAS funding, a student must have a matric certificate with at least 25 matric points and the total family household income should be at most R350,000. MP = 25 and INC = R350,000 are therefore the cut-off points for matric points and household income respectively. Thus, as described by [14], with two assignment variables, there are four treatment conditions that define four distinct regions in a two dimensional space spanned by $M{P}^C$ and $IN{C}^C$, the centered variables of MP and INC around their respective cut-off points.

1.

Treatment 1: If students score at least 25 matric points and family income is greater than R350,000 (Region 1): $W_{1i}=1\mathrm{and}{W}_{2i}=0$

2.

Treatment 2: If students score less than 25 matric points and family income is greater than R350,000 (Region 2): $W_{1i}=0\mathrm{and}{W}_{2i}=0$

3.

Treatment 3: If students score less than 25 matric points and family income is at most R350,000 (Region 3): $W_{1i}=0\mathrm{and}{W}_{2i}=1$

4.

Treatment 4: If students score at least 25 matric points and family income is at most R350,000 (Region 4): $W_{1i}=1\mathrm{and}{W}_{2i}=1$

The parameters that we estimate then become the population conditional mean probabilities of being eligible for NSFAS funding for students in each treatment condition at the appropriate cut-off point. For example, the causal effect of being eligible for NSFAS funding instead of not being eligible for NSFAS funding, for a student scoring on the income (INC) cut-off is then the difference between [2]:

$$u_l\left(c\right)=\underset{x\downarrow 0^{-}}{lim}E\left[NS{F}_i\right|M{P}^C=x,IN{C}^C=0]$$

and

$$u_r\left(c\right)=\underset{x\uparrow 0^{+}}{lim}E\left[NS{F}_i\right|M{P}^C=x,IN{C}^C=0]$$

(2)

2.2. Multiple Assignment Variables: Estimation Strategies

Equation (2) gives the basic analytic strategy for estimating treatment effects using either single or multiple assignment variables. Observed data is used to estimate the limits of the average potential outcomes at the boundaries of two treatment assignment regions, and then take the difference of the estimated limits. According to [5], these limits must be estimated at the boundary of the observed data for each treatment condition and fitting a regression model of the following form (assuming a sharp regression discontinuity):

$$Y_i=f(X_{1i},X_{2i},\dots ,X_{ji},W_i)+{ϵ}_i$$

(3)

where $X_{1i},X_{2i},\dots ,X_{ji}$∈D⊂S and D is the domain of observations used to estimate the model,S is the domain of observations in the full sample, and $W_i$ is a zero/one treatment-assignment indicator.

For MRDD with two assignment variables, we have the following:

$$Y_i=f(X_{1i},X_{2i},W_i)+{ϵ}_i$$

(4)

where $X_{1i},X_{2i}$∈D⊂S and D is the domain of observations used to estimate the model, S is the domain of observations in the full sample, and $W_i$ is a zero/one treatment-assignment indicator [15]. The authors point out that estimators of the MRDD differ in terms of:

(i)

the specification of the function f;

(ii)

the domain (D) of observations used in estimating the model.

3. Materials and Methods

3.1. Data

We focus on estimating the impact that matric points and household income have on the chance that a student qualifies for the NSFAS grant to support his or her bachelor’s degree studies using simulated data for household income (INC) and matric points (MP). There are similar studies that have used simulated data on regression discontinuity designs. For example, [16], developed automated local regression models using synthetic data, and only used real world data to evaluate the models. Ref. [3] simulated a dataset using summary statistics reported in a research paper by [12]. Ref. [3] indicate that they used summary statistics because the original data from [12] was no longer available. In this paper, we took a similar approach and used summary statistics to simulate South Africa’s household income data. The simulated data for household income was generated using the log-normal distribution. The use of the lognormal distribution is motivated by [3,17]. Ref. [17] report that income distribution datasets are usually fit using the lognormal distribution. This finding by [17] is also supported by [18], who state that most literature on income distributions indicate that country income distributions closely resemble the lognormal distribution. Therefore, to simulate income data for South Africa that follows a log-normal distribution, we estimate the mean and standard deviation of total household income from

Table 1. Average income distribution (Source: STATSSA: Living Conditions Survey 2).

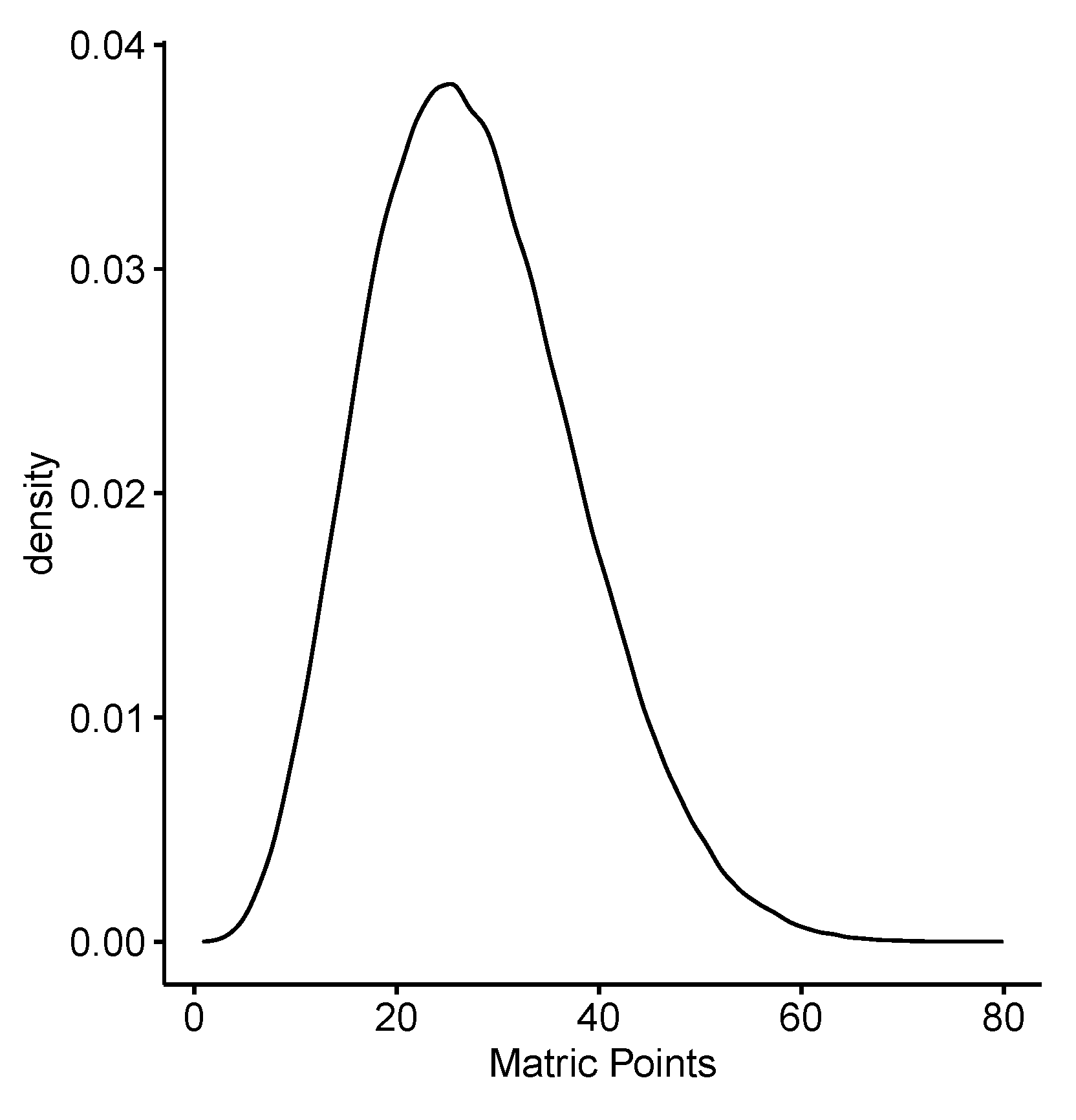
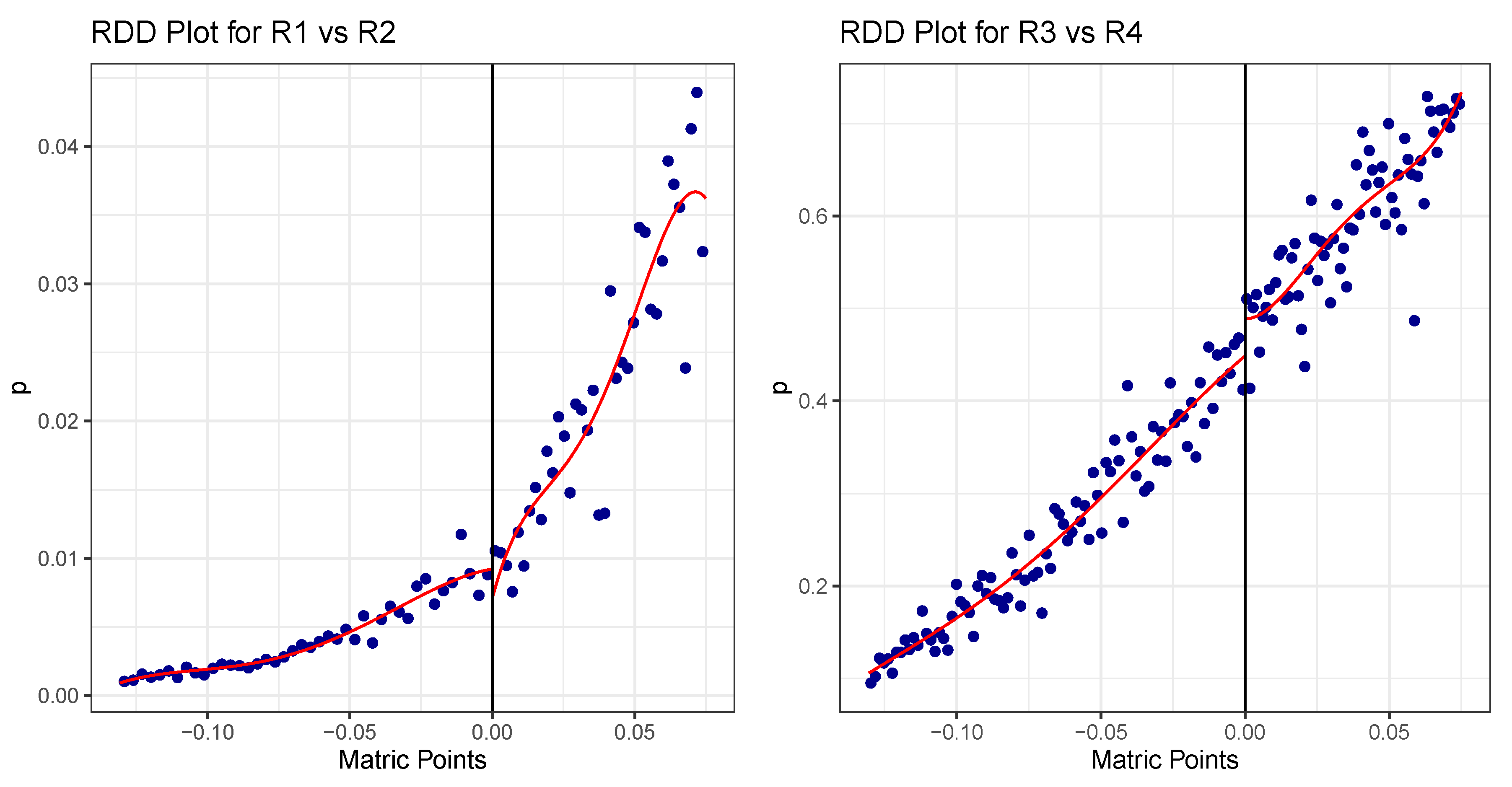
Population Group of Household	Average Income	% Households	Number of Households
Black African	92,983	80.42	18,800
Coloured	172,765	7.23	1690
Indian/Asian	271,621	2.31	540
White	444,446	10.04	2347
Total	981,815		23,377

of the average household incomes by population group in South Africa (http://www.statssa.gov.za/publications/P0310/P03102014.pdf), (accessed on 11 April 2021).

On the other hand, the use of the truncated beta distribution for the matric points (matric points are similar to GPA) was inspired by [19], who state that the normal assumption is usually employed in mordern educational data. However, the authors state that the normal distribution is not the best choice, and the logitnormal distribution and a scaled, shifted, and truncated beta distribution are better choices for modelling examination scores. Following [3], we chose a scaled, shifted, and truncated beta distribution as it is similar to the empirical distribution reported in [12]. Using

Table 2. Subject Passes Level System.

Level	Final Mark%	Achievement
7	80–100%	Outstanding
6	70–79%	Meritorius
5	60–69%	Substantial
4	50–59%	Moderate
3	40–49%	Adequate
2	30–39%	Elementary
1	0–29%	Not Achieved-Fail

, we consider seven matric subjects and generate matric points that range from 0 to 49. If a student does not achieve any of the subject pass levels that are shown in Table 2 in seven subjects, then the students scores a total of zero matric points. On the other hand, if a student achieves a subject pass level equal to seven in seven subjects, then the student will have a total of 49 matric points.

Different combinations of the scaled, shifted, and truncated beta distribution parameters $\alpha$ and $\beta$ were employed in simulating the matric points data. We chose $\alpha$ = 5, $\beta$ = 13 as the preferred parameters for simulating matric points as they give us the density of matric points slightly positively skewed to the right as shown in Figure 1.

After simulating the income and matric points data, we use the data generation process in Equation (5), to generate estimates of the probabilities of eligibility for NSFAS funding $P(NS{F}_i=1|IN{C}^c,M{P}^c)$:

$$P(NS{F}_i=1|IN{C}^c,M{P}^c)={\beta }_0+{\beta }_{1}IN{C}^c+{\beta }_{2}M{P}^c+IN{C}^c\times M{P}^c+{ϵ}_i$$

(5)

3.2. Estimating Causal Effects Using the Frontier Regression Discontinuity Design (FRDD)

The FRDD approach analyses samples of the data based on status (i.e., above or below the cut-off score), on all but one of the assignment variables and then models the discontinuity along the remaining assignment variable using the single assignment variable RDD methods [5]. Focusing on the $M{P}^c$ frontier method entails using sample points where $IN{C}^c\ge 0$. Because the assignment variable is centered on its cut-point value, sample points where $IN{C}^c\ge 0$ are used. For example, when estimating Treatment 1 versus Treatment 2 in Figure 2, we limit the sample only to individuals with $IN{C}^c\ge 0$.

Thereafter, we choose a sub-sample from the samples that lie within the optimal bandwidth on the left or right of $M{P}^c$. This sub-sample will be used in fitting linear probability models of the form:

$$P(NS{F}_i=1|M{P}^c,T_{m{p}_i})={\beta }_0+{\beta }_1{T}_{m{p}_i}+{\beta }_{2}M{P}_i^c+{\beta }_{3}M{P}_i^c\times T_{m{p}_i}+{ϵ}_i,$$

(6)

or

$$\begin{array}{c}\hfill P(NS{F}_i=1|M{P}^c,T_{m{p}_i},IN{C}^c)={\beta }_0+{\beta }_1{T}_{m{p}_i}+{\beta }_{2}M{P}_i^c+{\beta }_{3}M{P}_i^c\times T_{m{p}_i}+{\beta }_{4}IN{C}_i^c+{ϵ}_i,\hfill \end{array}$$

(7)

where $P(NS{F}_i=1|M{P}^c,T_{m{p}_i})$ is the probability of eligibility for NSFAS funding given $M{P}^c$ and the treatment assignment variable for matric points, $T_{m{p}_i}$. Equation (7) includes the covariate $IN{C}^c$ to improve the treatment effect, $\widehat{{\beta }_1}$’s precision. The equations are also adapted and expressed as a function of $IN{C}^c$, $T_{in{c}_i}$, and $M{P}^c$ as a covariate, to evaluate the effect of the income variable on the chance of eligibility for NSFAS funding.

We use the linear probability model (LPM) specification, rather than a logistic or probit, to model Equations (6) and (7) because in terms of model fit, LPM is just as good as logistic regression withing a certain range of probabilities to be modelled [20]. Ref. [20] recommends that the probabilities being modelled should be between between 0.20 and 0.80. A plot probability (p) versus the log-odds (Figure 3) illustrates the range of probabilities that was employed.

Figure 3 shows that between 0.20 and 0.80, the relationship between probability (p) and the log odds is almost linear. Therefore, we applied the LPM within this range. We use the linear probability model because according to [14,21], the model becomes more credible when it is applied within range 0.20 and 0.80 for the probability, and a narrow bandwidth for the independent variable(s), using local linear-regression analysis. Furthermore, refs. [14,21] report that the linear probability specification provides consistent and unbiased estimates of the fundamental trends for samples. We used LPM because it is easy to interpret as compared to the logistic model. This means that the regression parameters obtained from fitting LPM are easy to interpret in terms of the population differences in the probability of eligibility for NSFAS funding per unit difference in either matric points or household income. In addition, ref. [14] compared the linear probability model and logistic regression and found out that, within a narrow and optimal bandwidth, these two models produce identical results. Ref. [22] highlight that the linear probability model yields treatment estimates that are just as accurate as those estimated by logistic regression. As we are estimating the effect of matric points and household income on the probability of eligibility for NSFAS funding, the parameter of interest is the coefficient (${\beta }_1$) of the treatment variable(s) and not the coefficients of the assignment variables. This makes the linear probability model an appropriate analytic procedure for estimating the effect of matric points and household income since the treatment status is a binary variable [22]. Thus, the functional form concerns about the linear probability model may not necessarily apply because all that is required is to estimate the treatment effects, as opposed to estimating the effect of the continuous assignment variables.

4. Experiments

To implement the frontier multiple regression–discontinuity design, we consider three variables, namely, the matric points (MP), household income (INC), and NSFAS funding (NSF). Students apply for NSFAS funding in Grade 12 before their matric results are out and they do not know in advance whether or not they are going to achieve matric points that meet the requirement to study for a bachelor’s degree. This makes MP suitable as an assignment variable, as it cannot be manipulated precisely. MPs around the threshold then become as good as random. The other variable is total household income (INC), which is a measure of the total income of members of the household. The variable NSF indicates the chance of a student being eligible for NSFAS funding to study for a bachelor’s degree within one year after matriculation. Data is simulated that contains MP scores and Income (INC) values with cut-off points of 25 and R350,000 (≈US$25,000), respectively. We create continuous assignment variables (predictors) by centering the normalised MP and INC scores on the values of their respective cut-off points. The centered continuous predictors are labelled $M{P}^c$ and $IN{C}^c$. Thus, $M{P}^c$ = 0 and $IN{C}^c$ = 0 indicate that the student achieved the minimum requirements for qualifying for NSFAS funding. Following the approach by [14], we create dichotomous versions of the same predictors (MP and INC) labelled, $T_{mp}$ and $T_{inc}$, which are the treatment variables that indicate whether a student met the minimum passing standard (MP = 25 points) required in order to study for a bachelor’s degree and also met the maximum income threshold (INC = R350,000) for NSFAS funding. A binary outcome variable $Y_i$ was generated such that $Y_i$ = 1 if $M{P}_i^c\ge 0$ and $IN{C}_i^c\le 0$, i.e., a student receives NSFAS funding and 0 otherwise, i.e, a student does not receive NSFAS funding. The probabilities (between 0 and 1) of eligibility for NSFAS funding are then estimated by fitting a logistic regression to Equation (8), adapted from [4,14], thereby giving the outcome variable as a probability;

$$P(NS{F}_i=1|M{P}^c,IN{C}^c)=\widehat{{\gamma }_0}+\widehat{{\gamma }_1}M{P}_i^c+\widehat{{\gamma }_2}IN{C}_i^c+\widehat{{\gamma }_3}(M{P}_i^c\times IN{C}_i^c)+{ϵ}_i$$

(8)

Under normal conditions, the full functional forms of the data generation models are usually not known [5]. Therefore, choosing an estimation method and the best way to implement it could be challenging. Thus, we took a systematic approach where we have relied on programmed algorithms to select the bandwidth that ensures that the chosen functional form approximates our simulated data well. Equations (6) and (7) were used to specify the linear functional forms using an optimal bandwidth that minimises the mean squared error of $\widehat{{\beta }_1}$. This bandwidth is chosen by utilising a non-parametric density estimation algorithm [23]. The causal effects are then estimated by fitting a linear probability model to Equations (6) and (7), the data that lies within the chosen optimal bandwidths and then derive the estimates of $\widehat{{\beta }_1}$. Equation (6) specifies the outcomes as a linear function of, say $M{P}^c$, the treatment variable, $T_{mp}$, an interaction of $M{P}^c$ and $T_{mp}$. Equation (7) adds $IN{C}^c$ as a baseline covariate. Besides, we investigate whether adding $IN{C}^c\ge 0$ as a covariate improves the precision of the estimates of $\widehat{{\beta }_1}$.

Simulations were conducted based on the values of income, matric points, and Equations (6) and (7). $M{P}^c$ and $IN{C}^c$ were generated as continuous variables. We introduced different values of $\sigma$ ($\sigma$ = 0, 0.05, 0.1 and 0.15) to control for the amount of variation in the assignment variables. The simulated data was initially analysed without adding more variation to the simulated assignment variables, this represented $\sigma$ = 0. The variation in the assignment variables was gradually increased in steps of 0.05 from 0 to 0.15, and the models were rerun to give the new estimates of the parameters of interest. We will investigate whether or not increasing the variation in the assignment variables affects the treatment assignment mechanism and thus, the treatment effect estimates. Additionally, we considered different samples of sizes 5000, 10,000, 20,000 to determine whether or not increasing the sample size affects the estimated treatment effects. 1000 simulations were performed for each model, by varying the sample sizes and the variability $\sigma$ that controls the amount of variation in the assignment variables. Overall, the simulation scenarios were composed of three different levels of sample sizes, four error variances and four treatment regions (Figure 2) for each of Equations (6) and (7) giving a total of 96 scenarios. For each scenario we generated 1000 simulated data sets and used Equations (6) and (7) to estimate the the average coefficient ${\beta }_1$, which gives the estimate of the treatment effect. Because, the true relationship between a binary outcome and continuous explanatory variables is fundamentally not linear, the functional form of the linear probability model is generally not correctly specified. In this paper, we will show through supplementary analyses that within a narrow and optimal bandwidth, the linear specification model is still credible.

5. Results and Analysis

5.1. Estimation of the Causal Effects

The results obtained by fitting the simulated data in each treatment region (Figure 2) to Equation (6) are presented in

Table 3. Top: Simulation results for fitting Equation (6) to compare R3 vs. R4 which represents $M{P}^c$< 0 vs. $M{P}^c$≥ 0 for $IN{C}^c$< 0, and cut-off c = 0. Bottom: Simulation results for fitting Equation (6) to compare R1 vs. R2 which represents $M{P}^c$< 0 vs. $M{P}^c$≥ for $IN{C}^c$> 0 and cut-off, c = 0.

R3 vs. R4	N	${\mathit{h}}_{\mathit{l}}$	${\mathit{h}}_{\mathit{r}}$	${\mathit{\beta }}_1$	s.e	p-Value
	5000	−0.1307	0.1248	0.0388	0.0196	0.1607
$\sigma$ = 0.00	10,000	−0.1307	0.1248	0.0371	0.0139	0.0718
	20,000	−0.1307	0.1248	0.0371	0.0098	0.0119
	5000	−0.1307	0.1248	0.0293	0.0186	0.2276
$\sigma$ = 0.05	10,000	−0.1307	0.1248	0.0295	0.0131	0.1157
	20,000	−0.1307	0.1248	0.0293	0.0093	0.0349
	5000	−0.1307	0.1248	0.0169	0.0165	0.3484
$\sigma$ = 0.10	10,000	−0.1307	0.1248	0.0164	0.0117	0.2728
	20,000	−0.1307	0.1248	0.0161	0.0082	0.1631
	5000	−0.1307	0.1248	0.0086	0.0146	0.4283
$\sigma$ = 0.15	10,000	−0.1307	0.1248	0.0080	0.0103	0.4161
	20,000	−0.1307	0.1248	0.0082	0.0073	0.3301
R1 vs. R2
	5000	−0.1922	0.2859	−0.0763	0.0407	0.1061
$\sigma$ = 0.00	10,000	−0.1922	0.2859	−0.0790	0.0287	0.0171
	20,000	−0.1922	0.2859	−0.0786	0.0203	0.0008
	5000	−0.1922	0.2859	−0.0680	0.0393	0.1388
$\sigma$ = 0.05	10,000	−0.1922	0.2859	−0.0689	0.0276	0.0334
	20,000	−0.1922	0.2859	−0.0685	0.0194	0.0023
	5000	−0.1922	0.2859	−0.0474	0.0373	0.2668
$\sigma$ = 0.10	10,000	−0.1922	0.2859	−0.0475	0.0258	0.1139
	20,000	−0.1922	0.2859	−0.0468	0.0180	0.0274
	5000	−0.1922	0.2859	−0.0272	0.0346	0.4550
$\sigma$ = 0.15	10,000	−0.1922	0.2859	−0.0275	0.0243	0.3304
	20,000	−0.1922	0.2859	−0.0278	0.0171	0.1718

and

Table 4. Top: Simulation results for fitting Equation (6) to compare R2 vs. R3 which represents $IN{C}^c$≤ 0 vs. $IN{C}^c$> 0 for $M{P}^c$≤ 0, and cut-off c= 0. Bottom: Simulation results for fitting Equation (6) to compare R1 vs. R4 which represents $IN{C}^c$≤ 0 vs. $IN{C}^c$> 0 for $M{P}^c$> 0, and cut-off c= 0.

R2 vs. R3	N	${\mathit{h}}_{\mathit{l}}$	${\mathit{h}}_{\mathit{r}}$	${\mathit{\beta }}_1$	s.e	p-Value
	5000	−0.5097	0.5114	−0.0003	0.0040	0.6029
$\sigma$ = 0.00	10,000	−0.5097	0.5114	−0.0003	0.0028	0.6055
	20,000	−0.5097	0.5114	−0.0004	0.0019	0.5977
	5000	−0.5097	0.5114	−0.0004	0.0055	0.5924
$\sigma$ = 0.05	10,000	−0.5097	0.5114	−0.0004	0.0038	0.5874
	20,000	−0.5097	0.5114	−0.0004	0.0027	0.5802
	5000	−0.5097	0.5114	−0.0007	0.0098	0.5685
$\sigma$ = 0.10	10,000	−0.5097	0.5114	−0.0004	0.0068	0.5667
	20,000	−0.5097	0.5114	−0.0004	0.0048	0.5695
	5000	−0.5097	0.5114	−0.0002	0.0156	0.5554
$\sigma$ = 0.15	10,000	−0.5097	0.5114	−0.0003	0.0108	0.5637
	20,000	−0.5097	0.5114	−0.0003	0.0076	0.5615
R1 vs. R4
	5000	−0.4200	0.2970	−0.0014	0.1425	0.5046
$\sigma$ = 0.00	10,000	−0.4200	0.2970	−0.0017	0.0996	0.4979
	20,000	−0.4200	0.2970	−0.0007	0.0699	0.4798
	5000	−0.4200	0.2970	−0.0033	0.1365	0.4917
$\sigma$ = 0.05	10,000	−0.4200	0.2970	−0.0008	0.0960	0.4957
	20,000	−0.4200	0.2970	0.0007	0.0675	0.4890
	5000	−0.4200	0.2970	0.0041	0.1261	0.4851
$\sigma$ = 0.10	10,000	−0.4200	0.2970	−0.0014	0.0884	0.4938
	20,000	−0.4200	0.2970	0.0044	0.0620	0.4953
	5000	−0.4200	0.2970	0.0019	0.1134	0.4928
$\sigma$ = 0.15	10,000	−0.4200	0.2970	−0.0005	0.0792	0.4970
	20,000	−0.4200	0.2970	0.0003	0.0558	0.4791

. Table 3 shows that for treatment regions R3 vs. R4, the treatment coefficients ${\beta }_1$’s are statistically significant (p-value = 0.0119 < 0.05) when N= 20,000 for $\sigma$ = 0. Additionally, the coefficients are statistically significant (p-value = 0.0349 < 0.05) when N = 20,000 for $\sigma$ = 0.05. These findings suggest that Equation (6) requires a bigger sample size for it to start yielding significant treatment effects. However, using Equation (7), which includes $IN{C}^c$ as a covariate, yields significant treatment effects for all the levels of $\sigma$ and for all the different sample sizes as shown in

Table 5. Top: Simulation results for fitting Equation (7) to compare R3 vs. R4, which represents $M{P}^c$≤ 0 vs. $M{P}^c$> 0 for $IN{C}^c$$\le$ 0, and cut-off c = 0. Bottom: Simulation results for fitting Equation (7) to compare R1 vs. R2 which represents $M{P}^c$≤ 0 vs. $M{P}^c$> 0 for $IN{C}^c$> 0, and cut-off c = 0.

R3 vs. R4	N	${\mathit{h}}_{\mathit{l}}$	${\mathit{h}}_{\mathit{r}}$	${\mathit{\beta }}_1$	s.e	p-Value
	5000	−0.1307	0.1248	0.0375	0.0067	0.0001
$\sigma$= 0.00	10,000	−0.1307	0.1248	0.0374	0.0047	0.0000
	20,000	−0.1307	0.1248	0.0371	0.0033	0.0000
	5000	−0.1307	0.1248	0.0296	0.0056	0.0002
$\sigma$ = 0.05	10,000	−0.1307	0.1248	0.0292	0.0039	0.0000
	20,000	−0.1307	0.1248	0.0291	0.0028	0.0000
	5000	−0.1307	0.1248	0.0163	0.0037	0.0019
$\sigma$ = 0.10	10,000	−0.1307	0.1248	0.0162	0.0026	0.0000
	20,000	−0.1307	0.1248	0.0161	0.0018	0.0000
	5000	−0.1307	0.1248	0.0080	0.0022	0.0084
$\sigma$ = 0.15	10,000	−0.1307	0.1248	0.0080	0.0015	0.0001
	20,000	−0.1307	0.1248	0.0080	0.0011	0.0000
R1 vs. R2
	5000	−0.1922	0.2859	−0.0778	0.0362	0.0843
$\sigma$ = 0.00	10,000	−0.1922	0.2859	−0.0796	0.0256	0.0111
	20,000	−0.1922	0.2859	−0.0782	0.0181	0.0003
	5000	−0.1922	0.2859	−0.0682	0.0341	0.1078
$\sigma$ = 0.05	10,000	−0.1922	0.2859	−0.0692	0.0241	0.0200
	20,000	−0.1922	0.2859	−0.0685	0.0169	0.0012
	5000	−0.1922	0.2859	−0.0469	0.0298	0.1961
$\sigma$ = 0.10	10,000	−0.1922	0.2859	−0.0473	0.0210	0.0675
	20,000	−0.1922	0.2859	−0.0468	0.0147	0.0101
	5000	−0.1922	0.2859	−0.0273	0.0249	0.3434
$\sigma$ = 0.15	10,000	−0.1922	0.2859	−0.0275	0.0176	0.2041
	20,000	−0.1922	0.2859	−0.0278	0.0126	0.0746

. Therefore, we will report the results based on the statistically significant estimates obtained by fitting data to Equation (7) (with $IN{C}^c$ as a covariate ) that are shown in Table 5. Table 5 shows that when $\sigma$ = 0, the treatment effects (${\beta }_1$’s) for R3 vs. R4 are comparable and statistically significant for the different sample sizes. These results show that when $\sigma$ = 0 and N= 5000, 10,000 or 20,000, scoring matric points that are greater than or equal to 25 compared to scoring matric points that are less than 25, increases the probability of eligibility for NSFAS funding, i.e., $P(NS{F}_i=1)$ by 3.75, 3.74, and 3.71 percentage points, respectively, for a unit increase in matric points for students whose households income is less than or equal to R350,000 (≈US$25,000).

The results show strong evidence that scoring matric points that are greater than or equal to 25 and an income less than R350,000 (≈US$25,000) significantly increases the chance of eligibility for NSFAS funding. This makes achieving matric points greater than 25 and household income less than R350,000 important variables to be considered when awarding NSFAS funding. The estimated treatment effects decrease when the variability in the two assignment variables, $M{P}^c$ and $IN{C}^c$, is varied from $\sigma$ = 0 to $\sigma$ = 0.15 in steps of 0.05, while holding the cut-offs constant as shown in Table 5 for R3 vs. R4. Additionally, the treatment effects are all still statistically significant at 5% level of significance. These results suggest that the causal estimates obtained by using the frontier approach may be sensitive to the level of variation in the assignment variables, because increasing the variation in the assignment variables may cause the observations to move away from the cut-off points, thereby decreasing the treatment effects.

As shown in Table 5 for R1 vs. R2, when $\sigma$ = 0 and N = 10,000, scoring matric points that are greater than or equal to 25 compared to scoring matric points that are less than 25, decreases the probability of eligibility for NSFAS funding, i.e., $P(NS{F}_i=1)$ by a significant 7.96 (p-value = 0.0111 < 0.05) percentage points for a unit increase in matric points for students whose household income is greater than or equal to R350,000 (≈US$25,000). These students who just meet the matric point threshold but with a household income that is just greater R350,000 (≈US$25,000) do not receive NSFAS funding and yet they are not different from those whose income is just below R350,000 (≈US$25,000). These students are referred to as the “missing middle” [8]. The authors define the “missing middle” as the students who come from households whose incomes are between R350,000 and R600,000. These students do not qualify for NSFAS funding but at the same time they cannot afford to pay for their higher education.

Table 4 and

Table 6. Top: Simulation results for fitting Equation (7) to compare R2 vs. R3 which represents $IN{C}^c$≤ 0 vs. $IN{C}^c$> 0 for $M{P}^c$$\le$ 0, and cut-off c= 0. Bottom: Simulation results for fitting Equation (7) to compare R1 vs. R4 which represents $IN{C}^c$≤ 0 vs. $IN{C}^c$> 0 for $M{P}^c$$>0$, and cut-off c= 0.

R2 vs. R3	N	${\mathit{h}}_{\mathit{l}}$	${\mathit{h}}_{\mathit{r}}$	${\mathit{\beta }}_1$	s.e	p-Value
	5000	−0.5097	0.5114	−0.0004	0.0031	0.5879
$\sigma$ = 0.00	10,000	−0.5097	0.5114	−0.0004	0.0021	0.6032
	20,000	−0.5097	0.5114	−0.0004	0.0015	0.5758
	5000	−0.5097	0.5114	−0.0005	0.0041	0.5817
$\sigma$ = 0.05	10,000	−0.5097	0.5114	−0.0004	0.0029	0.5836
	20,000	−0.5097	0.5114	−0.0004	0.0020	0.5763
	5000	−0.5097	0.5114	−0.0004	0.0067	0.5835
$\sigma$ = 0.10	10,000	−0.5097	0.5114	−0.0005	0.0046	0.5589
	20,000	−0.5097	0.5114	−0.0005	0.0033	0.5558
	5000	−0.5097	0.5114	−0.0006	0.0093	0.5558
$\sigma$ = 0.15	10,000	−0.5097	0.5114	−0.0008	0.0065	0.5368
	20,000	−0.5097	0.5114	−0.0001	0.0045	0.5427
R1 vs. R4
	5000	−0.4200	0.2970	−0.0014	0.0842	0.5050
$\sigma$ = 0.00	10,000	−0.4200	0.2970	−0.0016	0.0591	0.4956
	20,000	−0.4200	0.2970	−0.0007	0.0414	0.5179
	5000	−0.4200	0.2970	−0.0009	0.0787	0.4877
$\sigma$ = 0.05	10,000	−0.4200	0.2970	−0.0003	0.0552	0.5116
	20,000	−0.4200	0.2970	−0.0006	0.0389	0.5114
	5000	−0.4200	0.2970	0.0011	0.0668	0.4903
$\sigma$ = 0.10	10,000	−0.4200	0.2970	0.0005	0.0470	0.4963
	20,000	−0.4200	0.2970	0.0035	0.0330	0.5022
	5000	−0.4200	0.2970	0.0037	0.0537	0.5147
$\sigma$ = 0.15	10,000	−0.4200	0.2970	−0.0005	0.0377	0.4982
	20,000	−0.4200	0.2970	0.0011	0.0265	0.4886

, explore the effects of having a household income greater than R350,000 compared to having an income less than or equal to R350,000 for students who are either scoring matric points greater than 25 or less than 25. These results show that all the ${\beta }_1$’s are small and not statistically significant at 5% level of significance. The implications of these results are that when awarding NSFAS funding, one must first look at whether or not a student has met the matric points threshold and then consider the household income. Considering the matric points first, makes it easier to quantify the number of students that have qualified for university entry. Consequently, NSFAS will then be in a position to quantify those that automatically qualify for NSFAS funding and also, quantify the “missing middle”.

5.2. Supplementary Analysis

The following supplementary analyses are considered in this paper, and they are based on the simulated data when $\sigma$ = 0 and N = 10,000.

5.2.1. Checking for Continuity of the Conditional Expectation of Exogenous Variables around the Cut-Off/Threshold Value

Graphical analysis is an integral part of any RDD design. It is assumed that the treatment effect or causal effect of interest is measured by the value of the discontinuity in the expected outcome at a particular cut-off point. This is a fundamental assumption that postulates that without an intervention, the outcome variable would have been continuous at the cut-off point. This means that any discontinuity in the outcome is credited only to the treatment or exposure. Graphical analysis provides insights into the RDD results for causal analysis. For example, if the graph has a discontinuity, this would suggest that the intervention had a causal effect on the outcome, whereas if the graph is continuous, then it would suggest that there is no causal effect that can be attributed to the intervention. Current literature that we are aware of on MRDD has limited discussion on a direct extension of the conventional RDD graphs to MRDD. Ref. [3] offers a sub-optimal extension to MRDD, as well as using a different approach, the “slicing” and “sliding window” plots. In this study we deploy two dimensional plots for each of the causal effects as shown in Figure 4 and Figure 5. The graphs compare two treatments at a time, yielding four plots in total (one for each pair of treatments being compared).

Using the function “rdplot()” in the R package “rdrobust” [24], the outcome variable is plotted as a function of the assignment variable, as shown in Figure 4 and Figure 5. The graphs show that there are discontinuities at the cut-off points, thereby providing evidence of a non-zero treatment effect. Additionally, the graphs show that the relationship between the outcome variable and the assignment variables is approximately linear within a very small bandwidth of the assignment variables. Thus, the graphs show that the linear specification model is a plausible and credible model for estimating the treatments effects within a narrow bandwidth.

5.2.2. Manipulation Testing Using Local Polynomial Density Estimation

Ref. [7] introduced the McCrary manipulation test to check for evidence of manipulation near the income or matric points cut-off points. However, in this paper, we employ a newer method proposed by [25] that uses local polynomial density estimators [23] for manipulation testing. The method uses the rddensity() function in the R package ‘rddensity’ to implement manipulation testing procedures. The test is robust to local polynomial order specifications and different bandwidths [25]. Manipulation testing using local polynomial density estimation tests the null hypothesis ($H_0$) of no discontinuity of density around cut-off point versus the alternative hypothesis that the density is discontinuous around cut-off points. A test statistic, $\mid T_q(h_l,h_r)\mid$, is computed for a given $\alpha$ level of significance [23]. $H_0$ is rejected if and only if $\mid T_q(h_l,h_r)\mid$≥${\varphi }_{1-\alpha /2}$. Thus, $H_0$ indicates that there should not be any difference in the chance of eligibility for NSFAS funding for students on either side of the income or matric points cut-off points. Any differences should be attributed to the treatment effect only. The manipulation test checks whether this is actually true in our data. If students are able to choose their side of the cut-off points in order to influence the outcome, then we might worry that students on either side of the cut-off points are not comparable. The results of the manipulation tests for $\sigma$ = 0 and N = 10,000 are shown in

Table 7. Examining Manipulation at the Income and Matric points cut-off points.

Causal Effect	Bandwidth	$\mid {\mathit{T}}_{\mathit{q}}({\mathit{h}}_{\mathit{l}},{\mathit{h}}_{\mathit{r}})\mid$	p-Value
R3 vs. R4	(−0.1307, 0.1248)	0.4809	0.6306
R1 vs. R2	(−0.1922, 0.2859 )	0.2300	0.8181
R2 vs. R3	(−0.5097, 0.5114)	0.9122	0.3617
R1 vs. R4	(−0.4200, 0.2970)	0.3571	0.721

.

For a given bandwidth, $T_q(h_l,h_r)$ is the final manipulation test statistic. For example, for R3 vs. R4 which represents $M{P}^c$< 0 vs. $M{P}^c$$\ge$ 0 when $IN{C}^c$$\le$ 0 and cut-off, c= 0, $\mid T_q(-0.1307,0.1248)\mid$ = 0.4809, with a p-value = 0.6306. This means that we fail to reject $H_0$, and conclude that there is no statistical evidence of systematic manipulation of the matric points. Additionally, the manipulation test results for R1 vs. R2, R2 vs. R3 and R1 vs. R4 indicate that there is no evidence of manipulation of the assignment variables.

5.2.3. Sensitivity to Optimal Bandwidth Selection

We investigate whether the causal estimates critically dependent on a particular bandwidth choice, i.e., how sensitive the causal estimates are to outcomes of the units that are located very close to the cut-off points. Ref. [26] describes the implementation of a newer method that employs local polynomial methods to analyse the sensitivity of the causal estimates to the bandwidth choice. The method investigates sensitivity to bandwidth choice by removing or adding units at the end-points of the neighborhood. This method is different to the the continuity-based approach that changes the bandwidths that are used for local polynomial estimation. Additionally, the newer approach uses finite-sample methods to select a bandwidth that is closer to the cut-off points where the local randomization assumption is probably justified. The “rdwinselect()" command contained in the “rdlocrand” R package [27] is employed to check for sensitivity of the causal estimates to the bandwidth that is used. The “rdwinselect()" command automatically selects a window around the cut-off where the treatment can plausibly be assumed to have been as-if randomly assigned [26]. If the causal estimates critically depend on a particular bandwidth, then they are less credible.

Table 8. Minimum window around the cut-off points where the treatment can plausibly be assumed to have been randomly assigned.

Treatment Region	Window
R3 vs. R4	(−0.0037, 0.0029)
R1 vs. R2	(−0.0455, 0.0541)
R2 vs. R3	(−0.095, 0.1336)
R1 vs. R4	(−0.0973, 0.1237)

shows the recommended windows around the cut-off points that were selected for each of the treatment region comparisons.

After choosing the appropriate minimum windows around the cut-off points using “rdwinselect()" function that are shown in Table 8, different statistical tests such as the difference-in-means (DM), Kolmogorov–Smirnov (KS), and Wilcoxon rank sum (RS) can be implemented to test whether or not the treatment effects are different from zero or not. In this paper, we implemented the difference-in-means (DM) of the outcomes on either side of the cut-off point using the “rdrandinf()" command in the “rdlocrand” R package. The DM procedure tests the Fisherian null hypothesis [26], that the treatment effect is zero for all units. Ref. [26] points out that the interpretation of the difference-in-means test statistic in the Fisherian framework is different because it tests the sharp null hypothesis of no treatment effect, and it should not be interpreted as an estimated treatment effect. Its main purpose is to test the null hypotheses that are sharp (e.g., no treatment effect), not on point estimation. This is much stronger than testing the hypothesis that the average treatment effect (ATE) is zero. If the treatment effects are not statistically significant using the minimum window when in the first place we obtained statistically significant treatment effects using the optimal bandwidths and vice versa, then it indicates that the treatment effects are sensitive to the bandwidth used.

Table 9. Difference-in-means (DM) test statistics for the treatment regions under investigation.

Treatment Region	DM Test Statistic (T)	p-Value
R3 vs. R4	0.383	0.000
R1 vs. R2	0.138	0.000
R2 vs. R3	−0.003	0.103
R1 vs. R4	−0.078	0.132

shows the results of DM for each treatment region.

The DM for treatment regions R3 vs. R4 and R1 vs. R2 significant at $\alpha =0.05$ using the automatically determined minimum bandwidths. Table 5 shows that the treatment effects for R3 vs. R4 and R1 vs. R2 are all significant for $\sigma$ = 0 and N = 10,000. These results show that the causal estimates do not critically depend on a particular bandwidth. Additionally, Table 9 shows that the DM for treatment regions R2 vs. R3, and R1 vs. R4 are not statistically significant at $\alpha =0.05$ using the automatically determined minimum bandwidths. The treatment effects for R2 vs. R3, and R1 vs. R4 are also not statistically significant for $\sigma$ = 0 and N = 10,000, as shown in Table 6. These results provide evidence that the causal estimates obtained in the simulation studies are credible as they are very robust to bandwidths that are close to the cut-off points for income and matric points.

6. Case Study

6.1. Application of the MRDD to the Graduate Admissions Data Set

The purpose of case study is apply the methods described earlier to a real world data set. The design for this case study is inspired by [28] who used the conventional RDD with grade points average (GPA) as the only running variable. Therefore, we determine whether using two the assignment variables, namely CGPA and GRE scores from the Indian graduate admissions data [29], produce significant and credible causal effects estimates of the chance of student getting admission for a master’s program in the USA. Ref. [30] recommends a total GRE score of 322 for a student to stand a higher chance of being admitted to a graduate program of choice. Thus, we set a GRE cut-off of 322. Similarly, [30] highly recommends CGPA of ≈8.5 in order for a candidate not to be directly rejected due to poor academic performance. Thus, we use 8.5 and 322 as cut-off points for CGPA and GRE, respectively.

6.2. Estimation of the Causal Effects of CGPA and GRE

To estimate the effect of scoring CGPA ≥ 8.5 over CGPA < 8.5 for students having GRE < 322 or GRE ≥ 322, Equation (9) (similar to Equation (7)) is fitted to the data.

$$\begin{array}{cc}\hfill P(Admit\hfill & =1|CGP{A}^c,T_{cgpa},GR{E}^c,TOE{F}^c)={\beta }_0+{\beta }_1{T}_{cgpa}+{\beta }_{2}CGP{A}^c\hfill \\ & +{\beta }_{3}CGP{A}^c\times T_{cgpa}+{\beta }_{4}GR{E}^c+{\beta }_{5}TOEF{L}_i^c+{ϵ}_i,\hfill \end{array}$$

(9)

The following causal effects are determined using the assignment variables “CGPA” and “GRE”, with respective cut-offs equal to 8.5 and 322. Additionally, the variables are centered around their respective cut-off points to give $CGP{A}^c$ and $GR{E}^c$. To estimate the effect of GRE, $CGP{A}^c$, and $T_{cgpa}$, variables are replaced by $GR{E}^c$ and $T_{gre}$ in Equation (9), respectively. The data used was of size, N = 500 at the time of writing this paper.

1

Causal Effect 1: $CGP{A}^c$< 0 vs. $CGP{A}^c$$\ge 0$ for $GR{E}^c$$\ge 0$

2

Causal Effect 2: $CGP{A}^c$< 0 vs. $CGP{A}^c$$\ge 0$ for $GR{E}^C$< 0

3

Causal Effect 3: $GR{E}^c$< 0 vs. $GR{E}^c$$\ge 0$ for $CGP{A}^c$$\ge 0$

4

Causal Effect 4: $GR{E}^c$<0 vs. $GR{E}^c$$\ge 0$ for $CGP{A}^c$< 0

The results (Causal Effects 1–4) of fitting to Equation (9) the Graduate Admissions data set are shown in

Table 10. The results of fitting to Equation (9) the Graduate Admissions Data Set.

Causal Effect	${\mathit{h}}_{\mathit{l}}$	${\mathit{h}}_{\mathit{r}}$	${\mathit{\beta }}_1$	s.e	p-Value
Causal Effect 1	−0.400	0.550	0.403	0.104	0.000
Causal Effect 2	−0.200	0.480	−0.035	0.016	0.025
Causal Effect 3	−24.0	18.0	0.607	0.028	0.000
Causal Effect 4	−23.0	13.0	0.118	0.018	0.000

.

Table 10 shows that Causal Effects 1–4 are significant at 5% level of significance. Causal Effect 1 is equal to the effect of having a CGPA score that is greater than or equal to 8.5 compared to having a CGPA score that is less than 8.5 for all the students whose GRE score is already greater than or equal to 322. The results show that having a having a CGPA score greater than 8.5 compared to having a CGPA that is less than 8.5 increases the chance of graduate college admission by a significant 40.3 (p-value = 0.000 < 0.05) percentage points for students from India who already have a GRE score that is greater than 322. Similarly, Causal Effect 3 shows that having a GRE score that is greater than 322 compared to having a GRE Score that is less than 322 increases the chance of graduate college admission by a significant 60.7 (p-value = 0.000 < 0.05) percentage points for students who already have a CGPA score greater than 8.5. The effect of scoring a CGPA score greater than 8.5 compared to scoring a CGPA less than 8.5 for students who already have a GRE score < 322 (Causal Effects 2) significantly reduces the chance of admission to a graduate master’s program by ≈3.5 ( p-value = 0.025 < 0.05 ) percentage points. On the other hand, obtaining a GRE score > 322 compared to obtaining a GRE score < 322 (Causal Effect 4) increases the chance of college admission by ≈11.8 percentage points for students who already have CGPA < 8.5 for students who already have a CGPA score that is less than 8.5. These results suggests that GRE and CGPA are very important obstacles that must be overcome if one is to have a realistic chance of being admitted to the graduate master’s program. This means that for students from India intending to apply to study for a graduate master’s programs in science and technology in the USA, they must achieve competitive GRE and CGPA of at least 322 and at least 8.5, respectively.

Table 11. Examining manipulation at the CGPA and GRE cut-off points.

Causal Effect	${\mathit{h}}_{\mathit{l}}$	${\mathit{h}}_{\mathit{r}}$	${\mathit{T}}_{\mathit{q}}$(${\mathit{h}}_{\mathit{l}}$, ${\mathit{h}}_{\mathit{r}})$	p-Value
Causal Effect 1	−0.400	0.550	−1.110	0.267
Causal Effect 2	−0.200	0.480	−0.701	0.483
Causal Effect 3	−24.0	18.0	0.921	0.357
Causal Effect 4	−23.0	13.0	1.505	0.133

shows the manipulation test results of the CGPA and GRE scores. The results show that there is insufficient evidence to reject the null hypothesis ($H_0$) of no discontinuity of density around the cut-off points for Causal Effects 1–4. This suggests that there is insufficient evidence of manipulation of the CGPA and GRE scores. Thus, the causal estimates are credible.

Table 12. Tests for difference in means (DM) using the minimum window (bandwidth).

Causal Effect	Minimum Window	DM Test	p-Value
	(Bandwidth)	Statistic (T)
Causal Effect 1	(−0.4, 0.42)	0.347	0.001
Causal Effect 2	(−0.2, 0.19)	0.005	0.035
Causal Effect 3	(−2, 1)	0.665	0.000
Causal Effect 4	(−4, 5)	0.310	0.000

shows the difference-in-means (DM) tests for the Fisherian null hypothesis [23], that the treatment effect is zero for all units. We reject the Fisherian null hypothesis that the treatment effect is zero for Causal Effects 1–4 and conclude that the causal effects that are all statistically significant at 5% level of significance since the p-values of the DM statistics (T) shown in Table 12 are all less than 0.05. This shows that causal estimates are not sensitive to the choice of bandwidth because the causal estimate shown in Table 10 are also statistically significant at 5% level. This means that the frontier MRDD produced credible causal estimates.

7. Discussion and Conclusions

7.1. Discussion

This paper has highlighted the importance of using an appropriate regression discontinuity approach when faced with the complexity brought about by having more than one assignment variable. In this study we have used the frontier MRDD because it is easy to implement. It reduces the assumptions checking process to a series of well-defined single assignment variables RDD, whose methods are well-defined in the literature [5]. A data-driven bandwidth selection method was deployed in selecting an optimal bandwidth, thus eliminating the possibility of manipulating the results by choosing an arbitrary bandwidth. Researchers seeking to use local linear regression must ensure that there is a sufficient density of points around the cut-off points. Not having enough density of points at the threshold point may result in less credible causal estimates. The simulation results produced significant causal estimates when the data was random with no induced variability in the assignment variables. For example, based on our analytical results, barely scoring matric points greater than or equal to 25 points compared to scoring matric points less than 25 for students whose household income is less than R350,000 increases the probability of eligibility for NSFAS funding by 3.75 percentage points (Table 5 for $\sigma$ = 0). When the level of variability in the two assignment variables, $M{P}^c$ and $IN{C}^c$ was increased from $\sigma$ = 0 to $\sigma$ = 0.15 in steps of 0.05, while holding the cut-offs constant, the estimated treatment effects decreased respectively for each level of $\sigma$. This showed that the frontier MRDD approach was not suitable for handling data with high variability. Thus, for future work we may consider developing methods that can handle variability in the assignment variables better. Besides, the frontier MRDD works very well when $\sigma$ = 0, i.e., when there is no induced variability in the assignment variables and the causal effect estimates were comparable and credible for the different sample sizes.

We have reported not only the causal effects, but also carried out supplementary analyses to assess the credibility of the primary causal effect estimates. We found evidence of a relationship between the outcome variable and the assignment variable(s) through graphical analysis. Figure 4 and Figure 5 show “visual” evidence of disturbances or discontinuities in the expected smooth relationship between the outcome variable and the assignment variable(s). This gives credibility to the causal estimates as it indicates that the treatments effects actually exist at the cut-offs. The relationship between the probability of eligibility for NSFAS funding and either one of the assignment variables (income or matric points) is assumed to exhibit smooth functions. This assumption of smooth functions is based on the continuity-based framework that is used to explain the required identification assumptions intuitively, and also in developing causal effect estimates. Additionally, we have assessed the existence of the causal effects through an alternative causal framework, making use of the local randomization framework [31]. The local randomisation framework is different from the continuity-based framework in that it formalises the idea of a local randomized experiment near the cutoff by embedding the RD design in a classical, Fisherian causal model, thereby giving interpretation and justification to randomization inference and related classical experimental methods [32]. By using the local randomisation framework, we analysed the units that are in a small window around the cut-off points “as-if” they were randomly assigned to treatment or control. This enabled us to use statistical tools such as the difference-in-means (DM) to test the Fisherian null hypothesis, that the treatment effect is zero for all units. The Fisherian null hypothesis of no treatment effect was applied in both the simulation and the case study. For example, in the case study, we did not apply graphical analysis to visually inspect whether a treatment effect existed or not, but we rejected the Fisherian null hypothesis of no treatment effect, thereby validating the presence of treatment effects for Causal Effects 1–4. The local randomisation assumption near the cut-off has allowed us to use a newer method proposed by [31] in assessing the credibility of causal estimates in a simulation study as well as in a real world data set. Besides, for the continuous assignment variables, $M{P}^c$ and $IN{C}^c$ in the simulation study, we have used graphical analysis (or the continuity-based framework) to detect the presence of a discontinuity or treatment effect and then used the local randomization approach (Fisherian null hypothesis) as a robustness check.

To test for evidence of manipulation of the assignment variables we used a newer intuitive and easy-to-implement non-parametric density estimator that is based on local polynomial techniques [23]. The authors indicate that the estimator is fully automatic and does not require any other transformation of the data. Students must not be able to influence their position relative to the cut-off scores. The local polynomial density manipulation testing results for both the simulation study (Table 7), and the case study (Table 11), show that students were not able to manipulate or choose their preferred side of the assignment variable(s) cut-off point, thus making the causal estimates more credible. Besides, the evidence of no manipulation holds because all students may not precisely manipulate their own matric points. This gives credibility to the causal effects estimated in both the simulation and case study.

Sensitivity to bandwidth choices was performed by examining the robustness of our causal estimates to changing bandwidths. Table 9 shows that when the causal estimates were estimated using narrow windows around the cut-off points, they were all significant at 5% level of significance. This suggests that our average causal estimates results remain largely robust to changing bandwidth choices.

The results of the case study have demonstrated that the frontier MRDD is a valid and it can be applied to a real world data set giving significant and credible causal effects of a treatment. Using the Indian graduate admissions data for master’s programs in science and technology studies in the USA, we obtained significant causal estimates (Table 10). Additionally, the manipulation test results (Table 11) indicated that there was insufficient evidence to reject the null hypothesis $H_0$ of no discontinuity. This suggests that there was no evidence of manipulation of the GRE or the CGPA in order to gain admission to graduate master’s programs for students from India. Additionally, Table 12 shows that when using the minimum window (bandwidth) around the cut-off points, the Fisherian null hypothesis of no treatment effect is rejected, thereby indicating that the causal estimates were credible and not sensitive to bandwidth choice.

The simulation studies described earlier ensured that we had enough data points on either side of the cutoff points. However, in real-world MRDD applications, the distribution of points around the cut-off points may be sparse and not optimal. Therefore, practitioners wishing to apply MRDD need to take into account the distribution of points around the cutoff points when they are determining the sample size(s) to use. Furthermore, the case study has shown that it essential to perform supplementary analyses such as the manipulation tests or sensitivity to bandwidth choice. This is because failure to perform supplementary analyses may affect the precision and bias of the causal effect estimates.

7.2. Limitations

A limitation of the study was that consolidated data of household income and matric points was not available from the department that handles the National Student Financial Aid Scheme (NSFAS) at the time of writing this paper and we could not directly apply our approach to real income and matric points data. However, we have demonstrated that the approach we have adopted still works for MRDD with two assignment variables and can unearth valuable causal effects of interest. For future work, we strongly recommend that further research should focus on the determination of the minimum sample size required for two or more assignment variables. Additionally, future simulation studies can be employed to examine the effect of variations in the correlation and distribution of the assignment variables. In the simulation studies we used samples of size 5000, 10,000, and 20,000 and in the case study we used data of size 500. Determining the minimum sample required to obtain credible causal estimates will assist those wishing to apply for MRDD. Determining the minimum sample size enables one to have enough density of data points around the cut-off point and thus generate more credible estimates. In generating the outcome variable, the possibility of using different combinations of the data generation distributions could be explored. Future work could also look at studying the effect of NSFAS grants on subsequent enrollment rates for a bachelor’s degree and not just focus of the probability of eligibility for NSFAS funding. One could also look at whether or not NSFAS grants influences the choice of the universities to attend or influence the number of years students spend studying for their bachelor’s degree.

8. Conclusions

In the absence of randomised controlled experiments, regression discontinuity designs offer more opportunities to estimate causal effects by making use of the variation in the treatment assignment induced by a cut-off point. One major finding of this paper is the discovery of new evidence that both matric points and income have a huge impact on the probability of getting NSFAS funding to study at any university in South Africa. This evidence will inform policy makers and educational practitioners on the effects of matric points and income on the chance of eligibility for NSFAS funding. The availability of the NSFAS grant has a huge impact on students’ decisions to attend university or seek other opportunities elsewhere. In summary, this paper makes valuable contributions to the literature on multiple regression discontinuity designs by conducting supplementary analyses that seek to add more credibility to the causal estimates obtained through primary analyses. If one is interested in determining causal effects of barely meeting the requirements of one assignment variable, among the subjects that either meet or fail to meet the requirements of the other assignment variable, then we strongly recommend the use of the frontier multivariate regression discontinuity design as it is easy to implement and it incorporates discontinuities in multiple assignment variables into single regression discontinuity designs along a number of frontiers of the treatment variables.