Abstract
This paper discusses a non-parametric resampling technique in the context of multidimensional or multiparameter hypothesis testing of assumptions of the Rasch model. It is based on conditional distributions and it is suggested in small sample size scenarios as an alternative to the application of asymptotic or large sample theory. The exact sampling distribution of various well-known chi-square test statistics like Wald, likelihood ratio, score, and gradient tests as well as others can be arbitrarily well approximated in this way. A procedure to compute the power function of the tests is also presented. A number of examples of scenarios are discussed in which the power function of the test does not converge to 1 with an increasing deviation of the true values of the parameters of interest from the values specified in the hypothesis to be tested. Finally, an attempt to modify the critical region of the tests is made aiming at improving the power and an R package is provided.
1. Introduction
Various resampling approaches have been suggested in the statistical literature, notably permutation tests, cross-validation, the jackknife, and the bootstrap. A taxonomy of resampling techniques is, for example, provided by Rodgers [1]. These approaches are applicable to a wide range of statistical problems. In principle, they are utilized in cases where the probability distribution of an estimator or a test statistic is unknown. In a number of practically relevant scenarios, the distribution can only be derived asymptotically, i.e., for large samples. When the sample size is small or in the case of sparse data resampling techniques can be used instead.
The jackknife, originally introduced by Quenouille [2] and Tukey [3], is a subsampling approach aimed at estimating or approximating only the variance (i.e., the random error) of an estimate and its potential bias. The bootstrap introduced by Efron [4] and Efron and Tibshirani [5] generalizes the basic idea of the jackknife for approximating the sampling distribution of a test statistic or, more generally, a root, i.e., a real-valued function of the parameters of interest and the data. Thus, it can also be used in hypothesis testing problems (e.g., [6]). The original bootstrap [4] is a non-parametric approach. There is also a model-based approach called parametric bootstrap [7]. An application-oriented introduction of the bootstrap is given by Chernick [8] and Chernick and LaBudde [9].
In the psychometric context or, more specifically, in problems of testing hypotheses or assumptions of a class of psychometric models known as Rasch models [10,11], bootstrap techniques have also been applied. Parametric bootstrap procedures have been discussed by Von Davier [12], Heene et al. [13], and Alexandrowicz and Draxler [14]. These have in common that parameters of the assumed model are estimated from the data, and these estimates are then used to generate the bootstrap samples. These estimates are biased for small samples (in principle, because of the logit transformation of response probabilities). Generally, they are only asymptotically unbiased. The dependence on biased estimates may affect the hypothesis testing procedure in an adverse manner like biasing the test and/or reducing its power. Other resampling procedures applied in this context are of a non-parametric nature [15,16,17,18,19,20,21]. These capitalize on the existence of sufficient statistics for all parameters in the Rasch model. The conditional distribution given the observed values of these sufficient statistics is discrete uniform and does not depend on any of the parameters of the model. Drawing samples from such a discrete uniform distribution to estimate or approximate the conditional distribution of any test statistic can be viewed as a non-parametric bootstrap approach. Such a procedure is fairly practical since the determination of the exact discrete conditional distribution of a test statistic is complicated and computationally very demanding [18]. Additionally, it has an advantage over the parametric bootstrap since it avoids the dependence on any potentially biased parameter estimates. Note that, strictly speaking, the procedure utilized in this paper is a redrawing or resampling from a known conditional distribution, rather than drawing from the observations themselves which is common with the classical bootstrap and which is typically used when the distribution of the data is not known.
The Rasch model is only one of a variety of psychometric models used to measure psychological quantities like abilities, proficiencies, and attitudes but it can also be viewed as a model that stands out against others. It formalizes desirable fundamental measurement principles like the generalizability of comparisons of persons over items and vice versa (e.g., [11]).
In the present paper, problems of testing multidimensional or multiparameter hypothesis in the Rasch modeling framework are discussed. In particular, tests of the invariance assumption of the item parameters in the Rasch model are discussed which are of great interest in the practice of psychometrics. Verhelst’s non-parametric Markov Chain Monte Carlo (MCMC) approach [17] is utilized. It is computationally the fastest compared to others and is easily accessible as an R package [22]. The bias and power function of the tests is also investigated. Finally, suggestions concerning the choice of the critical region to improve the power of the tests are given and an R package for the computations is provided.
Note that the novelty of this paper does not originate from the use of a resampling procedure or, specifically, Verhelst’s Rasch Sampler [17,22] but in providing remarks and a tentative guideline on potential improvements of the power of the tests in case of very small sample sizes and sparse data, respectively. Furthermore, an R package has been developed to achieve better dissemination and wider application of the procedures.
The remainder of this paper is organized as follows. Section 2 describes the theoretical background, and the statistical model, and introduces conditional tests of the hypothesis of invariance of item parameters in the Rasch model. Section 3 reviews common algorithms to sample binary matrices and addresses computational issues. Section 4 and Section 5 present the study design and results of size and power function of the tests. Section 6 hints tentatively at potential modifications of the tests. Final remarks are provided in Section 7.
2. Theoretical Background
In the Neyman–Pearson paradigm [23], which is considered in the present work, it is assumed that the true unknown probability distribution generating the observations (the data) in a sample space belongs to a family (or class) of distributions that is specified by a statistical model indexed by one or more parameters taking values in a parameter space . A statistical hypothesis is generally obtained by specifying a subset of this family or, equivalently, a subset of the parameter space .
2.1. Psychometric Model
In this work, data are assumed to be given by the binary responses of a number of persons to a number of items. It is assumed that every person responds to every item. Denote by the binary response of person to item . Let the binary responses of every person to every item be arranged in an matrix . Consider the following family of distributions specified by the model
where is a person parameter typically interpreted as an ability or attitude, is an item parameter, i.e., easiness or attractiveness of the respective item, and is a conditional effect of item j given . The latter is an observed covariate value of person i. The covariate may be binary or real-valued, e.g., gender and age. For the present purpose, the and parameters are treated as nuisances. The interest lies only in making inferences about the parameters. Setting all of them to 0 yields the Rasch model as a special case that assumes invariance of the item parameters, i.e., independence of the covariate. Further, the model given by (1) assumes that the k responses of each person are locally independent and that the persons are drawn independently from the population of interest, i.e., the k-vectors of responses of the n persons are independent vector-valued random variables. Then, the joint distribution of all responses is given by the product of (1) over all persons and items. By using matrix multiplication, one obtains
with , , , , and for identifiability. As can immediately be seen, it is a multiparameter exponential family of distributions and is its natural parameter space, i.e., an open subset of Euclidean space. The first factor is a normalizing constant not depending on the data, and the second factor depends on the data only through the respective sufficient statistics, i.e.,
are sufficient for the family distributions. Note that the former two statistics are the row and column sums of the response matrix . Hence, further considerations can be restricted to the distribution of the sufficient statistics. The marginal distribution of , which are the sufficient statistics for the nuisance parameters and , and the joint distribution of all sufficient statistics , , and are given by
and
In (2), denotes a finite set containing as elements all matrices satisfying the condition and , i.e., matrices with the same row and column sums. The subset additionally satisfies that , where , and denotes the cardinality of . Thus, (2) is composed of the union of all matrices satisfying and (3) of the union of all matrices satisfying . Note that
the summation on the right side being taken over all values of the statistic that can potentially be observed, i.e., with probability . Consider restricting the original sample space consisting of all possible binary matrices (with arbitrary row and column sums) to the set , i.e., consider the conditional distribution obtained by
Obviously, it does not depend on the nuisance parameters and . Note that one element of the vector is not free. One degree of freedom is lost because of the conditioning. When (when the invariance assumption of the Rasch model holds true) the conditional distribution (4) becomes , where is the cardinality of . Thus, it is simply given by the number of matrices for which divided by the number of all matrices in . It is also easily verified that every single matrix in has the same probability of being observed (given the invariance assumption). By drawing random samples from this discrete uniform distribution over all matrices in the proportion can be arbitrarily well approximated by carrying out a sufficient number of draws. Note that such an approach samples whole matrices with given row and column sums and not individual responses of the persons to the items. This constitutes the basic idea of the (non-parametric) resampling approach that is applied in the present work.
Note that the philosophical basis for conditioning on a statistic is strongest when the statistic is ancillary, i.e., when its distribution does not depend on the parameters of interest. This is, obviously, not the case. The distribution of depends on but, as indicated in Section 1, there are also other more technical arguments that may justify it, at least in the present context.
It may also be interesting to note that (4) reduces to the central hypergeometric distribution when , , and [24].
2.2. Statistical Tests
In the following, conditional tests based on (4) are discussed. Let the two subclasses of distributions
, be specified. Of interest is to test the hypothesis
against the alternative
or, briefly speaking, against . Note that the nuisance parameters and are left unspecified. Regardless of their true values, the tests to be considered in the sequel are not affected since their size and power are based on (4).
A test decides between these two hypotheses on the basis of the observed value of a test statistic. Since the alternative hypothesis is two-sided and concerns multiple parameters one may consider the following test statistics. Consider the score function first. Since (4) is also a multiparameter exponential family the vector-valued score function has the well-known simple form
where are the expected values of the -dimensional distribution (4). For the present purpose, the score function is evaluated at . The expected values of (4) are obtained by
where the summation has to be taken over all values of the statistic that can potentially be observed, i.e., with probability , and
with as the number of matrices in for which . Hence, the score function expresses the deviations of the observed values of the elements of from their expected values when (5) is true (when the invariance assumption of the Rasch model holds true). The vector of expected values of the score function itself is , as is well known. Thus, reasonable and very intuitive test statistics for the present purpose are obtained by
treating as a matrix and using matrix multiplication, and
Thus, is the sum of squared elements of the score function and is the sum of absolute values. The critical region of the tests shall be denoted by and is chosen to consist of those matrices in for which the 100 percent largest values of the respective test statistic is obtained, where denotes the probability of the error of the first kind. The conditional power of the tests is a function of the parameter of interest given and . The complete conditional power function is then given by
Note that these tests do generally not achieve the exact predetermined level unless one does not use randomization. This is because of the discrete nature of (4). Thus, one may also take conservatism issues and suggestions of resolving them into account (e.g., [25]).
The described choice of the critical region cannot be considered optimal. In the multiparameter case, in general, no optimal tests exist, e.g., no uniformly most powerful (UMP) and UMP unbiased tests. Basically, any other test statistic that is expected to have reasonable power against the alternative (6) may be utilized. Various suggestions have already been made by Ponocny [15]. In the present work, four other quadratic test statistics are investigated which are expected to have good power. These are the well-established trinity of the likelihood ratio (LR) [26,27], the Wald (W) [28], and the Rao score test (RS) [29,30], as well as the relatively new gradient test (G) [31,32,33]. As is well known, these tests are derived from asymptotic theory but, in the present case, the limiting distribution of these test statistics is not of relevance. They may also be used in small samples because their exact conditional distribution is simply obtained from (4). Since the computation of (4) can be time-consuming it may also be approximated by a resampling procedure.
3. Resampling Algorithms and Computational Issues
The utilization of resampling techniques is of critical importance for the practicality of the tests described in Section 2.2 This is mainly because of the time-consuming problem of counting the numbers of matrices in [18] and computing the exact conditional distribution (4). It is more practical to draw random samples of matrices from the uniform distribution over to approximate the conditional distribution (4), size, and the power function (10) of the tests. There are a number of algorithms serving this purpose.
Algorithms to approximate the uniform distribution of binary matrices with fixed row and column sums can be categorized. One class of algorithms suggested by Snijders [34], Chen et al. [35], and Chen and Small [16] are so-called sequential importance sampling procedures which are mainly utilized to approximate dynamic systems. Using such algorithms, the uniform distribution over all binary matrices in can be sequentially approximated. The other class of algorithms are Markov Chain Monte Carlo procedures. These consider the matrices in the sample space as states of a Markov chain and a sampling scheme defines the transition probabilities from one state to the other. The stationary distribution of the Markov chain is given by the (desired) discrete uniform distribution over all matrices in . For example, algorithms discussed by Besag and Clifford [36], Ponocny [15], and Verhelst [17] belong to this category. Strona et al. [37] introduced the Curveball algorithm, with more attention on matrix information content than on matrix structure. A modified version of the Curveball algorithm, called the good-shuffle Curveball algorithm, has been proposed by Carstens [38], showing a better performance in small matrices. An overview of MCMC algorithms is provided by, e.g., Rechner [39].
Finally, it should be remarked that Miller and Harrison [18] solved the complicated combinatorial problem of determining the exact total number of matrices in the sample space by deriving a recursive counting algorithm. Hence, in principal, the exact uniform distribution need not be approximated any more. It can be determined exactly and one can sample from it. Exact counting, as well as sampling from the exact distribution, has only a practical drawback. It is computationally more intensive and more time-consuming compared to some of the approximate approaches mentioned. The MCMC procedure by Verhelst [17] seems to be the most efficient algorithm up to date [20]. Verhelst’s so-called Rasch Sampler is also easily accessible as an R package [40].
As far as the necessary computations in the present work are concerned, the conditional distribution (4), size, and power of the tests can be approximated to a sufficient degree by using the Rasch Sampler. For this, the matrices in , , and are simply replaced by the respective matrices randomly drawn. In particular, the test statistic is computed from each of the matrices drawn. The observed distribution of the test statistic over all matrices then serves as an approximation of the exact conditional distribution (4) when the hypothesis (5) is true. For the computations of the test statistics LR, W, RS, and G, the R package tcl [41] can be used. Note that this package uses a conditional likelihood which, unlike in the present case, is obtained from conditioning only on (row sums of ). The choice of tcl has merely practical reasons since the routines are readily available. Nonetheless, the exact sampling distribution of the test statistics is determined from (4) and approximated using the Rasch Sampler.
4. Design
A number of typical scenarios concerning sample size n and item number k are investigated to illustrate the performance of the bootstrap tests described in Section 2.2 This includes illustrations of power function and bias of the tests. The objective is primarily to get an idea of the reduction of the power of the tests in small samples and data with low information, respectively. The following scenarios of small sample sizes are considered: 10, 15, 20, 25, 30, and 50. The numbers of items considered are 6, 8, 10, 12, 14 16, 18, 20, 25, and 30. In all scenarios, the person covariate is considered to be binary. When the sample size is even, the two groups of persons are of equal size. In the case of n being odd, one of the two groups is greater by 1, e.g., 7 vs. 8 when .
The data scenarios to be investigated are generated using (1) with . The person parameters are drawn randomly from the standard normal distribution in each scenario. The item parameters are chosen from the interval −1 to 1. Note that this range may be too narrow. In most applications, true item parameters are likely to be of a broader range. The reason for not using a broader interval is to avoid sum scores of the items, i.e., column sums of , of either 0 (no person responding correctly) or n (all persons responding correctly). The information in the sample becomes extremely low for more extreme true parameters (i.e., farther from 0) or, in other words, when the data are sparse. In small samples, items with more extreme true parameters are pretty likely to yield either a sum score of 0 or n. In such a case, the responses to the respective item do not contain any information at all. To include all items in the analysis, one has to make sure that the sum scores are greater than 0 and smaller than n. To make sure to investigate realistic data scenarios and to consider different degrees of sparsity in the data, the design considers items with extreme sum scores, i.e., near 0 or n, as well as items with sum scores in the middle of the possible range, i.e., near . Additional requirements for the data (to be informative) given by Fischer [42] have also been considered. Matrices not meeting these requirements have been excluded and replaced by new appropriate matrices.
Once a matrix of binary responses has been generated for each combination of sample size and item number scenario to be considered, it has been used as the input matrix (initial matrix) for Verhelst’s MCMC approach and the respective R package [40]. In every scenario, i.e., for every input matrix, 10,000 matrices with the same row and column sums as the respective input matrix have been drawn to approximate the conditional distribution (4) and the power function (10) of each of the six tests to be considered. Note that the R package [40] restricts the total number of draws to = 8191 but it can be extended. In the present work, drawing matrices has been continued until 10,000 matrices have been obtained.
An R package with all the source codes to carry out all necessary computations can be downloaded from https://github.com/akurz1/tclboot/, accessed on 31 August 2021.
5. Results
For the presentation of results and performance of the tests, respectively, the conditional power function given by (10) is considered. It is suitable for evaluating the tests with respect to a potential bias and power. Note that for a test to be unbiased its power function must be when the hypothesis (5) is true, and it must be when the alternative (6) is true. The complete conditional power (10) is a function of multiple parameters (when ). Therefore, the diagrams to be presented in the sequel display the power curves as a function of one parameter at a time while all respective others are set to 0. Thus, they only show the local power of the tests.
In general, the results can be summed up as follows. As expected from basic theory on inferential statistics, the power of the tests increases with an increasing deviation of the parameters from 0. The smaller the sample size, the lower the power becomes in general. In some scenarios not quite desirable results have been observed, meaning that the local power of the tests does not converge to 1 when only one parameter tends away from 0. Practically speaking, regardless of how much a single item is violating the invariance assumption, the power of the test is stagnating (when the other items are not violating the invariance assumption). Such a scenario occurs more frequently when the sample size is small and the respective item is extreme, i.e., when its sum score is near 0 or n, in other words, when the data are sparse. Concerning bias of the tests, similar results have been observed. A bias occurs more frequently when the sample size is small and items are extreme. The complete results, tables, and plots can be obtained from https://github.com/akurz1/tclboot/, accessed on 31 August 2021. In the following, only a few examples are presented.
In Figure 1 and Figure 2 it can be seen that the local power values are higher with respect to moderate items (with a sum score in the middle of the range of possible values) than extreme items (with a sum score near 0 or n) which is expected from theory. Note that regarding an extreme item the range of possible values of the respective T statistic is limited, relative to a moderate item. The T statistic is sufficient for the respective parameter. Thus, if the range of possible values of the T statistic is small, the information in the sample concerning the respective parameter will also be small, accounting for the low local power of the test.
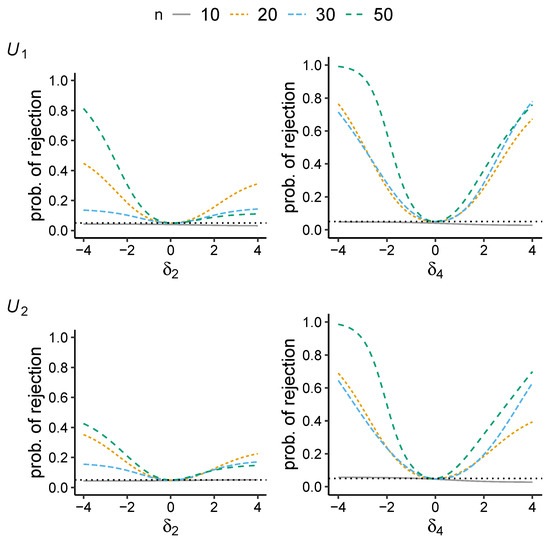
Figure 1.
Local power curve for tests and and sample sizes . Power curve displayed as a function of (item 2, an extreme item) and (item 4, a moderate item). The nominal level is set to 0.05 (dotted horizontal line).
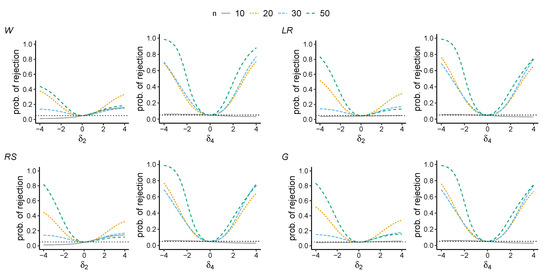
Figure 2.
Local power curve for tests and G and sample sizes . Power curve displayed as a function of (item 2, an extreme item) and (item 4, a moderate item). The nominal level is set to 0.05 (dotted horizontal line).
The examples shown in Figure 1 and Figure 2 also seem to reveal a counterintuitive result at first glance. It can be seen that the local power curves are mostly lower for (sometimes even for ) than , in particular, the local power as a function of which refers to item 2. Such a result may reasonably be explained by the degree of sparsity in the data. On closer inspection of the input matrices (that have been used to sample the 10,000 matrices), it turns out that the input matrix used in the example where (and also ) has more extreme column sum scores than the input matrix used for the case . This is specifically true for item 2. Thus, the information is lower and the degree of sparsity is higher in the data example where (and ). Despite the larger sample size, this accounts for the lower power.
In scenarios of very small sample sizes like , the local power curves are typically relatively flat. In such cases, the power only rarely converges to 1 when the respective parameter tends away from 0, in particular, with respect to extreme items. In Figure 1 and Figure 2 one can see typical examples. Thus, in these cases, the information in the sample seems to be too low. Acceptable power values can barely be achieved. Figure 1 and Figure 2 also show that the tests are (severely) biased in scenarios of . The probability of rejection drops below for some (sets of) values of the respective parameter .
As far as the comparison of the six test statistics is concerned it seems difficult to make definitive statements. The results show a mixed picture. In some scenarios some tests perform better than others in terms of bias and power, in other scenarios the same tests are worse.
6. Examples of Modifications of the Tests
The following remarks and suggestions are of a more heuristic, searching, and tentative character. To investigate possibilities to improve the power of the tests one may subject the critical region C to critical scrutiny. Recall that C has been chosen to consist of the 100 percent largest values of the respective test statistic.
Consider the following example shown in Figure 3. It shows the local power (fully-drawn curve) of a test based on the statistic as a function of , where all other parameters are set to 0. The critical region of this test consists of the 100 percent largest values of that are obtained from the 10,000 samples drawn, where . As can be seen in Figure 3 the local power of the test does not seem to converge to 1 for increasing . It seems to tend to a value between and . On closer inspection of the critical region of this test, one reveals that it does barely contain matrices yielding a value of the sufficient statistic for which is in the upper range of possible values. The range of possible values of , i.e., values with probability >0, are the integers from 2 to 10. The critical region does barely contain matrices for which is 9 or 10.
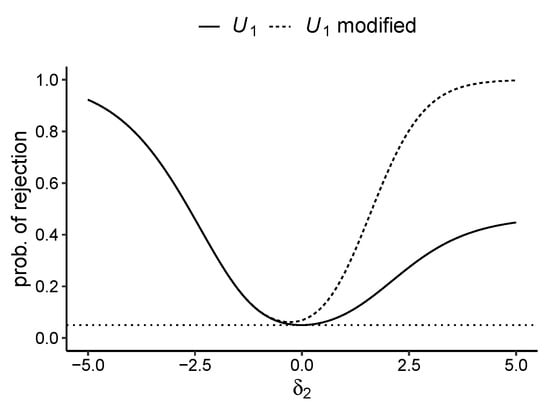
Figure 3.
Local power curve for the test and its modified version referring to an extreme item in a scenario with sample size n = 30 and number of items k = 10. The nominal level of is set to 0.05 (dotted horizontal line).
This is an obvious reason for the power function not to increase locally with increasing values (as can be seen in the diagram) since, in particular, the matrices with values of being in the upper range are those matrices that become more probable when is increased. Hence, one may suggest a modification of the critical region to improve the local power of the test by adding matrices to the critical region for which yields a value in the upper range, e.g., 9 and 10. Such a modification improves the local power of the test as can be seen by the dotted curve in Figure 3. The price of this improvement is an increase of the probability of the error of the first kind from 0.05 to 0.069 in the present case and a bias of the test, respectively. The bias is noticeable in Figure 3. The dotted curve shows that the power drops below the power at when is slightly negative.
To avoid too much of an increase of the probability of the error of the first kind , one may also consider removing matrices yielding values of being somewhere in the middle of the range of possible values from the critical region (as a compensation), in order to reduce again. Further, one may also have to take into account that an improvement of local power in the case of a particular parameter (or item) may yield a decrease in local power elsewhere in the parameter space, i.e., concerning another parameter (another item). Nonetheless, such a modification can be worthwhile, in particular, when a great improvement of power is achieved compared to a relatively small increase of and only a slight bias of the test. Of course, this will have to be evaluated in each specific case in practice.
Finally, Figure 4 shows an example of modifying the local power in respect of every free parameter (every item) in a scenario with and . This example involves adding matrices with the respective T statistic from both the lower and upper range for every item. In particular, denote by the -quantile and by the -quantile of the conditional distribution of given by (7). The modification procedure makes sure that the critical region C of the test contains all matrices that satisfy and for all free T statistics and parameters (for all items), respectively. For the determination of these quantiles, has been set to a lower value of to avoid too much of an increase beyond the desired level of . As can be seen in Figure 4, the improvement of the local power values is impressive regarding all items. The bias can also be kept limited, except for item 1.
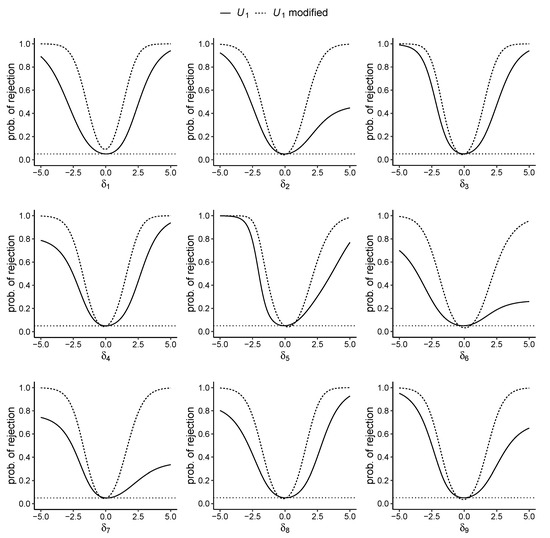
Figure 4.
Local power curve for the test and its modified version referring to all (free) items in a scenario with sample size n = 30 and number of items k = 10. The dotted horizontal line represents the desired level of .
7. Final Remarks
The non-parametric resampling approach that is applied in this paper [17,22] is easily accessible and applicable to problems of testing multiparameter hypotheses in the Rasch modeling framework. The sampling distribution of any suitable test statistic can be approximated in this way. Therefore, such an approach provides a good and practical alternative to asymptotic (large sample) procedures in case of small sample size and sparse data scenarios. Nonetheless, statistical tests do not have to be satisfactory in terms of basic properties such as bias and power, which is frequently the case in very small samples. Therefore, one of the objectives of this paper is to raise awareness of these problems and to point at possible improvements to the tests. These suggestions provide by no means definite solutions and shall rather be considered from a heuristic perspective. These attempts to improve the power of the tests may work satisfactorily in some cases, in others they may not. Of course, this has to be evaluated in each specific practical context on its own. For this purpose, an R package has additionally been developed to provide the necessary tools for applied researchers.
The procedures of testing hypotheses or assumptions of the Rasch model described in the present paper refer only to the invariance assumption of item parameters. These can be extended in many ways. For instance, if a binary person covariate is used, which divides the sample into two groups, where one group consists of persons with a low value of (low value of the row sum) and the other of persons with a high value, the alternative hypothesis given by (6) will basically be equivalent to assuming different discriminations of the items (e.g., [43,44]). Another example has been discussed by Draxler and Dahm [21], in which the influence of the average response time per item on the unidimensionality assumption of person parameters in the Rasch model has been investigated. Further examples of different tests have been discussed by Ponocny [15] and Draxler and Zessin [19].
Author Contributions
All authors contributed equally to the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
An R package with all source codes and simulation data to carry out all necessary computations can be downloaded from https://github.com/akurz1/tclboot/, accessed on 31 August 2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rodgers, J.L. The Bootstrap, the Jackknife, and the Randomization Test: A Sampling Taxonomy. Multivar. Behav. Res. 1999, 34, 441–456. [Google Scholar] [CrossRef]
- Quenouille, M.H. Notes on bias in estimation. Biometrika 1956, 43, 353–360. [Google Scholar] [CrossRef]
- Tukey, J. Bias and confidence in not quite large samples. Ann. Math. Stat. 1958, 29, 614. [Google Scholar]
- Efron, B. The 1977 RIETZ lecture: Bootstrap Methods. Ann. Stat. 1979, 7, 1–26. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Springer: New York, NY, USA, 1993. [Google Scholar]
- Romano, J.P.; Shaikh, A.M.; Wolf, M. Hypothesis Testing in Econometrics. Annu. Rev. Econ. 2010, 2, 75–104. [Google Scholar] [CrossRef] [Green Version]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Chernick, M.R. Bootstrap Methods: A Guide for Practitioners and Researchers, 2nd ed.; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Chernick, M.R.; LaBudde, R.A. An Introduction to Bootstrap Methods with Applications to R; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; Danish Institute for Educational Research: Kopenhagen, Demark, 1960. [Google Scholar]
- Fischer, G.H.; Molenaar, I.W. Rasch Models: Foundations, Recent Developments, and Applications; Springer: New York, NY, USA, 1995. [Google Scholar]
- Davier, M.V. Bootstrapping goodness-of-fit statistics for sparse categorical data: Results of a Monte Carlo study. Methods Psychol. Res. Online 1997, 2, 29–48. [Google Scholar]
- Heene, M.; Draxler, C.; Ziegler, M.; Bühner, M. Performance of the bootstrap Rasch model test under violations of non-intersecting item response functions. Psychol. Test Assess. Model. 2011, 53, 283–294. [Google Scholar]
- Alexandrowicz, R.W.; Draxler, C. Testing the Rasch model with the conditional likelihood ratio test: Sample size requirements and bootstrap algorithms. J. Stat. Distrib. Appl. 2016, 3, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Ponocny, I. Nonparametric goodness-of-fit tests for the Rasch model. Psychometrika 2001, 66, 437–459. [Google Scholar] [CrossRef]
- Chen, Y.; Small, D. Exact Tests for the Rasch Model via Sequential Importance Sampling. Psychometrika 2005, 70, 11–30. [Google Scholar] [CrossRef]
- Verhelst, N.D. An efficient MCMC algorithm to sample binary matrices with fixed marginals. Psychometrika 2008, 73, 705–728. [Google Scholar] [CrossRef]
- Miller, J.W.; Harrison, M.T. Exact sampling and counting for fixed-margin matrices. Ann. Stat. 2013, 41, 1569–1592. [Google Scholar] [CrossRef] [Green Version]
- Draxler, C.; Zessin, J. The power function of conditional tests of the Rasch model. AStA Adv. Stat. Anal. 2015, 99, 367–378. [Google Scholar] [CrossRef]
- Draxler, C.; Nolte, J.P. Computational Precision of the Power Function for Conditional Tests of Assumptions of the Rasch Model. Open J. Stat. 2018, 8, 873. [Google Scholar] [CrossRef] [Green Version]
- Draxler, C.; Dahm, S. Conditional or Pseudo Exact Tests with an Application in the Context of Modeling Response Times. Psych 2020, 2, 17. [Google Scholar] [CrossRef]
- Verhelst, N.D.; Hatzinger, R.; Mair, P. The Rasch Sampler. J. Stat. Softw. 2007, 20, 1–14. [Google Scholar] [CrossRef]
- Lehmann, E.L.; Romano, J.P. Testing Statistical Hypotheses, 3rd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Draxler, C. A Note on a Discrete Probability Distribution Derived from the Rasch Model. Adv. Appl. Stat. Sci. 2011, 6, 665–673. [Google Scholar]
- Agresti, A. Categorical Data Analysis, 3rd ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Neyman, J.; Pearson, E.S. On the Use and Interpretation of certain test criteria for purposes of statistical inference. Biometrika 1928, 20, 263–294. [Google Scholar]
- Wilks, S.S. The large-sample distribution of the likelihood ratio for testing composite hypotheses. Ann. Math. Stat. 1938, 9, 60–62. [Google Scholar] [CrossRef]
- Wald, A. Tests of statistical hypotheses concerning several parameters when the number of observations is large. Trans. Am. Math. Soc. 1943, 54, 426–482. [Google Scholar] [CrossRef]
- Rao, C.R. Large sample tests of statistical hypotheses concerning several parameters with applications to problems of estimation. Math. Proc. Camb. Philos. 1948, 44, 50–57. [Google Scholar]
- Silvey, S.D. The lagrangian multiplier test. Ann. Math. Stat. 1959, 30, 389–407. [Google Scholar] [CrossRef]
- Terrell, G.R. The gradient statistic. Comput. Sci. Stat. 2002, 34, 206–215. [Google Scholar]
- Lemonte, A.J. The Gradient Test. Another Likelihood-Based Test; Academic Press: London, UK, 2016; ISBN 978-0-12-803596-2. [Google Scholar]
- Draxler, C.; Kurz, A.; Lemonte, A.J. The gradient test and its finite sample size properties in a conditional maximum likelihood and psychometric modeling context. Commun. Stat. Simul. Comput. 2020, 1–19. [Google Scholar] [CrossRef]
- Snijders, T.A.B. Enumeration and simulation methods for 0–1 matrices with given marginals. Psychometrika 1991, 56, 397–417. [Google Scholar] [CrossRef]
- Chen, Y.; Diaconis, P.; Holmes, S.P.; Liu, J.S. Sequential Monte Carlo Methods for Statistical Analysis of Tables. J. Am. Stat. Assoc. 1991, 100, 109–120. [Google Scholar] [CrossRef]
- Besag, J.; Clifford, P. Generalized Monte Carlo significance tests. Biometrika 1989, 76, 633–642. [Google Scholar] [CrossRef]
- Strona, G.; Nappo, D.; Boccacci, F.; Fattorini, S.; San-Miguel-Ayanz, J. A fast and unbiased procedure to randomize ecological binary matrices with fixed row and column totals. Nat. Commun. 2014, 5, 4114. [Google Scholar] [CrossRef]
- Carstens, C.J. Proof of uniform sampling of binary matrices with fixed row sums and column sums for the fast Curveball algorithm. Phys. Rev. E 2015, 91, 042812. [Google Scholar] [CrossRef]
- Rechner, S. Markov Chain Monte Carlo Algorithms for the Uniform Sampling of Combinatorial Objects. Ph.D. Thesis, Martin-Luther-Universität Halle-Wittenberg, Halle, Germany, 2018. [Google Scholar] [CrossRef]
- Mair, P.; Hatzinger, R. Extended Rasch modeling: The eRm package for the application of IRT models in R. J. Stat. Softw. 2007, 20, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Draxler, C.; Kurz, A. Tcl: Testing in Conditional Likelihood Context, R Package Version 0.1.1; 2021. Available online: https://CRAN.R-project.org/package=tcl (accessed on 31 August 2021).
- Fischer, G.H. On the existence and uniqueness of maximum-likelihood estimates in the Rasch model. Psychometrika 1981, 46, 59–77. [Google Scholar] [CrossRef]
- Glas, C.A.W.; Verhelst, N.D. Testing the Rasch Model; Springer: New York, NY, USA, 1995; pp. 69–95. [Google Scholar]
- Draxler, C.; Alexandrowicz, R.W. Sample size determination within the scope of conditional maximum likelihood estimation with special focus on testing the Rasch model. Psychometrika 2015, 80, 897–919. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).