Evaluating the Performance of Multiple Imputation Methods for Handling Missing Values in Time Series Data: A Study Focused on East Africa, Soil-Carbonate-Stable Isotope Data
Abstract
1. Introduction
2. Review of SSA
- Set suitable initial values in place of missing data (e.g., mean of the non missing data).
- Choose reasonable values of window length (L) and the number of leading eigentriples (r).
- Reconstruct the time series where its missing data are replaced with initial values.
- Replace the values of time series at missing locations with their reconstructed values.
- Reconstruct the time series.
- Repeat steps 4 and 5 until the maximum absolute value of the difference between consecutive replaced values of the time series by their reconstructed value is less than ( is the convergence threshold and is a small positive number).
- Consider the final values replaced to be the imputed values.
3. Other Imputation Methods
- Interpolation: linear, spline and Stineman interpolation.
- Kalman smoothing (ARIMA): the Kalman smoothing on the state space representation of an ARIMA model.
- Kalman smoothing (StructTS): the Kalman smoothing on structural time series models fitted by maximum likelihood.
- Last observation carried forward (LOCF): each missing value is replaced with the most recent present value prior to it.
- Next observation carried backward (NOCB): the LOCF is done from the reverse direction, starting from the back of the series.
- Weighted moving average: Missing values are replaced by weighted moving average values. The average in this implementation is taken from an equal number of observations on either side of a missing value. For example, to impute a missing value at location i, the observations are used to calculate the mean for moving average window size 4 (2 left and 2 right). Whenever all observations in the current window are not available (NA), the window size is incrementally increased until there are at least 2 non-NA values present. The weighted moving average is used in the following three ways:
- Simple moving average (SMA): all observations in the moving average window are equally weighted for calculating the mean.
- Linear weighted moving average (LWMA): Weights decrease in arithmetical progression. The observations directly next to the ith missing value () have weight 1/2, the observations one further away () have weight 1/3, the next have weight 1/4 and so on. This method is the variation of inverse distance weighting.
- Exponential weighted moving average (EWMA): Weights decrease exponentially. The observations directly next to the ith missing value have weight , the observations one further away have weight , the next have weight and so on. This method is also the variation of inverse distance weighting.
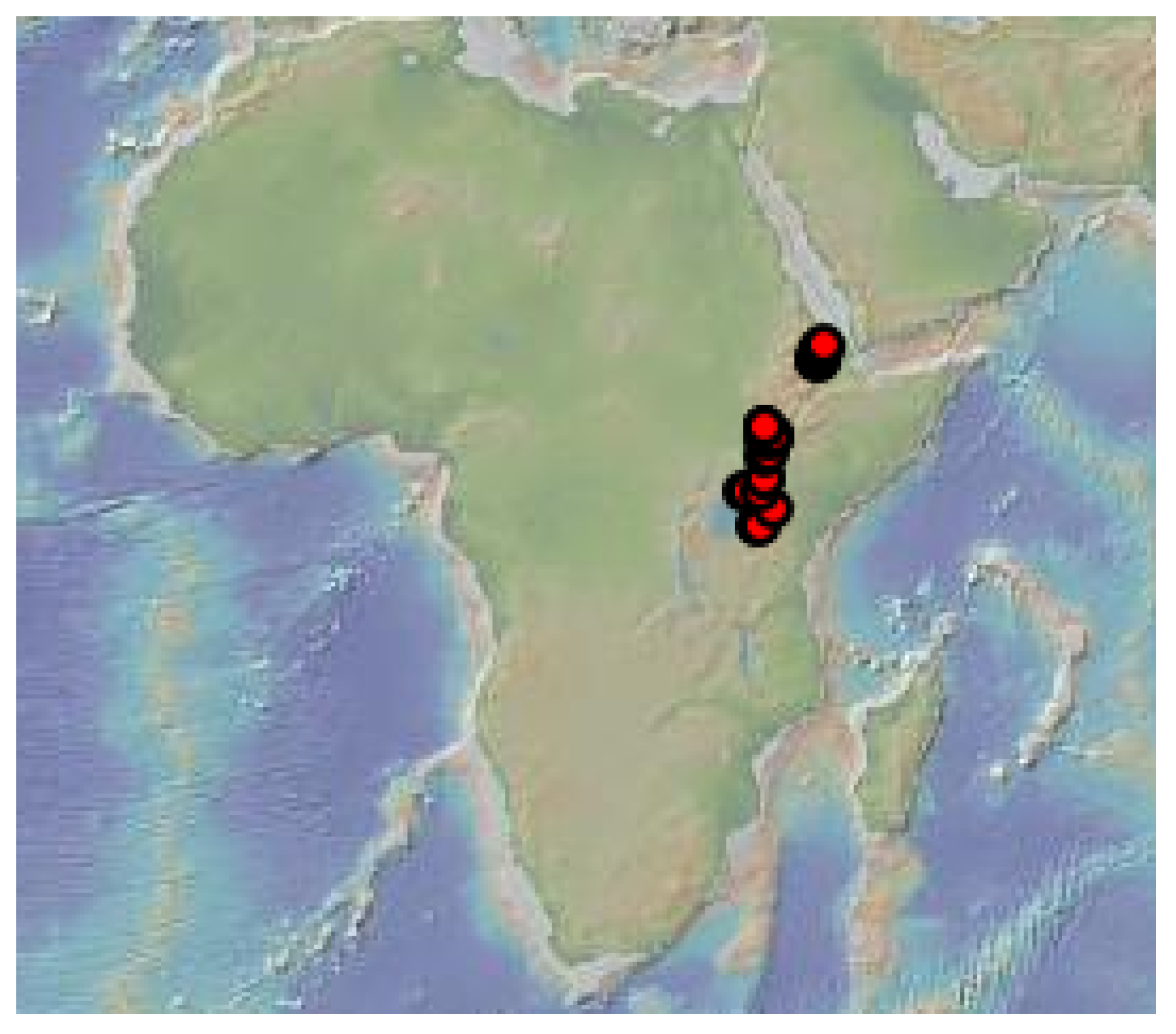
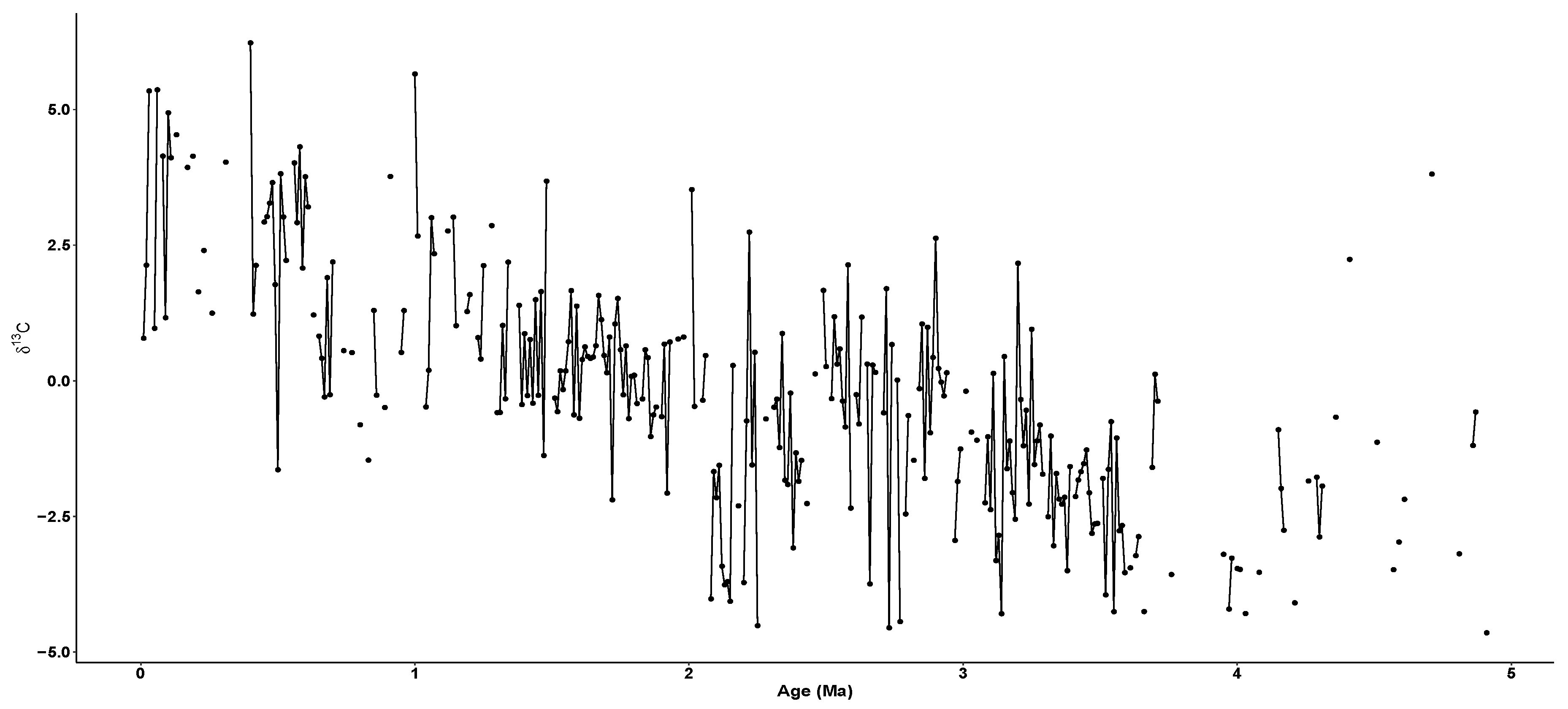
4. Data
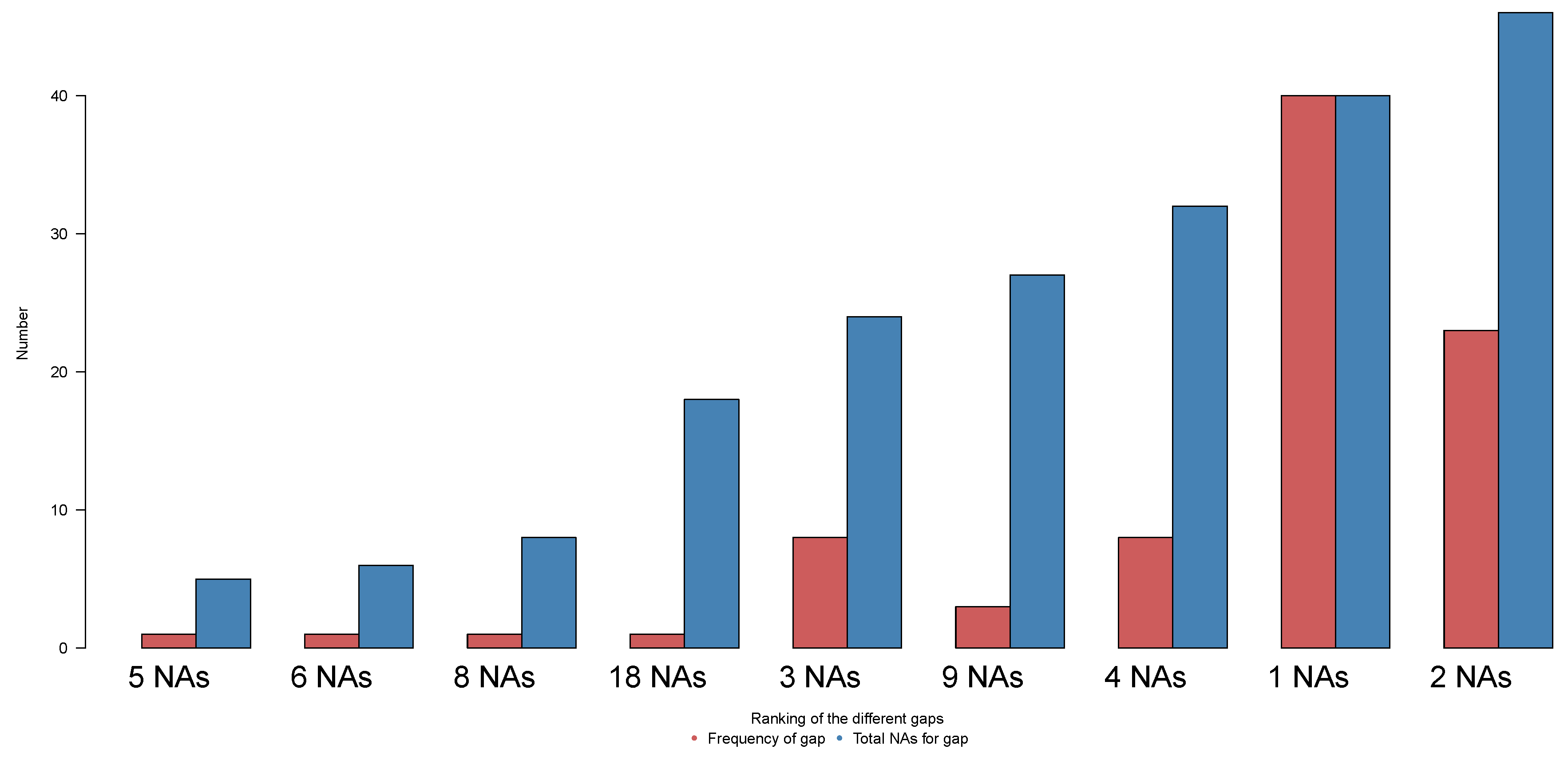
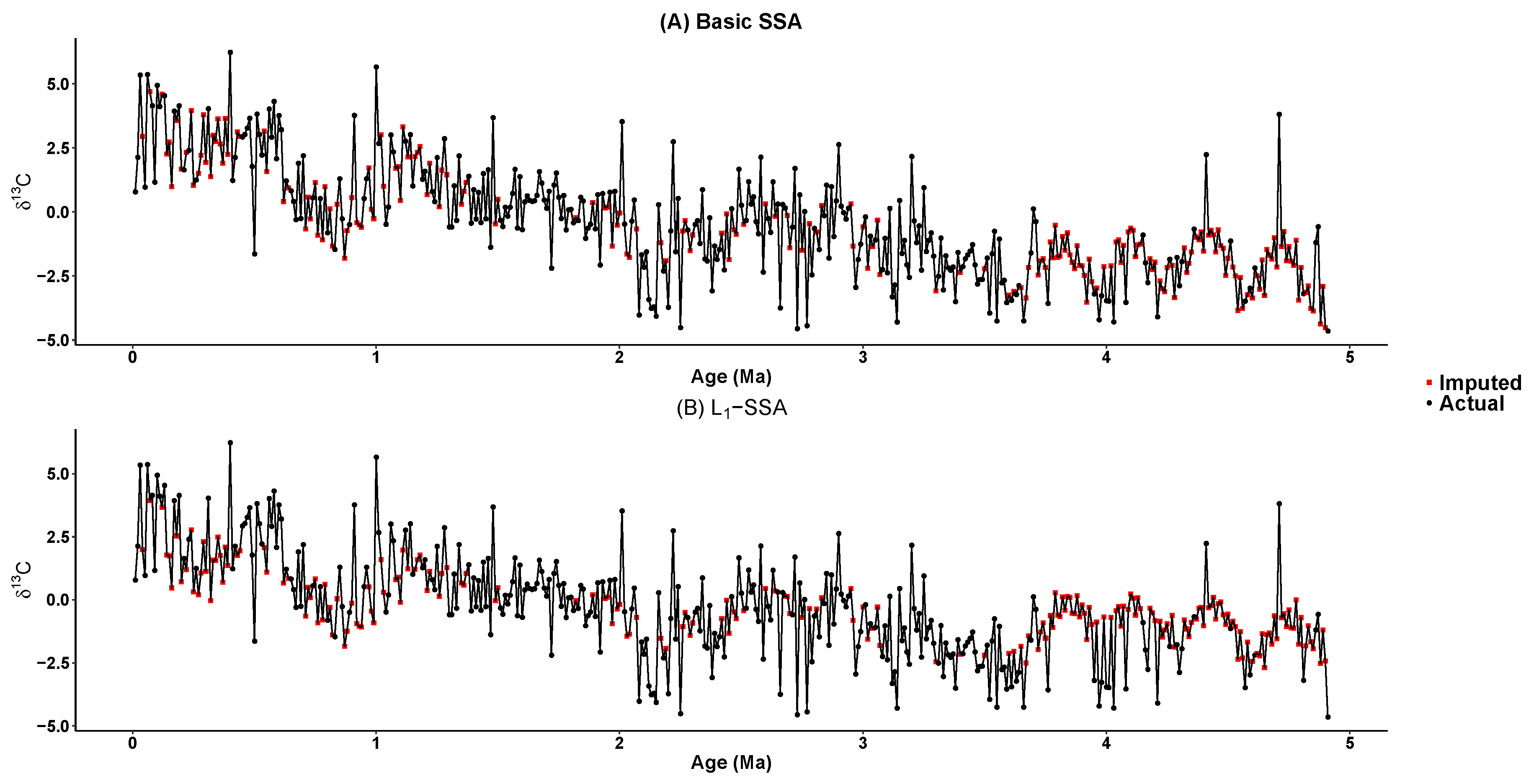
5. Imputing Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SSA | singular spectrum analysis |
| SVD | singular value decomposition |
| NA | not available |
| ARIMA | autoregressive integrated moving average |
| LOCF | last observation carried forward |
| NOCB | next observation carried backward |
| SMA | simple moving average |
| LWMA | linear weighted moving average |
| EWMA | exponential weighted moving average |
References
- Kossinets, G. Effects of missing data in social networks. Soc. Netw. 2006, 28, 247–268. [Google Scholar] [CrossRef]
- Donders, A.R.T.; Van Der Heijden, G.J.; Stijnen, T.; Moons, K.G. A gentle introduction to imputation of missing values. J. Clin. Epidemiol. 2006, 59, 1087–1091. [Google Scholar] [CrossRef] [PubMed]
- Montanari, A.; Mignani, S. Notes on the bias of dissimilarity indices for incomplete data sets: The case of archaelogical classification. Qüestiió Quaderns D’EstadíStica i Investigació Operativa 1994, 18, 39–49. [Google Scholar]
- Levin, N.E. Compilation of East Africa Soil Carbonate Stable Isotope Data. In Interdisciplinary Earth Data Alliance (IEDA); 2013; Available online: http://dx.doi.org/10.1594/IEDA/100231 (accessed on 2 November 2018).
- Holliday, V.T.; Gartner, W.G. Methods of soil P analysis in archaeology. J. Archaeol. Sci. 2007, 34, 301–333. [Google Scholar] [CrossRef]
- Guillerme, T.; Cooper, N. Effects of missing data on topological inference using a Total Evidence approach. Mol. Phylogenet. Evol. 2016, 94, 146–158. [Google Scholar] [CrossRef] [PubMed]
- Manos, P.S.; Soltis, P.S.; Soltis, D.E.; Manchester, S.R.; Oh, S.H.; Bell, C.D.; Dilcher, D.L.; Stone, D.E. Phylogeny of extant and fossil Juglandaceae inferred from the integration of molecular and morphological data sets. Syst. Biol. 2007, 56, 412–430. [Google Scholar] [CrossRef] [PubMed]
- Kalantari, M.; Yarmohammadi, M.; Hassani, H. Singular Spectrum Analysis Based on L1-norm. Fluct. Noise Lett. 2016, 15, 1650009. [Google Scholar] [CrossRef]
- Kwak, N. Principal component analysis based on L1-norm maximization. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1672–1680. [Google Scholar] [CrossRef] [PubMed]
- Silva, E.S.; Hassani, H. On the use of singular spectrum analysis for forecasting U.S. trade before, during and after the 2008 recession. Int. Econ. 2015, 141, 34–49. [Google Scholar] [CrossRef]
- Kondrashov, D.; Ghil, M. Spatio-temporal filling of missing points in geophysical data sets. Nonlinear Process. Geophys. 2006, 13, 151–159. [Google Scholar] [CrossRef]
- Korobeynikov, A. Computation- and space-efficient implementation of SSA. Stat. Interface 2010, 3, 257–368. [Google Scholar] [CrossRef]
- Golyandina, N.; Korobeynikov, A. Basic Singular Spectrum Analysis and forecasting with R. Comput. Stat. Data Anal. 2014, 71, 934–954. [Google Scholar] [CrossRef]
- Golyandina, N.; Korobeynikov, A.; Shlemov, A.; Usevich, K. Multivariate and 2D Extensions of Singular Spectrum Analysis with the Rssa Package. J. Stat. Softw. 2015, 67, 1–78. [Google Scholar] [CrossRef]
- Moritz, S.; Bartz-Beielstein, T. imputeTS: Time Series Missing Value Imputation in R. R J. 2017, 9, 207–218. [Google Scholar] [CrossRef]
- Moritz, S. imputeTS: Time Series Missing Value Imputation. R Package Version 3. 2019. Available online: https://CRAN.R-project.org/package=imputeTS (accessed on 15 October 2019).
- Harmand, S.; Lewis, J.E.; Feibel, C.S.; Lepre, C.J.; Prat, S.; Lenoble, A.; Taylor, N. 3.3-million-year-old stone tools from Lomekwi 3, West Turkana, Kenya. Nature 2015, 521, 310–315. [Google Scholar] [CrossRef] [PubMed]
- Antón, S.C.; Potts, R.; Aiello, L.C. Evolution of early Homo: An integrated biological perspective. Science 2014, 345, 1236828. [Google Scholar] [CrossRef] [PubMed]
- Lister, A.M. The role of behaviour in adaptive morphological evolution of African proboscideans. Nature 2013, 500, 331–334. [Google Scholar] [CrossRef] [PubMed]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A. Analysis of Time Series Structure: SSA and Related Techniques; Chapman & Hall/CRC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series; Springer Briefs in Statistics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Golyandina, N.; Korobeynikov, A.; Zhigljavsky, A. Singular Spectrum Analysis with R; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Hassani, H.; Yeganegi, M.R.; Silva, E.S. A New Signal Processing Approach for Discrimination of EEG Recordings. Stats 2018, 1, 11. [Google Scholar] [CrossRef]
- Ghodsi, Z.; Silva, E.S.; Hassani, H. Bicoid Signal Extraction with a Selection of Parametric and Nonparametric Signal Processing Techniques. Genom. Proteom. Bioinform. 2015, 13, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Hassani, H.; Silva, E.S.; Gupta, R.; Segnon, M.K. Forecasting the price of gold. Appl. Econ. 2015, 47, 4141–4152. [Google Scholar] [CrossRef]
- Sanei, S.; Hassani, H. Singular Spectrum Analysis of Biomedical Signals; Taylor & Francis, CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
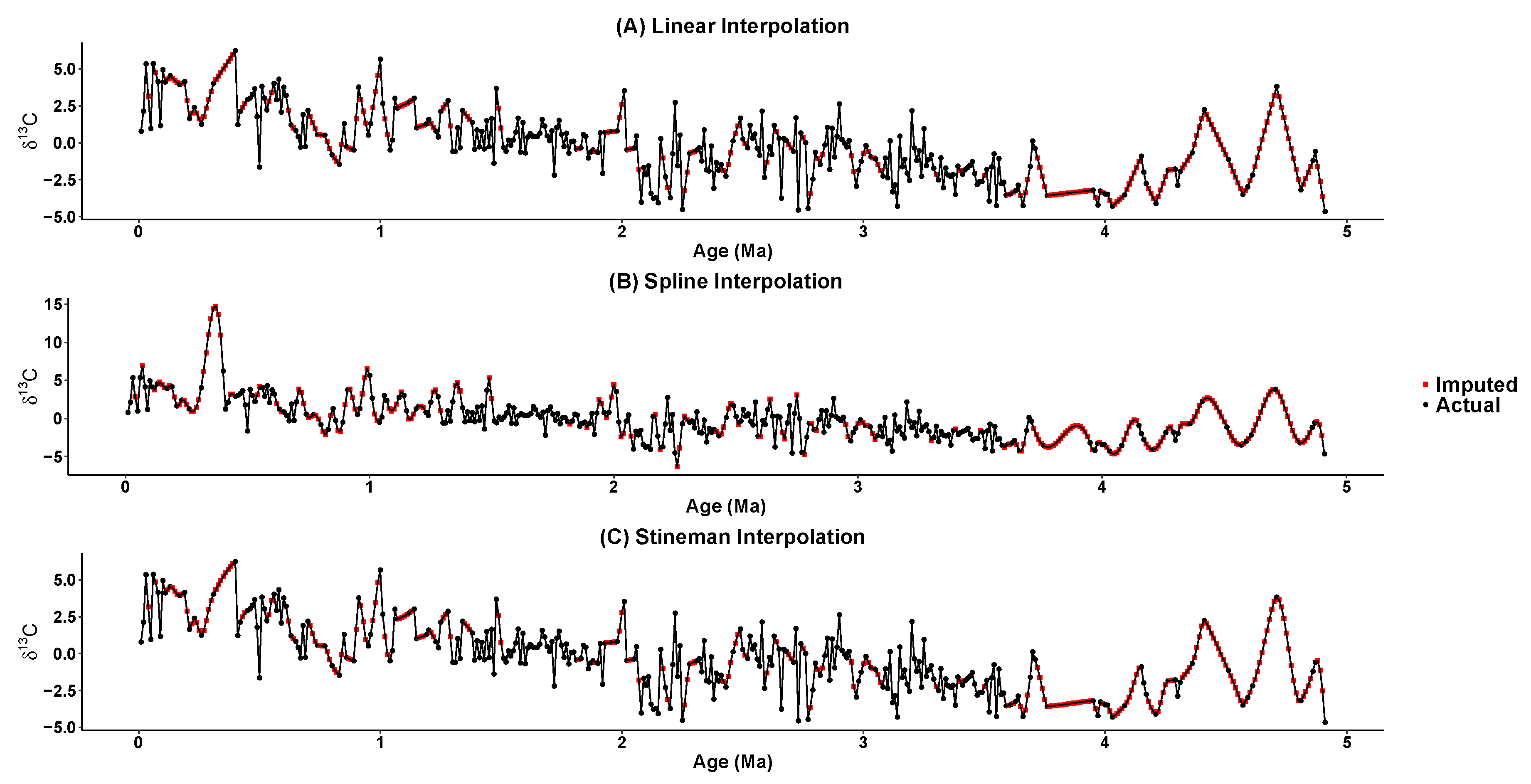

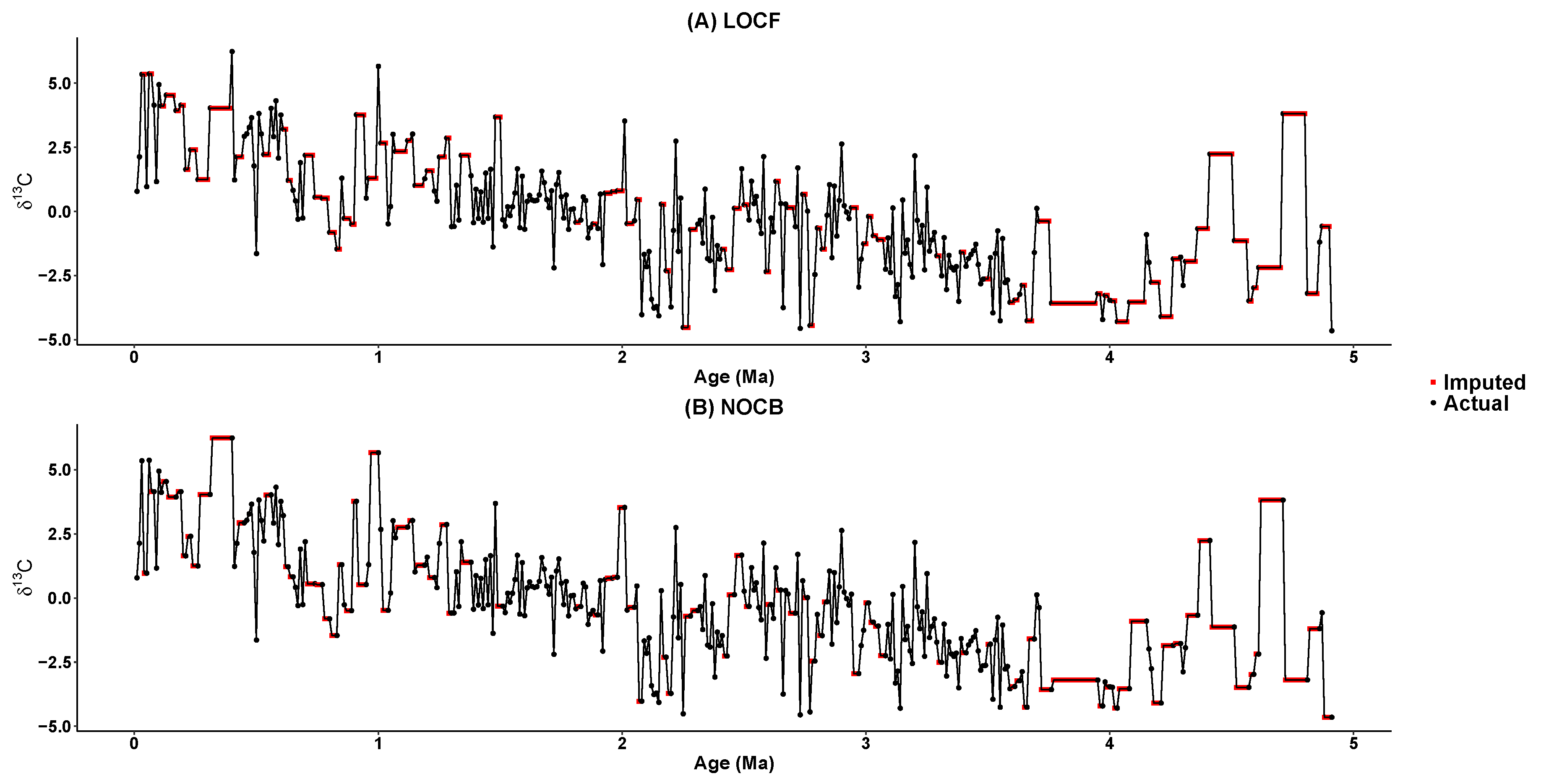
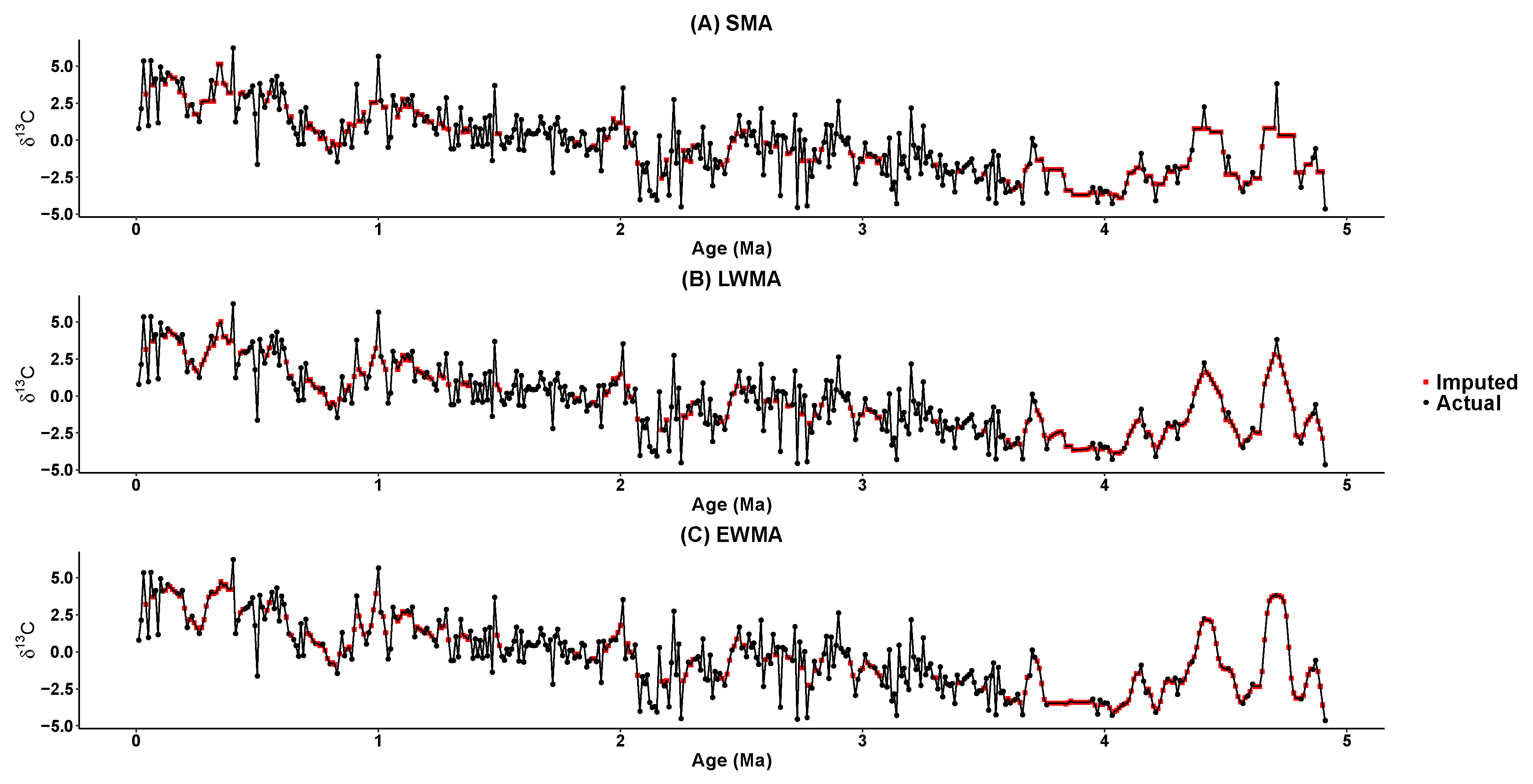
| Time Series | Mean | Standard Deviation | Median | Skewness | Kurtosis |
|---|---|---|---|---|---|
| Original | −0.25 | 2.21 | −0.33 | 0.30 | −0.18 |
| Basic SSA | −0.43 | 2.10 | −0.63 | 0.45 | −0.15 |
| -SSA | −0.29 | 1.85 | −0.39 | 0.40 | 0.57 |
| Linear Interpolation | −0.23 | 2.34 | −0.37 | 0.32 | −0.49 |
| Spline Interpolation | −0.04 | 2.85 | −0.34 | 1.35 | 4.36 |
| Stineman Interpolation | −0.23 | 2.36 | −0.38 | 0.33 | −0.48 |
| Kalman (ARIMA) | −0.28 | 2.14 | −0.35 | 0.31 | −0.40 |
| Kalman (StructTS) | −0.35 | 2.09 | −0.62 | 0.38 | −0.34 |
| LOCF | −0.23 | 2.43 | −0.36 | 0.21 | −0.72 |
| NOCB | −0.24 | 2.51 | −0.48 | 0.47 | −0.32 |
| SMA | −0.29 | 2.19 | −0.34 | 0.30 | −0.42 |
| LWMA | −0.27 | 2.24 | −0.36 | 0.28 | −0.54 |
| EWMA | −0.26 | 2.32 | −0.38 | 0.28 | −0.64 |
| Imputing | Percent of Missing Values | |||
|---|---|---|---|---|
| Method | 10% | 20% | 30% | 40% |
| Basic SSA | 1.12 | 1.15 | 1.20 | 1.24 |
| -SSA | 1.11 | 1.13 | 1.17 | 1.22 |
| Linear Interpolation | 1.37 | 1.38 | 1.43 | 1.48 |
| Spline Interpolation | 1.87 | 2.16 | 2.57 | 3.18 |
| Stineman Interpolation | 1.39 | 1.43 | 1.48 | 1.56 |
| Kalman (ARIMA) | 1.11 | 1.13 | 1.19 | 1.25 |
| Kalman (StructTS) | 1.22 | 1.25 | 1.27 | 1.29 |
| LOCF | 2.56 | 2.66 | 2.76 | 2.90 |
| NOCB | 2.53 | 2.68 | 2.77 | 2.92 |
| SMA | 1.21 | 1.24 | 1.27 | 1.33 |
| LWMA | 1.18 | 1.21 | 1.25 | 1.31 |
| EWMA | 1.23 | 1.26 | 1.31 | 1.38 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassani, H.; Kalantari, M.; Ghodsi, Z. Evaluating the Performance of Multiple Imputation Methods for Handling Missing Values in Time Series Data: A Study Focused on East Africa, Soil-Carbonate-Stable Isotope Data. Stats 2019, 2, 457-467. https://doi.org/10.3390/stats2040032
Hassani H, Kalantari M, Ghodsi Z. Evaluating the Performance of Multiple Imputation Methods for Handling Missing Values in Time Series Data: A Study Focused on East Africa, Soil-Carbonate-Stable Isotope Data. Stats. 2019; 2(4):457-467. https://doi.org/10.3390/stats2040032
Chicago/Turabian StyleHassani, Hossein, Mahdi Kalantari, and Zara Ghodsi. 2019. "Evaluating the Performance of Multiple Imputation Methods for Handling Missing Values in Time Series Data: A Study Focused on East Africa, Soil-Carbonate-Stable Isotope Data" Stats 2, no. 4: 457-467. https://doi.org/10.3390/stats2040032
APA StyleHassani, H., Kalantari, M., & Ghodsi, Z. (2019). Evaluating the Performance of Multiple Imputation Methods for Handling Missing Values in Time Series Data: A Study Focused on East Africa, Soil-Carbonate-Stable Isotope Data. Stats, 2(4), 457-467. https://doi.org/10.3390/stats2040032






