1. Introduction
One of the tasks statisticians face is extracting and possibly inferring biologically/clinically relevant information from published papers. This aspect of applied statistics is well developed, and one can choose to form many easy to use and performant algorithms that aid problem solving. Often, these algorithms aim to aid statisticians/practitioners to extract variability of different measures or biomarkers that is needed for power calculation and research design [
1,
2].
While these algorithms are efficient and easy to use, they mostly are not probabilistic in nature, thus they do not offer means for statistical inference. Yet another field of applied statistics that aims to help practitioners in extracting relevant information when only partial data is available propose a probabilistic approach with order statistics. This approach has a long history and special focus was/is paid for samples with censored observations [
3] or extremes [
4]. Arnold and collaborators [
5] offer a comprehensive overview or order statistics including how and when minimum and maximum of a sample may become sufficient statistic and some exact formulas and closed solution for the distribution of some order statistics.
The likelihood, the joint density of the observed data, is at the core of most statistical estimation and/or inference. Whereas formulation of the likelihood in most cases is based on complete samples there are situations when we observe only parts of the data. This could be due to censoring of different kind, or perhaps we do not have access at the full data but only at minimum and maximum values. Combination of the likelihood theory and order statistics is straightforward [
6].
Herein, we aim to investigate the performance of likelihood-based confidence intervals when only minimum–maximum and sample size is available. Using Monte Carlo simulations, we examine coverage and interval width for location parameters estimated form ranges. Additionally, we compare estimation and inference from ranges with estimation and inference based on full samples. Lastly, we examine if the effect of sample size on estimation and inference on ranges.
In the following, we give a brief background for likelihood, order statistics and likelihood for order statistics. Then outline the Monte Carlo simulation. Thereafter we list the results of the simulation, an illustrative application and conclude with a brief general discussion.
2. Likelihood and Order Statistics
We assume that each of the n iid random observations in the sample have probability mass function . In all cases the likelihood is the joint density of the observed data and
We aim to estimate the parameter that makes most probable, or most likely under the assumed probability mass function. Based on the likelihood function for the simple null-hypothesis of three test statistics can be formulated, the Wald (), score (), and likelihood ratio () statistics. These three test statistics are asymptotically equivalent and as , the test statistics converges in distribution to . Confidence regions for the parameter(s) of interest are given by which is a random set that contains the nonrandom true value with nominal probability of . Of the three alternative test statistics the Wald- statistics and the Wald (or approximate) confidence intervals are the most common. The Wald-statistics is estimated as . The Wald-interval is not invariant to the parametrization of the estimate of the interest.
The likelihood ratio statistic does not depend on model parametrization and the not necessary symmetric around the point estimate. The likelihood ratio statistic is given by .
For the confidence intervals based on the Wald statistics (or Score statistics in most cases) there are closed form solutions. The intervals derived from require numerical estimation. This is done on log scale , where is the log likelihood function
If we do not know the full
, but we only know
and
, the likelihood function and the test statistics cannot be calculated as described above. For iid continuous variables the distribution of the range is
where
is the cdf and
is the pdf of y. For simpler cases it is possible to obtain closed form solutions [
7]. However, this formulation can be rather unpractical with difficult optimization.
Glen [
8] offered a simpler solution, MLEOS, maximum likelihood estimation with order statistics defined as
, where K is the set of order statistic indices (in or case 1 and n) and
is the pdf for the order statistics. The pdf for the r
th order statistics is
We can obtain likelihood ratio statistics and confidence intervals by numerical optimization of MELOS. When full data is available, we can use closed form solutions for the Wald-statistics and approximate confidence intervals. It is possible to obtain exact formulas of the Information Matrix for MLEOS, however with considerable difficulty [
9] and this is not always needed as optimization routines return the value of the Hessian matrix at
.
3. Simulation Settings
We simulated a random variable
with sample sizes of 25, 50, 100, 500, and 1000. We assumed that the simulated
is iid following exponential and normal distribution. After simulating
with
we used maximum likelihood estimation to obtain likelihood ratio and Wald-type approximate confidence intervals. Thereafter we extracted
and
and used MELOS to obtain likelihood ratio and Wald-type approximate confidence intervals. Thereafter, we repeated the procedure 1000 times. For each iteration, we noted if the confidence interval covers the true parameter value and the width of the confidence interval. Assuming binomial distribution for the confidence interval coverage, we expect that the coverage should be within 1.96 standard errors of the nominal coverage probability. As we run 1000 simulations, we expect that the coverage should be between tolerance limits of 0.936 and 0.963 [
10].
For the normal distribution, we employed two types of estimation. First, we used MLEOS to estimate both mean and variance from the ranges. Second, we used the Wan-estimator to estimate the sample standard deviation from the ranges as
where
is the inverse function of standard normal distribution or equivalently, the upper
zth percentile of the standard normal distribution [
2]. All analyses were conducted in
R 3.5.1 [
11].
4. Results
4.1. Exponential Distribution
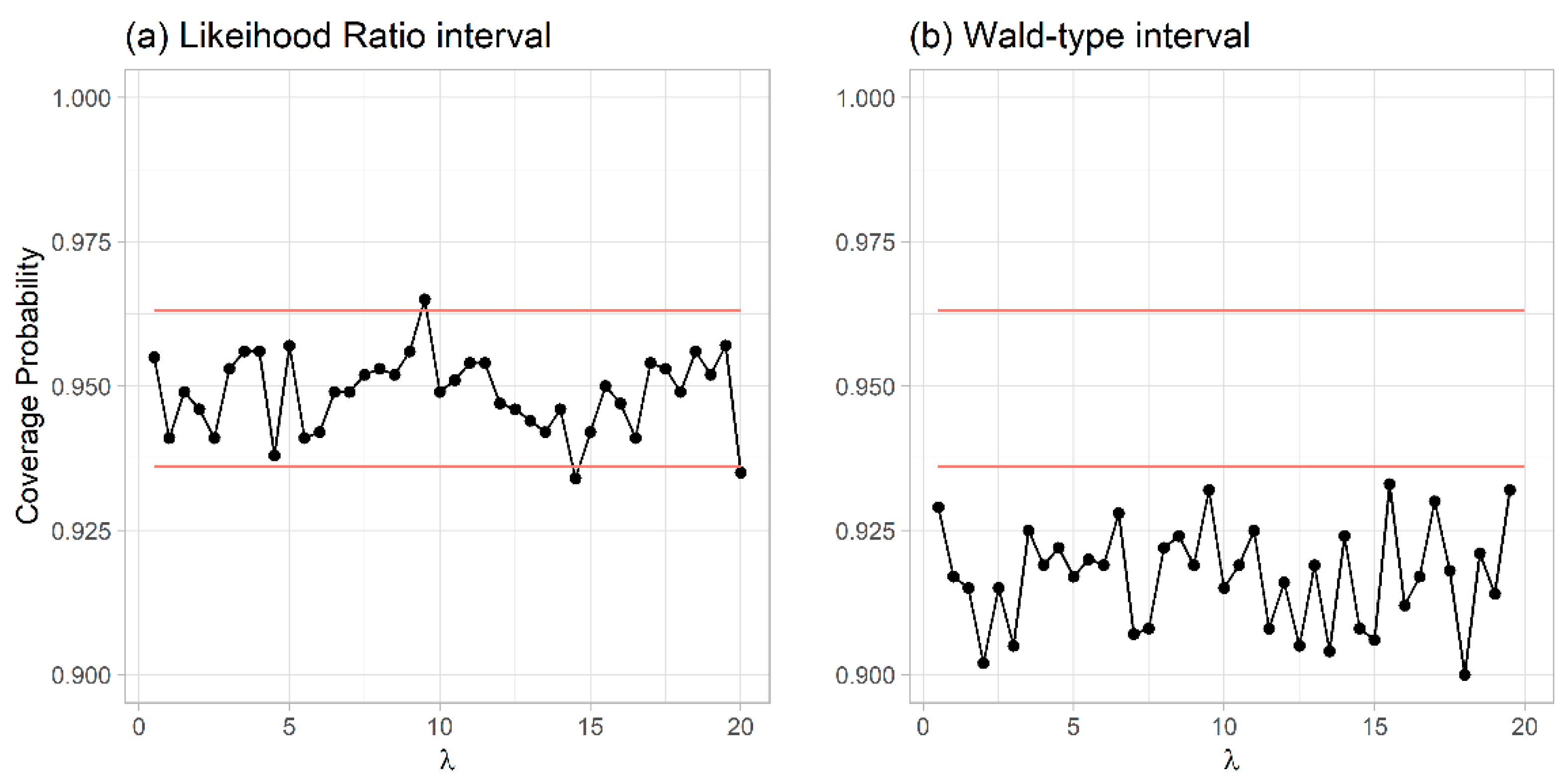
Table 1 presents the results for the exponential distribution with an intensity of 2. Likelihood ratio confidence intervals had coverage values within the tolerance limits Wald-type confidence intervals had coverage values under the lower tolerance limit of 0.936 when estimated either on full samples or ranges (
Table 1).
This pattern was consistent for different intensities (
Figure 1).
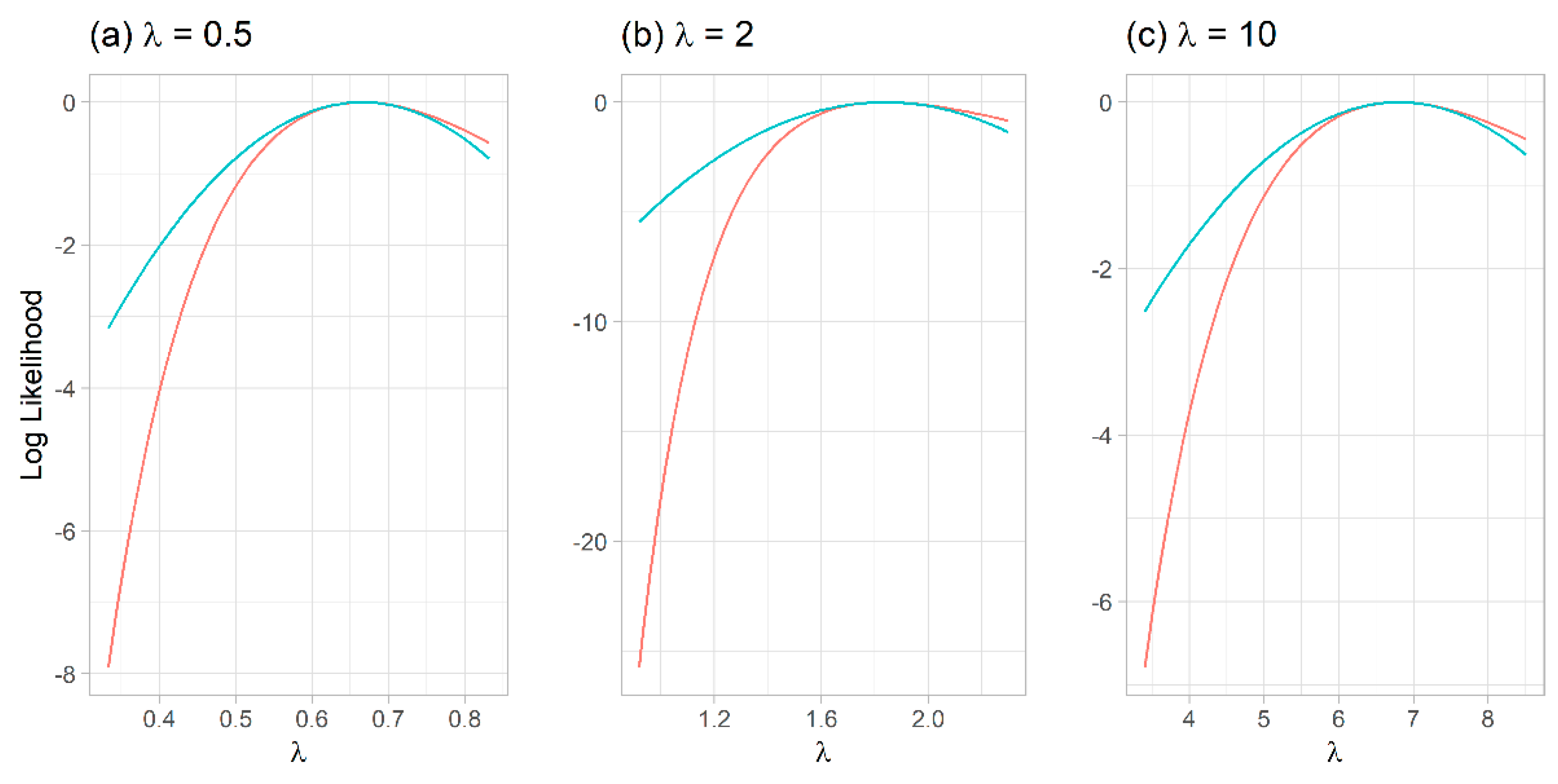
Quadratic (Taylor-series) approximation of the order statistics likelihood showed poor normal approximation, explaining the subpar performance of the Wald-type intervals (
Figure 2).
4.2. Normal Distribution
Table 2 summarizes the coverage probabilities for confidence intervals for the mean of a normally distributed variable with
and
. Apart from
n = 25 the coverage of both likelihood ratio and Wald-type intervals had coverage values within the tolerance limits.
Concomitant estimation of both means and associated standard deviations leads to a substantial under-coverage of likelihood ratio intervals based on ranges. The Wald-type confidence interval had coverage values within the tolerance limits. Using the Wan-estimator (Equation (5)) as a plug-in kept the coverage properties of the Wald-type confidence interval. The coverage of the likelihood ratio interval improved and attained coverage value within the tolerance limits and close to the nominal coverage. Additionally, likelihood ratio intervals were slightly narrower than Wald-type intervals, suggesting improvement in statistical power.
5. Illustrative Application
5.1. Exponential Distribution: Survival Data
In a recent abstract Okiror and collaborators [
12] reported survival statistics for patients undergoing pulmonary metastasectomy for sarcoma. The authors report that for the 66 patients with metastatic sarcoma that they followed up the median disease-free interval was 25 months, ranging between 0 and 156. We could assume that the disease-free survival is exponentially distributed with intensity λ. Of interest is to estimate λ and construct a 95 % confidence interval around it. In this case we have access to median and range so there are several ways to proceed. The range is the least robust statistics, as they are maximally sensitive to outliers. Thus, using the median to estimate λ, is the better option. The median of an exponentially distributed variable is given by
which in our case gives an intensity estimate of 0.0277. Additionally, we could use the ranges. The range reported can be used in two ways. First, knowing that the variance of an exponentially distributed variable is
and using the Wan [
2] equation for the standard deviation we can get an intensity estimate of 0.0301. Neither, approach offers straightforward way of inference, however Monte Carlo methods could be considered. Lastly, we could use MLEOS for point and interval estimation. This resulted in an intensity estimate of 0.0303 and associated 95 % confidence interval of 0.0192 to 0.0535. It is worth to note that this intensity underestimates the median, by two months (23 instead of 25). This can be due to multiple reasons. Partly the sensibility of ranges to outliers and equally importantly the possible deviation from the assumed distribution. However, a reparameterization to
and optimization with MLEOS gave a 95 % confidence interval for the median of 13 to 36 months. Thus, we cannot conclude without reasonable doubt that the two months’ deviation is a genuine one.
5.2. (Log) Normal Distribution: Exhaled Nitric Oxide Test
Early phase clinical trials for new asthma medicines often take advantage of allergen challenges. In these challenges healthy volunteers are subjected to allergens that cause adverse airway responses and different biomarkers are measured and compared between the placebo and active arms. Research planning often extracts data from published articles either for setting reasonable target values or for variance estimation that needed for power calculations. Barchuk and collaborators [
13] present such an allergen challenge study where among others they show data for F
ENO. F
ENO test (exhaled nitric oxide test) is a way to determine how much lung inflammation is present and how well inhaled steroids are suppressing this inflammation in allergic or eosinophilic asthma patients. Barchuk and collaborators [
13] present the geometric mean and range for FENO readings during a bronchial allergen challenge (BAC) (
Table 3).
We applied MLEOS in two different setting to this data. First, we used the range data to estimate standard deviations using the Wan-estimator and then assuming log-normally distributed data we estimated the geometric means and associated 95% confidence intervals. With one notable exception the estimation was acceptable. Second, using log-scale (normal distribution) we estimated standard deviations both with the Wan-estimator and MLEOS. FENO is modeled on log scale, thus we modeled σ, the standard deviation for the normal distribution and not the standard deviation of the log-normal distribution. Here, MLEOS provided standard deviation estimates that deviated only on third or fourth decimal from the Wan-estimator. As the later estimator is validated it can be used as a golden standard. Thus, we concluded that MLEOS is a feasible and easy way to obtain standard deviation estimates from ranges. In addition to the Wan-estimator MLEOS provides future inference that can be extremely valuable for a research planning.
6. Discussion
In this note, we showed that it is possible to construct likelihood-based confidence intervals for means when the only available data is the minimum and maximum value of a sample. The range caries more information than the values of the two measurements, it also indicates that the rest of the values are within these values. This combined with an assumed distribution allowed construction of the confidence intervals. Of course, confidence intervals have meaning only if the parameter estimates are unbiased or if the bias it relatively low compared to the variance of the estimate. MLEOS had been proved to provide unbiased point estimates [
8], and this was confirmed by or simulation (data not presented). Glen [
8] focused to show the value of MLEOS for various censorship scenarios. Building on his work, we took a step forward and assessed the feasibility of MLEOS not only for point estimates but for inference. For the one parameter distribution, like the exponential distribution where the intensity characterizes both the expected value and variance estimation is straightforward. Order statistics likelihood estimation for the normal distribution assumes estimation of two model parameters the mean and variance. If full data are available, this estimation is straightforward; however, if only minimum and maximum values are available, then the number of parameters to be estimated matches the number of data points. Additionally, the maximum likelihood estimate of the standard deviation is biased. Here it is recommended to use plug-in estimator for the variance, such as the Wan-estimator [
2]. Glen [
8] observed that the censoring pattern greatly influences the recorded bias. Unfortunately, he did not considered ranges. We expected that the standard deviation estimated by MLEOS would be higher than for the Wan-estimator, however this was not the case. While both estimators explicitly consider the sample sizes, their aim is somewhat differ. The Wan-estimator aims to give an estimate the sample standard deviation, MLEOS aims to estimate parameters that makes toe observed ranges most likely.
Here, we assumed that we know the distribution of the observations. However, this is not always the case. Confidence interval construction for ranked set samples [
14,
15,
16] including non-parametric interval received considerable attention. Confidence intervals for medians can be constructed based on adjacent order statistics with nonlinear interpolation [
17,
18]. Moreover, there are available routines for likelihood estimation for miss-specified or partially miss-specified models [
19]. Thus, it is of interest to assess in a future work the effect of model miss-specification and possible remedies.