Abstract
Disease emergence, in the last decades, has had increasingly disproportionate impacts on aquatic freshwater biodiversity. Here, we developed a new model based on Support Vector Machines (SVM) for predicting the risk of freshwater fish disease emergence in England. Following a rigorous training process and simulations, the proposed SVM model was validated and reported high accuracy rates for predicting the risk of freshwater fish disease emergence in England. Our findings suggest that the disease monitoring strategy employed in England could be successful at preventing disease emergence in certain parts of England, as areas in which there were high fish introductions were not correlated with high disease emergence (which was to be expected from the literature). We further tested our model’s predictions with actual disease emergence data using Chi-Square tests and test of Mutual Information. The results identified areas that require further attention and resource allocation to curb future freshwater disease emergence successfully.
1. Introduction
The worldwide pattern of river threats offers the most comprehensive explanation as to why freshwater biodiversity is considered to be in a state of crisis [,,]. Estimates suggest that at least 10,000–20,000 freshwater species are extinct or at risk [], with loss rates rivalling those of previous transitions between geological epochs such as the Pleistocene to Holocene []. Part of the key impacts on freshwater biodiversity arise from the emergence of diseases and thus an early prediction of freshwater disease emergence could underpin evidence based environmental management and cost optimisation.
Given the increasing importance of Big Data and Data Mining techniques in the modern age, supervised machine learning algorithm called Support Vector Machines (SVM) [,] are efficient tools to develop intelligent predicting models. SVM has the advantage of being a non-parametric and non-linear classification technique [], which is not bound by the parametric assumptions of normality, linearity or stationarity often missing in data mined. Moreover, SVM can model with small sample sizes and has proven to provide a high degree of prediction accuracy []. SVM models have previously been used for prediction based tasks in a variety of fields. Whilst it is not the intention of this paper to review all such efforts, we found it pertinent to provide some examples. There are considerable evidences of SVM’s varied application such as predicting medication adherence in heart failure patients [], detection of epileptic electroencephalogram [], financial distress and risk prediction [,], construction safety-risk assessment [,], revenue forecasting [], forecasting wind speed for wind farms [], groundwater simulation [] or apple disease detection []. The above examples not only illustrate the popularity of SVM across various fields, but also its competence at providing comparatively accurate predictions and classifications.
To the best of our knowledge, the application and evaluation of the suitability of SVM for predicting the risk of freshwater fish disease emergence is unique. However, few other studies have successfully used SVM in freshwater related scenarios, for example predicting freshwater algal blooms [,,], identifying freshwater species [] or even developing an early-warning protocol for predicting chlorophyll-a concentration in freshwater and estuarine reservoirs in Korea [].
Here, we used an existing database on fish diseases emergences and a database on fish introduction across England to predict the risk of freshwater disease emergence. The aim of the study was to build an intelligent model, which could predict and classify the risk of freshwater disease emergence in England as low, medium or high. The risk map would be based on the output from the chosen model to provide a graphical representation of the risk of freshwater disease emergence at a 10 km scale. Finally, we intended to compare the predicted to the observed distribution freshwater fish disease emergence in order to identify the high-risk areas. Such predictive output would be of great use to environmental agencies in order to set up cost effective early warning systems for managing the risk of fish emerging diseases.
2. Data
The first dataset (D1) included observed freshwater fish diseases emergence data collected for England by the Centre for Environment, Fisheries and Aquaculture Science (CEFAS) Weymouth. The data included fish and shellfish disease emergence on a global scale over the last 10 years and was published in []. The second dataset (D2) contained data for the time period 2000–2004 on native and non-native fish movement and introduction across England and was published in []. It contains information at 10 km scale, which is the lowest spatial resolution allowed in England for the release of commercially sensitive data, as the dataset identifies locations of pet shops, garden centres, fish farms, and fish consignment vendors and buyers []. Specifically, the dataset includes information on fish imports (intensity = numbers per annum of licensed fish consignments; diversity = number of ornamental varieties and of countries of origin) and for demographic information (i.e., numbers of humans, pet shops, garden centres, and fish farms per unit area).
3. Methodology
3.1. Classification of Disease Emergence Risk
For the purposes of fitting the model and analysis, we divided our data randomly (to reduce bias) into training, validation and test sets as defined in the seminal text by []. We set aside 1000 observations (which is approximately two thirds of the entire dataset) for training our SVM model. Out of the remaining, we selected 400 observations for validating the SVM model and leave aside 100 observations for testing. The training set of D2 was initially examined to develop a statistically reliable method for classifying the risk of freshwater fish disease emergence for each cell. We were interested in achieving a risk categorization of low, medium and high for freshwater disease emergence in England. The classification we developed in this study relies on a combination of a statistical reasoning and logical perceptions. Based on the accepted assumption (see []) that the increased numbers and frequencies of live freshwater fish introductions in an area, increases the risk of fish disease emergence, this database was used to train, validate and test model for the risk of freshwater fish disease emergence in England. According to [], and information provided by experts, the following factors and assumptions contribute towards freshwater fish disease emergence:
- The native and non-native fish movements into a cell increases the diversity of fish species in a cell.
- The diversity of fish in a cell contributes towards the likelihood of one of fish holding a pathogen. That is, the more varied the more likely they are to hold a pathogen.
- The higher is the number of fish movements into a cell, the higher is the possibility of a freshwater fish disease emerging in that cell.
Taking these factors and assumptions into consideration, we developed the following methodology for classifying the risk of freshwater fish disease emergence. For classification purposes, we were mainly interested in the variables titled “Number of varieties”, “1Native species moves to”, and “Non-native species moves to” variables which are found in D2. Next, we introduced a new column titled “Sum” into the database (Equation (1)), purely for classification purposes. The “Sum” column contains the following information and its creation was influenced by the assumption that a high number of fish movements (regardless of whether it is native or non-native) would increase the chances of a freshwater fish disease emerging.
Following its introduction, we analyzed the distribution of the “Sum” column to determine the cut off points for the proposed risk classification. The cumulative distribution function (c.d.f.) was used for this purpose. The c.d.f describes the relationship:
which is the probability that a real valued random variable X with a given probability distribution will be found at a value less than or equal to x. As such, the c.d.f for a continuous variable X can be defined as:
where f is the probability density function.
Figure 1 shows the c.d.f for the “Sum” column. The optimal cut off points shown here were generated based solely on the Sum variable, which is a combination of native and non-native fish movements. Prior to determining the cut off points as optimal, we also evaluated modelling with different points to ascertain the sensitiveness and robustness of the adopted points. Next, we analyzed this c.d.f to identify statistically reliable, optimal cut off points for low, medium and high risk classification of the database. Accordingly, the optimal cut off points generated was based on the “Sum” variable, which combines native and non-native fish movements into a particular cell (see Figure 1).
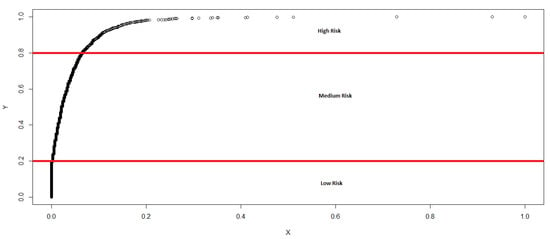
Figure 1.
Cumulative distribution function of the Sum.
The determination of the risk classifications can be further explained as follows. It is visible that up until , suggesting zero fish movements (Figure 1). When compared with the actual data, this converts into a cut off point of 1. Likewise, at , we arrive at the next cut off point, which is 28. Using such key information in combination with the logical perceptions relating to the variety of fish in a particular cell, we arrived at the final risk classification.
3.2. Support Vector Machine (SVM)
The foundations of SVM were developed by [] and those interested in a detailed elaboration of the theory underlying SVM are referred to []. In brief, SVM separates two classes by a function, which is induced from the available data observations, with the ultimate goal of producing a classifier that can be generalized. Note that, determining a class boundary using a separating hyperplane is adequate where classes are linearly separable, but there exists other less complex methods, which could provide satisfactory results in such situations. Therefore, SVM is most appropriate where classes are not linearly separable [].
An initial analysis of D2 showed that the classes were not linearly separable and thus prompted the use of an appropriate non-linear model in the form of SVM. Furthermore, there is evidence suggesting that, in general, freshwater ecological variables and their underpinning processes are very complicated and non-linear [], thereby further supporting the adoption of a non-linear model like SVM.
Following [,], the theory underlying SVM starts with the problem of separating a set of training vectors belonging to two separate classes:
with a hyperplane,
where denotes the inner product of the vectors and .
The simple solution to the problem is finding the hyperplane which the minimum distances between the hyperplane and the points is maximized in both classes. In other words, to find the solution to above mentioned problem, one may solve the following optimization problem:
The parameter M is called the margin and shows the minimum distance between the observation points and the hyperplane (the margin between two classes). Once the optimization problem in Equation (4) is solved, the classification function classifies the new observation as follows:
The classification function in Equation (5) is called linear support vector classifier. In optimization problem (Equation (4)), the second constraint guarantees all observations lie on the right side of the hyperplane. this constraint comes from the assumption “The observations are linearly separable (i.e.,: there exists a hyperplane which separates two classes)”. However, in real world problems (e.g., the problem in our hands), the linear classification is not always possible which means the optimization problem (Equation (4)) does not have a solution. To handle the problem, one needs to allow some of the points lie on the wrong side of the hyperplane. In this case, the optimization problem is formulated as follows:
The error term allows the observation to lie on the wrong side of the hyperplane. The parameter C is some nonnegative constant called tuning parameter. Once the optimization problem (Equation (6)) is solved, one may use the classification function (Equation (5)) to classify new observations.
Solving the optimization problem (Equation (6)), it turns out the optimal solution to the linear classification problem only involves all possible inner products of the observation vectors [], which implies one cane reformulate the linear support vector classifier as follows:
where the coefficients and the parameter b are estimated solving (Equation (6)), based on all inner products of observation vectors ( see [], Chapter 12 for more details on the solution).
Using the reformed classification function (Equation (7)), the linear support vector classifier can be extended for nonlinear problems by using a nonlinear function instead of inner product []:
where is, a symmetric, positive semi-definite function. The function is called Kernel and allows the support vector classifier (Equation (8)) to classify between two classes even if they are not linearly separable. Some popular choices for kernel function are:
- Linear Kernel: .
- dth-Degree polynomial: .
- Gaussian: .
- Radial basis: .
- Neural network: .
As can be seen, each kernel has its own extra parameters (i.e., polynomial kernel has the parameter d and the Gaussian kernel has the bandwidth matrix ). Cross-validation is a common method to select the appropriate kernel function and estimates its extra parameters [].
For the purposes of fitting the model and analysis, we divided our data according to [] randomly into training, validation and test sets. We set aside 1000 observations (which is approximately two thirds of the entire dataset) for training our SVM model. Out of the remaining, we selected 400 observations for validating the SVM model and leave aside 100 observations for testing. Out of the various SVM variants, we selected the ”nu-svc” classification variant (http://scikit-learn.org/stable/modules/svm.html#nusvc) for modeling the risk of freshwater fish disease emergence. Here, the parameter sets the upper bound on the training error and the lower bound on the fraction of data points to become Support Vectors (default: 0.2). A further interesting property of is that it is related to the ratio of support vectors and the ratio of the training error. We then used the risk categorization developed in this Section along with the following variables to develop the proposed SVM model.
Dependent Variable = Risk (classified as low, medium and high).
Independent Variables = Area, Population, Pop Per Ha, Pet Shops, Garden Centers, Fish Farms, No. Fish Importers, No. Fish Exporters, No of Varieties, Varieties per Ha, Origins, Total Imports, Total Species, Native species Fish Moves to, Non Natives Fish Moves to, Native species Fish Moves From, Non Natives Fish Moves From, and Species Group.
4. Empirical Results
4.1. Risk Classification
Risk classification for freshwater fish disease emergence in England are presented in Table 1. Using the cut off points identified in Section 3.1 in combination with the [] assumptions, which consider fish diversity in a particular cell, we set the cut off points for the risk categorization as follows:

Table 1.
Risk classification for freshwater disease emergence.
- The risk of disease emergence is categorized as low where each cell in the dataset for which the corresponding “Sum” and No. of Varieties equal zero.
- The risk is classified as medium when each cell in the dataset records a “Sum” greater than or equal to one and less than or equal to 28, in addition to the corresponding No. of Varieties equalling zero.
- The risk categorization is high when each cell in the dataset records a “Sum” greater than 28 and the No. of Varieties greater than or equal to zero. We categorize using the greater than or equal to sign for High risk because it appears reasonable (based on initial assumptions and expert opinions) to conclude that, even if the No. of Varieties equal zero, if the “Sum” is greater than 28, the movement of fish into that cell is statistically large enough (based on our c.d.f) for us to expect a high risk of disease emergence.
Next, we applied the developed risk categorization to the training set within D2 data to produce the distribution of the “Sum” column following the application of our risk categorization (Figure 2), enabling us to obtain a clear picture on how the risk is distributed based on our categorization.
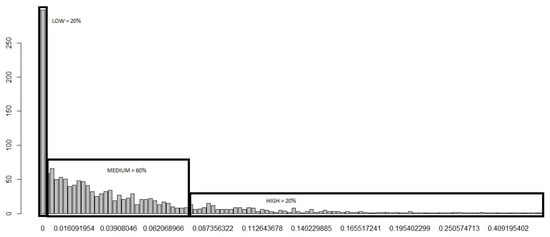
Figure 2.
Distribution of the “Sum” post risk categorization.
4.2. Output from the Proposed SVM Model
The model underwent a rigorous training process where we evaluated all possible classification variants of SVM as provided via the package (https://cran.r-project.org/web/packages/e1071/e1071.pdf) in R. A summary of the optimal SVM model is presented (Table 2). Eventually, the SVM model with the “nu-svc” classification was selected as the best model based on the lowest training error, highest sensitivity, specificity and accuracy.

Table 2.
SVM model summary.
The best classification is possible where the values of classification accuracy, sensitivity and specificity are closer to 1. In our case, the classification accuracy of the model was 90.99%, with a sensitivity of 0.84 and a corresponding specificity of 0.93. Thereafter, using the validation set, we simulated the fitted SVM model to provide an unbiased evaluation of the model’s fit on the training dataset. In the simulation process, we ensured the SVM model is held constant and fed it with 500 randomly generated validation sets (recall, the validation set includes 400 observations in total), recording its accuracy at each step and obtaining the overall average at the end. The results from the simulation are reported in Table 3. The accuracy figures reported here correspond to the ability of the model to correctly classify low risk as low, medium risk as medium and high risk as high.

Table 3.
SVM model simulation summary.
The simulation results in Table 3 suggest that the selected SVM model is able to achieve accuracy rates of over 90% on average in terms of correctly classifying low, medium and high risk of freshwater fish disease emergence. The associated standard deviations are relatively low and suggest that the SVM model is relatively stable. In addition, the standard deviations also suggest that the low risk prediction accuracy levels are most variable and that the medium risk accuracy prediction levels are more stable. The coefficient of variation (CV) statistic confirms the conclusions relating to the variability in accuracy levels reported above as low risk reports the highest CV and medium risk reports the lowest CV.
Finally, we went a step further to test the proposed SVM model by evaluating its performance at correctly classifying the 100 observations left aside as part of the test set. These results are reported in Table 4. The first observation is that the model was able to accurately classify 90.0% of the low risk outcomes as low risk, 91.0% of the medium risk outcomes as medium risk and 94.0% of the high risk outcomes as high risk. Accordingly, it is clear that the model shows promising results for future applicability in terms of predicting the risk of freshwater fish disease emergence in England as it records accuracy levels of over 90% across all three levels. Secondly, the accuracy variations among low, medium and high are higher than what was reported in the simulations at the validation stage, but, as before, low risk continues to report the most variable accuracy levels whilst medium reports the most stable accuracy levels. Moreover, we can ascertain that there is no overfitting problem in this model because the training accuracy and testing accuracy levels do not differ by a large amount. As such, we are confident that the model specification and tuning are appropriate.

Table 4.
SVM model validation summary.
4.3. Mapping Freshwater Disease Emergence in England
D1 relates to the period 2000–2010 and was used to map the actual freshwater disease emergence in England (Figure 3). The data suggest that diseases caused from bacteria have only been reported in the north of England during this period. Furthermore, whilst virus and parasite related diseases are widespread, there appears to be no diseases emerging towards the middle part of England and the majority of the diseases have been reported around the coastal belt.
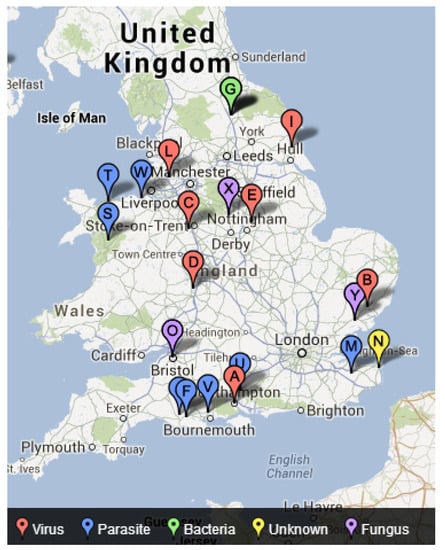
Figure 3.
Actual freshwater disease emergence in England (2000–2010).
Based on the risk categorization, we established a risk map of freshwater fish disease emergence in England (Figure 4). We tested for a relationship between observed freshwater fish disease emergence and our risk categorization of freshwater fish disease emergence in England.
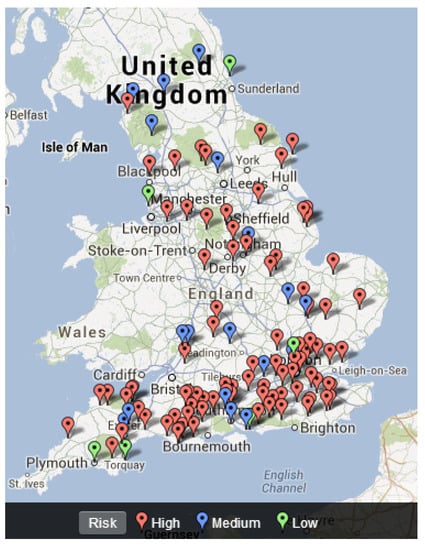
Figure 4.
Risk map for freshwater disease emergence in England.
A basic visual comparison between the two maps indicated that in certain parts of England the actual fish disease emergence and the predicted risk of a fish disease emergence matched according to the proposed model. However, a key difference is seen around the actual disease emergence and predicted risk of disease emergence around London. This is because in reality there have been no actual reported disease outbreaks (Figure 3) in London, whilst the model we built suggests a high risk of fish diseases emerging around this area (Figure 4).
This could be explained as follows. It is important to remember that the SVM model was built on the [] assumptions, according to which the very high fish movements and large number of varieties of fish found in the London area should increase the actual disease outbreaks. However, in England, the Environment Agency (EA) is known for regularly checking large fish importers and sellers of fish ensuring that disease outbreaks are curbed in such highly concentrated areas. This could suggest that the [] assumptions could be mitigated using robust disease surveillance programmes in some populated areas.
We then carried out further statistical tests, which involved Chi-square tests for association, and Mutual Information (MI). For the purpose of performing the statistical tests, the three risk levels were recoded as 0, 1 and 2 corresponding to “low”, “medium” and “high” risk. The next step involved matching all 1500 locations in D2 with D1 actual disease emergence locations. We then added a new variable, which took the value 1 if the actual disease emergence point matched with a location on D2 and 0 otherwise. This enabled us to perform an association test for matching the two maps and the results are reported in Table 5.

Table 5.
Association between risk of disease emergence and actual freshwater disease emergence by location.
The first observation is that there is a statistically significant association between the predicted risk of fish disease emergence and observed fish disease emergence for the entirety of England in general. However, when we performed a finer analysis by location, we found that statistically significant associations between our predicted risk levels and actual disease emergence can only be seen in Suffolk/Ipswich, Staffordshire, Worcestershire, Dorset, North Yorkshire, Eden, North Kent and Bristol.
These results provide two important insights. Firstly, given that the association between predicted risk of fish disease emergence and observed fish disease emergence for the entirety of England was found to be statistically significant, proves that the [] assumptions are globally valid, at least for England and that the risk classification developed in this study is valid. Secondly, the counties which show a statistically significant association between the predicted risk and actual disease emergence highlights the areas where special attention and resources can be diverted to control the emergence of diseases. It would be interesting to see whether the locations that were not found to have a statistically significant association with the proposed risk categorization correspond to locations where rigorous fish health checks are taking place to curb disease emergence. Next, we evaluated the association between our predicted risk and various pathogen lead diseases. These results are reported in Table 6.

Table 6.
Association between risk of disease emergence and actual freshwater disease emergence by type.
The prediction of risk has a statistically significant association with actual disease emergence resulting from viruses, bacteria and fungi (Table 6). However, there is no statistically significant association between the risk levels and parasite and other unknown diseases. This suggests further research is required into identifying the factors influencing the emergence of parasites in freshwaters as the factors on which our prediction of risk is based do not appear to have a significant association.
In addition, we also test our risk categorization and its association with actual freshwater fish disease emergence further by seeking to quantify the linear or non-linear dependency between the two maps. For this purpose, we used Shannon’s information theory [] combined with the concept of mutual information. Mutual information results are able to show how much knowing the value of one random variable (risk levels) reduces uncertainty about another random variable (actual disease emergence). According to [], Mutual Information (MI) can be summarised as:
where and are estimates of Shannon entropy of the two random variables X and Y calculated based on the counts, and are the related conditional entropies, and is the joint Shannon entropy of X and Y. Accordingly, we calculated the MI value for our random variables and the result was 0.99. However, interpreting this value alone can be misleading, and therefore we relied on the standard measure for MI as adopted by [];
As explained in [], the significance of the measure is that it captures the linear and nonlinear dependence between the two random variables. In this case, we are left with a = 0.93, which suggests a very strong association between the predicted risk of disease emergence and the actual freshwater disease emergence, and thereby confirms that our risk categorization is valid and statistically significant.
Finally, we sought to determine the association between risk of fish disease emergence and number of fish farms since the literature suggests that areas in which there is high fish movement are generally correlated with high disease emergence. Accordingly, a high number of fish farms would suggest high fish movements in a particular region. The Chi-square results for association suggested that there was in fact a statistically significant association between risk of a disease emerging and the number of fish farms in England. To validate this result and further confirm its accuracy, we relied on Fishers exact test. The results from Fisher’s exact test also confirmed that the findings based on the association test are indeed valid and reliable. Our results in this study confirm the related hypothesis is valid for England as reported in previous literature.
5. Conclusions
In this study, we propose a new categorization for classifying risk of freshwater fish disease emergence in England and test the validity of the classification using Chi-Square tests and Mutual Information. We found that our classification is indeed reliable and able to provide useful insights for freshwater disease management in England. Using the proposed risk classification, we then built a SVM model for predicting the risk of freshwater fish disease emergence in England.
The results show that our proposed model is able to accurately predict low risk as low, medium risk as medium and high risk of disease emergence as high with average accuracy rates of over 90%. Through our analysis, we also identify locations in England where there is likely to be an increased risk of freshwater disease emergence so that the relevant authorities could devote more time and resources to mitigate potential episodes of disease emergence. These areas include Suffolk/Ipswich, Staffordshire, Worcestershire, Dorset, North Yorkshire, Eden, North Kent and Bristol. The statistical analysis between the risk map and actual observed disease emergence map also shows that, in England, the current efforts by authorities to manage health check fish movements and could be leading to reduced recorded levels of freshwater fish disease emergence—the majority of the areas, which are predicted to have an increased risk do not correspond with actual disease emergence.
Whilst it would be beneficial to extrapolate the findings to the rest of the world, the fact that England is privy to a unique and advanced disease monitoring strategy hindered the expansion of the model to other parts of the world such as China and India which report the largest freshwater aquaculture use. This further highlights a limitation of the proposed SVM model as it can only work well in countries with advanced monitoring strategies such as England. However, the theory underlying this model is useful in predicting high and low risk areas with high accuracy levels and thereby shows the potential for predicting freshwater disease emergence globally in the future. Nevertheless, those intending on adopting this same model for extrapolating beyond England, should bear in mind that the local level of connectivity/human population density may influence the level of risk as established for England.
Author Contributions
E.S.S. and H.H. performed the statistical tests; E.S.S., R.E.G., D.A., H.H., M.C., M.R.Y. and M.G. wrote the paper; R.E.G., D.A. and H.H. jointly conceived and designed the project.
Funding
This research received no external funding.
Acknowledgments
We thank the reviewers whose insightful comments helped improve this paper as well as Gordon H. Copp from the Centre for Environment, Fisheries and Aquaculture Science UK, and E. Peeler and P. Dunn at Cefas–Weymouth for assisting in the compilation of the dataset, and comments on an earlier version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Raptis, C.E.; van Vliet, M.T.H.; Pfister, S. Global thermal pollution of rivers from thermoelectric power plants. Environ. Res. Lett. 2017, 11, 104011. [Google Scholar] [CrossRef]
- Shen, Y.; Cao, H.; Tang, M.; Deng, H. The Human Threat to River Ecosystems at the Watershed Scale: An Ecological Security Assessment of the Songhua River Basin, Northeast China. Water 2017, 9, 219. [Google Scholar] [CrossRef]
- Wen, Y.; Schoups, G.; van de Giesen, N. Organic pollution of rivers: Combined threats of urbanization, livestock farming and global climate change. Sci. Rep. 2017, 7, 43289. Available online: https://www.nature.com/articles/srep43289 (accessed on 21 August 2018). [CrossRef] [PubMed]
- Crist, E.; Mora, C.; Engelman, R. The interaction of human population, food production, and biodiversity protection. Science 2017, 356, 260–264. [Google Scholar] [CrossRef] [PubMed]
- Vorosmarty, C.J.; McIntyre, P.B.; Gessner, M.O.; Dudgeon, D.; Prusevich, A.; Green, P.; Glidden, S.; Bunn, S.E.; Sullivan, A.; Reidy Liermann, C.; et al. Global threats to human water security and river biodiversity. Nature 2010, 467, 555–561. [Google Scholar] [CrossRef] [PubMed]
- Cortes, C.; Vapnik, V. Support Vector Machines. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Auria, L.; Moro, R.A. Support Vector Machines (SVM) as a Technique for Solvency Analysis; Technical Report; Deutsche Bundesbank: Hannover, Germany; German Institute for Economic Research: Berlin, Germany, 2008; Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1424949 (accessed on 21 August 2018).
- Xie, Z.; Lou, I.; Ung, W.K.; Mok, K.M. Freshwater Algal Bloom Prediction by Support Vector Machine in Macau Storage Reservoirs. Math. Prob. Eng. 2012, 2012, 397473. Available online: https://www.hindawi.com/journals/mpe/2012/397473/ (accessed on 21 August 2018). [CrossRef]
- Son, Y.-J.; Kim, H.-G.; Kim, E.-H.; Choi, S.; Lee, S.-K. Application of Support Vector Machine for Prediction of Medication Adherence in Heart Failure Patients. Healthc. Inform. Res. 2010, 16, 253–259. [Google Scholar] [CrossRef] [PubMed]
- Nicolaou, N.; Georgiou, J. Detection of epileptic electroencephalogram based on Permutation Entropy and Support Vector Machines. Expert Syst. Appl. 2012, 39, 202–209. [Google Scholar] [CrossRef]
- Sun, J.; Li, H. Financial distress prediction using support vector machines: Ensemble vs. individual. Appl. Soft Comput. 2012, 12, 2254–2265. [Google Scholar] [CrossRef]
- Danenas, P.; Garsva, G. Selection of Support Vector Machines based classifiers for credit risk domain. Expert Syst. Appl. 2015, 42, 3194–3204. [Google Scholar] [CrossRef]
- Jiang, P.; Craig, P.; Crosky, A.; Maghrebi, M.; Canbulat, I.; Saydam, S. Risk assessment of failure of rock bolts in underground coal mines using support vector machines. Stat. Methods Min. Ind. 2018, 34, 293–304. [Google Scholar] [CrossRef]
- Zhou, Y.; Su, W.; Ding, L.; Luo, H. Predicting Safety Risks in Deep Foundation Pits in Subway Infrastructure Projects: Support Vector Machine Approach. J. Comput. Civ. Eng. 2017, 31. [Google Scholar] [CrossRef]
- Lin, K.-P.; Pai, P.-F.; Lu, Y.-M.; Chang, P.-T. Revenue forecasting using a least-squares support vector regression model in a fuzzy environment. Inf. Sci. 2013, 220, 196–209. [Google Scholar] [CrossRef]
- Santamaria-Bonfil, G.; Reyes-Ballesteros, A.; Gershenson, C. Wind speed forecasting for wind farms: A method based on support vector regression. Renew. Energy 2016, 85, 790–809. [Google Scholar] [CrossRef]
- Ebrahim, H.; Rajaee, T. Simulation of groundwater level variations using wavelet combined with neural network, linear regression and support vector machine. Glob. Planet. Chang. 2017, 148, 181–191. [Google Scholar] [CrossRef]
- Omrani, E.; Khoshnevisan, B.; Shamshirband, S.; Saboohi, H.; Anuar, N.B.; Nasir, M.H.N.M. Potential of radial basis function-based support vector regression for apple disease detection. Measurement 2014, 55, 512–519. [Google Scholar] [CrossRef]
- Lou, I.; Xie, Z.; Ung, W.K.; Mok, K.M. Integrating Support Vector Regression with Particle Swarm Optimization for numerical modeling for algal blooms of freshwater. Appl. Math. Model. 2015, 39, 5907–5916. [Google Scholar] [CrossRef]
- Lou, I.; Xie, Z.; Ung, W.K.; Mok, K.M. Integrating Support Vector Regression with Particle Swarm Optimization for Numerical Modeling for Algal Blooms of Freshwater. In Advances in Monitoring and Modelling Algal Blooms in Freshwater Reservoirs; Lou, I., Han, B., Zhang, W., Eds.; Springer: Dordrecht, The Netherlands, 2017. [Google Scholar]
- Wu, Y.; Yin, J.; Dai, Y.; Yuan, Y. Identification method of freshwater fish species using multi-kernel support vector machine with bee colony optimization. Trans. Chin. Soc. Agric. Eng. 2014, 30, 312–319. [Google Scholar]
- Park, Y.; Cho, K.H.; Park, J.; Cha, S.M.; Kim, J.H. Development of early-warning protocol for predicting chlorophyll-a concentration using machine learning models in freshwater and estuarine reservoirs, Korea. Sci. Total Environ. 2015, 502, 31–41. [Google Scholar] [CrossRef] [PubMed]
- Thrush, M.A.; Dunn, P.L.; Peeler, E.J. Monitoring Emerging Disease of Fish and Shellfish Using Electronic Sources. Transbound. Emerg. Dis. 2012, 59, 385–394. [Google Scholar] [CrossRef] [PubMed]
- Copp, G.H.; Vilizzi, L.; Gozlan, R.E. Fish Movements: The Introduction Pathway for Topmouth Gudgeon Pseudorasbora Parva and Other Non-Native Fishes in the UK. Aquat. Conserv. 2010, 20, 269–273. [Google Scholar] [CrossRef]
- Copp, G.H.; Vilizzi, L.; Gozlan, R.E. The demography of introduction pathways, propagule pressure and occurrences of non-native freshwater fish in England. Aquat. Conserv. 2010, 20, 595–601. [Google Scholar] [CrossRef]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Peeler, E.J.; Oidtmann, B.C.; Midtlyng, P.J.; Miossec, L.; Gozlan, R.E. Non-native aquatic animals introductions have driven disease emergence in Europe. Biol. Invasions 2011, 13, 1291–1303. [Google Scholar] [CrossRef]
- Vapnik, V. Statistical Learning Theory; Springer: New York, NY, USA, 1998. [Google Scholar]
- Brereton, R.G.; Lloyd, G.R. Support vector machines for classification and regression. Analyst 2010, 135, 230–267. [Google Scholar] [CrossRef] [PubMed]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- Shannon, C. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Hassani, H.; Dionisio, A.; Ghodsi, M. The effect of noise reduction in measuring the linear and nonlinear dependency of financial markets. Nonlinear Anal. Real World Appl. 2010, 11, 492–502. [Google Scholar] [CrossRef]
- Granger, G.; Lin, J. Using the mutual information coefficient to identify lags in nonlinear models. J. Time Ser. Anal. 1994, 15, 371–384. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).