1. Introduction
The cure fraction models are broadly used for analyzing survival data. In the literature, there are two major models to fit survival data with a cure fraction. The first one is the mixture cure rate model, also known as the standard cure rate model. This model was initially introduced by Boag [
1] in 1949 and further developed by Berkson and Gage [
2] in 1952 and later extensively studied by other authors. In this model, it is assumed that a certain proportion of the population is cured and the remaining is not cured. In order to estimate the cure fraction, parametric, semi-parametric and non-parametric methods have been studied by several authors. Farewell [
3] in 1982 used a Weibull distribution for uncured subjects and a logistic regression for cure probability. Goldman [
4] in 1984 discussed parametric survivorship analyses using maximum likelihood estimation and the likelihood ratio test. Taylor [
5] in 1995 proposed the semi-parametric method to a mixture model using the logistic regression for an incidence part and the Kaplan–Meier for the latency part. Peng and Dear [
6] in 2000 investigated the non-parametric approach to a mixture model to estimate parameter of interest in the model using EM algorithm, marginal likelihood approach, and multiple imputations. They also extended to Cox’s proportional hazards cure model. Kuk and Chen [
7] in 1992 also proposed the semi-parametric cure model using the logistic regression for cure probability and the proportional hazard regression model for failure time. Zhang and Peng [
8] in 2009 proposed a mixture cure model where the covariate effects on the proportion of cure and the distribution of the failure time of uncured patients are separately modeled. Patilea and Van Keilegom [
9] in 2017 proposed a general approach to estimate a mixture cure model for random right censoring data. They worked with a parametric model for the cure proportion and the conditional probability for the uncured subjects. Moreover, Kim and Jhun [
10] in 2008 investigated interval censored data based on a mixture cure model. They derived the likelihood in interval censored data based on an approximate likelihood approach suggested by Goetghebeur and Ryan [
11] in 2000.
The second one is a non-mixture cure rate model, also known as the bounded cumulative hazard model and promotion time cure model. In cancer study, this model was developed based on the assumption that the number of cancer cells that remain active after cancer treatment and that may grow slowly and produce a detectable cancer, which assumed to follows a Poisson distribution. This model was first proposed by Yakovlev et al. [
12] in 1993 and was further discussed by Chen et al. [
13] in 1999. The semi-parametric approaches of estimation for survival data with a cure fraction have been discussed by Chen et al. [
14] in 2001. Tsodikov et al. [
15] in 2003 provided a review of existing methodology of statistical inference based on the non-mixture model. They have highlighted that there are the distinct advantages of the non-mixture cure model: the non-mixture cure model has proportional hazard model structure, the non-mixture cure model presents a much more biologically meaningful interpretation of the results of the data analysis and the non-mixture cure model is easy in computations due to its simple structure for the survival function which can provide a certain technical advantage when developing maximum likelihood estimation procedures. Herring and Ibrahim [
16] in 2002 studied the parametric estimation of random effects for non-ignorable missing covariates in a non-mixture cure model. Uddin et al. [
17,
18] in 2006 approached both non-parametric and parametric methods in a non-mixture model for uncensored data. Liu et al. [
19] in 2009 investigated the semi-parametric non-mixture cure model for interval censored data using the EM method. Lopes et al. [
20] in 2012 studied both bayesian and classical approaches to long-term survivors and random effects based on a non-mixture cure model.
In this paper, we considered a generalized extreme value type II distribution for long-term survivors. The generalized extreme value distribution was introduced by Jenkinson [
21] in 1955 and its sub-models are widely used for modeling extreme events. The generalized extreme value distribution sub-models are Gumbel, Fréchet and Weibull distributions. An extreme value distributions play an important role in statistics. Ramos et al. [
22] in 2017, discussed some properties of the long-term Fréchet distribution. We study a long-term survival non-mixture cure model with Fréchet distribution for uncured population. The Fréchet distribution is one of the flexible distribution for survival analysis due to its properties. Its probability density function is skewed to the right and it has also increasing and decreasing hazard rate function depending on the values of a shape parameter. A simulation study is conducted to show the performance of the maximum likelihood estimators. Moreover, we compare the our proposed model with other established models using the real data-sets of leukemia for 46 allogeneic marrow transplantation patients presented by Kersey et al. [
23] in 1987 and ECOG phase III clinical trial e1684 available in R package
.
The rest of the article is organized as follows. In
Section 2 and
Section 3 we derive the likelihood function of a mixture cure model and a non-mixture cure model rspectively. In
Section 4 we introduce the Fréchet distribution and we derive the likelihood function of the non-mixture Fréchet distribution. In
Section 5 we conduct the simulation study of the non-mixture Fréchet distribution. In
Section 6 we present the leukemia dataset and melanoma dataset to compare the mixture cure model and the non-mixture cure model with different susceptible distributions and finally the conclusion is presented in
Section 7.
2. Likelihood Function of a Mixture Cure Model
A mixture cure model refers to a class of model for survival data with long-term survivors when some of them will not develop the event of interest. In a mixture cure model, the population consists of two types of subjects: uncured (susceptible) subjects who experience the event of interest and cured (non-susceptible) subjects who will never experience it. Those who are not going to develop the event of interest are referred to as “cured subjects”, or “long-term survivors”.
Let
T denote the survival time of a subject and let
be the cure indicator with
when the subject is cured and
when the subject is uncured. Let
p be the proportion of subjects that are cured, and
be the proportion of subjects that are not cured. That is,
and
. So,
and
, the cumulative distribution function of uncured subjects. Then the cumulative distribution function of the overall population
T is
and the survival function of
T is
where
denotes a proper survival function for the uncured patients. Notice that
is not proper. The corresponding density function of
T is
where
is the probability density function of uncured patients.
Suppose
be the right-censored survival time for subject
i, then
, where
be the failure time of the
subject and
be the right-censored variable of the
subject,
. The observed survival time of
subject is
and the censoring indicator is
, where
, for
. Then the likelihood function of the mixture model is
and the log-likelihood function is
3. Likelihood Function of a Non-Mixture Cure Model
In this section, we introduce a non-mixture cure model developed for survival data with long-term survivors in cancer study. Let
N be the number of cancer cells for a patient after cancer treatment. Since the number of cancer cells may grow rapidly and may later produce a detectable cancer disease, the number of cancer cells,
N, is assumed to have a Poisson distribution with mean
. Let
be the random time for the
jth cancer cell to produce a detectable cancer mass. Then, the time to relapse of cancer can be defined by the random variable
T such that
. Furthermore, we assume that
are independently and identically distributed with distribution and survival functions
and
, respectively. Then the survival function of
T is given by:
where
is the probability of cure or cure fraction in this model since
which implies that
is an improper survival function. The cumulative distribution, density and hazard functions of
T are given below respectively,
Since
is not proper survival function, then we can derive the following theorem:
Theorem 1. Let . For and is a strictly increasing proper distribution function, then has an improper uniform distribution over .
Proof of Theorem 1. Notice that as
,
. So,
Since
is strictly increasing which implies that
is also strictly increasing, it has an inverse, denoted by
. Then for
,
Therefore,
has an improper uniform distribution over
.
Case-1: If , this theorem is equivalent to the Inverse Transform Method.
Case-2: If , the result is not realistic for real life. □
We now consider the right-censored life time data and assume there are
n patients under cancer study. Let
refer to the right-censored survival time for individual
i and
where
be the right-censored variables. Then we observe
and the censoring indicator
. The likelihood function of
is
and the log-likelihood function is
4. Fréchet Susceptible Distribution
We used a generalized extreme value distribution as the susceptible distribution, i.e., the type II Fréchet distribution. The class of extreme value distributions essentially consists of three types of extreme value distributions: type I (Gumbel distribution), type II (Fréchet distribution) and type III (Weibull distribution). The extreme value distribution is useful in modeling and measuring the events which occur with very low probability. Moreover, extreme value distributions are widely used in finance, insurance, risk management, economics, material sciences and many other subjects which dealing with extreme events.
More specifically, we considered the Fréchet distribution, which was named after the French mathematician Maurice Fréchet (1878–1973), to fit the survival time of uncured individuals. The Fréchet distribution is also known as inverse Weibull distribution under some parametric constraints. The probability density function of Fréchet distribution is
where
is the shape parameter and
is the scale parameter. The survival and hazard functions are respectively
Denote
. Substituting the above functions into (4) of the non-mixture model with Fréchet susceptible distribution, we obtain the log-likelihood:
The maximum likelihood estimator (MLE) of
is one that maximizes
, denoted by
. The score functions are given below by taking partial derivatives of log-likelihood function (
5) with respect to
:
If the log-likelihood function has a global maximizer, then the MLE is the solution of the score equations. Since it is a non-linear system, numerical solution is computed by the Newton-Raphson method.
5. Simulation Study
We conducted simulation studies to examine the performance of the maximum likelihood estimator of in finite samples. The right-censored survival times were generated by using the inverse transform method to the survival function . We used the following algorithm to simulate a sample of size n from the non-mixture Fréchet distribution with right-censored data:
- Step 1:
Generate a simple sample of from .
- Step 2:
Suppose
p is a cure fraction. The random survival time can be calculated from the equation
if
, otherwise
is infinity.
- Step 3:
Generate the simple sample of the censoring times from a Fréchet distribution and adjust the parameters of the Fréchet distribution to obtain the desired censoring rates.
- Step 4:
The right-censored data is obtained from the minimum of censoring time and survival time. That is .
- Step 5:
The observed data-set is .
- Step 6:
Maximize the likelihood function with respect to to obtain . The standard optimization method, optim() in R is used.
We consider various simulation settings with different proportion of cure fractions and different censoring rates. The censoring variable follows a Fréchet distribution with parameter and , where the value of and would be adjusted to get the desired censoring rate in the right-censored survival data.
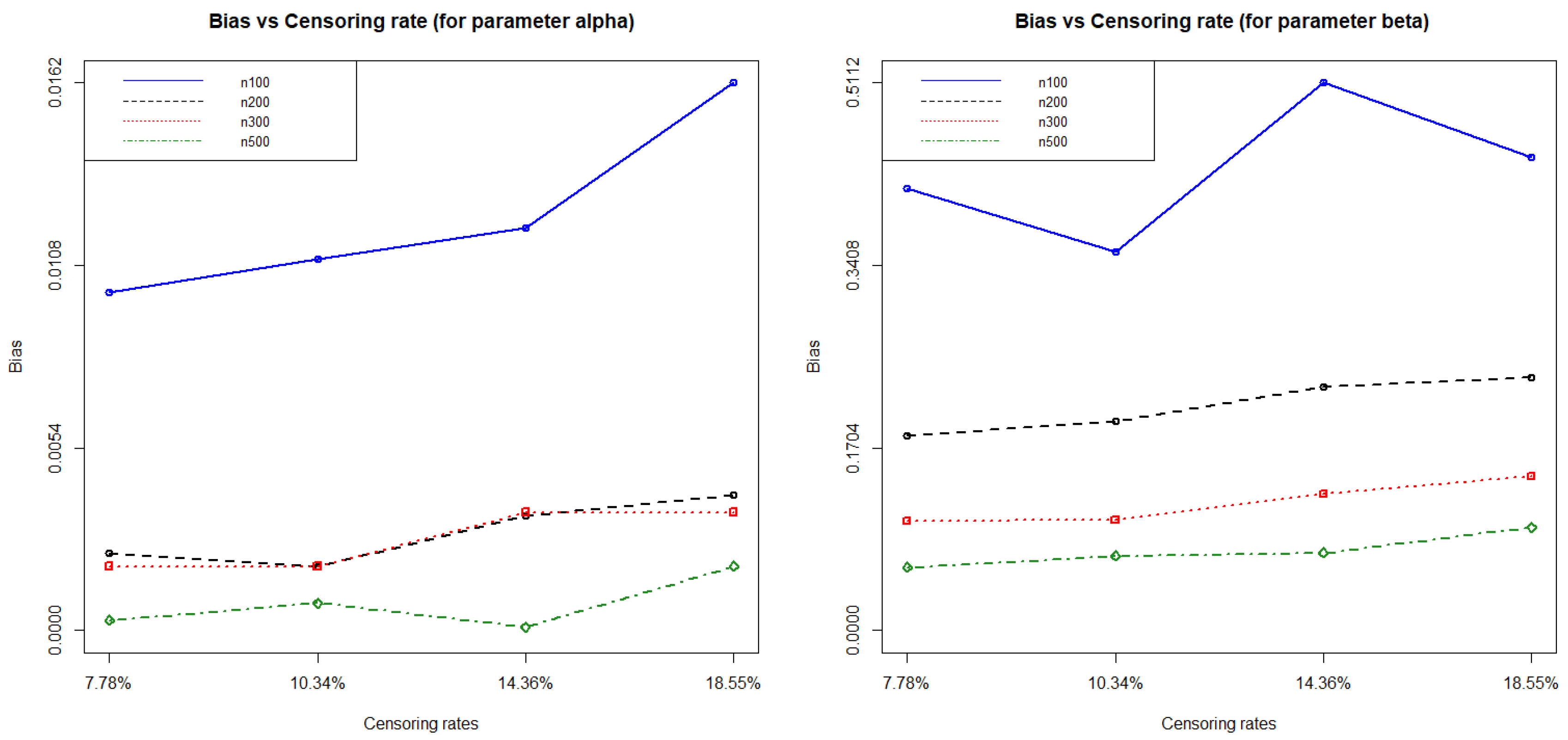
In this simulation study, we are interested in the bias, standard error, root mean square error, and 95% confidence interval as the performance measures. The bias is the difference between the expected value of an estimator and true parameter as given by bias = and the standard error is a measure of the dispersion of the values in the sampling distribution, which is a statistical term that measures the accuracy and is defined by the standard deviation divided by the square root of sample size. The mean square error (MSE) of an estimator is the expected squared deviation of the estimator of a parameter from the true parameter. The root mean square error (RMSE) is the squared root of MSE, where MSE(. The confidence intervals tell you about the parameter of interest and not about the values of the estimated parameter.
The simulation results are based on 500 replications with the sample sizes 100, 200, 300, and 500 for each parameter setting. Results are presented in
Table 1,
Table 2,
Table 3 and
Table 4, which show the values of mean, bias, standard error (SE), root mean square error (RMSE), and 95% confidence interval of MLE. The simulation results suggest that the proposed method has a good performance overall. The averages of the estimates are very close to respective true parameter values in all different settings of simulations. However, the simulation results for cure fractions of both
and
with lower censoring rates perform better than the higher censoring rates. The biases of estimates are small, and the estimates of the standard error (SE), and root mean square error (RMSE) of all examined parameters decreased with increasing sample size for all settings. The length of the confidence interval of each parameter also decreased with increasing sample size for all different setting. The estimates of all examined parameters perform better for low levels of censoring than high levels of censoring. Moreover, the estimates of all examined parameters performed well for low rates of cure proportion compared to high rates of cure proportion. Finally, we can conclude that the MLE works well for the non-mixture cure model with Fréchet susceptible distribution.
The overall censoring rate of
Table 1 is about 7.78%, while
Table 2 is about 10.34%. Moreover,
is the true parameter vector, CR the censoring rate, SE the standard error, RMSE a root mean square error and CI the confidence interval.
The overall censoring rates of
Table 3 is about 14.36%, and
Table 4 is about 18.55%. Moreover,
is the true parameter vector, CR the censoring rate, SE the standard error, RMSE a root mean square error and CI the confidence interval.
Figure 1 shows the relationship between the estimated bias against the censoring rate.
6. A Real Data Analysis
In this section, we would like to compare non-mixture and mixture models with different distributions. We use different susceptible assessments: the negative value of the log-likelihood function, the Akaike’s information Criterion
, the corrected Akaike’s information Criterion
, and the Bayesian Information Criterion
. The
is defined by
, where
is the vector of unknown parameters included in the model,
is the likelihood function and where
k is the number of free parameters in the model. The
is defined by
where
n is the sample size. The BIC is defined by
. A lower value of selection criterion indicates a better fit.
We consider the data-set of 46 patients with an HLA-matched donor-received allogeneic marrow presented by Kersey [
23] in 1987. Out of the 46 patients, 12 with allogeneic transplantation died during their observed periods. Those are the censored observations (26%). Using this data, we compare the non-mixture and mixture models with Fréchet, two parameters Weibull and two parameters Exponentiated Exponential (EE) susceptible distributions using the maximum likelihood method. The density function of Weibull distribution is defined by
and the density function of Exponentiated Exponential distribution is defined by
The notations , , and p are same as to the Fréchet distribution.
Table 5 and
Table 6 show the maximum likelihood estimates of the parameters and their standard errors of the above three susceptible distributions with both non-mixture and mixture models for allogenic marrow transplanted (leukemia) data, respectively.
Table 7 shows the values of
,
,
and
of three susceptible distributions using both mixture and non-mixture models for leukemia data.
Table 7 indicates that Fréchet Distribution is the best within both non-mixture and mixture cure models.
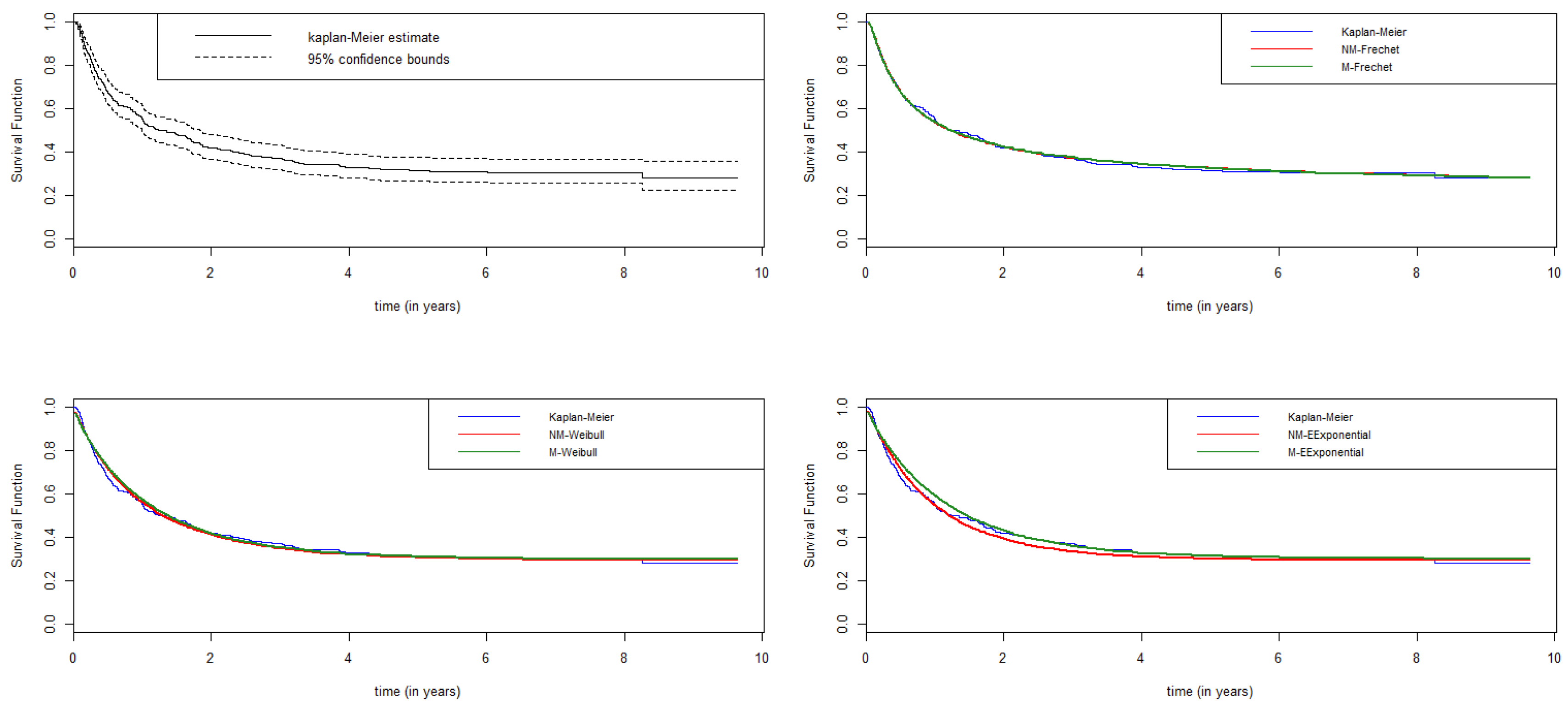
We also compared the Kaplan–Meier survival curves with the parametric curves. The models offer a better fit when they are closer to each other. The top left corner figure of
Figure 2 is the Kaplan–Meier survival curve of the allogenic marrow transplanted data. The top right corner of
Figure 2 is the Kaplan–Meier estimated curve overlaid with the estimated survival curves using Fréchet non-mixture and mixture models. The bottom left corner of
Figure 2 is the Kaplan–Meier estimated curve overlaid with the estimated survival curves using Weibull non-mixture and mixture models. The bottom right corner of
Figure 2 is the Kaplan–Meier estimated curve with survival curve of non-mixture and mixture models of Exponentiated Exponential Distribution. The curve of non-mixture Fréchet distribution is closer to the Kaplan–Meier survival curve in comparison to all other distributions, and the mixture model is a little bit over estimating the survival rate.
The second data-set we considered is the melanoma data without covariates from the Eastern Cooperative Oncology Group (ECOG) phase III clinical trial e1684 available in R package . In this trial, we found that a total of 69% patients are censored. This trial, e1684, was a two-arm clinical trial comparing high-dose interferon alpha-2b (IFN) regimen to observation. There were a total of 286 patients enrolled in the study, collected from 1984 to 1990, and the study was published in 1996. After deleting the missing data, we used a total of 284 observations without covariates for analyzing our models.
The statistical summaries under Fréchet susceptible distribution, two parameters Weibull, and Exponentiated Exponential susceptible distributions are presented in
Table 8 and
Table 9.
Table 10 shows the values of
,
,
and
of different distributions with both mixture and non-mixture models for melanoma data. From the result of
Table 10, we conclude that the Fréchet distribution non-mixture and mixture cure models are better fit, since
,
,
and
are smaller when compared to the other models.
The Kaplan–Meier estimate of survival curve and fitted survival curves of the Fréchet, Weibull and Exponentiated Exponential distributions for the melanoma data are given in
Figure 3. The top left corner figure of
Figure 3 is the Kaplan–Meier survival curve of the melanoma data. The top right corner of
Figure 3 is the Kaplan–Meier estimated curve overlaid with the estimated survival curves using Fréchet non-mixture and mixture models. The bottom left corner of
Figure 3 is the Kaplan–Meier estimated curve overlaid with the estimated survival curves using Weibull non-mixture and mixture models. The bottom right corner of
Figure 3 is the Kaplan–Meier estimated curve with survival curve of non-mixture and mixture model of Exponentiated Exponential distribution. The curve of non-mixture Fréchet distribution is closer to the Kaplan–Meier survival curve in comparison to all other distributions, and the mixture model is a little bit over estimating the survival rate.