Effect of Bend Spacing Configuration on the Vented Explosion Characteristics of Premixed Methane/Hydrogen in Pipelines with a Large Length-to-Diameter Ratio
Abstract
1. Introduction
2. Experimental Set-Up and Methodology
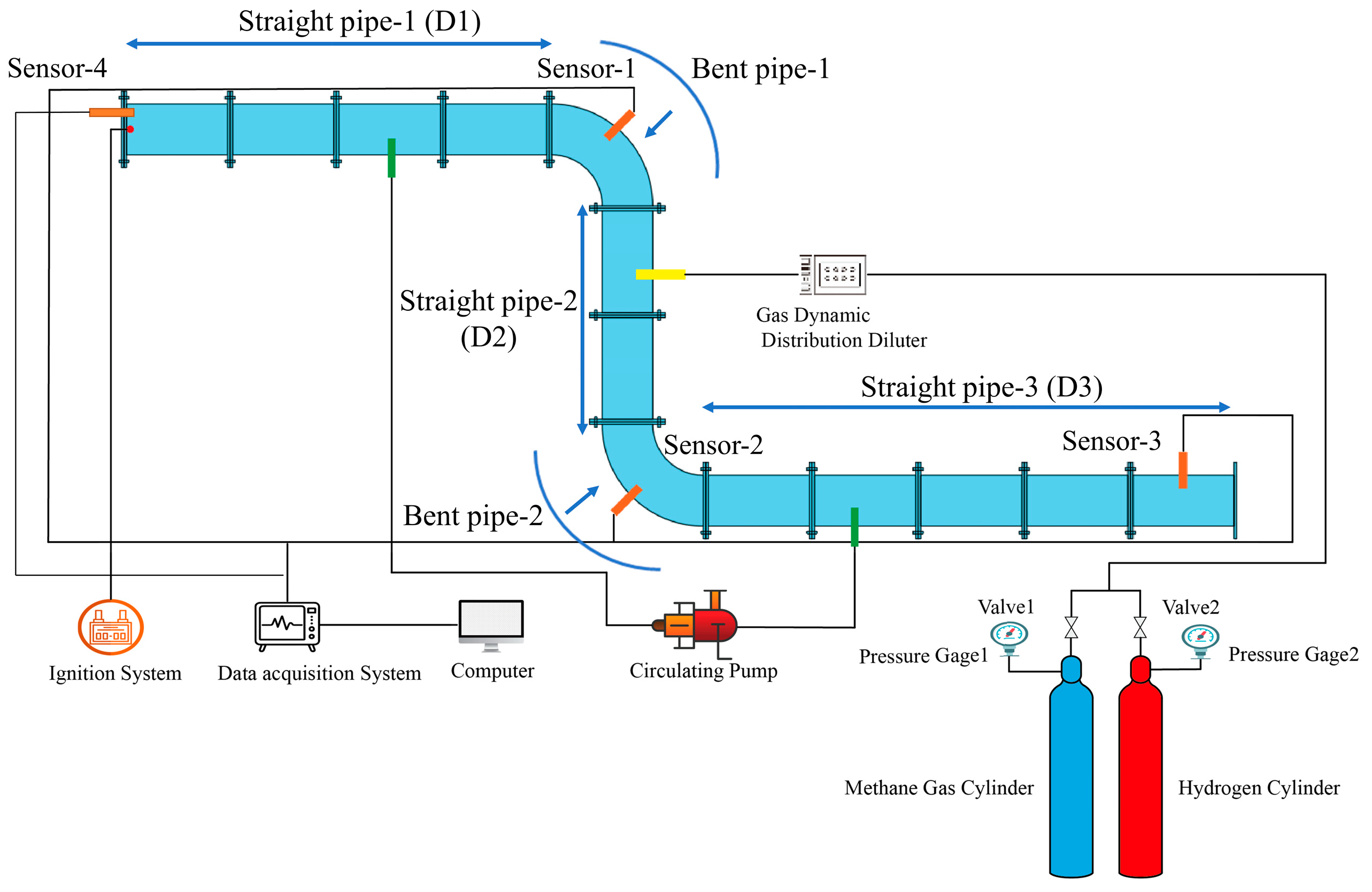
2.1. Experimental Set-Up
2.2. Experimental Methodology
3. Numerical Methods
3.1. Control Equations for Large Eddy Simulation
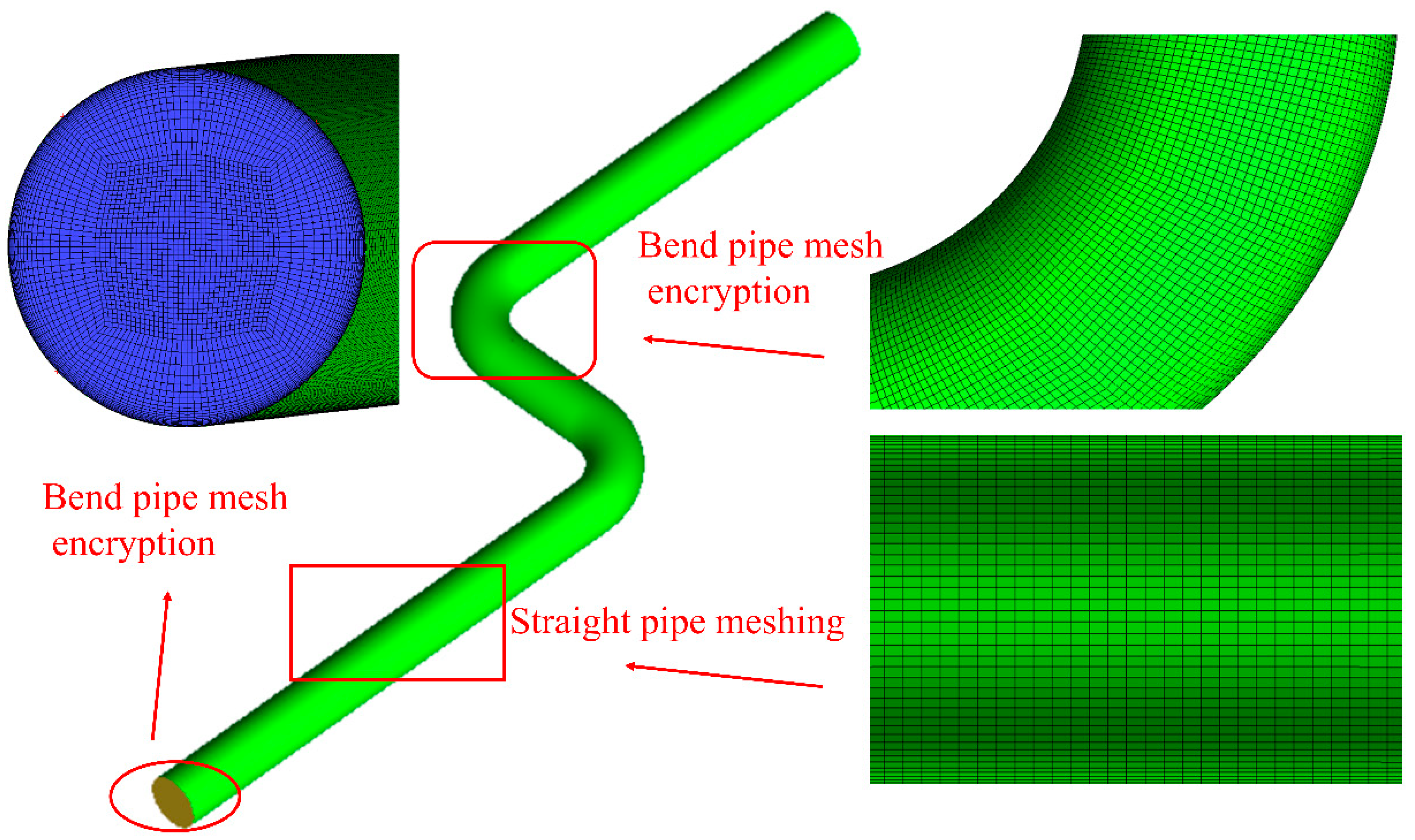
3.2. Computational Model and Meshing
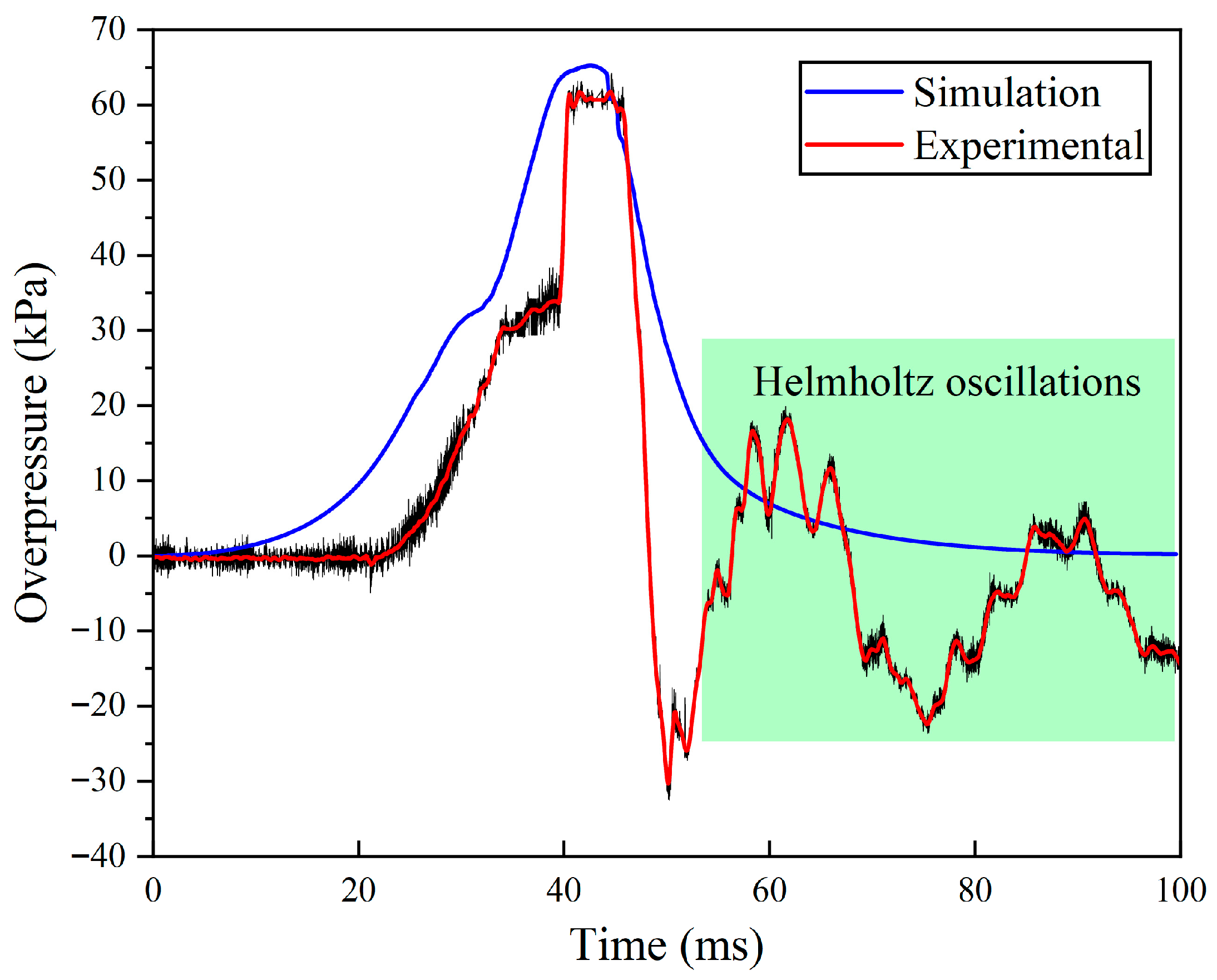
3.3. Numerical Validation
4. Results and Discussion
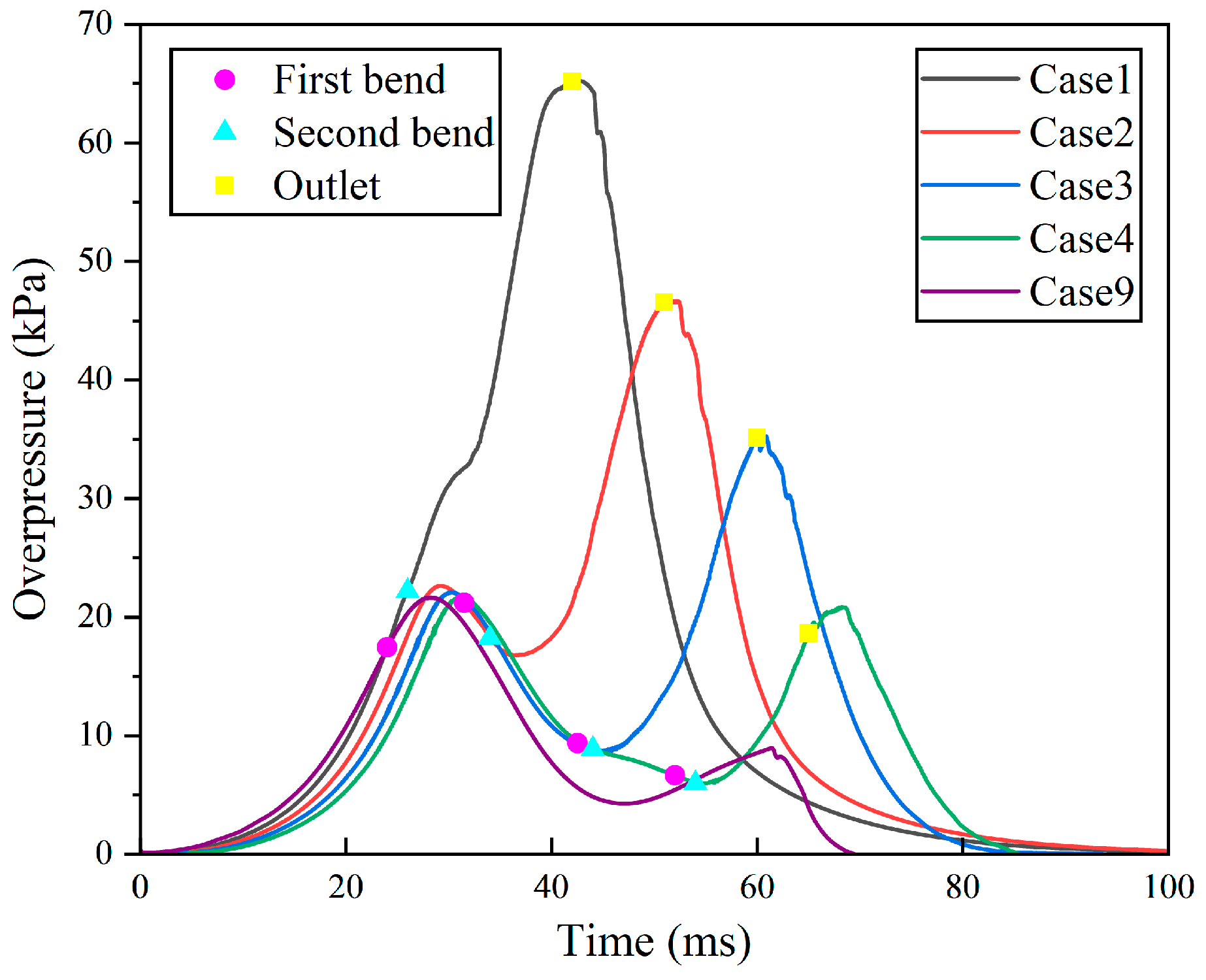
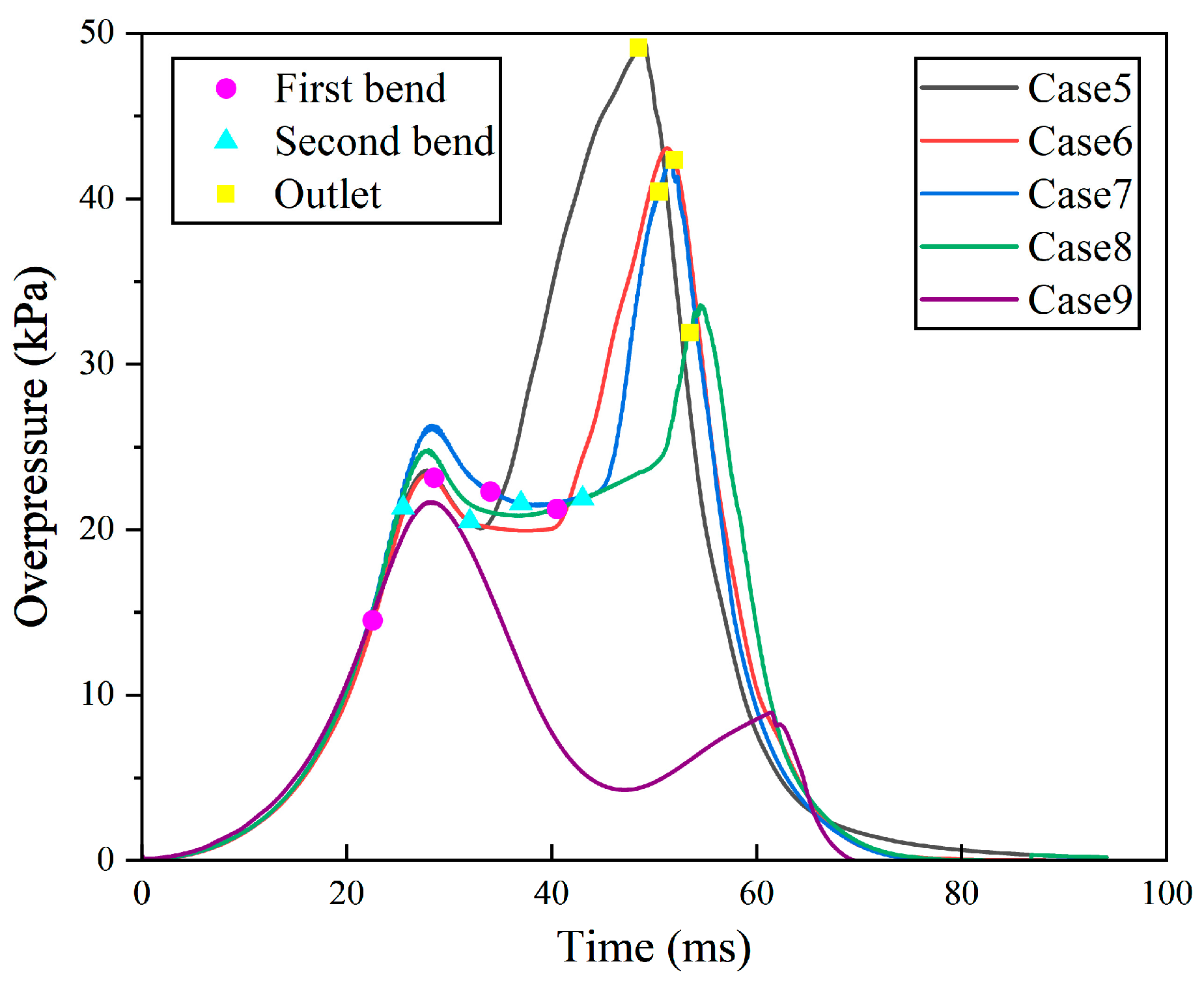
4.1. Effect of Bend Distance Configuration on Pressure Characteristics
4.1.1. Effect of Distance from Bent Pipe-1 to Ignition Source on Pressure
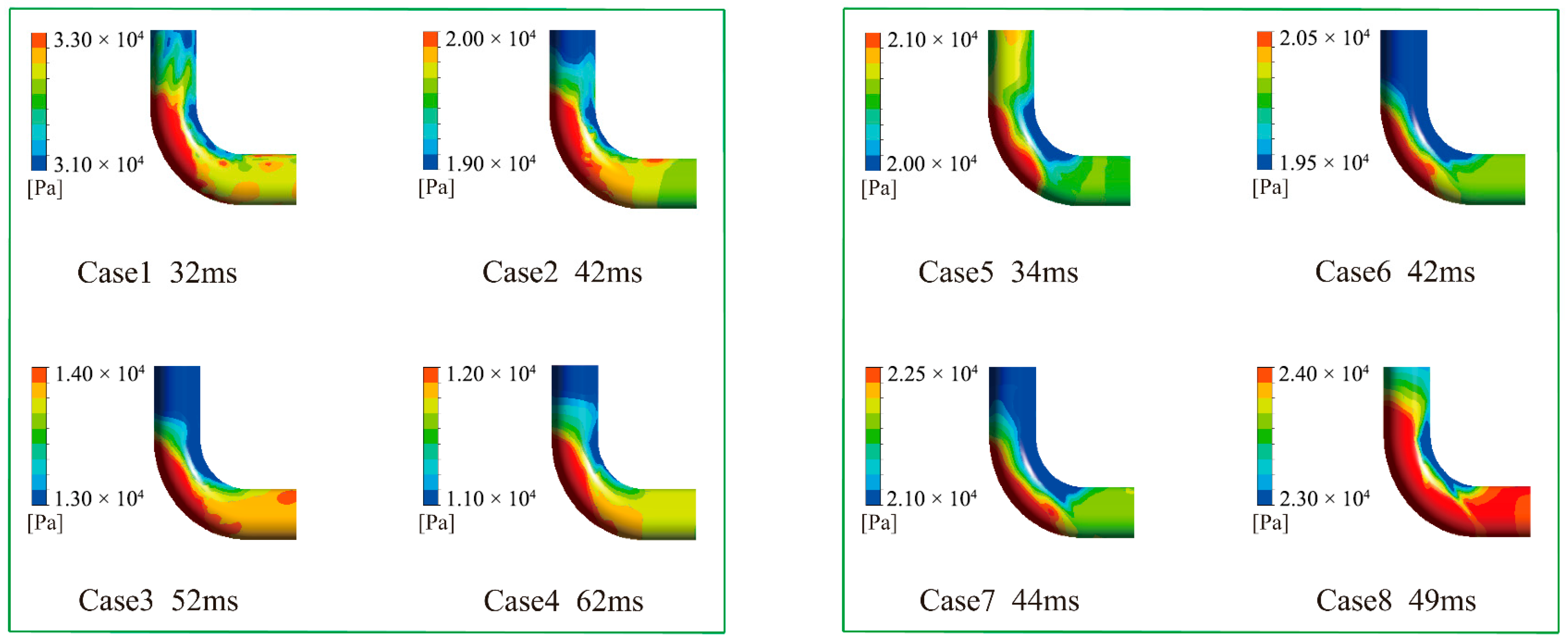
4.1.2. Effect of Distance Between the Bent Pipes on Pressure
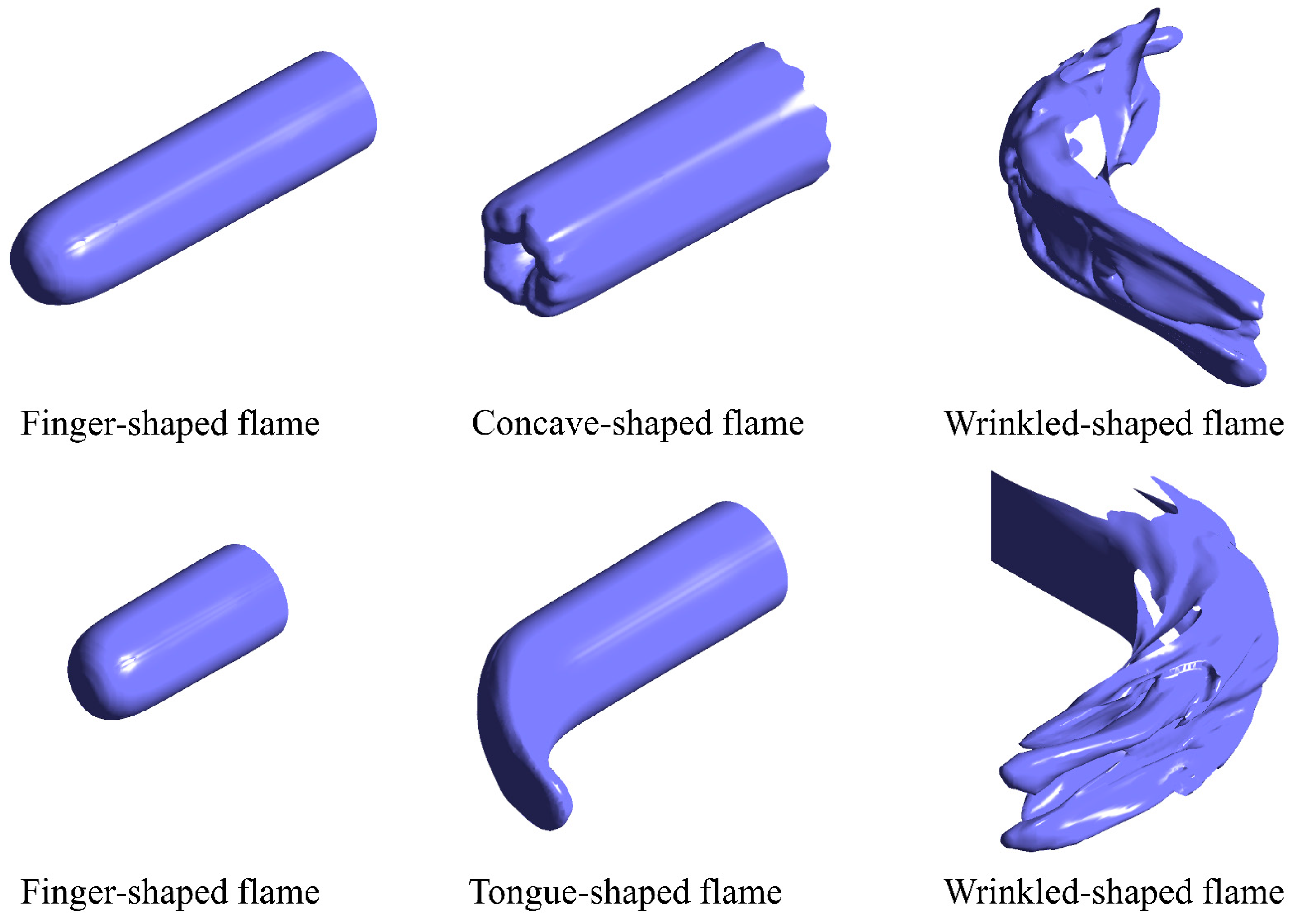
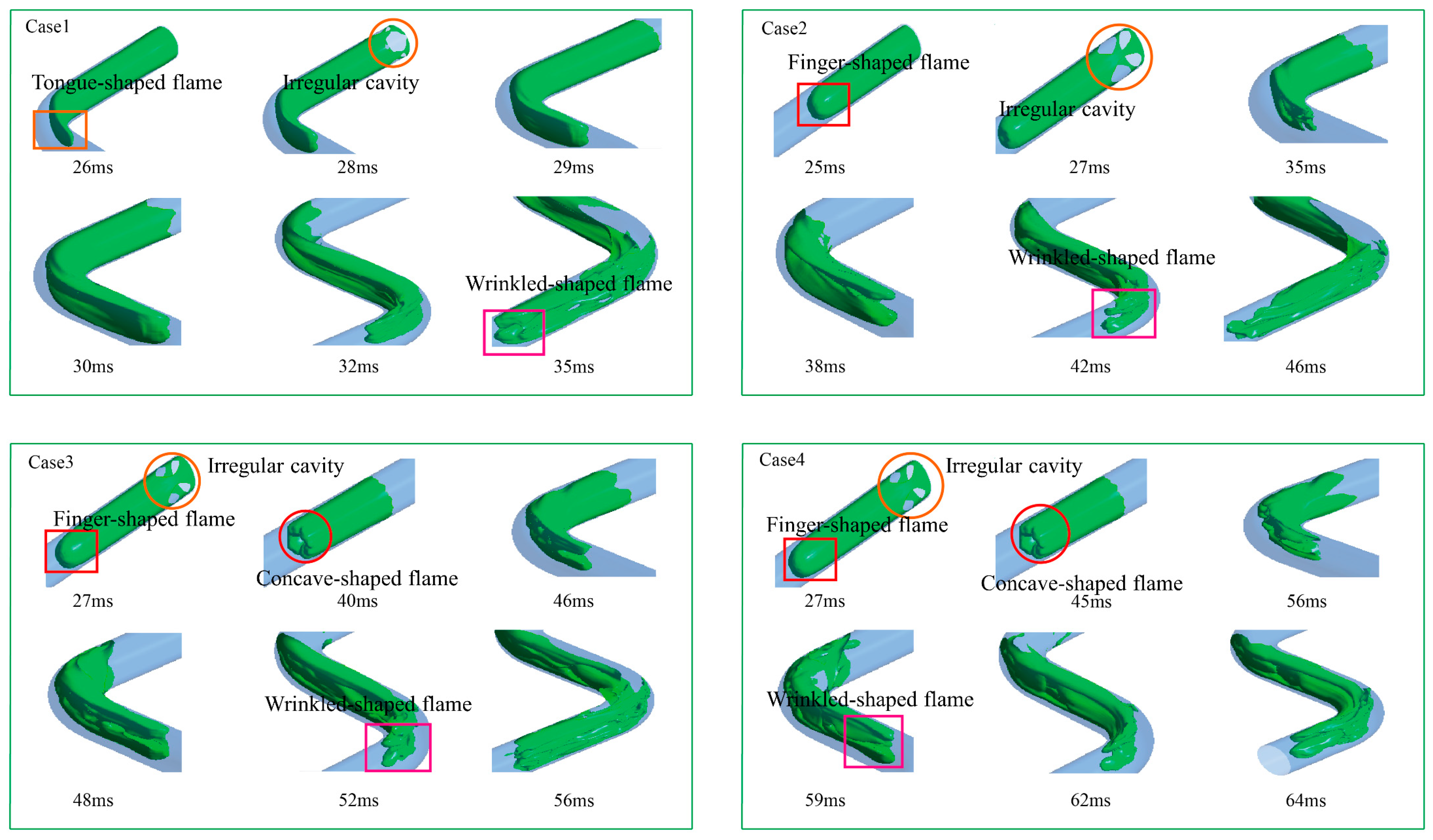
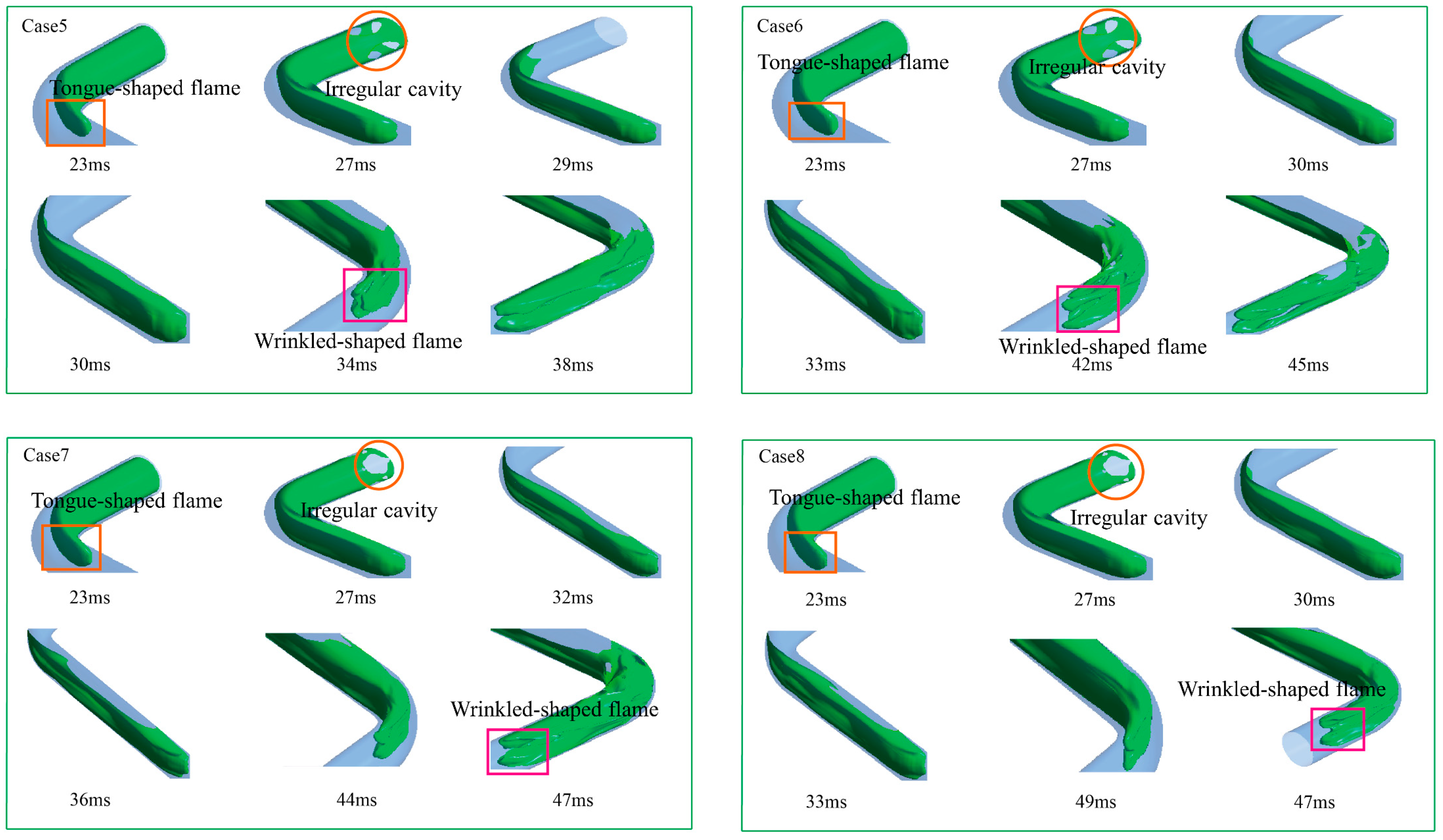
4.2. Effect of Bend Distance Configuration on Flame Morphology
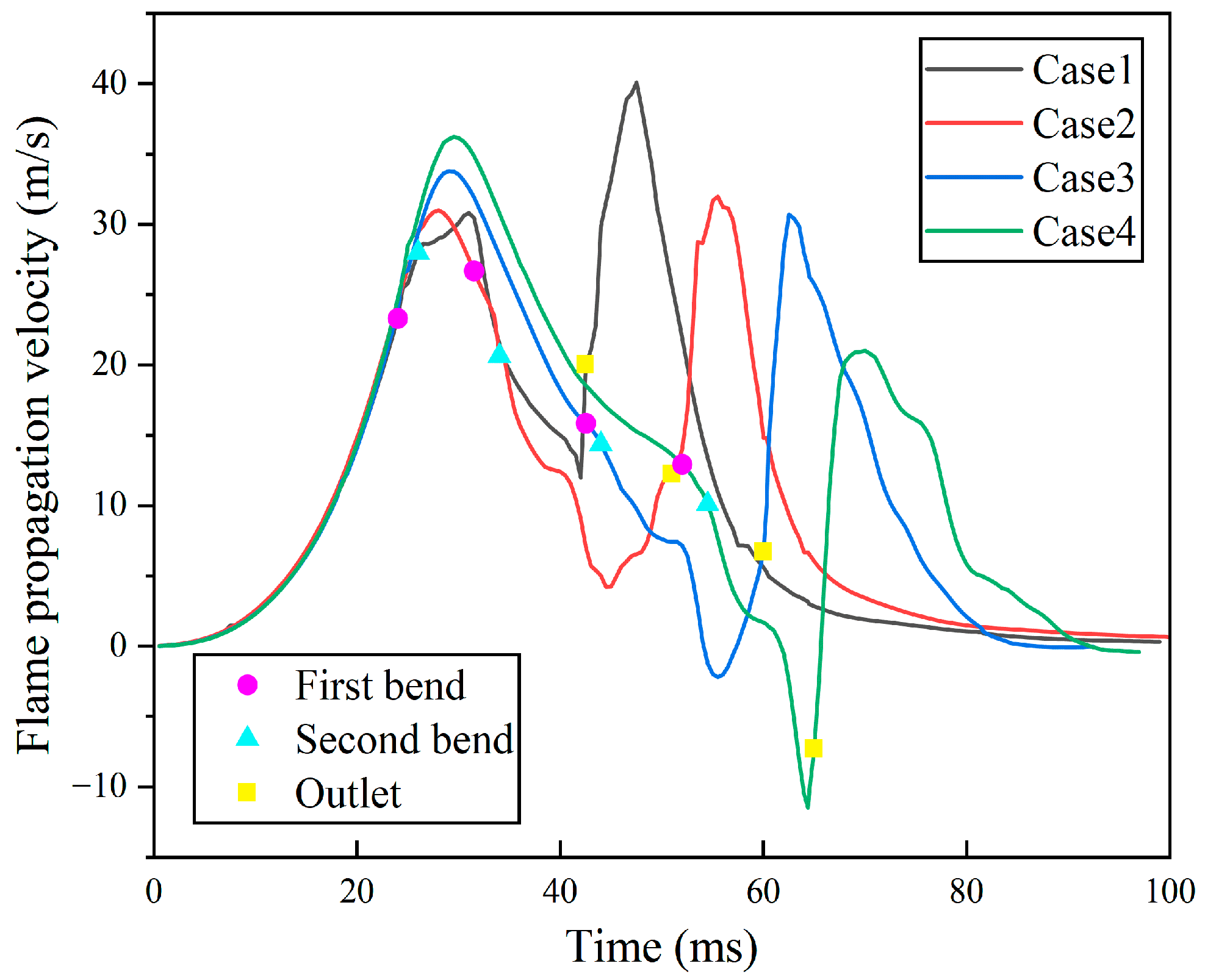
4.3. Effect of Bend Distance Configuration on Flame Propagation Dynamics
4.4. Effect of Bend Distance Configuration on Flame Area and Leading-Edge Position
5. Conclusions
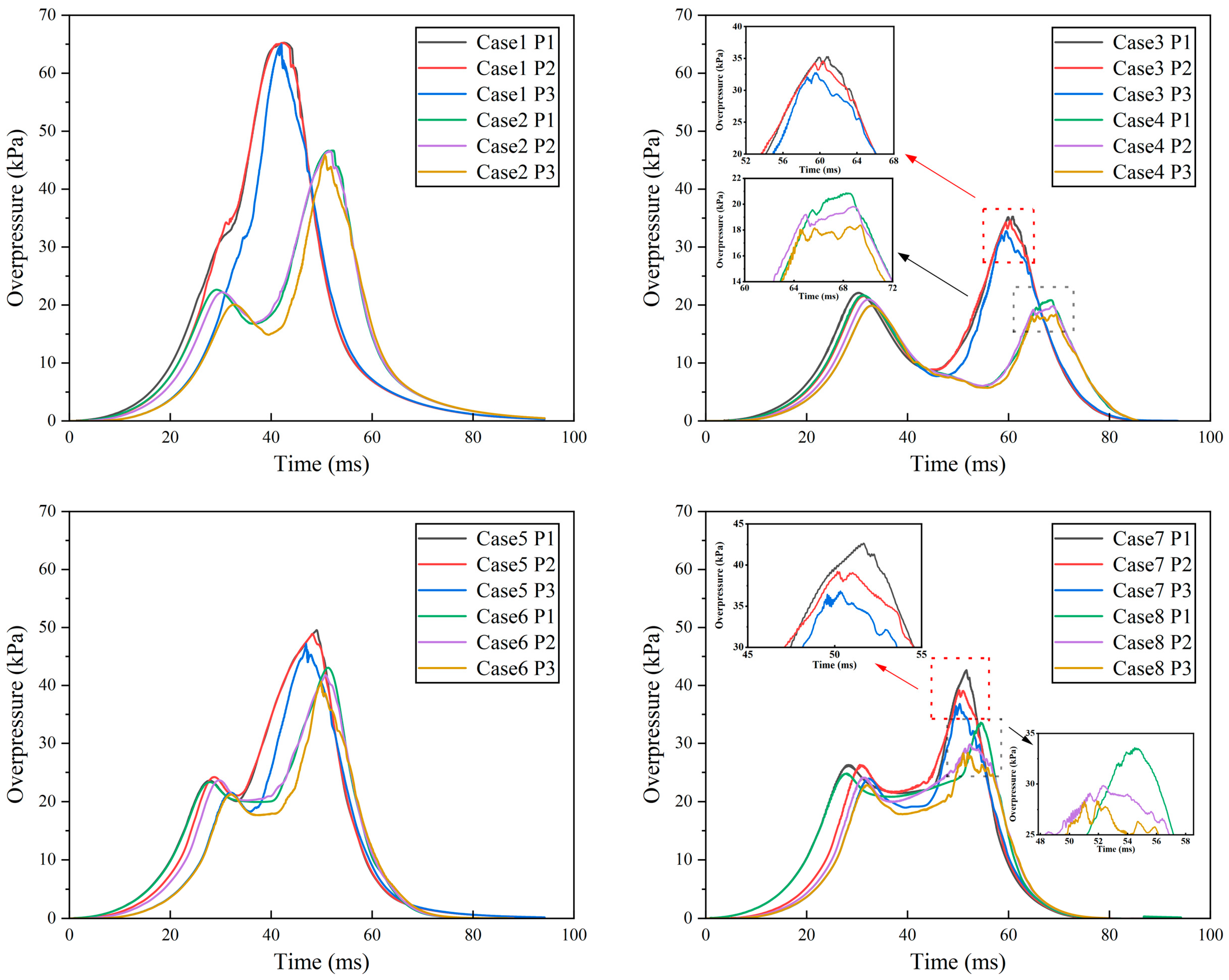
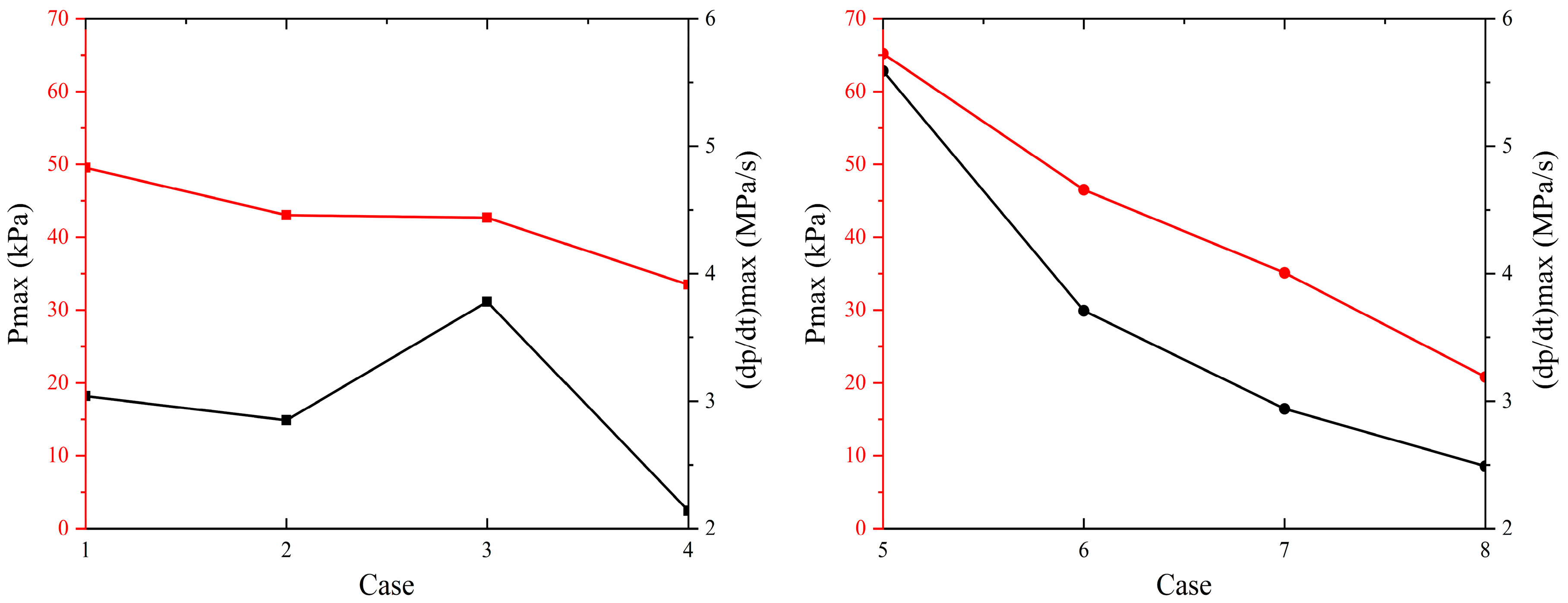
- The Pmax of the straight pipe is 21.7 kPa and the (dp/dt) max is 1.8 MPa/s. After adding the double-bent pipes, Pmax increases to 65.2 kPa, a 200% increase over the straight pipe, and (dp/dt) max increases to 3.7 MPa/s, a 108% increase over the straight pipe. Pmax and (dp/dt)max show an approximately linear decreasing law with the increase of D1 and can be used for explosion hazard prediction. The reflection, refraction, and diffraction of pressure waves at bends represent the primary mechanisms driving the elevation of pressure peaks. In engineering applications, the explosion pressure can be reduced by increasing the length of D1 or D2, among which the effect of the former is more significant.
- As the flame separates from the ignition source, an “irregular cavity” forms in the ignitor area. The high-pressure zone on the outer wall gives rise to the propagation of the flame front along the inner wall; meanwhile, it induces an uneven distribution of flow velocity, which in turn triggers flame wrinkles. Under the conditions of smaller D1 and any D2, the flame propagation presents the three-stage evolution characteristics of “finger-shaped” to “tongue-shaped” to “wrinkled-shaped”. When D1 is large, the flame evolution is a three-stage process of “finger-shaped” to “concave-shaped” to “wrinkled-shaped”.
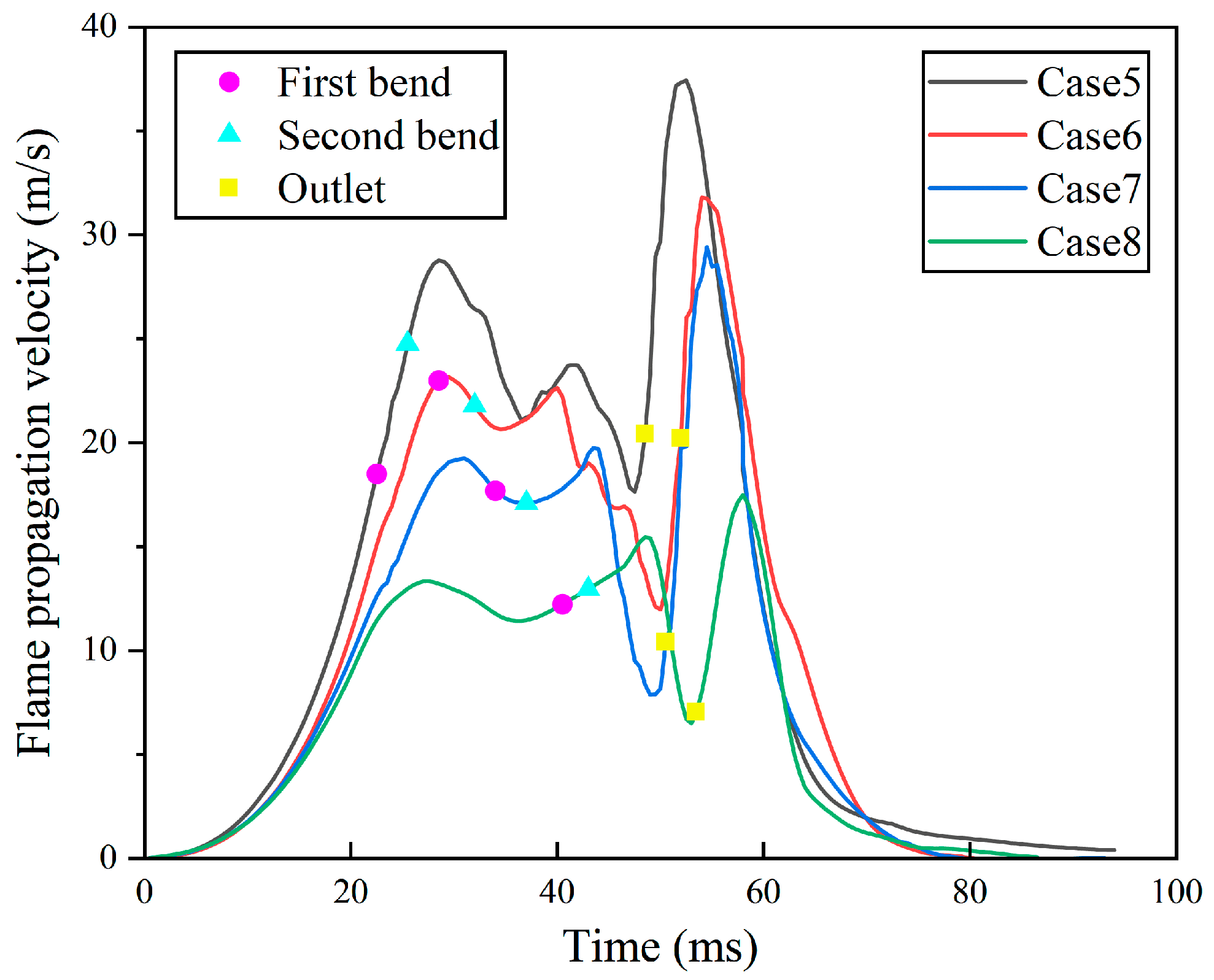
- Simulation results based on accurate and experimentally verified numerical models revealed that the velocity profile from Cases 1 to 4 has a pre- and post-phase, showing two significant velocity peaks. As D1 increases, the facilitative impact of the double-bent pipes on flame propagation weakens, causing speed peak-2 to decline progressively and its occurrence time to be delayed successively. The velocity profile from Cases 5 to 8 exhibits three characteristic peaks, corresponding to the pre, mid, and late stages. In the mid-term stage, due to the large D2, the turbulence intensity changes, providing more favorable conditions for combustion and promoting the formation of speed peak-2. However, its acceleration is significantly lower than that of the pre- and post-phases.
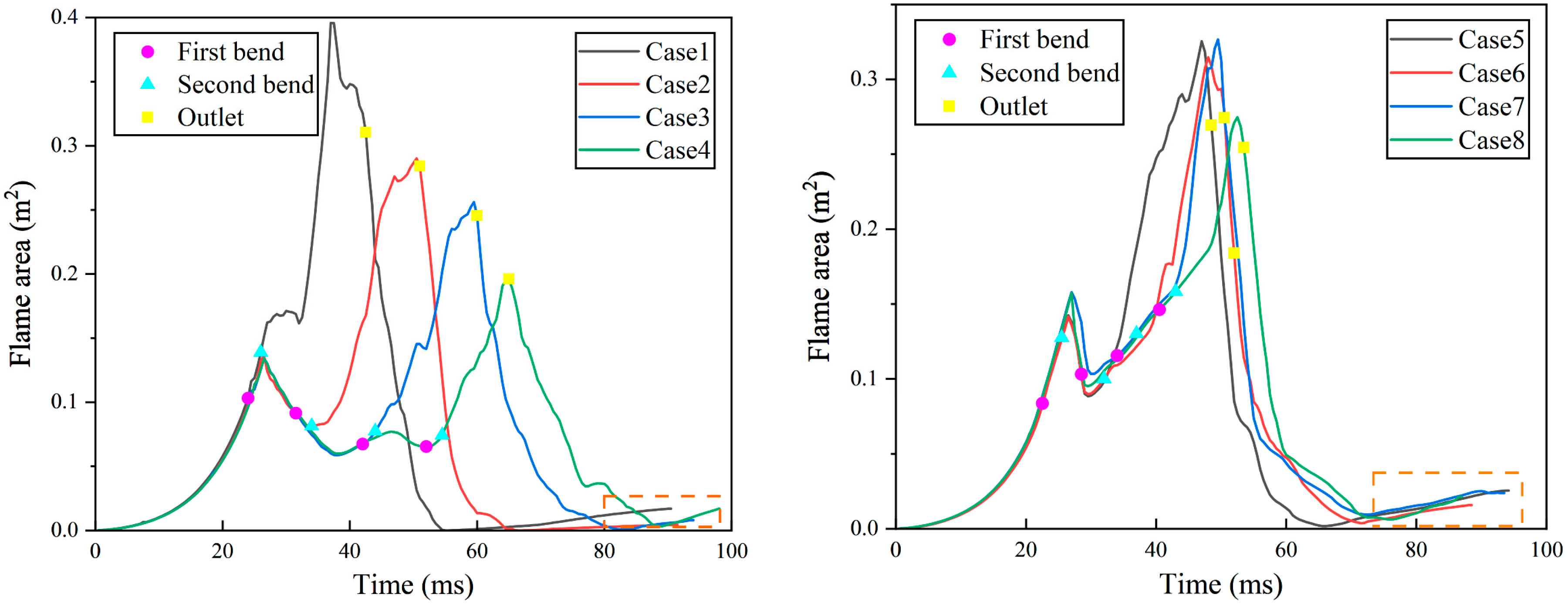
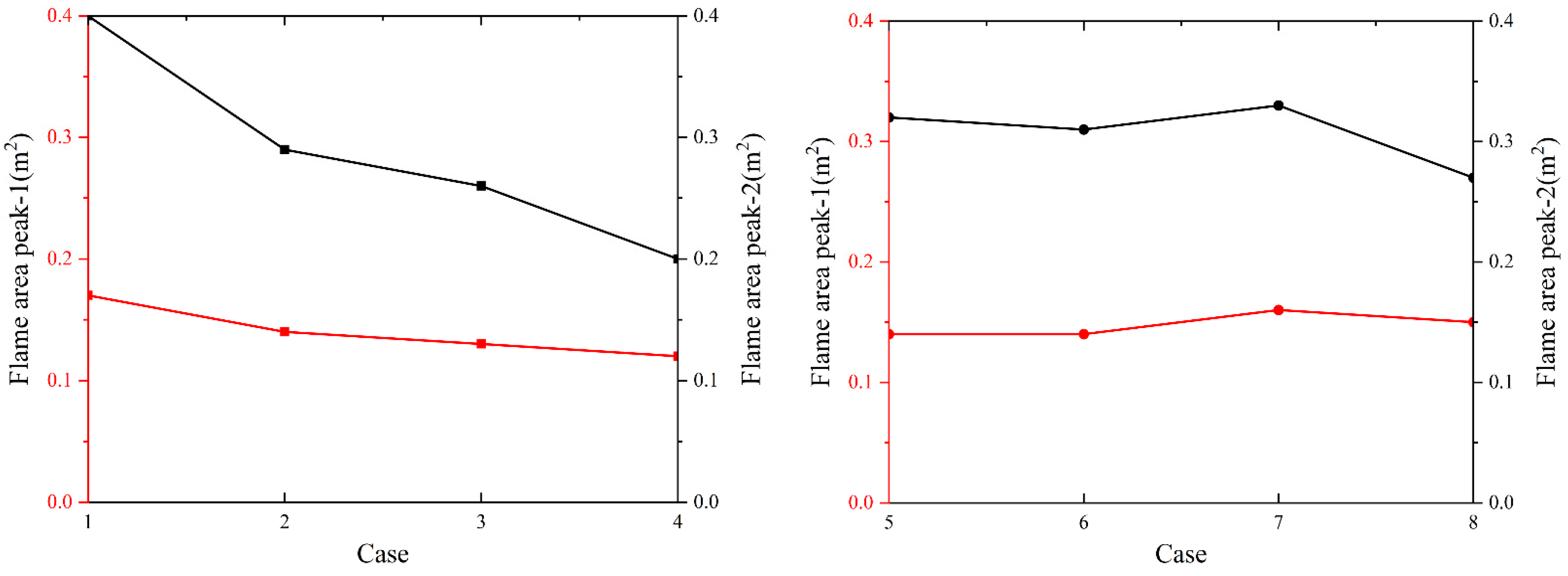
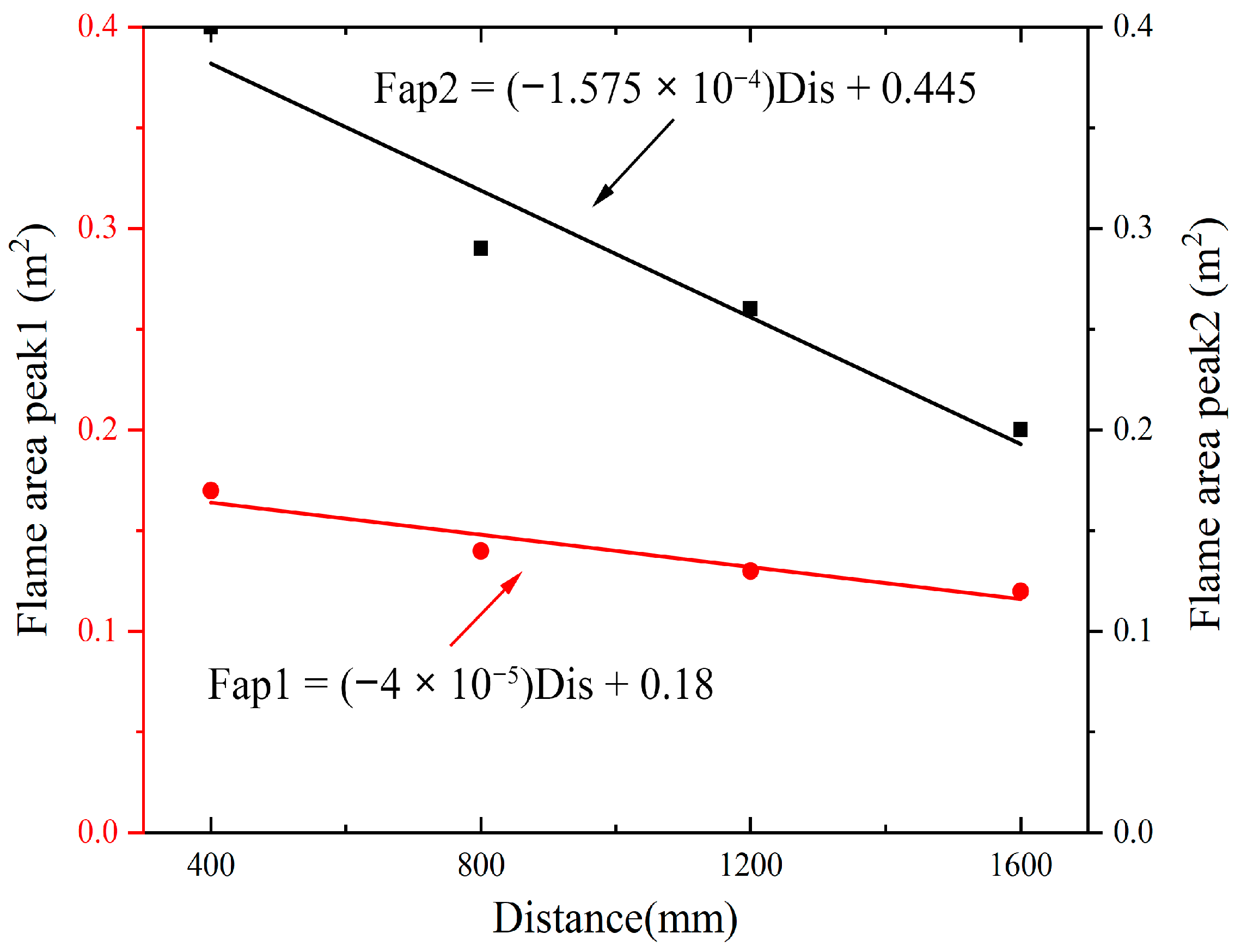
- As D1 increases, the area peak-2 shows a more obvious linear decrease than the area peak-1. For every 400 mm increase in D1, the average area peak-2 decreases by 0.067 m2 and the average area peak-1 decreases by 0.017 m2. No matter how D2 changes, the area peak remains within a relatively stable range. The time for the area curve to reach the area peak-2 is very short, and the flame reflux area is relatively large.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Panda, P.K.; Sahoo, B.; Ramakrishna, S. Electrospun nanofibers for photocatalytic water treatment and hydrogen generation application: A review. Int. J. Hydrogen Energy 2023, 48, 37193–37208. [Google Scholar] [CrossRef]
- Wolański, P. Detonative propulsion. Proc. Combust. Inst. 2013, 34, 125–158. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Q.; Shi, B.; Niu, Y.; Zhong, Z. Influences of a Pipeline’s Bending Angle on the Propagation Law of Coal Dust Explosion Induced by Gas Explosion. Combust. Sci. Technol. 2019, 193, 798–811. [Google Scholar] [CrossRef]
- Ma, Q.; Zhang, Q.; Pang, L.; Huang, Y.; Chen, J. Effects of hydrogen addition on the confined and vented explosion behavior of methane in air. J. Loss Prev. Process Ind. 2014, 27, 65–73. [Google Scholar] [CrossRef]
- Timmerberg, S.; Kaltschmitt, M. Hydrogen from renewables: Supply from North Africa to Central Europe as blend in existing pipelines–Potentials and costs. Appl. Energy 2019, 237, 795–809. [Google Scholar] [CrossRef]
- Xiu, Z.; Liu, Z.; Li, P.; Hao, B.; Li, M.; Zhao, Y.; Cai, P. Effects of combined obstacles on deflagration characteristics of hydrogen-air premixed gas. Int. J. Hydrogen Energy 2023, 48, 31008–31021. [Google Scholar] [CrossRef]
- Jia, W.; Ren, Q.; Zhang, H.; Yang, M.; Wu, X.; Li, C. Multicomponent leakage and diffusion simulation of natural gas/hydrogen mixtures in compressor plants. Saf. Sci. 2023, 157, 105916. [Google Scholar] [CrossRef]
- Crowl, D.A.; Jo, Y.-D. The hazards and risks of hydrogen. J. Loss Prev. Process Ind. 2007, 20, 158–164. [Google Scholar] [CrossRef]
- Molnarne, M.; Schroeder, V. Hazardous properties of hydrogen and hydrogen containing fuel gases. Process Saf. Environ. Prot. 2019, 130, 1–5. [Google Scholar] [CrossRef]
- Yao, Z.; Deng, H.; Dong, J.; Wen, X.; Zhang, X.; Wang, F.; Chen, G. On explosion characteristics of premixed syngas/air mixtures with different hydrogen volume fractions and ignition positions. Fuel 2021, 288, 119619. [Google Scholar] [CrossRef]
- Jeon, J.; Shin, D.; Choi, W.; Kim, S.J. Identification of the extinction mechanism of lean limit hydrogen flames based on Lewis number effect. Int. J. Heat Mass Transf. 2021, 174, 121288. [Google Scholar] [CrossRef]
- Shirvill, L.C.; Roberts, T.A.; Royle, M.; Willoughby, D.B.; Sathiah, P. Experimental study of hydrogen explosion in repeated pipe congestion–Part 1: Effects of increase in congestion. Int. J. Hydrogen Energy 2019, 44, 9466–9483. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Q.; Ma, Q.; Shen, S. Comparison of explosion characteristics between hydrogen/air and methane/air at the stoichiometric concentrations. Int. J. Hydrogen Energy 2015, 40, 8761–8768. [Google Scholar] [CrossRef]
- Chen, Q.; Zhao, K.; Li, B.; Zhang, D.; Mensah, R.A.; Das, O.; Xie, L.; Wang, Y. Effect of hydrogen concentration, vented area, and vented shape on vented hydrogen-air explosions and their consequence analysis. Exp. Therm. Fluid Sci. 2025, 167, 111484. [Google Scholar] [CrossRef]
- Jiang, B.; Tang, M.; Shi, S. Multiparameter acceleration characteristics of premixed methane/air explosion in a semi-confined pipe. J. Loss Prev. Process Ind. 2017, 49, 139–144. [Google Scholar] [CrossRef]
- Li, S.; Xiu, Z.; Li, R.; Ma, J.; Zhao, K.; Liu, Z.; Li, P.; Li, M.; Fan, T. Experimental and theoretical investigations into overpressure during confined space explosions of methane-hydrogen mixture. Process Saf. Environ. Prot. 2024, 187, 91–103. [Google Scholar] [CrossRef]
- Zhang, K.; Du, S.; Chen, H.; Wang, J.; Zhang, J.; Guo, Y.; Guo, J. Effect of hydrogen concentration on the vented explosion of hydrogen–air mixtures in a 5-m-long duct. Process Saf. Environ. Prot. 2022, 162, 978–986. [Google Scholar] [CrossRef]
- He, Q.; Gu, M.; Tang, F.; Sun, X.; Wang, Y. Ceiling radiation heat flux and downward received radiation heat flux of methane jet fire with hydrogen addition. Int. J. Hydrogen Energy 2024, 51, 741–753. [Google Scholar] [CrossRef]
- Cai, P.; Liu, Z.; Li, P.; Zhao, Y.; Li, M.; Li, R.; Wang, C.; Xiu, Z. Effects of fuel component, airflow field and obstacles on explosion characteristics of hydrogen/methane mixtures fuel. Energy 2023, 265, 126302. [Google Scholar] [CrossRef]
- Xiu, Z.; Liu, Q.; Liu, Z.; Li, M.; Li, P.; Hao, B. Coupled behavior of overpressure and vented flame in large-scale constrained spaces during methane deflagration: Effect of ignition position. Process Saf. Environ. Prot. 2025, 198, 107111. [Google Scholar] [CrossRef]
- Bin, H.; Xiu, Z.; Liu, Z. Optimization and improvement of Lee model and its application in large-scale constrained space of premixed methane/air deflagration dynamics analysis. Process Saf. Environ. Prot. 2025, 201, 107603. [Google Scholar] [CrossRef]
- Xiu, Z.; Liu, Z.; Li, P.; Li, M.; Ma, J.; Fan, T.; Hao, B. Research on the dynamics of flame propagation and overpressure evolution in full-scale residential gas deflagration. Case Stud. Therm. Eng. 2024, 62, 105204. [Google Scholar] [CrossRef]
- Pan, X.; Li, Y.; Jiang, Y.; Horri, B.A.; Zhang, T.; Wang, Z.; Wang, Q.; Jiang, J.; Wang, S. Self-ignition and flow characteristics of pressurized hydrogen in Y-shaped tubes. Int. J. Hydrogen Energy 2023, 48, 31412–31423. [Google Scholar] [CrossRef]
- Niu, Y.; Shi, B.; Jiang, B. Experimental study of overpressure evolution laws and flame propagation characteristics after methane explosion in transversal pipe networks. Appl. Therm. Eng. 2019, 154, 18–23. [Google Scholar] [CrossRef]
- Lei, B.; Wei, Q.; Pang, R.; Xiao, J.; Kuznetsov, M.; Jordan, T. The effect of hydrogen addition on methane/air explosion characteristics in a 20-L spherical device. Fuel 2023, 338, 127351. [Google Scholar] [CrossRef]
- Shamsadin Saeid, M.H.; Khadem, J.; Emami, S. Numerical investigation of the mechanism behind the deflagration to detonation transition in homogeneous and inhomogeneous mixtures of H2-air in an obstructed channel. Int. J. Hydrogen Energy 2021, 46, 21657–21671. [Google Scholar] [CrossRef]
- Xiao, H.; He, X.; Duan, Q.; Luo, X.; Sun, J. An investigation of premixed flame propagation in a closed combustion duct with a 90° bend. Appl. Energy 2014, 134, 248–256. [Google Scholar] [CrossRef]
- Mei, Y.; Shuai, J.; Zhou, N.; Ren, W.; Ren, F. Flame propagation of premixed hydrogen-air explosions in bend pipes. J. Loss Prev. Process Ind. 2022, 77, 104790. [Google Scholar] [CrossRef]
- Olugbemide, D.I. A CFD study of the effects of pipe bending angle on pressure piling in coal dust explosions in interconnected vessels. Fire Saf. J. 2022, 128, 103540. [Google Scholar] [CrossRef]
- Wang, Q.; Jin, S.; Wen, H.; Luo, Z.; Shu, C.-M.; Gao, W.; Wang, L.; Lu, X. Dynamic characteristics of methane explosion flame propagation in three types of pipe. Process Saf. Environ. Prot. 2023, 172, 1029–1047. [Google Scholar] [CrossRef]
- Li, S.; Liu, Z.; Zhao, Y.; Li, M.; Li, P. Flame propagation and overpressure characteristics of methane-hydrogen-mixed cloud explosion in unconfined area: Experimental and model study. Process Saf. Environ. Prot. 2025, 197, 106940. [Google Scholar] [CrossRef]
- Gong, L.; Jin, K.; Mo, T.; Zheng, X.; Yao, Y.; Zhang, Y. Numerical investigation on the shock wave propagation, hydrogen/air mixing and spontaneous ignition induced by high-pressure hydrogen release inside the tubes with different shaped cross-sections. Combust. Flame 2023, 252, 112770. [Google Scholar] [CrossRef]
- Ai, B.; Gao, J.; Hao, B.; Guo, B. Effect of Obstacle Length Variation on Hydrogen Deflagration in a Confined Space Based on Large Eddy Simulations. J. Appl. Fluid. Mech. 2024, 17, 384–397. [Google Scholar]
- Zheng, K.; Song, C.; Song, Z.; Ren, J.; Jia, Q. Experimental study on the explosion behavior of nonuniform hydrogen/methane/air mixtures in a duct. Fuel 2024, 368, 131655. [Google Scholar] [CrossRef]
- Hao, B.; Gao, J.; Guo, B.; Ai, B.; Hong, B.; Jiang, X. Numerical Simulation of Premixed Methane–Air Explosion in a Closed Tube with U-Type Obstacles. Energies 2022, 15, 4909. [Google Scholar] [CrossRef]
- Guo, B.; Gao, J.; Hao, B.; Ai, B.; Hong, B.; Jiang, X. Experimental and Numerical Study on the Explosion Dynamics of the Non-Uniform Liquefied Petroleum Gas and Air Mixture in a Channel with Mixed Obstacles. Energies 2022, 15, 7999. [Google Scholar] [CrossRef]
- Gao, J.; Ai, B.; Hao, B.; Guo, B.; Hong, B.; Jiang, X. Effect of Obstacles Gradient Arrangement on Non-Uniformly Distributed LPG–Air Premixed Gas Deflagration. Energies 2022, 15, 6872. [Google Scholar] [CrossRef]
- Han, O.; Zhang, Y.; Li, A.; Li, J.; Li, Y.; Liu, H. Experimental and numerical study on heavy gas contaminant dispersion and ventilation design for industrial buildings. Sustain. Cities Soc. 2020, 55, 102016. [Google Scholar] [CrossRef]
- Kazemi, M.; Brennan, S.; Molkov, V. Hydrogen-methane blends: Critical diameters and flame stability curves for non-premixed turbulent flames. Int. J. Hydrogen Energy 2025, 105, 693–700. [Google Scholar] [CrossRef]
- Su, Y.; Li, J.; Yu, B.; Zhao, Y. Numerical investigation on the leakage and diffusion characteristics of hydrogen-blended natural gas in a domestic kitchen. Renew. Energy 2022, 189, 899–916. [Google Scholar] [CrossRef]
- Long, F.; Duan, Y.; Yu, S.; Jia, H.; Bu, Y.; Huang, J. Effect of porous materials on explosion characteristics of low ratio hydrogen/methane mixture in barrier tube. J. Loss Prev. Process Ind. 2022, 80, 104875. [Google Scholar] [CrossRef]
- Blanchard, R.; Arndt, D.; Grätz, R.; Poli, M.; Scheider, S. Explosions in closed pipes containing baffles and 90 degree bends. J. Loss Prev. Process Ind. 2010, 23, 253–259. [Google Scholar] [CrossRef]
- Liu, L.; Luo, Z.; Su, B.; Hao, R.; Wang, T.; Deng, J.; Song, F. Flame propagation dynamic characteristics and mechanisms of methane–syngas–air mixtures in a semi-enclosed duct. Fuel 2024, 372, 132188. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, B. Characteristics of flame acceleration and deflagration-to-detonation transition enhanced by SF6 jet-in-cross-flow/flame interaction. Aerosp. Sci. Technol. 2023, 140, 108451. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, D.; Li, M.; Xiao, H. Effect of wall roughness on flame acceleration and deflagration-to-detonation transition in a narrow channel. Int. J. Hydrogen Energy 2024, 51, 880–893. [Google Scholar] [CrossRef]
- Luo, C.; Zanganeh, J.; Moghtaderi, B. A 3D numerical study of detonation wave propagation in various angled bending tubes. Fire Saf. J. 2016, 86, 53–64. [Google Scholar] [CrossRef]
- Du, Y.; Zhou, F.; Ma, L.; Zheng, J.; Xu, C.; Chen, G. Dynamic fracture response of pre-flawed elbow pipe subjected to internal hydrogen-oxygen detonation. Int. J. Hydrogen Energy 2018, 43, 19625–19635. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, Y.; Zeng, K.; Liu, B.; Wang, Q.; Jiang, D. Measurements of laminar burning velocities for natural gas–hydrogen–air mixtures. Combust. Flame 2006, 146, 302–311. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Y.; Gao, W. Experimental investigation on the effect of a barrier wall on unconfined hydrogen explosion. Int. J. Hydrogen Energy 2023, 48, 33763–33773. [Google Scholar] [CrossRef]
- Li, S.; Xu, Z.; Wang, F.; Xiu, Z.; Liu, Z.; Li, P.; Li, M. Flame propagation characteristics and thermal radiation hazards of methane-hydrogen-mixed cloud explosion in unconfined area: Experiment research and theoretical modeling. Int. J. Hydrogen Energy 2024, 54, 1563–1574. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Y.; Zhang, Z.; Shang, S.; Gao, W. Experimental and theoretical investigation on hydrogen cloud explosion subjected to external turbulence. Int. J. Hydrogen Energy 2023, 48, 15331–15340. [Google Scholar] [CrossRef]


| Case | Length (mm) | ||
|---|---|---|---|
| D1 | D2 | D3 | |
| 1 | 400 | 200 | 1400 |
| 2 | 800 | 200 | 1000 |
| 3 | 1200 | 200 | 600 |
| 4 | 1600 | 200 | 200 |
| 5 | 200 | 400 | 1400 |
| 6 | 200 | 800 | 1000 |
| 7 | 200 | 1200 | 600 |
| 8 | 200 | 1600 | 200 |
| 9 | 2000 (long straight pipe) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Gao, J.; Hao, B.; Han, Y.; Shao, X.; Wu, Y.; Wu, X.; Li, M. Effect of Bend Spacing Configuration on the Vented Explosion Characteristics of Premixed Methane/Hydrogen in Pipelines with a Large Length-to-Diameter Ratio. Fire 2025, 8, 328. https://doi.org/10.3390/fire8080328
Yang Y, Gao J, Hao B, Han Y, Shao X, Wu Y, Wu X, Li M. Effect of Bend Spacing Configuration on the Vented Explosion Characteristics of Premixed Methane/Hydrogen in Pipelines with a Large Length-to-Diameter Ratio. Fire. 2025; 8(8):328. https://doi.org/10.3390/fire8080328
Chicago/Turabian StyleYang, Yulin, Jianfeng Gao, Bin Hao, Yanan Han, Xiaojun Shao, Yang Wu, Xiao Wu, and Meng Li. 2025. "Effect of Bend Spacing Configuration on the Vented Explosion Characteristics of Premixed Methane/Hydrogen in Pipelines with a Large Length-to-Diameter Ratio" Fire 8, no. 8: 328. https://doi.org/10.3390/fire8080328
APA StyleYang, Y., Gao, J., Hao, B., Han, Y., Shao, X., Wu, Y., Wu, X., & Li, M. (2025). Effect of Bend Spacing Configuration on the Vented Explosion Characteristics of Premixed Methane/Hydrogen in Pipelines with a Large Length-to-Diameter Ratio. Fire, 8(8), 328. https://doi.org/10.3390/fire8080328






