New Experimental Approaches for the Determination of Flammability Limits in Methane–Hydrogen Mixtures with CO2 Inertization Using the Spark Test Apparatus
Abstract
1. Introduction
- USBM method: The explosion occurs in a cylindrical vertical tube with an inner diameter of 50 mm and a length of 1500 mm. The ignition is made by an electric spark or a pilot flame passing by the open lower end of the tube.
- ATSM 681-98 standard [31]: The explosion occurs in a 5 dm3 spherical glass; the ignition is made by a central spark igniter of 15 kV.
- German method according to DIN 51 649 [32]: The explosion occurs in a cylindrical vertical glass tube with an inner diameter of 60 mm and a length of 300 mm. An electric spark igniter of 15 kV was located at the tube bottom.
- Explosion vessel method: This method uses a closed volume chamber (spherical or cylindrical) into which a flammable mixture is introduced. Ignition is produced by an electric spark or a pilot flame, and the ignition criterion is usually based on the maximum pressure reached during combustion. This method is regulated by several standards such as ISO 10156 and EN 1839 [33] used to assess the flammability of gases and vapors.
- Shock tube method: In this method, the ignition of a mixture is studied in a long tube, where a shock wave causes combustion. It is mainly used in chemical kinetics and ignition dynamics investigations, rather than in standard industrial LFL and UFL studies.
- Moving vessel method: In this method, swelling is studied inside a vessel that moves or rotates during the process, allowing the simulation of flow or turbulent conditions. This type of technique is less common but is useful for studies in which flow dynamics affect the ignitable behavior.
- Pressure increase: In methods such as the explosion chamber method and ASTM E681-98, ignition is considered to have occurred when a sudden increase in pressure is detected in the chamber after application of the ignition source. Normally, a pressure increase of 5 to 10% above the initial value is taken as evidence of ignition.
- Flame visualization: In methods such as USBM and DIN 51 649, the propagation of a visible flame or explosion through a tube or chamber can be directly observed. If the flame travelled from the ignition point through the gaseous mixture, ignition was considered to have occurred.
- Burning rate: Some techniques, particularly in more detailed studies of combustion kinetics, use the fuel consumption rate or flame propagation speed as additional criteria for defining ignition.
- Temperature: In some experiments, thermocouples or temperature sensors may be used to detect a sudden rise in the temperature of the gas mixture, indicating a combustion reaction.
2. Materials and Methods
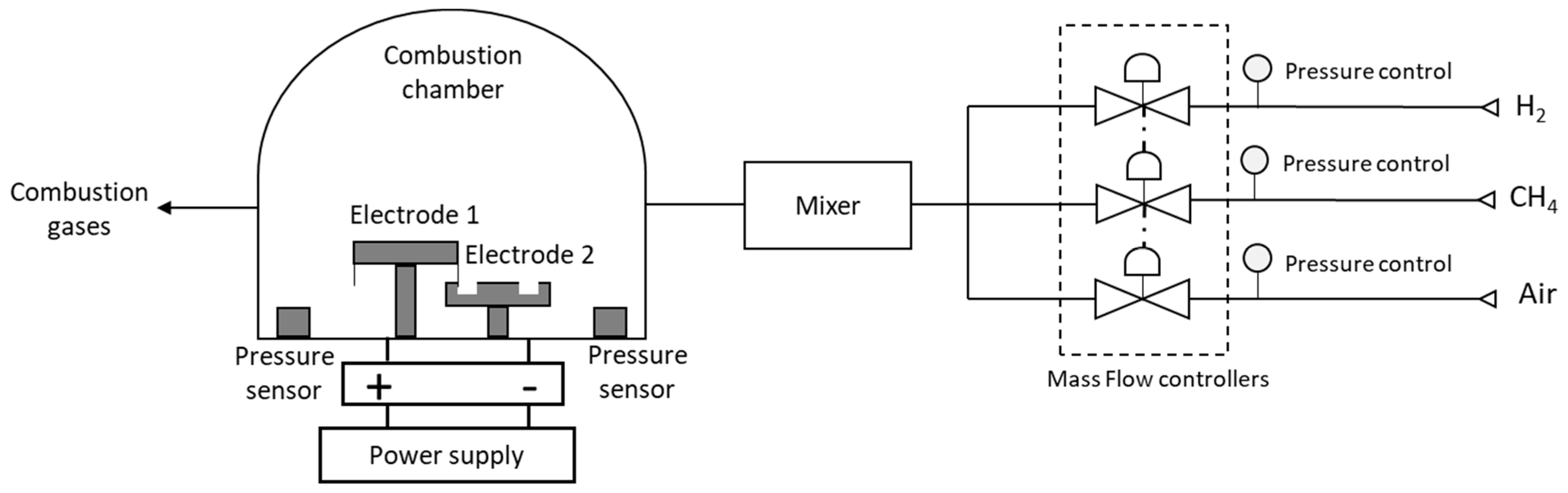
2.1. Experimental Development in the STA
2.2. Experimental System Validation
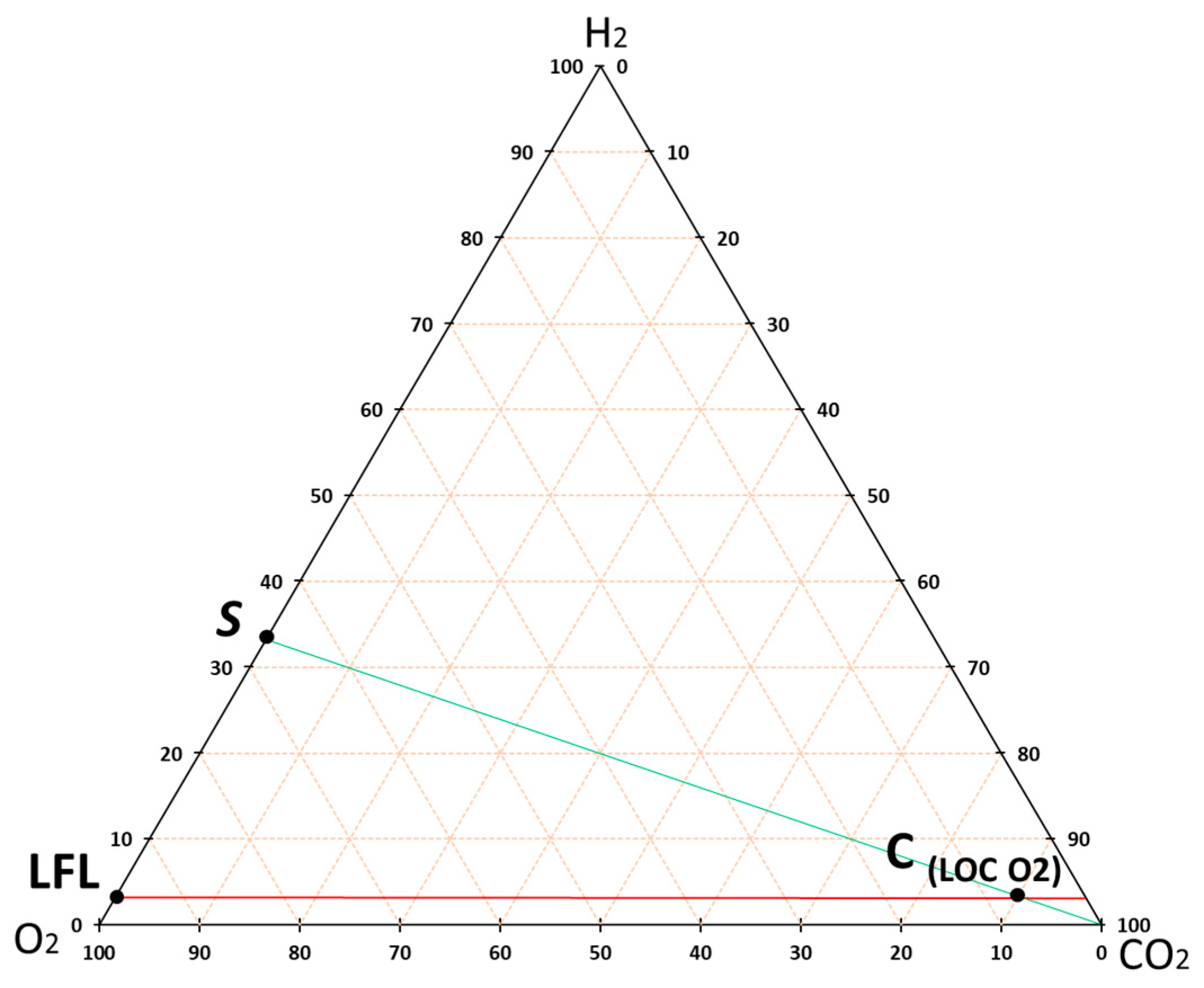
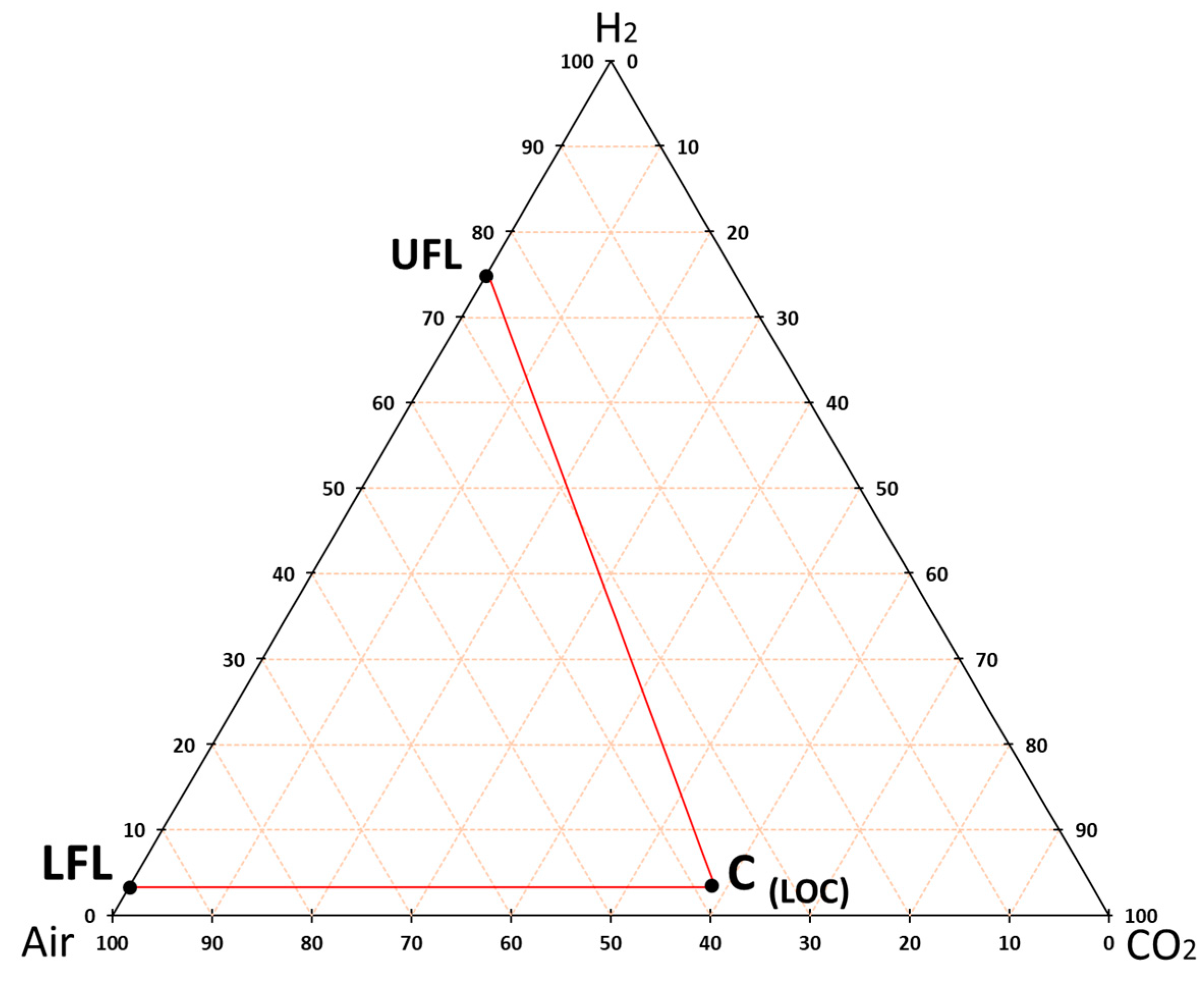
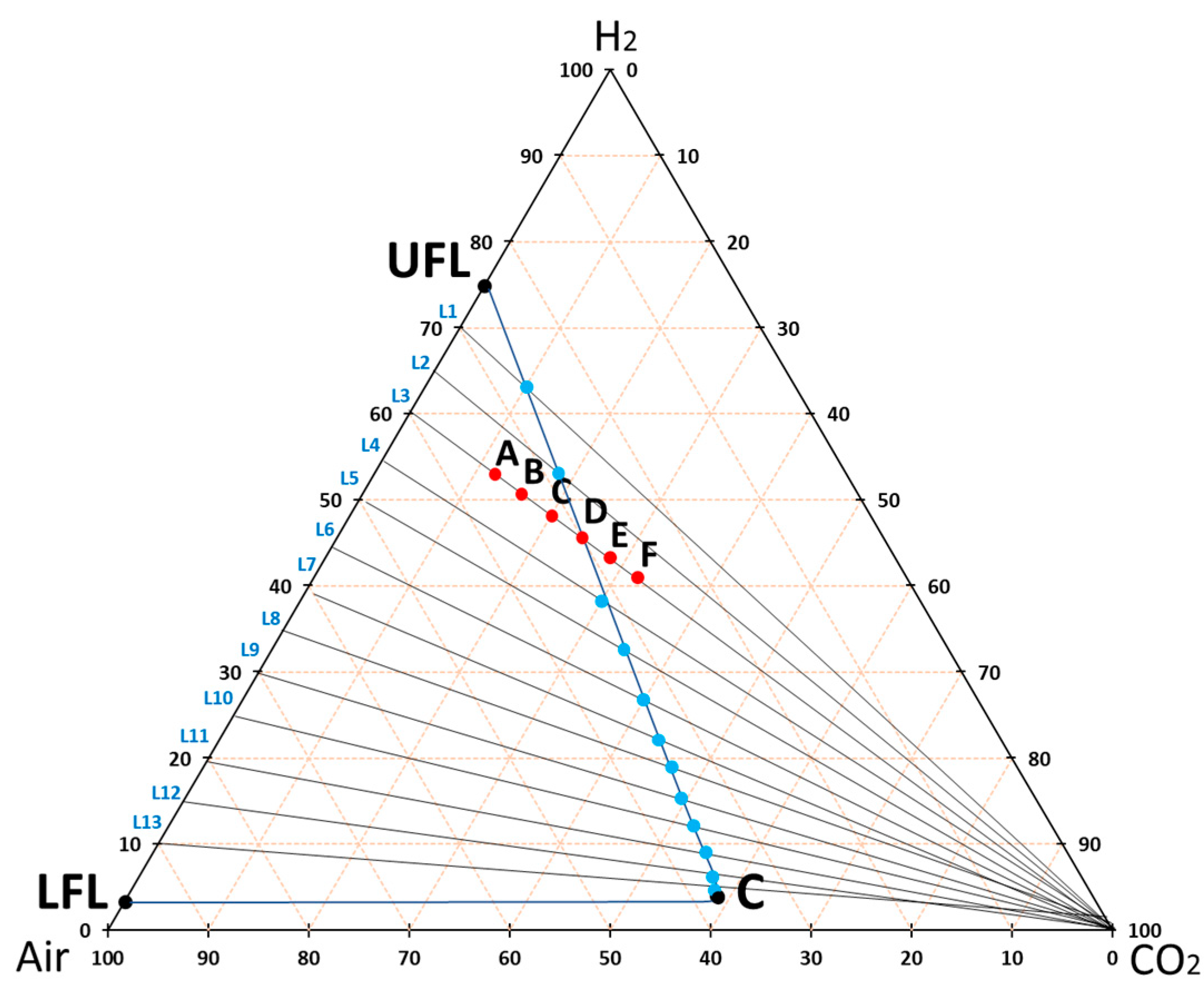
2.3. Experimental and Theoretical Methodology to Obtain the Flammability Intervals in the STA
3. Results and Discussion
3.1. Experimental Results of the Flammability Limits
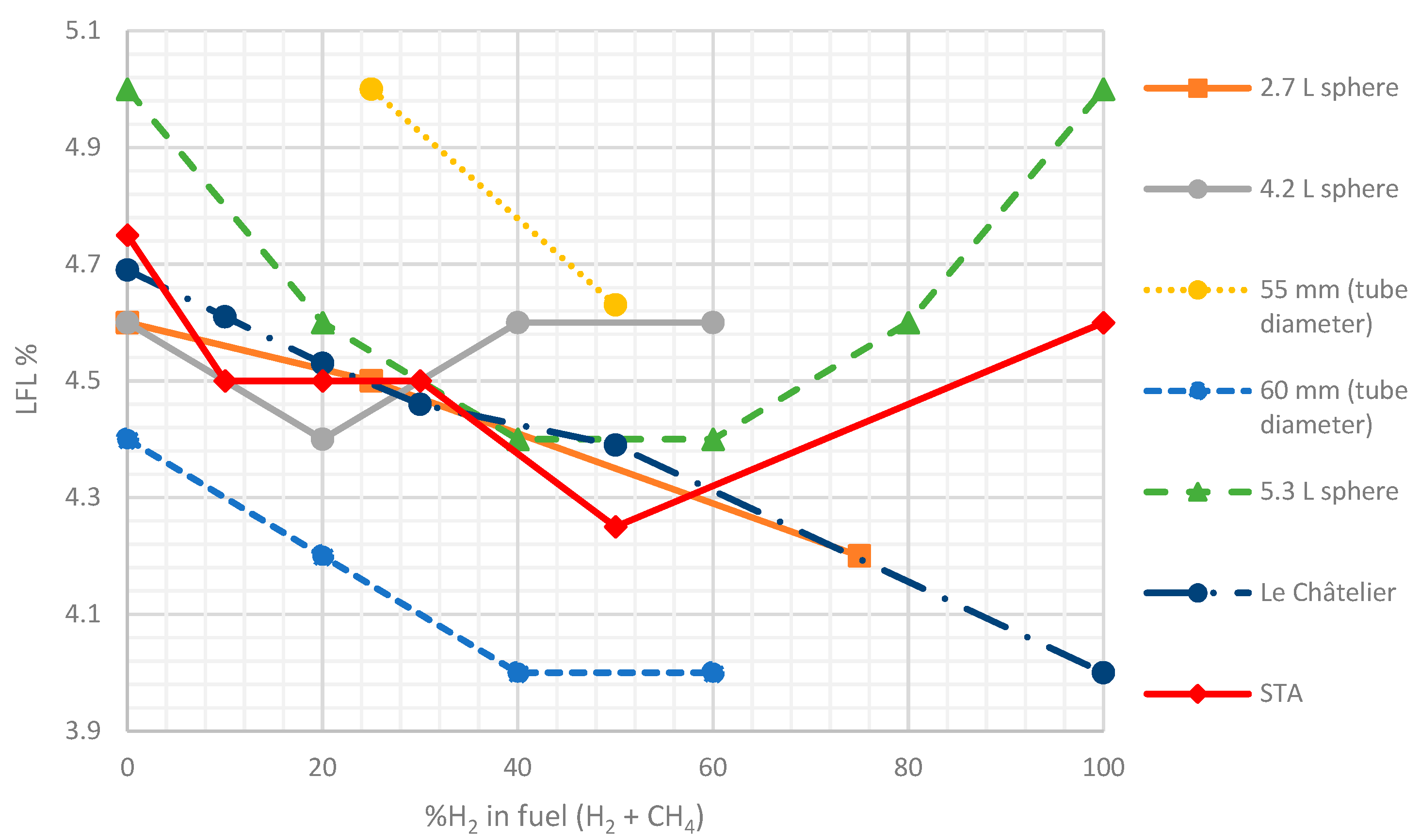
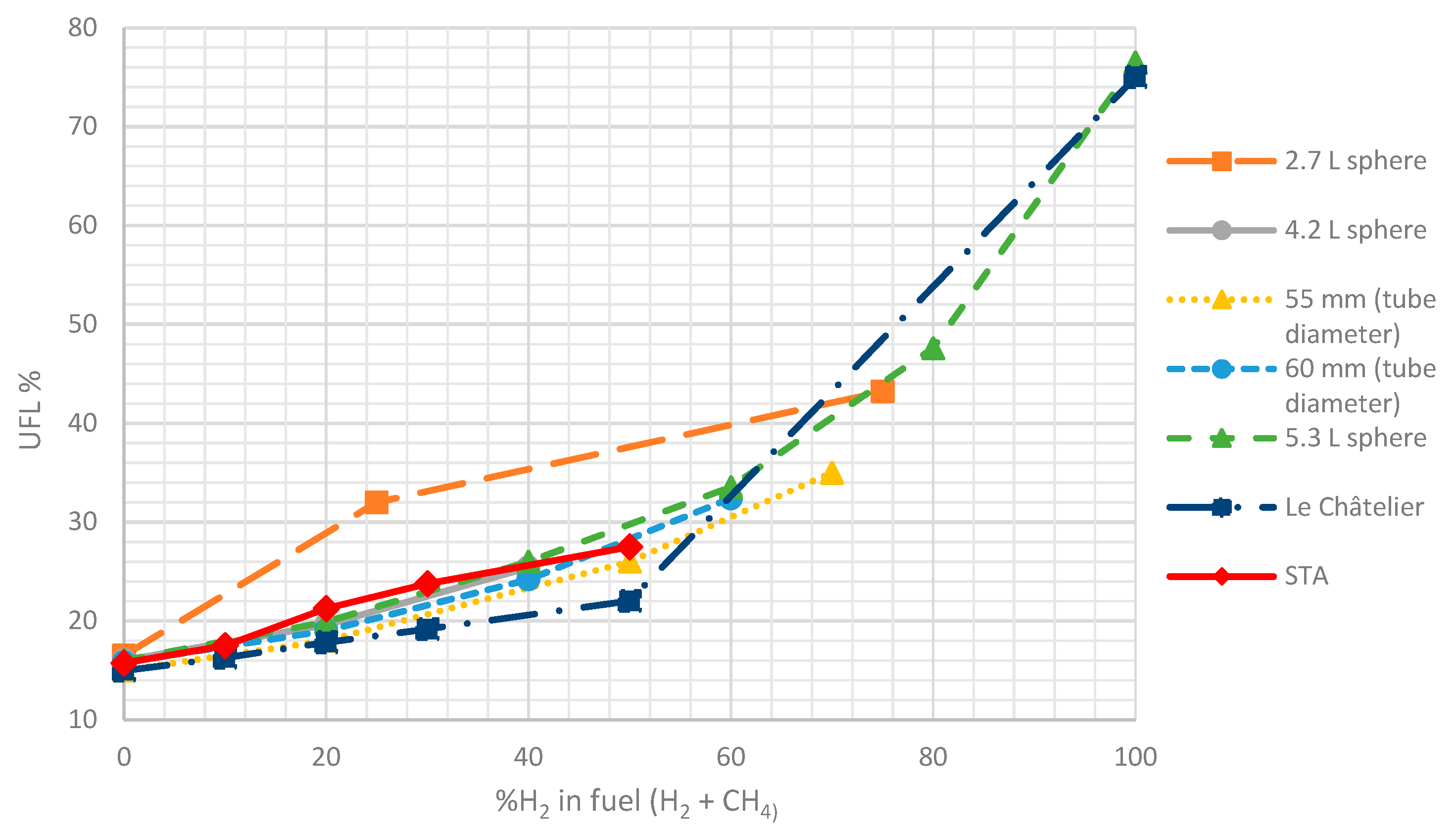
3.2. Experimental System Validation Results
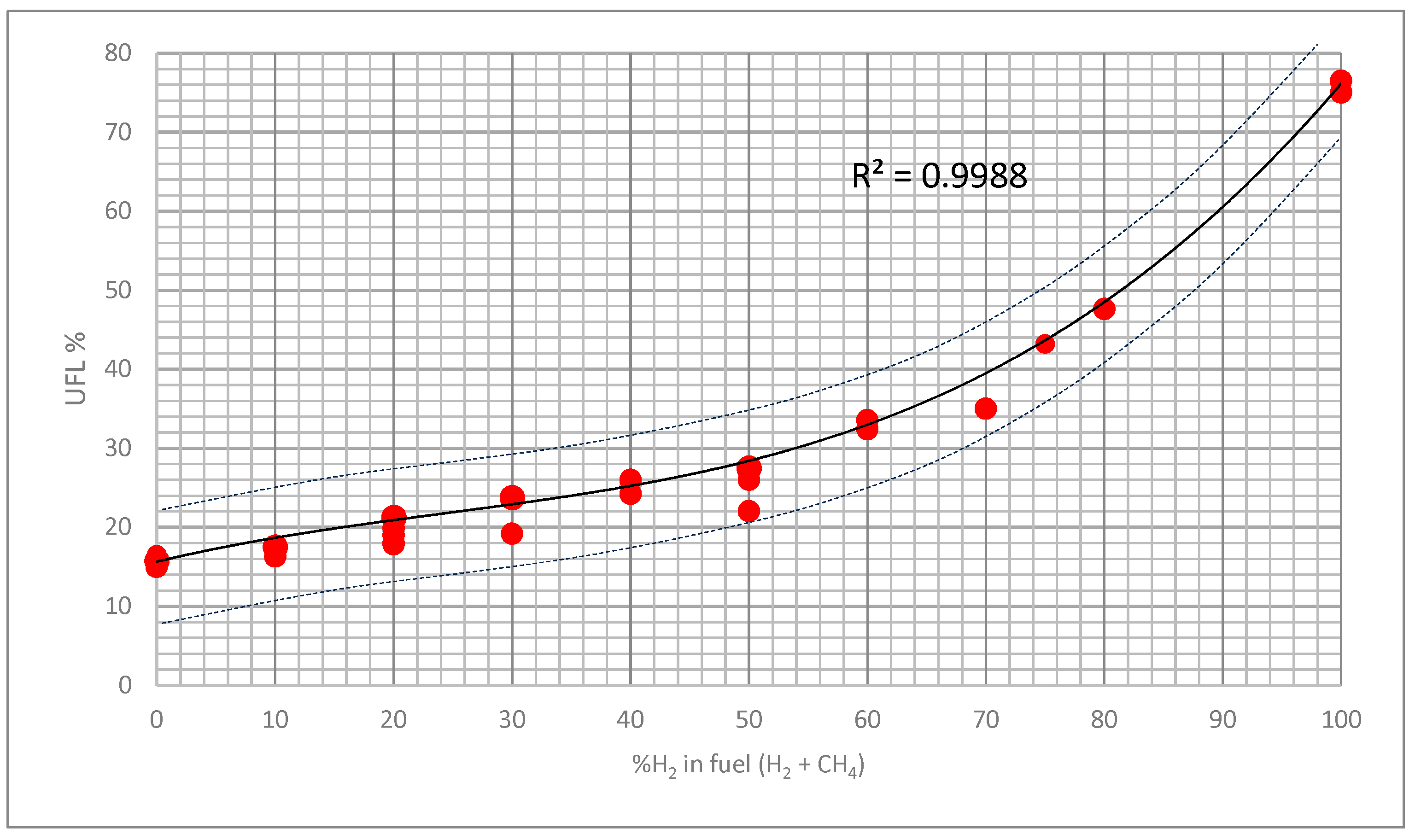
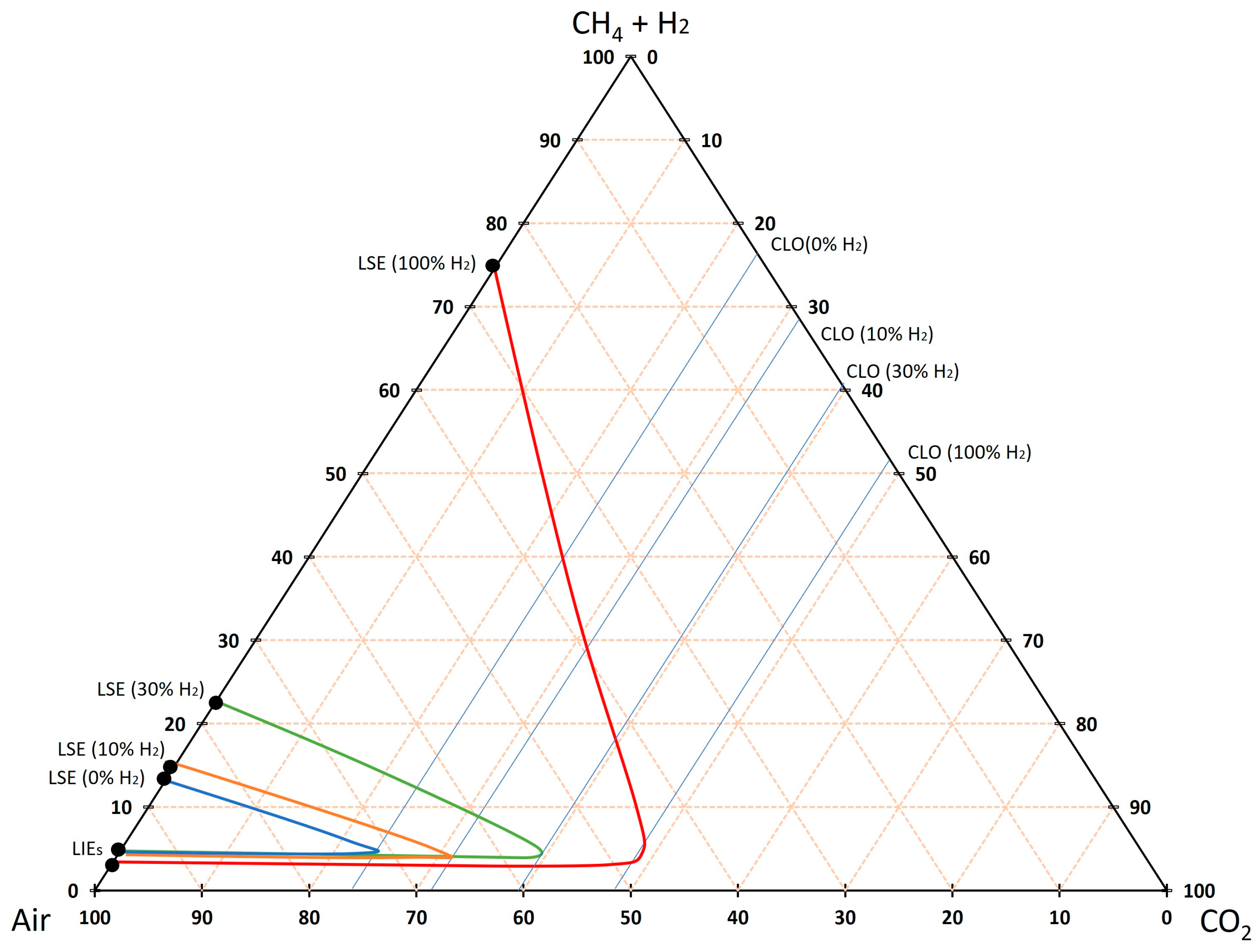
3.3. Theoretical Approximation of the FI
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Prajapati, L.K.; Tirkey, J.V.; Jena, P.; Giri, A. Parametric performance evaluation of SI engine using producer gas-biogas-hydrogen blend as a fuel: A thermodynamic modeling and optimization approach. Int. J. Hydrogen Energy 2024, 72, 268–287. [Google Scholar] [CrossRef]
- Arabzadeh, V.; Frank, R. Creating a renewable energy-powered energy system: Extreme scenarios and novel solutions for large-scale renewable power integration. Appl. Energy 2024, 374, 124088. [Google Scholar] [CrossRef]
- Xie, L.; Yuan, F.; Long, R.; Liu, Z.; Liu, W. Accelerating flammable gas cloud dissipation in hydrogen leakage during refilling hydrogen-powered vehicles via employing canopy fans. Int. J. Hydrogen Energy 2024. [Google Scholar] [CrossRef]
- Wang, X.; Zou, X.; Gao, W. Flammable gas leakage risk assessment for methanol to hydrogen refueling stations and liquid hydrogen refueling stations. Int. J. Hydrogen Energy 2024, 54, 1286–1294. [Google Scholar] [CrossRef]
- Sebai, S.; Tran, K.H.; Guibert, P. Experimental investigation of hydrogen-enriched biogas deflagration characteristics within a constant volume cylindrical vessel. Int. J. Hydrogen Energy 2024, 82, 1389–1401. [Google Scholar] [CrossRef]
- Wei, Z.; Liu, H.; Chen, Z.; Liu, Z.; Zhen, H. Quenching distance, wall heat flux and CO/NO thermochemical states in the wall vicinity of laminar premixed biogas-hydrogen impinging flame. Fuel 2022, 307, 121849. [Google Scholar] [CrossRef]
- Ryckebosch, E.; Drouillon, M.; Vervaeren, H. Techniques for transformation of biogas to biomethane. Biomass Bioenergy 2011, 35, 1633–1645. [Google Scholar] [CrossRef]
- Gieras, M.; Klemens, R.; Rarata, G.; Wolański, P. Determination of explosion parameters of methane-air mixtures in the chamber of 40 dm3at normal and elevated temperature. J. Loss Prev. Process Ind. 2006, 19, 263–270. [Google Scholar] [CrossRef]
- Tian, H.; Wu, M.; Shu, G.; Liu, Y.; Wang, X. Experimental and theoretical study of flammability limits of hydrocarbon–CO2 mixture. Int. J. Hydrogen Energy 2017, 42, 29597–29605. [Google Scholar] [CrossRef]
- Wang, W.Q.; Sun, Z.Y. Experimental studies on explosive limits and minimum ignition energy of syngas: A comparative review. Int. J. Hydrogen Energy 2019, 4, 5640–5649. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Zheng, L.; Yu, M.; Pan, R.; Shan, W. Study on the propagation characteristics of hydrogen/methane/air premixed flames in variable cross-section ducts. Process Saf. Environ. Prot. 2020, 135, 135–143. [Google Scholar] [CrossRef]
- Rajpara, P.; Shah, R.; Banerjee, J. Effect of hydrogen addition on combustion and emission characteristics of methane fuelled upward swirl can combustor. Int. J. Hydrogen Energy 2018, 43, 17505–17519. [Google Scholar] [CrossRef]
- Shirvill, L.C.; Roberts, T.A.; Royle, M.; Willoughby, D.B.; Sathiah, P. Experimental study of hydrogen explosion in repeated pipe congestion—Part 2: Effects of increase in hydrogen concentration in hydrogen-methane-air mixture. Int. J. Hydrogen Energy 2019, 44, 3264–3276. [Google Scholar] [CrossRef]
- Zhai, R.; Yang, Z.; Zhang, Y.; Lv, Z.; Feng, B. Effect of temperature and humidity on the flammability limits of hydrocarbons. Fuel 2020, 270, 117442. [Google Scholar] [CrossRef]
- Zlochower, I.A.; Green, G.M. The limiting oxygen concentration and flammability limits of gases and gas mixtures. J. Loss Prev. Process Ind. 2009, 22, 499–505. [Google Scholar] [CrossRef]
- Hussein, T.; Maxa, D. Flammability of complex hydrocarbon mixtures in air and nitrogen diluted atmosphere at ambient conditions and at elevated pressures. Fuel 2024, 357, 129555. [Google Scholar] [CrossRef]
- Wu, S.Y.; Lin, N.K.; Shu, C.M. Effects of Flammability Characteristics of Methane with Three Inert Gases. Process Saf. Prog. 2021, 25, 326–330. [Google Scholar] [CrossRef]
- García Torrent, J. Seguridad Industrial en Atmósferas Explosivas, 1st ed.; AUTOR-EDITOR-9788460774815; Laboratorio Oficial José María Madariaga: Madrid, Spain, 2003; ISBN 84-407-7481-3. [Google Scholar]
- Mitu, M.; Prodan, M.; Giurcan, V.; Razus, D.; Oancea, D. Influence of inert gas addition on propagation indices of methane-air deflagrations. Process Saf. Environ. Prot. 2016, 102, 513–522. [Google Scholar] [CrossRef]
- Mitu, M.; Giurcan, V.; Razus, D.; Oancea, D. Inert gas influence on the laminar burning velocity of methane-air mixtures. J. Hazard. Mater. 2017, 321, 440–448. [Google Scholar] [CrossRef]
- Wang, D.; Ji, C.; Wang, S.; Yang, J.; Tang, C. Experimental investigation on near wall ignited lean methane/hydrogen/air flame. Energy 2019, 168, 1094–1103. [Google Scholar] [CrossRef]
- Wen, X.; Wang, M.; Su, T.; Zhang, S.; Pan, R.; Ji, W. Suppression effects of ultrafine water mist on hydrogen/methane mixture explosion in an obstructed chamber. Int. J. Hydrogen Energy 2019, 44, 32332–32342. [Google Scholar] [CrossRef]
- Amez, I.; Castells, B.; Garcia-Torrent, J.; Medic, L. Influence of the addition of hydrogen on the flammability intervals of the methane, air and CO2 mixtures. In Proceedings of the Air and Waste Management Association’s Annual Conference and Exhibition, AWMA, Quebec, QC, Canada, 25–28 June 2019; p. 8. [Google Scholar]
- Wang, Q.; Zhao, Y.; Wu, F.; Bai, J. Study on the combustion characteristics and ignition limits of the methane homogeneous charge compression ignition with hydrogen addition in micro-power devices. Fuel 2018, 236, 354–364. [Google Scholar] [CrossRef]
- Ge, B.; Ji, Y.; Zhang, Z.; Zang, S.; Tian, Y.; Yu, H.; Chen, M.; Jiao, G.; Zhang, D. Experiment study on the combustion performance of hydrogen-enriched natural gas in a DLE burner. Int. J. Hydrogen Energy 2019, 44, 14023–14031. [Google Scholar] [CrossRef]
- Ghosh, A.; Munoz-Munoz, N.M.; Lacoste, D.A. Minimum ignition energy of hydrogen-air and methane-air mixtures at temperatures as low as 200 K. Int. J. Hydrogen Energy 2022, 47, 30653–30659. [Google Scholar] [CrossRef]
- Wilsdon, J. The politics of small things: Nanotechnology, risk, and uncertainty. IEEE Technol. Soc. Mag. 2004, 23, 16–21. [Google Scholar] [CrossRef]
- IEC 60079-11; Explosive Atmospheres—Part 11: Equipment Protection by Intrinsic Safety “i”. IEC: Geneva, Switzerland, 2011.
- Uber, C.; Hilbert, M.; Felgner, A.; Hüser, D.; Kurrat, M.; Gerlach, U. Electrical discharges caused by opening contacts in an ignitable atmosphere – Part I: Analysis of electrical parameters at ignition limits. J. Loss Prev. Process. Ind. 2019, 61, 114–121. [Google Scholar] [CrossRef]
- Janès, A.; Lesage, J.; Weinberger, B.; Carson, D. Experimental determination of minimum ignition current (MIC) ratio of hydrogen/methane (H 2 NG) blends up to 20 vol.% of hydrogen. Process. Saf. Environ. Prot. 2017, 107, 299–308. [Google Scholar] [CrossRef]
- ASTM E 681 98; Standard Test Method for Concentration Limits of Flammability of Chemicals (Vapors and Gases) 1. ASTM: West Conshohocken, PA, USA, 1998.
- DIN 51 69; Method for the Determination of Flammability Limits. DIN: Wittenbergplatz, Germany.
- EN 1839:2017; Determination of the Explosion Limits and the Lim-Iting Oxygen Concentration (LOC) for Flammable Gases and Vapours. European Committee for Standarization: Brussels, Belgium, 2017.
- Saito, N.; Ogawa, Y.; Saso, Y.; Liao, C.; Sakei, R. Flame-extinguishing concentrations and peak concentrations of N2, Ar, CO2 and their mixtures for hydrocarbon fuels. Fire Saf. J. 1996, 27, 185–200. [Google Scholar] [CrossRef]
- Uber, C.; Hilbert, M.; Felgner, A.; Hüser, D.; Kurrat, M.; Gerlach, U. Electrical discharges caused by opening contacts in an ignitable atmosphere – Part II: Spectroscopic investigation and estimation of temperatures. J. Loss Prev. Process. Ind. 2019, 61, 213–219. [Google Scholar] [CrossRef]
- Zhou, S.; Xiao, J.; Luo, Z.; Kuznetsov, M.; Chen, Z.; Jordan, T.; Banuti, D.T. Analysis of spontaneous ignition of hydrogen-enriched methane in a rectangular tube. Proc. Combust. Inst. 2024, 40. [Google Scholar] [CrossRef]
- Sekar, M.; Alahmadi, T.A.; Nithya, S. Numerical simulation of industrial gas burners fueled with hydrogen-methane mixtures for enhanced combustion efficiency and reduced greenhouse gas emissions. Fuel 2024, 370. [Google Scholar] [CrossRef]
- Miao, H.; Lu, L.; Huang, Z. Flammability limits of hydrogen-enriched natural gas. Int. J. Hydrogen Energy 2011, 36, 6937–6947. [Google Scholar] [CrossRef]
- Shekhar, R.; Boeck, L.R.; Uber, C.; Gerlach, U. Ignition of a hydrogen–air mixture by low voltage electrical contact arcs. Combust. Flame 2017, 186, 236–246. [Google Scholar] [CrossRef]
- Uber, C.; Shekhar, R.; Felgner, A.; Koenders, L.; Gerlach, U. Experimental investigation of low-voltage spark ignition caused by separating electrodes. J. Loss Prev. Process. Ind. 2017, 49, 822–831. [Google Scholar] [CrossRef][Green Version]
- Van den Schoor, F.; Norman, F.; Vandermeiren, K.; Verplaetsen, F.; Berghmans, J.; Van den Bulck, E. Flammability limits, limiting oxygen concentration and minimum inert gas/combustible ratio of H2/CO/N2/air mixtures. Int. J. Hydrogen Energy 2009, 34, 2069–2075. [Google Scholar] [CrossRef]
- EN 14756; Determination of the Limiting Oxygen Concentration (LOC) for Flammable Gases and Vapours. European Committee for Standarization: Brussels, Belgium, 2007.
- Razus, D.; Molnarne, M.; Fuß, O. Limiting oxygen concentration evaluation in flammable gaseous mixtures by means of calculated adiabatic flame temperatures. Chem. Eng. Process. Process. Intensif. 2004, 43, 775–784. [Google Scholar] [CrossRef]
- Kutcha, J.M. Investigation of Fire and Explosion Accidents in the Chemical Mining and Fuel-Related in-Dustries—A Manual; United states Department of the Interior, Bureau of Mines, Bulletin 680: Washington, DC, USA, 1985; Volume 30, pp. 876–878. [Google Scholar]
- Hodges, J.; Geary, W.; Graham, S.; Hooker, P.; Goff, R. Injecting Hydrogen into the Gas Network—A Lit-Erature Search; Health and Safety Laboratory: Buxton, UK, 2015; pp. 1–53. [Google Scholar]
- Schoor, F.V.D.; Hermanns, R.; van Oijen, J.; Verplaetsen, F.; de Goey, L. Comparison and evaluation of methods for the determination of flammability limits, applied to methane/hydrogen/air mixtures. J. Hazard. Mater. 2008, 150, 573–581. [Google Scholar] [CrossRef]
- Molnarne, M.; Schroeder, V. Hazardous properties of hydrogen and hydrogen containing fuel gases. Process. Saf. Environ. Prot. 2019, 130, 1–5. [Google Scholar] [CrossRef]

| Number of Rounds | Probability |
|---|---|
| 1–20 | Very high probability |
| 20–50 | High probability |
| 50–100 | Low probability |
| 100–200 | Very low probability |
| %H2 | 0 | 10 | 20 | 30 | 50 | 100 |
|---|---|---|---|---|---|---|
| LFL | 4.69 | 4.61 | 4.53 | 4.46 | 4.39 | 4.00 |
| UFL | 14.98 | 16.28 | 17.83 | 19.71 | 22.03 | 75.00 |
| %H2 | 10 | 20 | 30 | 50 |
|---|---|---|---|---|
| LFL | 4.50 | 4.50 | 4.50 | 4.25 |
| UFL | 16.25 | 21.25 | 23.75 | 27.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amez, I.; Paredes, R.; León, D.; Bolonio, D.; Pantelakis, D.; Castells, B. New Experimental Approaches for the Determination of Flammability Limits in Methane–Hydrogen Mixtures with CO2 Inertization Using the Spark Test Apparatus. Fire 2024, 7, 403. https://doi.org/10.3390/fire7110403
Amez I, Paredes R, León D, Bolonio D, Pantelakis D, Castells B. New Experimental Approaches for the Determination of Flammability Limits in Methane–Hydrogen Mixtures with CO2 Inertization Using the Spark Test Apparatus. Fire. 2024; 7(11):403. https://doi.org/10.3390/fire7110403
Chicago/Turabian StyleAmez, Isabel, Roberto Paredes, David León, David Bolonio, Dimitrios Pantelakis, and Blanca Castells. 2024. "New Experimental Approaches for the Determination of Flammability Limits in Methane–Hydrogen Mixtures with CO2 Inertization Using the Spark Test Apparatus" Fire 7, no. 11: 403. https://doi.org/10.3390/fire7110403
APA StyleAmez, I., Paredes, R., León, D., Bolonio, D., Pantelakis, D., & Castells, B. (2024). New Experimental Approaches for the Determination of Flammability Limits in Methane–Hydrogen Mixtures with CO2 Inertization Using the Spark Test Apparatus. Fire, 7(11), 403. https://doi.org/10.3390/fire7110403







