Fire Ignition and Propagation in Hidden Zones of Aircrafts: A Novel Confined Fire Apparatus (CFA) for Flame Spreading Investigation
Abstract
1. Introduction
2. Materials and Methods
2.1. Methods
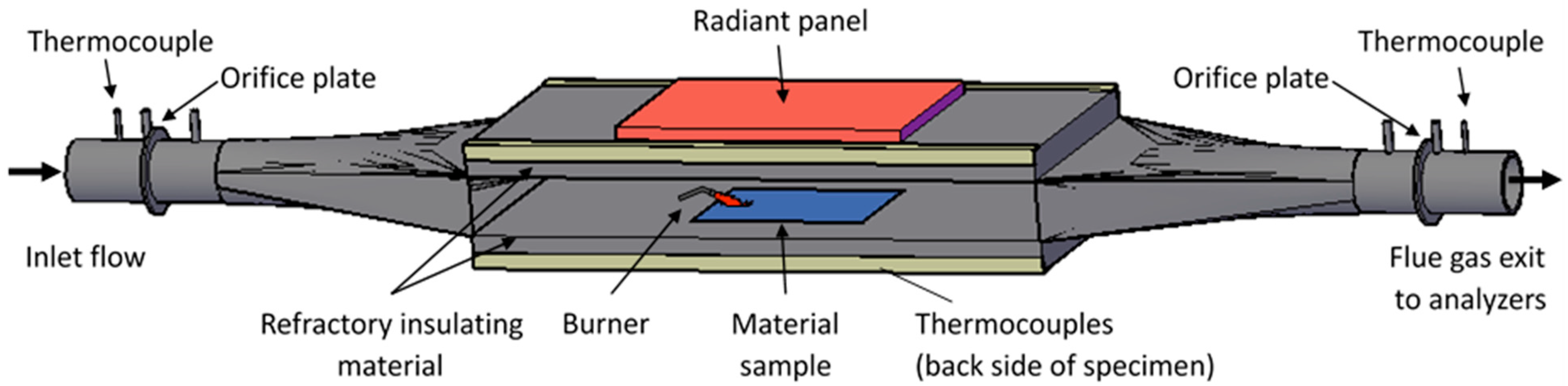
Confined Fire Apparatus
2.2. Materials
3. Experimental Setup
4. Results and Discussion
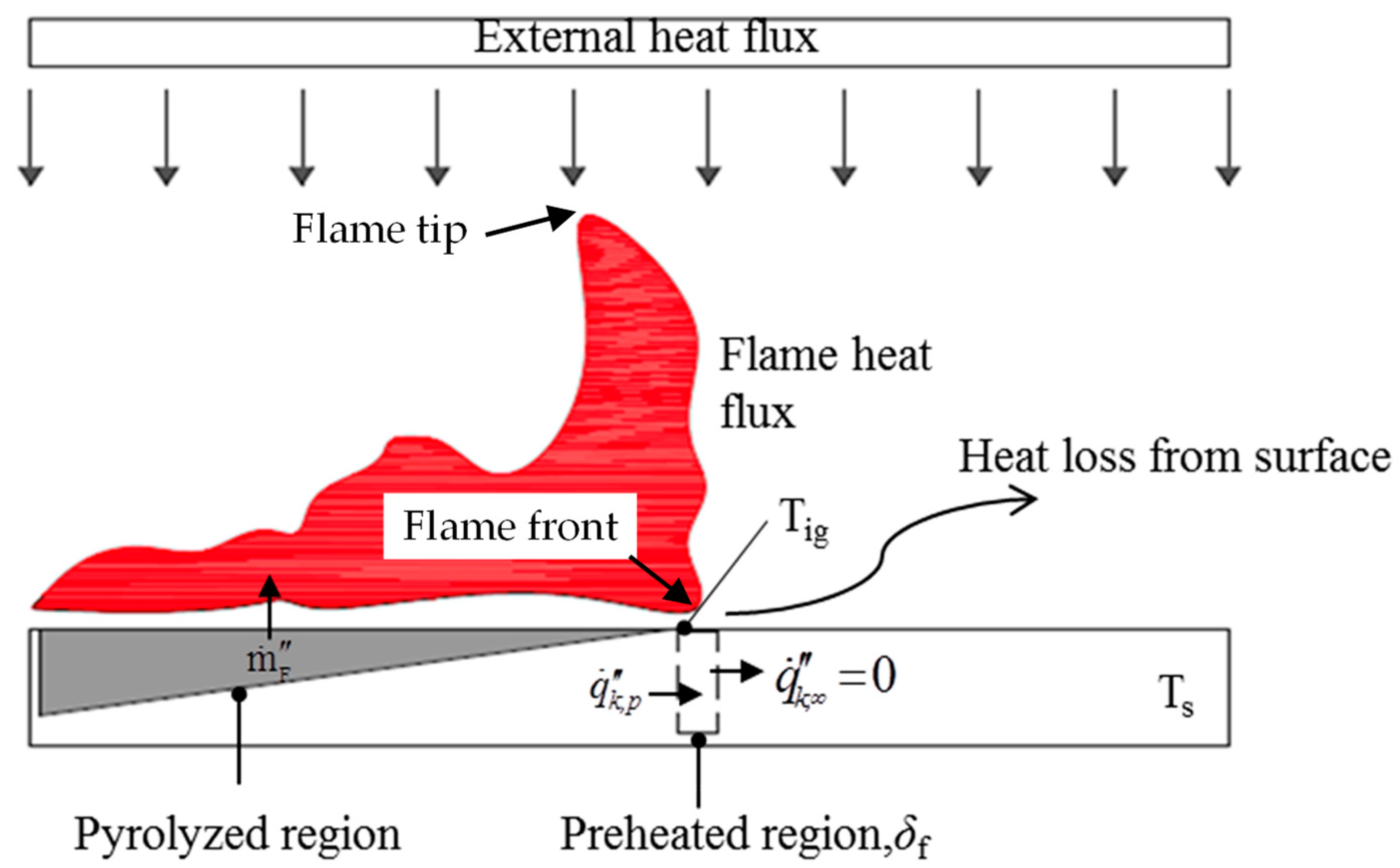
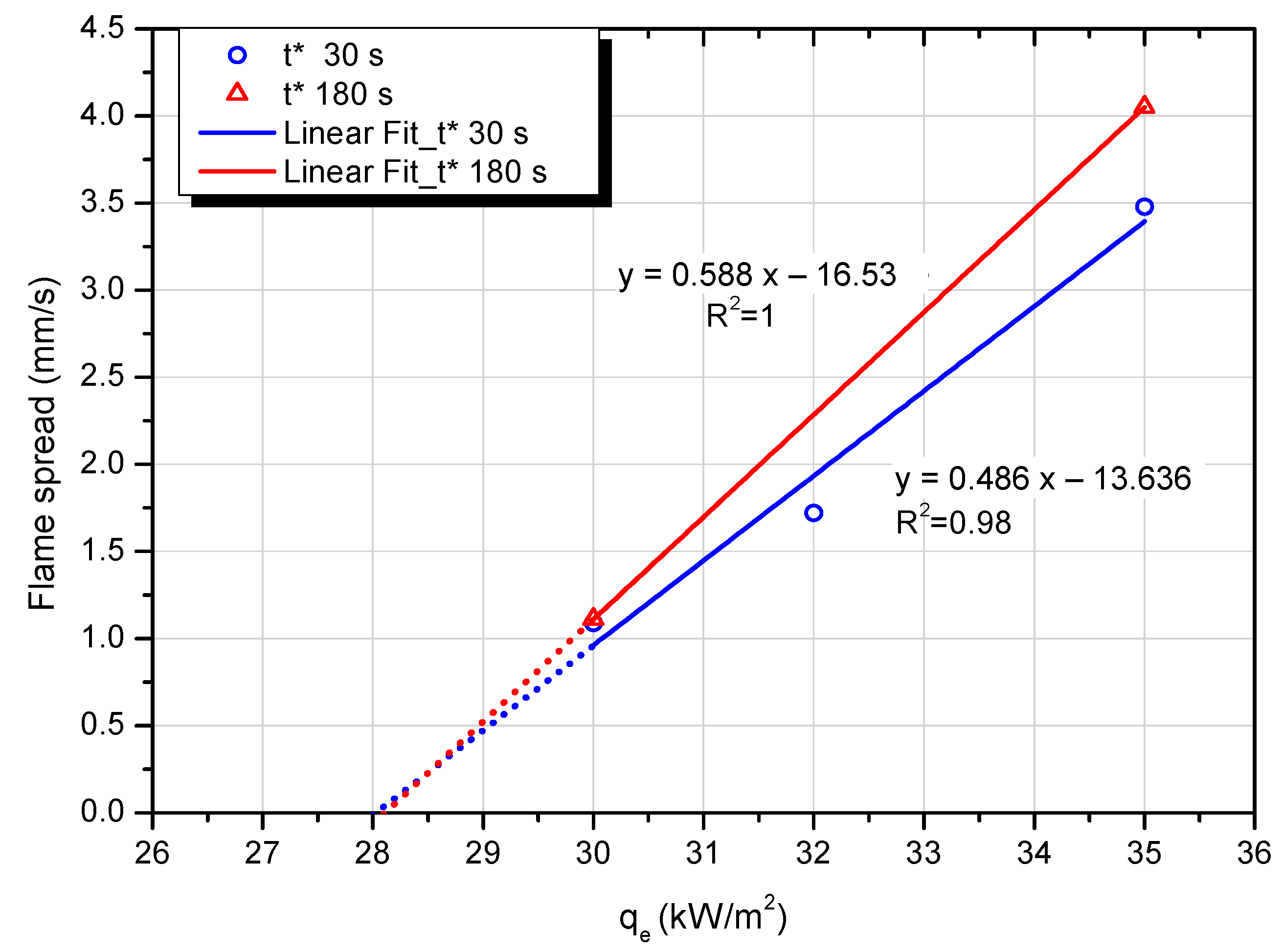
4.1. Flame Spread
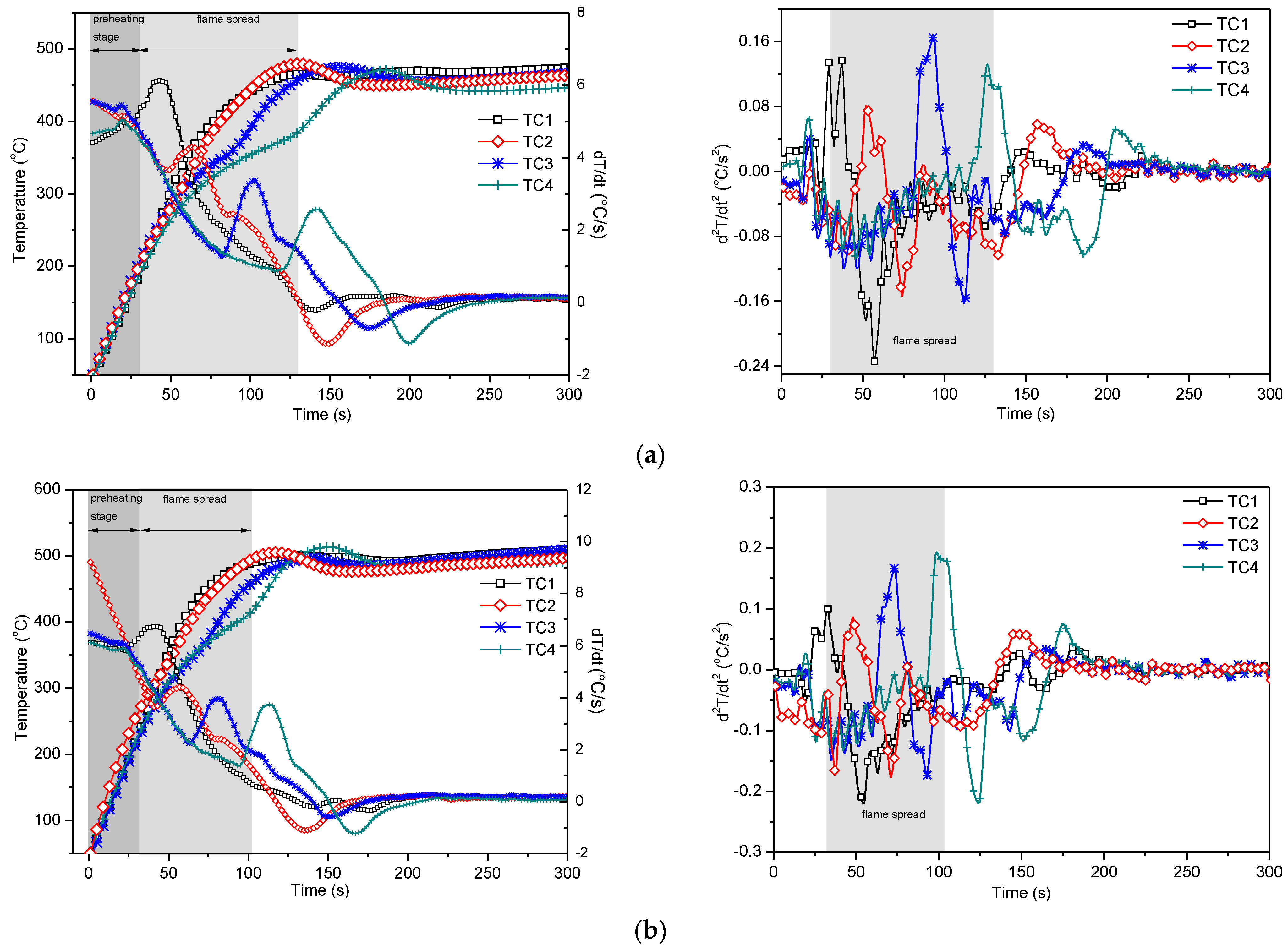
4.2. Temperature Profile Analysis
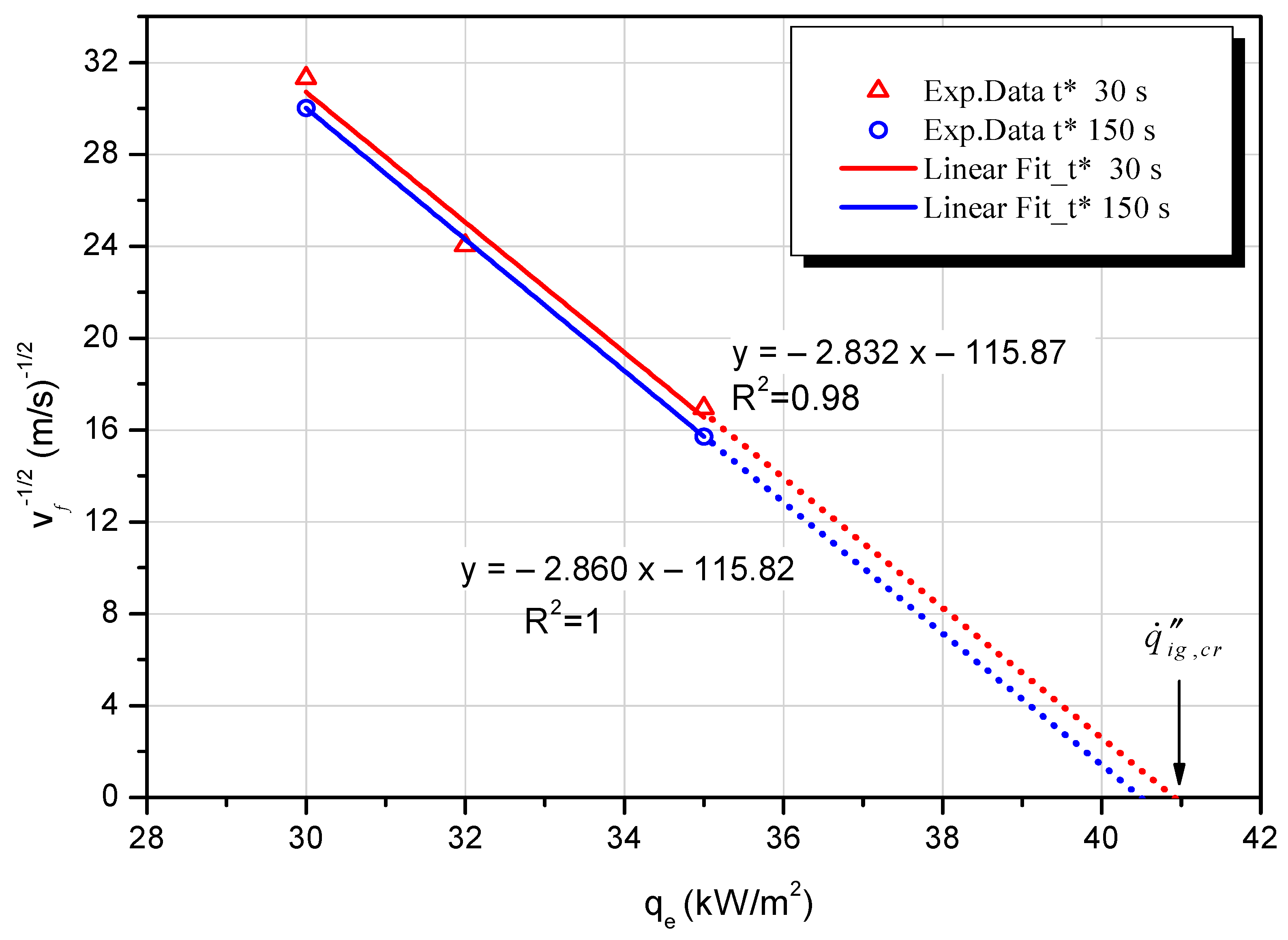
4.3. Flame Spread and Heat Transfer Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | Specific heat (kJ/kg K) | Greek | |
| kρc | Thermal inertia (kW/m2 K)2 s | α | Thermal diffusivity (m2/s) |
| k | Thermal conductivity (kW/m K) | δ | Sample thickness (m) |
| Critical heat flux for ignition (kW/m2) | δth | Thermal depth (m) | |
| Incident heat flux (kW/m2) | ε | Emissivity (-) | |
| To | Initial temperature (K) | ρ | Density (kg/m3) |
| Ts,min | Minimum surface temperature for flame spread | σ | Stefan–Boltzmann constant (W/m2 K4) |
| Tig | Ignition temperature (K) | δf | Flame heated length (m) |
| tig | Ignition time (s) | Φ | Flame spread parameter (kW2/m3) |
| b | Ignition parameter (s−1/2) | ||
| ht | Average heat transfer coefficient (kW/m2 K) | ||
| Critical heat flux for spreading (kW/m2) | |||
| t | Time (s) | ||
| t* | Preheating time (s) | Subscripts | |
| vf | Flame (front) spread rate (m/s) | ||
| vt | Flame (tip) spread rate (m/s) | ig | ignition |
References
- Transportation Safety Board (TSB) of Canada. In-Flight Fire Leading to Collision with Water—Swissair Transport Limited McDonnell Douglas MD-11 HB-IWF Peggy’s Cove, Nova Scotia 5 nm SW, 2 September 1998; Report Number A98H0003; Transportation Safety Board (TSB) of Canada: Gatineau, QC, Canada, 2003.
- Federal Aviation Administration—Fire Safety. Fire Research—Problem Statement. Available online: https://www.fire.tc.faa.gov/Research/Background (accessed on 15 December 2022).
- Reinhardt, J.W. Development of an Improved Fire Test Method for Aircraft Ducting Materials; Report Number DOT/FAA/AR-08/4; US Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2008.
- Marker, T. Development of Improved Flammability Criteria for Aircraft Thermal Acoustic Insulation; Report Number DOT/FAA/AR-99/44; US Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2000.
- U.S. Department of Trasnportation, Federal Aviation Administration. 14 CFR Part 25, 91, 121, 125 and 135. In Improved Flammability Standards for Thermal/Acoustic Insulation Materials Used in Transport Category Airplanes; Electronic Code of Federal Regulations; U.S. Department of Trasnportation, Federal Aviation Administration: Washington, DC, USA, 2003. [Google Scholar]
- Reinhardt, J.W. Development of an Improved Fire Test Method and Criteria for Aircraft Electrical Wiring; Report Number DOT/FAA/AR-10/2; US Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2010.
- Marker, T. Aircraft Materials Fire Test Handbook, Revision 3; Report Number DOT/FAA/TC-17/55; US Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2019.
- Ochs, R. Development of a Flame Propagation Test Method for Structural Composite Materials in Inaccessible Areas; FAA IAMFT Working Group: Bremen, Germany, 2011.
- Quintiere, J.A.; Walters, R.N.; Crowley, S. Flammability Properties of Aircraft Carbon-Fiber Structural Composite; Report Number DOT/FAA/AR-07/57; US Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2007.
- Panagiotou, J.; Quintiere, J.G. Generalizing Flammability of Materials. In Proceedings of the 10th International Conference, Interflam 2004, Edinburgh, SC, USA, 5–7 July 2004; pp. 895–906. [Google Scholar]
- Ochs, R. Vertical Flame Propagation (VFP) Test Method Update; FAA IAMFTWG Working Group: Kansas City, MO, USA, 2016.
- Emami, T.; Whedbee, R. VFP Update March 2019; FAA IAMFTF Working Group: Savannah, GA, USA, 2019.
- Magee, R.; McAlevy, R. The Mechanism of Flame Spread. J. Fire Flammabl. 1971, 2, 271–297. [Google Scholar]
- Zhou, L.; Fernandez-Pello, A.C. Concurrent Turbulent Flame Spread. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1990; Volume 23, pp. 1709–1714. [Google Scholar] [CrossRef]
- Hasemi, Y.; Yoshida, M.; Nohara, A.; Nakabayashi, T. Unsteady-State Upward Flame Spreading Velocity Along Vertical Combustible Solid And Influence Of External Radiation On The Flame Spread. Fire Saf. Sci. 1991, 3, 197–206. [Google Scholar] [CrossRef][Green Version]
- Fernández-Pello, A.; Williams, F.A. A Theory of Laminar Flame Spread over Flat Surfaces of Solid Combustibles. Combust. Flame 1977, 28, 251–277. [Google Scholar] [CrossRef]
- Cordova, J.L.; Walther, D.C.; Torero, J.L.; Fernandez-Pello, A.C. Oxidizer Flow Effects on the Flammability of Solid Combustibles. Combust. Sci. Technol. 2001, 164, 253–278. [Google Scholar] [CrossRef]
- Fereres, S.; Lautenberger, C.; Fernandez-Pello, C.; Urban, D.; Ruff, G. Mass Flux at Ignition in Reduced Pressure Environments. Combust. Flame 2011, 158, 1301–1306. [Google Scholar] [CrossRef]
- Pizzo, Y.; Consalvi, J.L.; Querre, P.; Coutin, M.; Porterie, B. Width Effects on the Early Stage of Upward Flame Spread over PMMA Slabs: Experimental Observations. Fire Saf. J. 2009, 44, 407–414. [Google Scholar] [CrossRef]
- Gollner, M.J.; Miller, C.H.; Tang, W.; Singh, A.V. The Effect of Flow and Geometry on Concurrent Flame Spread. Fire Saf. J. 2017, 91, 68–78. [Google Scholar] [CrossRef]
- Jiang, L.; Xiao, H.; Zhou, Y.; An, W.; Yan, W.; He, J.; Sun, J. Theoretical and Experimental Study of Width Effects on Horizontal Flame Spread over Extruded and Expanded Polystyrene Foam Surfaces. J. Fire Sci. 2014, 32, 193–209. [Google Scholar] [CrossRef]
- Liang, C.; Cheng, X.; Yang, H.; Zhang, H.; Yuen, K.K. Effects of Altitude and Inclination on Flame Spread over Poly(Methyl Methacrylate) Slabs. J. Fire Sci. 2013, 31, 511–526. [Google Scholar] [CrossRef]
- Zhao, K.; Zhou, X.; Yang, L.; Gong, J.; Wu, Z.; Huan, Z.; Liu, X. Width Effects on Downward Flame Spread over Poly(Methyl Methacrylate) Sheets. J. Fire Sci. 2015, 33, 69–84. [Google Scholar] [CrossRef]
- Williams, F.A. Mechanisms of fire spread. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1977; Volume 16, pp. 1281–1294. [Google Scholar] [CrossRef]
- Fernandez-Pello, A.C. Downward Flame Spread under the Influence of Externally Applied Thermal Radiation. Combust. Sci. Technol. 1977, 17, 1–9. [Google Scholar] [CrossRef]
- Hirano, T.; Sato, K. Effects of Radiation and Convection on Gas Velocity and Temperature Profiles of Flames Spreading over Paper. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1975; Volume 15, pp. 233–241. [Google Scholar] [CrossRef]
- Kashiwagi, T. A Study of Flame Spread over a Porous Material under External Radiation Fluxes. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1975; Volume 15, pp. 255–265. [Google Scholar] [CrossRef]
- Kashiwagi, T.; Newman, D.L. Flame Spread over an Inclined Thin Fuel Surface. Combust. Flame 1976, 26, 163–177. [Google Scholar] [CrossRef]
- Fernandez-Pello, A.C. Upward Laminar Flame Spread under the Influence of Externally Applied Thermal Radiation. Combust. Sci. Technol. 1977, 17, 87–98. [Google Scholar] [CrossRef]
- Quintiere, J. A Simplified Theory for Generalizing Results from a Radiant Panel Rate of Flame Spread Apparatus. Fire Mater. 1981, 5, 52–60. [Google Scholar] [CrossRef]
- ISO 554:1976; Standard Atmospheres for Conditioning and/or Testing—Specifications. International Organization for Standardization (ISO): Geneva, Switzerland, 1976.
- Papadogianni, V.; Romeos, A.; Perrakis, K.; Panidis, T. Fire behaviour of a Carbon/Nomex Honeycomb Sandwich Composite Used in Aircraft Interiors as Ceiling Panel. Heat Mass Transf. Stoffuebertragung 2022, 1–10, in press. [Google Scholar] [CrossRef]
- Koštial, P.; Jančíková, Z.K.; Frischer, R. Case Study on Fire Resistance of Sandwiches for Means of Transport. Coatings 2021, 11, 207. [Google Scholar] [CrossRef]
- Spearpoint, M.J.; Quintiere, J.G. Predicting the Piloted Ignition of Wood in the Cone Calorimeter Using an Integral Model—Effect of Species, Grain Orientation and Heat Flux. Fire Saf. J. 2001, 36, 391–415. [Google Scholar] [CrossRef]
- Delichatsios, M.A. Piloted Ignition Times, Critical Heat Fluxes and Mass Loss Rates at Reduced Oxygen Atmospheres. Fire Saf. J. 2005, 40, 197–212. [Google Scholar] [CrossRef]
- Quintiere, J.G. Fundamentals of Fire Phenomena; Wiley: New York, NY, USA, 2006; ISBN 9780470091135. [Google Scholar] [CrossRef]
- Ju, X.; Zhou, X.; Zhao, K.; Peng, F.; Yang, L. Experimental Study on Fire Behaviors of Flexible Photovoltaic Panels Using a Cone Calorimeter. J. Fire Sci. 2018, 36, 63–77. [Google Scholar] [CrossRef]
- Papadogianni, V.; Romeos, A.; Giannadakis, A.; Perrakis, K.; Panidis, T. Cone Calorimeter and Thermogravimetric Analysis of Glass Phenolic Composites Used in Aircraft Applications. Fire Technol. 2019, 56, 1253–1285. [Google Scholar] [CrossRef]
- Papadogianni, V.; Romeos, A.; Perrakis, K.; Panidis, T. Thermal Decomposition and Fire Behavior of Carbon Fiber/Nomex Honeycomb Composite. Int. Rev. Mech. Eng. 2021, 15, 1–12. [Google Scholar] [CrossRef]
- Drysdale, D. An Introduction to Fire Dynamics, 3rd ed.; John Wiley & Sons, Ltd.: England, UK, 2011; ISBN 9780470319031. [Google Scholar] [CrossRef]
- Chao, Y.H.C.; Fernandez-Pello, A.C. Concurrent Horizontal Flame Spread: The Combined Effect of Oxidizer Flow Velocity, Turbulence and Oxygen Concentration. Combust. Sci. Technol. 1995, 110–111, 19–51. [Google Scholar] [CrossRef]
- Orloff, L.; De Ris, J.; Markstein, G.H. Upward Turbulent Fire Spread and Burning of Fuel Surface. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1975; Volume 15, pp. 183–192. [Google Scholar] [CrossRef]
- Merryweather, G.; Spearpoint, M.J. Ignition of New Zealand Wood Products in the LIFT, RIFT and ISO 5657 Apparatus Using the ASTM e 1321-97 Protocol. J. Fire Sci. 2008, 26, 63–88. [Google Scholar] [CrossRef]
- Merryweather, G.; Spearpoint, M.J. Flame Spread Measurements on Wood Products Using the ASTME 1321 LIFT Apparatus and a Reduced Scale Adaptationof the Cone Calorimeter. Fire Mater. 2010, 34, 109–136. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer, 8th ed.; Wiley: New York, NY, USA, 2018; ISBN 978-1-119-35388-1. [Google Scholar]





| ρ (kg/m3) | k (W/mK) | cp (J/kgK) | kρc ((kW/m2 K)2 s) | Tig (°C) |
|---|---|---|---|---|
| 158 | 1.05 | 690 | 0.1136 | 596 |
| Heat Flux (kW/m2) | Pre-Heating Time (s) | Flame Spread Rate, vf (mm/s) (Visual) | Flame Tip Spread Rate, vt (mm/s) (Visual) | Flame Spread Rate, vf,T (mm/s) (Thermocouples) |
|---|---|---|---|---|
| 25 | 30/180 | n.s. * | ||
| 28 | 30/180 | n.s. * | ||
| 30 | 30/180 | 1.09/1.11 | 0.96/− | 1.17/− |
| 32 | 30/− | 1.72/− | 1.61/− | 1.70/− |
| 35 | 30/180 | 3.48/4.05 | 2.43/− | 3.63/− |
| (kW/m2) | Ts (°C, Exp. Calculated) | Ts (°C, Predicted) |
|---|---|---|
| 30 | 478 | 531 |
| 32 | 514 | 546 |
| 35 | 572 | 564 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadogianni, V.N.; Romeos, A.; Giannadakis, A.; Perrakis, K.; Panidis, T. Fire Ignition and Propagation in Hidden Zones of Aircrafts: A Novel Confined Fire Apparatus (CFA) for Flame Spreading Investigation. Fire 2023, 6, 292. https://doi.org/10.3390/fire6080292
Papadogianni VN, Romeos A, Giannadakis A, Perrakis K, Panidis T. Fire Ignition and Propagation in Hidden Zones of Aircrafts: A Novel Confined Fire Apparatus (CFA) for Flame Spreading Investigation. Fire. 2023; 6(8):292. https://doi.org/10.3390/fire6080292
Chicago/Turabian StylePapadogianni, Vasiliki N., Alexandros Romeos, Athanasios Giannadakis, Konstantinos Perrakis, and Thrassos Panidis. 2023. "Fire Ignition and Propagation in Hidden Zones of Aircrafts: A Novel Confined Fire Apparatus (CFA) for Flame Spreading Investigation" Fire 6, no. 8: 292. https://doi.org/10.3390/fire6080292
APA StylePapadogianni, V. N., Romeos, A., Giannadakis, A., Perrakis, K., & Panidis, T. (2023). Fire Ignition and Propagation in Hidden Zones of Aircrafts: A Novel Confined Fire Apparatus (CFA) for Flame Spreading Investigation. Fire, 6(8), 292. https://doi.org/10.3390/fire6080292





