Preliminary Study on Reconstruction of Building Thermal Field Based on Iterative Algorithm Acoustic CT

Abstract

Real-time acquisition and visualization of temperature anomalies in building spaces and 3D temperature field data during fires are of vital importance for fire danger warnings, early rescue operations, evacuation commands, and subsequent fire accident investigations. Taking into account the non-contact, global (planar and spatial), and high efficiency advantages of acoustic CT temperature measurement technology, this study involved the conducting of exploratory preliminary research in order to provide new ideas for the real-time global perception of information on building fires. The detailed research objective was as follows: obtain the temperature data at any time of a fire based on Fire Dynamics Simulator (FDS) and fit them to form the base temperature distribution diagram at that time. The large ill-conditioned matrix equation of acoustic flight under the scheme of multi-grid division was then constructed. The discrete temperature data of each grid in the building space was obtained by solving the matrix equation based on algebraic reconstruction algorithm (ART) and joint algebraic reconstruction algorithm (SART). The three-dimensional temperature field reconstruction of building space was realized by the interpolation of discrete temperature data. The reconstruction effect of each scheme was evaluated through the error analysis between the reconstruction data and the basic data. The results show that the real-time reconstruction of a 3D temperature field of a building thermal field can be realized based on acoustic CT temperature measurement technology, and the reconstruction algorithm and grid division scheme have a significant control effect on the reconstruction effect.

1. Introduction

With the increasing scope and degree of human economic activity, the types and densities of urban buildings, especially large public buildings, have also increased, making the problem of building fires increasingly prominent. In large public building fires, the early identification of the fire and timely reporting, efficient evacuation of personnel, and the effective command of firefighting and rescue operations are key to preventing the fire from spreading [1]. However, due to unclear information about the fire scene, such factors as accurate and timely warning, effective firefighting, rescue, and rapid evacuation command are severely hindered. These are also the main factors leading to the deaths of firefighters. The real-time distribution of a fire location, the temperature field, and the flue gas field in a building space fire are the key data for fire-fighting, personnel rescue and emergency evacuation plan formulation, and the fire temperature-flue gas information obtained in real time can also be used as a reliable basis for follow-up fire accident investigations. Related studies have shown that [2,3], in a fire environment, combustion will produce a large amount of heat and harmful gases, and harmful gases will suck up the surrounding air under the action of the fire plume to form a flue gas. The heat will contain the flue gas as the carrying medium, and the flue gas will spread in the building space. Under normal circumstances, the distribution of the temperature field and the flue gas flow field in the fire environment has good coincidence. Therefore, the real-time acquisition of temperature data of building fire space and transmission to the rescue command center is of great significance for the rapid determination of fire location, fire extinguishing and fighting, the rapid formulation of personnel rescue and emergency evacuation plans, and the follow-up investigation with regard to the cause of the fire.

At present, the acquisition of building fire temperature data mainly relies on sensor measurement and numerical model simulation calculation. The former has high precision and good timeliness, but can only obtain one-dimensional data (such as a resistance temperature sensor, thermoelectric temperature sensor, blackbody cavity thermal radiation pyrometer, etc.) or two-dimensional data on the surface of the object (such as an infrared thermometer), and lacks the ability to measure space temperature; the latter can simulate disaster changes in advance based on the numerical model of fire dynamics and specific boundary conditions, but the timeliness is poor and cannot support the rescue and evacuation command during a fire [4,5]. Therefore, improving the real-time measurement technology of three-dimensional temperature in building space to realize the global and real-time data presentation of the fire scene is one of the development trends in the field of intelligent fire extinguishing, rescue, and evacuation command of the fire scene.

The acoustic CT temperature field reconstruction technology based on computer tomography (CT) has the advantages of non-contact, wide temperature measurement range, high measurement accuracy, large spatial range of measurement objects, real-time continuous measurement, convenient maintenance, and it is not affected by radiation [6,7]. At present, acoustic CT temperature measurement technology has been applied in the field of combustion temperature detection of industrial boilers [8,9]; it also solves the technical problem of high temperature resistance of hardware such as acoustic transceiver devices, and provides the possibility for the subsequent application of this technology in other high temperature scenarios. In addition, the research on the technology involved in storage grain temperature detection [10], marine hydrothermal vent temperature detection [11,12], atmospheric temperature detection [13], and other aspects has gradually become popular.

Currently, in the field of information acquisition in building fires, the application and research of acoustic CT temperature reconstruction technology is in its infancy. This paper aims to use this technology for temperature field data acquisition in critical locations during the early stages of a fire in order to serve fire warnings, personnel evacuation, and firefighting rescue. To this end, we conducted some preliminary and preparatory research, mainly including the influence of grid partitioning schemes and iterative reconstruction algorithms on the reconstruction algorithm of the fire temperature field. Since this paper mainly explores the control effect of the reconstruction scheme and iterative reconstruction algorithm on the reconstruction effect, the combustion model of the building space is simplified. The specific content is based on the basic principle of acoustic CT temperature measurement; this paper takes the early temperature field of the building space fire as the reconstruction object, constructs a large ill-conditioned matrix equation under the multi-grid partitioning scheme, and uses algebraic reconstruction algorithm (ART) and the joint algebraic reconstruction algorithm (SART) to solve the large ill-conditioned matrix equation, realizing the reconstruction of the three-dimensional temperature field of the building space. By evaluating the relative error between the basic temperature field and the reconstructed temperature field, the reconstruction accuracy of each reconstruction scheme is analyzed. The research results of this paper provide a certain theoretical basis for the subsequent application of this technology in real and complex fire scenarios.

2. Principle of 3D Temperature Field Reconstruction for Acoustic CT

The measured space is meshed (N grids), and the acoustic sources and receivers (M acoustic rays) are arranged at multiple points to measure the time-of-flight (TOF) of each acoustic wave traveling under the temperature distribution condition, ${\tau }_{\mathrm{TOF},\mathrm{i}}$. The total flight time of a sound ray is equal to the sum of the time it takes for the sound ray to pass through each grid, and the time required to pass through each grid is equal to the length of the grid and the reciprocal of the speed of sound through the grid, as shown below.

$${\tau }_{TOF,i}={\displaystyle \sum _{j=1}^N{\omega }_{ij}}{f}_j i=1,2,\dots ,M$$

(1)

where ${\omega }_{ij}$ is the length of the i th path through the j th grid, in m; f_j is the Sound-slowness, whereby the acoustic wave ray passes through the reciprocal of the average velocity of each grid, in (m/s)⁻¹.

Each sonic generator is controlled sequentially to emit sound waves, and the relationship equation between the time of acoustic ray (M) passing through the grid (N) and the total time of acoustic ray flight is established after a period of measurement. Thus, the temperature field reconstruction problem is transformed into a matrix equation solution problem. The form is as follows.

$$\left\{\begin{array}{c}{\omega }_{11}{f}_1+{\omega }_{12}{f}_2+\cdots +{\omega }_{1N}{f}_N={\tau }_1\\ {\omega }_{21}{f}_1+{\omega }_{22}{f}_2+\cdots +{\omega }_{2N}{f}_N={\tau }_2\\ ⋮\\ {\omega }_{M1}{f}_1+{\omega }_{M2}{f}_2+\cdots +{\omega }_{MN}{f}_N={\tau }_M\end{array}\right.$$

(2)

Let $A=\left[\begin{array}{c}{\omega }_{11}\cdots {\omega }_{1N}\\ \begin{array}{ccc}⋮& ⋮& ⋮\end{array}\\ {\omega }_{M1}\cdots {\omega }_{MN}\end{array}\right]$, $x=(f_1,f_2,\cdots ,f_N)$; $b=({\tau }_1,{\tau }_2,\cdots ,{\tau }_M)$ is the M-dimensional data vector of time-of-flight (TOF) of acoustic wave traveling.

Therefore, Equation (2) above can be reduced to a linear matrix equation,

$$A\cdot x=b$$

(3)

The propagation speed of sound waves in the gas medium will be controlled by various factors such as temperature, humidity, atmospheric pressure, gas composition, etc., which are reflected in key parameters such as the gas adiabatic index, temperature, and the average molar mass of gas. This paper mainly focuses on the flue gas medium, focusing on the relationship between sound wave propagation speed and temperature in this medium. Therefore, the relationship between the propagation speed of sound waves and the temperature of the gas [14,15,16] is:

$$C=\sqrt{\gamma RT/m}=Z\sqrt{T}$$

(4)

where C is the velocity of sound propagation in the gas medium in m/s; γ is the adiabatic index of the gas, and its value is the ratio of constant pressure specific heat to fixed capacity specific heat; R is ideal gas universal constant of 8.3143 J/(mol·K); T is the absolute temperature of the gas medium, in K; and m is average molar mass of gas, in kg/mol.

Among them, the $Z=\sqrt{\gamma R/m}$ value is the key parameter that characterizes the comprehensive properties (composition) of the propagation medium, and is its state parameter and is a constant, so the speed of sound wave propagation in the medium only depends on the temperature of the medium. The Z value will vary for different propagation media, and for a given propagation medium, the Z value can be assumed to be a fixed constant. Relevant studies show that the Z of the flue mixture is 20.045 [17]. Therefore, the relationship between temperature and sound velocity is studied on this basis.

The solution temperature values of the n discrete grids are obtained by combining the matrix equation solution $x=(f_1,f_2,\cdots ,f_N)$ and Equation (4), and the solution temperature values of the N discrete grids are obtained. At this time, it can be assumed that the coordinate of each solution temperature data is the center point coordinate of the pixel grid, and then the reconstruction of the spatial 3D temperature field can be realized through the interpolation algorithm.

3. Acquisition of Building Fire Foundation Temperature Field Function

Suppose that the acoustic velocity and the propagation medium temperature follow the relationship of Formula (4) in order to explore the reconstruction accuracy of the acoustic CT 3D reconstruction technology for a building fire temperature field under different meshing schemes, and to analyze the error of reconstruction effect more conveniently, the basic temperature data of the fire field is obtained by the method of Fire Dynamics Simulator (FDS), and the discrete data is fitted by the BP neural network algorithm. The distribution function (black box function) of the base temperature data at a high fit is obtained in this paper.

By comparing the reconstruction temperature field distribution data with the basic temperature data obtained by FDS under different reconstruction schemes, the comparative study of the temperature field reconstruction effect under different reconstruction schemes can be realized. According to Formula (2), the total time-of-flight (TOF) of each acoustic wave traveling, ${\tau }_{\mathrm{TOF},\mathrm{i}}$, is a key parameter for solving the matrix equation, which can be obtained by local (ray) integration of the basic temperature distribution function.

$${\tau }_{TOF,i}={\displaystyle \underset{L_i}{\int }\frac{1}{v(x,y,z)}dl=}{\displaystyle \underset{L_i}{\int }f(x,y,z)dl}$$

(5)

The prerequisite for integrating to find the fly by time is to determine the specific function form of the temperature field distribution. Due to the complex temperature field distribution and the inability to achieve good fitting results in a single function form, this paper uses a BP neural network algorithm to fit the above discrete data in the MATLAB environment to obtain the basic temperature data distribution function (black box function) under high fit.

In order to obtain the complex temperature field distribution function of a building space fire, complete the local (ray) integration under the function distribution, and obtain the total flying time of each acoustic wave path, the following work was performed:

• The geometric model was established by FDS, and the simulation parameters such as fire power and grid size were set.
• The data acquisition sensors were arranged in each grid to calculate the discrete data of the fire base temperature.
• The discrete data was fitted by the BP neural network algorithm, and the distribution function (the form of neural network) of the base temperature data at ahigh fit was obtained.

(1)

The geometric model and the setting of key parameters was established

In this paper, the influence of reconstruction algorithms (ART, SART) and reconstruction schemes (mesh, rays) on the reconstruction effect is mainly explored through the error analysis (root mean square error, average error, and maximum error) between acoustic CT temperature reconstruction data and basal temperature data (numerical simulation acquisition). Therefore, in the process of basic temperature field construction, the boundary conditions of a fire scene and numerical simulation are simplified so as to obtain more targeted research algorithms and reconstruction schemes to control the reconstruction effect. In the future, on the basis of the maturity of relevant theoretical research, more research on working conditions and real natural convection fire scenarios will be carried out.

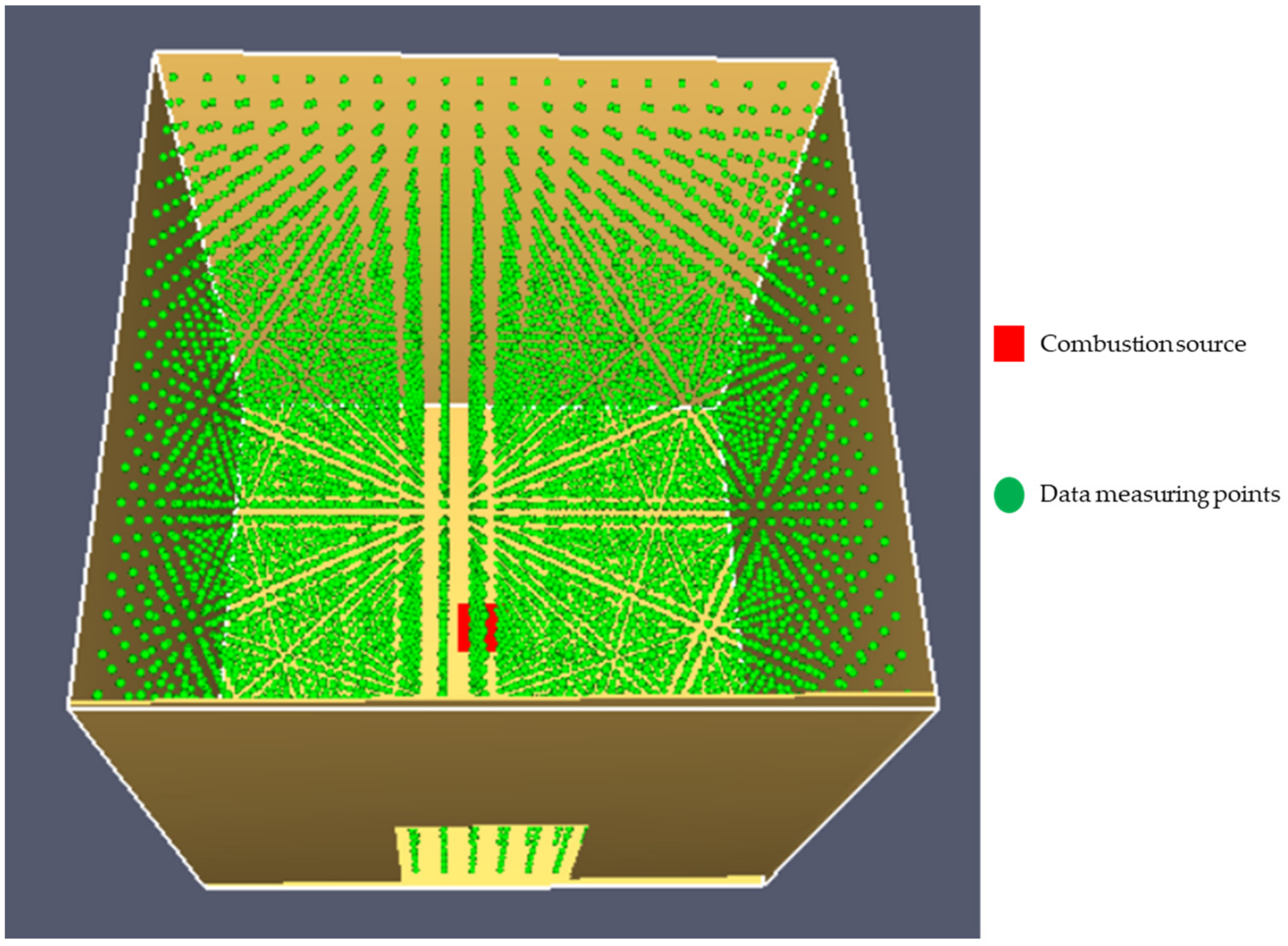
Build a large building space of 10 m × 10 m × 10 m, and mesh the geometry according to the dimensions of 0.5 × 0.5 × 0.5. Data collection points are set at the coordinates of each grid center point to calculate and obtain real-time temperature data during the fire. The specific parameters are shown in

Table 1. Geometry parameters setting of numerical simulation.

Parameter Category	Overall Size (m3)	Door Opening Size (m3)	Grid		Combustion Source
			Division Form	Mesh Size (m3)	Fire Source Location Coordinates(m)	Fire Source Size (m2)
Parameter value	10 × 10 × 10	3 × 0.2 × 4	Evenness	0.5 × 0.5 × 0.5	(0,0,−5)	1 × 1

and

Table 2. Calculation parameters setting of numerical simulation.

Parameter Category	Initial Temperature (K)	Air Humidity (%RH)	Burning Materials	Wall Material	Wall Thermal Conductivity (W/(m·k))	Ignition Source Power (MW/m2)
Parameter value	293.15	60%	Polyurethane_GM27	Concrete	1.8	10

:

The 3D layout is shown in Figure 1.

(2)

Acquisition of the base temperature field function and the fitting of the function

This technology can be used for the early warning of a fire, so in order to explore the sensitivity of the temperature measurement technology to the temperature of the fire stage within 1 min, and to consider the degree of flame temperature in the combustion process, this study selects the temperature of the fire stage t = 57 s as the basic data, but the technology can theoretically reconstruct the temperature distribution at any time.

The better fitting result cannot be achieved by a single functional form due to the complex temperature field distribution. In this paper, the above discrete data are fitted by the BP neural network algorithm in the MATLAB environment. A BP neural network [18] is a multi-layer feed-forward backpropagation network which uses a multi-layer feed-forward method for computing the output and uses error back-propagation correction for correcting the learning.

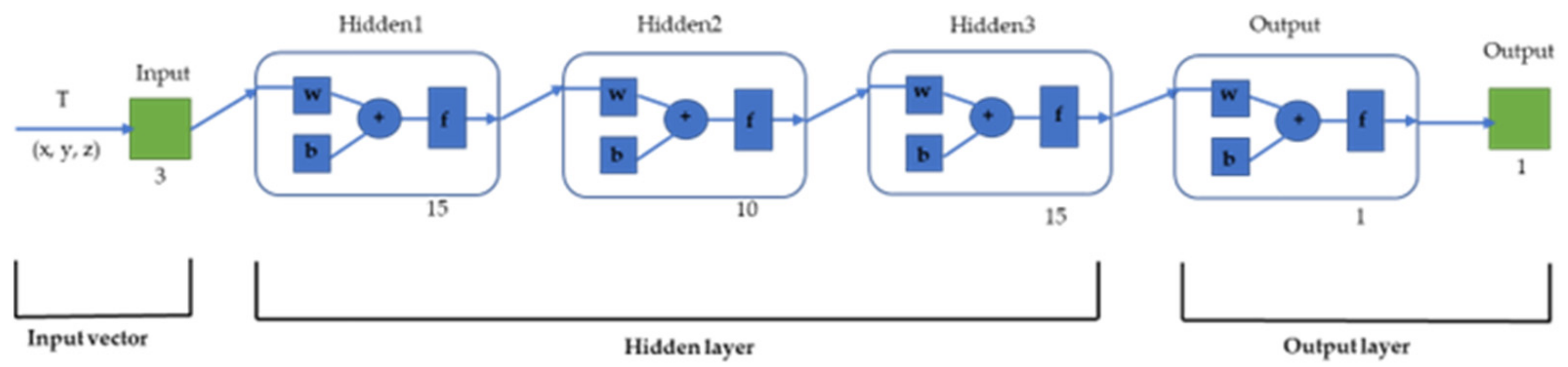
This time, the four-layer neurons network is used (three layers of hidden layer) for fitting based on the two functional forms of “logsig” and “purelin”, with 15, 10 and 15 neurons set in the hidden layer, respectively. After preliminary exploratory research and multiple forms of fitting, it was found that the four-layer neural network was selected with the highest fitting accuracy and the lowest fitting time. The specific setting is shown in Figure 2.

The fitting results are shown in Figure 3 below.

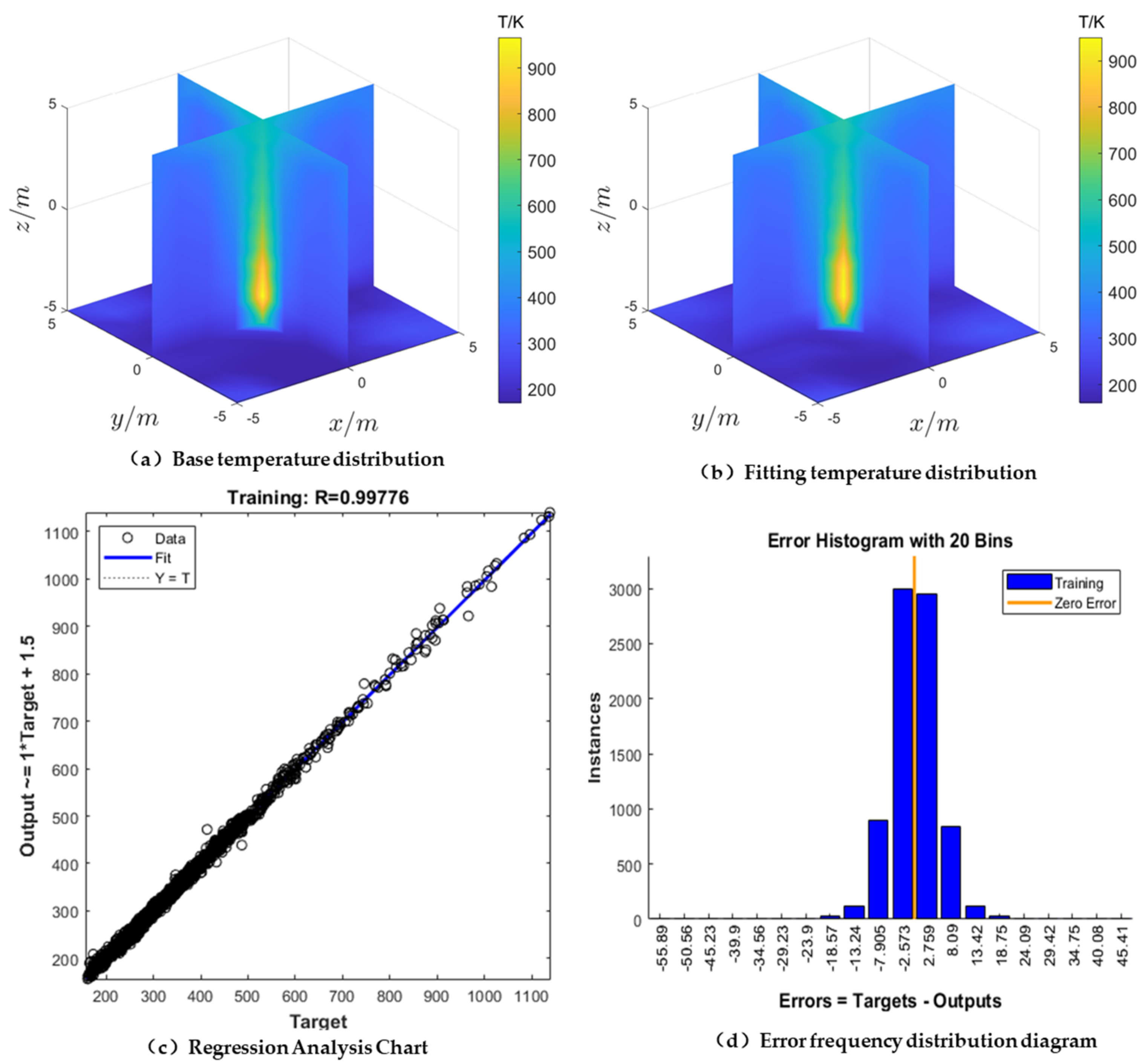
In the figure above, Figure 3a is a distribution cloud obtained by the linear interpolation of the basic temperature data obtained by FDS numerical simulation, and Figure 3b is a function distribution cloud obtained by fitting the basic temperature data by the BP neural network method. Figure 3c,d are the correlation coefficient R value and error frequency distribution plots of the fitting process, respectively. It can be seen from the figure that the correlation coefficient R value between the fitting function data and the basal temperature data is 0.99776, and most of the errors are concentrated between −2.573 K and 2.759 K. To reconstruct the temperature field, it is necessary to obtain the sound wave flight time, and the sound wave flight time needs to clarify the function form of the basic temperature field. The above data can show that the BP neural network fitting method using four layers of neurons can fit the complex temperature field discrete data well and obtain the black box function to support the integral acquisition of the sound wave flight time.

4. Reconstruction of the Fire Temperature Field Based on Acoustic CT

4.1. Arrangement of Acoustic Transceiver and Division of Grid

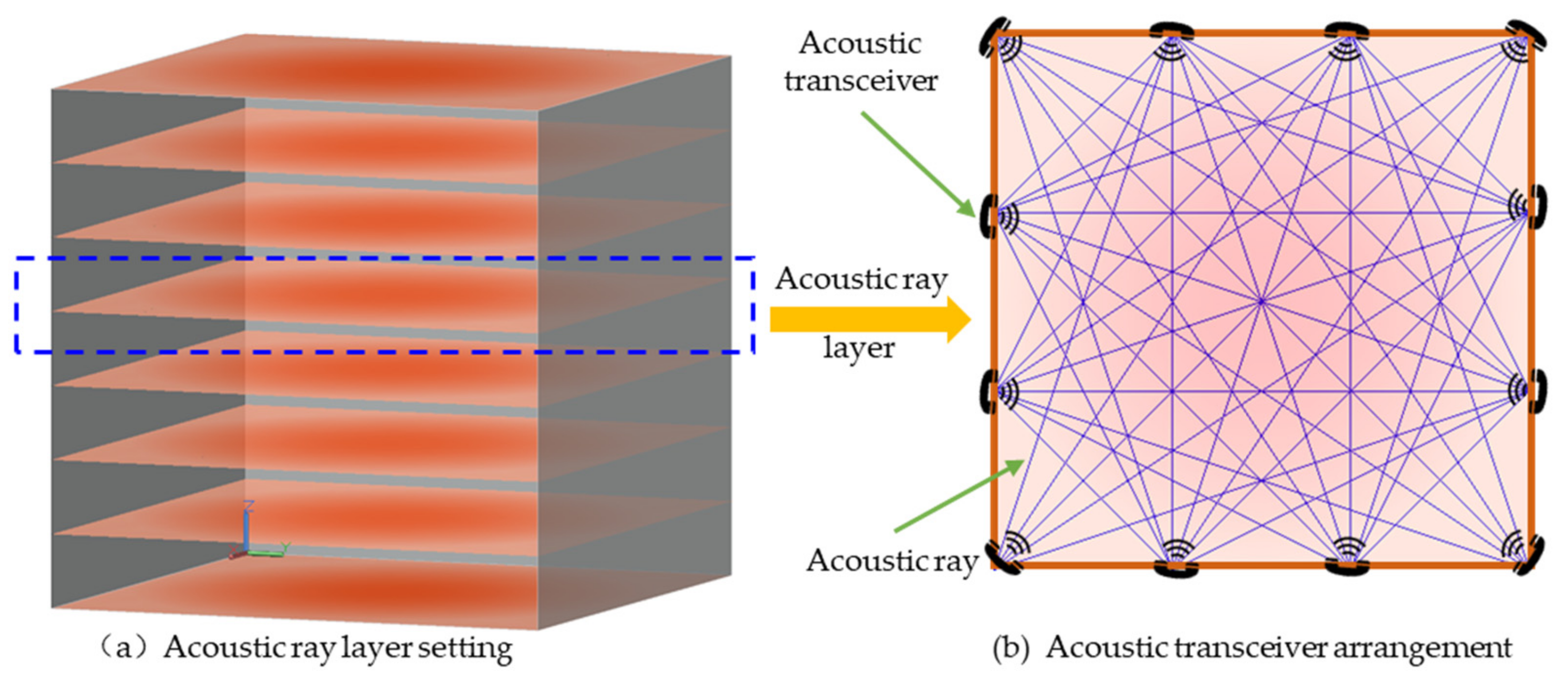
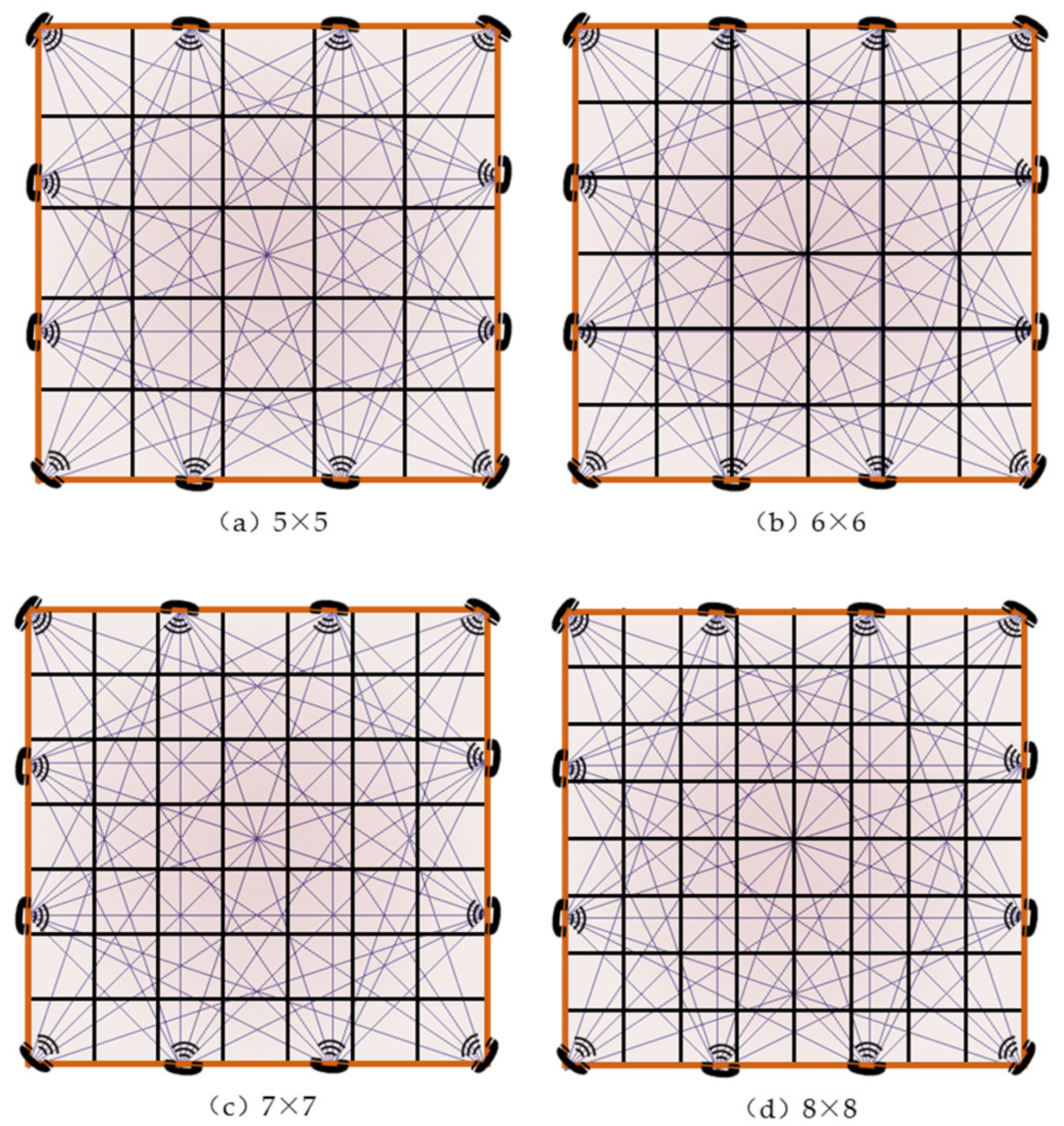
In this paper, acoustic CT temperature reconstruction technology is introduced into the field of building fire information acquisition for the first time, aiming to explore the influence of the reconstruction algorithm and the reconstruction scheme on the reconstruction effect from the perspective of basic research. In order to obtain more data on the error analysis of the reconstruction effect on the overall space, this article sacrifices some of the promotional applicability of this technology. The method of layered reconstruction and ensemble interpolation are used for 3D temperature field reconstruction. In the whole space area, eight sections are selected as the reconstruction unit layer. Twelve acoustic transceivers are evenly arranged on the boundary of each layer. There are 42 effective acoustic ray paths for each layer excluding acoustic rays at the boundary, as shown in Figure 4.

The temperature value in the reconstructed area grid is the solution obtained by the matrix equation (Equation (2), and it is also the basic pixel of the final imaging. In this paper, 5 × 5, 6 × 6, 7 × 7, 8 × 8 are set for each acoustic ray layer in order to explore the influence of the grid division scheme on the reconstruction effect of the 3D temperature field of a fire. In terms of exploratory research combined with relevant literature in other fields in the early stages, the four meshing schemes in this paper are more representative. As shown in Figure 5.

The average temperature inside each grid as a basic element is the unknown $x=(f_1,f_2,\cdots ,f_N)$ to be found in the matrix equation (Equation (3). The length of each ray passing through each grid is the matrix equation (Equation (3) coefficient matrix $A=\left[\begin{array}{ccc}{\omega }_{11}& \cdots & {\omega }_{1N}\\ ⋮& ⋮& ⋮\\ {\omega }_{M1}& \cdots & {\omega }_{MN}\end{array}\right]$. The overall flight time of each ray is the $b=({\tau }_1,{\tau }_2,\cdots ,{\tau }_M)$ vector of the matrix equation (Equation (2)).

4.2. Solution Method of the Acoustic Matrix Equation

It can be seen from the reconstruction scheme that the number of rays (equation number) is inconsistent with the unknown number (grid number), so Equation (2) belongs to the ill-conditioned matrix equation, and there is no definite solution. At present, there are many methods to solve the above ill-conditioned matrix equations, among which the iterative algorithm has the advantages of wide application range, relatively low computational complexity, the avoidance of dimensional disaster problems, and the controllable number of operations. Therefore, two iterative algorithms, the algebraic reconstruction techniques (ART) algorithm and the simultaneous algebraic reconstruction techniques (SART) algorithm, were selected to solve the ill-conditioned matrix equation under each reconstruction scheme so as to explore the accuracy of the equation solution of different solution methods under each scheme in this paper.

(1)

ART algorithm

The basic idea of the ART iterative algorithm is to discretize the continuous images first, and then reconstruct the images using a discrete model of CT imaging. An initial image is given, the projection image is obtained through the positive projection, and then the error between the current projection and the actual measurement projection is calculated to estimate the correction value of the current image. This correction value is iteratively corrected to each ray one by one and assigned to the pixels passed by the ray, and then the back projection and accumulation are processed. The iterative formula of ART is [19]:

$$f_j^{(k+1)}=f_j^{(k)}+\lambda \frac{{\tau }_i-{\displaystyle {\sum }_{n=1}^N{w}_{in}}{f}_n^{(k)}}{{\displaystyle {\sum }_{n=1}^N{w^2}_{in}}}{w}_{ij}$$

(6)

(2)

SART algorithm

Different from the ART algorithm, the SART algorithm makes some improvements, using the error of all the rays of the pixel through the pixel at the same projection angle to determine the correction value for that pixel, rather than considering only one ray. The effect is equivalent to smoothing out the error of the ART algorithm species, thus reducing the sensitivity of the reconstruction results to the measurement error. In the process of reconstructing the 3D temperature field, the solution process formula [20] of the SART algorithm is:

$$f_j^{(k+1)}=f_j^{(k)}+\lambda \frac{1}{{\displaystyle \sum _{i\in I}{w}_{ij}}}\cdot {\displaystyle \sum _{i\in I}\frac{{\tau }_i-{\displaystyle \sum _{n=1}^N{w}_{in}{f}_n^{(k)}}}{{\displaystyle \sum _{n=1}^N{w}_{in}}}}$$

(7)

where k is the number of iterations; λ is the relaxation factor; and $f_j^{(k)}$ and $f_j^{(k+1)}$ are the j th pixel value in the k th and (k + 1) th sub-iterations, respectively. In general, λ is a value between 0 and 2. The size of the relaxation factor is one of the factors affecting the reconstruction results and reconstruction speed. I is a set of projection indexes from a projection angle.

Considering the non-positive determinism of the large matrix equation solved in this paper, the iteration termination condition is set in the form of combining the highest consecutive equal number of values and the number of iterations. Under the 6 × 6 scheme, the highest value is equal in succession, and the iteration termination condition does not converge, so the iteration termination condition of the number of iterations is adopted.

Therefore, the research scheme of the 3D temperature field reconstruction of the thermal field of a building is shown in

Table 3. Research scheme for temperature field reconstruction.

Item	Content
Rebuild objects	Complex temperature field of building thermal field
Sound path	12 transceivers, 42 valid paths
Mesh subdivision	5 × 5, 6 × 6, 7 × 7, 8 × 8
Calculation method	ART, SART

.

5. Analysis of the Reconstruction Results

5.1. Comparative Analysis of Three-Dimensional Overall Reconstruction Temperature Field Cloud Map

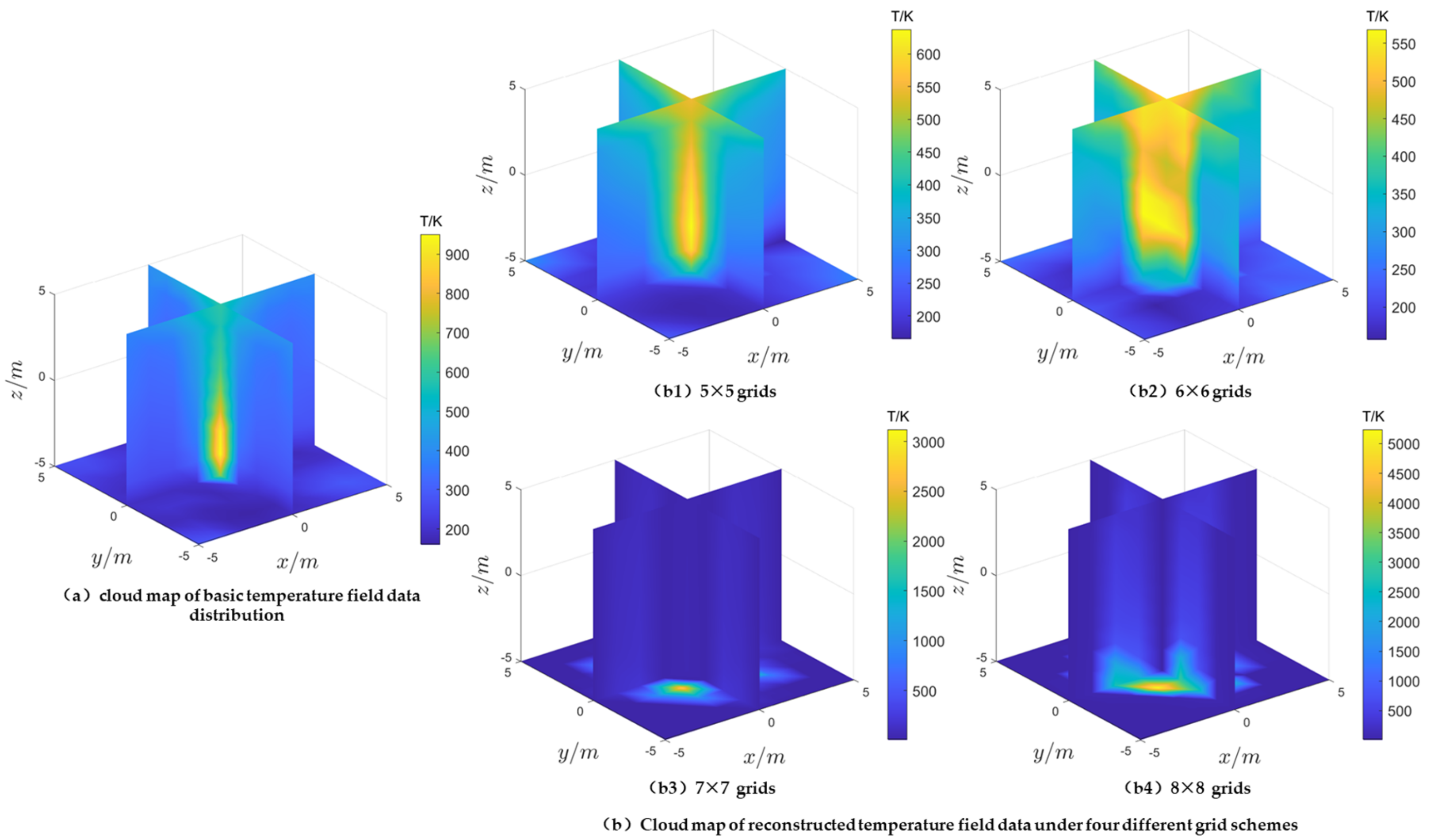
Figure 6 and Figure 7 show the contour plots of reconstructed temperature fields using the ART algorithm and the SART algorithm under different grid partitioning schemes, as well as the contour plots of the baseline temperature data (obtained by fitting a black box function using neural network methods, referred to as baseline temperature data thereafter). Figure 6a and Figure 7a display the distribution of the baseline temperature data, while Figure 6b and Figure 7b show the contour plots of the reconstructed temperature data using four grid schemes based on the ART and SART algorithms, respectively.

As can be seen from Figure 6, under the ART algorithm:

(1)

The reconstruction results under the 5 × 5 grid scheme (Figure 6(b1)) exhibit a high-temperature distribution pattern that is similar to the baseline temperature data (Figure 6a). The reconstruction results under the 6 × 6 grid scheme (Figure 6(b2)) also show significant high-temperature regions above and around the fire source, but with a distinctly different distribution pattern compared to the baseline temperature data (Figure 6a). It is evident that the reconstruction results under the 7 × 7 grid scheme (Figure 6(b3)) and the 8 × 8 grid scheme (Figure 6(b4)) do not show any high-temperature areas near the fire source, indicating that the reconstruction results are unsuccessful.

(2)

Under the 5 × 5 (Figure 6(b1)) and 6 × 6 (Figure 6(b2)) grid schemes, the maximum reconstructed temperatures are 600 K and 550 K, respectively. Both reconstructed temperatures are significantly lower than the baseline temperature data (Figure 6a), but the former demonstrates better reconstruction performance than the latter.

Therefore, based on the analysis of the distribution pattern of high-temperature regions and the overall reconstructed temperature, the reconstruction performance under the 5 × 5 grid scheme (Figure 6(b1)) using the ART algorithm is superior to the other three grid schemes. It can be observed that an increase in the number of unknowns in the ill-conditioned matrix equation is not conducive to the ART algorithm’s solution of the equation.

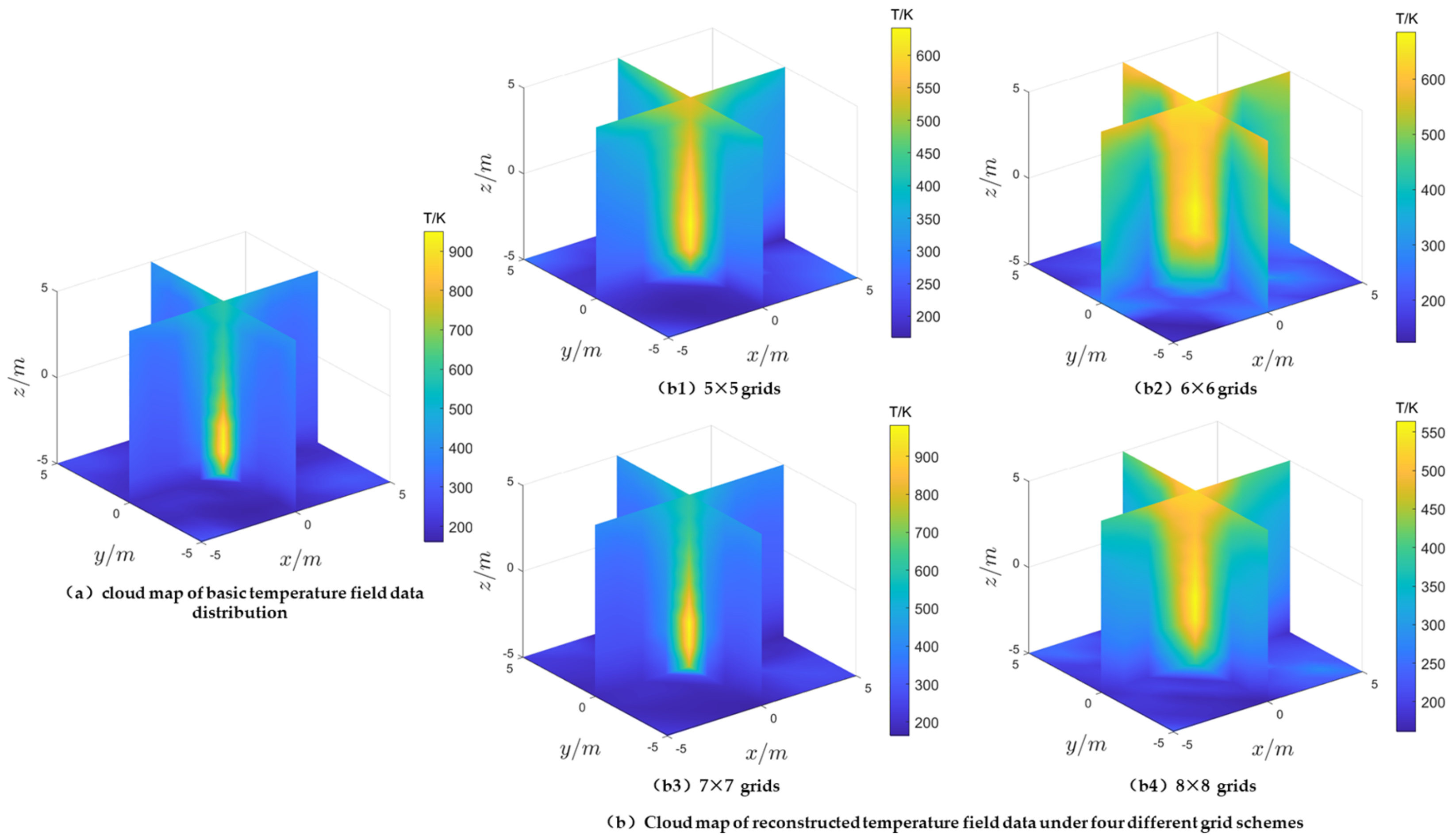
As can be seen from Figure 7, under the SART algorithm:

(1)

The reconstructions under the four grid schemes (Figure 7b) all exhibit significant high-temperature regions, with their locations consistent with the baseline temperature data (Figure 7a). However, the reconstruction performance, especially the distribution of high-temperature regions, varies significantly among the different grid schemes. Compared to the other two schemes, the high-temperature region morphology under the 5 × 5 (Figure 7(b1)) and 7 × 7 (Figure 7(b3)) grid schemes is more similar to the baseline temperature data.

(2)

The highest values of the reconstructed temperature field under the grid scheme of 5 × 5 (Figure 7(b1)), 6 × 6 (Figure 7(b2)) and 8 × 8 (Figure 7(b4)) were 600 K, 600 K and 550 K, respectively, which were lower than the maximum values of the baseline temperature data (Figure 7a). The morphology and maximum value of the high temperature zone under the 7 × 7 (Figure 7(b4)) meshing scheme are close to the baseline temperature (Figure 7a) data.

Therefore, from the analysis of high temperature zone morphology and overall reconstruction temperature, the meshing scheme and equation solving algorithm can control the final reconstruction effect to a large extent. Among them, compared with the case of a small number of meshes, a large number of grids will increase the pixels of the imaging, which will theoretically improve the imaging accuracy. However, when the number of equations (number of acoustic rays) is constant, there may be a problem of matrix singularity if the number of meshes (unknowns) is too great or too little, resulting in unsolvable or unstable solutions depending on the characteristics of the matrix and the solution method.

In addition, the reconstruction results show that under the same meshing scheme, the temperature field reconstruction effect based on the SART algorithm is better than that based on the ART algorithm.

5.2. Two-Dimensional Section Reconstruction Temperature Field Cloud Comparison Analysis

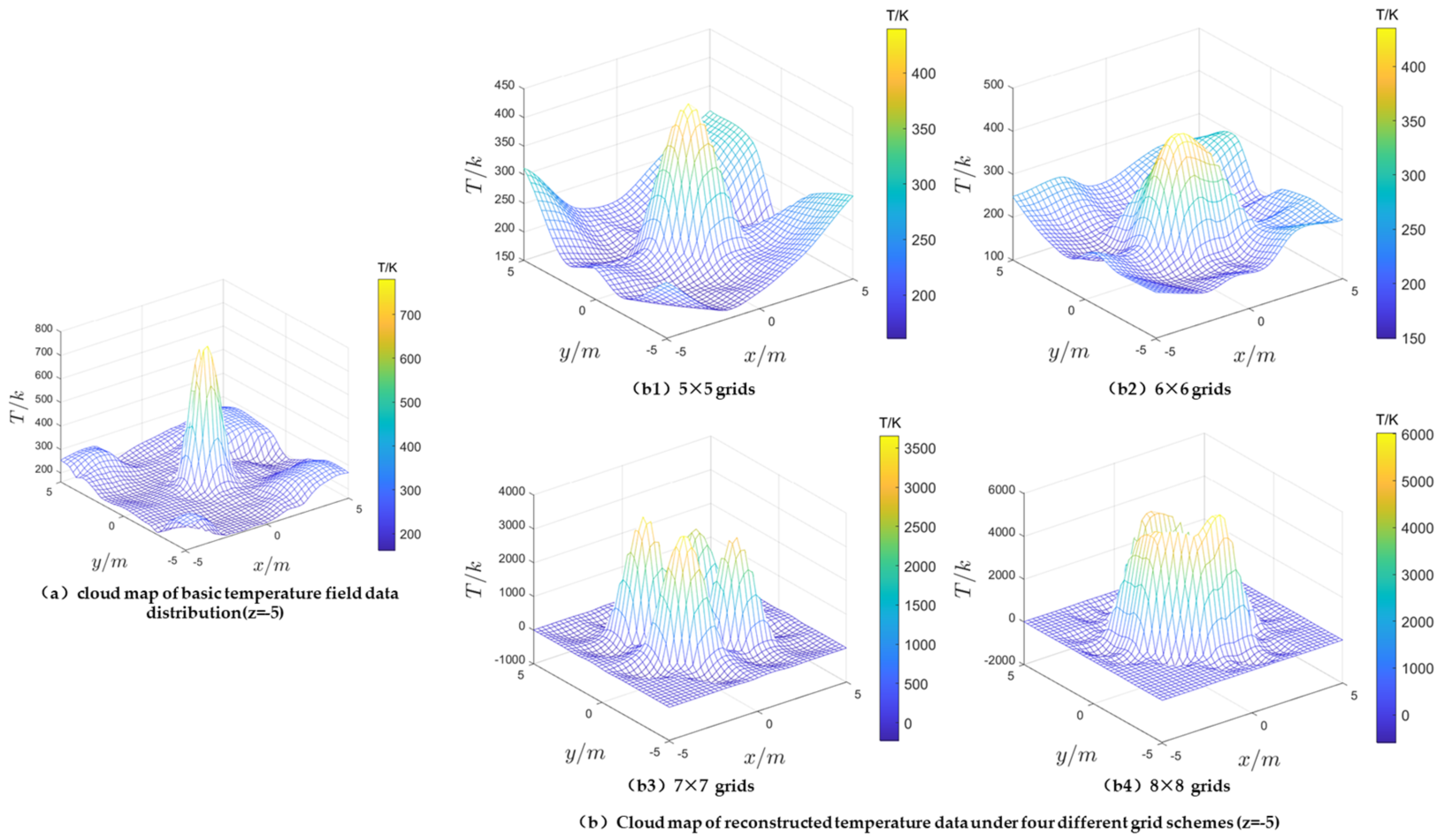
In order to compare the reconstructed temperature field and the basal temperature field more intuitively, the basic temperature field data cloud of a certain section (the z = −5 layer is selected here) and the reconstructed temperature field data cloud are selected for comparative analysis. Through preliminary exploratory research, the reconstruction accuracy of each layer under the same reconstruction scheme is basically the same, and the reconstruction effect of a single layer can represent the overall reconstruction effect, so the first layer is selected for analysis.

Figure 8a and Figure 9a show the base temperature data cloud maps for the z = −5 contour. Figure 8b and Figure 9b display the reconstructed temperature field data cloud maps for four different grid schemes using the ART and SART algorithms for the z = −5 contour, respectively.

As can be seen from Figure 8, under the ART algorithm:

(1)

Among the four grid schemes, the reconstruction results of the 5 × 5 (Figure 8(b1)) scheme and the 6 × 6 (Figure 8(b2)) scheme showed a unimodal high temperature region similar to the baseline temperature data (Figure 8a), but the maximum reconstruction temperature was significantly lower than the baseline temperature data (Figure 8a), and had a large error. The reconstruction results of the 7 × 7 (Figure 8(b3)) scheme and the 8 × 8 (Figure 8(b4)) scheme showed a multimodal phenomenon and an abnormally high temperature, so the reconstruction result failed.

(2)

Under the grid schemes of 5 × 5 (Figure 8(b1)) and 6 × 6 (Figure 8(b2)), the maximum distribution of the reconstruction temperature was 400 K. The reconstructed temperatures were significantly lower than the baseline temperature data (Figure 8a).

Therefore, the reconstruction failure of these two schemes is indicated from the two aspects of high temperature zone morphology and reconstruction maximum value, which is consistent with the previously discussed three-dimensional overall reconstruction temperature field analysis conclusion.

As can be seen from Figure 9, under the SART algorithm:

(1)

In the four meshing schemes, a single-peak high temperature region similar to the baseline temperature data appeared, the location of the high temperature zone was basically consistent with the baseline temperature data (Figure 9a), and the reconstruction effect was acceptable. The data fluctuations of the 6 × 6 (Figure 9(b2)) scheme and the 8 × 8 (Figure 9(b3)) scheme in the low temperature region were more obvious, and the temperature distribution pattern of the 5 × 5 (Figure 9(b1)) scheme and the 7 × 7 (Figure 9(b3)) scheme in the low temperature region was closer to the baseline temperature data, but the 5 × 5 (Figure 9(b1)) scheme may be the result of the overall flattening caused by fewer data pixels.

(2)

In terms of the maximum reconstruction temperature, the reconstruction result (700 K) under the 7 × 7 (Figure 9(b3)) scheme was basically consistent with the baseline temperature data (Figure 9a), and the maximum reconstruction temperature value of the other three schemes was significantly low. Therefore, the reconstruction effect under the 7 × 7 (Figure 9(b3)) grid scheme under this algorithm is the best.

Therefore, by comparing the reconstruction effects of different algorithms, the reconstruction effect of the SART algorithm is significantly better than that of the ART algorithm under the same grid scheme. In addition, the SART algorithm shows better robustness in terms of applicability to different grid schemes.

5.3. Quantitative Error Analysis of the Reconstruction Effect

The root-mean-square percent error E, mean relative error $E_{\mathrm{mean}}$, maximum relative error $E_{\max }$, and the correlation coefficient R are selected as the evaluation indexes of reconstruction quality to quantitatively evaluate the reconstruction effect of each reconstruction scheme [21].

$$E=\frac{\sqrt{\frac{1}{m}{\displaystyle \sum _{i=1}^m{[T_c(i)-T_M(i)]}^2}}}{T_{M\mathrm{m}\mathrm{a}\mathrm{v}\mathrm{e}}}\times 100\%$$

(8)

$$E_{\mathrm{mean}}=\left|\frac{T_{Cmean}-T_{Mmean}}{T_{Mmean}}\right|\times 100\%$$

(9)

$$E_{\max }=\left|\frac{T_{C\max }-T_{M\max }}{T_{M\max }}\right|\times 100\%$$

(10)

where M is the total number of grids divided by the measured region; $T_{c(i)}$ is the reconstruction temperature of the i th grid center point; $T_{M(i)}$ is the base temperature of the i th grid center point; $T_{Mave}$ is the average temperature of the foundation temperature field; $T_{Cave}$ is the average temperature of the reconstructed temperature field; $T_{M\max }$ is the highest temperature value of the foundation temperature field; and $T_{C\max }$ is the highest temperature value of the reconstructed temperature field.

In

Table 4. Reconstruction error of the three-dimensional temperature field of a building fire and the average calculation time of a single layer.

Algorithm	Grid Numbers	${\mathit{E}}_{\mathbf{mean}}$ (%)	${\mathit{E}}_{\mathbf{max}}$ (%)	$\mathit{E}$ (%)	Correlation Coefficient (R)	Single Layer Average Calculation Time (s)	Stopping Criterion for Iteration
ART algorithm	5 × 5 × 8	5.52	41.25	10.97	0.90	0.03	Normal convergence
	6 × 6 × 8	9.40	21.84	16.22	0.81	26.9	Iteration times
	7 × 7 × 8	—	—	—	—	—	Normal convergence
	8 × 8 × 8	—	—	—	—	—	Normal convergence
SART algorithm	5 × 5 × 8	5.51	40.82	10.91	0.90	0.12	Normal convergence
	6 × 6 × 8	25.81	36.78	30.64	0.59	32.5	Iteration times
	7 × 7 × 8	4.11	3.48	5.65	0.97	0.35	Normal convergence
	8 × 8 × 8	6.12	28.39	9.48	0.92	0.53	Normal convergence

, normal convergence represents the highest value of consecutive equal iteration termination conditions, and the number of iterations represents the number of iteration termination conditions.

From the reconstructed cloud image and error analysis data, it can be seen that:

• In the process of solving the sparse matrix equation under the reconstruction scheme, neither the ART algorithm nor the SART algorithm can converge independently under the 6 × 6 grid, and the number of iterations should be limited. Under other mesh division schemes, both methods can achieve autonomous convergence.
• For solving the sparse matrix equation under the complex distributed temperature field of a building fire, the ART algorithm takes less time than the SART algorithm in terms of single iteration time and overall convergence time, but the latter shows better robustness in overall reconstruction accuracy.
• Under the SART algorithm, the 7 × 7 meshing scheme achieves the best reconstruction effect. The correlation error index is within 6%, the correlation coefficient is 0.97, and the single-layer calculation time is within 0.5 s. This shows that the appropriate meshing scheme can realize the real-time and accurate reconstruction of the complex temperature field of a building fire under the SART algorithm.
• The meshing scheme has significant control over the reconstruction results. When the number of grids is small, the stability and convergence of the matrix equation solution will be better, but the reconstruction accuracy is poor due to the small number of reconstructed pixels. The reconstruction accuracy can be improved when there are many reconstruction pixels; however, higher requirements are proposed for solving the matrix equations. Therefore, the reconstruction effect of the fire temperature field is the result of the sparse matrix solution and the effective pixels. An optimal matching ratio between pixel meshing and effective acoustic path data exists.

6. Conclusions

In order to obtain temperature information from building fires more efficiently, and benefiting such factors as early warning, evacuation, firefighting and rescue, and the investigation of fire accidents, this paper explored the application of acoustic CT temperature measurement technology in the field of obtaining information from building fires. The main objective of this paper was to analyze the influence of grid partitioning schemes and iterative reconstruction algorithms on the temperature field reconstruction effect. After conducting preliminary preparatory research, the following conclusions were initially drawn:

• With the early fire stage and the relatively simple temperature field distribution constructed in this paper as the reconstruction object, the acoustic CT temperature measurement technology under the preferred reconstruction scheme was selected to achieve a good reconstruction effect.
• Under the reconstruction plan proposed in this paper, the SART algorithm has better stability compared with the ART algorithm. The SART algorithm has better reconstruction quality and is expected to be used for the 3D temperature field reconstruction of building fires in the practical application to a fire site.
• The number of effective pixel grids and the accuracy of matrix equations jointly determine the reconstruction quality of the three-dimensional temperature field of building fires. Therefore, there is an optimal matching ratio between the pixel grid division and the effective acoustic path data for a specific fire geometry space. It can be selected according to a 7 × 7 × 8 grid division under the condition of setting parameters in this paper.

This paper aims to explore the application of acoustic CT temperature measurement technology in the field of building fire information acquisition, and some preliminary preparatory research has been conducted. In order to realize the application of this technology in temperature information acquisition in fire scenes, further research needs to be carried out in the following aspects: firstly, to minimize the arrangement of acoustic transmitters and receivers and to achieve low-dose reconstruction while ensuring reconstruction accuracy in order to meet the needs of efficient rescue, emergency evacuation command, and fire accident investigation. Secondly, it is necessary to further explore the control law of the complexity of temperature field distribution on the reconstruction effect in order to improve the accuracy and reliability of reconstruction. Finally, it is necessary to conduct in-depth research on the propagation characteristics of sound waves in smoke environments in order to better cope with the complexity of fire environments. This research will help promote the application of acoustic CT temperature measurement technology in the field of building fire information acquisition and provide more accurate and reliable temperature information for fire rescue and investigation.