In-Depth Assessment of Cross-Passage Critical Velocity for Smoke Control in Large-Scale Railway Tunnel Fires
Abstract
1. Introduction
2. Current State of Tunnel Fire Smoke Control
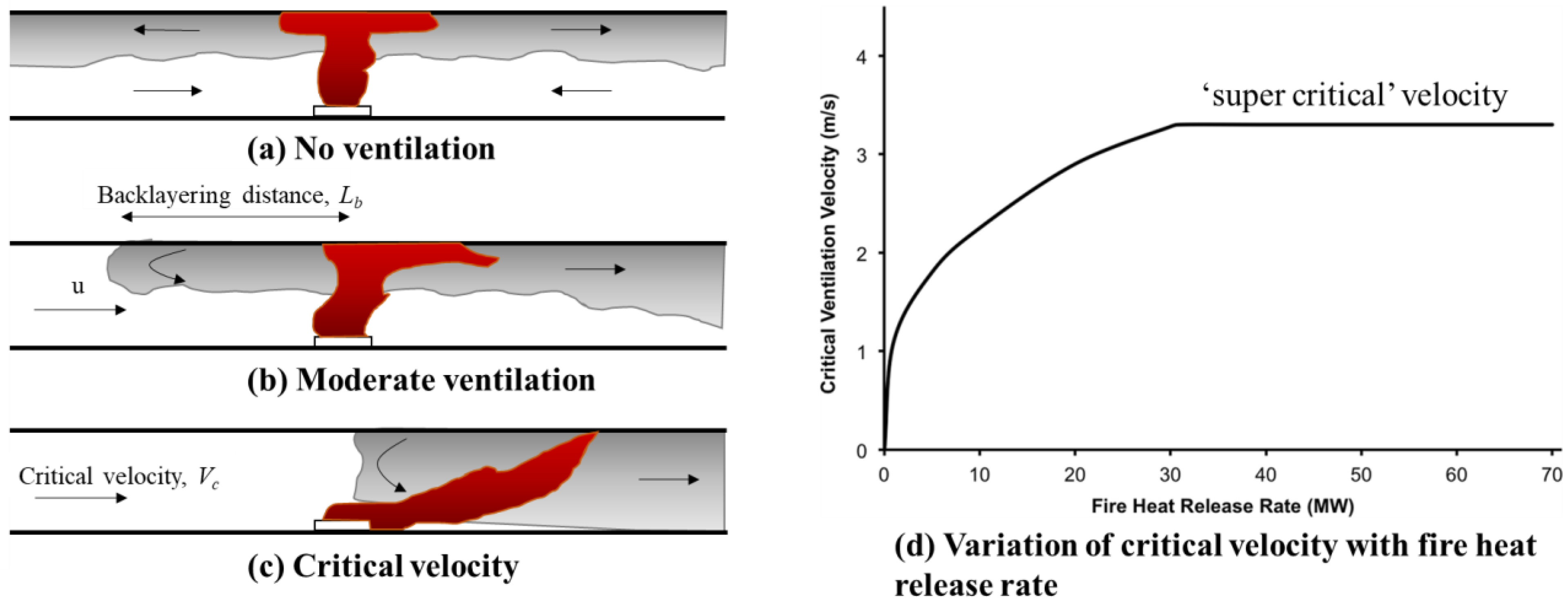
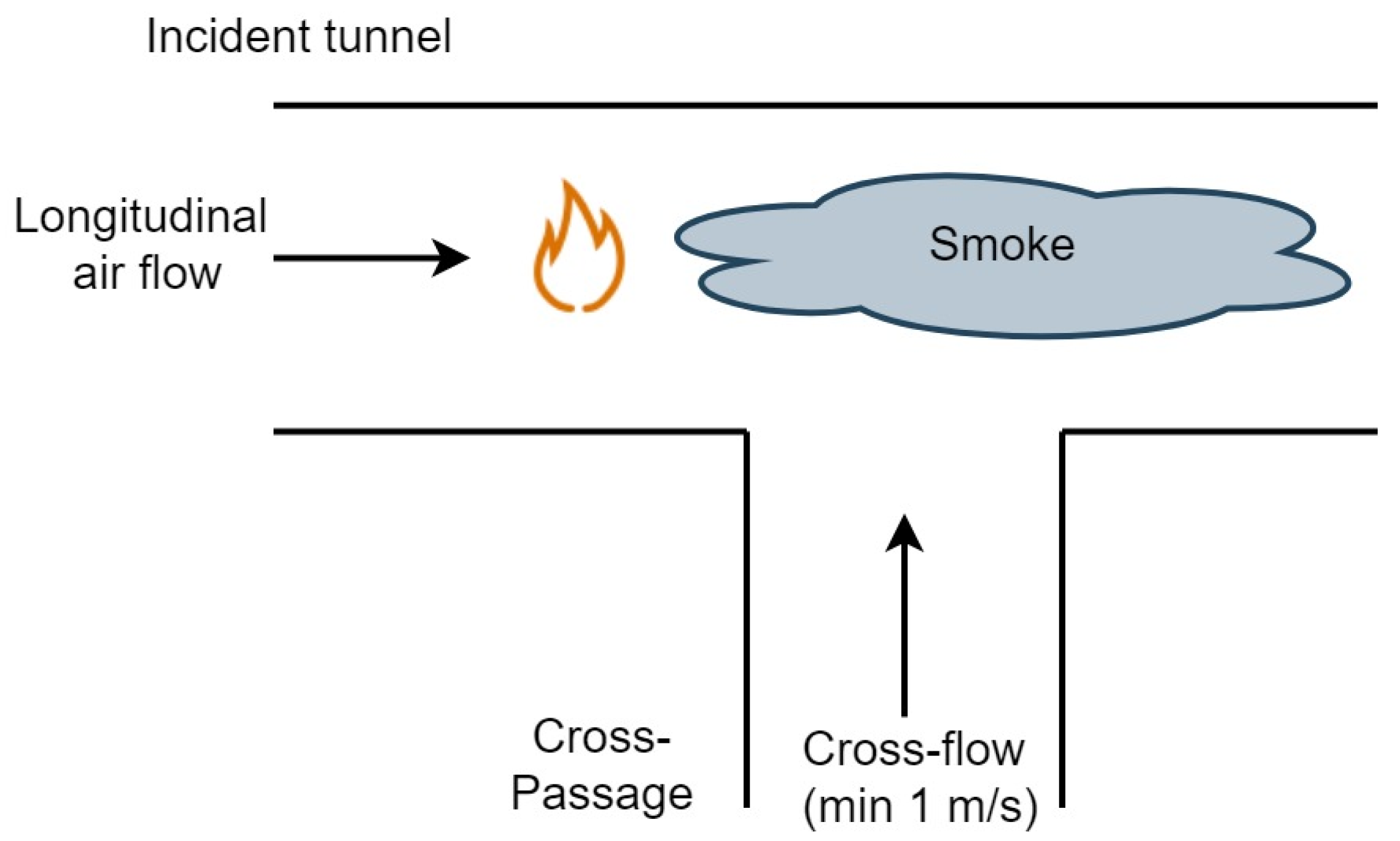
2.1. Critical Velocity in the Incident Tunnel and Cross-Passage
2.2. Computational Fluid Dynamics in Tunnel Fire Modelling
3. Computational Methods
3.1. Governing Equations
3.2. Subgrid-Scale Turbulence Model
3.3. Combustion Model
3.4. Radiation Model
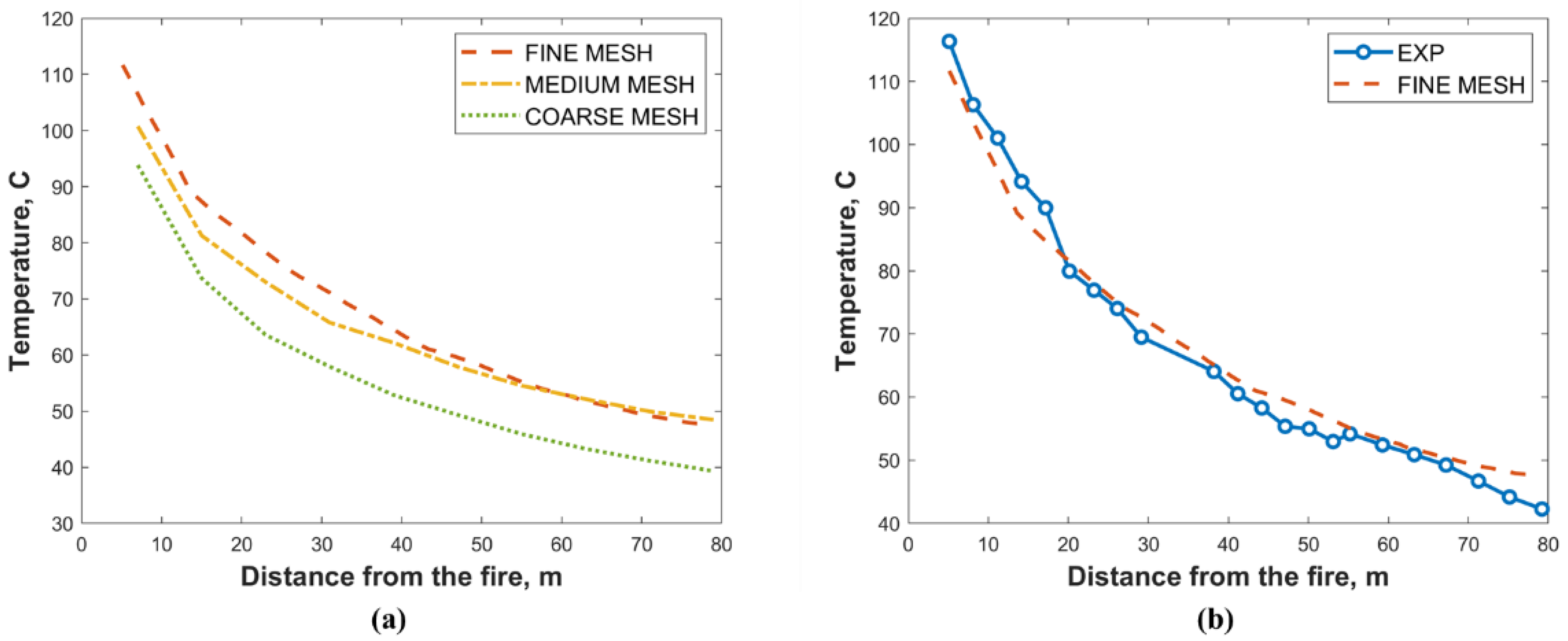
3.5. Model Validation for Tunnel Fire Cases
4. Model Configuration
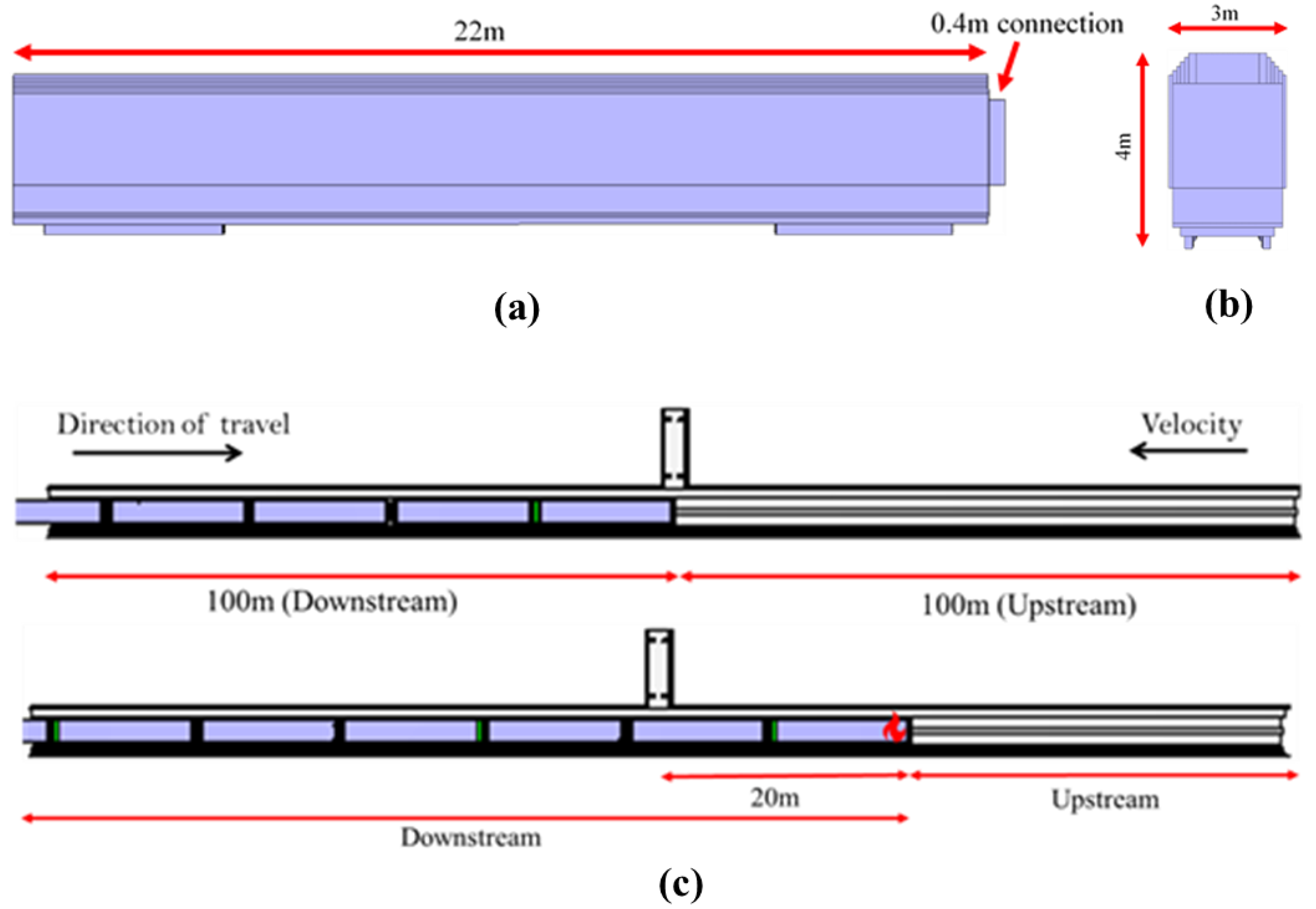
4.1. Rail Tunnel and Cross-Passage Geometry
4.2. Fire Location and Parameters
4.3. Boundary Conditions
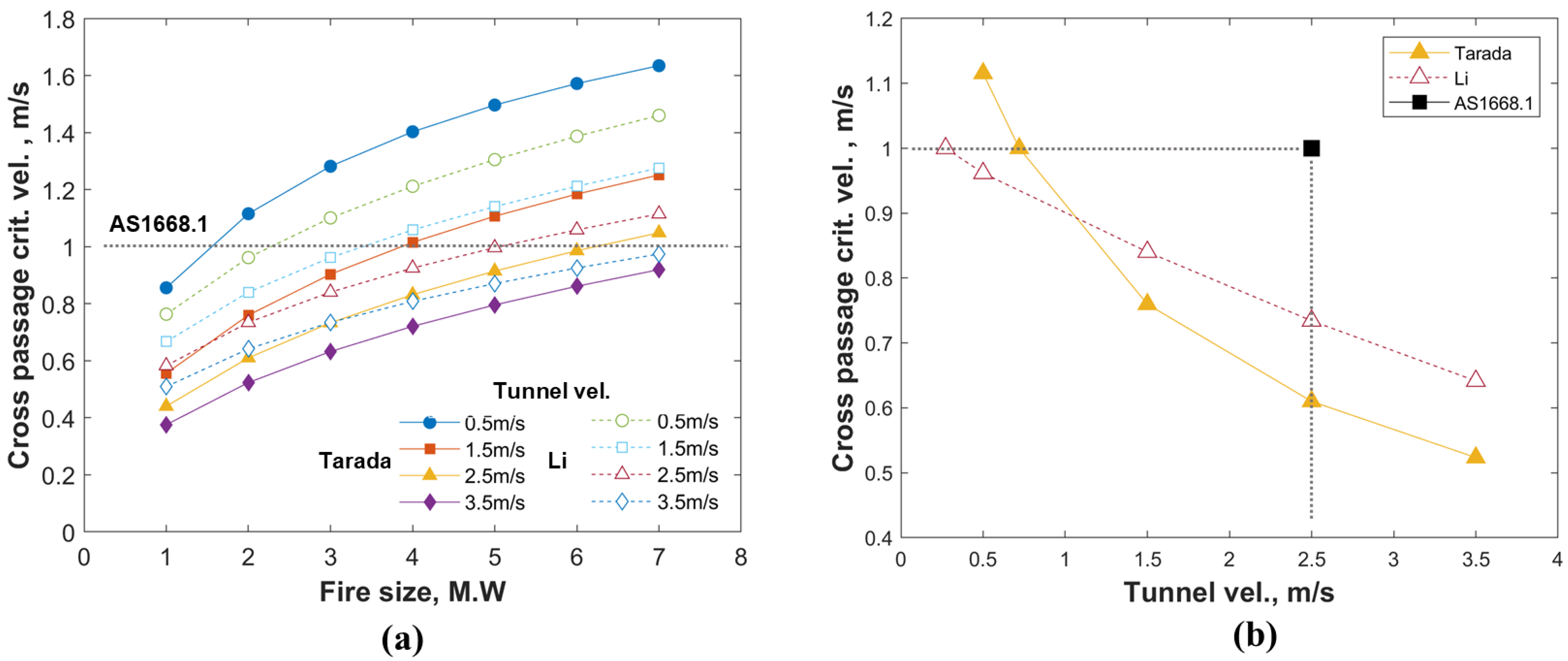
4.4. Determining the Cross-Passage Critical Velocity Based on Empirical Calculations
5. Results
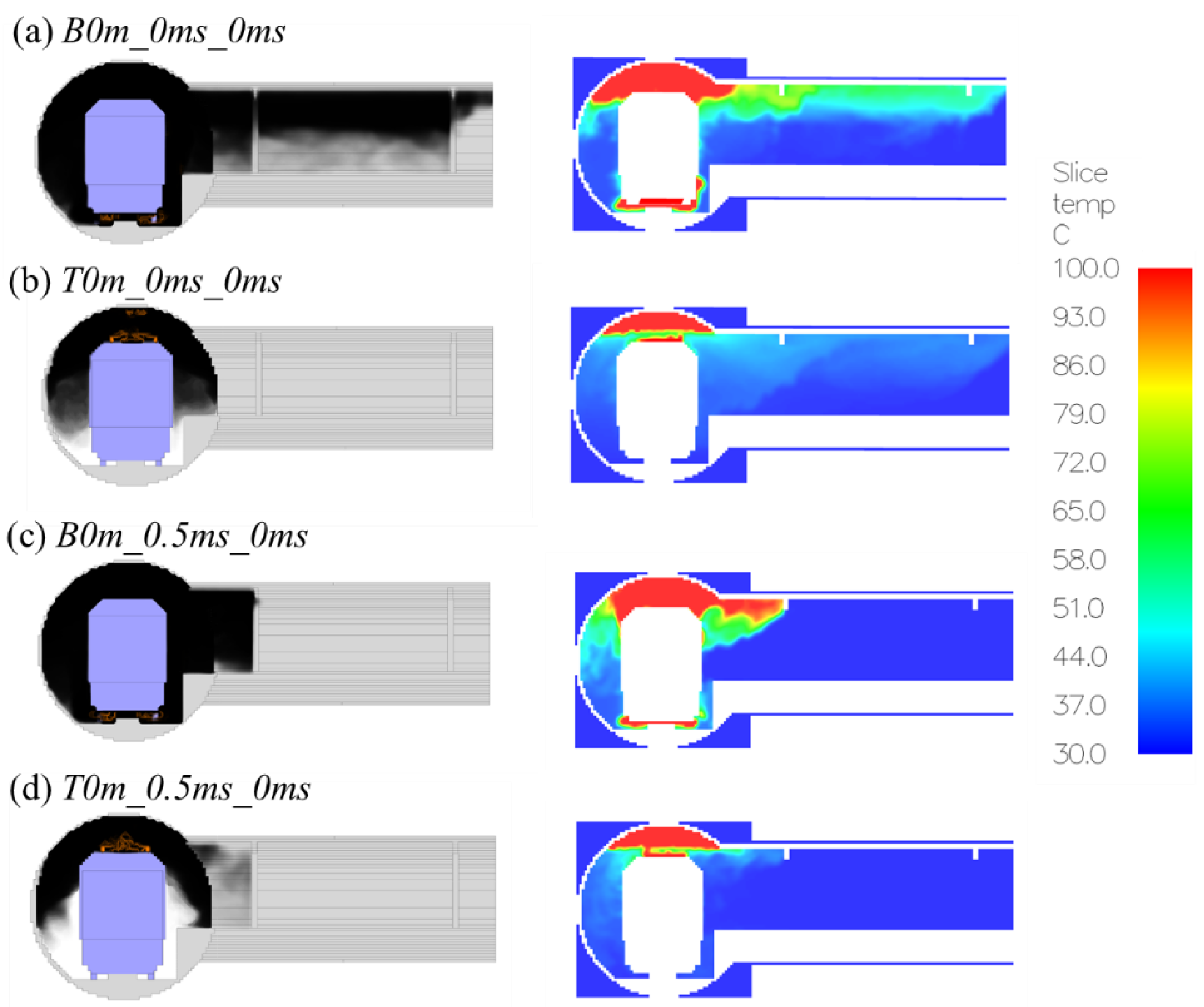
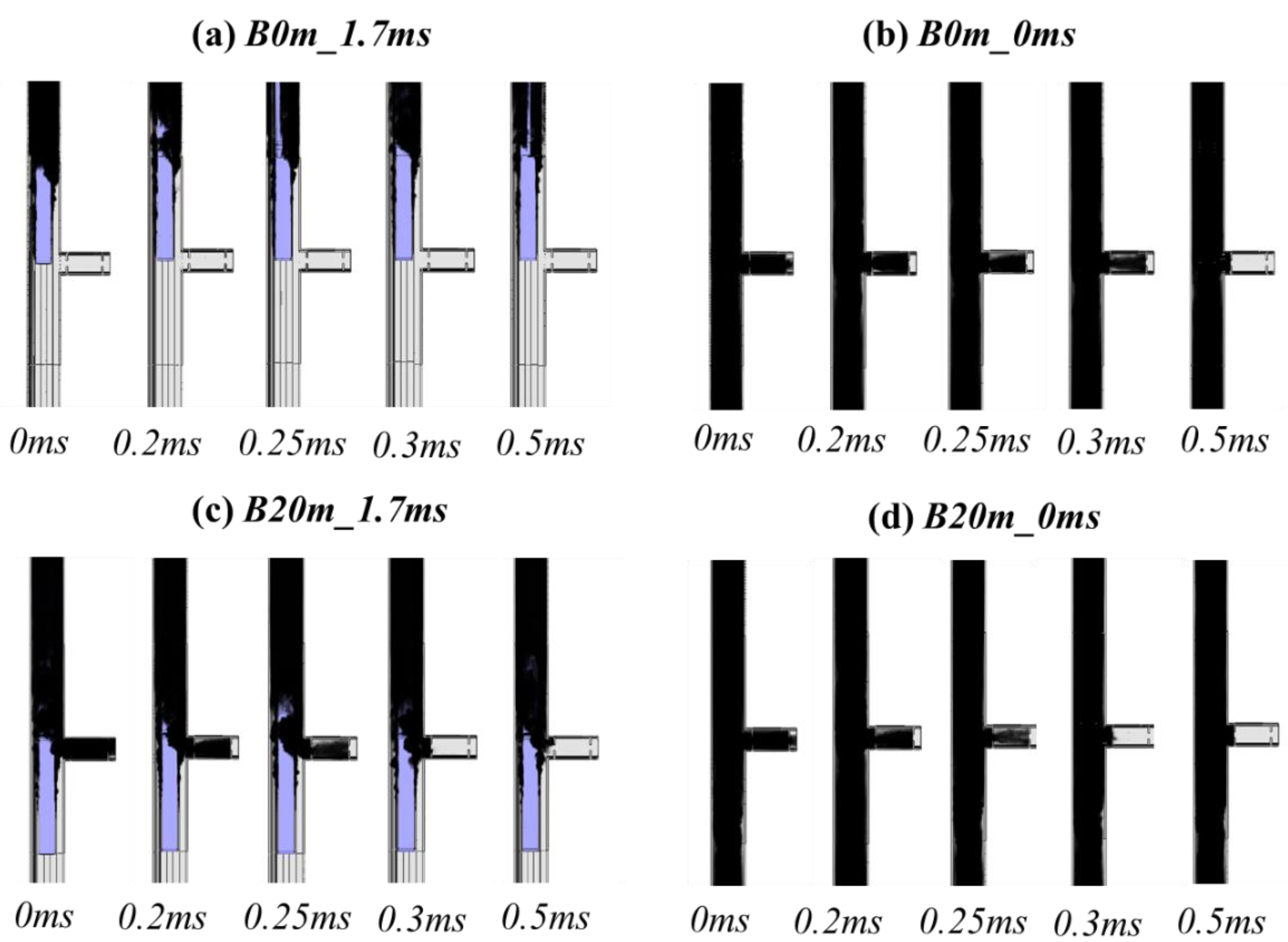
5.1. Smoke Distribution at the Cross-Passage
5.2. Temperature and Velocity Profile at the Cross-Passage Door
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Tunnel cross-sectional area (m2) | |
| Specific heat capacity (J/kg K) | |
| Characteristic length of the fire plume | |
| Acceleration due to gravity (m2/s) | |
| Critical Froude number | |
| Height of tunnel cross-section (m) | |
| Hydraulic diameter (m) | |
| thermal conductivity | |
| Backlayering length (m) | |
| Mass flow rate (m) | |
| Convective heat release rate (kW) | |
| Heat release rate | |
| Temperature | |
| Ambient temperature (K) | |
| Flame temperature (K) | |
| Horizontal gas velocity | |
| Critical velocity (m/s) | |
| Width of tunnel (m) | |
| Greek Symbols | |
| Density (kg/m3) | |
| Smoke density (kg/m3) | |
| Ambient density (kg/m3) | |
| Grid length | |
| Subscripts | |
| Subscript for ambient | |
| Subscript for cross-passage critical | |
| Subscript for cross-passage | |
| Subscript for tunnel | |
| Australian Standard | |
| Computer-Aided Design | |
| Computational Fluid Dynamics | |
| Fire Dynamics Simulator | |
| National Institute of Standards and Technology | |
| National Fire Protection Association | |
| wrt | with respect to |
| Cross-Passage |
References
- Gehandler, J. Road tunnel fire safety and risk: A review. Fire Sci. Rev. 2015, 4, 2. [Google Scholar] [CrossRef]
- Barbato, L.; Cascetta, F.; Musto, M.; Rotondo, G. Fire safety investigation for road tunnel ventilation systems–an overview. Tunn. Undergr. Space Technol. 2014, 43, 253–265. [Google Scholar] [CrossRef]
- Capote, J.; Alvear, D.; Abreu, O.; Lázaro, M.; Cuesta, A. Evacuation Modelling of Fire Scenarios in Passenger Trains; Springer: Berlin, Heidelberg, 2010; pp. 705–711. [Google Scholar]
- Standards Australia. AS/NZS 1668.1:2015—The Use of Ventilation and Air Conditioning in Buildings Fire and Smoke Control in Buildings; Standards Australia: Sydney, NSW, Australia, 2015. [Google Scholar]
- Li, Y.Z.; Lei, B.; Ingason, H. Scale modeling and numerical simulation of smoke control for rescue stations in long railway tunnels. J. Fire Prot. Eng. 2012, 22, 101–131. [Google Scholar] [CrossRef]
- Ingason, H. State of the art of tunnel fire research. In Proceedings of the 9th International Symposium on Fire Safety Science, Karlsruhe, Germany, 21–26 September 2008. [Google Scholar]
- Thomas, P.H. The movement of smoke in horizontal passages against an air flow. Fire Res. Stn. 1968, 723. [Google Scholar]
- Li, Y.Z.; Lei, B.; Ingason, H. Study of critical velocity and backlayering length in longitudinally ventilated tunnel fires. Fire Saf. J. 2010, 45, 361–370. [Google Scholar] [CrossRef]
- Kile, G.W.; Gonzalez, J.A. The Memorial tunnel fire ventilation test program: The longitudinal and natural tests. Ashrae Trans. 1997, 103, 701. [Google Scholar]
- Brinckerhoff, B.; Brinckerhoff, P. Memorial Tunnel Fire Ventilation Test Report; Massachusetts Highway Department: Boston, MA, USA, 1995. [Google Scholar]
- Ingason, H.; Li, Y.Z.; Lönnermark, A. Runehamar tunnel fire tests. Fire Saf. J. 2015, 71, 134–149. [Google Scholar] [CrossRef]
- Ingason, H.; Lönnermark, A. Heat release rates from heavy goods vehicle trailers in tunnels. Fire Saf. J. 2005, 40, 22. [Google Scholar] [CrossRef]
- Lönnermark, A.; Ingason, H. Fire spread and flame length in large-scale tunnel fires. Fire Technol. 2006, 42, 283–302. [Google Scholar] [CrossRef]
- Hu, L.H.; Huo, R.; Chow, W.K. Studies on buoyancy-driven back-layering flow in tunnel fires. Exp. Therm. Fluid Sci. 2008, 32, 1468–1483. [Google Scholar] [CrossRef]
- Stahlanwendung, S. Fires in Transport Tunnels: Report on Full-Scale Tests; Eureka-Project EU 499: FIRETUN; Conducted by the Following 9 European Countries: Austria, Finland, France, Germany, Great Britain, Italy, Norway, Sweden, Switzerland; Verlag u. Vertriebsges. mbH: Düsseldorf, Germany, 1995. [Google Scholar]
- Haack, A. Fire protection in traffic tunnels: General aspects and results of the EUREKA project. Tunn. Undergr. Space Technol. 1998, 13, 377–381. [Google Scholar] [CrossRef]
- Saleheen, Z.; Krishnamoorthy, R.R.; Nadjai, A. A review on behavior, material properties and finite element simulation of concrete tunnel linings under fire. Tunn. Undergr. Space Technol. 2022, 126, 104534. [Google Scholar] [CrossRef]
- Ingason, H. Fire development in large tunnel fires. In Proceedings of the 8th International Symposium on Fire Safety Science, Beijing, China, 18–23 September 2005; pp. 18–23. [Google Scholar]
- Oka, Y.; Atkinson, G.T. Control of Smoke Flow in Tunnel Fires. Fire Saf. J. 1995, 305–322. [Google Scholar] [CrossRef]
- NFPA (National Fire Protection Agency). NFPA 502: Standard for Road Tunnels, Bridges, and Other Limited Access Highways, Annex D; NFPA: Quincy, MA, USA, 2019. [Google Scholar]
- PIARC Committee on Road Tunnels (C5). Technical Committee 5 Road Tunnels, Fire and Smoke Control in Road Tunnels; World Road Association (PIARC): La Défense, France, 1999. [Google Scholar]
- European Parliament, Council of the European Union, Directive 2004/54/EC of the European Parliament and of the Council on Minimum Safety Requirements for Tunnels in the Trans European Road Network. 2004. Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=celex:32004L0054 (accessed on 8 September 2022).
- Sturm, P.; Beyer, M.; Rafiei, M. On the problem of ventilation control in case of a tunnel fire event. Case Stud. Fire Saf. 2017, 7, 36–43. [Google Scholar] [CrossRef]
- RABT 2016; Richtlinien fur die Ausstattung und den Betrieb von Strasentunneln [Guidelines for road tunnel equipment and operation]. RABT: Zella-Mehlis, Germany, 2016.
- ASTRA 13 001; Lüftung der Strassentunnel [Ventilation of Road Tunnels]. Bundesamt für Strassen (ASTRA): Ittigen, Switzerland, 2008.
- RVS 09.02.31; Tunnel, Tunnelausrüstung, Belüftung, Grundlagen, Österreich, [Tunnels, Tunnel Equipment, Ventilation, Basics, Austria]. Research Society Road—Rail—Transport (FSV): Vienna, Austria, 2014.
- Donald, M. Air Velocities Permitted in Road Tunnels, and Other Requirements for a Safe Escape Route in Case of Fire; World Road Association (PIARC): La Défense, France, 2018. [Google Scholar]
- Lee, C.K.; Chaiken, R.F.; Singer, J.M. Interaction Between Duct Fires and Ventilation Flow: An Experimental Study. Combust. Sci. Technol. 1979, 20, 59–72. [Google Scholar] [CrossRef]
- Kennedy, W.D. Critical Velocity: Past, Present and Future. In Proceedings of the One Day Seminar on Smoke and Critical Velocity in Tunnels, London, UK, 2 April 1996. [Google Scholar]
- Li, Y.Z.; Ingason, H. Discussions on critical velocity and critical Froude number for smoke control in tunnels with longitudinal ventilation. Fire Saf. J. 2018, 99, 22–26. [Google Scholar] [CrossRef]
- Tarada, F. Critical Velocities for Smoke Control in Tunnel Cross-Passages. In Proceedings of the First International Conference on Major Tunnel and Infrastructure Projects, Taipei, Taiwan, 22–24 May 2000. [Google Scholar]
- Langner, V.; Bopp, R.; Bailey, P.R. Minimum flow velocity through open cross passages in twin bore rail tunnels. In Proceedings of the 5th International Conference ‘Tunnel Safety and Ventilation’, Graz, Austria, 3–4 May 2010. [Google Scholar]
- Tarada, F. New Perspectives on the Critical Velocity for Smoke Control. In Proceedings of the Fourth International Symposium on Tunnel Safety and Security, Frankfurt am Main, Germany, 17–19 March 2010. [Google Scholar]
- Li, Y.Z.; Lei, B.; Ingason, H. Theoretical and Experimental Study of Critical Velocity for Smoke Control in a Tunnel Cross-Passage. Fire Technol. 2013, 49, 435–449. [Google Scholar] [CrossRef]
- Li, Y.Z.; Ingason, H. Effect of cross section on critical velocity in longitudinally ventilated tunnel fires. Fire Saf. J. 2017, 91, 303–311. [Google Scholar] [CrossRef]
- Yuen, A.C.Y.; Chen, T.B.Y.; Cordero, I.M.D.C.; Liu, H.; Li, A.; Yang, W.; Cheung, S.C.P.; Chan, Q.N.; Kook, S.; Yeoh, G.H. Developing a solid decomposition kinetics extraction framework for detailed chemistry pyrolysis and combustion modelling of building polymer composites. J. Anal. Appl. Pyrolysis 2022, 163, 105500. [Google Scholar] [CrossRef]
- De Cachinho Cordeiro, I.M.; Chen, T.B.Y.; Yuen, A.C.Y.; Wang, C.; Chan, Q.N.; Zhang, J.; Yeoh, G.H. Pyrolysis and combustion characterisation of HDPE/APP composites via molecular dynamics and CFD simulations. J. Anal. Appl. Pyrolysis 2022, 163, 105499. [Google Scholar] [CrossRef]
- Liu, H.; Cachinho Cordeiro, I.M.D.; Yin Yuen, A.C.; Chan, Q.N.; Kook, S.; Yeoh, G.H. Application of multi-parametric characterization to water-based fire suppression systems in compartment fire scenarios. Numer. Heat Transf. Part A Appl. 2022, 1–19. [Google Scholar] [CrossRef]
- Li, A.; Yuen, A.C.Y.; Wang, W.; Chen, T.B.Y.; Lai, C.S.; Yang, W.; Wu, W.; Chan, Q.N.; Kook, S.; Yeoh, G.H. Integration of Computational Fluid Dynamics and Artificial Neural Network for Optimization Design of Battery Thermal Management System. Batteries 2022, 8, 69. [Google Scholar] [CrossRef]
- Li, A.; Yuen, A.C.Y.; Wang, W.; Weng, J.; Yeoh, G.H. Numerical investigation on the thermal management of lithium-ion battery system and cooling effect optimization. Appl. Therm. Eng. 2022, 215, 118966. [Google Scholar] [CrossRef]
- Yuen, A.C.Y.; Chen, T.B.Y.; Yang, W.; Wang, C.; Li, A.; Yeoh, G.H.; Chan, Q.N.; Chan, M.C. Natural ventilated smoke control simulation case study using different settings of smoke vents and curtains in a large Atrium. Fire 2019, 2, 7. [Google Scholar] [CrossRef]
- Chen, T.B.Y.; Yuen, A.C.Y.; Yeoh, G.H.; Yang, W.; Chan, Q.N. Fire Risk Assessment of Combustible Exterior Cladding Using a Collective Numerical Database. Fire 2019, 2, 11. [Google Scholar] [CrossRef]
- Huo, Y.; Zou, G.W.; Gao, Y.; Li, S.S. Large eddy simulation of post-flashover room fires based on the Vreman subgrid-scale model. Int. J. Heat Mass Transf. 2015, 91, 872–884. [Google Scholar] [CrossRef]
- Sajid, Z.; Yang, Y.; You, P.; Deng, H.; Cheng, X.; Danial, S.N. An Explorative Methodology to Assess the Risk of Fire and Human Fatalities in a Subway Station Using Fire Dynamics Simulator (FDS). Fire 2022, 5, 69. [Google Scholar] [CrossRef]
- Cao, R.F.; Lee, E.W.M.; Yuen, A.C.Y.; Chen, T.B.Y.; De Cachinho Cordeiro, I.M.; Shi, M.; Wei, X.; Yeoh, G.H. Simulation of competitive and cooperative egress movements on the crowd emergency evacuation. Simul. Model. Pract. Theory 2021, 109, 102309. [Google Scholar] [CrossRef]
- Wang, W.; Zhu, Z.; Jiao, Z.; Mi, H.; Wang, Q. Characteristics of fire and smoke in the natural gas cabin of urban underground utility tunnels based on CFD simulations. Tunn. Undergr. Space Technol. 2021, 109, 103748. [Google Scholar] [CrossRef]
- Cheng, C.H.; Chow, C.L.; Chow, W.K. A simulation study of tenability for passengers in a railway tunnel with arson fire. Tunn. Undergr. Space Technol. 2021, 108, 103679. [Google Scholar] [CrossRef]
- Guo, X.; Pan, X.; Wang, Z.; Yang, J.; Hua, M.; Jiang, J. Numerical simulation of fire smoke in extra-long river-crossing subway tunnels. Tunn. Undergr. Space Technol. 2018, 82, 82–98. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Q. Analytical solution, experimental data and CFD simulation for longitudinal tunnel fire ventilation. Tunn. Undergr. Space Technol. 2014, 42, 307–313. [Google Scholar] [CrossRef]
- Tao, H.; Xu, Z.; Zhou, D. Investigation of the Temperature Beneath Curved Tunnel Ceilings Induced by Fires with Natural Ventilation. Fire 2022, 5, 90. [Google Scholar] [CrossRef]
- Li, Y.; Huang, F.; Ma, C.; Tang, K. A Simulation Study on the Smoke Control Effect with Different Smoke Exhaust Patterns and Longitudinal Air Supply for Ultra-Wide Tunnels. Fire 2022, 5, 72. [Google Scholar] [CrossRef]
- You, W.; Kong, J. Feasibility Analysis of Cross Passage Ventilation and Smoke Control in Extra-Long Submarine Tunnel. Fire 2022, 5, 102. [Google Scholar] [CrossRef]
- Hou, Y.-s.; Li, Y.-f.; Zhang, C. Influence of Train Location on Smoke Control in Tunnel Cross-passage. Procedia Eng. 2016, 135, 567–573. [Google Scholar] [CrossRef][Green Version]
- Feng, S.; Li, Y.; Houc, Y.; Li, J.; Huang, Y. Study on the critical velocity for smoke control in a subway tunnel crosspassage. Tunn. Undergr. Space Technol. 2020, 97, 103234. [Google Scholar] [CrossRef]
- McGrattan, K.B.; McDermott, R.J.; Weinschenk, C.G.; Forney, G.P. Fire Dynamics Simulator Technical Reference Guide; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2017.
- Smagorinsky, J. General circulation experiments with the primitive equations, i. the basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Lilly, D.K. The representation of small-scale turbulence in numerical simulation experiments. IBM Form. 1967, 320–1951, 195–210. [Google Scholar]
- Magnussen, B.F.; Hjertager, B.H. On mathematical modeling of turbulent combustion with special emphasis on soot formation and combustion. Symp. (Int.) Combust. 1977, 16, 719–729. [Google Scholar] [CrossRef]
- Khan, M.M.; Tewarson, A.; Chaos, M. Combustion characteristics of materials and generation of fire products. In SFPE Handbook of Fire Protection Engineering; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1143–1232. [Google Scholar]
- Grosshandler, W.L. RadCal: A Narrow Band Model for Radiation Calculations in a Combustion Environment; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1993.
- Hu, L.H.; Fong, N.K.; Yang, L.Z.; Chow, W.K.; Li, Y.Z.; Huo, R. Modeling fire-induced smoke spread and carbon monoxide transportation in a long channel: Fire Dynamics Simulator comparisons with measured data. J. Hazard. Mater. 2007, 140, 293–298. [Google Scholar] [CrossRef] [PubMed]
- McGrattan, K.; Miles, S. Modeling Fires Using Computational Fluid Dynamics (CFD). In SFPE Handbook of Fire Protection Engineering; Springer: New York, NY, USA, 2016; pp. 1034–1065. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, T.B.Y.; Yuen, A.C.Y.; Wang, C.; Chan, Q.N.; Yeoh, G.H. Investigation of door width towards flame tilting behaviours and combustion species in compartment fire scenarios using large eddy simulation. Int. J. Heat Mass Transf. 2020, 150, 119373. [Google Scholar] [CrossRef]
- Chen, Q.; Yuen, A.C.Y.; Chen, T.B.Y.; Cao, R.F.; Liu, H.; Yeoh, G.H. A Large-Eddy Simulation study on the effect of fuel configuration and pan distance towards chemical species for under-ventilated compartment fire scenario. Int. J. Heat Mass Transf. 2022, 184, 122306. [Google Scholar] [CrossRef]




| Fire Location Wrt Train Carriage | Train Head Location Wrt XP [m] | Longitudinal Tunnel Velocity [m/s] | XP Velocity [m/s] |
|---|---|---|---|
| Bottom, Top | 0, 20 | 0, 1.7 | 0, 0.2, 0.25, 0.3, 0.5 |
| Case | Simulation ID | Avg. XP Temperature [°C] | Avg. XP U-Velocity [m/s] | Smoke in XP |
|---|---|---|---|---|
| 1 | B0m_0ms_0ms | 44.93 | −0.12 | Yes |
| 2 | B0m_0ms_0.5ms | 34.47 | −1.41 | No |
| 3 | B0m_1.7ms_0ms | 30.01 | 2.61 | No |
| 4 | B0m_1.7ms_0.5ms | 30.00 | −1.41 | No |
| 5 | T0m_0ms_0ms | 35.96 | 0.10 | No |
| 6 | T0m_0ms_0.5ms | 30.71 | −1.40 | No |
| 7 | T0m_1.7ms_0ms | 30.18 | 2.46 | No |
| 8 | T0m_1.7ms_0.5ms | 30.05 | −1.41 | No |
| 9 | B20m_0ms_0ms | 40.26 | −0.17 | Yes |
| 10 | B20m_0ms_0.5ms | 32.59 | −1.40 | No |
| 11 | B20m_1.7ms_0ms | 88.19 | 1.42 | Yes |
| 12 | B20m_1.7ms_0.5ms | 30.58 | −1.40 | No |
| 13 | T20m_0ms_0ms | 33.61 | −0.08 | Yes |
| 14 | T20m_0ms_0.5ms | 30.92 | −1.41 | No |
| 15 | T20m_1.7ms_0ms | 36.16 | 1.38 | Yes |
| 16 | T20m_1.7ms_0.5ms | 30.02 | −1.41 | No |
| 17 | B0m_0ms_0.2ms | 42.72 | −0.56 | Yes |
| 18 | B0m_0ms_0.25ms | 41.31 | −0.70 | Yes |
| 19 | B0m_0ms_0.3ms | 41.48 | −0.85 | Yes |
| 20 | B0m_1.7ms_0.2ms | 30.00 | −0.56 | No |
| 21 | B0m_1.7ms_0.25ms | 30.00 | −0.71 | No |
| 22 | B0m_1.7ms_0.3ms | 30.00 | −0.84 | No |
| 23 | B20m_0ms_0.2m | 37.70 | −0.57 | Yes |
| 24 | B20m_0_ms_0.25m | 36.49 | −0.70 | Yes |
| 25 | B20m_0ms_0.3m | 35.52 | −0.84 | No |
| 26 | B20m_1.7ms_0.2m | 47.39 | −0.57 | Yes |
| 27 | B20m_1.7ms_0.25m | 45.50 | −0.71 | Yes |
| 28 | B20m_1.7ms_0.3m | 36.30 | −0.84 | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.B.Y.; Yuen, A.C.Y.; De Cachinho Cordeiro, I.M.; Liu, H.; Cao, R.; Ellison, A.; Yeoh, G.H. In-Depth Assessment of Cross-Passage Critical Velocity for Smoke Control in Large-Scale Railway Tunnel Fires. Fire 2022, 5, 140. https://doi.org/10.3390/fire5050140
Chen TBY, Yuen ACY, De Cachinho Cordeiro IM, Liu H, Cao R, Ellison A, Yeoh GH. In-Depth Assessment of Cross-Passage Critical Velocity for Smoke Control in Large-Scale Railway Tunnel Fires. Fire. 2022; 5(5):140. https://doi.org/10.3390/fire5050140
Chicago/Turabian StyleChen, Timothy Bo Yuan, Anthony Chun Yin Yuen, Ivan Miguel De Cachinho Cordeiro, Hengrui Liu, Ruifeng Cao, Amy Ellison, and Guan Heng Yeoh. 2022. "In-Depth Assessment of Cross-Passage Critical Velocity for Smoke Control in Large-Scale Railway Tunnel Fires" Fire 5, no. 5: 140. https://doi.org/10.3390/fire5050140
APA StyleChen, T. B. Y., Yuen, A. C. Y., De Cachinho Cordeiro, I. M., Liu, H., Cao, R., Ellison, A., & Yeoh, G. H. (2022). In-Depth Assessment of Cross-Passage Critical Velocity for Smoke Control in Large-Scale Railway Tunnel Fires. Fire, 5(5), 140. https://doi.org/10.3390/fire5050140











