Study on Coupled Combustion Behavior of Two Parallel Line Fires

Abstract

In this study, the interaction of two parallel line fires with a length-width ratio of greater than 50 was investigated and compared to a single line fire. Considering different length–width ratios and spacings between the fire sources, experiments were carried out to analyze the fire characteristics, such as the burning rate, the flame-merging state, the flame height, the flame tilt angle, and the flame length of the line fires. Its regularity was revealed by combining two mechanisms, namely, heat feedback enhancement and air entrainment restriction. The results revealed that the burning rate under different length–width ratios shows a uniform law, which increases first and then decreases with a greater spacing between the fire sources. There is a special relationship between the flame-merging probability P_m and the dimensionless characteristic parameters (S/Z_C)/(L/d)^0.27. Based on this relationship, a critical criterion of flame merging can be obtained as (S/Z_C)/(L/d)^0.27 = 2.38. In addition, the height and the length of the flame were studied to better describe the flame shape when the flame is tilted. Since the flame is bent, the flame length has an abrupt change at a specific position, and the inclination angle also has the same phenomenon. Finally, it was found that the influence of the length–width ratio on the line fires is relatively limited, which is further weakened under a greater length–width ratio.

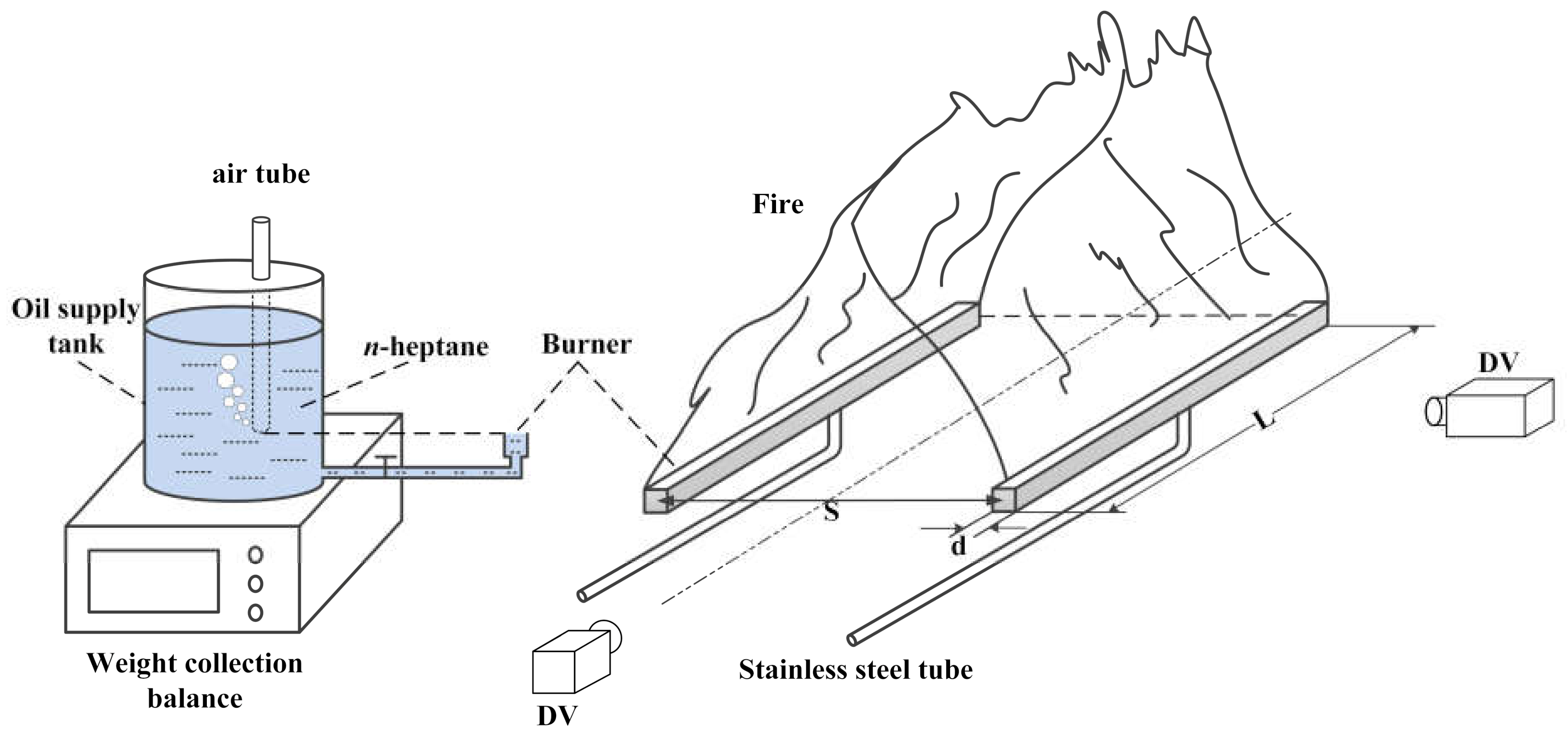
1. Introduction

A line fire is a special fire type, and its length is much larger than its width. According to previous studies, a fire source with a length–width ratio of more than ten can be considered as a line fire [1,2]. Its burning surface and flame can be regarded as two-dimensional. In practice, line fires are not uncommon, such as the cable fires and forest fires that spread along the ground and grass. The initial stage of the fire is often accompanied by multiple fires, and the interaction between the fires could lead to more-serious consequences. Therefore, investigating the burning characteristics of two parallel line fires is of great significance for the related fire hazards, such as forest fires and building fires.

The coupled combustion behavior of double (or multiple) fire sources is a complex process that has been examined by theoretical and numerical methods [3]. So far, numerous related works of the combustion-characteristic parameters focused on the simple shapes of fire sources such as centrosymmetric squares and circles fire sources. Kamikawa et al. [4] conducted many experiments using a series of square propane combustion arrays and analyzed the total heat-release rate and merged flame heights. Delichatsios [5] established a simple correlation of flame height of merging fires of an array of gaseous burners based on ref. [6] and developed a merging relation for merging flames to estimate the flame height of “group” fires. Liu et al. [7] conducted a large number of square fire arrays experiments. The results show that the burning rate of the pool fire arrays increased with the decrease in distance, but it began to decrease after the distance reached a critical value. Further, Liu et al. [8] presented a new approach to simulate fire propagation among discrete fuel sources and indicated that the surrounding new fire points have a positive effect on the burning rate of the original one. Vasanth et al. [9,10] studied the mass burning rate, the flame shape, the flame height, and the flame temperature of multiple round pool fires with small pool sizes (48, 68, and 83 mm). He found that in multiple pool fires, all these increased with the increase in the diameter of the participating pool. The flame temperature is unsymmetrical, while the double pool fire is set at a different height [11]. Wan et al. [12] investigated the flame-merging probability and flame height of two square gas burners under different spacing and established a flame-merging probability function. Li et al. [13] established the flame-merging probability function and flame-tilt-angle function from twin square propane burners under a cross wind. Jiao et al. [14] studied the fire-interaction mechanisms of n-heptane and ethanol multiple pool fires and found that the flame height of the former is larger than that of the latter.

With the increase in the length–width ratio, the research perspective is changed from the square fire source to the rectangular fire source and the line fire source. For two rectangular fires, Thomas and Baldwin [15] summarized a critical criterion of flame merging based on the force of the flame surface during flame interaction by simplified derivation. Hasimi and Nishihata [16] studied rectangular propane burners with a length–width ratio from 1 to 10 and observed an exponential relationship between the flame height and the heat-release rate. Yuan and Cox [17] developed a flame-height model consistent with the above-mentioned model, together with a model addressing the relationship among the temperature, the mass flow rate, and the heat release rate per unit length. Huang et al. [18] conducted experimental research by using rectangular propane burners with three different length–width ratios and established a modified expression for estimating flame height. Zhang et al. [19] found that there is a power-law relationship between the flame height and the heat-release rate per unit length by using a nozzle with dimensions that are 3 mm (width) × 95 mm (length). Tang et al. [20] studied the mean flame height and the radiative heat flux of four rectangular fire sources with different length–width ratios (1, 2, 4, and 8, respectively) under the same fire-source surface area. Liu et al. [21] analyzed the merging characteristics of two parallel rectangular burners under different fire-source spacings, length–width ratios, and heat-release rates and established a model among the flame-merging probability, the flame height, and the above-mentioned parameters. Tao et al. [22] conducted a series of experiments to investigate flame interaction and the merging flame length of double pool fires with the length–width ratios of 1:1, 1:2, 1:4, and 1:8, respectively.

For a larger length–width ratio, the burner changes from rectangular pool fires to diffusions of micro-slot burners, and the fuel changes from liquid to gaseous fuel, which may be because the liquid fuel is difficult to maintain in the experiment. Kuwana et al. [23] studied the heat-release rate and flame shape of two micro-slot flames with a size of 1 mm × 80 mm and found that the total heat-release rate basically increases and that the flame will eventually merge into a unified flame with the decrease in spacing. Hu et al. [24] conducted experiments to study the interaction between two identical slot-burners (length: 142.5 mm; width: 2 mm) and developed an analytical model to characterize the critical burner pitch for flame merging.

To sum up, there are few works on the combustion behavior of two parallel liquid line fires with large length–width ratios. Most of the previous work focused on the simple shapes of fire sources and rectangular fire sources with low length–width ratios, in addition to a few gaseous slot burners with a higher length–width ratio; studies mostly focus on the gas fire source, which may be because the liquid fuel is difficult to maintain in the experiment. The controllability of fire sources based on gaseous fuel is higher, but liquid fuel can better reflect the characteristics of free combustion. Therefore, a constant liquid burning system was developed. To reduce the effect of an insufficient length–width ratio on the two-dimensional linear fire, a 1 cm wide slot with a length–width ratio of greater than 50 was used as a burner in the experiment. The line-fire burning experiments at different spacings were conducted to explore the distribution and variation of burning characteristics, such as the burning rate, the flame-merging probability, the flame height, and the tilt angle. The research outcomes revealed line fire’s burning dynamics and behavioral characteristics, which provides theoretical guidance on the related fire-safety assessment.

2. Materials and Methods

2.1. Experimental Setup

All the tests were conducted in a 20 m-high closed hall in a stable environment. As depicted in Figure 1, two parallel rectangular burners were positioned on an experimental platform, which was 0.9 m above the ground. The rectangular burners had an identical rim height of 0.01 m, and a width (d) of 0.01 m, and were made of stainless steel (the thickness was 2 mm). The burners were embedded in a fireproofing board, and the top edge was aligned over the board, allowing only the fuel surface to receive the radiative heat and reduce the heat loss. Three groups of burners with lengths (L) of 0.6 m, 0.8 m, and 1.0 m were used. In contrast, the length–width ratio (L/d) of each burner was greater than 50. The rectangular burners, called line fires, were used to simulate the line-burning surface. Each line-fires group was tested with different fire spacings, denoted as S, varying from 0 to 0.45 m with an interval of 0.05 m. Each single line fire (with lengths of 0.6 m, 0.8 m, and 1.0 m) was also tested as a control.

High-purity (>98%) n-heptane was used as the fuel. Based on the siphon-pipe principle [14,25], the fuel levels were maintained at a fixed height by two identical reservoir and delivery systems. The mass loss throughout the burning processes was measured by an electronic balance (measuring range: 10 kg; accuracy: 0.1 g; and sampling frequency: 0.5 s) placed under a fuel-reservoir tank. The burning processes were recorded by two cameras (SONY FDR-AX700 and SONY FDR-AX100E, manufactured by SONY China Co., LTD, made in Shanghai, China) on both sides of the experimental platform for the possible inclined flame.

2.2. Measurement of the Burning Rate

The time-averaged burning rates were obtained from the electronic balance with a resolution of 0.1 g. Part of the tests was performed three times to verify the experimental repeatability. For example, Figure 2 shows the instantaneous fuel mass and the burning rate during the entire burning process when L/d = 60 and S = 20 cm. After a developing period, the burning rates of the line fire in three tests stabilized around a constant, about 0.3118 g/s. Similar test results under different length–width ratios and spacings indicated good experimental repeatability. Due to symmetry, the burning rates of two parallel identical line fires are theoretically the same. Therefore, the time-averaged burning rates in a steady period were used in the following analysis.

2.3. Flame Image Processing

The RGB images of the inclined flame during the steady period were obtained from video processed by MATLAB, while the burning processes were recorded at 25 frames per second. Each RGB image was converted to a grayscale image. Based on the OTSU algorithm [26], a suitable threshold value was chosen, and then the obtained grayscale image was changed to a binary image. The flame area can be obtained from the consequent binary image. Then, the flame-merging probability, the height, and the inclination angle can be investigated. Three kinds of images are shown in Figure 3.

The flame-merging probability P_m was defined as the number ratio of flame-merging frames to the total frames during the stable phase (see also Ref. [27]). The probability of flame merging ranges from 0, corresponding to no flame merging occurs, up to 1, corresponding to flames continuously merge together. The flame-merging judgment area was 0.5 mm wide on both sides of the centerline of the two parallel line flames, and the height is the distance from the burner surface to the ceiling When the flames are merged, this region contains a flame with a length greater than 0, otherwise the flames are not merged. Figure 4 is a schematic diagram of the judgment area. The width of the judgment area was 1 mm, and the height was much larger than the flame height of two parallel line fires.

2.4. Measurement of Flame Geometric Parameters

To obtain the relationship between the pixels in the video and the length in reality, before the start of the experiments, a ruler with a length of 60 cm was vertically fixed on the center symmetry line of the two burners as a reference for shooting. The fitting result is shown in Equation (1). The pixel value was read by a human; the error was within one pixel; and the result showed a good fitting. The proportional relationship of the captured image was: one pixel is equal to 0.134 cm.

$$h=0.134x-26.26,\hspace{1em}{R}^2=0.9999$$

(1)

where h is the actual scale value of the ruler; x is the pixel coordinate value of the scale value of the ruler on the image.

The average flame height H was defined as the vertical distance between the flame root and the highest position where the flame appearance probability is above 50% [28]. If the flame tips were not merged, the flame height was considered as the average of the two flame heights. As shown in Figure 5, the flame shape on the front side was slightly shorter on the two sides. Additionally, the shorter part on both sides occupied a small proportion in the joint flame, so only the middle part was considered when calculating the flame height. Therefore, the side image seen in Figure 6 can also present the average flame height, and the calculation process was relatively simple. The flame tilt angle $\theta$ was defined as the angle between the oblique flame and the vertical direction, determined by image recognition. The methods of determining H and $\theta$ in the flame merging and the non-merging state were slightly different. See Figure 6 for details.

3. Results

3.1. Combustion Behavior

For multiple pool fires, the burning behaviors are affected significantly by the fire interactions (i.e., competition of heat feedback enhancement and air entrainment restriction [7,8]), which is dominated by S/D (D is the diameter of the fuel pan) [8]. Due to the air-supply restriction among fires, the negative pressure in the interior of the burning area causes the flames to lean inward, and the flame tips could even be in touch with each other when S/D is small enough. Figure 7 shows the side view of the flames during the steady period from all the tests.

The flame was merged to a higher degree at a shorter distance $S$, which can be regarded as one flame when there is no gap at the bottom. For a given $L/d$, as $S$ increases, the flame gradually disengages from the merged state until it is completely separated, and the degree of the flame expansion is also reduced. The air-supply restriction between the fire sources gradually decreases as the spacing increases. The pressure drops between the flames decrease; the degree of the flame tilt decreases and the oxygen required for combustion can be obtained in a smaller space, so the degree of flame expansion is reduced.

Under the same S, there is no significant difference in the degree of flame merge and extension by comparing the flame morphology under different $L/d$. Obviously, the influences of the length–width ratio of the fire source on the shape of the two line-fires flames are limited. This phenomenon is different from Thomas et al. [15], which can be attributed to the huge length–width ratio of the fire source. The fire source in the experiment can be regarded as a two-dimensional structure under a large length–width ratio. It is also believed that the interaction between line fires is not dependent on the length–width ratio. However, because the experiment cannot reach the ideal state and cannot eliminate the influence from the short side of the fire source, the length–width ratio is still considered in the following discussion. However, it is foreseeable that its impact on the experimental results could be minimal on such a large scale.

Figure 8 shows the flame of line fires with different length–width ratios at the same spacing. Due to the air entrainment on the sides, there is a phenomenon that the flame on both sides slope to the middle, and the height is slightly lower than the middle part of the flame. However, with the different length–width ratios, the flame-inclination degree was almost the same. It was indicated, to some extent, that the effect of side air entrainment on these flames is similar. However, for the whole combustion process, the proportion of its influence gradually decreased with the increased length–width ratio. Therefore, for a line fire with a large length–width ratio, the effect of the length–width ratio on the burning processes becomes limited. It is further foreseeable that, as the length–width ratio increases, the effect will continue to decrease until it disappears. Besides, when the two flames are close together, there is an air-supply competition between the two flames. The air enters the cavity between the flames and moves upward with the fire plume, resulting in a weakened convective heat-transfer effect in the middle of the flame compared to the two ends of the flame. However, the enhancement effect of radiant heat in the central region is sufficient to offset the weakened effect of convective heat conduction, so the middle of the flame is higher than the two ends.

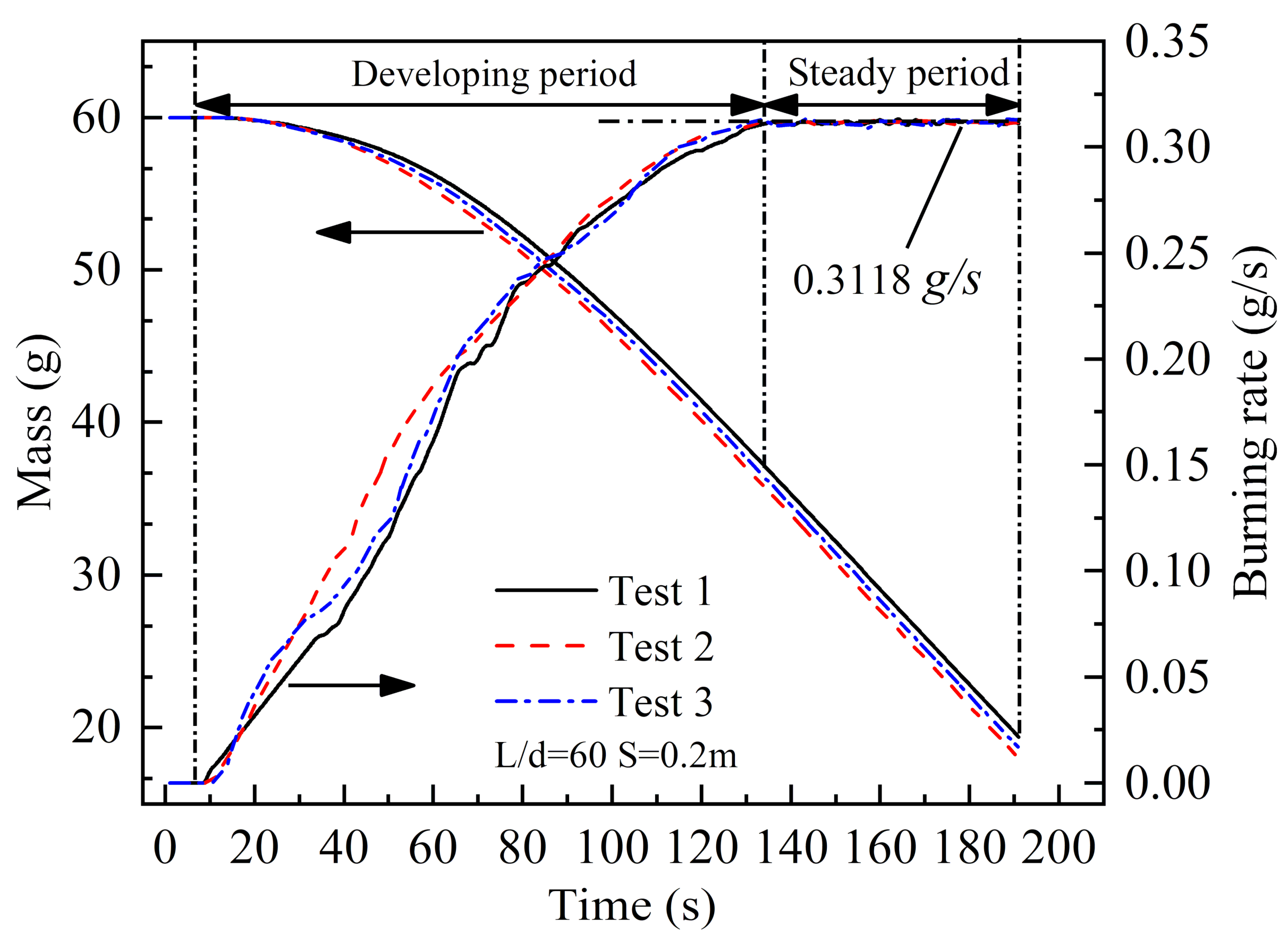
3.2. Steady-State Burning Rates

Air entrainment could cause the flame to tilt and merge. At this time, radiative heat feedback received on the fuel surface came from itself and another fire source. This situation is called the radiative-heat feedback-enhancement effect, which directly affects the burning intensity. The burning rate is an essential characteristic parameter reflecting the severity of burning. Therefore, this section discussed the variation in the burning rate under various spacings and length–width ratios of the fire sources.

Assuming a dimensionless burning rate $m^{*}=m/m_0$, where $m_0$ is the burning rate of a single fire source, the change in the burning rate under the influence of the two fire sources is explored. In this experiment, it was assumed that the interaction between fire sources depends on the two control variables, namely, the distance between the two fire sources and the length–width ratio of the fire sources. Figure 9 shows the data of $m^{*}$ under different $S$ and $L/d$.

It can be found that under different $L/d$, $m^{*}$ shows the same trend, namely, the overall trend increases at first and then decreases, and all of them are greater than 1. The interaction between the fires lead each of them to burn at a higher rate than those of a single, independent fire source. Although there is a competitive mechanism between the radiation-enhancement effect and the air entrainment limiting effect, it is evident that with the increasing S, the heat feedback enhancement increases first and then decreases, and the air entrainment restriction decreases all the time, which leads to the first increase and then the decrease in m*. When S is large enough, the burning rate of each fire source is equivalent to that of an independent fire source; there is no interaction between them, and the value of $m^{*}$ should be 1.

It can be seen from Figure 9 that the value of $m^{*}$ rises sharply when $S<0.05 \mathrm{m}$, indicating that the coupling result of the two action mechanisms are obvious, and $m^{*}$ reaches a peak at S = 0.05 m. The flame tilts as the spacing increases. Based on Ref. [29], the radiative heat feedback received by the fuel surface and another fire source begin to decrease, which is still higher than that of a single fire source. The space on the adjacent side of the two fires becomes larger; the air entrainment restriction is reduced; and the influence is weaker than the decrease in the radiation heat. Therefore, it shows a decreasing trend approaching 1, indicating that the interaction between the fire sources is getting weaker.

When $S$ is specified, the difference in $m^{*}$ under different $L/d$ is small. Since $m^{*}$ characterizes the growth rate of the burning rate compared with a single fire source, it can be inferred that the length–width ratio of the fire source has a limited effect on the $m^{*}$. In the case of the steady-state burning rate of the two parallel line fires under different $L/d$, besides the fuel type, spacing is a dominant factor.

4. Discussion

4.1. Flame Merging

When there is an interaction between fires, with the changed $S$, the fusion state of the flame can be divided into three stages: full merger, intermittent merger, and non-merger. Full merger means that the flame is always in contact with each other throughout the whole burning stage when the distance between fires is small, which can be considered as a single flame; with increased S, the flame begins to separate intermittently, which can no longer be considered as a single flame, and the flame is in the intermittent merge stage at this time; after the continually increased S, the flame is completely separated, which is considered as the non-merger stage.

The flame-merging probability $P_m$ is defined here to analyze and determine the fusion state of the flame. It can be found that the interaction between fire sources is related to $S$, $L/d$, and the heat-release rate. Therefore, the relationship between $P_m$ and appeal parameters was discussed. Liu et al. [8] considered that the flame-merging probability is relevant to the flame tilt angle, and a dimensionless model $S/Z_C$ was developed for characterization, where $Z_C$ is defined as

$$Z_C={\left(Q^{\prime }/\left({\rho }_{\infty }{c}_p{T}_{\infty }{g}^{1/2}\right)\right)}^{2/3}$$

(2)

in which $Q^{\prime }$ is the heat-release rate per unit length of the single fire source, and ${\rho }_{\infty }$, $c_p$, and $T_{\infty }$ are the density, specific heat, and temperature of the ambient air, respectively, while g is the gravitational acceleration.

Since the flame height is directly related to the test environment and fuel type, the characteristic scale can represent the flame height. This study used this characteristic quantity for the follow-up analysis. Since the tested fuel is liquid n-heptane with a calorific value of 44.56 KJ/kg [30], $Q^{\prime }$ can be calculated based on the burning rate per unit length. The flame height can affect the merging of the flames. During the data processing and experimental observation, it was found that in the intermittent merge stage of flame merging, as the $S$ increased, the probability of a merger showed a decreasing trend. For different $L/d$, the flame-merging probability also changed, and the inferred $P_m$ can be described by the characteristic quantities, such as $S$, $L/d$, and $Z_C$. Therefore, the dimensionless model $\left(S/Z\right)/\left(L/d\right)$ was constructed to analyze the function of the flame-fusion probability. A relationship between the flame intermittence merging stage and the parameters was observed:

$$P_m=K·{\left(S/Z_C\right)}^a·{\left(L/d\right)}^b+C$$

(3)

A fitting was performed based on Equation (3). Compared with the previous study [21] and data analysis, a fixed solution $a=1$ can be adopted to calculate the optimal solution:

$$P_m=-0.77\left(S/Z_C\right)/{\left(L/d\right)}^{0.27}+1.83\hspace{1em}{R}^2=0.99$$

(4)

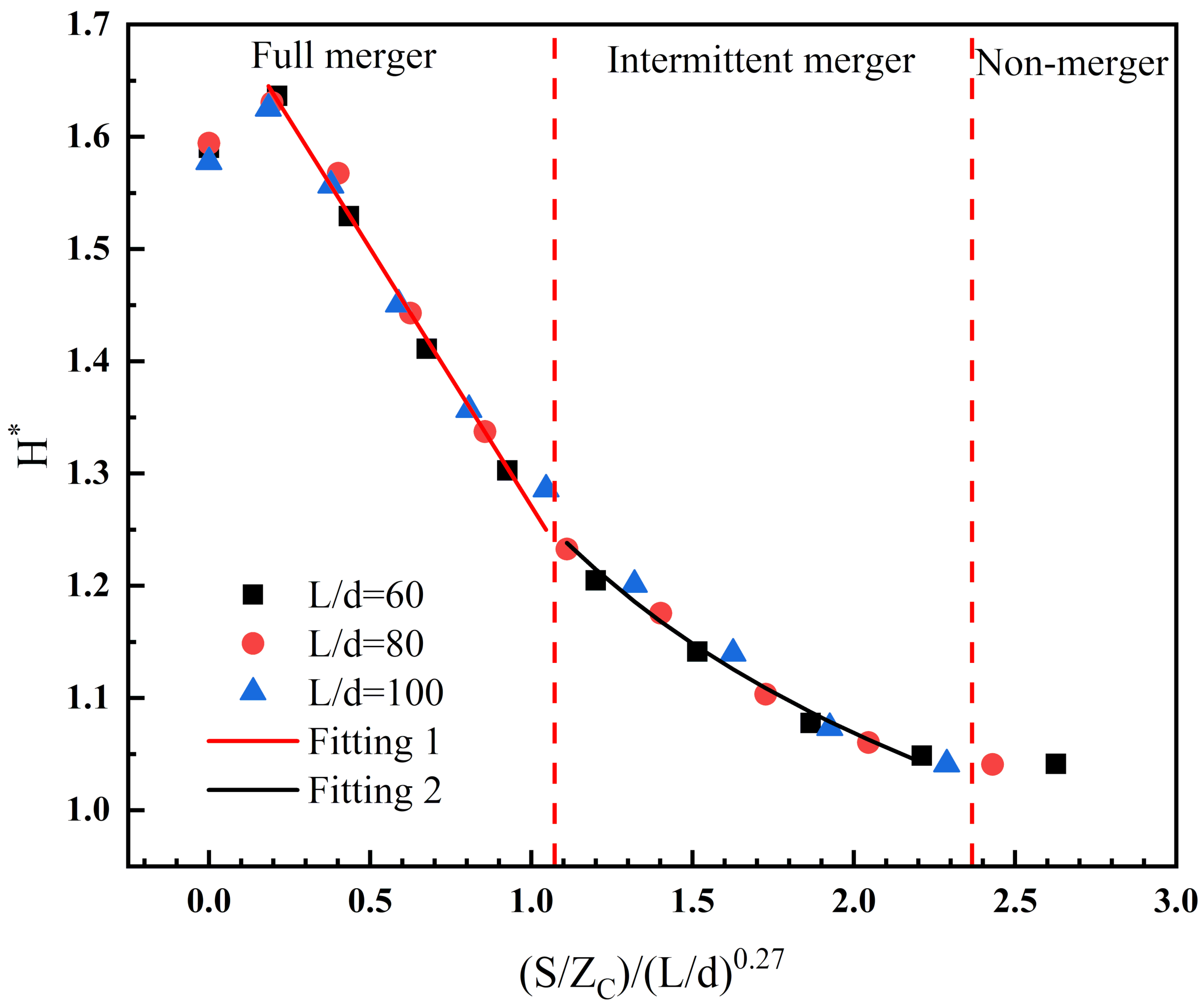
Figure 10 shows the $P_m$ with clear several stages. To benefit the analysis, we defined: $N=\left(S/Z_C\right)/{\left(L/d\right)}^{0.27}$. When $N$ is small, $P=1$, which means that the flame is completely merged; when $N$ is increasing, $P<1$; the flame is in an intermittent merge state; and the merging probability gradually decreases with the increased $N$; when $N$ is increasing to a certain value, $P_m$ decreases to 0, where the flame is no longer merged. Further analysis on the critical state of the flame merging shows that, when $P>0$, the flame shows a merging phenomenon, so $P=0$ can be used as the criterion for the flame merging. Combined with the appeal fitting result, $P=0, N=2.38$; so, in this, the criterion for flame merging was $N=2.38$. If we divide the entire combustion process into a merged and non-merged phase, $P_m=0.5$ can be used as the critical point determining if the flame is merged or not, where $N=1.73$. Furthermore, the power of $L/d$ was only 0.27. It can be seen that the influence of the length–width ratio of the fire source on the flame merging probability was weak. Therefore, the flame-merging probability is dominated by $S$ and the fuel type.

Based on the above analysis, the function of $P_m$ can be expressed as follows:

$$P_m=\left\{\begin{array}{cc}\hfill 1,& 0\le \left(S/Z_C\right)/{(L/d)}^{0.27}<1.08\hfill \\ \hfill -0.77\left(S/Z_C\right)/{(L/d)}^{0.27}+1.83,& 1.08\le \left(S/Z_C\right)/{(L/d)}^{0.27}<2.38\hfill \\ \hfill 0,& \left(S/Z_C\right)/{(L/d)}^{0.27}\ge 2.38\hfill \end{array}\right.$$

(5)

4.2. Dimensionless Analysis of Flame Height

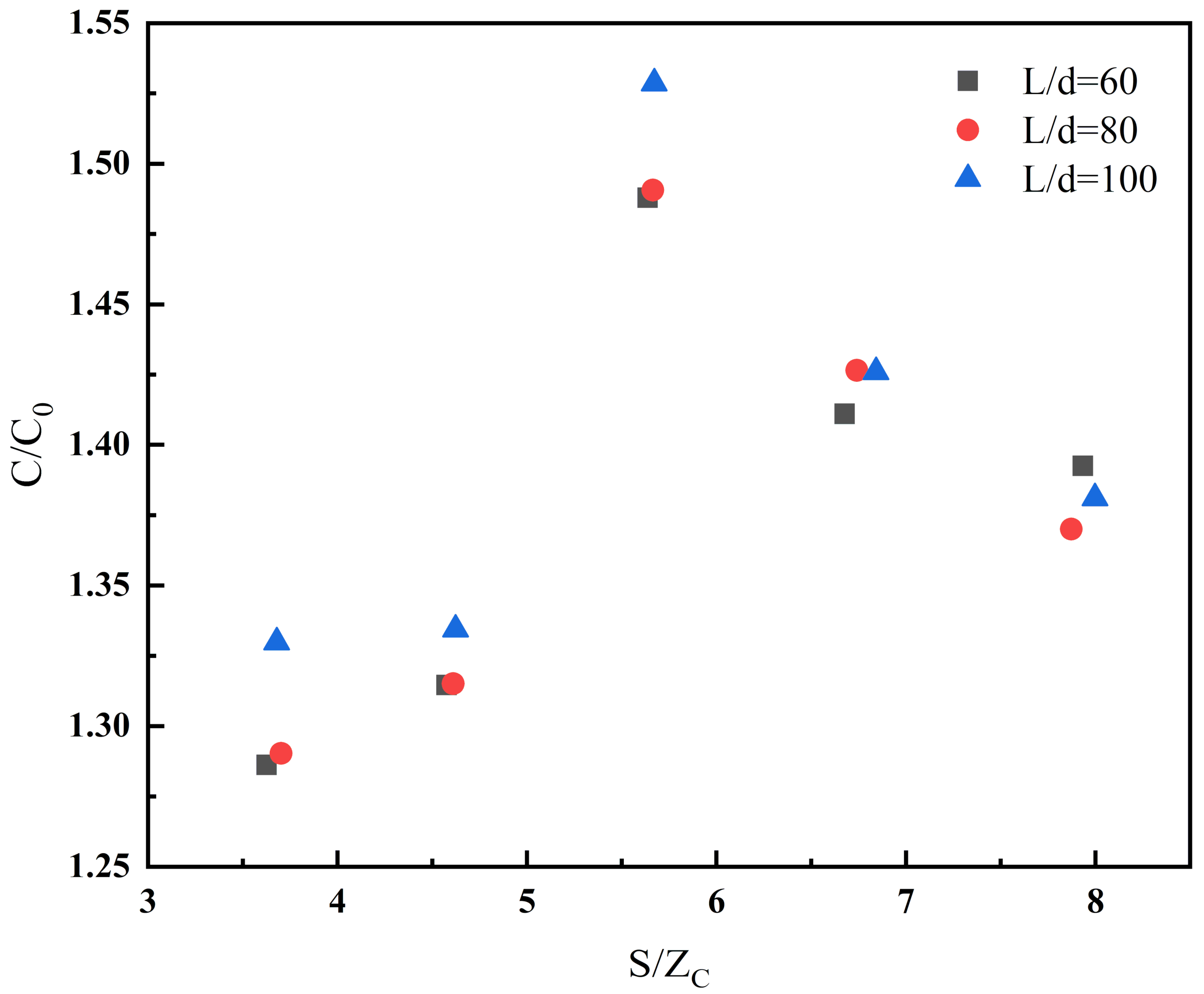
Compared with a single fire source, the effects of two mechanisms of action on the flame height were explored. A dimensionless parameter $H^{*}=H/H_0$ was proposed, where $H_0$ is the flame height of a single fire source. The flame height $H$ is also related to $S$, $L/d$, $Q$, and experimental conditions. Figure 11 shows the $H^{*}$ under different $\left(S/Z_C\right)/{\left(L/d\right)}^{0.27}$ and finds that the convergence is good.

The trend of flame height with $S$ is the same for those fire sources with different $L/d$. After rising in the initial stage, $H^{*}$ decreases regularly and gradually approaches 1. This is attributed to the interaction between fires. On the one hand, the enhanced radiative heat feedback leads to more fuel vapor and more air to support the burning processes. At this time, the air entrainment is limited, so it needs more space to complete combustion, which leads to a higher flame height. On the other hand, the pressure drop between fires leads to the flame inclination with the increased spacing between fires. The radiation-feedback intensity decreases, and the degree of air entrainment limitation decreases; so, the fire-source height decreases. This situation continues until the mutual influence between the fire sources disappears; it results in two independent fire sources, and $H^{*}$ equals 1. The reason for the presence of peaks is related to the burning rate, and the air-entrainment limitation is weak at smaller spacing, so the flame height depends on the burning rate.

The vertical line in Figure 11 is the boundary of the three merged stages according to the $P_m$. In Section 4.1, it was found that the law of interaction between the two fires can be reflected in the intermittent merge phase of the flame. The $H^{*}$ in the intermittent merge stage also shows a regular trend, so fitting the data of this phase can obtain the following functional relationship:

$$H^{*}=1.27{\left[\left(S/Z_C\right)/{(L/d)}^{0.27}\right]}^{-0.25}\hspace{1em}{R}^2=0.98$$

(6)

Figure 11 shows that there seems to be a clear rule in the complete merge phase after the peak appears. The data of this phase were fitted with the following functional relationship:

$$H^{*}=-0.46\left(S/Z_C\right)/{(L/d)}^{0.27}+1.73\hspace{1em}{R}^2=0.98$$

(7)

This test did not consider the flame height distribution during the non-merger phase of the flame, so it was not discussed here. In summary, the function of the flame height can be obtained:

$$H^{*}=\left\{\begin{array}{cc}\hfill 1.27{\left[\left(S/Z_C\right)/{(L/d)}^{0.27}\right]}^{-0.25},& 0.18\le \left(S/Z_C\right)/{(L/d)}^{0.27}<1.08\hfill \\ \hfill -0.46\left(S/Z_C\right)/{(L/d)}^{0.27},& 1.08\le \left(S/Z_C\right)/{(L/d)}^{0.27}<2.38\hfill \end{array}\right.$$

(8)

The flame height is still dominated by $S/Z_C$. When $S/Z_C$ increases, the $H^{*}$ decreases regularly. Under different $L/d$, $H^{*}$ shows the same law. It can be seen from the functional relationship that, although the effect of $L/d$ on the flame height exists, it is still weak.

4.3. Flame Length and Tilt Angle

With the increased $S$, the two flames can no longer be regarded as a fusion flame due to the gap at the flame root (approximately $S=25 \mathrm{cm}$). At this time, the flames are inclined to each other, and the flame height is insufficient to characterize the burning state. Therefore, the concept of the flame length $C$ is proposed to characterize the flame shape. Figure 12 shows the variation in the dimensionless flame length $C/C_0$ along with $S/Z_C$, where $C_0$ is the flame height of the single line fire.

Under increased $S/Z_C$, there is a sudden increasing phenomenon of $C/C_0$ when $S/Z_C$ approaches about 5. $C/C_0$ reaches its maximum value at S = 35 cm, which is just at the critical point of flame merging mentioned above, $P_m=0.5$. When $P_m>0.5$, the flame is tilted due to the interaction, and the flame tips were in contact with each other, so the flame shows a certain curvature due to the limited air entrainment. When $P_m<0.5$, the flame tips were no longer merging all the time, resulting in the air entrainment restriction and the flame bending decrease. As the spacing increased, the burning rate and the flame-merging probability decreased, making the flames in a critical state of merging and non-merging, and the mutual traction between the flames reached the maximum’ besides, the restriction of air supply decreased, resulting in the reduction in the pressure difference between the inside and the outside of the flame. So, the dimensionless flame length $C/C_0$ showed a sudden rise, which was consistent with the changing trend between the flame tilt angle $\theta$ and $S/Z_C$.

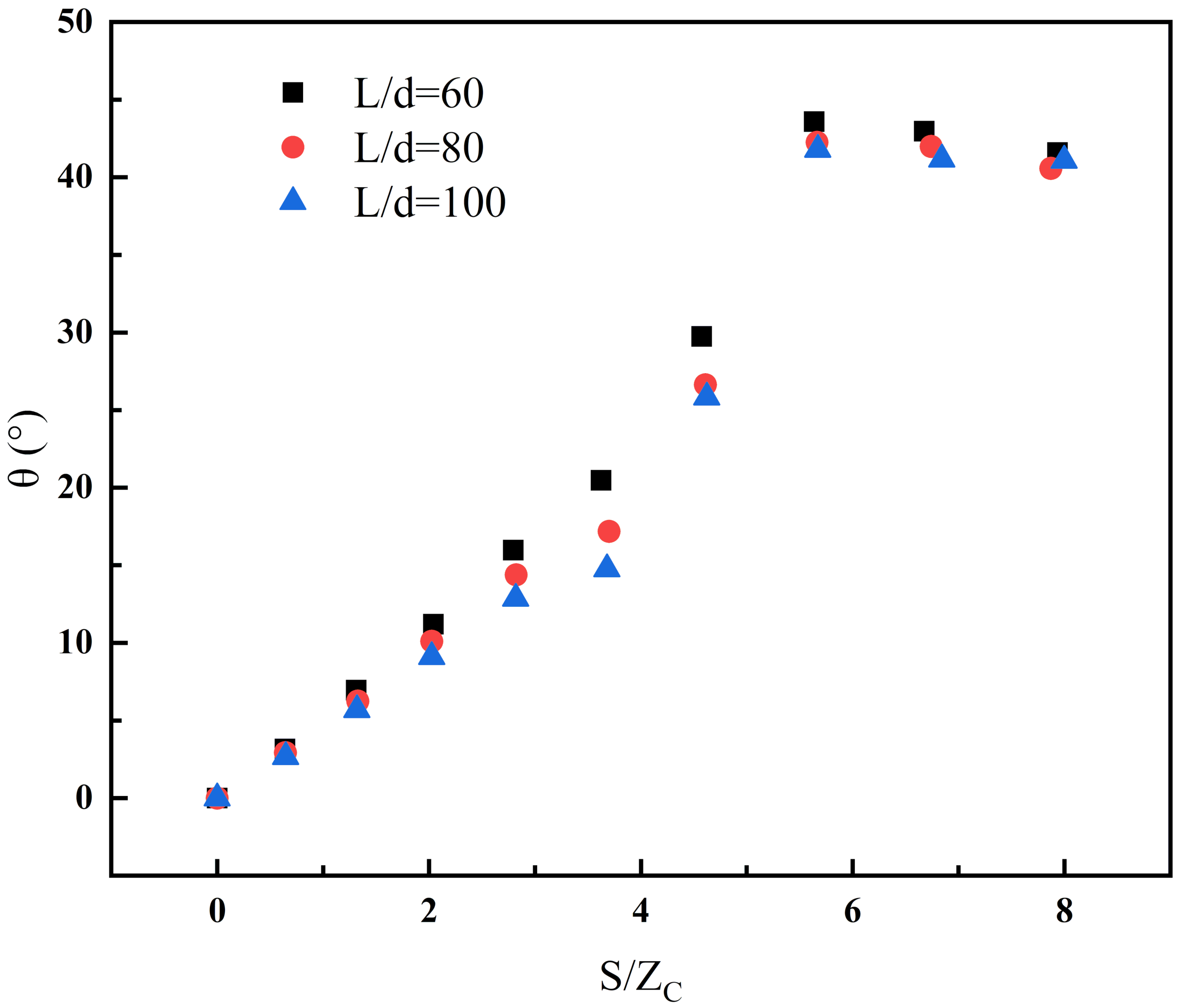
It can be seen from Figure 13 that $\theta$ tends to increase gradually and then decrease slowly with the increased $S/Z_C$. When the spacing is zero, the two fires can be regarded as a single fire source with a width of 2d. In other words, when $S/Z_C=0$, there is no flame mutual inclination, so the tilt angle is zero. As the spacing increases, the air entrainment is limited due to the separation of the flame root; the air-pressure difference exists between the flames; and the flames begin to appear oblique to each other. As the spacing becomes larger, the inclined space of the flame becomes larger as well. Since the air entrainment is always limited, $\theta$ increases gradually and reaches the maximum value when the flame bending disappears. At this time, the air-pressure difference on both sides of the line fire reaches the maximum value. Then, as the degree of air entrainment limitation is reduced, the pressure drop between the flames becomes smaller, and $\theta$ naturally decreases. In addition, it can be predicted that with the further increase in the spacing between the fires, the $\theta$ would continuously reduce. and the two fire sources can be regarded as independent fire sources. At that time, the $\theta$ will gradually approach 0 and the flame will be vertical, as in its natural state.

5. Conclusions

This work focused on the coupled combustion behavior of two parallel line fires. By considering the different length-width ratios ($L/d$) and spacings ($S$) of the fire sources, the interaction laws between two parallel line fires were studied and the main conclusions were summarized as follows.

(1)

In the real-time monitoring of the burning rate, each of the two parallel line fires had a higher burning rate than the independent fire source, indicating that the coupling effect of the two interaction mechanisms showed a promoting effect. Besides, under different $L/d$, the burning rate per unit length and its growth rate were basically the same, which was not affected by $L/d$ but enormously affected by the spacing $S$.

(2)

The image-processing method was used to obtain the merge probability of the flame. Three phases were divided into the full merger, the intermittent merger, and the non-merger. In addition, the three-segment function of the merging probability was proposed, and the critical criterion for determining the start of the flame fusion was determined.

(3)

In the analysis of the dimensionless flame height $H^{*}$, it was found that $H^{*}$ is dominated by $S/Z_C$, and the function expression was further obtained. In addition, there was an abrupt-change phenomenon of the flame length in a certain interval, which was attributed to the decrease in the air supply-restriction, and it had the same law in the flame tilt angle.