A DFT Study on the Structural, Electronic, Optical, and Elastic Properties of BLSFs XTi4Bi4O15 (X = Sr, Ba, Be, Mg) for Solar Energy Applications
Abstract
1. Introduction
2. Methodology
3. Results and Discussions
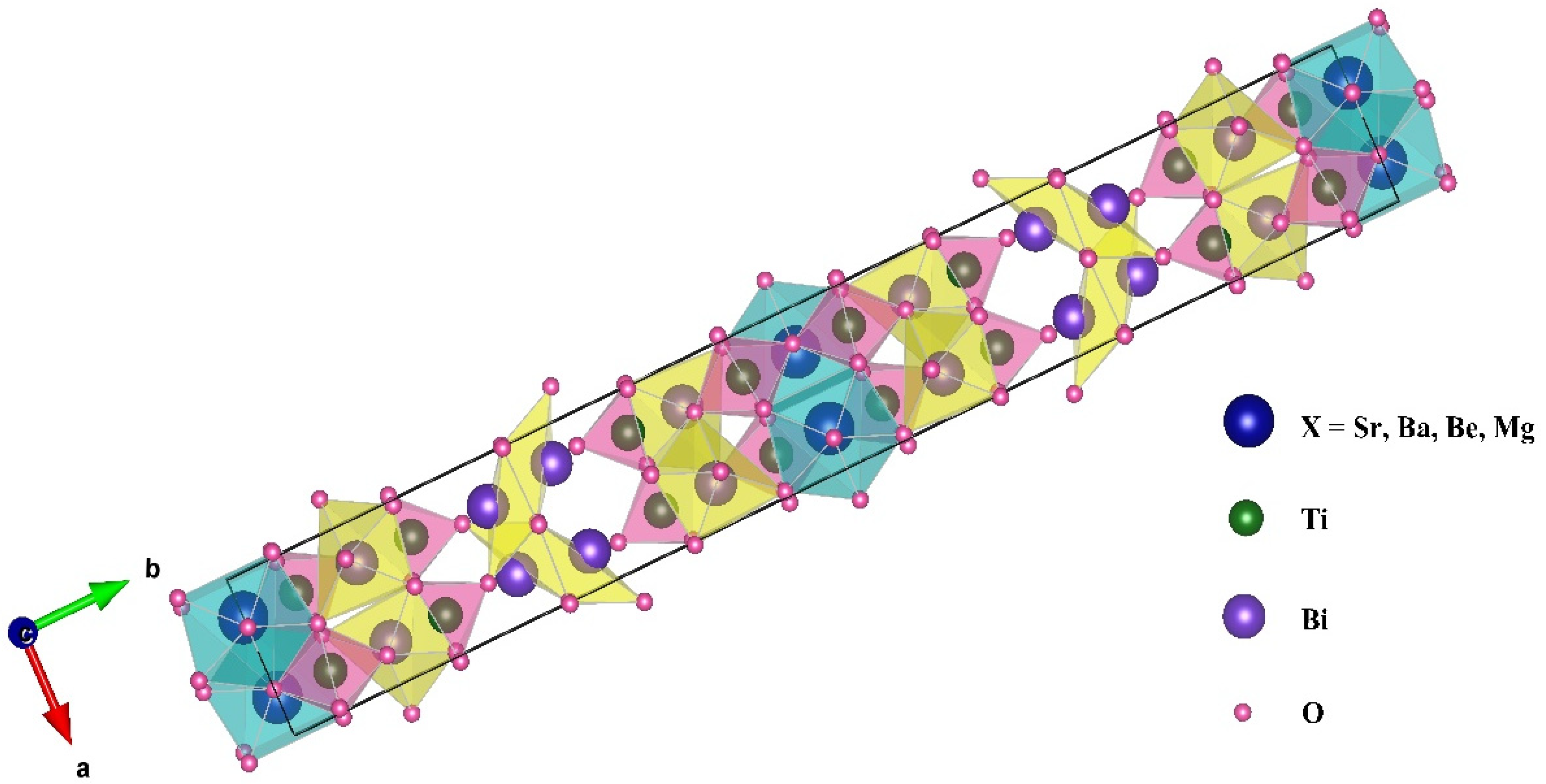
3.1. Structural Properties
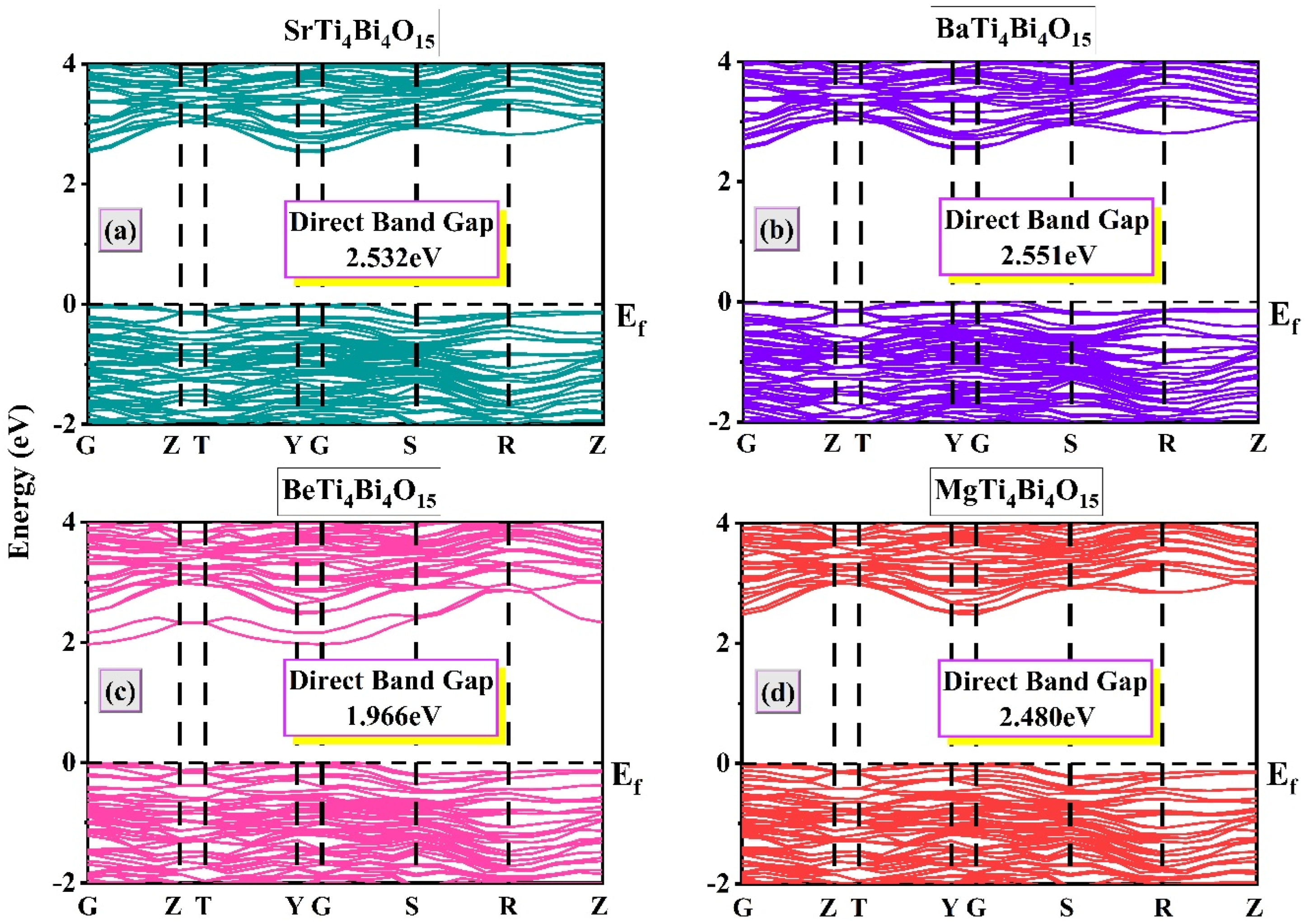
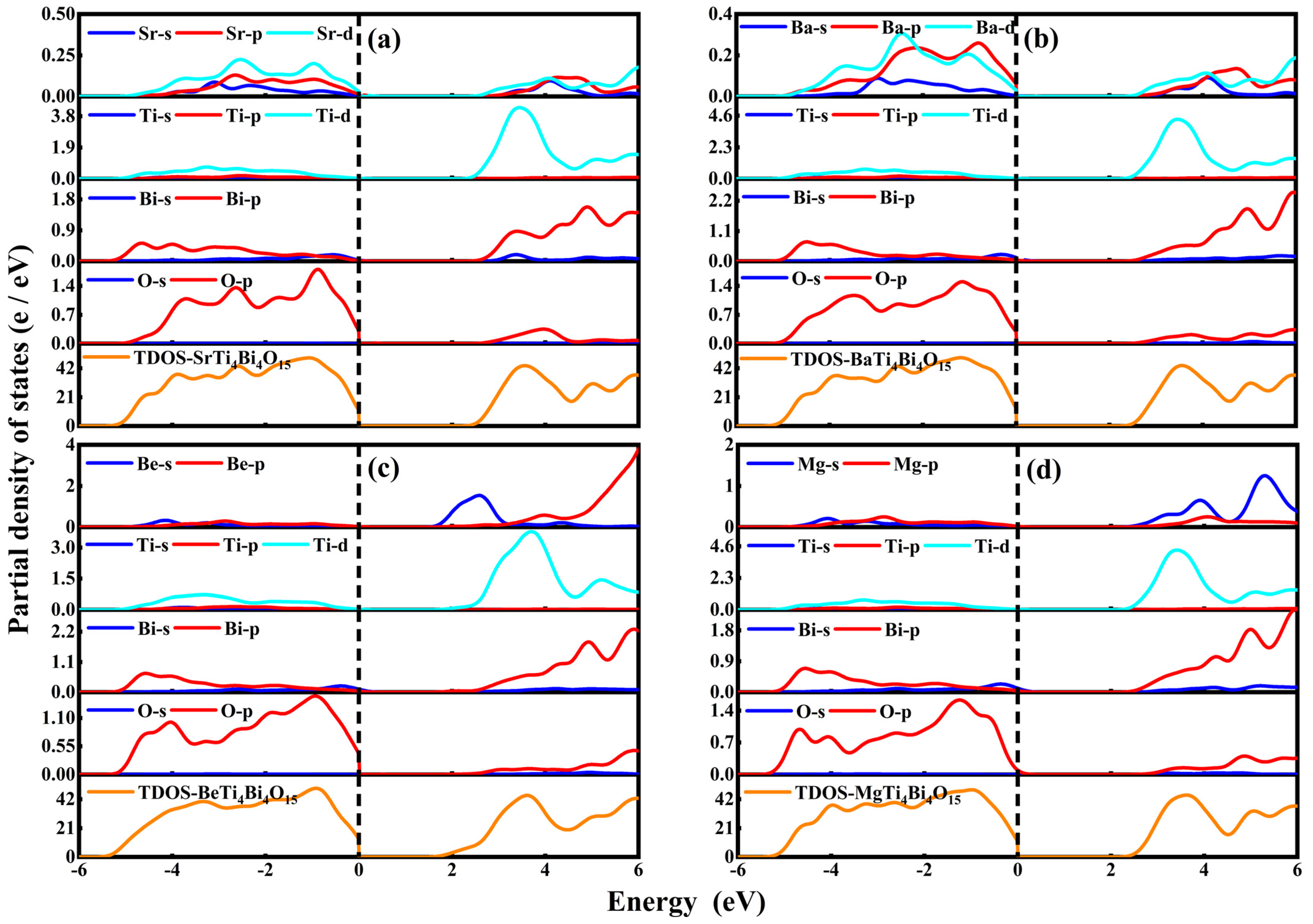
3.2. Electronic Properties
- ➢
- SrTi4Bi4O15
- ➢
- BaTi4Bi4O15
- ➢
- BeTi4Bi4O15
- ➢
- MgTi4Bi4O15
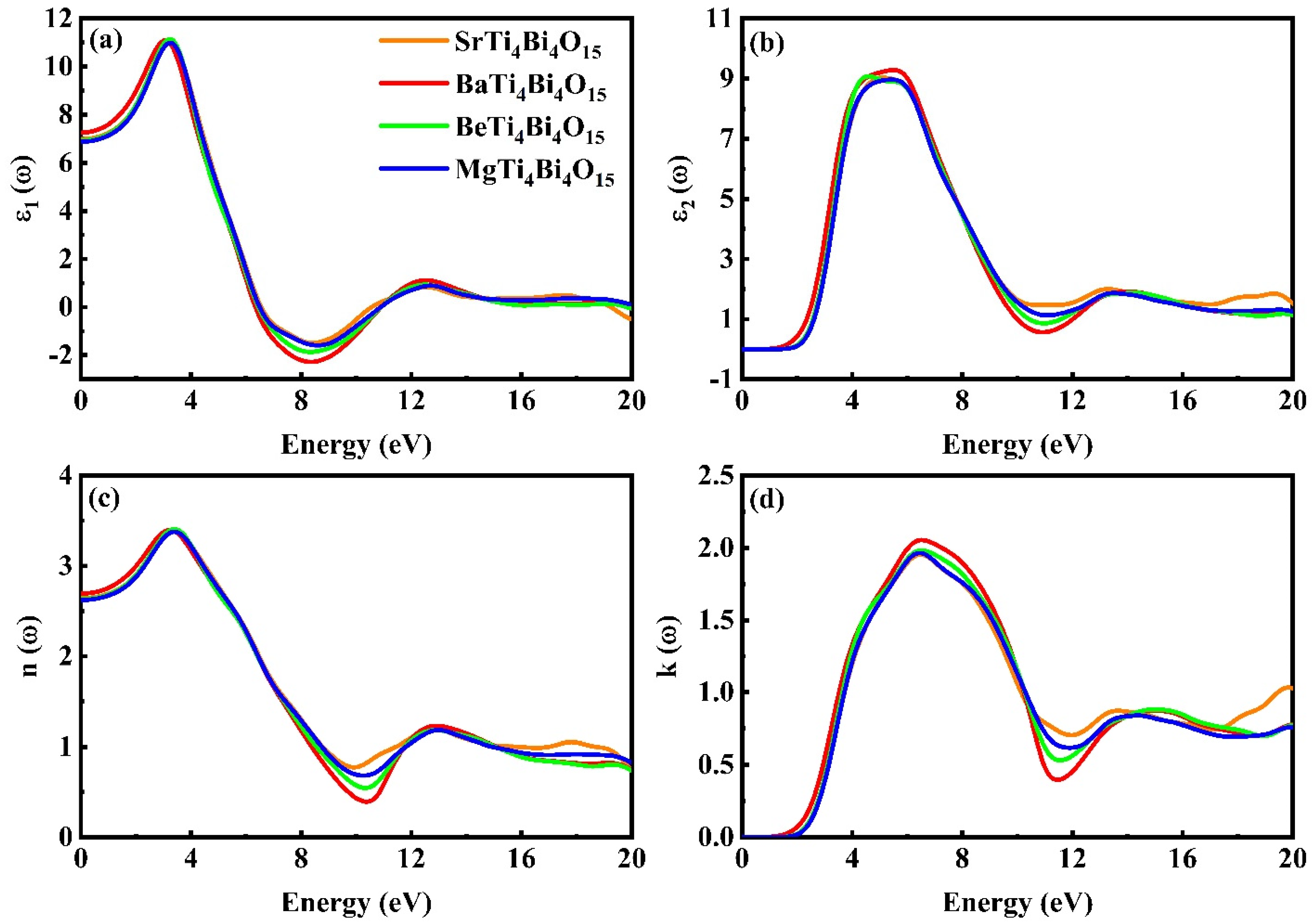
3.3. Optical Properties
3.4. Mechanical Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, K.L.; Liu, C.M.; Huang, F.Q.; Zheng, C.; Wang, W.D. Study of the electronic structure and photocatalytic activity of the BiOCl photocatalyst. Appl. Catal. B Environ. 2006, 68, 125–129. [Google Scholar] [CrossRef]
- Rajeshwar, K.; Osugi, M.E.; Chanmanee, W.; Chenthamarakshan, C.R.; Zanoni, M.V.B.; Kajitvichyanukul, P.; Krishnan-Ayer, R. Heterogeneous photocatalytic treatment of organic dyes in air and aqueous media. J. Photochem. Photobiol. C Photochem. Rev. 2008, 9, 171–192. [Google Scholar] [CrossRef]
- Chen, X.; Shen, S.; Guo, L.; Mao, S.S. Semiconductor-based photocatalytic hydrogen generation. Chem. Rev. 2010, 110, 6503–6570. [Google Scholar] [PubMed]
- Osterloh, F.E. Inorganic materials as catalysts for photochemical splitting of water. Chem. Mater. 2008, 20, 35–54. [Google Scholar] [CrossRef]
- Sohail, M.; Rauf, S.; Irfan, M.; Hayat, A.; Alghamdi, M.M.; El-Zahhar, A.A.; Ghernaout, D.; Al-Hadeethi, Y.; Lv, W. Recent developments, advances and strategies in heterogeneous photocatalysts for water splitting. Nanoscale Adv. 2024, 6, 1286–1330. [Google Scholar] [CrossRef]
- Morbec, J.M.; Narkeviciute, I.; Jaramillo, T.F.; Galli, G. Optoelectronic properties of Ta3N5: A joint theoretical and experimental study. Phys. Rev. B 2014, 90, 155204. [Google Scholar] [CrossRef]
- Ziani, A.; Harb, M.; Noureldine, D.; Takanabe, K. UV-Vis optoelectronic properties of α-SnWO4: A comparative experimental and density functional theory based study. APL Mater. 2015, 3, 096101. [Google Scholar] [CrossRef]
- Harb, M.; Masih, D.; Ould-Chikh, S.; Sautet, P.; Basset, J.M.; Takanabe, K. Determination of the Electronic Structure and UV–Vis Absorption Properties of (Na2–x Cux) Ta4O11 from First-Principle Calculations. J. Phys. Chem. C 2013, 117, 17477–17484. [Google Scholar] [CrossRef]
- Harb, M.; Sautet, P.; Nurlaela, E.; Raybaud, P.; Cavallo, L.; Domen, K.; Basset, J.-M.; Takanabe, K. Tuning the properties of visible-light-responsive tantalum (oxy) nitride photocatalysts by non-stoichiometric compositions: A first-principles viewpoint. Phys. Chem. Chem. Phys. 2014, 16, 20548–20560. [Google Scholar] [CrossRef]
- Harb, M.; Masih, D.; Takanabe, K. Screened coulomb hybrid DFT investigation of band gap and optical absorption predictions of CuVO3, CuNbO3 and Cu5Ta11O30 materials. Phys. Chem. Chem. Phys. 2014, 16, 18198–18204. [Google Scholar] [CrossRef]
- Kidchob, T.; Malfatti, L.; Marongiu, D.; Enzo, S.; Innocenzi, P. Sol–gel processing of Bi2Ti2O7 and Bi2Ti4O11 films with photocatalytic activity. J. Am. Ceram. Soc. 2010, 93, 2897–2902. [Google Scholar] [CrossRef]
- Patwardhan, J.S.; Rahaman, M.N. Compositional effects on densification and microstructural evolution of bismuth titanate. J. Mater. Sci. 2004, 39, 133–139. [Google Scholar] [CrossRef]
- Esquivel-Elizondo, J.R.; Hinojosa, B.B.; Nino, J.C. Bi2Ti2O7: It is not what you have read. Chem. Mater. 2011, 23, 4965–4974. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, S.; Ye, C. Leaching of copper from metal powders mechanically separated from waste printed circuit boards in chloride media using hydrogen peroxide as oxidant. Procedia Environ. Sci. 2016, 31, 917. [Google Scholar]
- Xue, K.H.; Fonseca, L.R.; Miao, X.S. Ferroelectric fatigue in layered perovskites from self-energy corrected density functional theory. RSC Adv. 2017, 7, 21856–21868. [Google Scholar] [CrossRef]
- Mircholi, F.; Moghadam, H.G. Study of electronic and optical properties of Bi0.5Na0.5TiO3, BiTiO3, NaTiO3 crystals using full potential linear argumented plane wave method. Optik 2015, 126, 1505–1509. [Google Scholar]
- Lardhi, S.; Noureldine, D.; Harb, M.; Ziani, A.; Cavallo, L.; Takanabe, K. Determination of the electronic, dielectric, and optical properties of sillenite Bi12TiO20 and perovskite-like Bi4Ti3O12 materials from hybrid first-principle calculations. J. Chem. Phys. 2016, 144, 134702. [Google Scholar] [CrossRef]
- Rizwan, M.; Qaiser, M.A.; Hussain, A.; Ghazanfar, U.; Dahshan, A. Influence of MnO2 on the ferroelectric properties, energy storage efficiency and piezoelectric properties of high-temperature Bi3TaTiO9 ceramics. New J. Chem. 2024, 48, 8158–8163. [Google Scholar] [CrossRef]
- Jabeen, N.; Hussain, A.; Rahman, A.U.; Faiza, I.; El-Bahy, S.M. Novel, diverse and ultra-high ferroelectric, piezoelectric and dielectric performances of Mn added La2Ti2O7-based ceramics for high-temperature applications. Solid State Ion. 2024, 414, 116637. [Google Scholar] [CrossRef]
- Hussain, A.; Jabeen, N.; Hassan, N.U.; Rahman, A.U.; Khan, M.U.; Naz, A.; Yousef, E.S. Influence of Mn Ions’ Insertion in Pseudo-Tetragonal Phased CaBi4Ti4O15-Based Ceramics for Highly Efficient Energy Storage Devices and High-Temperature Piezoelectric Applications. Int. J. Mol. Sci. 2022, 23, 12723. [Google Scholar] [CrossRef]
- Hussain, A.; Kainat, F.; Jabeen, N.; Yaqoob, A.; Abbas, T.; Khan, M.U.; Qaiser, M.A.; Mahmoud, M.H.H. First-Principles Calculations of the Structural, Mechanical, Optical, and Electronic Properties of X2Bi4Ti5O18 (X= Pb, Ba, Ca, and Sr) Bismuth-Layered Materials for Photovoltaic Applications. Crystals 2024, 14, 870. [Google Scholar] [CrossRef]
- Kainat, F.; Jabeen, N.; Yaqoob, A.; Hassan, N.U.; Hussain, A.; Khalifa, M.E. Effect of Ca, Ba, Be, Mg, and Sr Substitution on Electronic and Optical Properties of XNb2Bi2O9 for Energy Conversion Application Using Generalized Gradient Approximation–Perdew–Burke–Ernzerhof. Crystals 2024, 14, 710. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W.J.P.R. Density functional theory (DFT). Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.; Probert, M.A.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Wu, Z.; Cohen, R.E. More accurate generalized gradient approximation for solids. Phys. Rev. B—Condens. Matter Mater. Phys. 2006, 73, 235116. [Google Scholar] [CrossRef]
- White, J.A.; Bird, D.M. Implementation of gradient-corrected exchange-correlation potentials in Car-Parrinello total-energy calculations. Phys. Rev. B 1994, 50, 4954. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, A.J. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Benamrani, A.; Daoud, S.; Salam, M.M.A.; Rekab-Djabri, H. Structural, elastic and thermodynamic properties of YRh: DFT study. Mater. Today Commun. 2021, 28, 102529. [Google Scholar] [CrossRef]
- Benton, B.H.M.; Coyler, A.C.; Lee, D.L.; Moore, N.W.; Richardson Jr, T.L.; Saxon, D.T.; Yoder, J.L.; Kaufman, G.K. Electrofuels. In Encyclopedia of Inorganic and Bioinorganic Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 1–17. [Google Scholar]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Born, M. On the stability of crystal lattices. I. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1940; Volume 36, No. 2; pp. 160–172. [Google Scholar]
- Güler, E.; Güler, M. A theoretical investigation of the effect of pressure on the structural, elastic and mechanical properties of ZnS crystals. Braz. J. Phys. 2015, 45, 296–301. [Google Scholar] [CrossRef]
- Baaziz, H.; Ghellab, T.; Charifi, Z.; Güler, M.E.L.E.K.; Uğur, Ş.U.L.E.; Güler, E.M.R.E.; Uğur, G.Ö.K.A.Y. Full potential theoretical investigations for electronic, optical, mechanical, elastic and anisotropic properties of X2Se2C (X= Ta, Nb) compounds. Eur. Phys. J. B 2023, 96, 55. [Google Scholar] [CrossRef]
- Di Gennaro, M.; Saha, S.K.; Verstraete, M.J. Role of dynamical instability in the ab initio phase diagram of calcium. Phys. Rev. Lett. 2013, 111, 025503. [Google Scholar] [CrossRef] [PubMed]
- Royo, M.; Stengel, M. First-principles theory of spatial dispersion: Dynamical quadrupoles and flexoelectricity. Phys. Rev. X 2019, 9, 021050. [Google Scholar] [CrossRef]
- Du, X.; He, D.; Mei, H.; Zhong, Y.; Cheng, N. Insights on electronic structures, elastic features and optical properties of mixed-valence double perovskites Cs2Au2X6 (X= F, Cl, Br, I). Phys. Lett. A 2020, 384, 126169. [Google Scholar] [CrossRef]
- Guechi, N.; Bouhemadou, A.; Bin-Omran, S.; Bourzami, A.; Louail, L. Elastic, optoelectronic and thermoelectric properties of the lead-free halide semiconductors Cs2AgBiX6 (X= Cl, Br): Ab initio investigation. J. Electron. Mater. 2018, 47, 1533–1545. [Google Scholar] [CrossRef]
- Hussain, M.; Rashid, M.; Ali, A.; Bhopal, M.F.; Bhatti, A.S. Systematic study of optoelectronic and transport properties of cesium lead halide (Cs2PbX6; X= Cl, Br, I) double perovskites for solar cell applications. Ceram. Int. 2020, 46, 21378–21387. [Google Scholar] [CrossRef]


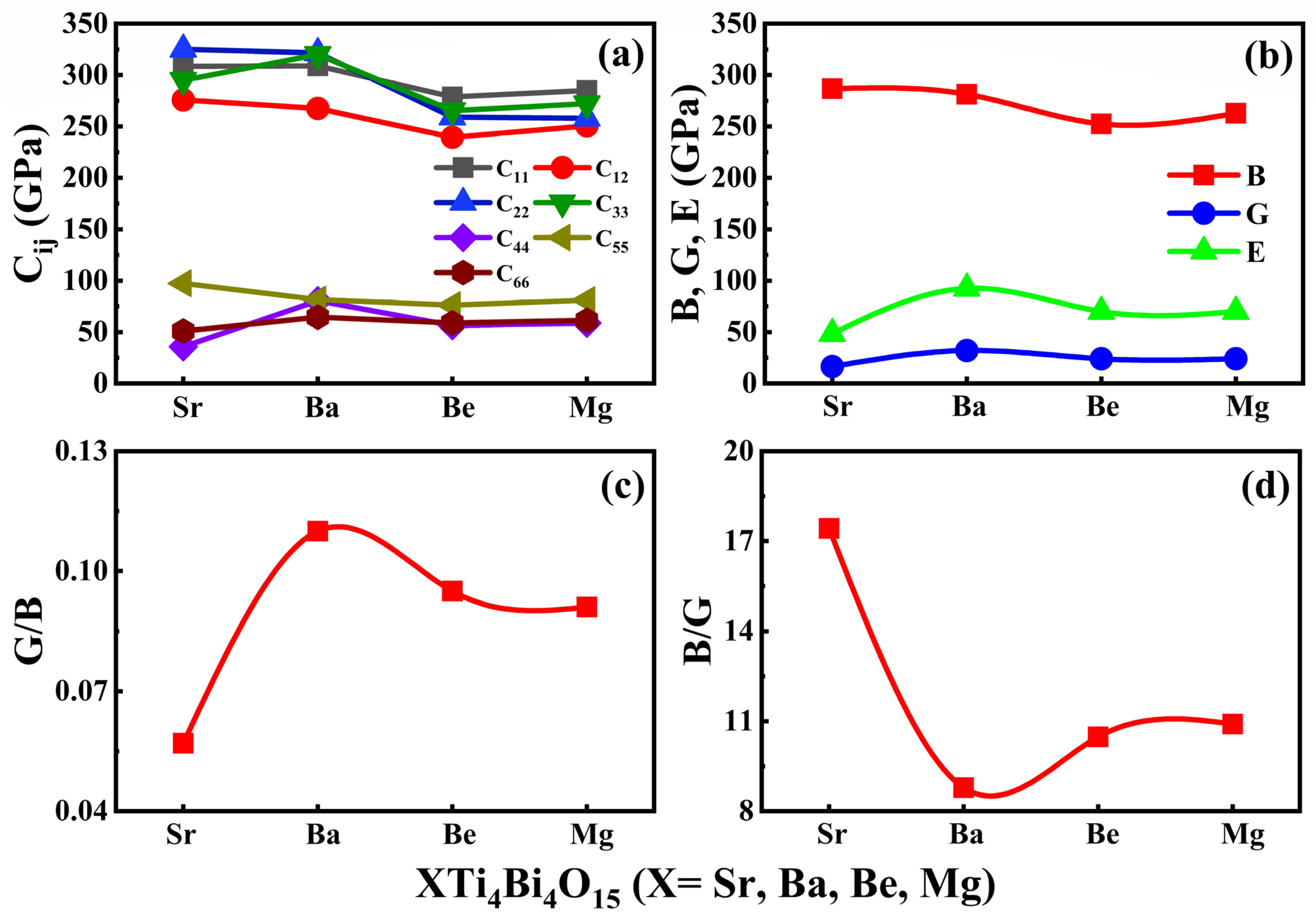
| NAME | SrTi4Bi4O15 | BaTi4Bi4O15 | BeTi4Bi4O15 | MgTi4Bi4O15 |
|---|---|---|---|---|
| C11 | 308.61 | 309.02 | 278.90 | 285.10 |
| C12 | 275.85 | 267.58 | 239.51 | 250.68 |
| C22 | 325.12 | 321.62 | 259.26 | 257.94 |
| C33 | 294.90 | 320.07 | 265.49 | 272.27 |
| C44 | 35.83 | 80.45 | 56.41 | 58.66 |
| C55 | 97.43 | 81.74 | 76.31 | 81.05 |
| C66 | 51.01 | 64.48 | 58.86 | 61.49 |
| B | 286.77 | 281.39 | 252.64 | 262.15 |
| G | 16.45 | 32.01 | 24.09 | 24.02 |
| E | 48.43 | 92.54 | 70.04 | 69.92 |
| B/G | 17.42 | 8.78 | 10.48 | 10.91 |
| G/B | 0.05 | 0.11 | 0.09 | 0.09 |
| ῡ | 0.47 | 0.44 | 0.45 | 0.45 |
| Materials | Functional | Electronic Properties | Optical Property Peak Values | Mechanical Property Comparison | References | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Band Gap (eV) | Band-Gap Type | ε1(ω) | α(ω) cm−1 | n(ω) | Ν | B/G | Nature | |||
| SrTi4Bi4O15 | GGA-PBE | 2.53 | Direct | 11 at 3.3 eV | 2.29 × 105 at 8.5 eV | 3.38 at 3.45 eV | 0.47 | 17.42 | Ductile | This Work |
| BaTi4Bi4O15 | GGA-PBE | 2.55 | Direct | 11 at 3.3 eV | 2.27 × 105 at 8.27 eV | 3.38 at 3.50 eV | 0.44 | 8.78 | Ductile | This Work |
| BeTi4Bi4O15 | GGA-PBE | 1.96 | Direct | 11.1 at 3.1 eV | 2.45 × 105 at 8.38 eV | 3.39 at 3.29 eV | 0.45 | 10.48 | Ductile | This Work |
| MgTi4Bi4O15 | GGA-PBE | 2.48 | Direct | 11.1 at 3.4 eV | 2.35 × 105 at 8.26 eV | 3.41 at 3.38 eV | 0.45 | 10.91 | Ductile | This Work |
| Pb2Bi4Ti5O18 | LDA-CA-PZ | 1.84 | Indirect | 10.9 at 4.18 eV | 2.08 × 105 at 7.90 eV | 3.58 at 3.7 eV | -- | 10.25 | Ductile | [21] |
| SrNb2Bi2O9 | GGA-PBE | 2.49 | Direct | 10.3 at 3.38 eV | 1.99 × 105 at 9 eV | 3.29 at 3.54 eV | Research Gap | [22] | ||
| Cs2Au2F6 | HSE06 | 2.41 | Direct | 2.52 at 2.01 eV | 7.6 × 104 at 8.7 eV | 1.68 at 2.04 eV | 0.26 | 1.756 | Critical value | [39] |
| Cs2Au2Cl6 | HSE06 | 2.01 | Direct | 3.8 at 1.76 eV | 9.5 × 104 at 9 eV | 1.96 at 1.82 eV | 0.33 | 2.514 | Ductile | [39] |
| Cs2AgBiCl6 | GGA-PBEsol | 1.61 | Indirect | 5.4 at 2.6 eV | 22.0 × 105 at 16 eV | 2.5 at 2.6 eV | 0.35 | 2.96 | Ductile | [40] |
| Cs2AgBiBr6 | GGA-PBEsol | 1.11 | Indirect | 6.5 at 2.5 eV | 18.7 × 105 at 17 eV | 2.7 at 2.5 eV | 0.34 | 2.88 | Ductile | [40] |
| Cs2PbBr6 | GGA-TB-mbj | 2.36 | Direct | 5.3 at 4.2 eV | 5.8 × 105 at 4.5 eV | 2.4 at 4.3 eV | 0.33 | 2.6 | Ductile | [41] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, A.; Kainat, F.; Hamza, A.; Naz, A.; Jabeen, N.; Munawar, T.; Qaiser, M.A. A DFT Study on the Structural, Electronic, Optical, and Elastic Properties of BLSFs XTi4Bi4O15 (X = Sr, Ba, Be, Mg) for Solar Energy Applications. Ceramics 2024, 7, 1727-1741. https://doi.org/10.3390/ceramics7040110
Hussain A, Kainat F, Hamza A, Naz A, Jabeen N, Munawar T, Qaiser MA. A DFT Study on the Structural, Electronic, Optical, and Elastic Properties of BLSFs XTi4Bi4O15 (X = Sr, Ba, Be, Mg) for Solar Energy Applications. Ceramics. 2024; 7(4):1727-1741. https://doi.org/10.3390/ceramics7040110
Chicago/Turabian StyleHussain, Ahmad, Fatima Kainat, Ameer Hamza, Adeela Naz, Nawishta Jabeen, Tuba Munawar, and Muhammad Adnan Qaiser. 2024. "A DFT Study on the Structural, Electronic, Optical, and Elastic Properties of BLSFs XTi4Bi4O15 (X = Sr, Ba, Be, Mg) for Solar Energy Applications" Ceramics 7, no. 4: 1727-1741. https://doi.org/10.3390/ceramics7040110
APA StyleHussain, A., Kainat, F., Hamza, A., Naz, A., Jabeen, N., Munawar, T., & Qaiser, M. A. (2024). A DFT Study on the Structural, Electronic, Optical, and Elastic Properties of BLSFs XTi4Bi4O15 (X = Sr, Ba, Be, Mg) for Solar Energy Applications. Ceramics, 7(4), 1727-1741. https://doi.org/10.3390/ceramics7040110








